Detecting the Effects of Early-Life Exposures: Why Fecundity Matters

Abstract

Prenatal exposures have meaningful effects on health across the lifecourse. Innovations in causal inference have shed new light on these effects. Here, we motivate the importance of innovation in the characterization of fecundity, and prenatal selection in particular. We argue that such innovation is crucial for expanding knowledge of the fetal origins of later life health. Pregnancy loss is common, responsive to environmental factors, and closely related to maternal and fetal health outcomes. As a result, selection into live birth is driven by many of the same exposures that shape the health trajectories of survivors. Lifecourse effects that are inferred without accounting for these dynamics may be significantly distorted by survival bias. We use a set of Monte Carlo simulations with realistic parameters to examine the implications of prenatal survival bias. We find that even in conservatively specified scenarios, true fetal origin effects can be underestimated by 50% or more. In contrast, effects of exposures that reduce the probability of prenatal survival but improve the health of survivors will be overestimated. The absolute magnitude of survival bias can even exceed small effect sizes, resulting in inferences that beneficial exposures are harmful or vice-versa. We also find reason for concern that moderately sized true effects, underestimated due to failure to account for selective survival, are missing from scientific knowledge because they do not clear statistical significance filters. This bias has potential real-world costs; policy decisions about interventions to improve maternal and infant health will be affected by underestimated program impact.

“the fact that something is difficult to measure is no reason not to try to think clearly about it”

- James Wood (1994) on fetal loss

Research into the early life origins of later life outcomes now spans the biological, behavioral, and social sciences (Barker 1998; Elo and Preston 1992; Finch and Crimmins 2004; Gluckman and Hanson 2006; Heckman 2012; Martinez 2016). The broad appeal of these questions reflects the breadth of their implications. For population scientists, understanding early-life origins is critical to understanding the evolution of cohort health, the dynamics of lags in period morbidity and mortality, the alignment of population and environmental traits, and even the intergenerational persistence of disadvantage (Doblhammer et al. 2013; Heckman 2012; Kuzawa and Sweet 2009; Kuzawa and Eisenberg 2014; Steckel 2013).

In order to understand these dynamics, population researchers rely on innovative designs to use data for causal inference (Almond and Currie 2011; Lindeboom et al. 2010; Lin and Lin 2010; Mazumder et al. 2010; Torche 2011) and inference of potential effect remediation (Heckman 2012; Duque and Rueda 2016).

However, little of this research accounts explicitly for fecundity—including the processes that affect which implanted pregnancies become live births. The likelihood that humans having uncontracepted sex will have a live birth is unusually low relative to other primates. As many as half of otherwise chromosomally viable pregnancies do not survive to live birth (Boklage 1990; Larsen 2013; Wilcox et al. 1988). Furthermore, survival almost certainly varies systematically within the population. The same mechanisms believed responsible for many of the lasting effects of early adversity—namely those operating through the neuroendocrine and immune systems like corticosteroid and cytokine exposure—are documented predictors of whether a healthy pregnancy will be established and maintained (Nepomnaschy et al. 2006; Bansal 2010; Arck et al. 2008; Michael and Papageorghiou 2008; Nakamura, Sheps, and Arck 2008).

Many research designs in population studies implicitly or explicitly assume away any population variation in fecundity, because this assumption allows researchers to draw counterfactual inferences from a comparison of traits across cohorts as long as the prenatal environment varies exogenously. If selection into live birth varies with the environment, inference becomes more complex. For any single study, selection has implications for the direction and magnitude of potential bias in the findings. For science as a whole, it structures the types of effects that are detected and published.

In this study, we aim to explicate how selection into live birth may shape the findings reported in early-life origins research. We discuss the effectiveness of data approaches to detect signatures of prenatal selection, and finally, we offer some ideas about what we need to learn about the prenatal period to shore up causal inference about the early life origins of later life outcomes.

We begin by briefly reviewing research on a subset of prenatal exposures and their later life effects on health and mortality. We then extend a simple model of cohort health (Bozzoli, Deaton, and Quintana-Domeque 2009) and use a set of Monte Carlo simulations with a parameter space bounded by published estimates to demonstrate how prenatal selection could shape reported findings about the effects of early-life exposures. Our findings have four implications.

First, if prenatal selection is in fact nonrandom, then assuming it is random can produce nontrivial estimate bias. Many effects will be underestimated. However bias can operate in either direction, depending on the selection dynamics related to the specific exposure under study. Some evolutionary models indicate positive selection dynamics for exposures that have been analyzed (Gluckman and Hanson 2006; Kuzawa and Quinn 2009; McDade et al. 2009); the effects inferred in those analyses may be biased upwards. Second, the magnitude of bias may be large. In some cases, evidence appears to be masked by this process. Results that are biased downwards will be less likely to clear a statistical significance filter, which could mean that science fails to record a nontrivial fraction of true early-life origin effects.

Third, accounting for prenatal survival bias has an impact on effect estimates that may be as substantively important as confounding or treatment selection bias. Researchers invest significant effort to sweeping out bias driven by endogeneity in the exposure process. Since the magnitude of bias resulting from selection may be comparable, it may be worth investing comparable effort to account for it. Finally, our findings imply that trait variability provides some opportunity to detect the signatures of prenatal selection in population data. We demonstrate that this requires data with large samples to detect. We conclude by discussing research designs that may improve inference through the integration of prenatal selection.

THE EARLY ORIGINS OF ADULT HEALTH

Research has linked early-life investments to a number of chronic conditions in adulthood (Gluckman and Hanson 2006; Bateson and Gluckman 2012). Relevant exposures take many forms: maternal environmental exposures to pesticides may affect neurodevelopment (Young et al. 2005), intrauterine growth restriction may predispose infants to later-life chronic inflammation and forms of chronic illness, including Type II diabetes and cardiovascular disease (Barker 1995, 1998; Langley-Evans et al. 2004; Whincup et al. 2008; McDade et al. 2014); exposure to maternal infection may increase the risk of ischemic heart disease (Mazumder et al. 2010), and may increase risk of mental illness, including schizophrenia (Brown et al. 2002, 2004). In some cases, exposures may generate forms of adaptation to local conditions that are advantageous (Gluckman and Hanson 2006; Kuzawa and Quinn 2009; McDade et al. 2009). Mismatches, however, between the prenatal environment (e.g., maternal deprivation) and the conditions of childhood (e.g., caloric abundance) could increase the long-run risk of chronic disease (Barker et al. 2002).

Several pathways have been proposed for these effects, including those that influence organ development, biological system maturation, and gene expression (Bateson and Gluckman 2012). Restriction of maternal nutrition, for example, is believed to affect placental development and fetal oxidative stress in the first trimester (Bailey et al. 2006, Ramakrishnan et al. 2012). These, in turn, affect fetal growth through pregnancy. Maternal exposures that either increase the production of glucocorticoids (Nepomnaschy et al. 2006) or reduce production of enzymes that inhibit it from crossing the placental barrier (Räikkönen et al. 2017) may impact the development of fetal systems, including the HPA-axis.

Measuring these relationships requires creative approaches to assemble data. Scholars must link evidence on individuals as adults in one period to information about the conditions surrounding their mothers’ pregnancies many decades earlier. In some cases, this has been done by linking current health measures with historical administrative data (Barker 1995, 2002, Whincup et al. 2008). Another approach uses information about adults’ birthdate and birth location from sample surveys and adult administrative data to link contextual conditions prevailing at the time of gestation that may have downstream effects on fetal health (Maccini and Yang 2009; McEniry and Palloni 2010, Hoynes et al. 2016).

At least two issues have been raised for both types of study designs. One is that the data support for estimates can be thin in light of sample demands. For example, a review of the effect of birthweight on cardiovascular disease in Nordic cohorts identifies twenty studies, ten of which use data on fewer than 500 persons (Gamborg et al. 2007). A review of birthweight effects on type-II diabetes discusses 30 studies, 21 of which include fewer than 100 persons with type-II diabetes (Whincup et al. 2008). Studies that creatively leverage cohort variation in birth timing among ongoing data collection efforts initiated for other purposes must also rely on small numbers of exposed persons (e.g., Ravelli et al. 1998, Almond and Mazumder 2005).

A second issue is the likely joint association between health at birth, health in adulthood and other confounding parental variation, like wealth (see Gage et al. 2016). To address this, scholars have put considerable effort into leveraging exogenous variation in conditions prevailing during pregnancy: war, natural disaster, famine, epidemic, or the roll out of safety net programs (Almond 2006, McEniry and Palloni 2010; Lumey, Stein, and Susser 2011, Kim et al. 2016). Others use intra-sibling comparisons to pin down effects adjusting for stable parental or family-level variation (Conley, Strully, and Bennet 2003). These innovations have revealed associations with meaningful implications. For example, Hoynes and colleagues (2016) document a 0.3-0.4 standard deviation reduction in metabolic syndrome in older age as a result of being born to a mother who had access to the Food Stamp Program during pregnancy.

Attention to omitted variable bias is now fairly widespread. We reviewed 50 studies of the effects of intrauterine exposures on adult health published between 1995 and 2018 in top epidemiology, sociology, and economics journals. All of the 50 discussed confounding and more than three-fourths of these used some approach to address it. We argue that survival bias requires similar attention. Of the 50 studies, 7 discussed prenatal survival bias—most commonly noting that estimated effects provide a lower bound—and 4 used a method to detect or address it.¹ If this reflects attention to prenatal selection among scientists pursuing early-life effects, then related, but potentially bigger issues are the findings that are not published because they fail to clear statistical significance filters. To elaborate, we turn to a discussion of fecundity and cohort traits.

HUMAN FECUNDITY AND SELECTION INTO BIRTH COHORTS

Parental Exposures and Pregnancy Survival

The fraction of fertilized eggs that survive to live birth may be as low as one third. Roughly 30% of fertilized eggs fail to implant.² Following successful implantation, 30-40% of pregnancies terminate. Half of these terminations have detectable chromosomal abnormalities and likely would not survive under any condition (Choi et al. 2014, Goddijn & Leschot 2000, Hardy & Hardy 2015, Zhang et al. 2018). The other half—15-20% of pregnancies overall—appear chromosomally viable with current detection technology but regardless, result in spontaneous loss. Survival in the first trimester is difficult to observe, but several landmark studies have followed small cohorts of non-contracepting women and administered regular blood or urine HCG tests to detect implanted pregnancies. These women were then followed forward, and 40-75% of pregnancies became live births (Wilcox et al. 1988, Zinaman et al. 1996, Nepomnaschy et al. 2006).

Evidence suggests that multiple mechanisms may be involved in pregnancy survival, including those that affect placental development and function, fetal oxidative stress, fetal neurological development, and likely many others (Ramakrishnan et al. 2012). These, in turn, are shaped by more distal processes that affect maternal nutrition, maternal exposure to biological and psychosocial stress, maternal exposure to infection, and maternal management of chronic conditions. Pregnancy survival varies with women’s body mass index (Maconochie et al. 2007; Arck et al. 2008, Kawwas et al. 2016), consumption of folic acid (Bailey et al. 2005), and in some studies, reports of stressful life events (Arck et al. 2008).

Whether prenatal selection is relevant for the study of early life effects rests on the magnitude of survival difference predicted by such exposures. Some studies find modest associations; e.g., in one cohort study with recruitment early in pregnancy, being underweight increased the risk of early pregnancy loss by a few percentage points (Arck et al. 2008).

Bruckner and colleagues’ (2016) analysis of Danish data found a small association between increases in regional unemployment and increased pregnancy loss. Other studies have found larger effects. Nepomnaschy et al. (2006) found that 10/12 implanted pregnancies to women with normal cortisol peaks became live births, whereas only 1/9 implanted pregnancies to women with evidence of dysregulated cortisol reactivity became a live birth. A study using linked registry and medical record data in Finland indicated that maternal flu infection during the 2009 pandemic doubled the risk of fetal death (Håberg et al. 2013). Edwards (2013) found that exposure to lead-contaminated water in Washington D.C. was associated with a 32-63% increase in fetal death in 2001. Zahran et al. (2014) documented a 260% increase in fetal death in Orleans parish attributed to Hurricane Katrina. In this study, we will explore a more conservative space—that in which survival is reduced or increased by up to one-third (33%).

To the extent that health is correlated across generations, evidence of selection on maternal health implies potential selection on fetal health. Though difficult to measure, some direct evidence indicates selection on fetal traits. For example, PAPP-A (pregnancy-associated plasma protein A) collected from maternal serum draws in the first trimester of pregnancy is a known predictor of pregnancy survival (Kaitu’u-Lino et al. 2013). PAPP-A is also predictive of fetal growth and birthweight (Canini et al. 2008, Salvig et al. 2010).

This evidence is consistent with a larger body of research that uses inferential approaches to describe intrauterine selection against frail members of pregnancy cohorts. These studies find evidence that signatures of pregnancy loss—lower than expected live birth counts, shifted ratios of more frail to less frail population subgroups, and higher rates of stillbirth and fetal death—are correlated with deleterious exposures (e.g., Casey et al. 2018) and with the health of surviving cohort members (e.g., Catalano & Bruckner 2006; Catalano et al. 2008; Gørgens, Meng, Vaithianathan 2012; Bruckner et al. 2014, 2015; James & Grech 2018, Catalano, Gemmill, & Bruckner 2018; Grossman & Slusky, forthcoming). Yet at present, neither direct nor inferred evidence of prenatal selection is routinely incorporated into research on the origins of adult health.

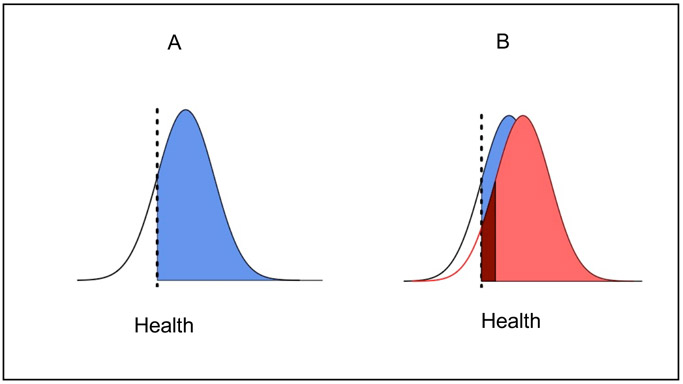
This omission has potential costs. When cohort loss is sizeable and non-random on maternal or fetal traits, survival bias is likely. Figure 1 illustrates survival for a hypothetical conception cohort with a distributed trait associated with long-run health and survival. The dashed lines represent the value of a latent health-associated trait needed to survive pregnancy. Panel A represents the outcome in some base scenario. When first observed at birth, the cohort is endowed with the distribution shown in blue. Panel B represents the counterfactual outcome in the presence of a health-improving exposure which improves gestational health equally across the board. Health endowments improve for all those who would have been born either way (light red). However, the cohort has grown. Those in dark red survive because of maternal health improvements. Even in an identification strategy that generates a perfect comparison between the blue and red distributions, failure to account for the fact that the dark red mass is only born in the counterfactual scenario would underestimate the exposure impact. If the blue and red distributions end up with statistically indistinguishable means, researchers might falsely conclude that the intervention had no effect on cohort health.

Figure 1. Survival Bias Illustration.

Note: In panel A, a cohort in dark blue survives the prenatal period as a function of health endowment values that exceed some threshold indicated by the dashed line. In panel B, a salutary “fetal origin effect” improves the health of the exposed cohort (light red). The cohort grows because additional members have health values that exceed the dashed line (dark red). Summary measures of cohort health—e.g., the difference in average health between the blue and red cohorts—will underestimate health returns of the fetal origin effect because of changes to survival, i.e. the cohort members in dark red. Note that this illustration holds K, mortality exogeneity, at 0. That is, all prenatal loss comes from the left tail of the health distribution. The simulations used in the present study are more flexible, allowing mortality exogeneity to be larger, generating more conservative estimates of survival bias.

In the real world, estimating the impact of variability in survival on the health of cohorts requires knowledge of characteristics and outcomes that are rarely measured in large cohort studies. These include the distribution of traits at the beginning of pregnancy, the fraction of fertilizations that survive, and the selectivity of loss with respect to traits of interest. It is currently difficult to prospectively model prenatal cohort attrition, as has been usefully done with panel data for later parts of the life course (e.g., Zajacova and Burgard 2013). Instead, we can consider the conditions under which variation in survival would and would not have substantial effects on estimated fetal origin effects detected using standard regression approaches.

Birth Cohort Traits: a Scarring-Selection Model

Figure 1 illustrates one version of a larger class of scarring-selection models, in which exposures contribute to cohort health by affecting the health of individuals and also by removing cohort members (e.g. Vaupel and Yashin 1985, Wrigley-Field 2014). The reduced-form version illustrated in Figure 1 has been used in recent applications to describe the relationship between exposures that increase child mortality and also shape lifecourse health trajectories. In these models, the underlying health parameter is defined as capturing robustness (or proclivity to survive, or the opposite of “frailty”). From that definition, it follows that mortality selects individuals from the left tail of the health endowment distribution. This introduces a particularly stark version of survival bias; those who survive and those who do not have non-overlapping values on the underlying health parameter (see Figure 1). The model we consider here includes this arrangement. But for the study of pregnancy, we must also consider that some losses will occur for reasons other than a particular underlying health condition. Pregnancy loss may be triggered by accidents or violence (Kvarnstrand et al. 2008; Mendez-Figueroa et al. 2013). If the researcher is interested in the health endowments associated with later-life heart disease, it is not clear that accidents will select pregnancies exclusively out of the left tail of that distribution. Similarly, some cytogenic abnormalities may predict pregnancy loss but may not perfectly overlap with the cytogenic predictors of height or dementia. If we assume that losses exclusively have the lowest values on the health construct of interest, we may overstate the severity of survival bias, even in the highly stylized model used here. For this reason, we will consider variation in the degree to which pregnancy loss is selected on the health endowment.

We follow the standard parsimonious approach to modeling scarring-selection (or heterogeneity in frailty) by beginning with a unidimensional endowment of health that also predicts risk of mortality. As in Bozzoli et al. (2009): let h_ic0 indicate the endowment of health for individual i in a cohort c of pregnancies beginning when fertilized eggs implant (t=0). The cohort experiences period-specific maternal environmental conditions, like caloric availability and infectious illness. These vary across cohorts and are represented by v_c, which is positive when it is beneficial to health and negative when it is detrimental to health. Health at birth, h_ic1, is given by

$$h_{ic1}=h_{ic0}+v_c$$ (1)

Let z be a threshold of health necessary to survive. A pregnancy survives when

$$h_{ic0}+v_c\ge z$$ (2)

If health endowment at implantation and environmental exposures were all that affected survival prospects, prenatal mortality in the cohort would be represented by the cumulative distribution function

$$m_c=\mathrm{F}(z-v_c)$$ (3)

Here, we build on prior research by relaxing the assumption that mortality exclusively occurs in the left tail of the h_ic0 distribution. We allow mortality in a cohort of pregnancies is shaped by at least two separate sets of processes:

1. The combination of h_ic0 and v_c represented in (1)-(3)

2. A process, ε_ic0, that is uncorrelated with h_ic0

We let the relative contribution of each of these two processes vary with a parameter K, which takes values between 0 and 1, and captures the exogeneity of survival with respect to the initial health endowment. This allows a more flexible representation of the mortality process in (3).

At the individual level, a pregnancy terminates before birth (m_ic=1) if

$$(1\text{-}K)(h_{ic0}+v_c)+K{\epsilon }_{ic0}<z$$ (4)

And survives (m_ic=0) if

$$(1\text{-}K)(h_{ic0}+v_c)+K{\epsilon }_{ic0}\ge z$$ (5)

The left-hand side of these inequalities represents latent “heartiness” or “survivability” of a cohort member, which could be succinctly represented as s_ic

$$s_{ic}≔(1\text{-}K)(h_{ic0}+v_c)+K{\epsilon }_{ic0}$$ (6)

Mortality in the cohort is then represented by the cumulative distribution function

$$m_c=F\left(\frac{z}{1-K}-\frac{K}{1-K}{\epsilon }_{ic0}-v_c\right)$$ (7)

Note that including this second process, ε_ic0, and varying its contribution to survival is intended to make the estimates in this study more conservative. By definition, survival bias is lessened as K approaches 1 and the ε_ic0 process is upweighted. Note that the parameter space explored in this study includes the more commonly used model (Eq. 1-3) which the proposed model is equivalent to when K=0.

METHODS

We build from the model defined above, in which the distribution of cohort traits at any age depends upon (i) initial conditions, (ii) the fetal origin “effect”—that is, the degree of damage or improvement generated by cohort-specific prenatal conditions manifest through any set of mechanisms, (iii) the fecundity effects of these same conditions, and (iv) the selectivity of cohort attrition induced by these same conditions.

We use a set of parsimonious simulations to ask: under what circumstances do true cohort averages for various health measures differ substantially from those estimated using standard analytical approaches? We then discuss whether and how additional complexity might change the inferences drawn here. With distributional assumptions, these equations have analytic solutions. The simulations here provide a simple expositional tool to describe bias across the parameter space and across features of the data generating process that may be relevant for others working in the area; e.g., we vary sample sizes, introduce spurious confounding, and discuss detectable variance.³

Each of the simulations involves four pregnancy cohorts: one treatment cohort and three control cohorts. The choice of three is inconsequential, beyond generating estimate precision in the control cohorts. The simulation is initiated by populating the cohorts with 100, 1000, or 10,000 observations. These three orders of magnitude approximately capture sample sizes for smaller sample surveys, larger sample surveys, and administrative data.

The simulations represent alternative scenarios of some event affecting both pregnancy survival probabilities and later life health. In each simulation, we set the three central parameters in equation (4)—v, K, and z. The key parameter is v, the fetal origin effect on later life health, which represents the truth that fetal origin research would aim to uncover. K describes the weight of the exogenous component of pregnancy survival. We determine the fraction of the cohort that will survive to live birth (m_c) and then set the survival threshold (z) that yields that fraction, given the values of v and K. When presenting results, we classify each simulation run by its chosen values of v, K, and m_c. We discuss simulations by focusing the value of m_c implied by the three parameters together, rather than reporting the value of z itself, because m_c is an intuitive construct; our central message is that improving measurement of m_c (prenatal cohort mortality) is crucial for accurate measurement of v_c (fetal origin health effects). We measure the combined impacts of these parameters by describing ratio of mortality in different scenarios. We describe forms of bias indexed over the ratio of mortality, r_m, in treatment versus control cohorts:

$$r_c≔(m_c^{trt}\text{-}{m}_c^{ctrl})∕m_c^{ctrl}$$ (8)

As described below, the range of values of each of these parameters is taken from the research on fetal origins effects (v) and pregnancy loss (r_m) reviewed earlier. K is a parameter about which we have the least evidence; we allow it to take all possible values between 0-1 in the simulation.

The simulation begins when fertilized eggs in the pregnancy cohort implant; at that point, each pregnancy is endowed with a health trait, h_ic0 drawn from a standard normal distribution, as well as a parameter, ε_i, drawn from an independent uniform distribution between −2 and 2 to produce two measures with overlapping densities. The treatment cohort experiences the fetal origin effect, v_c. We explore the implications of v_c having values across the range from −1 to 1 standard deviations of h_ic0.

In control cohorts, m_c=0.4, which means that 40% of pregnancies terminate between implantation and live birth. These are the 40% of the cohort with the lowest values on latent heartiness, s_ic in [6]. We allow cohort mortality in the treatment cohort to vary between 60% and 20%.

Because early-origins research is typically focused on adult health, we then age the live births forward to age 60. For simplicity, we use parameters from the contemporary U.S. population. We set m_c between birth and age 60 to 0.146, the probability of death by age 60 from the 1950 cohort lifetable. We assume that mortality over these 60 years is again the result of two distinct processes: the initial health endowment and a second process between birth and death that affects survival but is uncorrelated with h_ic0 or ε_ic0 – e.g., accidental death. We calculate a second value of latent heartiness for the birth to age 60 period, s_ic, in which K is conservatively set to 0.2 (20% of deaths before age 60 are due to accidents (NVSS 2015)) and ε_ic1 comes from an additional random draw of a parameter uniformly distributed between −2, 2.

Each simulation produces four cohorts of 60 year olds with values on a health trait, h_ic1 that is a function of their endowment, the fetal origin effect in [1], and two processes uncorrelated with h_ic0, ε_ic0 and ε_ic1.⁴ We pool the four cohorts and estimate regression equation [9] to compare average health values for individuals in control cohorts (T=0) with those in the treated cohort (T=1):

$$h_{ic1}=\alpha +{\beta }_1{\mathrm{T}}_{\mathrm{c}}+{\zeta }_{ic}$$ (9)

Since T is randomly assigned in these simulations, the regression would return the true value of the fetal origin effect, v_c in the absence of survival bias. We quantify the magnitude of survival bias with the ratio of the detected effect to the true effect:

$$\mathrm{b}≔{\beta }_1∕v_c$$ (10)

We keep several values from these simulations, the variance of h_ic1 among survivors, σ_c, as well as the estimate of β₁ and the standard error of β₁ from Eq. 9. To ensure that the results are not sensitive to the stochastic element of the h_ic0 and the epsilon parameter draws, we simulate each unique combination of m_c, K, and v_c 100 times and report the mean values of β₁ / v_c and σ_c across combinations.

To compare the magnitude of survival bias in relation to the potential magnitude of treatment selection bias, which much greater effort has been made to address, we introduce a confounder (X_i) that is correlated with both the treatment assignment T and with the initial health endowment. Consider, for example, examining the effect of prenatal exposure to maternal smoking on birthweight. It would be necessary to adjust for maternal education (the confounder), which is correlated both the exposure (smoking) and the health outcome (birthweight).

$$h_{ic1}=\alpha +{\beta }_1\mathrm{T}+{\beta }_2{\mathrm{X}}_i+{\zeta }_{ic}$$ (11)

In a context like this, if one were to estimate [9] even with perfect accounting for survival bias—i.e., selection based on s_ic as defined in [6] —the estimate of the health effect would be biased, since the omitted variable X_i is correlated with ζ. Alternatively, if one were to account for X_i perfectly but fail to account for survival selection, the estimate would be skewed by survival bias. What would be the consequences of properly estimating [11], but failing to account for selection based on s_ic? What about properly accounting for s_ic, but ignoring X_i entirely?

To shed light on these questions, we simulate scenarios in which X_i is correlated with ζ and with T to varying degrees. In each case, we estimate β₁ from [11], with and without accounting for selection based s_ic and with and without the inclusion of X_i in the specification. To properly account for s_ic we use a Heckman selection equation (Wooldridge 2003). By construction, we have ideal instruments for selection, ε_ic0 and ε_ic1, which predict latent heartiness but not health. We present β₁ as well as its deviation from v_c, the quantity it is intended to estimate, for of all four of these specifications. This allows us to gauge the relative importance of accounting for each source of bias.

RESULTS

Finding 1: Survival bias may be as large as half of true effects

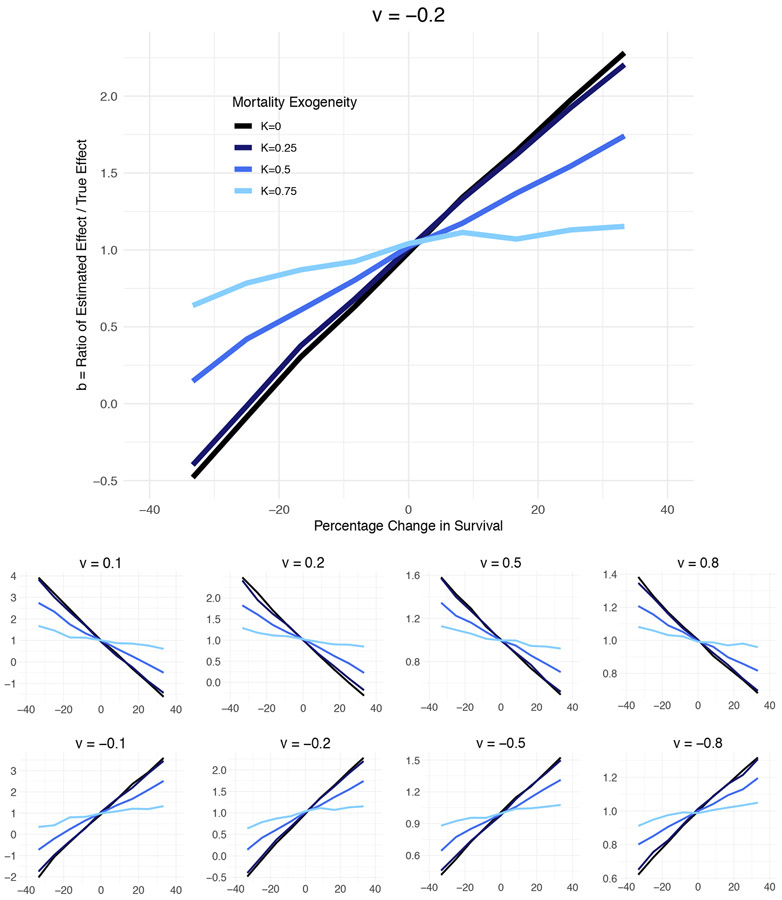
Figure 2 illustrates how much estimated fetal origin effects may be biased, as a function of the three key parameters: the magnitude of true effect, the associated changes to survival, and the degree to which pregnancy loss is selected on the health endowment. The plots are displayed separately by the magnitude of the true fetal origin effect (v) measured in standard deviations of the initial health endowment draw. In the top panel, the early-life event reduces health by one-fifth of a standard deviation (v = −0.2); this would be akin to a roughly 120 gram reduction in average cohort birthweight in the U.S. The horizontal axis represents the proportionate change in survival caused by the fetal origin effect (r_m, Eq. 8): the right side of the figure describes fetal origin effects that increase pregnancy survival, the left side describes fetal origin effects that reduce pregnancy survival. The vertical axis is survival bias in the estimated effect (b, Eq. 9).

Figure 2. Estimate Bias by True Effect Size (v), Survival Change (r), and Mortality Exogeneity (K).

Note: Figure represents results of 57,267 simulations across the v, s, K parameter space. The true fetal origin effect, v, is scaled in standard deviations of the cohort health endowment. Fetal origin effects that improve health represented in the top row, fetal origin effects that worsen health represented in the bottom row. Higher values of K (lighter blue) describe a mortality selection process with a larger degree of randomness with respect to the health endowment.

If the exposure driving the reduction in health does not reduce survival, the ratio of the estimated to the observed effect is 1.0, reflecting an absence of survival bias. When the exposure reduces survival, the estimated effects are smaller than the true effect size; the ratio falls below 1.0. How much bias is created by excess mortality is a function of how selected (or how “frail”) the lost pregnancies are. When K is closer to 1 (lighter blue line) cohort pregnancy loss and cohort survivor health later in life are almost independent of each other, and survival bias is minimized. When K is closer to 0 (darker blue line), the least healthy pregnancies are the least likely to survive. The black line (K=0) describes the model used in more standard scarring-selection models, in which all loss comes from the left tail of the health distribution.

The slopes of the lines highlight how important it is to quantify prenatal survival when interpreting early-life origin analyses. Consider an estimate indicating that an exposure worsens health by about one-tenth of one standard deviation—roughly akin to the estimated effects of exposure to extreme temperatures during pregnancy on birthweight for infants born in Bolivia, Colombia, and Peru (Molina & Saldarriaga 2017). If the same exposure reduces survival by 15-30%, the true effect size could be twice as large (v_c= −0.2) as the estimated effect. Even when the probability of loss is driven in part by factors uncorrelated with the health endowment (K=0.5), survival bias can mask up to half of the true health impact (v_c) of the early life event.

Consider a second example: an analysis by the Michigan Department of Health and Human Services (2017) found little evidence of an effect of water poisoning on low birthweight of infants born in Flint. The claim that water poisoning “Didn’t Affect Flint Birth Outcomes” was picked up in the press (Bouffard 2017). However the increase in pregnancy loss in Flint resulting from the change in water supply may have been large enough to contribute to a 12% reduction in fertility rates (Grossman and Slusky forthcoming). Depending on the exogeneity of prenatal selection (K), the Michigan DHHS estimates may mask a health impact on the survivors. In the top panel, for example, a true effect of −0.2 standard deviations in birthweight (~120 grams) could be estimated as zero with as little as a 25% reduction in survival. A true effect of one-tenth of a standard deviation (~60 grams) could be estimated as zero with a 12% reduction in survival. In one of the few analyses of early life effects to explicitly integrate prenatal survival, Grossman and Slusky (forthcoming) use similar logic to conclude that water poisoning almost certainly reduced birthweight in Flint; they bound the estimate at close to a 5% reduction in birthweight.

Comparing the lower set of smaller panels highlights the importance of selection dynamics for structuring bias by more and less powerful prenatal events. In general, smaller estimates are subject to larger proportionate bias and may mask either positive or negative true effect estimates under different mortality selection conditions. For example, if the health effects are in fact positive (e.g., v = 0.1), but small relative to the population variance in health, survival bias can confound researchers into concluding that an event that improved cohort health had no effect at all, or actually harmed health (b ≤ 1.0). This underestimate would be troubling, for example, in the evaluation of a social program aimed at improving health in pregnancy that might improve both prenatal survival and the postnatal health of survivors. As example of potential small effect underestimates: several studies have concluded that the impact of the Special Supplementary Nutrition Program for Women, Infants, and Children (WIC), which supports 50% of U.S. pregnancies, has small effects on birth outcomes (e.g., Joyce et al. 2008 estimate a 39.5 gram birthweight for gestational age association with WIC enrollment during pregnancy, and a 13.5 gram return to enrollment in the first trimester relative to the third; Sonchak (2016) estimates a 7 gram increase in birthweight association with enrollment using sibling comparisons). Yet a study of California pregnancies found maternal WIC enrollment reduced perinatal death by 22-31% (Fingar et al. 2017). If this survival improvement applies to the first-half of pregnancy as well, the true effects of WIC may be substantially underestimated.

For larger effects, survival bias is proportionately smaller. Compare the y-axis of the panels on the right to those on the left. Using the model described here, it would be difficult for true effects of 0.5 or 0.8 standard deviations to be estimated close to zero. Because of the proportionately smaller nature of bias, it is also the case that larger estimated effects are unlikely to mask true effects that are so large, their magnitude would be implausible. That is: smaller estimated effects that fail to address survival bias can easily mask true effects that are double the size of the estimate in magnitude (left panels in Figure 2). A larger estimated effect (−0.8 standard deviations) is unlikely to mask a true estimate that is two times as large (−1.6 standard deviations). Consider the estimated effects of prenatal exposure to the 1959-1961 famine in China, which was accompanied by a 25-40% increase in miscarriage (Cai and Feng 2005) and a 21-53% decrease in birth cohort size, relative to 1958 (Chen and Zhou 2007). Effects of the famine on adult height are estimated to be large: a reduction in adult height of 3 cm, or 0.4 standard deviations (Chen and Zhou 2007) and an increase in mental health symptoms index for adult women of 1.5 points or 0.84 standard deviations (Huang et al. 2013). If we mistakenly assumed that survival bias introduced the same proportionate error as we observe for smaller effects (left panels in Figure 2), it might raise concern that the study produced implausibly large estimates. Instead, the simulation results here suggest these effects could be underestimated by 10-30%, suggesting true effects that are still quite large but not beyond the realm of possibility.

Finding 2: Prenatal selection exacerbates the problem of a statistical significance filter.

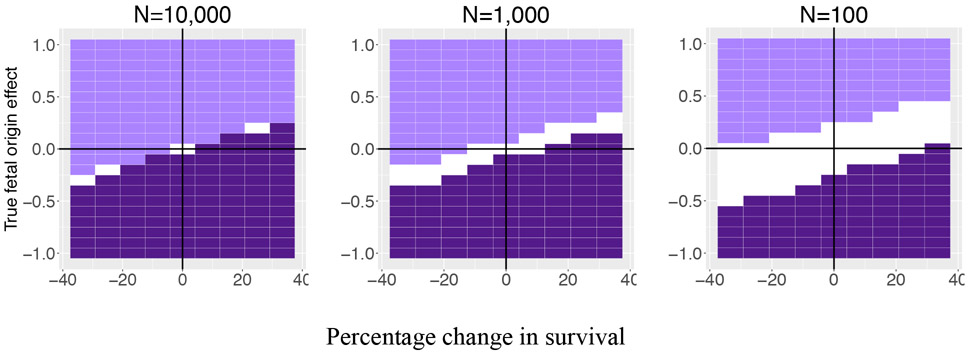
The bias described above may make inference a problem for any individual study, but it also raises the possibility of another level of “survival bias”—estimates which are selected into discourse based on p-value cut-offs. To describe this issue, we denote parameter space in which an estimate would meet the p<0.05 filter for a negative (dark purple) or positive (light purple) effect. Figure 3 displays this separately for estimates in which the exposed cohort sample (a quarter subset of the full sample) is 10,000, 1,000, or 100 persons. In this figure, the upper right and lower left quadrants capture fetal origin processes that improve cohort health and survival, and worsen cohort health and survival, respectively.

Figure 3. Negative (dark purple) and positive (light purple) estimates that would reach conventional levels of significance (p<0.05), by the sample size of exposed cohort.

Note: Figure depicts estimates of fetal origin effects generated from simulations that vary the true fetal origin effect magnitude (y-axis), the change in prenatal survival associated with exposure to the fetal origin effect (x-axis), and the size of the exposed cohort (N), or one-fourth of the total sample size used in the estimation. The dark purple space describes combinations in which estimates are signed negatively and reach a p<0.05 cut-off. The light purple space describes combinations in which estimates are signed positively and reach p<0.05. White area references space in which estimates would fail to meet conventional levels of significance. K, the exogeneity parameter, is held at 0.25.

The white space captures the type of effects that would be unlikely to be observed by scientists because survival bias would result in estimates that are sufficiently small as to become statistically indistinguishable from zero. With large samples on the order of those used in studies with administrative data, and a mortality process that has a moderate to high degree of health selectivity, even small negative effects will clear the p-value hurdle, but they will be incorrectly signed. By contrast, the right panel has sizeable white space in both the top right and bottom left quadrant, where we would expect health improving and health reducing fetal origin effects to cluster. An effect that reduces cohort health by up to half a standard deviation and also reduces survival from .6 to .5, would not reach conventional levels of significance. The earlier literature review described studies that used samples with sizes much closer to that depicted in the right panel (if not smaller) than that depicted in the left. It is possible, then, that prenatal selection masks a large set of small to moderately sized fetal origin effects.

Finding 3: Survival bias is likely to be comparable to the bias created by endogenous treatment selection

In many applications, researchers devote significant attention and effort to finding research designs to minimize potential confounding. As we have discussed, much less attention is typically paid to the potential impacts of survival bias. Is this disparity in attention warranted? We explore this question with a parsimonious but realistic simulation of conditions where both sources of bias are operating.

We draw a confounder, X_i, that is correlated with the probability of exposure to the fetal origin effect and to the health endowment. We allow these correlations to range in absolute magnitude from 0.1-0.5, because the degree of omitted variable bias will increase as the correlation moves from a small value (0.1) to a large one (0.5). Reasonable magnitudes of omitted variable correlations are difficult to reference because we typically only observe correlations among pregnancies that become live births. However, for example, among 3.5 million U.S. births in 2010, maternal education (confounder) has a correlation with birthweight (health) that is less than 0.1 and a correlation with smoking during pregnancy (exposure) of - 0.19.⁵

Table 1 describes estimates from a set of simulations in which the fetal origin effect is fixed at −0.5 standard deviations and the excess mortality (r_m) experienced by the treated cohort takes values of 18% or 33%. We assume that at least half of the process driving mortality is uncorrelated with the initial health endowment (K=0.5). This is intended to make the comparison of survival bias relative to omitted variable bias conservative. By definition, the magnitude of survival bias increases with mortality endogeneity.

Table 1.

Estimates of Fetal Origin Effect on Adult Health (of known value v=−0.5), with and without adjustment for treatment selection bias and prenatal survival bias.

% Addtl mortality exposed cohort			Bias Correction
	Correlation Xi and		(1) None		(2) Omitted variable bias		(3) Survival bias		(4) Survival + omitted var. bias
	Health	Exposure
			β1	% error	β1	% error	β1	% error	β1	% error
33	0.1	−0.1	−0.18	64	−0.17	65	−0.53	−6	−0.51	−3
33	0.2	−0.2	−0.22	55	−0.20	59	−0.57	−14	−0.50	−1
33	0.3	−0.3	−0.30	40	−0.25	51	−0.67	−33	−0.51	−1
33	0.4	−0.4	−0.41	17	−0.31	37	−0.78	−57	−0.51	−1
33	0.5	−0.5	−0.56	−12	−0.40	20	−0.93	−86	−0.51	−1
18	0.1	−0.1	−0.36	29	−0.35	30	−0.52	−4	−0.50	0
18	0.2	−0.2	−0.40	19	−0.38	24	−0.57	−13	−0.50	1
18	0.3	−0.3	−0.50	−1	−0.44	11	−0.68	−35	−0.51	−3
18	0.4	−0.4	−0.60	−21	−0.49	2	−0.78	−55	−0.50	1
18	0.4	−0.4	−0.75	−51	−0.57	−14	−0.93	−86	−0.49	2

Note: Results summarize estimates from 10 scenarios in which health at age 60 is a function of a fetal origin effect, T, and a confounder, X_i (see equation [11]). These scenarios vary the level of additional prenatal mortality, the correlation of the confounder with the health endowment, and the correlation between the confounder and the probability of exposure to the fetal origin effect. For each scenario, we estimate four specifications that are variations of equation 11; in each, β₁ is intended to estimate the true fetal origin effect, which has a known value of −0.5 standard deviations of the cohort health endowment. Estimates of β₁ shown above from:

⁽¹⁾specifications that neither include X_i nor adjust for survival bias

⁽²⁾that correct for omitted variable bias by including X_i but do not correct for survival bias

⁽³⁾that exclude X_i but correct for survival with a Heckman correction using ε_ic0 and ε_ic1 in the selection equation (these values come from equations [4]-[7] and the discussion on page 11)

⁽⁴⁾that correct for both omitted variable bias by including X_i and also correct for survival with a Heckman correction using ε_ic0 and ε_ic1 in the selection equation. Each of the scenarios is simulated 100 times and holds the exogeneity of prenatal mortality at 0.5 (see [4]-[7]). Estimates above are the mean values of β₁ across the 100 simulations for each parameter combination.

The results are indexed by the size of omitted variable correlations. The four columns display the estimates of β₁, and the percentage discrepancy between β₁ and −0.5 across four specifications. In column 1, neither omitted variable bias nor survival bias is addressed. Column 2 displays results from specifications in which omitted variable bias is corrected but survival bias is not. Column 3 displays results from specifications in which omitted variable bias is not corrected but survival bias is. In column 4, both types of bias are corrected and, as expected, the estimates are close to −0.5.

If omitted variable bias were substantially larger than survival bias, we would expect the error in column 3 (in which only survival bias is corrected) to be much larger than the error in column 2 (in which only omitted variable bias is corrected). It is not. When the correlations with the omitted variable are small in magnitude (0.1-0.2), survival bias is much larger than omitted variable bias. In column 2, we observe survival bias of 25-30% with a small increase in excess mortality (18%) and 55-60% with a larger increase in excess mortality (33%). By contrast, omitted variable bias (column 3) is 5-15%. Only when the correlations between the omitted variable are large in magnitude (approaching 0.5), is omitted variable bias much larger than survival bias. Additional simulations with varying values of K and v_c produce similar results. The correlation of treatment and outcome with the omitted variable must be large (>0.5) to create omitted variable bias that would justify the disparity in attention that the two problems receive in typical research designs.

Finding 4. In large samples, narrowed variance may provide a detectable signature of prenatal selection.

In some studies, scholars are able to detect evidence of changes in prenatal survival accompanying fetal origin exposures via reductions in birth counts or increases in fetal death. In other types of data, this information is not available. One way to detect evidence of selective changes in prenatal survival may be with evidence of reduced variance in health measures for exposed cohorts. The simulations used here speak to the viability of this strategy when the researcher can reasonably assume that the exposed and unexposed cohorts are drawn from distributions with similar variance.

In each simulation described in Figures 2 and 3, we compare the variance of the h_ic distribution at age 60 between the exposed and unexposed cohorts. We test whether these would be detected as statistically distinguishable at p<0.10 and p<0.05. Because of the relevance of sample size and attendant estimate precision to this task, we draw additional sets of simulations in which cohorts are 2500, 5000, and 7500 persons.

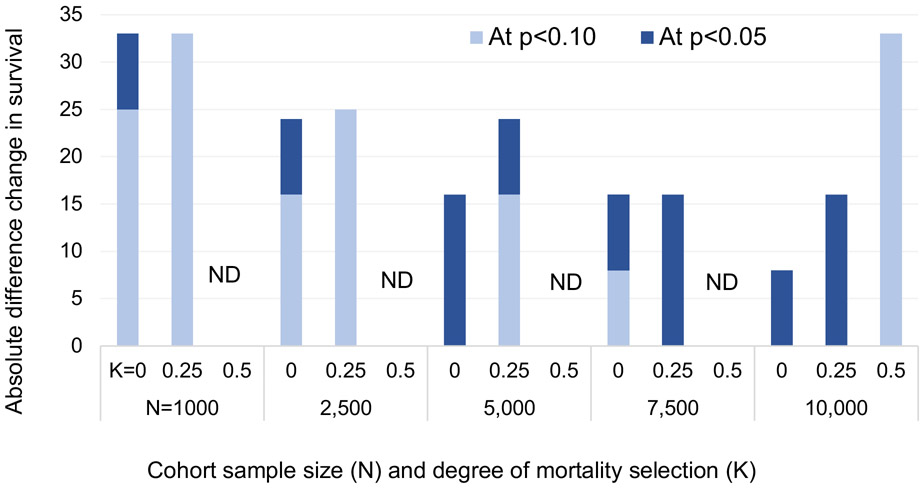
The results from this exercise are described in Figure 4. Light blue bars indicate difference in survival between exposed and unexposed cohorts necessary to detect a variance difference in the outcome distribution at p<0.10. Dark blue bars indicate the difference needed to detect variance changes at p<0.05. The bars are grouped by the sample size of the exposed cohort and by the exogeneity of prenatal survival (K).

Figure 4. Sample size, degree of mortality selection, and magnitude of effect on survival needed to detect variance change in outcome distribution.

Note: Light blue bars indicate difference in survival between exposed and unexposed cohorts necessary to detect a variance difference in the outcome distribution at p<0.10. Dark blue bars indicate difference needed to detect variance changes at p<0.05. ND = survival difference than 35% required to detect variance difference. K captures degree of mortality selection on outcome measure, 0=all mortality comes out of the left tail of h_ic0, .5 = half of mortality is driven by a process that is random with respect to h_ic0. Survival in unexposed cohorts held at 0.6. Estimates assume h_ic0 is normally distributed with variance=1 at conception.

When samples are small (e.g., 100 persons in the exposed cohort), it is not possible to detect variance differences in the outcome distributions with <35% change in survival. At 1000 and 2500, the selectivity of mortality must be high to detect these differences. When K=0.5, variance differences are not reliably detectable with sample sizes smaller than 10,000. However, when mortality is more selective of the least healthy (e.g., when K is 0.25) it is possible to detect variance differences in smaller samples. The findings are promising for research using administrative data. Of course, any particular health dimension may have a distribution with variance exceeding that in a standard normal distribution. In these cases, variance detection may be possible with smaller samples as well.

DISCUSSION

Fetal origins research over the past half century has generated findings with wide-ranging implications. These include cohort patterns in adult health, the intergenerational reach of disadvantage, and the evaluation of programs targeting adult nutrition and reproductive health (Palloni and Milesi 2009, Kuzawa and Sweet 2009, Hoynes et al. 2016). Despite a number of important conceptual and methodological advances in this research, the field only rarely takes seriously the role of survival bias. In many studies, it isn’t even discussed. This blind spot likely holds science back from understanding many effects of intrauterine exposure. Patterns in confounding may also help explain apparently contradictory results between studies of apparently similar exposures. Addressing survival bias directly may point the way to analytical innovations to separately identify compositional and direct effects.

Our argument builds on a long history of research on mortality selection. Scarring-selection models are standard tools in population science (Vaupel and Yashin 1985, Bozzoli et al. 2009, Wrigley-Field 2014, Domingue et al. 2017). Here, we argue that these models are also applicable for the period before birth (Bruckner and Catalano 2018, Liew et al. 2015). We attempt to quantify the effects of failure to routinely incorporate prenatal selection into the study of lifecourse health. We demonstrate that the magnitude of prenatal cohort loss can be sufficiently large to generate substantial survival bias in estimates linking prenatal exposures to later-life health. And because of this, a large class of moderately sized effects may not even be detectable with standard analytic approaches.

This bias has real-world implications. Consider the aforementioned WIC program that includes support for pregnancy health. Active debate about the returns to this program and the value of investing in it are ongoing (Besharov and Germanis 2000, Bitler and Currie 2005, Jackson 2015, Chorniy et al. 2018). The current federal administration has released multiple budget proposals with significant cuts to WIC funding.⁶ If the benefits of the program are either underestimated or worse, not detected, findings may undermine efforts to keep the program fully funded. Similarly, the assessment of harmful environmental impacts on population health, like contaminated drinking water, may be underestimated to the point that they cannot be detected if survival bias is not integrated into the analysis. In this case, families with infants—as well as those who lose pregnancies—may be deemed ineligible for damages if the costs of environmental negligence are not fully documented.

We have arrived at these conclusions with a skeletal scarring-selection model, though one that is more flexible than used elsewhere. We emphasize a unidimensional, latent measure of “health” that is predictive of the types of health characteristics measured at birth and at later ages—birthweight, functional limitations, chronic disease. This is similar to the “frailty” construct used in classic demographic research, though here we allow the latent variable to interact flexibly with cohort mortality. In reality, of course, human health is multidimensional and insults and investments during pregnancy are likely correlated with development in complex ways, some of which may be adaptive (Bateson and Gluckman 2012, Kuzawa and Quinn 2009). We use the parsimonious model to make the general point that prenatal selection is worthy of attention; research employing scarring-selection models may require a more complex formulation.

We initiate the model with pregnancy cohorts followed from implantation. We choose this starting point for two reasons. One, a large proportion of cytogenic abnormalities are removed from pregnancy cohorts before implantation (Larsen et al. 2013), leaving a group of pregnancies that are more likely sensitive to fetal origins exposures. Note that the control cohorts in the simulations also lose 40% of pregnancies and our analysis is on the marginal differences in survival—in an attempt to capture termination that is sensitive to exposures. Two, some research is able to measure pregnancy loss from implantation forward (Wilcox 1988, Zinaman 1996), providing some real-world estimates to bound the parameter space in the simulations.

Despite the advantages of starting the simulation with implanted pregnancies, fecundity encompasses a larger set of biological processes, including meiosis, fertilization, and implantation. The kinds of exposures that have been used to document fetal origin effects may also have effects on these other key elements of fecundity. They may also have effects on other proximate determinants of fertility, like partnership and coital frequency. In general: it is necessary to understand how a cohort of live births is produced to properly document the effects of fetal exposures. In this sense, we have moved the cohort clock start earlier and argue that doing so is essential. However our work does not preclude a look further back to understand how exposures in one generation pattern adult health in the next.

Looking ahead, several innovations promise to facilitate the incorporation of fecundity into fetal origins research. The single most important step needed is to improve measurement of fecundity, including pregnancy loss and prenatal selection. Existing research provides some estimates of the probability of pregnancy loss in human cohorts and how much it may vary by exposures that are considered important in structuring long-run health outcomes (Arck et al. 2008; Nepomnaschy 2006; Bruckner and Catalano 2018; Wilson 2018; Wilcox 2010; Wise et al. 2015). Now it is necessary to scale this research to non-clinical populations, and to track time series in representative samples.

While the research community develops improvements in measurement of fertilization and pregnancy loss, scholars can still use a number of tools for the study of fetal origin effects that correct for survival bias. The best approach will depend on data availability (e.g., are high resolution vital statistics data available during the exposure period?) and the nature of the exposure of interest (e.g., is it discrete in time and/or space?). There is not one algorithm that will work for every application. Proper accounting for survival bias, just like proper accounting for other sources of confounding, requires creativity, contextual expertise, and judgment.

The first set of tools are those that may help the researcher detect evidence of the magnitude of pregnancy loss associated with an exposure. We have suggested that variance reductions (or expansions) on outcome measures may provide some evidence of increases (or decreases) in pregnancy loss. Other inferential approaches may provide a retrospective window into the prenatal period. When the fetal origins exposure of interest is discrete in time and/or space, it may be possible to use time series of high-resolution birth count data to look for deviations. Because new pregnancies can follow early pregnancy loss in the next menstrual cycle, birth count data would need to be observable at a higher resolution than annual data. And much like the variance estimate exercise above, it would be necessary to work with an exposure that covered a large enough set of births to produce deviations that could be statistically detected. The observation that no detectable shift in birth counts is observed when counts are small is not likely sufficient evidence that no change in pregnancy survival occurred.

A third inferential approach relies on evidence in trends in the secondary sex ratio—the ratio of female to male births—based on the observation that higher prenatal mortality tends to disproportionately affect male fetuses and therefore increases the SSR (Song 2016; Sanders & Stoecker 2015; James & Grech 2017). Torche and Kleinhaus (2012), for example, simultaneously examine the effects of exposure to a major earthquake in Chile on preterm birth and pregnancy loss via the secondary sex ratio of exposed birth cohorts. By simulating counterfactual gestational age distributions, they conclude that exposure to the disaster in the third month of gestation increased the relative loss of male pregnancies and reduced gestational age for female pregnancies. This strategy of inferring loss from the SSR will benefit from the ongoing search for conclusive evidence about population sex ratios early in pregnancy (Mondal et al. 2014; Orzack et al. 2015; James & Grech 2017) and the accompanying implications for evidence of sex-specific vulnerability to pregnancy termination.

Other inferential approaches take advantage of characteristics of individuals and parent-child dyads that may be insensitive to the inputs that shape development between implantation and live birth. For example, the distribution of polygenic scores in observed cohorts with different intrauterine exposures and attendant levels of mortality may be informative of the nature of prenatal selection (see Munafò et al. 2017 for a similar approach to address postnatal selection). Gørgens, Meng, and Vaithianathan (2012) build on this logic and argue that selection could be detected by studying characteristics of the children of adults who were themselves exposed in utero. They argue that highly heritable traits should depict the selection and not the scarring effect of exposures in the first generation. Whether this approach is informative depends a great deal on the heritability of epigenetic change—a subject about which we still have much to learn (Bateson and Gluckman 2012, Heard and Martienssen 2014; Blake et al. 2018).

With some information about the magnitude of excess pregnancy loss generated by an exposure in hand, several approaches can be used to recover fetal origin effects. Some of these can be imported from the study of other phenomena. For example, a number of tools have been developed to study average treatment effects in the presence of sample attrition. These include tools for point-identification (Huber 2014) as well as more flexible approaches that bound estimates (Zhang and Rubin 2003, Lee 2009). Each of these requires some assumptions about the underlying relationship between health and pregnancy loss (e.g., the assumption of weak survival monotonicity); some of these can be varied by the researcher to test results sensitivity.

If stratified information about fetal death can be observed in the data, it is also possible to model fetal loss and this information to weight estimates derived from survivors (see for example Domingue et al. 2017 with inverse probability weighting). Finally, a simple, flexible approach to incorporating fecundity into fetal origins research would be to simulate the terminated pregnancies, vary assumptions about the underlying correlation structure, and bound estimates of fetal origin effects appropriately. This type of approach will of course be more informative when the parameter space can be bounded by published estimates or other information about the exposure at hand.

In combination, advances in the measurement of fecundity and the explicit incorporation of this information promises to advance our understanding of the links between early-life exposures and later life health. Together, these innovations will clarify the direction and magnitude of estimate bias, thereby uncovering fetal origin effects which may have significant, real-world implications but be otherwise hidden.