Abstract
The reproductive number (or , the initial reproductive number in an immune-naïve population) has long been successfully used to predict the likelihood of pathogen invasion, to gauge the potential severity of an epidemic, and to set policy around interventions. However, often ignored complexities have generated confusion around use of the metric. This is particularly apparent with the emergent pandemic virus SARS-CoV-2, the causative agent of COVID-19. We address some misconceptions about the predictive ability of the reproductive number, focusing on how it changes over time, varies over space, and relates to epidemic size by referencing the mathematical definition of and examples from the current pandemic. We hope that a better appreciation of the uses, nuances, and limitations of and facilitates a better understanding of epidemic spread, epidemic severity, and the effects of interventions in the context of SARS-CoV-2.
Keywords: , SARS-CoV-2, COVID-19, Interventions, Epidemic size, Heterogeneity
1. Introduction
With the emergence of SARS-CoV-2, the novel coronavirus responsible for COVID-19, much attention has been given to the reproductive number, , and its initial state, (Viceconte and Petrosillo, 2020). is the expected number of infections generated by an infected individual in an otherwise fully susceptible population and in the absence of interventions (Anderson and May, 1991, Diekmann et al., 1990). Since each infection produces an average of new infections, describes the exponential growth of infections during the early phase of an epidemic. Under relatively general assumptions, can be used to determine the probability an emerging disease will cause an epidemic, the final size of an epidemic, and what level of vaccination would be required to achieve herd immunity (Anderson and May, 1991, Delamater et al., 2019, Heffernan et al., 2005, Roberts, 2007). In many cases, has been invaluable such as for predicting the risk of measles resurgence (Béraud et al., 2018, Hens et al., 2015) and for managing emerging infectious diseases such as SARS-CoV-1 (Lipsitch et al., 2003) and foot-and-mouth disease (Ferguson et al., 2001). When interpreted correctly, and in conjunction with additional relevant information, it can yield valuable insight. However, misinterpretation may lead to faulty conclusions regarding disease dynamics.
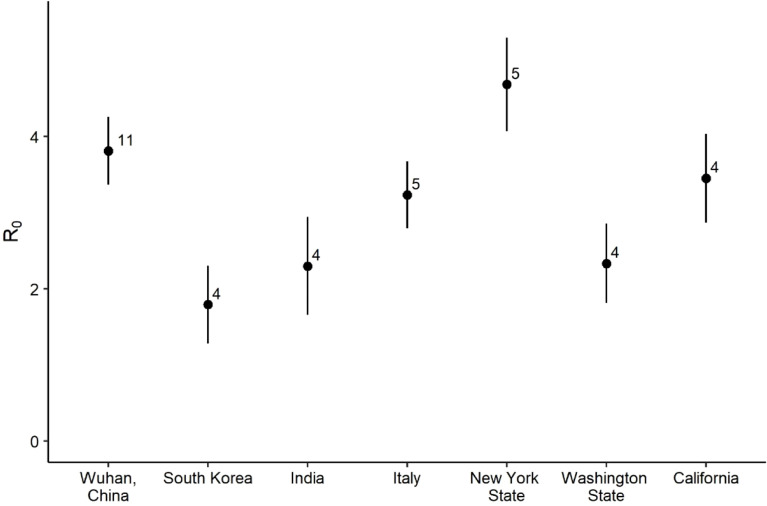
The virus SARS-CoV-2 emerged in Wuhan, China in late 2019 and has since become pandemic causing over one million deaths worldwide by September 30th, 2020 (Johns Hopkins University & Medicine Coronavirus Resource Center, 2020) in addition to severe economic distress. Policy makers have relied on estimates of to tailor control measures (e.g. Ferguson et al., 2020), but these estimates vary tremendously within and between populations around the globe (Fig. 1). It is important to understand why these estimates vary. It is also important to understand how the utility of the reproductive number is limited. Here, we derive and explain some of the key nuances of and , paying particular attention to insights and limitations with respect to the emerging pathogen SARS-CoV-2.
Fig. 1.
Estimates of the of SARS-CoV-2 vary substantially between locations (Binny et al., 2020, Chen et al., 2020, Choi and Ki, 2020, Deb and Majumdar, 2020, Giordano et al., 2020, Johndrow et al., 2020, Ke et al., 2020, Korolev, 2021, Lewnard et al., 2020, Li et al., 2020b, Majumder and Mandl, 2020, Mizumoto et al., 2020, Peirlinck et al., 2020, Pitzer et al., 2020, Ranjan, 2020, Read et al., 2020, Riou and Althaus, 2020, Sanche et al., 2020, Senapati et al., 2020, Shim et al., 2020, Singh and Adhikari, 2020, Tang et al., 2020, Wu et al., 2020, Xiao et al., 2020, Yuan et al., 2020, Zhao et al., 2020). Each point represents a literature-compiled average estimate for a different geographic area (sample size noted alongside means, error bars show plus or minus 1 standard error). For individual studies that provided multiple estimates for a single geographic area, the median estimate was used to avoid pseudo-replication. An analysis (not shown) confirmed that estimation method (transmission model, exponential growth model, or stochastic simulation method) did not drive the pattern of variation in by location. Recent meta-analyses of values for SARS-CoV-2 consider the effects of estimation methods in more detail (Alimohamadi et al., 2020, Barber et al., 2020).
2. Deriving and
2.1. A general definition
How many new infections will be caused by a single infected individual? For a directly transmitted pathogen, the answer to this question can be written as:
| (1) |
Above, is the reproductive number, is the rate of contacts that an infected individual has with susceptible individuals at time post infection, is the probability that a contact at time results in a new infection, and is the probability of still being infected at time . Notably, we could have combined and into a single parameter since the probability of infection given contact falls to zero after an individual recovers, but we prefer this more explicit formulation. Eq. (1) yields , the total number of infections one infected individual would generate over the course of their infection. When the population is fully susceptible and when no preventative interventions have been imposed, as would be expected at the beginning of a novel outbreak, Eq. (1) yields . Note that we have neglected to explicitly incorporate individual variation and temporal variation in contact rates, the probability that a contact results in a new infection, and the time to recovery. However, and , are intended to be averages, and so this variation is inherently a part of the reproductive number calculation. This variation could be explicitly included with additional subscripts to denote all possible infected hosts, noninfected hosts, times since the epidemic began, and ages of infections. For simplicity, we will not use any subscripts for , , and when we discuss how they relate to the reproductive number of SARS-CoV-2 in the remaining sections of this commentary.
2.2. Calculating the reproductive number using an epidemiological model
Estimating the individual parameters in Eq. (1) requires extensive data collection for a specific pathogen, host population, and time. Alternative approaches to estimating and therefore frequently rely on epidemiological models and epidemic data.
Following the lead of Kermack and McKendrick (1927), epidemics are often modeled as a set of ordinary differential equations such as for the classical Susceptible–Infected–Recovered (SIR) model. To illustrate the derivation of the reproductive number, we present a model of SARS-CoV-2 transmission that captures some of the key characteristics of the system. Unlike in the classic SIR model, in our model, infected individuals can be asymptomatic or not, and all non-asymptomatic infections progress through two stages, a pre-symptomatic and a symptomatic stage. Transmission is possible from each of these infected classes, but at different rates. Individuals showing symptoms are detected through testing (e.g. fever checks or diagnostic testing), and these individuals are quarantined. We assume no transmission from the quarantined class, and we assume that only symptomatic or quarantined individuals die from infection. Otherwise, all infected individuals eventually recover. In our model, the state variables , , , , , and are respectively the densities of susceptible, asymptomatically infected, pre-symptomatic, symptomatic (subscript “” used to denote COVID-19), quarantined, and recovered individuals in a population. Note that “” here is distinct from the reproductive number “”, but we use both for historical reasons.
| (2.1) |
| (2.2) |
| (2.3) |
| (2.4) |
| (2.5) |
| (2.6) |
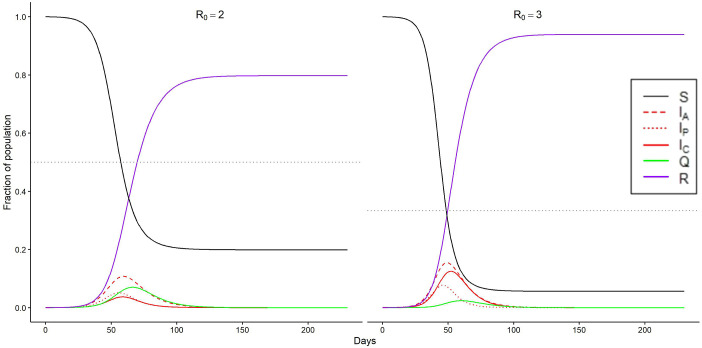
Here, the subscripts , , , and denote parameters for asymptomatic, pre-symptomatic, COVID-19 symptomatic, and quarantined individuals respectively. The parameters are transmission coefficients, the parameters are virus-induced death rates, and the parameters are recovery rates. is the fraction of new infections that are asymptomatic, is the infection progression rate from pre-symptomatic to symptomatic, and is the detection rate of symptomatic infections. Parameter values can, in principle, be estimated from data (e.g. Ferretti et al., 2020). Note that further complexity could be added to this model, for example, to incorporate spatial structure, hospitalization, age structure, host-specific exposure risk, superspreading, or time-varying mortality. Simulations of our model are shown in Fig. 2.
Fig. 2.
Simulation of transmission model of SARS-CoV-2 presented in Eqs. (2.1)–(2.6) for (left) and (right) . We achieved this change in by altering the parameter , which is the per day detection rate of symptomatic cases, thus illustrating the potential value of rapid case detection. Note that a larger leads to a faster epidemic and a greater fraction of the population becoming infected. The horizontal, dotted gray line in each panel indicates the herd immunity threshold (i.e. the value of that corresponds to ). Note that infection declines, but does not immediately disappear, after crossing the herd immunity threshold. Parameter values: ,(left) , (right) . Initial conditions: .
Numerous methods can be used to derive from a model (Heffernan et al., 2005). Perhaps most famously, is the dominant eigenvalue of the next generation matrix (Diekmann et al., 1990). In the following text, we use the survival function to calculate because of its intuitive connection to Eq. (1), but if we had used the next generation matrix, we would have derived the exact same . The survival function uses three components to determine the number of new infections caused by an initial case: (1) the rate at which an individual in a particular class causes new infections (from Eq. (1), ), (2) the probability that an individual is still in the class at time (from Eq. (1), ), and (3) the probability that an initial infected individual will enter that class. Note that this third term is implicitly assumed to be one in Eq. (1). The integral of the product of the first two terms multiplied by the third term yields the contribution to that comes from a focal class. Deriving the overall requires summing over all possible classes. To illustrate, consider the asymptomatic contribution for an average initial infection. Here, (1) is equal to , (2) is equal to , and (3) the probability that the initial case enters the asymptomatic class is equal to . Using these values, and extending the same methods to all infectious classes we derive:
| (3.1) |
where is the time since entering class . Since changes slowly at the beginning of an epidemic when few individuals are infected, we can treat as a constant with respect to time. This assumption allows us to analytically solve Eq. (3.1), which yields
| (3.2) |
Evaluating Eq. (3.2) at time rather than time 0 yields . Notice that the reproductive number has contributions from the asymptomatic, pre-symptomatic, and symptomatic classes, but not from the other classes because the other classes cannot cause new infections. If transmission were possible from these classes, additional terms would need to be included in Eq. (3.2). Alternatively, if we simplified our model by assuming that all infections were symptomatic () and pre-symptomatic individuals were not infectious (), then Eq. (3.2) would simplify to .
2.3. Calculating the reproductive number without an epidemiological model
can also be estimated without an epidemiological model, which can be especially useful if parameter estimates or even an appropriate model structure is not yet known. In principle, one could calculate by simply counting the cases attributed to infected individuals at or near the beginning of an outbreak. In practice, this method is rarely employed since contact tracing networks are rarely established during the earliest phase of an emerging disease outbreak (but see Pung et al., 2020) and estimates could be inaccurate due to bias towards observing large chains of transmission.
can also be inferred from the growth rate of cases early in an outbreak. Since the number of susceptible individuals changes slowly during the initial stages of an outbreak, early case growth rates can be approximated by exponential growth: the number of cases , where is the epidemic growth rate. If the number of cases is known for at least two time points, one could calculate the epidemic growth rate . The relationship between and depends on the distribution of the generation interval , which is defined as the amount of time between infection of two individuals where the second infection is caused by the first. can be approximated by direct observation or specified by an epidemiological model (Wallinga and Lipsitch, 2007). For the classical SIR model, the generation interval is exponentially distributed, leading to (Wallinga and Lipsitch, 2007), where is the mean of . Other relationships can be calculated for other distributions of (Wallinga and Lipsitch, 2007). See Zhao et al. (2020) for an example of this method used to calculate the of SARS-CoV-2. It is important to recognize however that emerging epidemics often grow more slowly than exponential due to stochastic effects, small population sizes, network effects, or preventative measures (Chowell et al., 2016). In these cases, a generalized growth model may more accurately reflect epidemic growth (Viboud et al., 2016).
After epidemics have started (i.e. when populations are no longer fully susceptible and when interventions may have been imposed), it is still useful to calculate to understand if cases will continue to grow or decline. A recent review explored various methods for this calculation (Gostic et al., 2020). Gostic et al. (2020) recommended two methods. The first, developed by Cori et al. (2013) uses time series incidence data and the serial interval to calculate in real time, which is particularly useful for assessing the impact of interventions as they are employed. The second, developed by Wallinga and Teunis (2004) uses similar data and is useful for the retrospective calculation of .
No matter the method used to calculate it, limited data or unreliable data early in an epidemic can make it difficult to constrain . The World Health Organization originally estimated the of SARS-CoV-2 to be between 1.4 and 2.5 (WHO, 2020). More recent estimates of have varied from 2.2 to 6.47 for the beginning of the Wuhan outbreak (Fig. 1). This represents tremendous uncertainty when attempting to use for public health planning. For example, if we were using these estimates to design a vaccine campaign capable of achieving herd immunity for a vaccine with perfect efficacy, our vaccination target (calculated as under assumptions of Eq. (2.1)–(2.6)) would be 29% of the population at or 85% at . Even with better estimates of , however, misconceptions around this metric lessen its practical utility.
3. Misconception 1: The reproductive number alone explains future dynamics
As we have explained, is calculated during the early stages of an epidemic because of its value in determining future infection dynamics in the absence of intervention (Anderson and May, 1991, Ma and Earn, 2006). is similarly useful for assessing changes in transmission over time and the potential impacts of interventions. However, and cannot fully explain future dynamics under particular circumstances. We discuss two important situations in which their value is limited: first, when hosts become aware of infection and alter their behavior, and second, when individual infection risk is heterogeneous.
Shifts in behavior that influence contact rates or the probability of infection given contact can alter over extremely short timescales (see Eq. (1)). For example, as awareness of the SARS-CoV-2 epidemic grew in the United States in March 2020, human mobility ground to a near halt (Gao et al., 2020, Warren and Skillman, 2020), presumably reducing contact rates . Other individual behavioral changes such as increased handwashing and mask wearing (Belot et al., 2020, Goldberg et al., 2020) have reduced the probability of transmission given contact (Eikenberry et al., 2020, Liang et al., 2020). Such bottom-up forces combined with top-down government-imposed interventions (e.g. school closures, banned gatherings) reduced to below 1 (the threshold for epidemic persistence) by late April 2020 in some states (Johndrow et al., 2020, Miller et al., 2020). Similar reductions to were documented in China (Li et al., 2020a, Tian et al., 2020) and other countries (Ensser et al., 2020, Giordano et al., 2020, Kupferschmidt, 2020, Yuan et al., 2020). Indeed, in models of the 1918 influenza pandemic, incorporating a behavioral response to death rates improved model fits (Bootsma and Ferguson, 2007, He et al., 2013). For SARS-CoV-2, behavioral changes have caused to fluctuate above and below 1 at different times based on the perceived threat of COVID-19 (Santamaría and Hortal, 2021).
While behavioral changes can temporarily reduce as described above, more sustainable reductions in are typically achieved when susceptible individuals are removed from populations either through naturally acquired immunity or vaccination. When hosts are heterogeneous such that some individuals are more likely to contract infection than others, declines faster than predicted by Eq. (2.1)–(2.6) or other SIR models lacking host heterogeneity (May and Anderson, 1987). This is because those most susceptible (for example, due to high exposure or low inherent immunity) will become infected earlier in an epidemic, leaving individuals that are on average more resistant (Langwig et al., 2017, May and Anderson, 1987). Thus, the classical formulation of the “herd immunity” threshold, , does not apply to populations with heterogeneity in risk of infection. To illustrate this point, Britton et al. (2020) developed a COVID-19 model with heterogeneous mixing between age classes and additional heterogeneity in contact rates. Under their assumptions, herd immunity was reached after 43% of the population acquired immunity through natural exposure, rather than the 60% that would be required under their assumptions in the absence of heterogeneity. Other studies have predicted that heterogeneity could have an even larger effect if susceptibility was correlated with infectivity (Gomes et al., 2020, Tkachenko et al., 2020). In some of the hardest hit areas, an appreciable fraction of people have been infected with SARS-CoV-2 (e.g. 22.7% in New York City, USA (Rosenberg et al., 2020) and over 44% in Manaus, Brazil (Buss et al., 2020)). However, the impact of these levels of infection on future disease dynamics is unknown, since for SARS-CoV-2, heterogeneity in infection risk is still highly uncertain (Randolph and Barreiro, 2020). Moreover, heterogeneity is likely to change through time due to changes in individual or government-mandated responses (Dolbeault and Turinici, 2020). Thus, even after herd immunity has been reached, additional waves of infection could occur if heterogeneity changes (Tkachenko et al., 2020).
4. Misconception 2: The reproductive number is constant over space
The of many pathogens are often referred to as known values. For example, the of measles is 12–14, polio is 5–7, and pertussis is 12–17 (Doherty et al., 2016). For SARS-CoV-2, estimates typically range from 2–3 (Liu et al., 2020a). However, the parameters (, , and in Eq. (1)) that make up can differ substantially from place to place (Figure 1, Delamater et al., 2019). It follows that interventions to reduce to less than 1 may need to vary in aggressiveness across locations (Stier et al., 2020).
Since differs between groups of people, combining multiple groups together to estimate a population-wide can produce misleading notions of disease spread. For example, a high average measles vaccination rate in the United States keeps below 1 nation-wide, but localized communities with high rates of vaccine refusal still experience serious outbreaks (Leslie et al., 2018). In the current COVID-19 pandemic, disease transmission has so far been much higher in refugee and low income populations compared to non-refugee and high income populations (Chopra and Sobel, 2020, Lau et al., 2020, Ruiz-Euler et al., 2020) and has been documented to vary between US counties (Sly et al., 2020). Since is an average, combining communities with high and low transmission may yield an estimate of , yet disease may still readily spread (Li et al., 2011). On the other hand, splitting populations may mean missing transmission events that occur between populations, thus underestimating (Smith et al., 2009).
Awareness of the consequences of how people are grouped can help us interpret values of the reproductive number. Within groups, behavior associated with work, home, and recreation affects contact rates . As we have discussed above, SIR models often assume that contact rates, and thus and , depend on host density. Although, evidence is mixed as to whether larger cities have higher values of and for SARS-CoV-2 (Heroy, 2020, Stier et al., 2020), built environments (e.g. hospitals, airport terminals, factories) do often have high values of (Dietz et al., 2020). This may partially explain patterns of explosive SARS-CoV-2 transmission in venues such as cruise ships and meat packing facilities (Althouse et al., 2020, Dyal et al., 2020, Mizumoto and Chowell, 2020). Household contacts have also been particularly important to the transmission dynamics of the virus (Bi et al., 2020). Therefore, differences in between populations can be partially explained by differences in household sizes between countries and cultures (Singh and Adhikari, 2020). For example, large, multigenerational households in Italy may have contributed to the large and deadly outbreak there relative to other European countries where multigenerational households are less common (Dowd et al., 2020). Similarly, the probability a new infection results from contact and the probability of remaining infected over time may vary by population. For SARS-CoV-2, individuals with severe symptoms have 60 times more viral RNA in nasal swabs, which likely increases both their ability to transmit the virus and the amount of time they remain infected (Liu et al., 2020b). Since older individuals are more likely to develop severe infection (Yang et al., 2020), is likely to be greater in populations with older individuals, such as in nursing homes (McMichael et al., 2020) or in developed countries (Dowd et al., 2020).
5. Misconception 3: The reproductive number is enough to tell us how large an epidemic will be
It is tantalizing to imagine that can be used to predict the extent of an outbreak, since it can be calculated during the early stages of an epidemic. Indeed, is related to final epidemic size (Kermack and McKendrick, 1927), but this relationship can be substantially affected by the fraction of the population infected initially and by heterogeneity in transmission.
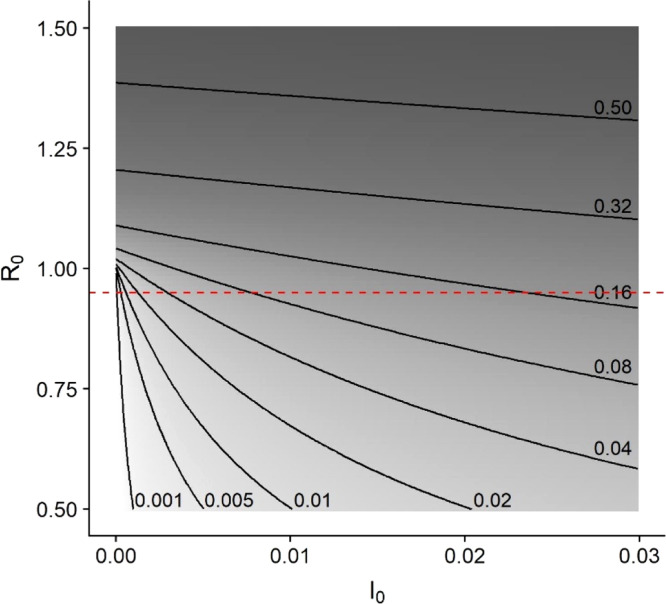
If we rescale population sizes such that the initial susceptible population size , and we assume that population sizes are sufficiently large to neglect demographic stochasticity (Hartfield and Alizon, 2013, Tildesley and Keeling, 2009), then the fraction of the population infected during an epidemic can be determined from the final epidemic size equation. This equation, , is not sensitive to the epidemic model used to calculate so long as the model assumes that the population is well-mixed with homogeneous susceptibility. Note that this equation prominently features , the fraction of the population infected at the beginning of the outbreak (or at the beginning of an intervention). Efforts to reduce the reproductive number below 1 are understandably a high priority, but when is close to or less than 1, the final outbreak size is more sensitive to changes in the fraction of infected individuals than it is to changes in (Fig. 3). This is because more infected individuals will fuel the outbreak for longer, infecting a greater proportion of the susceptible population even when each case produces on average less than one new infection. Now that SARS-CoV-2 infection rates are already substantial in populations around the globe, must be considered in addition to . For example, Pei et al. (2020) estimated that implementing social distancing policies one week earlier could have reduced the cases in the United States by early May, 2020 by 55% (over 700,000 cases) by keeping the number of infected individuals low at the time such policies were implemented.
Fig. 3.
Epidemic size contours and shading show that when is close to 1, the epidemic is more strongly influenced by a reduction of than by a reduction of . For instance, if (dashed line), the epidemic could infect from less than 0.1% to greater than 16% of the population as ranges from just above 0% to 3% of the population. Epidemic size was calculated using the final size equation, , where . Shading indicates the cube root of epidemic size with lighter colors corresponding to smaller outbreaks.
While a final epidemic size can be calculated using and , the final size equation above does not apply to populations with heterogeneous infection risk (Andreasen, 2011, Ball, 1985, Hébert-Dufresne et al., 2020, Ma and Earn, 2006). Given the inherent heterogeneity in human social networks, it is surprising that the final size equation is so accurate for many diseases such as childhood diseases (Caudron et al., 2015). This may be because transmission networks among children are close to random (Bjørnstad et al., 2002) or have other features that allow the final size equation to be accurate (Bansal et al., 2007). For diseases where this is not the case (e.g. many sexually transmitted diseases), heterogeneity could in principle be incorporated into the final epidemic size equation (Dwyer et al., 2000), but estimating heterogeneity early in an epidemic can be challenging. Moreover, as we describe in misconception 1, heterogeneity in infection risk can change over time as a result of human behavior or interventions, such as the shutdowns in response to the COVID-19 epidemic (Dolbeault and Turinici, 2020, Ruiz-Euler et al., 2020). Estimates of how future government restrictions and behavioral changes will alter heterogeneity in infection risk are thus critical for assessing the likely impact of the outbreak (Gomes et al., 2020). Such estimates are also key in determining thresholds for herd immunity (Randolph and Barreiro, 2020) and in prioritizing the distribution of interventions such as vaccines when they first become available (Atkinson and Cheyne, 1994, Giambi et al., 2019).
6. Conclusions
As we have discussed, the reproductive number and its initial value can be used to assess the potential for disease invasion and persistence, to predict the extent of an epidemic, and to infer the impact of interventions and of relaxing control measures. Determining in real time is especially helpful for the latter goals. For example, the of SARS-CoV-2 was used to justify implementations of lockdowns in the United Kingdom (Ferguson et al., 2020), and is one factor that is considered in lockdown relaxation policies (Thompson et al., 2020).
However, the utility of and can easily be overstated. Though we have focused on three misconceptions that we felt were particularly important for the COVID-19 pandemic, there are additional considerations to appreciate for accurate interpretation of and (Heffernan et al., 2005, Li et al., 2011, Roberts, 2007). These include complications associated with stochasticity (Keeling and Grenfell, 2000), superspreading (Lloyd-Smith et al., 2005), metapopulation dynamics (Cross et al., 2007), seasonality (Bjørnstad et al., 2002), multiple hosts (Roberts, 2007), and pathogen evolution (Hartfield and Alizon, 2014). Some of these nuances may also be important for SARS-CoV-2 dynamics. For example, superspreading events appear to be common with this virus (Althouse et al., 2020). Although superspreading affects epidemic dynamics, masks this feature of disease spread because it only represents average transmission.
The reproductive number is a valuable tool for understanding disease dynamics. describes early disease growth, and it can be estimated when little else is known about a pathogen. Later, can be used to measure the effectiveness of interventions. However, a singular focus on and can lead to inaccurate conclusions. Considering the nuances of disease dynamics when interpreting the reproductive number allows for a stronger understanding of the patterns with which the SARS-CoV-2 virus has traversed the globe, why it has impacted some populations more than others, and how best to limit future transmission.
Acknowledgments
We thank Amrita Bhattacharya and two anonymous reviewers for feedback on earlier versions of the text. This work was supported by startup funds from The Pennsylvania State University, United States. DAK was also partially supported by National Science Foundation, United States grant DEB-1754692. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- Alimohamadi Y., Taghdir M., Sepandi M. The estimate of the basic reproduction number for novel coronavirus disease (COVID-19): a systematic review and meta-analysis. J. Prev. Med. Public Heal. 2020;53:151–157. doi: 10.3961/jpmph.20.076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Althouse B.M., Wenger E.A., Miller J.C., Scarpino S.V., Allard A., Hébert-Dufresne L., Hu H. Superspreading events in the transmission dynamics of SARS-CoV-2: opportunities for interventions and control. PLoS Biology. 2020;18(11) doi: 10.1371/journal.pbio.3000897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson R.M., May R.M. Oxford University Press; Oxford, New York: 1991. Infectious Diseases of Humans: Dynamics and Control. [Google Scholar]
- Andreasen V. The final size of an epidemic and its relation to the basic reproduction number. Bull. Math. Biol. 2011;73:2305–2321. doi: 10.1007/s11538-010-9623-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Atkinson S.J., Cheyne J. Immunization in urban areas: issues and strategies. Bull. World Health Organ. 1994;72:183–194. [PMC free article] [PubMed] [Google Scholar]
- Ball F. Deterministic and stochastic epidemics with several kinds of susceptibles. Adv. Appl. Probab. 1985;17:1–22. doi: 10.2307/1427049. [DOI] [Google Scholar]
- Bansal S., Grenfell B.T., Meyers L.A. When individual behaviour matters: homogeneous and network models in epidemiology. J. R. Soc. Interface. 2007;4:879–891. doi: 10.1098/rsif.2007.1100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barber A., Griffin J.M., Casey M., Collins A., Lane E.A., Bosch Q.T., Jong M.D., Mc Evoy D., Byrne A.W., McAloon C.G., Butler F., Hunt K., More S.J. The basic reproduction number of SARS-CoV-2: a scoping review of available evidence. medRxiv. 2020 doi: 10.1101/2020.07.28.20163535. [DOI] [Google Scholar]
- Belot M., Choi S., Jamison J.C., Papageorge N.W., Tripdoi E., van den Broek-Altenburg E. Six-country survey on COVID-19. IZA Institute of Labor Economics. 2020 [Google Scholar]
- Béraud G., Abrams S., Beutels P., Dervaux B., Hens N. Resurgence risk for measles, mumps and rubella in France in 2018 and 2020. Eurosurveillance. 2018;23 doi: 10.2807/1560-7917.ES.2018.23.25.1700796. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bi Q., Mei S.Wu.Yongsheng., Ye C., Zou X., Zhang Z., Liu X., Wei L., Truelove S.A., Zhang T., Gao W., Cheng C., Tang X., Wu X., Sun B., Wu Yu, Huang S., Sun Y., Zhang J., Ma T., Lessler J., Feng T. Epidemiology and transmission of COVID-19 in 391 cases and 1286 of their close contacts in Shenzhen, China: a retrospective cohort study. Lancet Infect. Dis. 2020;20:911–919. doi: 10.1016/S1473-3099(20)30287-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Binny R.N., Hendy S.C., James A., Lustig A., Steyn N. Effect of Alert Level 4 on : review of international COVID-19 cases. medRxiv. 2020 doi: 10.1101/2020.04.30.20086934. [DOI] [Google Scholar]
- Bjørnstad O.N., Finkenstädt B.F., Grenfell B.T. Dynamics of measles epidemics: estimating scaling of transmission rates using a time series SIR model. Ecol. Monogr. 2002;72:169–184. doi: 10.2307/3100023. [DOI] [Google Scholar]
- Bootsma M.C.J., Ferguson N.M. The effect of public health measures on the 1918 influenza pandemic in U.S. cities. Proc. Natl. Acad. Sci. 2007;104:7588–7593. doi: 10.1073/pnas.0611071104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Britton T., Ball F., Trapman P. A mathematical model reveals the influence of population heterogeneity on herd immunity to SARS-CoV-2. Science. 2020;369(80):846–849. doi: 10.1126/science.abc6810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buss L.F., Prete C.A., Jr., Abrahim C.M.M., Mendrone A., Jr., Salomon T., de Almeida-Neto C., França R.F.O., Belotti M.C., Carvalho M.P.S.S., Costa A.G., Crispim M.A.E., Ferreira S., Fraiji N.A., Gurzenda S., Whittaker C., Kamaura L.T., Takecian P.L., Oikawa M.K., Nishiya A.S., Rocha V., Salles N.A., de Souza-Santos A.A., da Silva M.A., Custer B., Barral-Netto M., Kraemer M.U.G., Pereira R.H.M., Pybus O.G., Busch M.P., Castro M.C., Dye C., Nascimento V.H., Faria N.R., Sabino E.C. COVID-19 herd immunity in the Brazilian Amazon. medRxiv. 2020 doi: 10.1101/2020.09.16.20194787. [DOI] [Google Scholar]
- Caudron Q., Mahmud A.S., Metcalf C.J.E., Gottfredsson M., Viboud C., Cliff A.D., Grenfell B.T. Predictability in a highly stochastic system: final size of measles epidemics in small populations. J. R. Soc. Interface. 2015;12 doi: 10.1098/rsif.2014.1125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen N., Zhou M., Dong X., Qu J., Gong F., Han Y., Qiu Y., Wang J., Liu Y., Wei Y., Xia J., Yu T., Zhang X., Zhang L. Epidemiological and clinical characteristics of 99 cases of 2019 novel coronavirus pneumonia in Wuhan, China: a descriptive study. Lancet. 2020;395:507–513. doi: 10.1016/S0140-6736(20)30211-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choi S., Ki M. Estimating the reproductive number and the outbreak size of COVID-19 in Korea. Epidemiol. Health. 2020;42 doi: 10.4178/epih.e2020011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chopra T., Sobel J. Detroit under siege, the enemy within: the impact of the covid-19 collision. Infect. Control Hosp. Epidemiol. 2020;41(9):1122. doi: 10.1017/ice.2020.154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chowell G., Sattenspiel L., Bansal S., Viboud C. Mathematical models to characterize early epidemic growth: a review. Phys. Life Rev. 2016;18:66–97. doi: 10.1016/j.plrev.2016.07.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cori A., Ferguson N.M., Fraser C., Cauchemez S. A new framework and software to estimate time-varying reproduction numbers during epidemics. Am. J. Epidemiol. 2013;178:1505–1512. doi: 10.1093/aje/kwt133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cross P.C., Johnson P.L.F., Lloyd-Smith J.O., Getz W.M. Utility of as a predictor of disease invasion in structured populations. J. R. Soc. Interface. 2007;4:315–324. doi: 10.1098/rsif.2006.0185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deb S., Majumdar M. 2020. A time series method to analyze incidence pattern and estimate reproduction number of COVID-19.arXiv:2003.10655 [Google Scholar]
- Delamater P.L., Street E.J., Leslie T.F., Yang Y.T., Jacobsen K.H. Complexity of the basic reproduction number () Emerg. Infect. Diseases. 2019;25(1):1–4. doi: 10.3201/eid2501.171901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diekmann O., Heesterbeek J.A.P., Metz J.A.J. On the definition and the computation of the basic reproduction ratio in models for infectious diseases in heterogeneous populations. J. Math. Biol. 1990;28:365–382. doi: 10.1007/BF00178324. [DOI] [PubMed] [Google Scholar]
- Dietz L., Horve P.F., Coil D.A., Fretz M., Eisen J.A., Van Den Wymelenberg K. 2019 novel coronavirus (COVID-19) pandemic: built environment considerations to reduce transmission. Appl. Environ. Sci. 2020;5 doi: 10.1128/mSystems.00245-20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doherty M., Buchy P., Standaert B., Giaquinto C., Prado-Cohrs D. Vaccine impact: benefits for human health. Vaccine. 2016;34:6707–6714. doi: 10.1016/j.vaccine.2016.10.025. [DOI] [PubMed] [Google Scholar]
- Dolbeault J., Turinici G. Heterogeneous social interactions and the COVID-19 lockdown outcome in a multi-group SEIR model. Math. Model. Natural Phenomena. 2020;15:36. doi: 10.1051/mmnp/2020025. [DOI] [Google Scholar]
- Dowd J.B., Andriano L., Brazel D.M., Rotondi V., Block P., Ding X., Liu Y., Mills M.C. Demographic science aids in understanding the spread and fatality rates of COVID-19. Proc. Natl. Acad. Sci. 2020;117:9696–9698. doi: 10.1073/pnas.2004911117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dwyer G., Dushoff J., Elkinton J.S., Levin S.A. Pathogen-driven outbreaks in forest defoliators revisited: building models from experimental data. Am. Nat. 2000;156:105–120. doi: 10.1086/303379. [DOI] [PubMed] [Google Scholar]
- Dyal J.W., Grant M.P., Broadwater K., Bjork A., Waltenburg M.A., Gibbins J.D., Hale C., Silver M., Fischer M., Steinberg J., Basler C.A., Jacobs J.R., Kennedy E.D., Tomasi S., Trout D., Hornsby-Myers J., Oussayef N.L., Delaney L.J., Patel K., Shetty V., Kline K.E., Schroeder B., Herlihy R.K., House J., Jervis R., Clayton J.L., Ortbahn D., Austin C., Berl E., Moore Z., Buss B.F., Stover D., Westergaard R., Pray I., DeBolt M., Person A., Gabel J., Kittle T.S., Hendren P., Rhea C., Holsinger C., Dunn J., Turabelidze G., Ahmed F.S., DeFijter S., Pedati C.S., Rattay K., Smith E.E., Luna-Pinto C., Cooley L.A., Saydah S., Preacely N.D., Maddox R.A., Lundeen E., Goodwin B., Karpathy S.E., Griffing S., Jenkins M.M., Lowry G., Schwarz R.D., Yoder J., Peacock G., Walke H.T., Rose D.A., Honein M.A. COVID-19 among workers in meat and poultry processing facilities - 19 States, April 2020. MMWR. Morb. Mortal. Wkly. Rep. 2020;69:557–561. doi: 10.15585/mmwr.mm6918e3. [DOI] [PubMed] [Google Scholar]
- Eikenberry S.E., Mancuso M., Iboi E., Phan T., Eikenberry K., Kuang Y., Kostelich E., Gumel A.B. To mask or not to mask: modeling the potential for face mask use by the general public to curtail the COVID-19 pandemic. Infect. Dis. Model. 2020;5:293–308. doi: 10.1016/j.idm.2020.04.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ensser A., Überla P., Überla K. Modest effects of contact reduction measures on the reproduction number of SARS-CoV-2 in the most affected European countries and the US. medRxiv. 2020 doi: 10.1101/2020.04.20.20067538. [DOI] [Google Scholar]
- Ferguson N.M., Donnelly C.A., Anderson R.M. Transmission intensity and impact of control policies on the foot and mouth epidemic in Great Britain. Nature. 2001;413:542–548. doi: 10.1038/35104594. [DOI] [PubMed] [Google Scholar]
- Ferguson N.M., Laydon D., Nedjati-Gilani G., Imai N., Ainslie K., Baguelin M., Bhatia S., Boonyasiri A., Cucunubá Z., Cuomo-Dannenburg G., Dighe A., Dorigatti I., Fu H., Gaythorpe K., Green W., Hamlet A., Hinsley W., Okell L.C., van Elsland S., Thompson H., Verity R., Volz E., Wang H., Wang Y., Walker P.G.T., Walters C., Winskill P., Whittaker C., Donnelly C.A., Riley S., Ghani A.C. 2020. Impact of non-pharmaceutical interventions (NPIs) to reduce COVID-19 mortality and healthcare demand. Imperial College COVID-19 Response Team. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferretti L., Wymant C., Kendall M., Zhao L., Nurtay A., Abeler-Dörner L., Parker M., Bonsall D., Fraser C. Quantifying SARS-CoV-2 transmission suggests epidemic control with digital contact tracing. Science. 2020;368 doi: 10.1126/science.abb6936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gao S., Rao J., Kang Y., Liang Y., Kruse J. Mapping county-level mobility pattern changes in the United States in response to COVID-19. SIGSPATIAL Special. 2020;12:16–26. doi: 10.1145/3404820.3404824. [DOI] [Google Scholar]
- Giambi C., Del Manso M., Dalla Zuanna T., Riccardo F., Bella A., Caporali M.G., Baka A., Caks-Jager N., Melillo T., Mexia R., Petrović G., Declich S. National immunization strategies targeting migrants in six European countries. Vaccine. 2019;37:4610–4617. doi: 10.1016/j.vaccine.2018.01.060. [DOI] [PubMed] [Google Scholar]
- Giordano G., Blanchini F., Bruno R., Colaneri P., Di Filippo A., Di Matteo A., Colaneri M. Modelling the COVID-19 epidemic and implementation of population-wide interventions in Italy. Nat. Med. 2020;26:855–860. doi: 10.1038/s41591-020-0883-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldberg M.H., Gustafson A., Maibach E.W., Ballew M.T., Bergquist P., Kotcher J.E., Marlon J.R., Rosenthal S.A., Leiserowitz A. Mask-wearing increases after a government recommendation: a natural experiment in the U.S. during the COVID-19 pandemic. Front. Commun. 2020;5:1–6. doi: 10.3389/fcomm.2020.00044. [DOI] [Google Scholar]
- Gomes M.G.M., Aguas R., Corder R.M., King J.G., Langwig K.E., Souto-Maior C., Carneiro J., Gonçalves G., Penha-Gonçalves C., Ferreira M.U., Aguas R. Individual variation in susceptibility or exposure to SARS-CoV-2 lowers the herd immunity threshold. medRxiv. 2020 doi: 10.1101/2020.04.27.20081893. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gostic K.M., McGough L., Baskerville E., Abbott S., Joshi K., Tedijanto C., Kahn R., Niehus R., Hay J.A., De Salazar P.M., Hellewell J., Meakin S., Munday J.D., Bosse N.I., Sherratt K., Thompson R.N., White L.F., Huisman J.S., Scire J., Bonhoeffer S., Stadler T., Wallinga J., Funk S., Lipsitch M., Cobey S. Practical considerations for measuring the effective reproductive number, . PLoS Comput. Bio. 2020;16(12) doi: 10.1371/journal.pcbi.1008409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hartfield M., Alizon S. Introducing the outbreak threshold in epidemiology. PLoS Pathog. 2013;13(5) doi: 10.1371/journal.ppat.1003277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hartfield M., Alizon S. Epidemiological feedbacks affect evolutionary emergence of pathogens. Am. Nat. 2014;183:E105–E117. doi: 10.1086/674795. [DOI] [PubMed] [Google Scholar]
- He D., Dushoff J., Day T., Ma J., Earn D.J.D. Inferring the causes of the three waves of the 1918 influenza pandemic in England and Wales. 2013;280 doi: 10.1098/rspb.2013.1345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hébert-Dufresne L., Althouse B.M., Scarpino S.V., Allard A. Beyond : heterogeneity in secondary infections and probabilistic epidemic forecasting. J. Royal Soc. Interface. 2020;17 doi: 10.1098/rsif.2020.0393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heffernan J.M., Smith R.J., Wahl L.M. Perspectives on the basic reproductive ratio. J. R. Soc. Interface. 2005;2:281–293. doi: 10.1098/rsif.2005.0042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hens N., Abrams S., Santermans E., Theeten H., Goeyvaerts N., Lernout T., Leuridan E., Van Kerckhove K., Goossens H., Van Damme P., Beutels P. Assessing the risk of measles resurgence in a highly vaccinated population: Belgium anno 2013. Eurosurveillance. 2015;20 doi: 10.2807/1560-7917.ES2015.20.1.20998. [DOI] [PubMed] [Google Scholar]
- Heroy S. 2020. Metropolitan-scale COVID-19 outbreaks: how similar are they?arXiv:2004.01248 [Google Scholar]
- Johndrow J., Lum K., Gargiulio M., Ball P. Estimating the number of SARS-CoV-2 infections and the impact of mitigation policies in the United States. Harvard Data Sci. Rev. 2020 doi: 10.1162/99608f92.7679a1ed. [DOI] [Google Scholar]
- Johns Hopkins University & Medicine Coronavirus Resource Center . 2020. WWW document. URL https://coronavirus.jhu.edu/map.html (Accessed 30 september 20) [Google Scholar]
- Ke R., Sanche S., Romero-Severson E.O., Hengartner N. Estimating the reproductive number of SARS-CoV-2 in the United States and eight European countries and implications for vaccination. medRxiv. 2020 doi: 10.1101/2020.07.31.20166298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keeling M.J., Grenfell B.T. Individual-based perspectives on . J. Theoret. Biol. 2000;203:51–61. doi: 10.1006/jtbi.1999.1064. [DOI] [PubMed] [Google Scholar]
- Kermack W.O., McKendrick A.G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. A. 1927;115:700–721. doi: 10.2307/2304150. [DOI] [Google Scholar]
- Korolev I. Identification and estimation of the SEIRD epidemic model for COVID-19. J. Econom. 2021:63–85. doi: 10.1016/j.jeconom.2020.07.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kupferschmidt K. The lockdowns worked-but what comes next? Science. 2020;368(80):218–219. doi: 10.1126/science.368.6488.218. [DOI] [PubMed] [Google Scholar]
- Langwig K.E., Wargo A.R., Jones D.R., Viss J.R., Rutan B.J., Egan N.A., Sá-Guimarães P., Kim M.S., Kurath G., Gomes M.G.M., Lipsitch M. Vaccine effects on heterogeneity in susceptibility and implications for population health management. MBio. 2017;8 doi: 10.1128/mBio.00796-17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lau L.S., Samari G., Moresky R.T., Casey S.E., Kachur S.P., Roberts L.F., Zard M. COVID-19 in humanitarian settings and lessons learned from past epidemics. Nat. Med. 2020;26:647–648. doi: 10.1038/s41591-020-0863-y. [DOI] [PubMed] [Google Scholar]
- Leslie T.F., Delamater P.L., Yang Y.T. It could have been much worse: the Minnesota measles outbreak of 2017. Vaccine. 2018;36:1808–1810. doi: 10.1016/j.vaccine.2018.02.086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lewnard J.A., Liu V.X., Jackson M.L., Schmidt M.A., Jewell B.L., Flores J.P., Jentz C., Northrup G.R., Mahmud A., Reingold A.L., Petersen M., Jewell N.P., Young S., Bellows J. Incidence, clinical outcomes, and transmission dynamics of severe coronavirus disease 2019 in California and Washington: prospective cohort study. BMJ. 2020;369 doi: 10.1136/bmj.m1923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li J., Blakeley D., Smith R.J. The failure of . Comput. Math. Methods Med. 2011;2011 doi: 10.1155/2011/527610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Q., Guan X., Wu P., Wang X., Zhou L., Tong Y., Ren R., Leung K.S.M., Lau E.H.Y., Wong J.Y., Xing X., Xiang N., Wu Y., Li C., Chen Q., Li D., Liu T., Zhao J., Liu M., Tu W., Chen C., Jin L., Yang R., Wang Q., Zhou S., Wang R., Liu H., Luo Y., Liu Y., Shao G., Li H., Tao Z., Yang Y., Deng Z., Liu B., Ma Z., Zhang Y., Shi G., Lam T.T.Y., Wu J.T., Gao G.F., Cowling B.J., Yang B., Leung G.M., Feng Z. Early transmission dynamics in Wuhan, China, of novel coronavirus-infected pneumonia. N. Engl. J. Med. 2020;382:1199–1207. doi: 10.1056/NEJMoa2001316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li R., Pei S., Chen B., Song Y., Zhang T., Yang W., Shaman J. Substantial undocumented infection facilitates the rapid dissemination of novel coronavirus (SARS-CoV2) Science. 2020;493(80):489–493. doi: 10.1126/science.abb3221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liang M., Gao L., Cheng C., Zhou Q., Uy J.P., Heiner K., Sun C. Efficacy of face mask in preventing respiratory virus transmission: a systematic review and meta-analysis. J. Travel Med. 2020;36 doi: 10.1016/j.tmaid.2020.101751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lipsitch M., Cohen T., Cooper B., Robins J.M., Ma S., James L., Gopalakrishna G., Chew S.K., Tan C.C., Samore M.H., Fisman D., Murray M. Transmission dynamics and control of severe acute respiratory syndrome. Science. 2003;300(80):1966–1970. doi: 10.1126/science.1086616. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Ying, Gayle A.A., Wilder-Smith A., Rocklöv J. The reproductive number of COVID-19 is higher compared to SARS coronavirus. J. Travel Med. 2020;27 doi: 10.1093/jtm/taaa021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Yang, Yan L.M., Wan L., Xiang T.X., Le A., Liu J.M., Peiris M., Poon L.L.M., Zhang W. Viral dynamics in mild and severe cases of COVID-19. Lancet Infect. Dis. 2020;2019:656–657. doi: 10.1016/S1473-3099(20)30232-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lloyd-Smith J.O., Schreiber S.J., Kopp P.E., Getz W.M. Superspreading and the effect of individual variation on disease emergence. Nature. 2005;438:355–359. doi: 10.1038/nature04153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma J., Earn D.J.D. Generality of the final size formula for an epidemic of a newly invading infectious disease. Bull. Math. Biol. 2006;68:679–702. doi: 10.1007/s11538-005-9047-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Majumder M., Mandl K.D. Early transmissibility assessment of a novel coronavirus in Wuhan, China. SSRN. 2020 doi: 10.2139/ssrn.3524675. [DOI] [Google Scholar]
- May R.M., Anderson R.M. Transmission dynamics of HIV infection. Nature. 1987;326:137–142. doi: 10.1038/326137a0. [DOI] [PubMed] [Google Scholar]
- McMichael T.M., Currie D.W., Clark S., Pogosjans S., Kay M., Schwartz N.G., Lewis J., Baer A., Kawakami V., Lukoff M.D., Ferro J., Brostrom-Smith C., Rea T.D., Sayre M.R., Riedo F.X., Russell D., Hiatt B., Montgomery P., Rao A.K., Chow E.J., Tobolowsky F., Hughes M.J., Bardossy A.C., Oakley L.P., Jacobs J.R., Stone N.D., Reddy S.C., Jernigan J.A., Honein M.A., Clark T.A., Duchin J.S. Epidemiology of Covid-19 in a long-term care facility in King County, Washington. N. Engl. J. Med. 2020;382:2005–2011. doi: 10.1056/NEJMoa2005412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller A.C., Foti N.J., Lewnard J.A., Jewell N.P., Guestrin C., Fox E.B. Mobility trends provide a leading indicator of changes in SARS-CoV-2 transmission. medRxiv. 2020 doi: 10.1101/2020.05.07.20094441. [DOI] [Google Scholar]
- Mizumoto K., Chowell G. Transmission potential of the novel coronavirus (COVID-19) onboard the diamond Princess Cruises Ship 2020. Infect. Dis. Model. 2020;5:264–270. doi: 10.1016/j.idm.2020.02.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mizumoto K., Kagaya K., Chowell G. Early epidemiological assessment of the transmission potential and virulence of coronavirus disease 2019 (COVID-19) in Wuhan City, China, January–February 2020. BMC Med. 2020;18:217. doi: 10.1101/2020.02.12.20022434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pei S., Kandula S., Shaman J. Differential effects of intervention timing on COVID-19 spread in the United States. Science. 2020;6 doi: 10.1126/sciadv.abd6370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Peirlinck M., Linka K., Sahli Costabal F., Kuhl E. Outbreak dynamics of COVID-19 in China and the United States. Biomech. Model. Mechanobiol. 2020;19:2179–2193. doi: 10.1007/s10237-020-01332-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pitzer V.E., Chitwood M., Havumaki J., Menzies N.A., Perniciaro S., Warren J.L., Weinberger D.M., Cohen T. The impact of changes in diagnostic testing practices on estimates of COVID-19 transmission in the United States. medRxiv. 2020 doi: 10.1101/2020.04.20.20073338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pung R., Chiew C.J., Young B.E., Chin S., Chen M.I.-C., Clapham H.E., Cook A.R., Maurer-Stroh S., Toh M.P.H.S., Poh C., Low M., Lum J., Koh V.T.J., Mak T.M., Cui L., Lin R.V.T.P., Heng D., Leo Y.-S., Lye D.C., Lee V.J.M. Investigation of three clusters of COVID-19 in Singapore: implications for surveillance and response measures. Lancet. 2020;395:1039–1046. doi: 10.1016/S0140-6736(20)30528-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Randolph H.E., Barreiro L.B. Herd immunity: understanding COVID-19. Immunity. 2020;52:737–741. doi: 10.1016/j.immuni.2020.04.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ranjan R. Predictions for COVID-19 outbreak in India using epidemiological models. medRxiv. 2020 doi: 10.1101/2020.04.02.20051466. [DOI] [Google Scholar]
- Read J.M., Bridgen J.R.E., Cummings D.A.T., Ho A., Jewell C.P. Novel coronavirus 2019-nCoV: early estimation of epidemiological parameters and epidemic predictions. medRxiv. 2020 doi: 10.1101/2020.01.23.20018549. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Riou J., Althaus C.L. Pattern of early human-to-human transmission of Wuhan 2019 novel coronavirus (2019-nCoV), December 2019 to January 2020. Eurosurveillance. 2020;25 doi: 10.2807/1560-7917.ES.2020.25.4.2000058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roberts M.G. The pluses and minuses of . J. R. Soc. Interface. 2007;4:949–961. doi: 10.1098/rsif.2007.1031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenberg E., Tesoriero J., Rosenthal E., Chung R., Barranco M., Styer L., Parker M., Leung S.-Y.J., Morne J., Greene D., Holgrave D., Hoefer D., Kumar J., Udo T., Hutton B., Zucker H. Cumulative incidence and diagnosis of SARS-CoV-2 infection in New York. Ann. Epidem. 2020;48:23–29. doi: 10.1016/j.annepidem.2020.06.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruiz-Euler A., Privitera F., Giuffrida D., Lake B., Zara I. Mobility patterns and income distribution in times of crisis. SSRN. 2020 doi: 10.2139/ssrn.3572324. [DOI] [Google Scholar]
- Sanche S., Lin Y.T., Xu C., Romero-Severson E., Hengartner N.W., Ke R. High contagiousness and rapid spread of Severe Acute Respiratory Syndrome Coronavirus 2. Emerg. Infect. Diseases. 2020;26:1470–1477. doi: 10.3201/eid2607.200282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Santamaría L., Hortal J. COVID-19 effective reproduction number dropped during Spain’s nationwide dropdown, then spiked at lower-incidence regions. Sci. Total Environ. 2021;751 doi: 10.1016/j.scitotenv.2020.142257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Senapati A., Rana S., Das T., Chattopadhyay J. 2020. Impact of intervention on the spread of COVID-19 in India: a model based study.arXiv:2004.04950v1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shim E., Tariq A., Choi W., Lee Y., Chowell G. Transmission potential and severity of COVID-19 in South Korea. Int. J. Infect. Dis. 2020;93:339–344. doi: 10.1016/j.ijid.2020.03.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Singh R., Adhikari R. 2020. Age-structured impact of social distancing on the COVID-19 epidemic in India.arXiv:2003.12055 [Google Scholar]
- Sly K.T.L., White L.F., Nichols B. Population density and basic reproductive number of COVID-19 across United States counties. medRxiv. 2020 doi: 10.1101/2020.06.12.20130021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith R.J., Li J., Gordon R., Heffernan J.M. Can we spend our way out of the AIDS epidemic? A world halting AIDS model. BMC Publ. Health. 2009;9:S15. doi: 10.1186/1471-2458-9-S1-S15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stier A.J., Berman M.G., Bettencourt L.M.A. 2020. COVID-19 attack rate increases with city size.arXiv:2003.10376 [Google Scholar]
- Tang B., Wang X., Li Q., Bragazzi N.L., Tang S., Xiao Y., Wu J. Estimation of the transmission risk of the 2019-nCoV and its implication for public health interventions. J. Clin. Med. 2020;9(462) doi: 10.3390/jcm9020462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thompson R.N., Hollingsworth T.D., Isham V., Arribas-Bel D., Ashby B., Britton T., Challenor P., Chappell L.H.K., Clapham H., Cunniffe N.J., Dawid A.P., Donnelly C.A., Eggo R., Funk S., Gilbert N., Gog J.R., Glendinning P., Hart W.S., Heesterbeek H., House T., Keeling M., Kiss I.Z., Kretzschmar M., Lloyd A.L., McBryde E.S., McCaw J.M., Miller J.C., McKinley T.J., Morris M., O’Neill P.D., Pearson C.A.B., Parag K.V., Pellis L., Pulliam J.R.C., Ross J.V., Tildesley M.J., Toomba G.S., Silverman B.W., Struchiner C.J., Trapman P., Webb C.R., Mollison D., Restif O. Key questions for modelling COVID-19 exit strategies. Proc. R. Soc. B. 2020;287 doi: 10.1098/rspb.2020.1405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tian H., Liu Y., Li Y., Wu C.-H., Chen B., Kraemer M.U.G., Li B., Cai J., Xu B., Yang Q., Wang B., Yang P., Cui Y., Song Y., Zheng P., Wang Q., Bjornstad O.N., Yang R., Grenfell B.T., Pybus O.G., Dye C. An investigation of transmission control measures during the first 50 days of the COVID-19 epidemic in China. Science. 2020;642(80) doi: 10.1126/science.abb6105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tildesley M.J., Keeling M.J. Is a good predictor of final epidemic size: Foot-and-mouth disease in the UK. J. Theoret. Biol. 2009;258:623–629. doi: 10.1016/j.jtbi.2009.02.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tkachenko A.V., Maslov S., Elbanna A., Wong G.N., Weiner Z.J., Goldenfeld N. Persistent heterogeneity not short-term overdispersion determines herd immunity to COVID-19. medRxiv. 2020 doi: 10.1101/2020.07.26.20162420. [DOI] [Google Scholar]
- Viboud C., Simonsen L., Chowell G. A generalized-growth model to characterize the early ascending phase of infectious disease outbreaks. Epidemics. 2016;15:27–37. doi: 10.1016/j.epidem.2016.01.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Viceconte G., Petrosillo N. COVID-19 : Magic number or conundrum? Infect. Dis. Rep. 2020;12:8543. doi: 10.4081/idr.2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wallinga J., Lipsitch M. How generation intervals shape the relationship between growth rates and reproductive numbers. Proc. R. Soc. B Biol. Sci. 2007;274:599–604. doi: 10.1098/rspb.2006.3754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wallinga J., Teunis P. Different epidemic curves for severe acute respiratory syndrome reveal similar impacts of control measures. Am. J. Epidemiol. 2004;160:509–516. doi: 10.1093/aje/kwh255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Warren M.S., Skillman S.W. 2020. Mobility changes in response to COVID-19.arXiv:2003.14228 [Google Scholar]
- WHO M.S. 2020. Statement on the meeting of the international health regulations (2005) emergency committee regarding the outbreak of novel coronavirus (2019-nCoV) [www document] URL https://www.who.int/news-room/detail/23-01-2020-statement-on-the-meeting-of-the-international-health-regulations-(2005)-emergency-committee-regarding-the-outbreak-of-novel-coronavirus-(2019-ncov). (Accessed 6 December 20) [Google Scholar]
- Wu J.T., Leung K., Leung G.M. Nowcasting and forecasting the potential domestic and international spread of the 2019-nCoV outbreak originating in Wuhan, China: a modelling study. Lancet. 2020;395:689–697. doi: 10.1016/S0140-6736(20)30260-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xiao J., Hu J., He G., Liu T., Kang M., Rong Z., Lin L., Zhong H., Huang Q., Deng A., Zeng W., Tan X., Zeng S., Zhu Z., Li J., Gong D., Wan D., Chen S., Guo L., Li Y., Li Y., Sun L., Liang W., Song T., He J., Ma W. The time-varying transmission dynamics of COVID-19 and synchronous public health interventions in China. Int. J. Infect. Diseases. 2020 doi: 10.1016/j.ijid.2020.11.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang X., Yu Y., Xu J., Shu H., Xia J., Liu H., Wu Y., Zhang L., Yu Z., Fang M., Yu T., Wang Y., Pan S., Zou X., Yuan S., Shang Y. Clinical course and outcomes of critically ill patients with SARS-CoV-2 pneumonia in Wuhan, China: a single-centered, retrospective, observational study. Lancet Respir. Med. 2020;8:475–481. doi: 10.1016/S2213-2600(20)30079-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuan J., Li M., Lv G., Lu Z.K. Monitoring transmissibility and mortality of COVID-19 in Europe. Int. J. Infect. Dis. 2020;95:311–315. doi: 10.1016/j.ijid.2020.03.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao S., Lin Q., Ran J., Musa S.S., Yang G., Wang W., Lou Y., Gao D., Yang L., He D., Wang M.H. Preliminary estimation of the basic reproduction number of novel coronavirus (2019-nCoV) in China, from 2019 to 2020: a data-driven analysis in the early phase of the outbreak. Int. J. Infect. Dis. 2020;92:214–217. doi: 10.1016/j.ijid.2020.01.050. [DOI] [PMC free article] [PubMed] [Google Scholar]