Mixed-effects models for the design and analysis of stepped wedge cluster randomized trials: An overview

Abstract

The stepped wedge cluster randomized design has received increasing attention in pragmatic clinical trials and implementation science research. The key feature of the design is the unidirectional crossover of clusters from the control to intervention conditions on a staggered schedule, which induces confounding of the intervention effect by time. The stepped wedge design first appeared in the Gambia hepatitis study in the 1980s. However, the statistical model used for the design and analysis was not formally introduced until 2007 in an article by Hussey and Hughes. Since then, a variety of mixed-effects model extensions have been proposed for the design and analysis of these trials. In this article, we explore these extensions under a unified perspective. We provide a general model representation and regard various model extensions as alternative ways to characterize the secular trend, intervention effect, as well as sources of heterogeneity. We review the key model ingredients and clarify their implications for the design and analysis. The article serves as an entry point to the evolving statistical literatures on stepped wedge designs.

1 Introduction

Cluster-randomized trials (CRTs), also known as group-randomized trials, are frequently designed to evaluate the effect of an intervention administered at the cluster level, such as clinics, hospitals or geographical units.^1–4 Common reasons for randomizing at the cluster level include minimization of treatment contamination, administrative convenience, among others. The design and analysis of CRTs have been an active area of research over the past four decades and comprehensive reviews of recent methodological developments can be found in Turner et al.^5,6 and Murray et al.⁷ In parallel designs, usually half of the clusters are randomized to each arm. While parallel randomization ensures valid comparisons of post-treatment outcomes at the same point in time, concurrent implementation of the intervention may demand extensive administrative planning and logistical infrastructure.⁸

The stepped wedge CRT is an alternative design that allows for phased implementation of an intervention. In a stepped wedge CRT, clusters are randomized to intervention sequences that differ by the time points when the intervention starts to roll out.^9,10 An attractive feature of the stepped wedge CRT is that all clusters eventually receive the intervention, which can help facilitate recruitment when cluster stakeholders perceive the intervention to be beneficial.^11–13 Stepped wedge designs have also received increasing attention in recent pragmatic clinical trials (PCTs) embedded in health care delivery systems; see, for example, the Lumbar Imaging with Reporting of Epidemiology study (LIRE)¹⁴ and the Trauma Survivors Outcomes and Support study (TSOS)¹⁵ as two recent Demonstration Projects supported by the U.S. National Institutes of Health (NIH) Health Care Systems Research Collaboratory.¹⁶ Because of their unique features, stepped wedge CRTs usually require more complex statistical considerations compared to parallel CRTs. Mixed-effects regression is one of several approaches proposed for CRTs, and has been the most commonly used approach in analyzing stepped wedge CRTs. The objective of this article is to provide an overview of mixed-effects models developed for stepped wedge CRTs. In an effort to clarify their assumptions and implications, this article provides an entry point to the evolving statistical literatures on stepped wedge CRTs.

Several systematic reviews emphasized the conducting and reporting related to both the design and analysis of stepped wedge CRTs. For example, Martin et al.¹⁷ and Grayling et al.¹⁸ assessed the quality of reporting and design features of stepped wedge CRTs and found that many studies did not adhere to the guidelines recommended in the earlier CONSORT extension to CRTs.¹⁹ In particular, statistical methods for the sample size determination varied across studies, and insufficient details on modeling assumptions were provided. Variations in statistical models had been first observed in an earlier systematic review by Brown and Lilford,²⁰ even before the standard method was published in Hussey and Hughes.⁹ Davey et al.²¹ and Barker et al.²² surveyed the statistical methodology used for stepped wedge CRTs in practice and also noticed substantial variations in model specification, to which the sample size calculation and model-based inference could be sensitive. The various model specifications in practice motivated us to integrate the current toolkit of analytical models for stepped wedge designs.

Hemming et al.^23,24 recently introduced the CONSORT extension for the stepped wedge CRTs and encouraged clear reporting of analytical models specified for sample size calculation (item 7a) as well as for the primary and secondary analyses (items 12a and 12 b). In what follows, we consider the specification of the secular trend, the intervention, and sources of heterogeneity as three essential components of a model, and describe different formulations of each component. Our overview complements the CONSORT extension in clarifying the similarities and differences among models and in facilitating their proper application. The scope of this article differs from previous systematic reviews due to the fact that it is focusing on the statistical formulations and assumptions of the models used to describe the individual-level outcome trajectories. We took a top-down approach by providing a general model representation that separates the three essential components (i.e. secular trend, intervention effect, and sources of heterogeneity). We then cast a number of model variants as special cases of the general representation to explain their assumptions and implications for the design and analysis.

The rest of this article is organized as follows. Section 2 introduces the notation and the general model representation. Section 3 provides an overview of existing mixed-effects models and clarifies their assumptions and properties. Section 4 reviews the estimation and inference strategies in stepped wedge trials, and Section 5 concludes with a discussion.

2 A general model representation

2.1 Notation

Throughout the paper, we consider a stepped wedge CRT with I participating clusters followed over J ($J\ge 3$) time periods. We assume that individuals are included in each cluster and the outcome assessment is scheduled during each period at the individual level; in other words, we only consider complete designs,²⁵ and refer readers to Kasza and Forbes²⁶ and Kasza et al.²⁷ for methodological developments on incomplete designs. Based on the terminology of Murray and Hannan²⁸ and Feldman and Mckinlay,²⁹ we will distinguish between cross-sectional and closed-cohort stepped wedge designs. In a cross-sectional design, different individuals are observed in each cluster over time, whereas in a closed-cohort design, individuals are identified at the start of the trial and scheduled for repeated outcome assessment. In addition, Copas et al.³⁰ discussed a third option, the open-cohort design, which allows for attrition of members from and addition of new members to the original cohort in each cluster. We will describe the notation for each one of these three designs, and consistently use these notation when discussing model development.

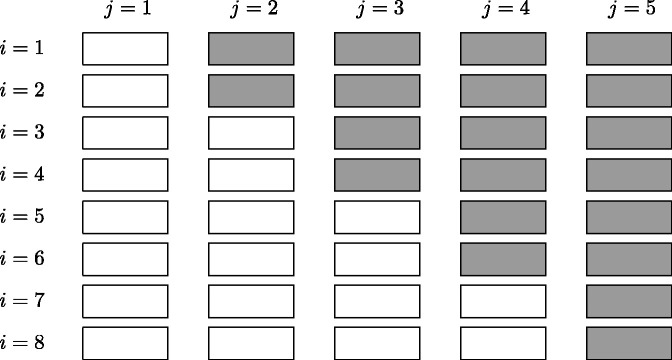
For the cross-sectional design, we assume N_ij individuals are included during period j ($j=1,\dots ,J$) in cluster i ($i=1,\dots ,I$); the cluster-period sizes may vary. For the closed-cohort design, we define N_i as the cohort size in cluster i as repeated measurements are taken from the same individuals. The open-cohort design can be considered as a mix of a cross-sectional design and a closed-cohort design, and we still assume N_ij individuals are included during period j in cluster i. However, in this case, there exists an overlapping number $\left(0\le n_i(j,l)\le \min \{N_{ij},N_{il}\}\right)$ of individuals for period j and period l in cluster i, depending on the degree of cohort openness. The notation of the open-cohort design generalizes that of the previous two designs, because the cross-sectional design is obtained as a special case with $n_i(j,l)=0$ for all j and l (maximum degree of openness) and the closed-cohort design is obtained with $n_i(j,l)=N_{ij}=N_{il}$ for all j and l (minimum degree of openness). Such notation becomes useful in Section 3.6. For all three types of designs, each cluster typically starts out in the control condition; clusters or sets of clusters are then randomized to intervention sequences and all clusters will be exposed to the intervention condition before the end of the trial. Figure 1 provides a schematic illustration of a design with I = 8 clusters and J = 5 periods. Notably, each one of the four distinct intervention sequences is fully determined by the time period during which the intervention is first implemented. We define the total number of distinct intervention sequences by S ($S\le J-1$), and there are in total S = 4 pre-planned sequences in Figure 1.

Figure 1.

A schematic illustration of a stepped wedge CRT with I = 8 clusters and J = 5 periods. Each white cell indicates a cluster-period under the control condition and each gray cell indicates a cluster-period under the intervention condition. There are in total S = 4 distinct intervention sequences.

2.2 Outcome model

The analysis of stepped wedge CRTs usually involves the characterization of a cluster-level, time-specific outcome trajectory. Here, we focus on the class of conditional models that require specification of fixed effects for the group-average structure and random effects for the heterogeneity. We will return to a brief discussion of marginal models in Section 5. The conditional models and marginal models have their own advantages and disadvantages, and our experience suggests there are more off-the-shelf software routines to fit conditional models with a complex random-effects structure. The review of Barker et al.²² also suggested that 61 out of 102 stepped wedge CRTs specified a linear or generalized linear mixed model for the primary analysis.

We define $Y_{ijk}(s)$ as the potential outcome of individual k during period j in cluster i, had cluster i received, possibly to contrary to fact, an intervention sequence s.³¹ We borrow the potential outcome framework of Rubin³² to clearly indicate the dependence of elements on intervention sequences. We index each distinct sequence by s, which is defined as the time interval when the intervention will be first introduced. Formally, $s\in \mathcal{S}\subseteq \{2,\dots ,J\}$, and the total number of sequences is the cardinality, $S=\text{card}(\mathcal{S})$. Define ${\mu }_{ijk}(s)$ as the expectation of $Y_{ijk}(s)$. We use a generalized linear mixed model to characterize the mean potential outcome as

$$g[{\mu }_{ijk}(s)]={\mathit{F}}_i(j,s)\prime \mathit{\theta }+{\mathit{R}}_{ik}(j,s)\prime {\mathit{\alpha }}_i$$ (1)

where g is a link function. Similar model representation has been previously introduced by Sitlani et al. in the context of longitudinal observational studies.³³

On the link function scale, ${\mathit{F}}_i(j,s)\prime \mathit{\theta }$ represents the group-average component and vector $\mathit{\theta }$ includes the parameter of interest (i.e. the intervention effect), while ${\mathit{R}}_{ik}(j,s)\prime {\mathit{\alpha }}_i$ represents the cluster-specific, time-specific, and/or individual-specific departure from the group average. By design, the assignment of intervention to clusters is monotone and confounded with time. Hence, it is common practice to separate ${\mathit{F}}_i(j,s)$ into a baseline component ${\mathit{F}}^0(j)$ characterizing the background secular trend in the absence of intervention, and a time-dependent intervention component $F_i^1(j,s)={\mathbb{I}}_{[j\ge s]}$. Then, the group-average component can be expressed as

$${\mathit{F}}_i(j,s)\prime \mathit{\theta }={\mathit{F}}^0(j)\prime \mathit{\beta }+F_i^1(j,s)\Delta (j,s)$$ (2)

where $\mathit{\beta }$ is the parameter encoding the secular trend without intervention, and $\Delta (j,s)$ is the change in the mean outcome at period j due to sequence s. To summarize, the ingredients for a potential mean outcome model are

$$g[{\mu }_{ijk}(s)]=︸\underset{\text{secular trend}}{{\mathit{F}}^0(j)\prime \mathit{\beta }}+︸\underset{\text{intervention effect}}{F_i^1(j,s)\Delta (j,s)}+︸\underset{\text{heterogeneity}}{{\mathit{R}}_{ik}(j,s)\prime {\mathit{\alpha }}_i}$$ (3)

With such a formulation, the potential outcome $Y_{ijk}(s)$ is then assumed to follow a parametric distribution with mean ${\mu }_{ijk}(s)$ and variance as a function of ${\mu }_{ijk}(s)$. For example, if the potential outcome is continuous and assumed normally distributed, we use an identity link for g and obtain the linear mixed model

$$Y_{ijk}(s)={\mathit{F}}^0(j)\prime \mathit{\beta }+F_i^1(j,s)\Delta (j,s)+{\mathit{R}}_{ik}(j,s)\prime {\mathit{\alpha }}_i+{\text{ϵ}}_{ijk}$$ (4)

where ϵ_ijk’s are independent and identically distributed as $N(0,{\sigma }_{\text{ϵ}}^2)$. Assume that there are no hidden variations of the intervention (i.e. the intervention is well defined), and we can link the observed outcome to the potential outcome by equating $Y_{ijk}=Y_{ijk}(s)$, if cluster i receives sequence s. This allow us to use the observed data to estimate all model parameters. As will be seen in Section 3, another typical assumption of models (3) and (4) is that the heterogeneity parameter ${\text{α}}_i$ is assumed independent across clusters and follows a common parametric distribution. This assumption implies that the potential outcomes are independent across clusters, and would not be affected by the intervention sequences received by other clusters.³¹ On the other hand, the heterogeneity parameter ${\text{α}}_i$ can induce correlation between potential outcomes of different individuals in the same cluster. Finally, because the majority of the literature on stepped wedge designs has focused on a continuous outcome, we will start with the identity link function and review existing models as special cases of the general representation (4).

3 Modeling considerations and implications

3.1 The Hussey and Hughes model

The standard analytical model for stepped wedge designs was proposed in the seminal paper by Hussey and Hughes.⁹ Assuming an identity link function g, the observed outcome Y_ijk is modeled as

$$Y_{ijk}=\mu +{\beta }_j+\delta X_{ij}+{\alpha }_i+{\text{ϵ}}_{ijk}$$ (5)

where μ is the grand mean, β_j is the jth period effect (with ${\beta }_1=0$ for identifiability), X_ij is a time-varying intervention indicator for cluster i during period j (X_ij = 1, if exposed to intervention; and X_ij = 0, otherwise), δ is the intervention effect, α_i is the random cluster effect assumed to follow $N(0,{\tau }_{\alpha }^2)$, and ${\text{ϵ}}_{ijk}\sim N(0,{\sigma }_{\text{ϵ}}^2)$ is the residual error independent of α_i.

The Hussey and Hughes model is a special case of model (4). We observe that the secular trend is assumed as

$${\mathit{F}}^0(j)\prime \mathit{\beta }=\mu +{\beta }_2{\mathbb{I}}_{[j=2]}+\cdots +{\beta }_J{\mathbb{I}}_{[j=J]}$$

where ${\mathbb{I}}_{[·]}$ is an indicator function. Because the average secular trend is assumed to be a distinct value during each period, this representation requires J parameters and is considered saturated. Further, the intervention effect, $\Delta (j,s)=\delta$, does not depend on the time interval during which the intervention was initiated. Finally, inherited from the models for analyzing parallel CRTs, the heterogeneity term, ${\mathit{R}}_{ik}(j,s)\prime {\mathit{\alpha }}_i={\alpha }_i$, captures the cluster-specific departure from the average but is assumed to be homogeneous across time periods, intervention sequences, and individuals.

The assumptions of the Hussey and Hughes model may be considered restrictive. For example, the intervention effect $\Delta (j,s)$ could be cumulative and explicitly depend on the time when the intervention was initiated, which is not captured by a constant intervention effect. In addition, the single cluster random effect postulates a simple exchangeable within-cluster correlation structure. In other words, the correlation between any pair of observations k, m in any two periods j, l and across all sequences s is assumed to be a nonnegative constant

$$\text{corr}[Y_{ijk}(s),Y_{ilm}(s)]=\rho ={\tau }_{\alpha }^2/({\tau }_{\alpha }^2+{\sigma }_{\text{ϵ}}^2)$$ (6)

where $\text{corr}[x,y]$ is a symmetric correlation operator. The value of ρ is referred to as the intraclass correlation coefficient (ICC).¹ Such a simple correlation structure also does not account for repeated measurements from the same individual, and so applies only to the cross-sectional setting.

The Hussey and Hughes model has been frequently used to estimate the required sample size for cross-sectional stepped wedge CRTs. Assuming equal cluster-period sizes $N_{ij}=N$ and known variance components, Hussey and Hughes derived the variance of the intervention effect estimator.⁹ Let ${\lambda }_1=1-\rho$ and ${\lambda }_2=1+(JN-1)\rho$, we can re-write the variance of the intervention effect estimator as

$$\text{var}(\widehat{\delta })=\frac{({\sigma }_{\text{tot}}^2/N)IJ{\lambda }_1{\lambda }_2}{(U^2+IJU-JW-IV){\lambda }_2-(U^2-IV){\lambda }_1}$$ (7)

where ${\sigma }_{\text{tot}}^2={\tau }_{\alpha }^2+{\sigma }_{\text{ϵ}}^2$ is the total variance, $U={\displaystyle {\sum }_{i=1}^I{\displaystyle {\sum }_{j=1}^J{X}_{ij}}},W={\displaystyle {\sum }_{j=1}^J{\left({\displaystyle {\sum }_{i=1}^I{X}_{ij}}\right)}^2}$ and $V={\displaystyle {\sum }_{i=1}^I{\left({\displaystyle {\sum }_{j=1}^J{X}_{ij}}\right)}^2}$ are design constants that depend on the assignment of intervention sequences to clusters. Using the results in Li et al.,³⁴ we can show that λ₁ and λ₂ are two distinct eigenvalues of the simple exchangeable correlation matrix. In fact, we will see in due course that expression (7) is a general form that applies to several other model variants, with slight changes in values for the total variance and the eigenvalues. The Hussey and Hughes variance formula is the basis for a number of subsequent methodological investigations. For instance, Woertman et al.³⁵ used the variance to derive a design effect, or variance inflation factor, relative to the individually randomized trial, under a balanced allocation of clusters to intervention sequences. The variance formula or design effect also motivated the study of optimal stepped wedge designs in the cross-sectional setting; see, for example, Lawrie et al.³⁶ and Thompson et al.³⁷ Girling and Hemming³⁸ considered optimal designs within a larger design space that includes hybrid designs (i.e. designs having both parallel and stepped wedge components), and found that the most efficient design was a hybrid design. Grayling et al.³⁹ proposed a group sequential design for stepped wedge CRTs. Rhoda et al.⁴⁰ and Hemming and Girling⁴¹ studied the relative efficiency between stepped wedge and parallel designs, and found that the relative efficiency depends on the number of periods J, cluster-period sizes N and the intraclass correlation coefficient ρ. The impact of variable cluster sizes, based on the Hussey and Hughes model, was studied in Kristunas et al. and Martin et al.^42,43 Even though the reduction in efficiency due to unequal cluster sizes can be dramatic in a given randomization scheme,⁴³ the average reduction in efficiency is generally smaller in a stepped wedge CRT compared to that in a parallel CRT. Harrison et al.⁴⁴ further developed an optimization algorithm for power calculation that accounts for unequal cluster sizes.

Taljaard et al.⁴⁵ and Bond⁴⁶ pointed out a possible limitation of the Hussey and Hughes model from a variance perspective. Specifically, one can show that the variance of the intervention effect estimator, $\text{var}(\widehat{\delta })$, converges to zero if the cluster-period sizes $N\to \infty$. This implies that the required number of clusters for an anticipated power converges to unity as N increases indefinitely, which may not be realistic. Nevertheless, both Barker et al.²² and Martin et al.¹⁷ found in their systematic reviews that the Hussey and Hughes model was the most widely used approach for designing and analyzing stepped wedge CRTs.

In what follows, we will review extensions of the Hussey and Hughes model, with an emphasis on alternative considerations on modeling ${\mathit{F}}^0(j)\prime \mathit{\beta },\Delta (j,s)$ and ${\mathit{R}}_{ik}(j,s)\prime {\mathit{\alpha }}_i$. The considerations for modeling the group-average component (i.e. secular trend and intervention effect) are typically the same between cross-sectional, closed-cohort and open-cohort designs; therefore, we will not consider them separately. However, the considerations for modeling heterogeneity can differ between designs, and will be separately discussed in Sections 3.4, 3.5 and 3.6.

3.2 Considerations for modeling the secular trend

Because the intervention is confounded with time, modeling the background secular trend is necessary to remove the bias in estimating the effect attributed solely to the intervention.^9,47 Recall that ${\mathit{F}}^0(j)\prime \mathit{\beta }$ models the group-average secular trend in the absence of intervention across J time periods, and one may generally write

$${\mathit{F}}^0(j)\prime \mathit{\beta }={\beta }_1{B}_1(j)+···+{\beta }_p{B}_p(j)$$ (8)

where ${\mathit{F}}^0(j)=(B_1(j),\dots ,B_p(j))\prime$ is a p-dimensional basis function, and p is generally no larger than J for identifiability. Different choices of the basis function results in different formulations of the average secular trend. For instance, the Hussey and Hughes model assumes a saturated J-dimensional basis function with

$${\mathit{F}}^0(j)=(1,{\mathbb{I}}_{[j=2]}\dots ,{\mathbb{I}}_{[j=J]})\prime$$

while Hemming et al.⁴⁷ explored a linear trend specification such that p = 2 and ${\mathit{F}}^0(j)=(1,j)\prime$. In principle, as long as $p\le J$ is required for identifiability, one could expand on the linear trend specification by including higher-order polynomial terms or their orthogonal counterparts.⁴⁸ In a recent simulation study, Nickless et al.⁴⁹ examined the quadratic specification with ${\mathit{F}}^0(j)=(1,j,j^2)\prime$ and found that such models performed generally well in terms of bias when the approximation to the true secular trend was adequate, even if the data were generated from complex nonlinear time effects.

From a bias perspective, it is natural to consider a nonparametric representation of ${\mathit{F}}^0(j)\prime \mathit{\beta }$, which would favor the saturated specification as in the Hussey and Hughes model. For example, when the true secular trend is nonlinear, the saturated specification could adequately control for the time effect, while the linear trend specification may lead to a biased intervention effect estimate. While the saturated time parameterization is adequate for trials with a limited number of discrete periods (J = 5) such as in the Washington State EPT Study,⁵⁰ it may not be the most efficient if there are a large number of periods relative to the number of clusters, due to the reduced degree of freedom available for estimating the intervention effect. For example, Hemming et al.⁴⁷ analyzed a stepped wedge CRT of 10 midwifery teams (with each team forming a cluster) to evaluate the effectiveness of a training package to promote sweeping membranes in post-term women in the UK. The trial collected outcomes from each team during each of the 40 weeks of the study, and would have required 39 categorical time parameters if the Hussey and Hughes model had been considered. In general, including many fixed-effects parameters with a limited number of clusters may decrease the precision of the intervention effect, so that it becomes much less likely to locate a true effect signal.^47,51 In this particular case, it seems attractive to look at a parsimonious specification of ${\mathit{F}}^0(j)\prime \mathit{\beta }$, such as the linear trend or a polynomial specification to a fixed degree.

Grantham et al.⁵² provided an interesting result on time parameterization in stepped wedge CRTs from a variance perspective. In the planning stage, sample size and power calculation critically depend on the variance of the intervention effect, $\text{var}(\widehat{\delta })$. In the linear mixed model setting with equal cluster-period sizes $N_{ij}=N$, Grantham et al.⁵² showed that $\text{var}(\widehat{\delta })$ was invariant to time parameterization as long as the sum of the intervention sequences across clusters

$$\left({\displaystyle \sum _{i=1}^I{X}_{i1}},\dots ,{\displaystyle \sum _{i=1}^I{X}_{iJ}}\right)\prime$$

lay in the column space of ${\mathit{F}}^0$, where ${\mathit{F}}^0=({\mathit{F}}^0(1),\dots ,{\mathit{F}}^0(J))\prime$ is the design matrix for the secular trend. An implication from this result is that, if there is a balanced allocation of clusters to each sequence ranging from $(0,\dots ,0,1)\prime$ to $(0,1,\dots ,1)\prime$, the saturated time specification in the Hussey and Hughes model and the linear trend specification yield the same expression for $\text{var}(\widehat{\delta })$. Further, $\text{var}(\widehat{\delta })$ does not change with polynomial specifications as long as the linear time term is included. This invariance property suggests that, with the same trial configuration, the sample size estimates become identical irrespective of the above two time parameterizations.⁵² However, it is important to realize that such variance comparisons assume known variance components, and are relevant only for design purposes. In the analysis stage, under-specification of the secular trend could result in bias relative to the true intervention effect, and thus variance appears to be a secondary consideration.⁴⁹

For sample size and power calculation, Heo et al.⁵³ used a linear mixed model that forwent any secular trend, namely assuming ${\mathit{F}}^0(j)\prime \text{β}=0$. While Zhou et al.⁵⁴ argued that ignoring the secular trend might be reasonable in trials with a very short duration, a number of authors^9,47 have cautioned against the general application of models without a secular trend due to the potential of bias. In fact, one can show analytically that, holding all other conditions equal, the variance of the intervention effect estimator, $\text{var}(\widehat{\delta })$, becomes strictly smaller when the secular trend is omitted.⁵⁴ This implies that the required sample size could be underestimated when it is incorrectly assumed that there is no time effect.

3.3 Considerations for modeling the intervention effect

In the general model formulation (4), the intervention effect, $\Delta (j,s)$, depends on both period index j and sequence index s, which suggests the possibility for going beyond a constant treatment effect. Formal extensions on modeling a time-varying intervention effect appeared in Hussey and Hughes⁹ and Hughes et al.⁵⁵ From Hughes et al.,⁵⁵ a saturated but stationary intervention effect representation is given by the general time-on-treatment effect, where

$$\Delta (j,s)={\delta }_{j-s}={\delta }_0{\mathbb{I}}_{[j=s]}+{\delta }_1{\mathbb{I}}_{[j=s+1]}+\cdots +{\delta }_{J-s}{\mathbb{I}}_{[j=J]}$$ (9)

We call this representation stationary because $\Delta (j,s)$ is not a saturated function of (j, s) but a saturated function of j – s for $j\ge s$. The general time-on-treatment effect allows the group-average intervention effect to be different depending on the elapsed number of time intervals since the intervention was first introduced. For example, the model assumes that the intervention effect at time $j\ge s$ is ${\delta }_{j-s}$, if the intervention is introduced at time s. In this case, the global test for H₀: ${\delta }_0={\delta }_1=···={\delta }_{J-2}=0$ is used to assess the overall intervention effect. Nickless et al.⁴⁹ reported that a linear mixed model with the time-on-treatment effect assumption had minimum bias and carried close-to-nominal coverage in estimating the average intervention effect under a wide range of scenarios. Further, because the constant intervention effect representation is nested within equation (9), a global test for H₀: ${\delta }_0={\delta }_1=···={\delta }_{J-2}$ provides a mechanism to assess the plausibility of constant intervention effect assumption.

The general time-on-treatment model requires J – 2 parameters for the intervention effect (as compared to only 1 parameter in the Hussey and Hughes model (5)), and could be challenging to estimate in trials with a limited number of clusters. Parsimonious versions of the time-on-treatment effect model have been suggested. Assuming that the periods are equally spaced, Hughes et al.⁵⁵ introduced the linear time-on-treatment effect representation, where

$$\Delta (j,s)={\delta }_0+{\delta }_1(j-s)$$ (10)

or more simply, $\Delta (j,s)=\delta (j-s+1)$, which was assumed as a linear function of the elapsed number of periods since the intervention was first introduced. Such parameterizations are especially useful when the intervention takes more than a single time period to fully develop, or when there is a strengthening or weakening of intervention effect over time. Alternatively, representation (10) can be considered as a constant treatment effect plus a treatment-by-linear-time interaction.

In the presence of a delayed treatment effect, one could also incorporate prior knowledge to such delay and model

$$\Delta (j,s)=\delta {\pi }_0{\mathbb{I}}_{[j=s]}+\delta {\mathbb{I}}_{[j>s]}$$ (11)

where ${\pi }_0\in [0,1]$ is a constant value representing how effective the intervention will be during the time interval when it is just introduced.⁵⁵ For example, if the intervention is known to be 50% effective when it is first introduced and 100% effective afterwards, we can set ${\pi }_0=1/2$. Had one known from prior knowledge that the intervention will be $100{\pi }_{j-s}$ percent effective when it has been introduced j – s periods (with ${\pi }_{j-s}=0$ if j < s), the general delayed treatment effect representation can be formalized as

$$\Delta (j,s)=\delta {\pi }_0{\mathbb{I}}_{[j=s]}+\delta {\pi }_1{\mathbb{I}}_{[j=s+1]}+\cdots +\delta {\pi }_{J-s}{\mathbb{I}}_{[j=J]}$$ (12)

Clearly, when prior knowledge suggests an arithmetic increase in effectiveness such that ${\pi }_1-{\pi }_2={\pi }_2-{\pi }_3=\dots ={\pi }_{J-s-1}-{\pi }_{J-s}$, representation (12) is an equivalent parameterization to equation (10).

Finally, Hughes et al.⁵⁵ provided an example of a nonlinear model for the time-on-treatment effect, where the intervention effect is considered to increase nonlinearly over time until it reaches the maximum long-term effect. In that model, the time indicator j indexes the exponential rate of increase, and so the model is no longer nested within equation (9). To facilitate the understanding of various intervention effect assumptions, we provide schematic illustrations of four typical examples in Figure 2 .

Figure 2.

Schematic illustrations of four intervention effect representations in a stepped wedge design with I = 4 clusters and J = 5 periods. Each cell with a zero entry indicates a control cluster-period and each cell with a non-zero entry indicates an intervention cluster-period.

3.4 Considerations for modeling heterogeneity in cross-sectional designs

There have been extensive discussions of alternative strategies for modeling the random-effects structure in stepped wedge trials, especially for those involving cross-sectional designs. Because such discussion has been centered on extensions to the Hussey and Hughes model, they have almost exclusively adopted the constant intervention effect and the categorical time parameterization. We conjecture that assuming no treatment-by-time interaction in the analytical model has gained popularity since trial planning and sample size estimation are more convenient once a scalar target parameter is assumed. To focus on ideas and stay consistent with the current literature, we will review variants of random-effects structures by assuming a linear link, categorical secular trend (except for the random coefficient model which uses a linear trend specification) as well as a time-invariant intervention effect. To provide a quick reference, we also list selected model variants in Table 1 .

Table 1.

Example extensions to the Hussey and Hughes model for stepped wedge cluster randomized trials in cross-sectional and closed-cohort designs; all models assume a continuous outcome and an identity link function.

Design	Extension	Feature	Example references
Cross-sectional	Nested Exchangeable$*$	Distinguish between within-period and between-period ICCs	Hooper et al.;56 Girling and Hemming38
	Exponential Decay$*$	Allow the between-period ICC to decay at an exponential rate over time	Kasza et al.57 Kasza and Forbes61
	Random Intervention	Include random cluster-specific intervention effects, and ICC depends on intervention status	Hughes et al.55 Hemming et al.47
	Random Coefficient	Include random cluster-specific time slopes; ICC tends to be an increasing function of distance in time	Murray et al.58
Closed-cohort	Basic	Include cluster-level and subject-level random effects to separate between-individual ICC and within-individual ICC	Baio et al.65
	Block Exchangeable$*$	Include three random effects to distinguish between within-period ICC, between-period ICC, and within-individual ICC	Hooper et al.56 Girling and Hemming38
	Proportional Decay$*$	Allow the between-period ICC and within-individual ICC to decay over time at the same exponential rate	Li60
	Random Intervention	Include random cluster-specific intervention effects, and ICC depends on intervention status	Kasza et al.27

Note: The choice of terminology with the ‘*’ symbol is based on the following. The nested exchangeable correlation model was defined in Teerenstra et al.⁵⁹ and Li et al.⁶⁰ in the context of three-level CRTs and crossover CRTs. Li et al.³⁴ introduced the block exchangeable correlation model for closed-cohort design and pointed out the nested exchangeable correlation model is a special case. The exponential decay correlation model is proposed in Kasza et al. and Kasza and Forbes.^57,61 The proportional decay correlation model is introduced in Li⁶⁰ and dates back to the earlier work of Liu et al.⁷² in the context of longitudinal parallel CRTs.

3.4.1 Nested exchangeable correlation model

The first notable extension to the Hussey and Hughes model was found in Hooper et al.⁵⁶ and Girling and Hemming.³⁸ This model has also been referred to as the Hooper/Girling model,⁵⁷ and is written as

$$Y_{ijk}=\mu +{\beta }_j+\delta X_{ij}+{\alpha }_i+{\gamma }_{ij}+{\text{ϵ}}_{ijk}$$ (13)

Compared to the Hussey and Hughes model, there is an additional term, ${\gamma }_{ij}\sim N(0,{\tau }_{\gamma }^2)$, representing the random cluster-by-time interaction. This additional random effect is assumed independent of the random cluster effect α_i. As a special case of the general model representation, the nested exchangeable correlation model specifies the heterogeneity term as

$${\mathit{R}}_{ik}(j,s)\prime {\mathit{\alpha }}_i={\alpha }_i+{\gamma }_{ij}$$ (14)

and therefore allows the deviation from the group average to be both cluster-specific and period-specific. Notice that similar ideas on random cluster-by-time interaction date back to the earlier work of Murray et al.⁵⁸ for parallel CRTs with repeated measurements. Hemming et al.⁴⁷ pointed out that it might be convenient to consider γ_ij as a latent factor arising from the unmeasured time-varying characteristics within a cluster.

The nested exchangeable correlation model distinguishes between two different types of correlation parameters: the within-period ICC and the between-period ICC. Specifically

$$\text{corr}[Y_{ijk}(s),Y_{ilm}(s)]=\left\{\begin{array}{ll}{\rho }_{\text{w}}=({\tau }_{\alpha }^2+{\tau }_{\gamma }^2)/({\tau }_{\alpha }^2+{\tau }_{\gamma }^2+{\sigma }_{\text{ϵ}}^2),& j=l\\ {\rho }_{\text{b}}={\tau }_{\alpha }^2/({\tau }_{\alpha }^2+{\tau }_{\gamma }^2+{\sigma }_{\text{ϵ}}^2), & j\ne l\end{array}\right.$$

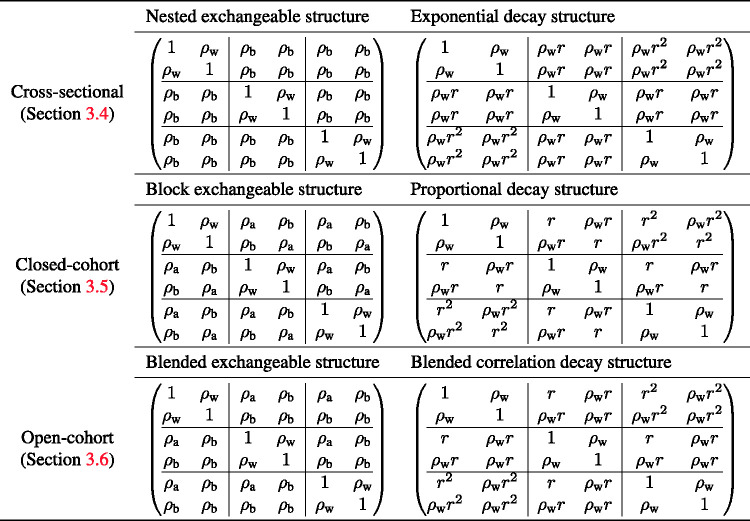
where the within-period ICC, ${\rho }_{\text{w}}$, describes the correlation between two within-cluster observations collected during the same period, and the between-period ICC, ${\rho }_{\text{b}}$, describes the correlation between two within-cluster observations collected in different periods. Since the variance components are positive, the between-period ICC is constrained to be no larger than the within-period ICC. Such a nested exchangeable correlation model has also been previously studied in three-level and crossover CRTs.^59,60 An example matrix form of the nested exchangeable correlation structure is provided in Table 2 .

Table 2.

Illustration of the non-decaying (exchangeable) and decaying within-cluster correlation structure implied by the random-effects model in cross-sectional, closed-cohort, and open-cohort designs.

Note: In each correlation matrix, each block represents the correlation structure in a given cluster-period or between two cluster-periods, and the total number of periods is T = 3. The cluster-period sizes are assumed to be equal (N_ij = 2). In the open-cohort design, we assume only one individual is followed through all periods, and a new individual will be supplemented in each period. Each correlation matrix is defined for the vector of observations collected across all periods in the same cluster.

On the other hand, Hooper et al.⁵⁶ characterized the nested exchangeable correlation structure based on ${\rho }_{\text{w}}$ and the cluster autocorrelation (CAC), which was defined as

$$\text{CAC}={\tau }_{\alpha }^2/({\tau }_{\alpha }^2+{\tau }_{\gamma }^2)={\rho }_{\text{b}}/{\rho }_{\text{w}}$$ (15)

Different from the individual-level correlation ${\rho }_{\text{b}}$, the CAC has been interpreted as the correlation between two population means from the same cluster at different times (also see Feldman and Mckinlay²⁹ for this interpretation). Here we clarify that CAC should actually be interpreted as the limit of the correlation between two cluster-period means. Specifically, if we define the cluster-period mean as ${\overline{Y}}_{ij+}=N_{ij}^{-1}{\displaystyle {\sum }_{k=1}^{N_{ij}}{Y}_{ijk}}$, then the variance, covariance and correlation of cluster-period means can be calculated as

$$\begin{array}{l}\text{var}({\overline{Y}}_{ij+})={\sigma }_{\text{tot}}^2\left\{\frac{1+(N_{ij}-1){\rho }_{\text{w}}}{N_{ij}}\right\},\text{cov}({\overline{Y}}_{ij+},{\overline{Y}}_{il+})={\sigma }_{\text{tot}}^2{\rho }_{\text{b}}\\ \text{corr}({\overline{Y}}_{ij+},{\overline{Y}}_{il+})=\frac{\text{cov}({\overline{Y}}_{ij+},{\overline{Y}}_{il+})}{\sqrt{\text{var}({\overline{Y}}_{ij+})}\sqrt{\text{var}({\overline{Y}}_{il+})}}\\ =\frac{N_{ij}{\rho }_{\text{b}}}{1+(N_{ij}-1){\rho }_{\text{w}}}\to \text{CAC},\text{as} N_{ij}\to \infty \end{array}$$

and CAC is the limit of correlation between ${\overline{Y}}_{ij+}$ and ${\overline{Y}}_{il+}$ when the cluster-period size N_ij increases indefinitely. Girling and Hemming³⁸ also defined the cluster mean correlation (CMC) as the proportion of the variance of a cluster mean ${\overline{Y}}_{i++}={\displaystyle {\sum }_{j=1}^J{\displaystyle {\sum }_{k=1}^{N_{ij}}{Y}_{ijk}}}$ that came from random effects that were independent of time. Assuming equal cluster-period sizes $N_{ij}=N$, the CMC is the proportion of variability of ${\overline{Y}}_{i++}$ explained by α_i, and can actually be rewritten as

$$\begin{array}{l}\text{CMC}=\frac{NJ{\rho }_{\text{b}}}{1+(N-1){\rho }_{\text{w}}+N(J-1){\rho }_{\text{b}}}\\ =\frac{NJ\times \text{CAC}}{1/{\rho }_{\text{w}}+(N-1)+N(J-1)\text{CAC}}\end{array}$$ (16)

which is a function of CAC, within-period ICC, number of periods and the cluster-period size. In what follows, we will use the individual-level ICCs to characterize different correlation structures, but the CAC and CMC are two alternative parameterizations.

Hooper et al.⁵⁶ and Girling and Hemming³⁸ provided a closed-form expression for the variance of the intervention effect based on model (13). Assuming equal cluster-period sizes $N_{ij}=N$, one can use the results in Li et al.³⁴ to show that the form of the variance formula is identical to equation (7), except that we replace

$$\begin{array}{l}{\sigma }_{\text{tot}}^2={\tau }_{\alpha }^2+{\tau }_{\gamma }^2+{\sigma }_{\text{ϵ}}^2\\ {\lambda }_1=1+(N-1){\rho }_{\text{w}}-N{\rho }_{\text{b}}\\ {\lambda }_2=1+(N-1){\rho }_{\text{w}}+N(J-1){\rho }_{\text{b}}\end{array}$$

In particular, the two parameters, λ₁ and λ₂, have been shown to be two distinct eigenvalues of the nested exchangeable correlation matrix.³⁴ Interestingly, the cluster mean correlation (16) also depends only on the two eigenvalues as we can show $\text{CMC}=1-{\lambda }_1/{\lambda }_2$. Further, unlike the Hussey and Hughes model, the nested exchangeable correlation model is considered to be more realistic for cross-sectional studies since the limit of the variance

$$\underset{N\to \infty }{\lim }\text{var}(\widehat{\delta })=\frac{{\sigma }_{\text{tot}}^{2}I({\rho }_{\text{w}}-{\rho }_{\text{b}})\{{\rho }_{\text{w}}+(J-1){\rho }_{\text{b}}\}}{(IU-W)\{{\rho }_{\text{w}}+(J-1){\rho }_{\text{b}}\}+(U^2-IV){\rho }_{\text{b}}}>0$$ (17)

is a positive quantity as long as ${\rho }_{\text{w}}\ne {\rho }_{\text{b}}$.

3.4.2 Exponential decay model

Kasza et al.⁵⁷ extended the nested exchangeable correlation model (13) by allowing the between-period correlation to decay exponentially over time. The model is written as

$$Y_{ijk}=\mu +{\beta }_j+\delta X_{ij}+{\gamma }_{ij}+{\text{ϵ}}_{ijk}$$ (18)

where the heterogeneity term is

$${\text{R}}_{ik}(j,s)\prime {\mathit{\alpha }}_i={\gamma }_{ij}$$

The collection of random effects in cluster i is assumed to follow ${\mathit{\gamma }}_i=({\gamma }_{i1},\dots ,{\gamma }_{iJ})\prime \sim N(0,{\tau }_{\gamma }^2\tilde{\mathbf{M}})$, and $\tilde{\mathbf{M}}$ had a symmetric Toeplitz structure

$$\tilde{\mathbf{M}}=\left(\begin{array}{ccccc}1& r_{12}& r_{13}& \dots & r_{1J}\\ r_{21}& 1& r_{23}& \dots & r_{2J}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ r_{J1}& r_{J2}& r_{J3}& \dots & 1\end{array}\right)$$ (19)

where r_jl = r_lj for all l and j.

Clearly, an unrestricted Toeplitz correlation structure could include up to $J(J-1)/2$ unknown parameters, which may not be easy to interpret from a design perspective. Therefore, Kasza et al.⁵⁷ focused on the following autoregressive structure for trial planning. Specifically, the structure matrix $\tilde{\mathbf{M}}$ could include two parameters r₀ and r and is written as

$$\tilde{\mathbf{M}}=\mathbf{M}(r_0,r)=\left(\begin{array}{ccccc}1& r_{0}r& r_0{r}^2& \dots & r_0{r}^{J-1}\\ r_{0}r& 1& r_{0}r& \dots & r_0{r}^{J-2}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ r_0{r}^{J-1}& r_0{r}^{J-2}& r_0{r}^{J-3}& \dots & 1\end{array}\right)$$ (20)

The Hussey and Hughes model and the nested exchangeable correlation model are returned by $\mathbf{M}(1,1)$ and $\mathbf{M}(r_0,1)$, while the exponential decay model of Kasza et al.⁵⁷ is returned by $\mathbf{M}(1,r)$. Although the Hussey and Hughes model is a special case of the nested exchangeable correlation model, it is important to realize that the exponential decay and nested exchangeable correlation models do not have a clear nesting relationship. The exponential decay model implies the following correlation structure

$$\text{corr}[Y_{ijk}(s),Y_{ilm}(s)]=\left\{\begin{array}{ll}{\rho }_{\text{w}}={\tau }_{\gamma }^2/({\tau }_{\gamma }^2+{\sigma }_{\text{ϵ}}^2),& j=l\\ {\rho }_{\text{b},|j-l|}={\tau }_{\gamma }^2{r}^{|j-l|}/({\tau }_{\gamma }^2+{\sigma }_{\text{ϵ}}^2),& j\ne l\end{array}\right.$$

An example matrix form the exponential decay correlation structure is provided in Table 2.

For sample size estimation, the variance of $\widehat{\delta }$ may not be obtained analytically with the exponential decay model, but could be computed numerically following the general variance formula of Kasza et al.⁵⁷ Kasza et al.⁵⁷ compared $\text{var}(\widehat{\delta })$ using the nested exchangeable correlation model and the exponential decay model, and concluded that $\text{var}(\widehat{\delta })$ was sensitive to the random-effects assumptions. Specifically, when the exponential decay model is the true model, the variance could either be overestimated or underestimated if the nested exchangeable correlation model is incorrectly assumed, and vice versa. Therefore, Kasza et al.⁵⁷ recommended examination of the plausibility of alternative correlation structures based on preliminary data, whenever possible. From a data analytic perspective, Kasza and Forbes⁶¹ further considered the misspecification of the random-effects structure on the estimation of the treatment effect and variance components. They found that incorrectly omitting the decay parameter r (namely assuming the Hussey and Hughes model or the nested exchangeable correlation model when the true model induces an exponential correlation decay) might lead to an inflated type I error rate and invalid inference.

The exponential decay model (18) assumes that the correlation decay is a function of the distance between time periods, which is considered appropriate if all individuals in the same period are measured at approximately the same time. For this reason, this model is also more explicitly referred to as the discrete-time exponential decay model. Grantham et al.⁶² extended the discrete-time exponential decay model to accommodate continuous enrollment, and allowed for the correlation decay to depend on the distance between the actual measurement times of each individual. They concluded that incorrectly assuming the Hussey and Hughes model in the presence of continuous-time correlation decay would likely underestimate the required sample size in the design stage. We are not aware of any existing numerical studies that examine the implications for the statistical analysis due to continuous correlation decay. In fact, Hooper and Copas indicated that the current literature on stepped wedge designs had not differentiated between continuous enrollment and discrete individual sampling, and therefore new statistical models and methods would be required to address the challenges associated with continuous enrollment.⁶³

3.4.3 Random intervention model

Several authors have suggested extensions to the Hussey and Hughes model and accounted for potential variation across clusters in the magnitude of intervention effects.^47,55,64 For example, Hemming et al.^47,64 considered a model parameterized as

$$Y_{ijk}=\mu +{\beta }_j+\delta X_{ij}+{\alpha }_{1i}{X}_{ij}+{\alpha }_{0i}(1-X_{ij})+{\text{ϵ}}_{ijk}$$ (21)

where

$$\left(\begin{array}{c}{\alpha }_{1i}\\ {\alpha }_{0i}\end{array}\right)\sim N\left[\left(\begin{array}{c}0\\ 0\end{array}\right),\left(\begin{array}{cc}{\tau }_1^2& {\sigma }_{10}\\ {\sigma }_{10}& {\tau }_0^2\end{array}\right)\right]$$

and σ₁₀ is the possibly non-zero covariance between random effects ${\alpha }_{1i}$ and α₀₁. Within our general model representation (4), this model assumes the heterogeneity term to be

$${\mathit{R}}_{ik}(j,s)\prime {\mathit{\alpha }}_i={\alpha }_{1i}{\mathbb{I}}_{[j\ge s]}+{\alpha }_{0i}{\mathbb{I}}_{[j<s]}$$

and now depends on the intervention sequence assigned for cluster i. The heterogeneity term can also be considered as an interaction between the random cluster effect and treatment assignment. An implication of this interaction term is that the intervention not only affects the group average through $F_i^1(j,s)\prime \Delta (j,s)=\delta X_{ij}$, but also affects the marginal dispersion through the variance components. Hemming et al.⁶⁴ showed that the following within-cluster correlation structure holds

$$\text{corr}[Y_{ijk}(s),Y_{ilm}(s)]\left\{\begin{array}{ll}{\rho }_0={\tau }_0^2/({\tau }_0^2+{\sigma }_{\text{ϵ}}^2),& j<s,l<s\\ {\rho }_1={\tau }_1^2/({\tau }_1^2+{\sigma }_{\text{ϵ}}^2),& j\ge s,l\ge s\\ {\rho }_{10}={\sigma }_{10}/\left\{\sqrt{{\tau }_0^2+{\sigma }_{\text{ϵ}}^2}\sqrt{{\tau }_1^2+{\sigma }_{\text{ϵ}}^2}\right\},& j\ge s,l<s, \text{or} j<s,l\ge s\end{array}\right.$$

where ρ₀ is the correlation for two observations collected under the control condition, ρ₁ is the correlation for two observations collected under the intervention condition, and ρ₁₀ is the correlation for two observations collected under different conditions (one under control and the other under intervention condition). The random intervention model does not permit a closed-form derivation of the variance, $\text{var}(\widehat{\delta })$, and therefore sample size estimates must proceed by numerical calculations. To date, only simulation-based approaches have been examined to estimate sample size from the random intervention model.⁶⁵

An alternative parameterization of (21) is to directly include a random cluster-by-treatment interaction in the Hussey and Hughes model.⁵⁵ The model can be written as

$$Y_{ijk}=\mu +{\beta }_j+(\delta +{\nu }_i)X_{ij}+{\alpha }_i+{\text{ϵ}}_{ijk}$$ (22)

where

$$\left(\begin{array}{c}{\alpha }_i\\ {\nu }_i\end{array}\right)\sim N\left[\left(\begin{array}{c}0\\ 0\end{array}\right),\left(\begin{array}{cc}{\tau }_{\alpha }^2& {\sigma }_{\alpha \nu }\\ {\sigma }_{\alpha \nu }& {\tau }_{\nu }^2\end{array}\right)\right]$$

and ${\sigma }_{\alpha \nu }$ is a possibly non-zero covariance between α_i and ν_i. This model assumes the heterogeneity term

$${\mathit{R}}_{ik}(j,s)\prime {\mathit{\alpha }}_i={\alpha }_i+{\nu }_i{\mathbb{I}}_{[j\ge s]}$$

Hemming et al.⁶⁴ discussed alternative parameterizations that allowed for treatment effect heterogeneity, and recommended the use of equations (21) and (22) because other parameterizations induced unnecessary and sometimes implausible assumptions on the correlation structure. Baio et al.⁶⁵ pointed out that term $(\delta +{\nu }_i)$ in model (22) could be interpreted as a cluster-varying random slope for the intervention effect.

3.4.4 Random coefficient model

Another modeling technique, proposed for analyzing parallel longitudinal CRTs, is the random coefficient model.⁵⁸ Although such a model has not yet been formally investigated in the context of stepped wedge designs, there has been recent interest in exploring their operating characteristics (Section 4 of Kasza and Forbes⁶¹ mentioned such models), and we briefly discuss the model assumptions here. The random coefficient model usually specifies a linear secular trend but allows for cluster-specific time slopes

$$Y_{ijk}=\mu +(\beta +{\xi }_i)T_j+\delta X_{ij}+{\alpha }_i+{\text{ϵ}}_{ijk}$$ (23)

In this model, we use $T_j=j$ to represent the linear time basis function, β as the fixed time slope and ξ_i as the random slope. Within the general model representation, the heterogeneity term is written as

$${\mathit{R}}_{ik}(j,s)\prime {\mathit{\alpha }}_i={\alpha }_i+j{\xi }_i$$

The random intercept and slope are assumed to be independent of the residual error, but could covary following a bivariate normal distribution

$$\left(\begin{array}{c}{\alpha }_i\\ {\xi }_i\end{array}\right)\sim N\left[\left(\begin{array}{c}0\\ 0\end{array}\right),\left(\begin{array}{cc}{\tau }_{\alpha }^2& {\sigma }_{\alpha \xi }\\ {\sigma }_{\alpha \xi }& {\tau }_{\xi }^2\end{array}\right)\right]$$

The following within-cluster correlation structure between a pair of outcomes results from the above model

$$\text{corr}[Y_{ijk}(s),Y_{ilm}(s)]={\rho }_{jl}=\frac{{\tau }_{\alpha }^2+(j+l){\sigma }_{\alpha \xi }+jl{\tau }_{\xi }^2}{\sqrt{{\tau }_{\alpha }^2+2j{\sigma }_{\alpha \xi }+j^2{\tau }_{\xi }^2+{\sigma }_{\text{ϵ}}^2}\sqrt{{\tau }_{\alpha }^2+2l{\sigma }_{\alpha \xi }+l^2{\tau }_{\xi }^2+{\sigma }_{\text{ϵ}}^2}}$$

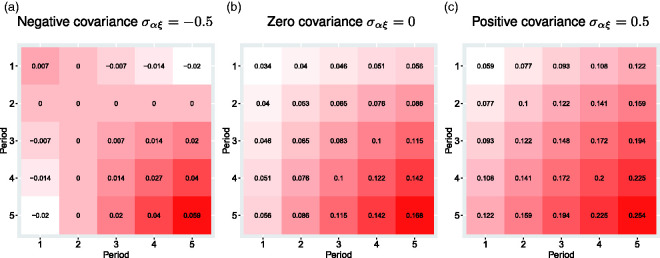
which is specific to both time period indices j and l. It is not immediate what correlation pattern is implied from the above expression, except that it is symmetric, namely, ${\rho }_{jl}={\rho }_{lj}$. Therefore, we plot the within-period and between-period ICCs in a hypothetical trial with J = 5 periods in Figure 3 under different assumptions of the covariance parameters. When ${\sigma }_{\alpha \xi }\ge 0$ as in panels (b) and (c), our finding suggests that the within-period ICC is often an increasing function of time j. In addition, the between-period ICC also increases as the distance in time, $|j-l|$, increases, which is opposite to the correlation structure implied by the exponential decay model. Finally, when the covariance ${\sigma }_{\alpha \xi }<0$, the random coefficient model could imply negative between-period ICCs. These observations point out that the within-cluster correlation structure induced from the random coefficient model may be challenging to interpret, especially because the pattern of the between-period ICC contradicts that of the exponential decay model, and the latter has been considered plausible in several settings.⁵⁷ Further simulation and methodological investigations are required to study the performance and interpretation of the random coefficient model versus other alternatives in the context of stepped wedge designs.

Figure 3.

Three examples of within-cluster correlation patterns implied by the random coefficient model. A trial with J = 5 is assumed throughout; the diagonal cells present the within-period ICC values, while the off-diagonal cells present the between-period ICC values. White color indicates a smaller ICC value while red color indicates a larger ICC value. The variance components parameters are assumed as ${\sigma }_{\text{ϵ}}=6,{\tau }_{\alpha }=1,{\tau }_{\xi }=0.5$ and the covariance parameter (a) ${\sigma }_{\alpha \xi }=-0.5$, (b) ${\sigma }_{\alpha \xi }=0$, (c) ${\sigma }_{\alpha \xi }=0.5$. (a) Negative covariance σ_αξ = − 0.5; (b) Zero covariance σ_αξ = 0; (c) Positive covariance σ_αξ = 0.5.

3.5 Considerations for modeling heterogeneity in closed-cohort designs

3.5.1 The basic model

Considerations for closed-cohort designs were discussed in Copas et al.,³⁰ and a simple extension to the Hussey and Hughes model was introduced in Baio et al.⁶⁵ Specifically, the basic model is written as

$$Y_{ijk}=\mu +{\beta }_j+\delta X_{ij}+{\alpha }_i+{\varphi }_{ik}+{\text{ϵ}}_{ijk}$$ (24)

where ${\varphi }_{ik}\sim N(0,{\tau }_{\varphi }^2)$ is the random effect for the repeated measures from individual k in cluster i, and it is assumed to be independent of random cluster effect α_i. The heterogeneity term

$${\mathit{R}}_{ik}(j,s)\prime {\mathit{\alpha }}_i={\alpha }_i+{\varphi }_{ik}$$ (25)

is modeled as a function of cluster index i and individual index k. This model assumption induces the following nested exchangeable within-cluster correlation structure

$$\text{corr}[Y_{ijk}(s),Y_{ilm}(s)]=\left\{\begin{array}{ll}{\rho }_{\text{a}}=({\tau }_{\alpha }^2+{\tau }_{\varphi }^2)/({\tau }_{\alpha }^2+{\tau }_{\varphi }^2+{\sigma }_{\text{ϵ}}^2),& k=m\\ {\rho }_{\text{d}}={\tau }_{\alpha }^2/({\tau }_{\alpha }^2+{\tau }_{\varphi }^2+{\sigma }_{\text{ϵ}}^2), & k\ne m\end{array}\right.$$

where ${\rho }_{\text{a}}$ is the correlation between two repeated measurements from the same individual (termed the within-individual ICC following Li et al.³⁴) and ${\rho }_{\text{d}}$ is the correlation between two observations collected from different individuals, regardless of time periods. Although not directly pointed out by Baio et al.,⁶⁵ the additive random structure permits a closed-form derivation of the variance of the intervention effect for trial planning once we assume equal cohort sizes, N_i = N. In particular, using the results of Li et al.,³⁴ one can show that $\text{var}(\widehat{\delta })$ shares the same form with expression (7), except that we replace

$$\begin{array}{l}{\sigma }_{\text{tot}}^2={\tau }_{\alpha }^2+{\tau }_{\varphi }^2+{\sigma }_{\text{ϵ}}^2,\\ {\lambda }_1=1-{\rho }_{\text{a}},\\ {\lambda }_2=1+J(N-1){\rho }_{\text{d}}+(J-1){\rho }_{\text{a}}\end{array}$$

where λ₁ and λ₂ are again the two eigenvalues of the within-cluster correlation matrix implied by model (24).

This basic model suggested in Baio et al.⁶⁵ has the same limitation as the Hussey and Hughes model, that is, the limit of the variance, $\underset{N\to \infty }{\lim }\text{var}(\widehat{\delta })$, converges to zero as the cohort size approaches infinity. In other words, the required number of clusters converges to one for any given level of power as long as one increases the cohort sizes indefinitely, which may not be realistic. Nevertheless, models assuming the heterogeneity term (25) appeared in a few previous investigations, including all models used in the simulation study of Nickless et al.⁴⁹

3.5.2 Block exchangeable correlation model

The nested exchangeable correlation model was extended to include a similar individual-level random intercept to account for the correlations between repeated measures. The model appeared in Hooper et al.⁵⁶ and Girling and Hemming³⁸ as

$$Y_{ijk}=\mu +{\beta }_j+\delta X_{ij}+{\alpha }_i+{\gamma }_{ij}+{\varphi }_{ik}+{\text{ϵ}}_{ijk}$$ (26)

where ${\varphi }_{ik}\sim N(0,{\tau }_{\varphi }^2)$ is the random effect for the repeated measures from individual k in cluster i, and is assumed to be independent of α_i and γ_ij (α_i and γ_ij are defined earlier in equation (13)). Using the notation of the general model, the block exchangeable correlation model represents the heterogeneity by

$${\mathit{R}}_{ik}(j,s)\prime {\mathit{\alpha }}_i={\alpha }_i+{\gamma }_{ij}+{\varphi }_{ik}$$

which depends on cluster i, period j as well as individual k. Three ICC parameters are implied by the block exchangeable correlation model in the cohort setting, as we can write

$$\text{corr}[Y_{ijk}(s),Y_{ilm}(s)]=\left\{\begin{array}{ll}{\rho }_{\text{a}}=({\tau }_{\alpha }^2+{\tau }_{\varphi }^2)/({\tau }_{\alpha }^2+{\tau }_{\gamma }^2+{\tau }_{\varphi }^2+{\sigma }_{\text{ϵ}}^2),& j\ne l,k=m\\ {\rho }_{\text{w}}=({\tau }_{\alpha }^2+{\tau }_{\gamma }^2)/({\tau }_{\alpha }^2+{\tau }_{\gamma }^2+{\tau }_{\varphi }^2+{\sigma }_{\text{ϵ}}^2),& j=l,k\ne m\\ {\rho }_{\text{b}}={\tau }_{\alpha }^2/({\tau }_{\alpha }^2+{\tau }_{\gamma }^2+{\tau }_{\varphi }^2+{\sigma }_{\text{ϵ}}^2), & j\ne l,k\ne m\end{array}\right.$$

where ${\rho }_{\text{a}}$ is the within-individual ICC for repeated measures, ${\rho }_{\text{w}}$ and ${\rho }_{\text{b}}$ are the within-period and between-period ICCs which have the same interpretations as their corresponding counterparts in the cross-sectional model. Constant values are assumed for three types of ICCs, and therefore the correlation structure does not depend on the intervention sequence s. An example matrix form the block exchangeable correlation structure is provided in Table 2.

In the closed-cohort setting, model (26) induces the so-called block exchangeable correlation structure, due to the fact that if the correlation structure is written in a matrix form, the exchangeability holds both within and across periods.³⁴ The variance expression for the treatment effect was derived in Hooper et al.,⁵⁶ Girling and Hemming,³⁸ and Li et al.,^34,66 using different notation. In our notation, the expression of $\text{var}(\widehat{\delta })$ is the same as equation (7), except that we will redefine the total variance and eigenvalues by

$$\begin{array}{l}{\sigma }_{\text{tot}}^2={\tau }_{\alpha }^2+{\tau }_{\gamma }^2+{\tau }_{\varphi }^2+{\sigma }_{\text{ϵ}}^2,\\ {\lambda }_1=1+(N-1)({\rho }_{\text{w}}-{\rho }_{\text{b}})-{\rho }_{\text{a}},\\ {\lambda }_2=1+(N-1){\rho }_{\text{w}}+(J-1)(N-1){\rho }_{\text{b}}+(J-1){\rho }_{\text{a}}\end{array}$$

Further, as the cohort size N increases to infinity, the limit of the variance, $\underset{N\to \infty }{\lim }\text{var}(\widehat{\delta })$, is given in equation (17), which is a positive constant as long as ${\rho }_{\text{b}}\ne {\rho }_{\text{w}}$. Therefore, the block exchangeable correlation model is considered more realistic than the basic model in the cohort setting, for the same reason argued in Taljaard et al.⁴⁵ Finally, we can see that models (5), (13) and (24) are all nested in the block exchangeable correlation model (26).

The block exchangeable correlation model has facilitated the investigation of several design questions in the closed-cohort settings. For example, Li et al.³⁴ reported the roles of the three ICC parameters for design efficiency. In particular, they found that larger values of the within-period ICC reduced the design efficiency, just as the traditional ICC did in a parallel design. However, larger values of both the between-period ICC and/or within-individual ICC increase the design efficiency. Further, optimal closed-cohort designs were reported in Li et al.,⁶⁶ who generalized the earlier findings in Lawrie et al. based on the Hussey and Hughes model.³⁶ Girling and Hemming³⁸ derived the optimal design within a larger design space that includes hybrid designs, and found the hybrid design to be the most efficient within the larger design space. Their results apply to both cross-sectional and closed-cohort designs. Grayling et al.⁶⁷ developed an algorithm to search for admissible (cohort) stepped wedge designs in the presence of multiple intervention arms.⁶⁸ Girling⁶⁹ studied the relative efficiency of unequal cluster sizes versus balanced cluster sizes in closed-cohort designs, and reported that the loss of precision due to unequal cluster sizes was usually no more than 12%, which was consistent with prior investigations in cross-sectional designs.⁴² Defining CV as the coefficient of variation for cohort sizes, Girling⁶⁹ showed that inflating the required cohort size by a factor of $(1+{\text{CV}}^2)$, as one would do in a parallel CRT,⁷⁰ provided a valid but conservative sample size estimate for cohort stepped wedge trials. Finally, because the nested exchangeable correlation model is a special case of the block exchangeable correlation model, these results derived under the latter model apply to the cross-sectional setting by setting ${\tau }_{\varphi }^2=0$.

3.5.3 Proportional decay model

Li⁷¹ proposed a model for the design and analysis of cohort stepped wedge designs that allowed the exponential decay of between-period ICC and within-individual ICC over time. However, Li⁷¹ focused on a population-averaged model that allowed the direct characterization of the within-cluster correlation structure, but did not consider a mixed-effects model counterpart. With a continuous outcome Y_ijk, we are able to find a conditional model that leads to the same inference as the marginal model discussed in Li.⁷¹ Specifically, the conditional model that allows correlation decay in the closed-cohort design setting shares the same form as the exponential decay model

$$Y_{ijk}=\mu +{\beta }_j+\delta X_{ij}+{\gamma }_{ij}+{\text{ϵ}}_{ijk}$$ (27)

where the heterogeneity term is

$${\mathit{R}}_{ik}(j,s)\prime {\mathit{\alpha }}_i={\gamma }_{ij}$$

However, in addition to assuming ${\text{γ}}_i=({\gamma }_{i1},\dots ,{\gamma }_{iJ})\prime \sim N(0,{\tau }_{\gamma }^2\mathit{M}(1,r))$, we could further assume a similar autoregressive structure for residual errors of the kth person in cluster i as

$${\mathit{ϵ}}_{ik}=({\text{ϵ}}_{i1k},\dots ,{\text{ϵ}}_{iJk})\prime \sim N(0,{\sigma }_{ϵ}^2\mathit{M}(1,r)), {\mathit{ϵ}}_{ik}\perp {\mathit{ϵ}}_{im}, k\ne m$$

where r is the decay rate shared by ${\mathit{\gamma }}_i$ and ${\text{ϵ}}_{ik}$, and ${\mathit{\gamma }}_i\perp {\text{ϵ}}_{ik}$.

The above decay model implies a proportional decay correlation structure that dates back to the analysis of multilevel longitudinal data.^72,73 The within-cluster correlations between each pair of observations is

$$\text{corr}[Y_{ijk}(s),Y_{ilm}(s)]=\left\{\begin{array}{ll}{\rho }_{\text{a},|j-l|}=r^{|j-l|},& j\ne l,k=m,\\ {\rho }_{\text{w}}={\tau }_{\gamma }^2/({\tau }_{\gamma }^2+{\sigma }_{\text{ϵ}}^2),& j=l,k\ne m,\\ {\rho }_{\text{b},|j-l|}={\tau }_{\gamma }^2{r}^{|j-l|}/({\tau }_{\gamma }^2+{\sigma }_{\text{ϵ}}^2),& j\ne l,k\ne m\end{array}\right.$$

where ${\rho }_{\text{a},|j-l|}$ is the within-individual ICC that decays exponentially over time, ${\rho }_{\text{w}}$ and ${\rho }_{\text{b},|j-l|}$ are the within-period and between-period ICCs just as their counterparts in the exponential decay model. This correlation model is termed the proportional decay model as the same decay rate r applies to both the within-individual ICC and the between-period ICC for different individuals. An example matrix form the proportional decay correlation structure is provided in Table 2. A unique feature of the proportional decay correlation structure is that the correlation matrix can be written as a Kronecker product between an exchangeable correlation and a first-order autoregressive matrix.⁷³ This separability property allows one to derive a closed-form variance for the intervention effect to facilitate sample size and power calculation.

Under equal cohort sizes N_i = N, Li⁷¹ showed that

$$\text{var}(\widehat{\delta })=\frac{({\sigma }_{\text{tot}}^2/N)I(1-r^2)\{1+(N-1){\rho }_{\text{w}}\}}{(IU-W)(1+r^2)-2(IP-Q)r}$$ (28)

where $U={\displaystyle {\sum }_{i=1}^I{\displaystyle {\sum }_{j=1}^J{X}_{ij}}}$ and $W={\displaystyle {\sum }_{j=1}^J{\left({\displaystyle {\sum }_{i=1}^I{X}_{ij}}\right)}^2}$ are defined earlier as in the Hussey and Hughes model,⁹ and $P={\displaystyle {\sum }_{i=1}^I{\displaystyle {\sum }_{j=1}^{J-1}{X}_{ij}}}{X}_{i,j+1},Q={\displaystyle {\sum }_{j=1}^{J-1}\left({\displaystyle {\sum }_{i=1}^I{X}_{ij}}\right)\left({\displaystyle {\sum }_{i=1}^I{X}_{i,j+1}}\right)}$ are cross-product terms resulting from the first-order autoregressive decay. As the cohort size increases to infinity

$$\underset{N\to \infty }{\lim }\text{var}(\widehat{\delta })=\frac{{\sigma }_{\text{tot}}^{2}I(1-r^2){\rho }_{\text{w}}}{(IU-W)(1+r^2)-2(IP-Q)r}>0$$

which is a positive constant as long as $\left|r\right|<1$. This variance expression suggests that the proportional decay model is not subject to the same criticism as the basic model (24). The variance expression also permits us to study the role of decay, r, on design efficiency. Li⁷¹ further presented a closed-form expression of the design effect based on equation (27), and demonstrated the parabolic relationship between $\text{var}(\widehat{\delta })$ and r, when all other parameters were held constant.

3.5.4 Random intervention model

The random intervention model in the closed-cohort design has been considered in Kasza et al.,²⁷ although in the context of incomplete designs where outcomes may not be measured in certain cluster-periods (e.g. trials with implementation periods where outcome data are not collected). The model can be represented by

$$Y_{ijk}=\mu +{\beta }_j+(\delta +{\nu }_i)X_{ij}+{\gamma }_{ij}+{\varphi }_{ik}+{\text{ϵ}}_{ijk}$$ (29)

where ${\varphi }_{ik}\sim N(0,{\tau }_{\varphi }^2)$ is the random effect for the repeated measures from individual k in cluster i, ${\text{ϵ}}_{ijk}\sim N(0,{\sigma }_{\text{ϵ}}^2)$ is the residual error, ν_i is the cluster-specific random intervention effect, and γ_ij is the cluster-period-specific random deviation from the group average, as in the exponential decay model. Clearly, the heterogeneity term is modeled as

$${\mathit{R}}_{ik}(j,s)\prime {\mathit{\alpha }}_i={\gamma }_{ij}+{\varphi }_{ik}+{\nu }_i{\mathbb{I}}_{[j\ge s]}$$

Kasza et al.²⁷ assumed the following correlation pattern for the remaining set of random effects

$$({\gamma }_{i1},{\gamma }_{i2},\dots ,{\gamma }_{iJ},{\nu }_i)\prime \sim N\left[\left(\begin{array}{c}{\mathbf{0}}_{J\times 1}\\ 0_{1\times 1}\end{array}\right),\left(\begin{array}{cc}{\tau }_{\gamma }^2\tilde{\mathit{M}}& {\sigma }_{\gamma \nu }\mathbf{1}\\ {\sigma }_{\gamma \nu }\mathbf{1}\prime & {\tau }_{\nu }^2\end{array}\right)\right]$$

and the vector $({\gamma }_{i1},{\gamma }_{i2},\dots ,{\gamma }_{iJ},{\nu }_i)\prime$ was assumed to be independent of ${\varphi }_{ik}$ and ϵ_ijk. In the above covariance structure, ${\tau }_{\gamma }^2,{\tau }_{\nu }^2$ are variance components for γ_ij and ν_i, ${\sigma }_{\gamma \nu }$ is the possibly non-zero covariance between them, 1 is the $J\times 1$ matrix of ones, and $\tilde{\mathit{M}}$ is the symmetric Toeplitz matrix defined in equation (19). The complicated random-effects structure in fact distinguishes between eight types of ICC parameters. Specifically, when two observations are measured under the control condition (namely, $j<s,l<s$), the within-period, between-period and within-individual ICCs are

$$\text{corr}[Y_{ijk}(s),Y_{ilm}(s)]=\left\{\begin{array}{cc}{\rho }_{\text{w}}=\frac{{\tau }_{\gamma }^2}{{\tau }_{\gamma }^2+{\tau }_{\varphi }^2+{\sigma }_{\text{ϵ}}^2},& j=l,k\ne m\\ {\rho }_{\text{b}}=\frac{{\tau }_{\gamma }^2{r}_{jl}}{{\tau }_{\gamma }^2+{\tau }_{\varphi }^2+{\sigma }_{\text{ϵ}}^2},& j\ne l,k\ne m\\ {\rho }_{\text{a}}=\frac{{\tau }_{\gamma }^2{r}_{jl}+{\tau }_{\varphi }^2}{{\tau }_{\gamma }^2+{\tau }_{\varphi }^2+{\sigma }_{\text{ϵ}}^2}, & j\ne l,k=m\end{array}\right.$$

When two observations are measured under the intervention condition (namely, $j\ge s,l\ge s$), the within-period, between-period, and within-individual ICCs become

$$\text{corr}[Y_{ijk}(s),Y_{ilm}(s)]=\left\{\begin{array}{cc}{\rho }_{\text{w}}=\frac{{\tau }_{\gamma }^2+{\tau }_{\nu }^2+2{\sigma }_{\gamma \nu }}{{\tau }_{\gamma }^2+{\tau }_{\varphi }^2+{\tau }_{\nu }^2+2{\sigma }_{\gamma \nu }+{\sigma }_{\text{ϵ}}^2},& j=l,k\ne m\\ {\rho }_{\text{b}}=\frac{{\tau }_{\gamma }^2{r}_{jl}+{\tau }_{\nu }^2+2{\sigma }_{\gamma \nu }}{{\tau }_{\gamma }^2+{\tau }_{\varphi }^2+{\tau }_{\nu }^2+2{\sigma }_{\gamma \nu }+{\sigma }_{\text{ϵ}}^2},& j\ne l,k\ne m\\ {\rho }_{\text{a}}=\frac{{\tau }_{\gamma }^2{r}_{jl}+{\tau }_{\nu }^2+2{\sigma }_{\gamma \nu }+{\tau }_{\varphi }^2}{{\tau }_{\gamma }^2+{\tau }_{\varphi }^2+{\tau }_{\nu }^2+2{\sigma }_{\gamma \nu }+{\sigma }_{\text{ϵ}}^2}, & j\ne l,k=m\end{array}\right.$$

Finally, when one observation is measured under the control condition while the other one under the intervention condition ($j\ge s,l<s$ or $j<s,l\ge s$), the correlations are

$$\text{corr}[Y_{ijk}(s),Y_{ilm}(s)]=\left\{\begin{array}{cc}{\rho }_{\text{b}}=\frac{{\tau }_{\gamma }^2{r}_{jl}+{\sigma }_{\gamma \nu }+{\tau }_{\varphi }^2}{\sqrt{{\tau }_{\gamma }^2+{\tau }_{\varphi }^2+{\tau }_{\nu }^2+2{\sigma }_{\gamma \nu }+{\sigma }_{\text{ϵ}}^2}\sqrt{{\tau }_{\gamma }^2+{\tau }_{\varphi }^2+{\sigma }_{\text{ϵ}}^2}},& k=m\\ {\rho }_{\text{a}}=\frac{{\tau }_{\gamma }^2{r}_{jl}+{\sigma }_{\gamma \nu }}{\sqrt{{\tau }_{\gamma }^2+{\tau }_{\varphi }^2+{\tau }_{\nu }^2+2{\sigma }_{\gamma \nu }+{\sigma }_{\text{ϵ}}^2}\sqrt{{\tau }_{\gamma }^2+{\tau }_{\varphi }^2+{\sigma }_{\text{ϵ}}^2}},& k\ne m\end{array}\right.$$

As we explained when we reviewed the exponential decay model in Section 3.4, parsimonious parameterization of $\tilde{\mathbf{M}}$ may lead to simpler and more interpretable models. For example, when $\tilde{\mathbf{M}}=\mathbf{M}(1,1)$, model (29) is a direct extension of model (22) by the addition of the random intercept ${\varphi }_{ik}$. When $\tilde{\mathbf{M}}=\mathbf{M}(r_0,1)$, model (29) extends the block exchangeable correlation model (26) with the addition of a random intervention component. When $\tilde{\mathbf{M}}=\mathbf{M}(1,r)$, model (29) extends the exponential decay model (18) by the addition of random intercept ${\varphi }_{ik}$ and random intervention effect ν_i. Notice that in the last case, there is no guarantee that the between-period ICC for any pair of observations decays at an exponential rate, and therefore model (29) does not nest the proportional decay model (27), even though both models are developed for closed-cohort designs.

3.6 Considerations for modeling heterogeneity in open-cohort designs

The model development in the cross-sectional and closed-cohort designs have important implications for the open-cohort design, as an open-cohort design can be considered a mix of the former two. Kasza et al.⁷⁴ recently discussed several open-cohort sampling schemes for stepped wedge designs and proposed a corresponding sample size calculation procedure based on a linear mixed model. We will review the related model variants and their connections to the results in Sections 3.4 and 3.5.

3.6.1 Blended exchangeable correlation model

In principle, the block exchangeable model developed for the closed-cohort design can still be used to represent the outcome trajectory in the open-cohort design, except for a few notational caveats. Specifically, the outcome model can still be written as

$$Y_{ijk}=\mu +{\beta }_j+\delta X_{ij}+{\alpha }_i+{\gamma }_{ij}+{\varphi }_{ik}+{\text{ϵ}}_{ijk}$$ (30)

where all the parameters are defined in Section 3.5.2. Importantly, under the attrition of members from and addition of new members to the original cohort, we shall use a distinct subscript k to represent a distinct individual in each cluster. The implied within-cluster correlation matrix is neither nested exchangeable nor block exchangeable, but becomes a blend of these two. We call such a matrix a blended exchangeable correlation structure and an example formulation is provided in Table 2.

Assuming that the cluster-period sizes were identical ($N_{ij}=N$) and there existed the same number of overlapping individuals between any two periods $\left(n_i(j,l)=n\right)$, Kasza et al.⁷⁴ derived a closed-form variance of the intervention effect, which could be rewritten in our notation as

$$\text{var}(\widehat{\delta })=\frac{({\sigma }_{\text{tot}}^2/N)IJ\{{\lambda }_1+\chi ({\rho }_{\text{a}}-{\rho }_{\text{b}})\}\{{\lambda }_2-\chi (J-1)({\rho }_{\text{a}}-{\rho }_{\text{b}})\}}{(U^2+IJU-JW-IV)\{{\lambda }_2-\chi (J-1)({\rho }_{\text{a}}-{\rho }_{\text{b}})\}-(U^2-IV)\{{\lambda }_1+\chi ({\rho }_{\text{a}}-{\rho }_{\text{b}})\}}$$ (31)

where U, V, W were design constants defined in Section 3.1

$$\begin{array}{l}{\sigma }_{\text{tot}}^2={\tau }_{\alpha }^2+{\tau }_{\gamma }^2+{\tau }_{\varphi }^2+{\sigma }_{\text{ϵ}}^2,\\ {\lambda }_1=1+(N-1)({\rho }_{\text{w}}-{\rho }_{\text{b}})-{\rho }_{\text{a}},\\ {\lambda }_2=1+(N-1){\rho }_{\text{w}}+(J-1)(N-1){\rho }_{\text{b}}+(J-1){\rho }_{\text{a}}\end{array}$$

and $\chi =1-n/N\in [0,1]$ was the common rate of attrition or churn rate. This expression permits a convenient sample size formula for open-cohort designs, and unifies the variance expressions derived under models (5), (13), (24) and (26). For example, as the churn rate approaches one, the open-cohort design reduces to the cross-sectional design and the variance (31) reduces to the variance derived under the nested exchangeable model (13). On the other hand, as the churn rate approaches zero, the open-cohort design reduces to the closed-cohort design and variance (31) reduces to the one derived under the block exchangeable correlation model. This unified perspective represents a continuum between cross-sectional and closed-cohort designs, and may help with the efficiency comparisons between these two designs. In fact, when the within-individual ICC ${\rho }_{\text{a}}$ is larger than the between-period ICC ${\rho }_{\text{b}}$, variance (31) is a monotonically increasing function of χ over $[0,1]$. Within a random-effects model (30), ${\rho }_{\text{a}}$ is constrained to be no smaller than ${\rho }_{\text{b}}$, and therefore the closed-cohort design is usually more efficient than the cross-sectional design, provided other parameters are all held equal. On the contrary, if the within-individual ICC ${\rho }_{\text{a}}$ is smaller than the between-period ICC ${\rho }_{\text{b}}$, variance (31) becomes a monotonically decreasing function of χ over $[0,1]$. In this case, the closed-cohort design becomes less efficient than the cross-sectional design, providing the remaining parameters are held equal. However, even though the latter case is mathematically valid (because the resulting correlation matrix can still be positive definite, see the eigenvalue conditions of Li et al.³⁴), it may not be plausible in practice because serial correlation defined for the same individual is usually believed to be stronger than correlation between individuals.

3.6.2 Blended correlation decay model

Kasza et al.⁷⁴ introduced a linear mixed model that allowed correlation decay in open-cohort designs. The model has the same conditional mean structure as the exponential decay and the proportional decay model and is written as

$$Y_{ijk}=\mu +{\beta }_j+\delta X_{ij}+{\gamma }_{ij}+{\text{ϵ}}_{ijk}$$ (32)

where ${\mathit{\gamma }}_i=({\gamma }_{i1},\dots ,{\gamma }_{iJ})\prime \sim N(0,{\tau }_{\gamma }^2\mathit{M}(1,r))$ and r is the decay rate at the cluster-period level. Here, we use a distinct subscript k to represent a distinct individual in each cluster to allow for open-cohort sampling. If individual k in cluster i contributes outcome observations in a total of $J_k\le J$ periods, the model assumes an autoregressive structure for errors of that individual as

$${\mathit{ϵ}}_{ik}=({\text{ϵ}}_{i1k},\dots ,{\text{ϵ}}_{i{J}_{k}k})\prime \sim N(0,{\sigma }_{\text{ϵ}}^2\mathbf{M}(1,\eta )), {\mathit{ϵ}}_{ik}\perp {\mathit{ϵ}}_{im}, k\ne m$$

where η is the decay rate at the individual level, and the two random effects are independent, ${\text{γ}}_i\perp {\mathit{ϵ}}_{ik}$. Notice that this blended correlation decay model is more general than the proportional decay model because the individual-level decay rate η is allowed to differ from the cluster-period-level decay rate r.

The blended correlation decay model implies the following correlation structure

$$\text{corr}[Y_{ijk}(s),Y_{ilm}(s)]=\left\{\begin{array}{ll}{\rho }_{\text{a},|j-l|}=({\tau }_{\gamma }^2{r}^{|j-l|}+{\sigma }_{\text{ϵ}}^2{\eta }^{|j-l|})/({\tau }_{\gamma }^2+{\sigma }_{\text{ϵ}}^2),& j\ne l,k=m,\\ {\rho }_{\text{w}}={\tau }_{\gamma }^2/({\tau }_{\gamma }^2+{\sigma }_{\text{ϵ}}^2),& j=l,k\ne m,\\ {\rho }_{\text{b},|j-l|}={\tau }_{\gamma }^2{r}^{|j-l|}/({\tau }_{\gamma }^2+{\sigma }_{\text{ϵ}}^2),& j\ne l,k\ne m\end{array}\right.$$

where ${\rho }_{\text{a},|j-l|}$ is the within-individual ICC that decays over time depending on both η and r. Furthermore, ${\rho }_{\text{w}}$ and ${\rho }_{\text{b},|j-l|}$ are the within-period and between-period ICCs just as their counterparts in the exponential decay model and the proportional decay model. The blended correlation decay model unifies the exponential decay and proportional decay models. For instance, when the churn rate approaches one, the open-cohort design reduces to the cross-sectional design, and the blended correlation decay structure reduces to the exponential decay structure. On the other hand, as the churn rate approaches zero, the open-cohort design reduces to the closed-cohort design, and the blended correlation decay structure becomes the proportional decay structure when the two decay rates are identical, namely $\eta =r$. This indicates that the blended correlation decay model represents a continuum between cross-sectional and closed-cohort designs, and will be helpful for comparing efficiency between cross-sectional and closed-cohort designs under a range of correlation decay parameters. We provide an illustrative matrix form of the blended correlation decay structure in Table 2, where we assume an equal decay rate at each level ($\eta =r$). This illustrative formulation in Table 2 also shows that the blended correlation decay structure is a “blend” of the exponential decay and proportional decay structures. Unlike the blended exchangeable correlation model, the blended correlation decay structure does not admit a closed-form variance expression of the intervention effect, even when the churn rate is assumed to be a constant. Kasza et al.⁷⁴ provided a general matrix-based variance formula for numerically computing sample size and power, with the two decay parameters as key input. However, empirical estimates of these decay rates are lacking, and additional research effort is necessary to examine the operating characteristics of model (32) for estimating these decay parameters in stepped wedge designs with realistic sample sizes.

3.7 Considerations for modeling binary outcomes

The literature on stepped wedge designs has largely focused on the application of linear mixed models and a continuous outcome, and includes few focused discussions of binary outcomes. For sample size estimation, Hussey and Hughes⁹ used variance expression (5) derived from the linear mixed model, but approximated ${\sigma }_{\text{ϵ}}^2\approx \mu (1-\mu )$. In this particular case, the link function g is still identity and thus the intervention effect could be interpreted as the risk difference. Although this variance approximation may be adequate when there is minimal secular trend and a small intervention effect,^25,75 it may either underestimate or overestimate the true power in other parameter regions.⁷⁶ To accurately estimate sample size, Zhou et al.⁷⁶ proposed the following variant of the Hussey and Hughes model

$${\mu }_{ij}=\mu +{\beta }_j+\delta X_{ij}+{\alpha }_i$$ (33)

where μ_ij is the proportion of responses in cluster i during period j, and the heterogeneity term ${\mathit{R}}_{ik}(j,s)\prime {\mathit{\alpha }}_i={\alpha }_i$ now follows a truncated normal distribution with density

$$f({\alpha }_i|{\tau }_{\alpha }^2)\propto \mathbb{I}\{-l_0<{\alpha }_i<1-l_1\}\exp \left(-\frac{{\alpha }_i^2}{2{\tau }_{\alpha }^2}\right)$$

where the truncation points $l_0=\min \{\mu +{\beta }_j,\mu +{\beta }_j+\delta ;j=1,\dots ,J\}$ and $l_1=\max \{\mu +{\beta }_j,\mu +{\beta }_j+\delta ;j=1,\dots ,J\}$ are defined to ensure that the probability μ_ij is strictly bounded between zero and one. Based on this model, Zhou et al.⁷⁶ proposed a maximum likelihood approach to compute the sample size. It was shown that their approach provided more accurate characterization of the required sample size than the binomial approximation in Hussey and Hughes.⁹

Since μ_ij is a proportion, other common choices of the link function include the log link and the logit link, with the respective interpretations of the intervention effect as a risk ratio and as an odds ratio. Although sample size methods based on these nonlinear link functions have not yet been extensively discussed (except for the simulation-based approach of Baio et al.⁶⁵), there have been some investigations of the operating characteristics of these models as tools for data analysis. For example, in the cross-sectional setting, Thompson et al.⁷⁷ compared the performance between three logistic linear mixed models in a simulation study with varying parameter constellations. The three models they examined could be considered as the logistic version of the Hussey and Hughes model (5), nested exchangeable correlation model (13) and the random intervention model (22). They found that the following logistic counterpart of the nested exchangeable correlation model

$$\text{logit}({\mu }_{ij})=\mu +{\beta }_j+\delta X_{ij}+{\alpha }_i+{\gamma }_{ij}, {\alpha }_i\sim N(0,{\tau }_{\alpha }^2), {\gamma }_{ij}\sim N(0,{\tau }_{\gamma }^2)$$

had more robust performance in terms of bias and type I error rates across a number of data generating processes. Finally, the extension of the exponential decay model to binary outcomes and its operating characteristics have not yet been investigated.

4 Estimation and inference for the intervention effect

Estimation and inference for the parameters in mixed-effects models have been extensively discussed in a number of textbooks.^48,78–80 The basic principles, such as maximum likelihood, apply to all model formulations we have reviewed in Section 3. Although not our focus, the Bayesian approach is an alternative option, and could potentially be attractive especially in the presence of complex random-effects structures.⁴⁸ Using the general model (4) and assuming that the heterogeneity parameter ${\text{α}}_i$ follows a parametric distribution $f({\text{α}}_i;\Theta )$, one could define the likelihood of the observed outcomes by generic notation as

$$L(\mathit{\theta },\Theta )={\displaystyle \prod _{i=1}^I{\displaystyle \int \left[{\displaystyle \prod _{j=1}^J{\displaystyle \prod _{k=1}^{N_{ij}}f}}(Y_{ijk}|\text{θ},{\text{α}}_i)\right]}}f({\text{α}}_i;\Theta )\text{d}{\text{α}}_i$$ (34)

and numerically search for the values of fixed-effects parameter $\text{θ}$ and variance components $\Theta$ that maximize the likelihood. With continuous outcomes and the normality assumption for $f(Y_{ijk}|\text{θ},{\text{α}}_i)$, it is often possible to obtain closed-form expressions for iterative updates between $\text{θ}$ and $\Theta$.⁸⁰ More often than not, equation (34) is modified to obtain the restricted maximum likelihood (REML), because the estimates of the variance component parameters $\Theta$ will be unbiased. With binary outcomes and binomial assumptions for $f(Y_{ijk}|\text{θ},\Theta )$, approximation to (34) can be carried out via the Laplace method,⁷⁸ penalized quasi-likelihood⁸¹ or adaptive Gauss-Hermite Quadrature,⁸² among others. The variance of the MLE can be obtained from computing the approximate information matrix for $(\text{θ},\Theta )$. Testing the null hypothesis of no intervention effect (i.e. certain components of $\text{θ}$ equal zero) can proceed by the Wald, likelihood ratio or score statistic based on the large-sample normality theory. These procedures are available in standard software packages, such as SAS and R.

Cluster randomized trials usually involve a limited number of clusters, and therefore the desired frequentist properties may not be guaranteed for the hypothesis testing procedures derived from large-sample theory. Recent systematic reviews confirmed that most stepped wedge CRTs recruited fewer than 30 clusters,^17,18 and so there could be an emerging interest in developing small-sample adaptation of existing testing procedures for better performance. In the recent CONSORT extension to stepped wedge CRTs, Hemming et al.²³ encouraged the incorporation of small-sample corrections in the analysis of stepped wedge designs, whenever appropriate (item 12a). Although there has not yet been much investigation of small-sample corrections for mixed-effects model-based tests applied to stepped wedge trials, there were previous reports of small-sample corrections in parallel CRTs that may inspire ideas. For example, Li and Redden⁸³ considered the Wald t-statistic (or the equivalent F-statistic) from the logistic linear mixed model in the analysis of parallel CRTs with 10 to 30 clusters. They compared five degree-of-freedom approximations in terms of type I error rates and power, across scenarios with varying ICCs and cluster sizes. They concluded that the between-within degree of freedom⁸⁴ carried the nominal type I error rates and had higher power than its competitors. The between-within approach divides the residual degree of freedom into the between-cluster and within-cluster portions. If a fixed-effect covariate changes within any cluster, the within-cluster degree of freedom is assigned to that effect; otherwise, the between-cluster degree of freedom is assigned to the effect. Such findings may or may not be directly generalizable to stepped wedge trials, because unlike the parallel CRT, the intervention status actually changes over time within a cluster. In fact, we can compute the between-within degree of freedom for testing the intervention effect in the Hussey and Hughes model to be $(I-1)J$, which tends to be larger than its counterpart in parallel CRTs. It remains to be explored which degree of freedom approximation would be adequate in small stepped wedge designs.

The permutation test is another attractive tool for the inference in CRTs due to its robustness in controlling test size.⁸⁵ Under the strong null hypothesis of no intervention effect, Gail et al.⁸⁶ demonstrated that the type I error rate of the permutation test will not exceed the nominal level, even in CRTs with a limited number of clusters. Murray et al.⁸⁷ and Li et al.^88,89 also showed that the permutation test could achieve a similar level of power as the model-based F-test, but had better control of test sizes. Several authors have considered permutation-based inference for the analysis of stepped wedge trials; the general idea is to obtain the reference distribution of a given test statistic by permuting the intervention sequences across clusters. For example, Wang and DeGruttola⁹⁰ and Ji et al.³¹ considered the estimated treatment effect and the corresponding z-score (Wald statistic) as the test statistic for testing H₀: δ = 0 based on the Hussey and Hughes model (5) and the nested exchangeable correlation model (13); they obtained the exact distribution of the statistic from randomly shuffling the intervention sequences within the randomization space characterized by the design configuration. They found that the specification of the random-effects structure (or more generally the heterogeneity term ${\mathit{R}}_{ik}(j,s)\prime {\mathit{\alpha }}_i$) only affected the power of the test, but not the validity, and therefore demonstrated its superiority over the model-based test. Ren et al.⁹¹ considered permuting the estimated treatment effect and the corresponding z-score obtained from a random intervention model (22), but reported an inflated type I error rate even when the random intervention model is correctly specified. This phenomenon arises likely because the intervention sequence affects both the mean and covariance structures, and the exchangeability assumption fails to hold under the null hypothesis. Others have considered more nonparametric test statistics. For example, Thompson et al.⁹² proposed a test statistic based on combining the optimally weighted within-period comparisons (i.e. the vertical comparisons defined in Davey et al.²¹ and Matthews and Forbes⁹³), and developed a permutation test with fewer modeling assumptions. Their test can be applied to both continuous and binary outcomes, and has demonstrated adequate control of type I error rate in simulations. Kennedy-Shaffer et al.⁹⁴ proposed an ensemble test statistic that combined the within-period and between-period contrasts via the Synthetic Control method (their SC method) and difference-in-differences (their crossover method). The corresponding permutation test based on the ensemble statistic demonstrated higher power than the permutation test in Thompson et al.⁹² and the permutation test based on mixed-effects models^31,90 when those models were misspecified. Hughes et al.⁹⁵ provided a design-based test statistic and characterized the closed-form variances of the statistic under permutation; they showed that the resulting test carried the nominal size even under misspecification of both the mean and covariance structures. Furthermore, since the closed-form permutation variance is derived analytically, the permutation test in Hughes et al.⁹⁵ dispenses with intensive enumerations and is considered computationally more efficient than previous proposals. To date, there has not been a comprehensive simulation study that evaluates the comparative performance of all of the above permutation tests under different data generating processes, and more investigations are needed to offer practical recommendations on optimal ways to conduct randomization-based inference for stepped wedge designs.

5 Discussion

We have provided an overview of mixed-effects models that have been applied to the design and analysis of stepped wedge CRTs. We offered a unified perspective from a general model formulation and illustrated that existing models in the literature were its special cases with different assumptions about the secular trend, intervention effect and sources of heterogeneity. Our overview suggests that the current literature on stepped wedge designs has placed more emphasis on modeling the between-cluster and between-time heterogeneity, compared to modeling the secular trend or the intervention effect. We conjecture that this is because a number of discussions have focused on sample size calculation, which becomes convenient based on a scalar intervention effect but still remains sensitive to the assumptions for the random-effects structure. However, given the possibility of a time-varying intervention effect, it will be important for future work to address implications of the alternative methods reviewed in Section 3.3 on sample size planning and data analysis. In addition, there is currently limited guidance on how to select the most appropriate random-effects structure in the context of stepped wedge designs. Murray et al.⁵⁸ explored the use of information criteria to select appropriate mixed-effects models for the analysis of parallel longitudinal CRTs, but recommended against them due to their unreliable performance. More research on identifying the appropriate random-effects structure in both the design and analysis stages would be of substantial interest.

We found that there is more development for continuous outcomes than for binary, count or time-to-event outcomes, likely due to the availability of closed-form expressions for variance and ICCs. Although these closed-form expressions have helped us generate knowledge and insights on the role of various design parameters and facilitated the application of these new designs, the generalizability of such knowledge to binary or count outcomes requires further exploration. Zhou et al.⁷⁶ pointed out that binary outcomes were fairly common in stepped wedge trials, especially in health care studies with an implementation endpoint. However, accurate sample size methods for binary outcomes have only been developed based on the risk difference scale and a single random cluster intercept, as considered in Zhou et al.⁷⁶ It would be important to extend such approaches for risk ratio and odds ratio measures, and to accommodate more complex assumptions on the heterogeneity, such as a model with a random cluster-by-time interaction or correlation decay.^56,57 Regarding the analysis of stepped wedge trials, Thompson et al.⁷⁷ conducted simulation studies with binary outcomes and suggested that the logistic extension of the nested exchangeable correlation model performed well in terms of bias and coverage across several data generating processes. To date, there has been little work on count or rate outcomes. We are only aware of a simulation study by Scott et al.,⁹⁶ who used a Poisson log-linear mixed-effects model to simulate outcomes and examine the operating characteristics of population-averaged models estimated by generalized estimating equations (GEE).⁹⁷

Methods for designing and analyzing stepped wedge trials with time-to-event outcomes also need further attention. In the THRio study,⁹⁸ Moulton et al.⁹⁹ discussed a log-rank type analysis to compare the incidence between intervention and control clusters within each period, analogous to the vertical comparison methods^21,93 in non-survival settings. They used a simulation-based approach to estimate the design effect relative to parallel cluster randomization which was then used to compute sample size and power. Zhan et al.¹⁰⁰ developed a discrete-time survival model for analyzing stepped wedge CRTs with terminal endpoints and interval censoring (as the exact event time could be unknown within each discrete period). The key insight is to reformulate the likelihood using a generalized linear mixed model for the binary event history indicators. In this regard, considerations in Section 3 may still apply, but additional research is necessary. Importantly, closed-form sample size estimation procedures and optimal design configurations based on such discrete-time survival models remain unavailable and are open questions for future studies.¹⁰¹

As an alternative to mixed-effects models, population-averaged models have been proposed to design and analyze parallel CRTs.^6,102 While the conditional model we discussed requires the specification of a conditional mean structure with an association structure induced by random-effects, the population-averaged model counterpart requires the specification of a marginal mean and a separate correlation model for the association structure.^103,104 The conditional intervention effect from the mixed-effects model and the marginal intervention effect from the population-averaged model are identical with an identity link but could be different with a nonlinear link function.^104,105 Further, the interpretation of the marginal intervention effect remains the same regardless of the correlation model, while the interpretation of the conditional intervention effect may change according to specifications of random effects.¹⁰⁶ Though the population-averaged model has several attractive features, it has not been as extensively studied in stepped wedge CRTs, with a few exceptions.^34,71,96,107 Specifically, Li et al.³⁴ and Li⁷¹ used GEE to estimate the population-averaged intervention effect, coupled with the block exchangeable correlation structure (the correlation structure implied by model (13) and (26)), and the proportional decay structure (the correlation structure implied by model (27)). The GEE has been known to be prone to bias with a small number of clusters, both in terms of estimation of correlation parameters and variances,^108,109 therefore finite-sample corrections have been carefully studied and recommended.^34,71,96,107

There are other aspects of the applications of models to stepped wedge designs that we have not reviewed. Above all, we have restricted the current article to models without cluster-level or individual-level covariates, although they could in principle be included in the analytical stage, especially when stratification or covariate-constrained randomization is carried out to minimize chance imbalance.^43,88,89,110 We have also only reviewed models applicable to stepped wedge trials with a single level of clustering, while Hemming et al.²⁵ and Teerenstra et al.¹¹¹ proposed extensions of the Hussey and Hughes model that accounted for multiple levels of clustering (e.g. patients nested in clinics and clinics nested in counties). Third, we have presented models assuming complete outcome information is available for all individuals and assumed away individual non-response. In practice, especially in closed-cohort designs, patient drop-out may occur given that the trial could last for a few years. When the drop-out mechanism can be considered as missing at random,¹¹² one may use inverse probability weighting or multilevel multiple imputation to reduce the bias due to missing outcomes. Turner et al.¹¹³ recently studied the relative merits of these two mainstream missing data approaches for parallel CRTs, and it would be of interest to consider their extensions to stepped wedge CRTs.

Finally, in stepped wedge trials, reporting the values of various ICCs or variance components is also critically important to help inform the design of future studies with similar endpoints. Our experiences suggest that, although the correlations or variance components are essential input in virtually any sample size procedure derived from mixed-effects models in Section 3, only a very limited number of stepped wedge trials report such values. Accurate reporting of correlation estimates or variance components has been recommended in the CONSORT extension to stepped wedge designs,²³ and an example where the within-period and between-period correlations are reported can be found in Martin et al.¹¹⁴ and Hemming et al.⁴⁷ We need more studies to report estimates of ICCs and variance components, in particular for the correlation decay and random intervention models, to facilitate the design of trials based on these more recent extensions of the Hussey and Hughes model.

Declaration of conflicting interests

The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.

Funding

The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: This work is supported within the National Institutes of Health (NIH) Health Care Systems Research Collaboratory by the NIH Common Fund through cooperative agreement U24AT009676 from the Office of Strategic Coordination within the Office of the NIH Director and cooperative agreement UH3DA047003 from the National Institute on Drug Abuse. This work is also supported by the administrative supplement 3-UH3-DA047003-02S2 from the NIH Office of Disease Prevention and PCORI contract ME-1507-31750. The content is solely the responsibility of the author and does not necessarily represent the official views of the National Institutes of Health or PCORI. Karla Hemming is funded by the U.K. National Institute of Health Research Senior Research Fellowship SRF-2017-10-002. The authors are grateful to Dr. David Murray for participating in discussions leading up to this article as part of the work of the NIH Collaboratory Biostatistics and Study Design Working Group, for which Dr. Murray is the NIH representative. The authors thank the Editor and two anonymous reviewers for providing helpful comments.

ORCID iDs

Fan Li https://orcid.org/0000-0001-6183-1893

Karla Hemming https://orcid.org/0000-0002-2226-6550