Evaluation of Single Sample Network Inference Methods for Metabolomics-Based Systems Medicine

Abstract

Networks and network analyses are fundamental tools of systems biology. Networks are built by inferring pair-wise relationships among biological entities from a large number of samples such that subject-specific information is lost. The possibility of constructing these sample (individual)-specific networks from single molecular profiles might offer new insights in systems and personalized medicine and as a consequence is attracting more and more research interest. In this study, we evaluated and compared LIONESS (Linear Interpolation to Obtain Network Estimates for Single Samples) and ssPCC (single sample network based on Pearson correlation) in the metabolomics context of metabolite–metabolite association networks. We illustrated and explored the characteristics of these two methods on (i) simulated data, (ii) data generated from a dynamic metabolic model to simulate real-life observed metabolite concentration profiles, and (iii) 22 metabolomic data sets and (iv) we applied single sample network inference to a study case pertaining to the investigation of necrotizing soft tissue infections to show how these methods can be applied in metabolomics. We also proposed some adaptations of the methods that can be used for data exploration. Overall, despite some limitations, we found single sample networks to be a promising tool for the analysis of metabolomics data.

Introduction

Humans exhibit great phenotypic diversity in both healthy and pathophysiological conditions as a result of molecular regulatory and metabolic systems underlying the functioning of living organisms. It is now widely recognized that phenotypic diversity cannot be understood and characterized by analyzing single molecular markers such as genes, metabolites, or proteins alone: what is relevant is the complex web of interactions underlying the molecular mechanisms maintaining the functioning of the organism.¹⁻³

These molecular interactions are well captured and modeled using the formalism of network inference and analysis,⁴⁻⁶ where molecular entities such as genes, proteins, and metabolites are represented as nodes and their mutual relationships as edges, which can be different in nature, representing physical interactions, as in protein–protein interaction networks, regulation, as in gene regulatory networks, or similar concentration patterns, as in metabolite–metabolite association networks.⁷

It has been shown that network-based biomarkers, for example, sub-network markers,⁸ network biomarkers,⁹ and edge biomarkers¹⁰ are superior to the traditional single-molecule biomarkers for accurately characterizing disease states due to their additional information on interactions and networks.

In the quest for personalized medicine,¹¹ it is of paramount importance to elucidate the molecular mechanisms which underlay the subject-specific response to pathophysiological stimuli, resulting from the dysfunction of individual-specific networks/systems rather than just the malfunction of a singular biological entity. In this light, networks and network analyses have the potential of being pivotal in personalized medicine if there exists the possibility of their extension from a population level to the individual-specific level.

However, since several samples are required to define the associations (like in the form of correlations¹²) among molecular elements, such as metabolites or genes, there exists no straightforward approach to infer an individual-specific network by profiling metabolite concentrations or gene expression from a single sample. If such an approach was demonstrated, it would be a very desirable situation due to the fact that it is rarely possible to obtain multiple samples from the same subjects, given the necessity of designing complex and expensive longitudinal studies. On the contrary, a single bio-fluid sample (such as blood and urine) is usually easy to obtain even in common clinical practice.

There is growing research interest in the possibility of the construction of such individual-specific networks by expression profiling of a single sample and several methods have been proposed.¹³⁻¹⁶

Here, we present a comparative review of two methods for single sample network inference with the aim of evaluating their possible application to metabolomics data to obtain metabolite–metabolite single-sample association networks. We focused on LIONESS proposed by Kuijjer et al.(14) and ssPCC by Liu et al.(13) We chose these two approaches among others since they adopt similar albeit different philosophies and thus are directly comparable, both are (or may be) based on correlations, and are easy to implement.

We analyzed these two methods for their ability to produce single sample or sample-specific networks from metabolite concentrations, and we explored and compared their characteristics on data generated from

• i)Numerical simulations
• ii)A dynamic metabolic model
• iii)22 publicly available metabolomic data sets.

We then applied the two methods on a study case pertaining to the metabolomics investigation of necrotizing soft tissue infections (NSTIs)¹⁷ in order to showcase the deployment of single sample network inference in real-life metabolomics applications. Additionally, we suggest some potentially new use of single sample networks for sample exploration and classification.

Material and Methods

Basics of Networks

A network is a graphical representation of relationships among objects. A network consists of nodes which represent biological features (genes, proteins, and metabolites) connected by links or edges which represent pair-wise relationships between the biological features.

This representation shifts the focus toward the relationships among biological entities rather than on their levels; in this light, network and network analysis are fundamental tools from the systems biology toolbox to investigate and understand metabolomics data.¹² When the nodes are metabolites, the networks can be termed metabolite–metabolite association networks.

Methods for Single Sample Networks Inference

LIONESS: Linear Interpolation to Obtain Network Estimates for Single Samples

LIONESS is an approach developed by Kuijjer et al. in the context of gene regulatory networks.^14,18

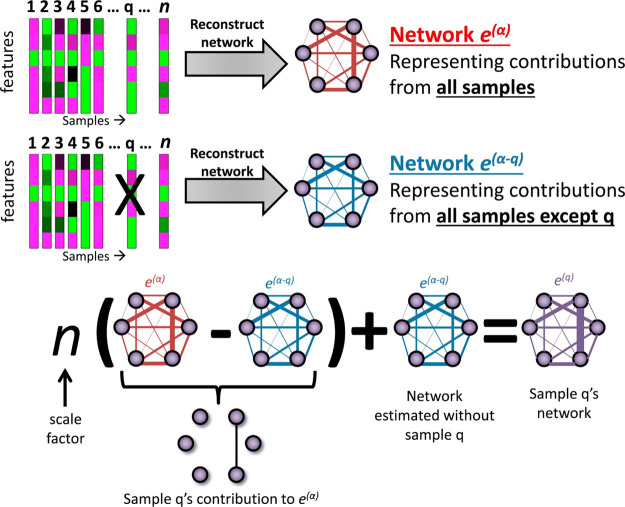
This approach starts by considering a n × m data matrix X_(α) and the corresponding m × m network E^(α) (i.e,. the so-called aggregate network) with edges e_ij between nodes i and j and the network E^(α–q) constructed from the (n – 1) × m data matrix X_(α–q), that is a matrix with all but the qth sample, which we refer to as the q-sample for the sake of simplicity. A graphical illustration of the LIONESS procedure is given in Figure 1.

Figure 1.

Visual illustration of the Lioness estimation of a single sample based on two aggregate network models, one reconstructed using all biological samples in a given data set and the other using all except the sample of interest (q, q-sample). Figure reproduced and adapted from the original publication,¹⁴ published under Creative Commons license CC BY-NC-ND 4.0.

LIONESS assumes that the aggregate network E^(α) built from n samples is the mean of networks constructed from every single sample from the data set X^(α) containing n samples. This assumption is then extrapolated to define the edge e_ij^(α) in E^(α) as the linear combination of the weights of that edge across a set of n networks

1

where w_(s) represents the relative contribution of each single sample network to the aggregate network and

2

Similarly, for the network E^(α–q) constructed from all but the q-sample, the edge between e_ij^α–q is defined as

3

where

From eqs 1 and 3, the authors defined

4

as long as the assumption holds that every sample makes an equal proportional contribution to the aggregate networks E^(α), which makes w_q^(α) constant.

Combining eqs 4 and 3 and solving for the edge e_ij^(q) for the q-sample gives the general LIONESS equation

5

which defines the edge between node i and j of the single sample network for the q-sample. The term 1/w_q^(α) gives the weight of each sample, and can be set to n if all samples are given the same weight, obtaining

6

which will be used throughout this study. In matrix notation, eq 6 becomes

7

The LIONESS equation does not depend on the particular methods used to infer the networks which can be estimated with any approach or different association measures; the most common approach is to use correlation, but mutual information can also be used. However, the authors reported sub-optimal performance when using mutual information to measure associations and single sample edges. In a related study, we also reported the sub-optimal performance of mutual information for metabolite association network estimation.¹⁹ For this reason, we will focus on Pearson’s correlation also because this will allow direct comparison with the ssPCC method (see the section ssPCC: Single Sample Network Based on Pearson’s Correlation). In this case, the LIONESS eq 6 becomes

8

where r_ij is the Pearson correlation between variable (metabolite) i and j. A summary of the notation used is given in Table 1.

Table 1. Summary of the Notation Used in the Paper to Define the Lioness and ssPCC Edges.

		original notation	definition	alternative notation	correlation notation	definition
ssPCC	network built using all samples in the reference data set	PCCn			rij(n)
	aggregated network built using all samples in the reference plus the q-sample	PCCn+1			rij(n+q)
	single sample network for the q sample	ΔPCCn	PCCn+1 – PCCn		rij(q)	rij(n+q) – rij
Lioness	aggregated network built using all samples	eij(α)		eij(n)	rij(α)
	network built using all samples but the q-sample	eij(α–q)		eij(n–q)	rij(α–q)
	single sample network for the q-sample	eij(q)	n(eij(α) – eij) + eij(α–q)		rij(q)	n(rij(α) – rij) + rij(α–q)

Choice of the Aggregate Network

The LIONESS algorithm outputs a single sample network for each sample in a given data set given an aggregate network. If the data set contains n₁ samples from group 1 and n₂ samples from group 2, there is the legitimate question of whether to build the aggregate network using all n₁ + n₂ samples or to build two different separate reference networks, one for group 1 and one for group 2. In the original paper,¹⁴ the authors investigate the use of non-homogeneous background (page 13 of the Supporting Information¹⁴) and reported minimal differences. However, in this study we explored both implementations that we dubbed, for convenience, as LIONESS single (LIONESS-S) and LIONESS double (LIONESS-D)

• 1.LIONESS-S Consider all samples to build the aggregated network and build single sample networks referring to the pool of all samples, or
• 2.LIONESS-D Consider two different aggregate networks E₁^(α) and E₂ from the two group samples and use them to build two sets of single sample networks, one for group 1 and one for group 2.

ssPCC: Single Sample Network Based on Pearson’s Correlation

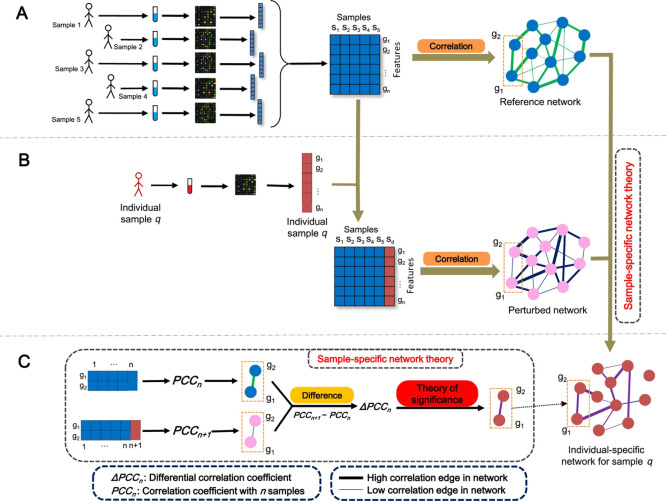
The single sample network based on Pearson’s correlation (which we abbreviate as ssPCC) was proposed by Liu et al.(13) for building sample specific networks in the context of gene regulatory networks for disease characterization. As such, it relies on the availability of a n × mX_n set of reference or control samples to contrast a set of case (possibly disease, in general from a different condition) q-samples. The ssPCC aims to define the single sample network specific to the q-sample(s).

Using the same notation used in the original publication, the single specific network for the q-samples obtained using as reference the n samples in X_n is given by

9

where PCC_n is the Pearson’s correlation matrix²⁰ calculated from the reference set X_n, and PCC_n+1 is the correlation matrix calculated from the (n + 1) × m set made of X_n + the q-sample. The PCC_n is referred to as the “Reference network”, while PCC_n+1 is referred to as the “Perturbed network”. Thus, the single sample network for the q-sample is considered to be the perturbation of the correlation of the m variables in X_n caused by the addition of the q-sample which comes from a different population. A graphical illustration of the ssPCC procedure is given in Figure 2.

Figure 2.

Visual illustration of the ssPCC estimation of single sample network. (A) For a group of n reference samples, a reference network PCC_n can be constructed using Pearson’s correlations. (B) A new sample q is added and the perturbed network PCC_n+1 with this additional sample is calculated. The difference between PCC_n and PCC_n+1 is due to sample q. (C) Differential network ΔPCC_n is constructed taking the difference between perturbed and the reference network PCC_nn + 1 – PCC_n. Figure reproduced and adapted from the original publication,¹³ published under Creative Commons license CC BY-NC-ND.

Using an edge notation similar to the one used for LIONESS, the single sample network for the q-sample can be rewritten as

10

where the superscript n + q indicates the addition of the sample q to the n samples of the reference matrix X_n and r_ij indicates Pearson’s sample correlation between variables i and j. A summary of the notation used is given in Table 1.

The authors proposed to assess the significance of an edge in the single sample network by means of permutation but found that the procedure could be conveniently substituted with a Z-test which is much faster and gives equivalent results (see the section in the original paper¹³). They propose the following Z statistic test

11

which, considering eq 10, can be conveniently rewritten using the edge notation in terms of the sample correlation between variable i and j

12

The Z-statistic is then confronted with the critical values of a standard normal distribution to assess significance.

ssPCC for a two Group Case

The ssPCC algorithm outputs single sample networks only for the case group and not for the reference group. This setting does not allow, per se, to build single sample networks for all samples (i.e., case and reference samples) as in LIONESS. We attempted to bypass this limitation by building single sample networks also for the reference data set by contrasting each sample in the reference data set against the remaining samples, that is, considering each reference sample as a q-sample.

Data Simulations

Numerical Simulations

Simulation Scheme 1

We simulate n × 2 reference data set X_n by sampling from a bivariate normal distribution

13

with population μ₀ = (0, 0) and

14

where ρ₀ is the population (expected) value of r_ij⁽ⁿ⁾ (i.e., of PCC_n) from ssPCC eqs 9 and 10.

We let ρ₀ vary over the values −0.9, −0.7, −0.5, −0.3, 0, 0.3, 0.5, 0.7, and 0.9 to define 9 different reference covariance/correlation structures. The q-sample for which the single sample network is sought using ssPCC, that is, the sample to be added to X_n to calculate PCC_n+1 is also drawn from a bivariate normal distribution with

15

with population mean μ_q = (0, 0) and correlation matrix

16

We let ρ_q vary in the range [0, +1] in increments of 0.1 to define 11 different covariance/correlation structures for variables x and y. We take the difference

17

as a measure of the perturbation effect when a sample q is added to X_n to estimate r_ij^(n+q) (i.e., PCC_n+1): when ρ_q = ρ₀, the q-samples and the reference samples come from the same distribution, which implies that there is no perturbation, hence the expected value of r_ij and r_ij⁽ⁿ⁾ is the same. As ρ_q increases with respect to ρ₀, the perturbation increases, and in consequence ΔPCC_n also increases.

Simulation Scheme 2

This simulation is similar to the Simulation Scheme 1. The only difference is that

18

that is the q-samples come from a population with both different mean and correlation structure.

Simulation Scheme 3

We generated m × m (with m = 20) random correlation matrices Σ_m (with elements ρ_ij ≥ 0 and ρ_ij ≠ ρ_i′j′ for all possible variable pairs) satisfying the property

19

This was achieved using the vine method^21,22 by sampling from a beta distribution Beta(α,β). The variance σ² of the beta distribution was set to 0.1, and the mean μ was numerically optimized to have the sampled data obtain the required average correlation ρ equal to 0.1 to 0.9 in steps of 0.1, within a 5% precision. The mean μ and variance σ² link the α and β parameters by the relationships

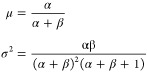20

The optimized μ^opt values (0.113, 0.116, 0.123, 0.135, 0.163, 0.201, 0.262, and 0.382) were used to calculate the α and β shape parameters to be passed to the algorithm.

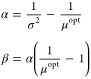21

The correlation matrices Σ_m were used to simulate multivariate normally distributed data N(μ,Σ_m) to be used as a reference and as q-samples. In particular, data with an average correlation of 0.6 and 0.9 were used as reference data sets and data with an average correlation in the range 0.1–0.9 were used as q-samples.

Multivariate Data Simulation

The covariance/correlation matrices defined in the Simulation Schemes 1–3 were used to generate normally distributed multivariate data using the Matlab mvnrnd function.

Data Simulation Using a Dynamic Metabolic Model

To generate metabolites with plausible concentration patterns as observed in metabolomics data, we used a dynamic metabolic model, as described in ref (19). For the sake of completeness, we report here the full simulation strategy.

The model describes the activation of NF-κβ complex (nuclear factor kappa-light-chain-enhancer of activated B cells) and the corresponding response of the intracellular signaling pathway when exposed to lipo-polysaccharide that activates an inflammatory response. It consists of 59 ordinary differential equations recounting the reactions involving 35 metabolites. The model was obtained from the BioModels database²³ (www.ebi.ac.uk/biomodels/) with accession number BIOMD0000000489. Full details on the model building and accessory files can be found in the original publication.²⁴

The model dynamics were constructed and simulated using ordinary differential equations representing 3 types of reactions, namely

• i)Reversible reactions using mass action law
• ii)Irreversible reactions using mass action law
• iii)Enzymatic reactions using Michaelis–Menten kinetics.

We give three reactions used in the model to showcase examples of ordinary differential equations corresponding to each type of reaction and the kinetics involved.

22

23

24

where IRF3 (Interferon Regulatory Factor 3), IKK(IkB kinase), and TAK1:TAB1:TAB2:TRAF6 (complex of mitogen-activated protein kinase kinases) are three of the metabolites/compounds utilized in the NF-κβ activation and corresponding signaling pathway, [P] represents the addition of phosphoryl group via the process of phosphorylation, [metabolite] represents the concentration of the metabolites, and i is the reaction number. For detailed description and information on all metabolites and reactions involved in the NF-κβ model, we refer the reader to the original publication and its Supporting Information.²⁴

Subject-specific concentration profiles were obtained by varying the kinetic constants Km_i, k_i, kf_i, and kr_i for all of the 59 reactions and the initial concentrations c_m for the 4 metabolites with non-null initial concentrations in order to generate subject-specific profiles. All these constants, Km_i, k_i, kf_i, kr_i, and c_m were varied between bounds (a, b) ± 10% of the original values (see eq 25 and following) presented in the original publication. This was achieved by sampling from a uniform distribution U(a,b) to obtain values for each subject. For the j-th individual, the values kf_i, kr_i, k_i, km_i, and c_m for the i-th reaction were defined as

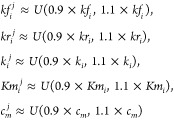25

The rationale of this approach is that models with different parameters will produce different metabolite profiles, like those observed when sampling different subjects in real-life metabolomics experiments.

Using this approach, we generated 500 individual profiles from which we built data sets of different sizes by random sampling.

To mimic different conditions, we introduced perturbations to the model by manipulating the kinetic constants in the following manner

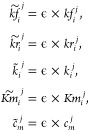26

here ϵ is used as a scaling parameter, the same for all reactions. The value of ϵ was varied over the values 1/10, 1/5, 1/3, 1/2, 1/1.5, 1, 1.5, 2, 3, 5, and 10 which were used to create subject-specific profiles in a similar manner as described above.

Using the same ϵ for all reactions allows us to investigate the performance of the SSN method as a function of the perturbation. From the pool of 500 samples, we randomly sampled (with replacement) subsets of different sizes (n = 10, 25, 50, 100, 250, and 500).

Power of the ssPCC Test

We investigated the actual power of the test (i.e., the probability of rejecting the null hypothesis H₀ when actually false) by means of the Simulation Schemes 1 and 2.

For each combination of Σ_n and Σ_q, we generated a n × 2 reference data set X_n from which we calculated PCC_n and k q-samples to obtain k values of ΔPCC_n which were tested for significance at the 0.05 level and recorded how many times H₀ was correctly rejected to calculate the actual power of the test. In our Simulation Scheme 1, the Null hypothesis H₀ is always false, except when Σ_q = Σ_n. The overall procedure was repeated 1000 times, and the results were averaged over the repetitions. The actual power was calculated for n = 25, 250, and 25,000.

The relative frequency of the rejection of H₀ when Σ_q = Σ_n (i.e.,H₀ true) is the actual α level of test, that is, the actual false positive rate (Type I error).

Principal Component Analysis

We explored differences among single sample networks with principal component analysis (PCA). Each single sample matrix was vectorized and PCA was applied on the edges to investigate the patterns of similarity/difference among the networks. Networks were vectorized by taking only the upper diagonal part of the network (given the symmetry) so that only 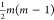edges are considered instead of m². Every m × m single sample network was then collapsed to a 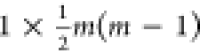vector, and the different networks were then collected in a matrix form suitable for PCA.

Random Forest Prediction Models

Random Forest²⁵ was used to build classification models to explore the use of single sample network edges in a prediction context, that is, to explore whether the use of the edge weights between pair of metabolites possesses higher predictive power than the original metabolite concentrations. We focused on two-group scenarios, which are also the most commonly encountered in metabolomics applications, applying this approach to several public metabolomics data sets.

We built single sample networks using both LIONESS implementations (Single and Double, see the section Choice of the Aggregate Network) and ssPCC (see the section ssPCC for a Two Group Case).

The single sample networks were processed for Random Forest as described in the case of PCA (see the section Principal Component Analysis).

We used the standard Breiman’s Random Forest implementation which uses the Gini impurity as loss.²⁶ We set the number of trees to 1000 and used the default value of 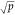(where p is the number of variables) for the “mtry” parameter. We used a 2/3 + 1/3 data split (training + validation) to obtain an unbiased estimation of the classification. We took into account data unbalance using the “strata” option. Each model fitting was repeated 100 times to take into account the variability due to the resampling step used by the RF algorithm to randomly select the same number of subjects from each group and so to build the model on balanced data. The resampling was nested within the cross-validation step used to assess the quality of the prediction models. All results are given as the arithmetic mean over 100 iterations.

Pathway Enrichment Analysis

Pathway enrichment analysis was performed using the built-in function available in the MetaboAnalyst 4.0²⁷ online server (www.metaboanalyst.ca) using the hypergeometric test. The Benjamini–Hochberg method was used for the false discovery rate (fdr) correction.²⁸ We considered significantly enriched those pathways with fdr < 0.01.

Experimental Data

Metabolomic Study Case

As a study case, we considered a data set from a metabolomic investigation of NSTIs. The data set consists of plasma metabolite profiles acquired via GC–MS on 34 NSTI patients enrolled in the INFECT project (Clinicaltrials.gov, NCT01790698). In addition, 24 patients with no known infections were included as controls.

The patients had NSTI of different microbial etiology and were classified into polymicrobial and monomicrobial NSTI.

This data is available at the NIH Common Fund’s National Metabolomics Data Repository (NMDR) website, the Metabolomics Workbench (www.metabolomicsworkbench.org) with Project ID ST00127 where it can be accessed via the Project DOI (DOI: 10.21228/M85H5H). We refer to the original publication¹⁷ for more details on the study design, sample collection, and processing, GC–MS experiments, and clinical information.

Compendium of Publicly Available Metabolomics Data

To explore further the characteristics of the two methods for inference of single sample networks, we used a compendium of 22 data sets that we compiled for a previous study.¹⁹

Ten of these data sets were derived from the compendium assembled by Mendez et al.(29) including studies representative of three of the most frequent metabolomic experimental platforms (nuclear magnetic resonance, NMR; gas chromatography mass spectrometry, GC–MS; and liquid chromatography mass spectrometry, LC–MS) concerning the metabolomic profiling of varying biofluids (serum, plasma, urine, and feces). All studies follow a two-group design (either as primary design or secondary result of the publication or as a subset of a multi-class study) and have varying sample sizes and number of metabolites (variables) present. We have made use of the processed and cleaned data available in Mendez et al.(29) to which we refer the reader for more detailed information on the processing and cleaning of data sets. Metabolites having missing values were either deleted (e.g., dataset MTBLS136) or imputed using the Random Forest procedure implemented in the R package missForest³⁰ (e.g., data set ST001047). We also included other data sets derived from tissue (fat), plant, and fruit extracts along with microbiome data (16S sequencing) and other chemical-based assays on various fluids such as coffee, wine, and oil and finally two transcriptomic data sets. Relevant references and attributes for all data sets are shown in Table 3.

Table 3. Random Forest Classifications of 22 Case-Control Metabolomics Data Sets Using Metabolite Concentrations and Single Sample Network Edges as Described in the Section Random Forest Prediction Models^a.

								classification accuracy
	study ID	refs	platform	type	obs	var	design	conc	ssPCC	LIONESS-S	LIONESS-D
1	KODAMA	(39)	NMR	urine	80 (40/40)	490	subject (A/B)	96.9	100.0	87.5	100.0
2	MTBLS123	(40)	NMR	urine	151 (79/72)	63	shock (pre/post)	99.1	97.4	56.3	81.5
3	MTBLS136	(41)	LC–MS	serum	668 (337/331)	371	postmenopausal hormone (estrogen/estrogen + progesterone)	99.1	99.6	59.4	89.8
4	MTBLS161	(42)	NMR	serum	59 (34/25)	30	chronic fatigue syndrome (case/control)	96.0	96.6	67.8	86.4
5	MTBLS404	(43)	LC–MS	urine	184 (101/83)	120	sex (M/F)	98.3	100.0	67.4	100.0
6	MTBLS547	(44)	LC–MS	caecal	97 (46/51)	35	high fat diet (case/control)	99.9	97.9	84.5	94.8
7	MTBLS90	(45)	LC–MS	plasma	968 (485/483)	189	sex (M/F)	99.4	90.8	63.6	91.3
8	MTBLS92	(46)	LC–MS	plasma	253 (142/111)	138	breast cancer chemotherapy (before/after)	98.3	92.5	62.7	89.3
9	pgmm	(47)	assay	oil	50 (25/25)	7	region (A/B)	100.0	97.3	92.0	98.7
10	pgmm	(48)	assay	coffee	43 (36/7)	12	variety (Arabica/Robusta)	100.0	97.7	95.3	83.7
11	pgmm	(49)	assay	wine	130 (59/71)	27	type (Barolo/Grignolino)	100.0	100.0	81.5	94.6
12	ST000061		GC–MS	tissue	118 (59/59)	157	subcutaeus/visceral fat	94.7	99.1	78.6	87.2
13	ST000369	(50)	GC–MS	serum	80 (49/31)	181	adenocarcinoma (case/control)	89.9	100.0	55.0	80.0
14	ST000496	(51)	GC–MS	saliva	100 (50/50)	69	debridement (pre/post)	99.3	96.0	63.0	91.0
15	ST001000	(52)	LC–MS	stool	121 (68/53)	124	inflammatory bowel diseases (CD/UC)	91.7	98.3	66.9	96.7
16	ST001047	(53)	NMR	urine	83 (43/40)	149	gastric cancer (gastric cancer/healthy)	93.4	100.0	61.4	88.0
17	ST001243	(54)	GC–MS	plasma	98 (48/50)	69	trisomy 21 (yes/no)	99.0	100.0	79.2	91.7
18		(55)	NMR	urine	50 (25/25)	200	cachexia (case/control)	92.2	93.5	70.1	94.8
19		(55)	NMR	urine	77 (47/30)	63		94.4	94.0	96.0	98.0
20		(55)	NMR	urine	60 (30/30)	63		99.4	96.2	67.4	86.6
21		(56)	GC–MS	urine	301 (129/172)	324	sex (M/F)	98.2	99.0	72.4	90.0
22		(57)	GC–MS	plant	70 (35/35)	67	light/dark	91.5	94.3	62.9	84.3

^aAbbreviations: CD: Crohn’s disease. UCL=: Ulcerative colitis. Assay stands for chemical assay.

Software

Calculations were performed using R,³¹ Matlab,³² and Python.³³ Our R implementations for LIONESS and ssPCC are available at www.systemsbiology.nl under the software tab. Original R package for LIONESS by Kuijjer et al.(18) can be also obtained at github.com/kuijjerlab/lionessR and bioconductor.org/packages/lionessR.

Results and Discussion

We begin by noticing that LIONESS and ssPCC are not context or data dependent or depending on how the networks are inferred. Both methods have been originally applied to gene regulatory networks but the statistical framework is totally general; they are both based on “manipulation” of correlations but the way the correlations are calculated and manipulated is totally independent of their origin. There is nothing in how the methods are formulated that is specifically depending on or descending from the correlations originating from gene regulation patterns. The two frameworks are fully generalizable to different biological contexts and applications. Here, we explore their applicability to metabolite–metabolite correlation networks; different approaches can be used to calculate the reference networks depending on the applications, but the way the single sample networks are obtained does not depend on the application.

Power of the ssPCC Test

We investigated the actual power of the ssPCC test (i.e., the probability of rejecting a null hypothesis when actually false) using the Simulation Scheme 1 described in the Material and Methods section.

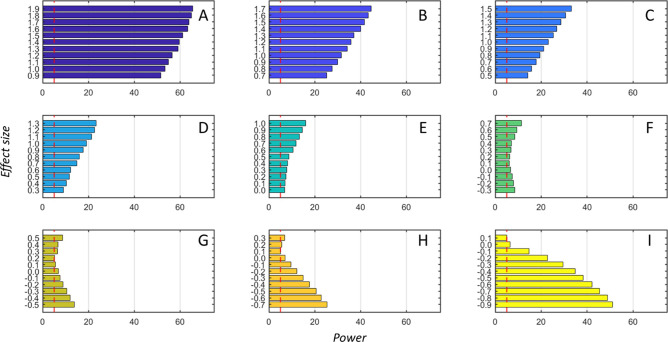
As shown in Figure 3 we observed limited power when the reference samples and the q-samples are drawn from a multivariate normal distribution with different population covariance–correlation matrices but with the same population means (Simulation 1). The results shown are for n = 250.

Figure 3.

Actual power of the ssPCC proposed testing procedure based on a Z-test (see the section ssPCC: Single Sample Network Based on Pearson’s Correlation and eq 12) as a function of the effect size defined in the section Power of the ssPCC Test using the Simulation Scheme 1. The nine panels (A–I) correspond to the different correlation ρ₀ of the ssPCC reference network (PCC_n, see eq 14): the values are −0.9, −0.7, −0.5, −0.3, 0, 0.3, 0.5, 0.7, and 0.9, respectively. For each value of ρ₀, we let ρ_q (see eq 16) to vary in the range [0:1] with increments of 0.1. The effect size is defined as ρ_q – ρ₀, so that for each ρ₀ there are 11 effect size values, indicated on the y-axis of the bar plots. Results are shown for sample size n = 1. The actual power is calculated over 1000 tests. The vertical dashed red lines indicate the 5% level.

The power of the test is heavily dependent on the correlation among x and y in the reference set, that is, on PCC_n; the maximum power achieved is slightly higher than 60% when r_ij⁽ⁿ⁾ = 0.9(PCC_n) (panel A) and reaches its minimum when r_ij is below 0.5 (panels E–G).

Unfortunately, this is the most common case in metabolomics studies: metabolomics correlations are mostly positive and smaller than 0.6 as also shown in Table 2 where the distribution characteristics of correlation values (that is, r_ij⁽ⁿ⁾, PCC_n are given for 10 case-control metabolomics data sets. Thus the most common situation observed in real-life metabolomics studies is the situation in which the test has less power to detect differences between the q-sample and the reference set.

Table 2. Association Between Metabolite Differential Expression and Single Sample Edges Found to Be Significant with the Proposed ssPCC Test^a.

		% SSN edges associated with DE metabolites			average ssPCC SSN edge			correlation in reference Data
	data set	mean	95% CI		mean	95% CI		mean	95% CI
1	MTBLS136	56.1	39.6	77.8	0.01	0.01	0.01	0.03	–0.17	0.43
2	MTBLS161	82.3	42.6	98.3	0.02	0.00	0.12	0.35	–0.38	0.79
3	MTBLS404	67.9	0.0	97.3	0.01	0.00	0.05	0.30	–0.05	0.73
4	MTBLS547	76.3	0.0	100.0	0.01	0.00	0.07	0.29	–0.22	0.84
5	MTBLS90	84.7	69.3	97.8	0.01	0.00	0.01	0.06	–0.18	0.62
6	MTBLS92	85.0	65.3	98.3	0.01	0.00	0.03	0.21	–0.09	0.80
7	ST000369	39.5	14.6	68.1	0.11	0.08	0.17	0.03	–0.31	0.50
8	ST000369	54.1	32.0	77.8	0.02	0.01	0.08	0.03	–0.29	0.45
9	ST001000	75.3	0.0	98.2	0.02	0.00	0.09	0.14	–0.28	0.95
10	ST001047	75.3	0.0	98.2	0.02	0.00	0.09	0.14	–0.28	0.95

		% SSN edges associated with DE metabolites			average Lioness SSN edge			correlation in aggregate data
	data set	mean	95% CI		mean	95% CI		mean	95% CI
1	MTBLS136	55.10	49.1	62.4	0.55	0.33	0.95	0.03	–0.16	0.43
2	MTBLS161	80.02	42.7	88.2	0.63	0.34	1.22	0.30	–0.19	0.67
3	MTBLS404	79.34	62.3	87.5	0.60	0.32	1.20	0.24	–0.05	0.66
4	MTBLS547	81.20	63.9	88.6	0.62	0.33	1.22	0.31	–0.13	0.77
5	MTBLS90	82.46	76.5	87.8	0.63	0.34	1.16	0.06	–0.17	0.62
6	MTBLS92	82.92	76.5	88.8	0.63	0.34	1.23	0.19	–0.07	0.80
7	ST000369	31.98	23.7	42.6	0.59	0.32	1.88	0.04	–0.23	0.60
8	ST000369	51.28	35.7	61.5	0.54	0.32	0.95	0.03	–0.22	0.53
9	ST001000	81.10	65.2	87.8	0.60	0.33	1.10	0.15	–0.25	0.93
10	ST001047	81.10	65.2	87.8	0.60	0.33	1.10	0.15	–0.25	0.93

^aThe % of edges associated with differential expressed metabolites is shown together with the average ssPCC edges and with the average correlation of the reference network calculated on 10 case-control metabolomics data sets. More information on the data can be found in Table 3.

The power of the test depends of course on n and should tend to 1 as n → ∞. However, we did not observe any strong dependence on n: for n = 25, the maximum power was ≈64% which increased to ≈66% for n = 25,000 when PCC_n = 0.9, which indicates that the size of the reference data set has little influence on the actual power of the test.

The limited power of the test under Simulation Scheme 1 can be understood by considering eq 4 in the original publication.

The authors derived an interesting relationship (in the case n ≫ 1) linking the ΔPCC_n, that is, r_ij^(q) and the difference of the level of variable i and j measured on the q-sample with respect to the average level of the same variables in the reference data

27

where

28

Several interesting observations can be derived from eq 27:

• 1.ΔPCC_n → 0 if Δx and Δy are zero, that is if the q sample is from a population with the same average level (μ_q = μ_n) of the reference population as in Simulation 1.
• 2.PCC_n+1 does not appear in the (re)definition of ΔPCC_n: only the difference in the levels of X and Y with respect to the correlation of X and Y in the reference define ΔPCC_n.

This explains the very limited power observed in Figure 3. If the reference samples and the q-samples are drawn from a multivariate distribution with the same population, it means that both Δx and Δy tend to 0 and ΔPCC_n tends to zero even if PCC_n ≠ 0.

• 3.If the number of samples in the reference data set n is very large, adding the q sample has practically no influence: it is not the perturbation of the correlation (i.e., PCC_n+1 – PCC_n) that it is tested, but some function of the differences of X and Y with respect to the average values in reference data. This observation is supported by empirical evidence shown in Table 2 where SSN networks were built for 10 case-control metabolomics data sets: the vast majority of significant SSN edges are associated with metabolites whose concentrations are significantly different between the two conditions.
• 4.If we plug eq 27 in eq 11, we obtain the following expression for the Z-statistic

29

which does not depend explicitly on n, since PCC_n is fixed a priori, this explains why increasing the dimensionality of the reference data set X_n has little influence on the power of the test.

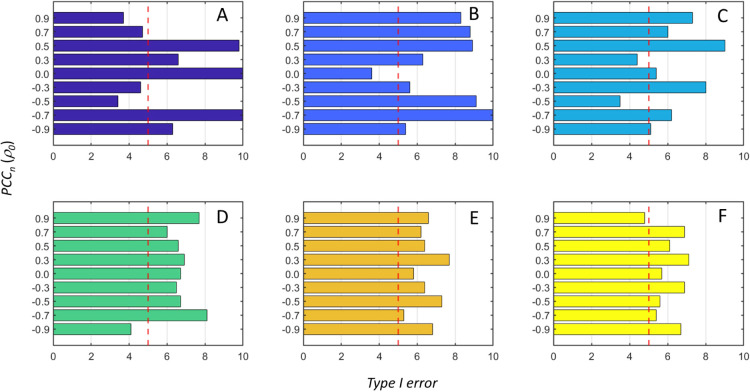
• 5.ΔPCC_n can be different from zero also when PCC_n is zero, that is when the reference samples and the q-samples are from populations with the same covariance–correlation structure; this happens when Δx, Δy ≠ 0. This explains the slightly inflated Type I error observed in Figure 4.
• 6.ΔPCC_n can be zero even if Δx, Δy, and PCC_n are all different from zero. This can happen, for instance, when

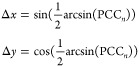30

or

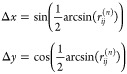31

Figure 4.

Actual Type I error (α) of the ssPCC proposed testing procedure based on a Z-test (see the section ssPCC: Single Sample Network Based on Pearson’s Correlation and eq 12) as a function of the effect size defined in the section Power of the ssPCC Test. The nominal 5% level is indicated by the vertical dashed red line. The six panels (A–F) correspond to the different sample sizes used, which are 10, 50, 100, 500, 1000, and 10,000, respectively. The actual α is calculated over 1000 tests.

Relationship between LIONESS and ssPCC Single Sample Networks

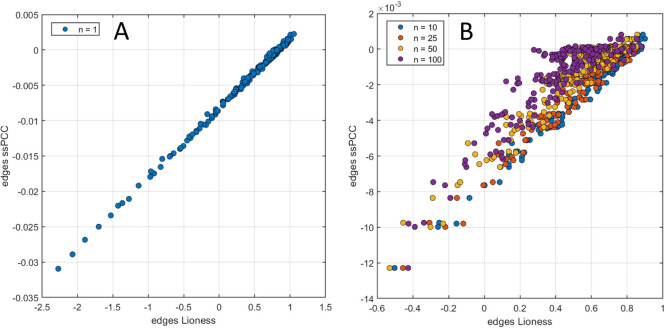
If a correlation is used as a measure of variable association, the two methods are functionally related, and from the definition of the ssPCC and LIONESS edges, it follows that the latter can be written as a function of the ssPCC edges. In particular, when the data set X^(α) used to build the aggregated network in LIONESS is equivalent to the reference data set used in ssPCC, there is an almost perfect linear relationship between the edges of the q-sample network estimated using LIONESS and using ssPCC, as can be seen in Figure 5 panel A. This relationship deteriorates when X^(α) is not equal to X_n, that is when there is more than one sample belonging to a group different from the reference (Figure 5 panel B). Note the different scale of the edge weights: for ssPCC, the edges are bounded between −2 and +2, being defined as the difference between two correlations; and for LIONESS, if correlations are used, the edges are bounded between 1 – 2n and 2n – 1.

Figure 5.

Comparison of the Lioness and ssPCC single sample edges. (A) Scatter plot of the edges for a q-sample obtained when the data set X^(α) used to build the aggregated network in Lioness is equivalent to the reference data set used in ssPCC. (B) Scatter plot of the edges for a q-sample obtained when X^(α) is not equal to X_n, i.e., when there is more than one sample belonging to a group different from the reference. Note the different scale of the edge weights.

A relationship similar to eq 27 can be derived also for LIONESS. It is enough to note that r_ij⁽ⁿ⁺¹⁾ is actually the correlation calculated using all samples (thus including the q-samples i.e., r_ij) in LIONESS, and PCC_n is the correlation calculated using all but the q-sample, that is r_ij^(α–q). The LIONESS edge can be rewritten as

32

This also establishes that the edges of a single sample network estimated with LIONESS are a function of both the perturbation of the correlation and the difference between the levels of the q-sample and the mean of the remaining n – 1 samples.

Comparison of ssPCC and LIONESS on Simulated Data

Simulated Data with Different Levels of Correlation

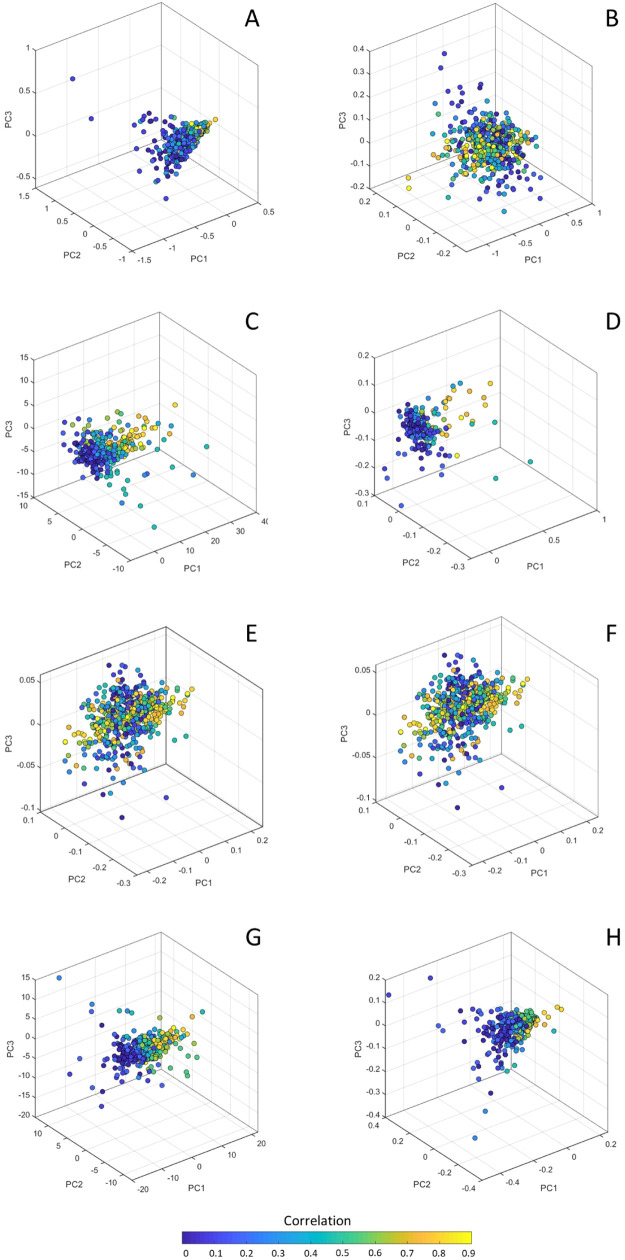
The first simulation entails the case of the reference data (m = 20 variables) with zero mean and average correlation equal to 0.6; this value was chosen because most parts of the observed metabolomic correlations are smaller than 0.6.³⁴ The q-sample comes from data with an average correlation between 0 and 0.9 and a mean equal to 0 or 10. The results are shown in Figure 6, panels A–D. As can be seen, there is no obvious separation of the single sample networks as a function of the effect size; although, a slight separation appears when the mean of the reference and q-sample differ, especially between single sample networks from a sample with extreme average correlation (i.e., 0 and 0.9).

Figure 6.

Scatter plot from PCA of the single sample networks obtained with LIONESS-S (left column) and ssPCC (right column). Panels (A–D) refer to simulation with reference data (20 variables) with average correlation equal to 0.6, while the q-sample is from a population with correlation between 0 and 0.9 and mean equal to 0 (panels A,B) or 10 (panels C,D). Panels (E–H) refer to simulation with reference data with average correlation 0.9, while the q-sample is from a population with correlation between 0 and 0.9 and mean equal to 0 [i.e., data from simulation 1, panels (E,F)] or 10 [i.e., data from simulation 2, panels (G,H)]. Each point in the PCA plot is a vectorized version of the single sample networks, color-coded according to the population correlation from which the q-samples are sampled.

When the same exercise is repeated with reference data with an average correlation equal to 0.9 (Figure 6, panel E–H), the results are similar with a slight separation emerging only when the reference samples and the q-samples come from populations with different means.

Comparison on NF-κβ Dynamic Model Data

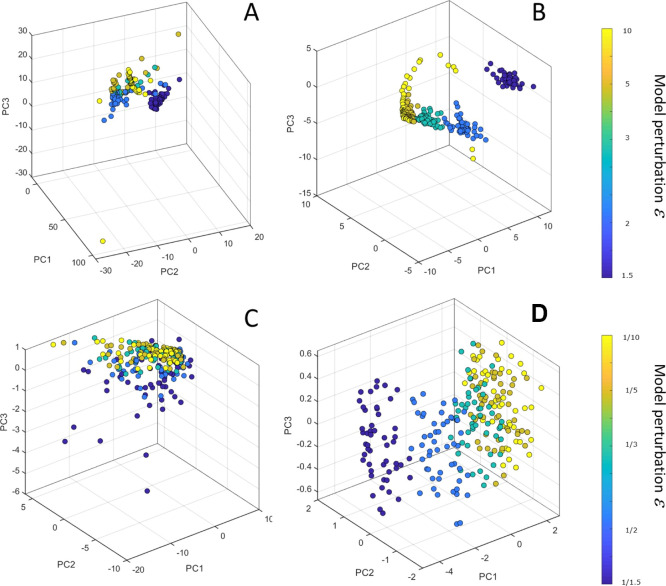
We compared the LIONESS and ssPCC on data simulated from a dynamic model for the NF-κβ pathway where model parameters were manipulated to introduce increasing levels of perturbation with respect to the original unperturbed model; this was accomplished by multiplying/dividing the kinetic parameter (see eqs 27 with ϵ = 1, 1.5, 2, 3, 5, and 10). Results are shown in Figure 7; n = 50 samples were considered for each configuration.

Figure 7.

Scatter plot from PCA of the single sample networks obtained with LIONESS-S (left column) and ssPCC (right column) on data simulated using a dynamic model of the NF-kB metabolic pathway. Panels (A,B) give results on data obtained by multiplying the kinetic parameters by a factor ϵ = 1, 1.5, 2, 3, 5, and 10; see eq 27. Panels (C,D) give results on data obtained by multiplying the kinetic parameters by a factor ϵ = 1/10, 1/5, 1/3, 1/2, and 1/1.5). Each point in the PCA plot is a vectorized version of the single sample network, color-coded by the magnitude of the perturbation. For each ϵ configuration, n = 50 samples were considered.

In the case of the multiplicative perturbation of the model, networks tend to cluster according to the level of perturbation with highly perturbed networks clustering away from those corresponding to low perturbation. This is particularly evident for ssPCC-derived networks with very clear separation among the clusters (Figure 7 panel B); however, the separation among LIONESS-based networks is much less evident (panel A).

For data from the perturbed model obtained by dividing the kinetic constants (see eq 27 with ϵ = 1/10, 1/5, 1/3, 1/2, and 1/1.5), the single sample networks obtained with LIONESS are not resolved, and it is not possible to distinguish among the different groups corresponding to the different perturbation levels (Figure 7, panel C). On the contrary, the networks obtained with ssPCC are very well resolved, and clear differences appear among the groups (Figure 7, panel D).

Use of Single Sample Edges for Group Prediction and Classification

We explored the potential of single sample network edges for classification purposes by replacing actual observed metabolite concentrations with the pairwise edges, the rationale being that, as follows from eqs 27 and 32, single-sample edges are a function of both difference in correlation and in level and thus, in some case, can bear more information than level alone.

To this scope, we compared the accuracy of Random Forest classification models on 25 publicly available data sets (see the section Compendium of Publicly Available Metabolomics Data). For each data set, we built four different Random Forest classification models using:

• 1.Original concentration/abundance profiles.
• 2.The edges of the single sample networks built using ssPCC.
• 3.The edges of the single sample networks built using LIONESS and all samples to build the aggregate network (LIONESS-D).
• 4.The edges of the single sample networks built using LIONESS and only group-specific samples to build the aggregate network (LIONESS-S).

In total, we have three ways to build single sample network edges for a two-class problem to be used for classification purposes.

The results are given in Table 3. Under the assumption that single sample edges hold more information content than the concentration profiles, we expected the Random Forest models built on edges to have higher accuracy than those built on the original concentration values.

We observed that in general, classification accuracy is already very high when using the original values. However, in 13 cases out of 22, the use of ssPCC edges gives better (or equal) classification accuracy.

For some data sets, the use of single-sample edges in place of concentrations resulted in better discrimination. For instance, for data 13 the accuracy increases from 89.9 to 100% and better discrimination between cases and controls is also obtained for data sets 1, 3, 4, 5, 12, 15, 16, 17, 18, 20, and 22. In other cases, a reduction in accuracy can be observed.

When using the LIONESS-D approach (akin to the strategy we devised for ssPCC), the accuracy was better only in 5 cases out of 22, while when using the LIONESS-S accuracy was better only in one case (data set 19): in all other cases the accuracy was remarkably lower.

When Random Forest was run on edges from LIONESS-S, discrimination accuracy was lower with the sole exception of data set 19. This can be explained by the process of separating case and control data before running the LIONESS algorithm. In this format, the matrix E^q is built as a function of E^(α) as shown in eq 7; however, here all samples in E^(α) come from the same classification group causing the variation between single samples to be much lower due to the lower difference in E^α and E^(α–q) as compared to that in LIONESS-D.

There is a large difference depending on how the aggregate network is built. In the original publication,¹⁴ the authors discussed the problem of how to build the aggregate network when in the presence of samples from non-homogeneous populations (basically considering the two approaches used here). They found minimal difference (verbatim) in the accuracy of the reconstruction of the single sample networks but did not explore the edge reconstruction in a discriminant/classification setting.

We can also comment that calculating correlations from a non-homogeneous population is not statistically a sound strategy since sample correlation must be calculated from samples drawn from the same population. It is simple to show with simulations that if half of the samples come from a population with correlation ρ = 1 and half from a population with ρ = 0, the sample correlation will be around 0.5 and this will lower the single sample edge.

Classification models built from ssPCC and LIONESS-D edges often yielded similar albeit lower accuracy. This is not too unexpected as when LIONESS is expressed as a function of ssPCC, as shown in eq 32, it descends that the LIONESS single sample edge also depends on Δx_i and Δx_j which are the deviations of the q-sample from the average of the reference data. In the LIONESS-D approach, the deviations Δx_i and Δx_j are calculated from each q-sample from data sets that are homogeneous to the q-sample and thus can be expected to be small, and this also lowers the edges’ values. This is not the case for all ssPCC edges; in our modification, the deviations for q-samples in the control group are estimated from samples homogeneous to the q-samples, but for the control group, the q-samples are not homogeneous to the reference (which is made from control samples) and this makes the edges larger. This can explain the markedly different behavior of the different single sample edges when used for discrimination between two groups.

We shall conclude by remarking that in a classification setting the use of single sample edges as derived from ssPCC and LIONESS-D can be used only in an exploratory or confirmatory setting but not to predict new, unknown, q-samples; the network must be constructed by contrasting the unknown sample either with the case or the control group without knowing to which group the q-sample actually belongs. Unknown q-samples can be predicted using the edges from LIONESS when the aggregates network is constructed using all samples from both groups simultaneously.

Metabolomics Case Study: NSTIs

In order to delve deeper into the characteristics of the two methods and to investigate whether (possibly) new biological information can be gained from the use of single sample network, we analyzed in detail metabolomics data concerning metabolite plasma profiles collected from patients suffering from NSTIs, fast-spreading, aggressive bacterial infections associated with high morbidity and mortality.^35,36 The study comprised 34 NSTI patients and 24 surgery patients with no known infection or morbidity acting as controls. This data has been previously analyzed using standard statistical (univariate) approaches and differential correlation analysis.¹⁷

Single Sample Network Analysis

We began by building the aggregate reference networks for ssPCC and LIONESS: we used the LIONESS-S approach here as referenced in section LIONESS: Linear Interpolation to Obtain Network Estimates for Single Samples, as this is the approach put forth in the original publication.¹⁴ The reference networks are given in Figures 9A and 10A, respectively.

Figure 9.

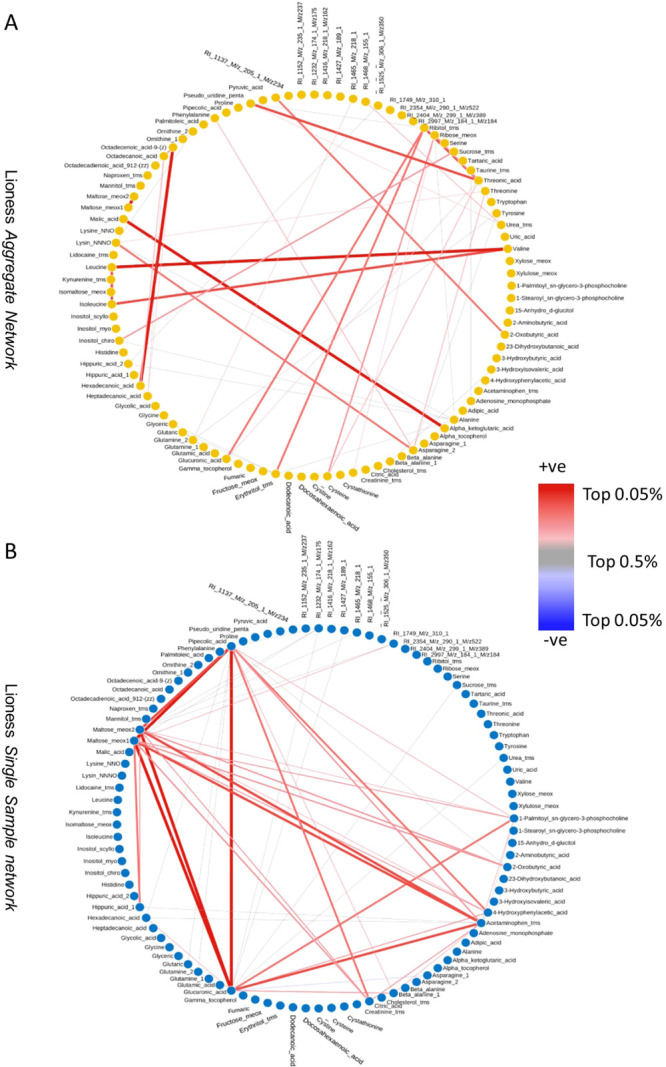
(A) Aggregate (reference) network for Lioness (B) Lioness single sample network for NSTI patient n. 24. The top (in absolute value) 0.05% edges are shown. The link width is proportional to the edge weight.

Figure 10.

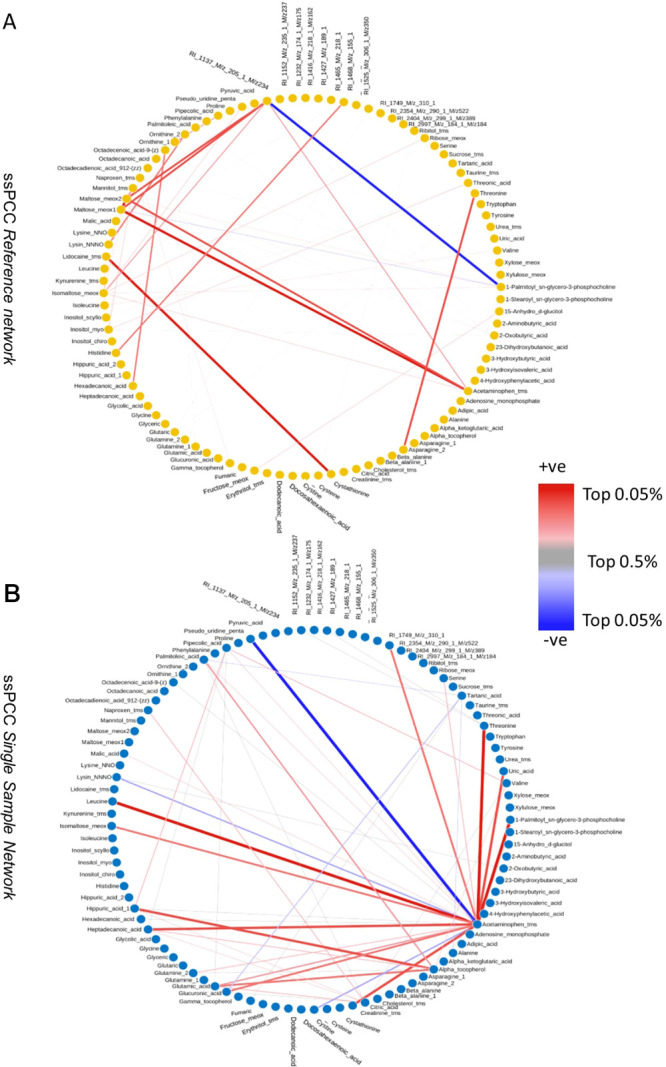
(A) Aggregate (reference) network for ssPCC (B) ssPCC single sample network for NSTI patient n. 24. The top (in absolute value) 0.05% edges are shown. The link width is proportional to the edge weight.

As expected, the two aggregate results/reference networks are rather different with different relevant patterns of correlations. We recall that in this case, for ssPCC the reference network is the correlation matrix obtained from the control group, while for LIONESS, the aggregate is obtained from the correlation of the complete data set (NSTI + control samples).

As can be seen, there are obvious differences. While the ssPCC reference network seems to cluster around Maltose, the LIONESS aggregate network seems to cluster around valine and ribitol.

We performed pathway analysis on the top 25 perturbed edges for both networks with the aim of assessing network properties and identifying structural and functional units in the metabolic networks.³⁷ We found significant enrichment for aminoacyl-tRNA biosynthesis (P-value = 3.29 × 10^–5, fdr = 0.0028) and lysine degradation pathways (P-value = 1.33 × 10^–4, fdr = 0.0056) for the LIONESS aggregate network (Figure 9A) and significant enrichment for the aminoacyl-tRNA biosynthesis (P-value = 2.45 × 10^–5, fdr = 0.002) and valine, leucine, and isoleucine biosynthesis pathways (P-value = 1.15 × 10^–4, fdr = 0.005) for the ssPCC reference network (Figure 10A). These results indicate that the single sample networks are going to be constructed against a background that may encode for different biological phenomena and as such, they will bear different biological information. This can be seen also from the results shown in Figure 5 where ssPCC and LIONESS edges are contrasted: two different reference networks result in related but different single sample edges.

It is interesting to note that no significant enrichment (after adjustment for multiple corrections) was found when pathway enrichment analysis was performed only on differentially abundant metabolites (see Table 3 in Afzal et al.(17)). This is a clear indication that information on metabolic rewiring and/or disruption is reflected not only in a change in metabolite levels but also in changes in the correlations between metabolite concentrations. In this case, single sample edges carry more information about changes in metabolism in NSTI than simple metabolite abundances.

We constructed the single sample networks for the 34 NSTI patients; as shown in Figure 8 the single sample networks obtained using ssPCC and LIONESS are markedly different, confirming what was observed using simulated data (see the sections Numerical Simulations and Data simulation using a dynamic metabolic model and Figures 6 and 7). LIONESS and ssPCC networks cluster separately and, in general, LIONESS sample edges show higher variability than the corresponding ssPCC edges. In particular, there is a group of networks (corresponding to samples 5, 6, 10, 15, 20, 28, and 29) that are markedly different from the others. This is particularly evident for the LIONESS edges. All samples belong to patients with concurrent comorbidities with NSTI; all these patients are female, except patients 28 and 29.

Figure 8.

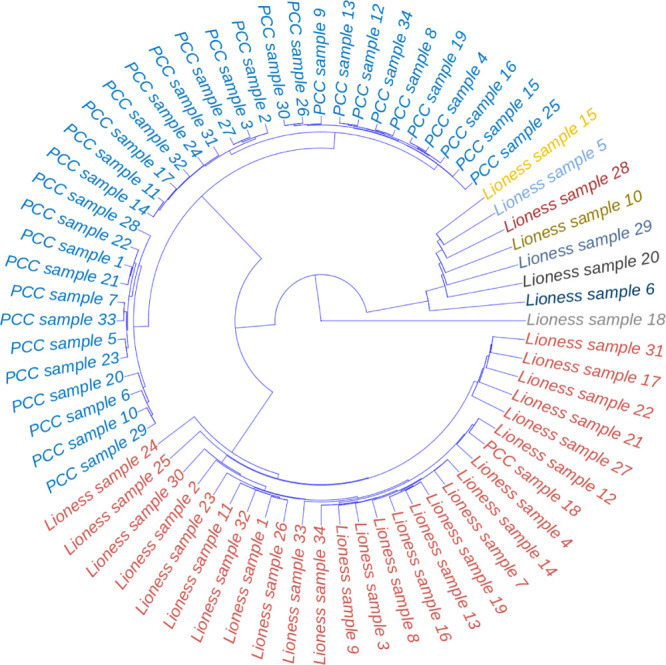
Clustering dendrogram of the single sample networks for the metabolomics study case. The single samples for the subjects affected by NSTIs are shown. Samples are color-coded by distance/similarity: red, for LIONESS (using LIONESS-S implementation) and blue for ssPCC single sample networks. Distances are calculated on the vectorized networks.

Moreover, the ssPCC edges of sample 18 are more similar to LIONESS edges than to the other ssPCC samples.

We then focused on single sample networks built from the same sample profile using the two methods. We built correlation matrices among ssPCC and LIONESS edges and selected the NSTI patient for whom the single sample networks obtained with ssPCC and LIONESS were most different (i.e., the least correlated). We recovered from this analysis the single sample network for sample 24 who is a NSTI patient having a polymicrobial etiology. The corresponding single sample networks for ssPCC and LIONESS are given in Figures 9B and 10B where only the largest edges are shown (see figure caption for more details).

As can be seen, there are obvious differences. In the LIONESS single sample network (Figure 9B), the edges connecting acetaminophen and glucuronic acid are the most disrupted. In the ssPCC single sample network (Figure 10B), the edges connecting acetaminophen, α-tocopherol (vitamin E), maltose, and proline are altered. In the original publication,¹⁷ standard differential network analysis was performed to compare metabolite–metabolite connectivity in NSTI and surgery control (see Table 4 in Afzal et al.¹⁷); glucuronic acid, and maltose were among the most differentially connected metabolites but not acetaminophen and α-tocopherol.

Table 4. Accuracy of the Random Forest Models Constructed Using the Concentration/Abundance Profiles and the Edges of Single Sample Networks Built from the Metabolomics Data Set Investigating NSTIs.

	classification accuracy
Model	Conc	ssPCC	LIONESS-S	LIONESS-D
NSTI vs Controls	94.7	98.3	98.3	100.0
mono vs poly	87.1	82.5	82.5	82.5
StreptococcusvsStaphylococcus	85.6	75.9	75.9	79.3

Univariate Analysis of the Single Sample Network Edges

Furthermore, we compared the edges of LIONESS and ssPCC single sample networks between NSTI patients and controls using a t-test and we compared the results with those obtained in the original publication using the metabolite concentrations. In particular, we compared NSTI and control group on:

• 1.Metabolite concentrations
• 2.Metabolite–metabolite single sample network edges defined using ssPCC
• 3.Metabolite–metabolite single sample network edges defined using LIONESS-S
• 4.Metabolite–metabolite single sample network edges defined using LIONESS-D.

Results are given in Table 6 that contains the top 10 metabolites/edges (sorted by P-value). In general, we observed that metabolites whose concentration is different between NSTI patients and controls are in general those whose single sample edges are found to discriminate among the two groups.

Table 6. Results of t-Test on the Single Sample Edges Obtained Using Lioness (Two Implementations, Mono and Double) and ssPCC Together with Results from a t-Test on the Metabolite Concentrations (Column “Conc”)^a.

	Concentrations	ssPCC edges	LIONESS-S edges	LIONESS-D edges
1	1-stearoyl sn-glycro-3-phosphocholine	RI 2997 m/z 184 1 m/z 184 & RI 2354 m/z 290 1 m/z 522	cystathionine & glutaric acid	RI 2997 m/z 184 1 m/z 184 & RI 2354 m/z 290 1 m/z 522
2	1-palmitoyl sn-glycero-3-phosphocholine	RI 2997 m/z 184 1 m/z 184 & RI 1232 m/z 174 1 m/z 175	cystathionine & naproxen tms	RI 2997 m/z 184 1 m/z 184 & RI 1232 m/z 174 1 m/z 175
3	isomaltose meox	alpha tocopherol & RI 2997 m/z 184 1 m/z 184	lidocaine tms & glutaric acid	alpha tocopherol & RI 2997 m/z 184 1 m/z 184
4	RI 1416 m/z 218 1 m/z 162	alpha tocopherol & tryptophan	cystathionine & lidocaine tms	α-tocopherol & tryptophan
5	α-tocopherol	1-palmitoyl sn-glycero-3-phosphocholine & maltose meox2	pseudo uridine penta & threonic acid	1-palmitoyl sn-glycero-3-phosphocholine & maltose meox2
6	tryptophan	isomaltose meox & RI 1232 m/z 174 1 m/z 175	3-hydroxyisovaleric acid & beta alanine	isomaltose meox & RI 1232 m/z 174 1 m/z 175
7	ribose meox	1-palmitoyl sn-glycero-3-phosphocholine & maltose meox1	2,3-dihydroxybutanoic acid & glycine	1-palmitoyl sn-glycero-3-phosphocholine & maltose meox1
8	glucoronic acid	RI 2997 m/z 184 1 m/z 184 & fumaric acid	heptadecanoic acid & asparagine	RI 2997 m/z 184 1 m/z 184 & fumaric acid
9	RI 1427 m/z 189 1	citric acid & glutamine-2	octadecanoic acid & asparagine	citric acid & glutamine-2
10	RI 2354 m/z 290 1 m/z 522	alpha tocopherol & RI 1416 m/z 218 1 m/z 162	octadecenoic acid-9-(z) & asparagine	alpha tocopherol & RI 1416 m/z 218 1 m/z 162

^aThe top 10 edges (sorted by P-values) are given.

Random Forest Analysis on Single Sample Network Edges

Following the same strategy outlined in Section Random Forest Prediction Models, we performed Random Forest classifications to analyze the prediction accuracy of single sample edges in comparison with the simple correlations. In particular, Random Forest classification models were built for the following two-group comparisons:

• 1.NSTI (n = 34) versus controls (n = 24)
• 2.Mono-microbial NSTI (n = 26) versus poly-microbial NSTI (n = 7)
• 3.Streptococcus NSTI (n = 20) versus Staphylococcus aureus NSTI (n = 8)

The models were built using the original concentration/abundance profiles, the edges of the single sample networks were built using ssPCC, the edges of the single sample networks were built using LIONESS-S, and the edges of the single sample networks were built using LIONESS-D. Classification accuracies are given in Table 4. Regarding the comparison between NSTI and controls, the use of the single sample network edges increases the accuracy (up to 100%), although the use of simple concentrations gives excellent classification (94.7%). The logic behind the use of single sample network edges is that additional information is contained in the relationships (or disruption thereof) among (pairs of) metabolites that is contained in, or is additional to, the metabolite levels and thus better accuracy should be, in principle, obtained. However, this is not always the case. For the comparison between mono versus poly microbial infection and Streptococcus versus Staphylococcus infection, the use of single sample network results in decreased accuracy. This may well depend on the limited sample size used to build the aggregated/reference networks that can lead to instability in the estimation of these networks¹² and, as a consequence, low-quality estimation of the single sample networks. We also compared the edge and metabolite importance in the Random Forest models using the mean decrease Gini index as the importance measure. The top metabolites and edges from the models are shown in Table 5. The metabolites whose edges mostly contribute to the separation between NSTI and controls tend to be the metabolites whose concentration is also different between the two groups, confirming that the single sample edges bear content of both concentration and pairwise relationships as also discussed in the section ssPCC: Single Sample Network Based on Pearson’s Correlation.

Table 5. Random Forest Classification of NSTI Patients and Controls Using Metabolite Concentrations and ssPCC and LIONESS Single-Sample Network Edges^a.

	Concentrations	ssPCC edges	LIONESS-S edges	LIONESS-D edges
1	1-palmitoyl sn-glycero-3-phosphocholine	1-stearoyl sn-glycero-3-phosphocholine & 1-palmitoyl sn-glycero-3-phosphocholine	lidocaine tms & glutaric acid	alpha tocopherol & RI 2997 m/z 184 1 m/z184
2	1-stearoyl sn-glycero-3-phosphocholine	RI 2997 m/z 184 1 m/z184 & RI 2354 m/z 290 1 m/z522	Naproxen tms & Lidocaine tms	RI 2997 m/z 184 1 m/z184 & maltose meox1
3	RI 2997 m/z 184 1 m/z184	1-palmitoyl sn-glycero-3-phosphocholine & RI 2354 m/z 290 1 m/z522	pseudo uridine penta & threonic acid	RI 2997 m/z 184 1 m/z184 & RI 2354 m/z 290 1 m/z522
4	RI 1416 m/z 218 1 m/z162	1-palmitoyl sn-glycero-3-phosphocholine & Citric acid	cystathionine & lidocaine tms	RI 2354 m/z 290 1 m/z522 & tryptophan
5	isomaltose meox	1-stearoyl sn-glycero-3-phosphocholine & RI 2354 m/z 290 1 m/z522	naproxen tms & glycine	1-stearoyl sn-glycero-3-phosphocholine & 1-palmitoyl sn-glycero-3-phosphocholine
6	pibose meox	1-palmitoyl sn-glycero-3-phosphocholine & RI 2997 m/z 184 1 m/z184	naproxen tms & glutamine	1-palmitoyl sn-glycero-3-phosphocholine & RI 2354 m/z 290 1 m/z522
7	citric acid	1-stearoyl sn-glycero-3-phosphocholine & citric acid	cystathionine & glutaric acid	RI 2354 m/z 290 1 m/z522 & RI 1416 m/z 218 1 m/z162
8	tryptophan	alpha tocopherol & tryptophan	naproxen tms & glutaric acid	RI 2354 m/z 290 1 m/z522 & citric acid
9	alpha tocopherol	1-stearoyl sn-glycero-3-phosphocholine & tryptophan	octadecenoic acid-9-(z) & asparagine-2	alpha tocopherol–tryptophan
10	RI 2354 m/z 290 1 m/z522	tryptophan & RI 1416 m/z 218 1 m/z162	naproxen tms & lysine	RI 1416 m/z 218 1 m/z162 & glyceric acid

^aThe top 10 metabolites and metabolite–metabolite edges are shown in decreasing order of importance (given by the Mean Decrease Gini Index).

Conclusions

In this study, we investigated and assessed the utility of two methods for the inference of single sample networks in a metabolomics context: LIONESS (Linear Interpolation to Obtain Network Estimates for Single Samples)¹⁴ and ssPCC (single sample network based on Pearson’s correlation).¹³

The two methods are functionally related and when compared on simulated data with different correlative properties, we found both methods to have limited ability to describe different situations. However, on data from a NF-kB dynamic metabolic model, we found that only the ssPCC single sample networks are able to describe different situations arising from perturbations of the model.

We found the statistical procedure proposed in ssPCC to have limited power and to be heavily dependent on the particular reference networks and of little utility for practical applications.

We explore the potential of single sample edges to be used in place of concentration to discriminate between groups in a case–control scenario. To this scope, we used two different implementations of LIONESS and proposed a work-around to adapt ssPCC to this scenario. Using Random Forest as a classification algorithm, we found that in 13 cases out of 22 the use of ssPCC edges gives better (or equal) classification accuracy than (to) the use of actual metabolite concentrations, while, overall, the use of LIONESS sample resulted in worse prediction models.

We found that single sample networks built off of a control group (like ssPCC and LIONESS-S) yield better results than those built off of similar samples in a classification setting; however, this approach does not allow for generalization and as such should be used as an exploratory tool.

We finally applied the two methods to analyze a metabolomics study pertaining to NSTIs.

NSTI-specific single sample networks obtained with the two methods are markedly different and are likely to describe different ongoing biological processes. We found that single sample edges, either from ssPCC or LIONESS, gave better prediction results in distinguishing between NSTI patients and controls but not in other comparisons aimed to distinguish between disease etiology. In general, ssPCC edges found to be important in discriminating groups involve metabolite pairs that are found important when comparing groups with a standard t-test performed on concentrations.

There are still some aspects of single sample networks to be elucidated, the most important being a proper statistical validation for both ssPCC and LIONESS.

We used both methods taking Pearson’s correlation as an association measure and building networks using the standard correlation matrix, but the two methods are general. Other measures of association can be used, such as partial correlation, as proposed by the authors of ssPCC,³⁸ or mutual information, although the latter measure does not give any improvements, at least for what concerns metabolomics data.¹⁹ In addition, more sophisticated approaches can be used for network inference as proposed by Kuijjer et al.(14)

Overall, we think single sample networks seem to be a promising tool for the analysis of metabolomics data. For instance, we have shown that single sample edges provide more information than simple concentrations for pathway analysis since they encode both levels and relationships between metabolites. Single sample networks can be used as exploratory tools and can be paired with standard univariate and multivariate tools.

Author Contributions

E.S. designed the study and supervised the work. S.J. and E.S. performed data analysis. S.J and E.S. wrote the manuscript. All authors read and approved the final version of the paper.

The authors declare no competing financial interest.