Effect of ultrasonic frequency and surfactant addition on microcapsule destruction

Highlights

• •The destruction of microcapsules was frequency dependent.
• •The resonance frequencies of the microcapsules were calculated using elastic modulus measurements.
• •Cavitation bubble size changed with surfactant addition.
• •Sonoluminescence was used to evaluate bubble activity.

Abstract

In a previous study, we found that cavitation bubbles cause the ultrasonic destruction of microcapsules containing oil in a shell made of melamine resin. The cavitation bubbles can be smaller or larger than the resonance size; smaller bubbles cause Rayleigh contraction, whereas larger bubbles are not involved in the sonochemical reaction. The activity in and around the bubble (e.g., shear stress, shock wave, microjet, sonochemical reaction, and sonoluminescence) varies substantially depending on the bubble size. In this study, we investigated the mechanism of the ultrasonic destruction of microcapsules by examining the correlations between frequency and microcapsule destruction rate and between microcapsule size and cavitation bubble size. We evaluated the bubbles using multibubble sonoluminescence and the bubble size was changed by adding a surfactant to the microcapsule suspension. The microcapsule destruction was frequency dependent. The main cause of microcapsule destruction was identified as mechanical resonance, although the relationship between bubble size and microcapsule size suggested that bubbles smaller than or equal to the microcapsule size may also destroy microcapsules by applying shear stress locally.

1. Introduction

Cavitation bubbles produce various physical and chemical effects [1], [2], [3], [4]. The main physical effects include shock waves, microjets, and shear stress, which have been applied in several fields, such as emulsification, extraction, and cleaning [5], [6], [7], [8]. The chemical effects arise from the formation of free radicals in collapsing cavitation bubbles [8]. The contraction rate is high owing to the Rayleigh contraction, and during collapse, the inside of the bubble is subjected to high temperatures and pressures [9], [10], [11]. Light, known as sonoluminescence (SL), is emitted during cavitation and may provide information about bubble activity [12], [13], [14], [15], [16], [17]. The huge number of cavitation bubbles that are generated move in a complex manner, repeatedly splitting and coalescing, owing to the ultrasonic radiation pressure, the flow of the liquid, the force exerted by the pressure gradient of the sound field, and the forces of attraction and repulsion acting between the bubbles. The properties of the bubbles depend on factors including the ultrasonic frequency, sound pressure, liquid temperature, dissolved gas, dissolved substances, and irradiation time [1], [2], [3], [4], [18], [19]. The cavitation bubble sizes vary substantially, and the type of activity in and around the bubble, such as shear stress, shock waves, microjets, sonochemical reactions, and SL, varies greatly [13], [20]. Algae and bacteria samples have been used as indicators for investigating the complex activity of bubbles, particularly cavitation bubbles. Yamamoto et al. [21] and Kurokawa et al. [22] reported that cavitation bubbles are involved in the ultrasonic inactivation of microscopic organisms. The inactivation mechanism is thought to involve both the chemical and physical effects of cavitation bubbles and depends on the type of sample and the frequency of the ultrasonic waves [23], [24].

In this study, to investigate the destruction mechanism under sonication, different size microcapsules consisting of a melamine shell containing oil and fat were used as a model for algae and bacteria. The frequency dependence of the destruction rate and the correlation between bubble size and bubble activity were investigated using MBSL measurements as an indicator of microcapsule destruction with and without a surfactant. These results indicate a correlation between MBSL intensities, bubble size, and the microcapsule destruction rate.

2. Materials and methods

2.1. Microcapsules

Microcapsules (Chemitec) consisting of fat and oil in a melamine resin shell with a shell-to-content volume ratio of 1:4 were used, and the shell thickness was approximately 7% of the radius. All microcapsules were spherical before ultrasonic irradiation. The samples were microcapsules with particle sizes of 1–2 and 3–5 μm, and polydisperse microcapsules with a particle size distribution of 0.3–50 μm. The elastic modulus E was measured using a scanning probe microscope (SPM-9700, Shimadzu Corporation) at 200 MPa. The samples were suspended in Milli-Q water, and the microcapsule concentration was adjusted to 10⁷ capsules/mL. Sodium dodecyl sulfate (SDS; Wako Pure Chemical Corporation) was dissolved in the microcapsule suspension at concentrations of 0.01, 0.1, 2, and 10 mM to change the sizes and activities of the cavitation bubbles in the ultrasonic field.

2.2. Ultrasonic treatment

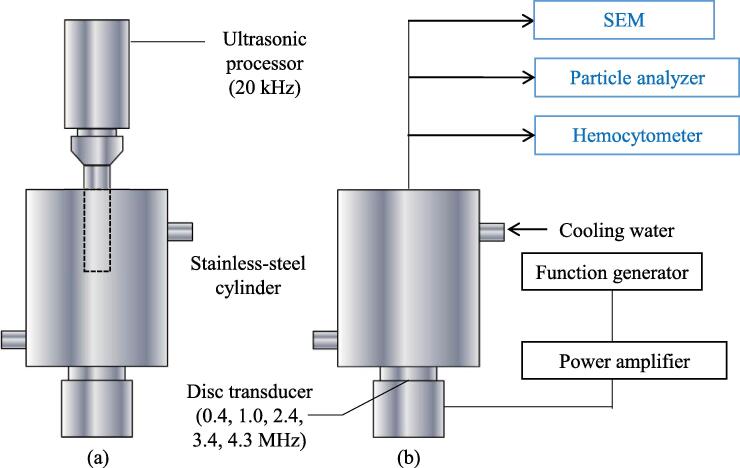
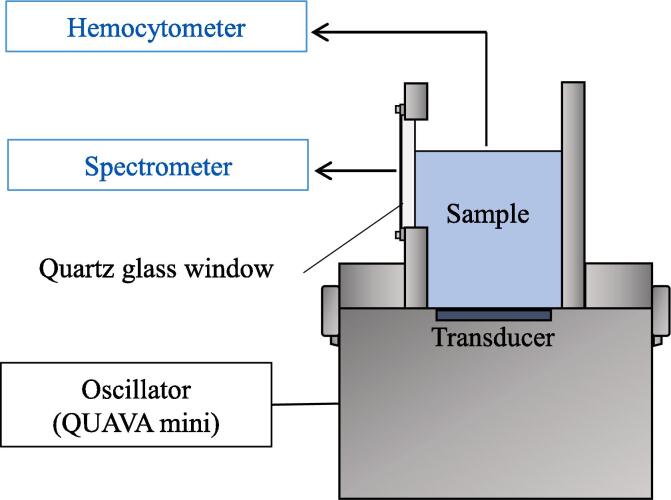
Fig. 1 shows a diagram of the ultrasonic reactors for ultrasonic frequencies of 20 kHz and 0.4, 1.0, 2.4, 3.4, and 4.3 MHz. A sample was placed in a stainless-steel cylinder. A horn transducer (VC750, Sonic & Materials, Inc.) was used at 20 kHz, and the suspension was directly irradiated from the upper part of the sample tank. This was used for comparison with previous results [21], [22]. For other frequencies, a PZT ceramic disk transducer (Fuji Ceramics) with a diameter of 30 mm was placed at the bottom of the sample tank, and the suspension was irradiated directly. Fig. 2 shows a diagram of the ultrasonic irradiation system for irradiation at 430 and 950 kHz. A 430 or 950 kHz ultrasonic transducer (QUAVA mini, KAIJO) was installed with a stainless-steel rectangular parallelepiped sample tank (60 × 60 × 100 mm). A quartz glass window was attached to the center of the side of the sample tank to measure the multibubble sonoluminescence (MBSL). The acoustic power was measured by the calorimetric method [28] and was constant at 10 ± 1 W in all experiments. The sample temperature was kept constant at 15 ± 1 °C by circulating cooling water outside the sample tank. The experimental device in Fig. 1 irradiated a 300 mL sample for 30 min. The device in Fig. 2 irradiated a 100 mL sample for 30 min, and samples were taken every 10 min.

Fig. 1.

Diagram of ultrasonic reactors used to irradiate samples at (a) 20 kHz and (b) 0.4, 1.0, 2.4, 3.4, and 4.3 MHz.

Fig. 2.

Schematic of the ultrasonic irradiation system for irradiating samples at 430 and 950 kHz.

2.3. Analytical methods

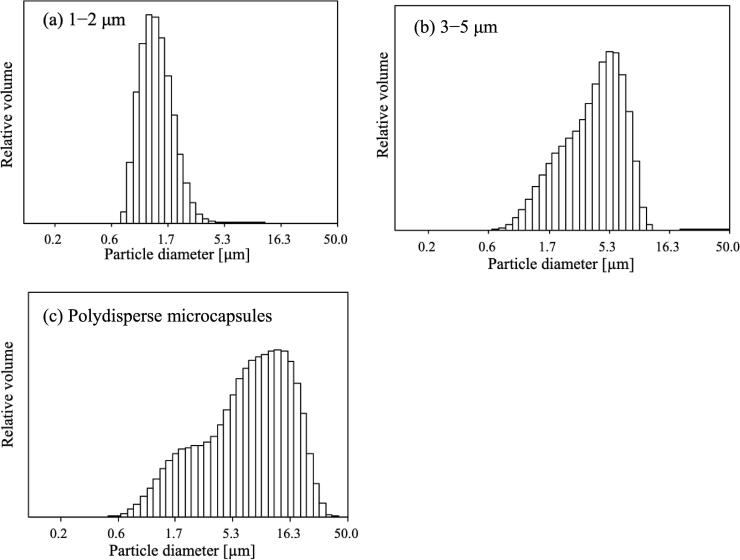
All experiments were performed in triplicate to ensure reproducibility. To evaluate the destruction, particle size distribution measurements were performed using a laser-diffraction particle size analyzer (SALD-2300, Shimadzu Corporation) and the state of the microcapsules was observed by scanning electron microscopy (SEM; TM3030Plus, Hitachi). The destruction rate was calculated using an optical microscope (IX73, Olympus) and a hemocytometer (EM Techcolor, Hirschmann). Four optical micrographs were taken for each sample and undamaged microcapsules were counted before and after ultrasonic irradiation. Fig. 3(a) and (b) show the particle size distribution of the microcapsules with average particle sizes of 1–2 and 3–5 μm. The microcapsule particle size ranged from 1 to 10 μm, and the peak values of the particle size distributions were 1.4 μm for the 1–2 μm microcapsules and 5.3 μm for the 3–5 μm microcapsules. Fig. 3(c) shows that the particle size distribution of the polydisperse microcapsules was 0.3–50 μm, and microcapsules of various sizes are mixed.

Fig. 3.

Particle diameter of microcapsules before ultrasonic irradiation for (a) 1–2 and (b) 3–5 μm microcapsules, and (c) polydisperse microcapsules with a size distribution 0.3–50 μm.

The MBSL intensity was observed using a spectrometer (SP 2300i, Princeton Instruments) and a CCD detector (Pixis100, Princeton Instruments). The diffraction grating was 300 g/mm, the slit width was 1 mm, and the wavelength ranged from 257 to 540 nm. Immediately after ultrasonic irradiation, the emission spectrum was obtained with 2 min exposure. The MBSL intensity was normalized by integrating the spectrum intensity and setting the intensity of the microcapsule suspension in pure water as 1.

3. Frequency dependence of ultrasonic destruction of microcapsules

3.1. Results

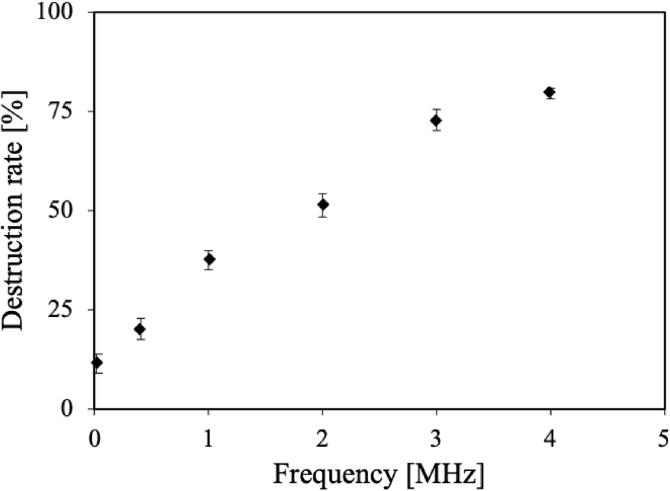
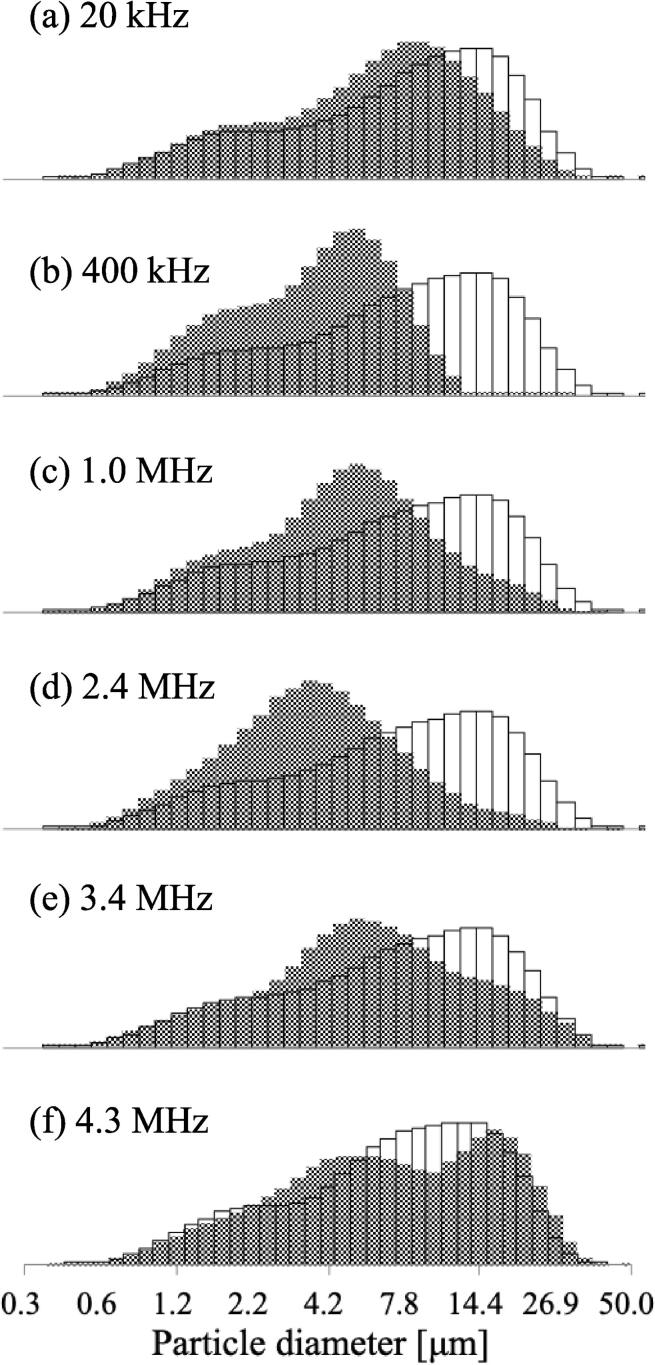
Fig. 4 shows the destruction rate of microcapsules with average particle sizes of 3–5 μm as a function of frequency. The destruction rate increased with frequency and the highest destruction rate was observed at 4.3 MHz. Fig. 5 shows the particle size distribution of the polydisperse microcapsules before and after 30 min ultrasonic irradiation at each frequency. Before ultrasonic irradiation, the particle size distribution was 0.3–50 μm. After irradiation at 400 kHz to 3.4 MHz, the distribution of microcapsules above 10 μm was reduced substantially as the frequency decreased. At 4.3 MHz, there was no change in the particle size distribution above 15 μm, which resulted in a decrease in the particle sizes of 5–15 μm. At 20 kHz, the distribution was largely unchanged after ultrasonic irradiation.

Fig. 4.

Destruction rate of microcapsules with particle diameters of 3–5 μm as a function of frequency.

Fig. 5.

Particle size distribution of microcapsules before (open histograms) and after (closed histograms) sanitation for 30 min at (a) 20 kHz, (b) 400 kHz, (c) 1.0 MHz, (d) 2.4 MHz, (e) 3.4 MHz, and (f) 4.3 MHz.

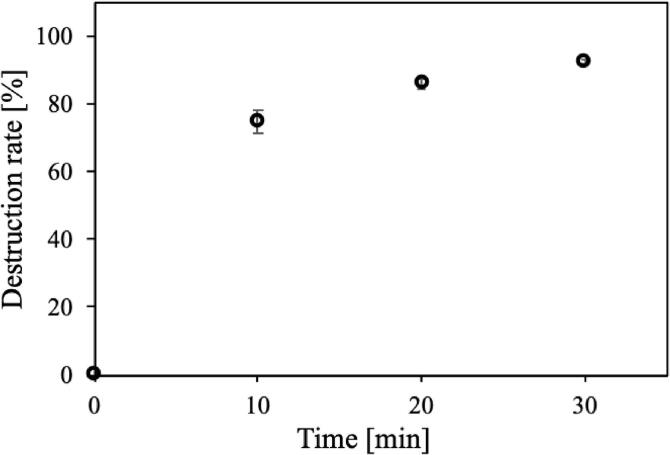
The type of destruction depended on the frequency (Fig. 6). At 20 kHz, concave microcapsules were observed at particle sizes of 8 μm or more, whereas at 400 kHz, more concave particles than ruptured particles were observed at particle diameters of 5 μm or more and few particles with holes were observed. From 1.0 to 3.4 MHz, all types of destruction were observed at particle sizes of 5 μm or more, and ruptured particles were particularly dominant. Destruction was observed at particle sizes of 5 μm or less only at 4.3 MHz, and all types of destruction were observed above 5 μm. Fig. 7 shows the destruction rate as a function of time for 3–5 μm microcapsules sonicated at 950 kHz for 30 min. The destruction rate reached about 75% after 10 min, gradually increased, and reached a rate of 92% after 30 min.

Fig. 6.

SEM images of types of deformation observed. (a) Concave, (b) rupture destruction, (c) and holes.

Fig. 7.

Destruction rate of microcapsules with particle diameter of 3–5 μm at 950 kHz as a function of time.

3.2. Discussion

Based on the results in Section 3.1, we discuss the relationship between microcapsule destruction and frequency from the perspective of bubble vibration and microcapsule vibration.

3.2.1. Resonant frequency of the bubble vibration

We used the Minnaert formula [29], [30] for the resonant frequency of a single bubble in a sound field to calculate the bubble equilibrium radius, R₀ [m],

$$f_0=\frac{1}{2\pi R_0}\sqrt{\frac{1}{{\rho }_0}\left(3\gamma P_0+\frac{2\sigma }{R_0}\left(3\gamma -1\right)\right)}$$ (3.2.1.1)

where f₀ is the resonance frequency [Hz], ρ₀ is the density of the liquid [kg/m³], γ is the specific heat ratio of the gas, P₀ is the sound pressure [Pa], and σ is the surface tension [N/m]. Table 1 shows the relationship between the main frequencies used in this study and the equilibrium radius. The calculated equilibrium radii were 163.1, 8.2, 3.3, and 1.7 μm at frequencies of 20, 400, 1000, and 2000 kHz, respectively. At frequencies above 400 kHz, the average sizes of the polydisperse microcapsules and the bubbles were similar.

Table 1.

Correlation between the main frequencies used in this study and the equilibrium radius.

Frequency [kHz]	Equilibrium radius [μm]
20	163.1
400	8.2
1000	3.3
2000	1.7

3.2.2. Oscillation analysis

Cavitation bubbles cause the vibration of microorganisms and cells during ultrasonication, and thus oscillation analysis was performed assuming that the microcapsule shells are vibrated via the same mechanism [31], [32], [33]. The microcapsule was assumed to be a thin elastic shell, and the oscillation was considered. In the low-order mode, the degree of deformation reached a maximum at n = 2. This oscillation mode is called the quadrupole mode and is used in the following analysis.

The relationship between particle size and frequency was considered using a shell model. For a hard shell, the approximate mechanical resonance frequency, f_K, of the shell is expressed as

$$f_K\approx \frac{1}{2\pi }\sqrt{\frac{K_A}{{\rho }_i{a}^3}}$$ (3.2.2.1)

$$K_A=\frac{\mathit{Eh}}{2(1-\upsilon )}$$ (3.2.2.2)

where ρ is the density in the shell [kg/m³], E is elastic modulus [N/m²], h is the film thickness [m], ν is Poisson's ratio, and a is the shell radius [m]. The shear modulus, μ, is calculated by

$$\mu =\frac{\mathit{Eh}}{2\left(1+\upsilon \right)}$$ (3.2.2.3)

where the thickness, h, is 7% of the microcapsule radius.

The mechanical resonance frequency of the microcapsule was calculated with Eq. (3.2.2.1).

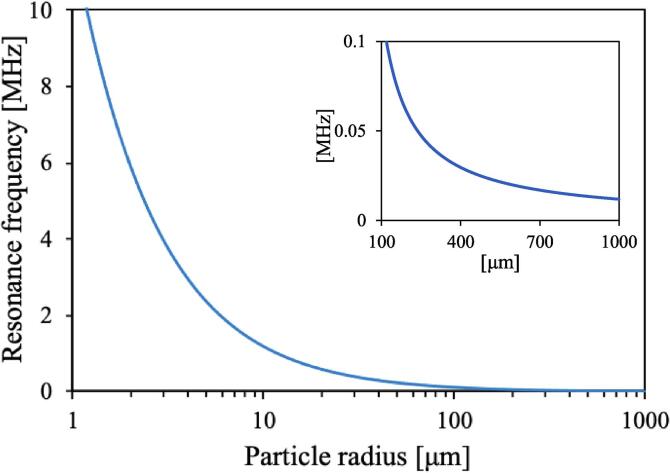
Fig. 8 shows the analysis results for the microcapsules used in this experiment. However, it is difficult to measure E accurately because scanning probe microscopy has a high error of approximately 50%. Therefore, the curve shown in Fig. 8 could be shifted to the left or right. The calculation results showed that the frequency at which the high destruction rate was obtained in this experiment was similar to the order of the mechanical resonance frequency of the microcapsule, and a smaller particle would have a higher resonance frequency. This result agreed with the polydisperse microcapsule distributions at larger diameters not decreasing at higher frequencies (Fig. 5). Ruptured microcapsules were observed at particle sizes over 5 μm (Fig. 6(b)). The calculation results are consistent with the destruction observed at frequencies from 1.0 to 3.4 MHz. These results suggested that the microcapsules were ruptured by mechanical resonance because the spherical shell of the microcapsule could not withstand the surface area change accompanying the resonance. The lack of destruction at 20 kHz was because the particle size of the microcapsules in Fig. 8 was much larger than that of the microcapsules. Yasui et al. [34] revealed that the resonance frequency was reduced by bubble–bubble interactions. The microcapsule concentration of the sample used in the present study was 10⁷ capsules/mL. Considering the interactions between microcapsules, between bubbles in the bubble cloud, and between microcapsules and bubbles, the real resonance frequency should be lower than the resonance frequency calculated by the simple theoretical formula (Eq. (3.2.2.1)).

Fig. 8.

Resonance frequency calculated using the shell model for each microcapsule particle size. The elastic modulus was 200 MPa. The inset shows a magnification of the curve from 100 to 1000 μm.

3.2.3. Surface area change rate of the elastic shell

Because microcapsules are excited by oscillation via the expansion and contraction of cavitation bubbles and are damaged because they cannot withstand the surface area change, the type of destruction can be evaluated based on the magnitude of the vibration.

L is the distance between the centers of the cavitation bubble and the elastic shell in the ultrasonic field in the water. The oscillation of the shell at this time was estimated from the change in the surface area, S. Based on Zinin and Allen [31], Eq. (3.2.3.1) was used for the analysis. We assumed that the bubble shows a respiratory vibration that vibrates linearly with a change in sound pressure [31], [35], [36].

$$\frac{\mathrm{\Delta }S}{S}(\omega ,\theta )=\frac{\mathrm{\Delta }R}{R_0}\frac{R_0^2}{a^2}\frac{R_0}{L}\sum _{n=1}^{\infty }n(2n+1){\gamma }_o{\left(\frac{a}{L}\right)}^n\frac{d_S^n(\omega )}{d^n(\omega )}{P}_n(cos\theta )$$ (3.2.3.1)

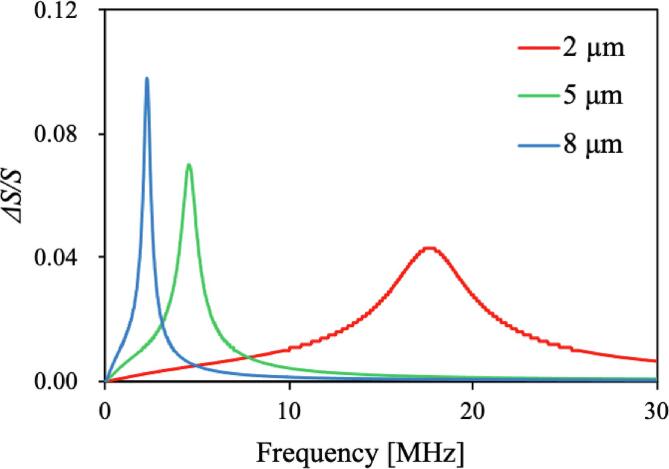
Fig. 9 shows the surface area change rate of microcapsules with particle diameters of 2, 5, and 8 μm calculated using Eq. (3.2.3.1) with elastic modulus E of 200 MPa and sound pressure P of 2.06 × 10⁵N/m², which was an average value for an acoustic power of 10 W. Generally, the sound pressure should be measured by a hydrophone, but the average sound pressure estimated from the acoustic power was used because of the formation of standing waves in the reactor and the complexity of the sound pressure distribution. The smaller the microcapsule particle size, the higher the maximum surface area change rate was. In contrast, the mechanical Quality factor increased with the microcapsule particle size. This shows that the resonance frequency of large microcapsules was limited to a narrow region. These results suggest that the mechanical resonance of the microcapsule excited by the bubble vibration is a factor in the destruction of the microcapsule. In addition to this destruction mechanism, the presence of concave particles and holes indicate that other destruction factors may exist. Yasui et al. [34] observed rupturing and fragmentation in hollow microcapsules. In our work, the concave particles could be formed by the local force applied to the microcapsule and the holes may be formed by microjets [13], [20]. These destruction mechanisms are discussed in Section 4.

Fig. 9.

Surface area change rates of 2, 5, and 8 μm microcapsules (E = 200 MPa).

3.2.4. Time dependence of the destruction rate

Fig. 7 shows that the destruction rate increased rapidly in the first 10 min, and then gradually. After 30 min irradiation, the destruction rate was 92%. Yasui et al. [34] reported a stochastic destruction process in hollow microcapsules. The probability that a microbubble will burst is approximately 1 over several microseconds, and microcapsules that vibrate at the resonant frequency are more likely to burst within a few cycles. We propose that the destruction due to mechanical resonance is caused by the vibration of the microcapsules by adjacent cavitation bubbles. Therefore, if the conditions described by Yasui et al. are satisfied, the microcapsules should be destroyed within several cycles. In Fig. 7, the destruction rate increases rapidly in the first 10 min because the cavitation bubbles and microcapsules have a high probability of encountering each other, and there is a high probability that the oscillation of the bubbles and the resonance frequency of the microcapsules will match. The destruction rate did not reach 100% because the microcapsules contained oil, had different shell thicknesses, and some microcapsules were not the resonant size due to the size dispersion.

4. Microcapsule particle size and bubble size

Section 3 describes a destruction model in which mechanical resonance arising from bubble oscillation around the microcapsule causes microcapsule destruction. This indicates that the ultrasonic destruction of microcapsules is caused by cavitation bubbles. The relationship between the resonance frequencies of the bubble oscillation and the microcapsule suggests that the bubble contributing to destruction has stable linearly oscillating cavitation. Because this mechanism is likely to rupture the microcapsule owing to the change in surface area, this explains the ruptured microcapsules we observed. However, we also observed microcapsules with concave damage and holes, and thus we investigated other destruction mechanisms. In particular, the hole damage was probably caused by shear stress acting as a local force on the microcapsule.

This section discusses the effects of the size and activity of cavitation bubbles on the ultrasonic destruction of microcapsules. Cavitation bubble sizes vary from those smaller than the resonance diameter, which causes Rayleigh contraction, to those larger than the resonance diameter, which do not participate in sonochemical reactions. The activity in and around the bubble, such as shear stress, shock waves, microjets, sonochemical reactions, and sonoluminescence, depends on the bubble size [1], [2], [3], [4], [18], [19]. To change the bubble activity, the surfactant SDS was added to the sample [25], [26], [27]. The MBSL intensity was measured to evaluate the contribution of cavitation bubbles to the destruction of microcapsules qualitatively.

4.1. Results

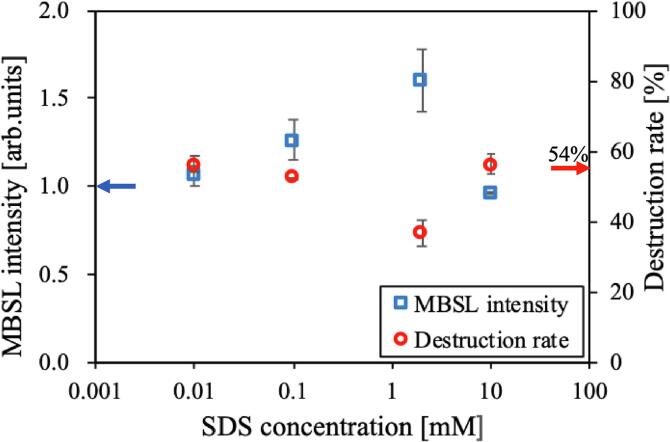
Fig. 10 shows the destruction rates and MBSL intensities of samples with particle sizes of 3–5 μm for various SDS concentrations at 430 kHz. The MBSL intensity was normalized by setting the emission intensity of the microcapsule suspension in pure water to 1. The destruction rate of the microcapsule suspension in pure water was 54%. The luminescence intensity and the microcapsule destruction rate were highest in the 2 mM SDS suspension. At concentrations lower than 2 mM, the MBSL intensity and destruction rate were almost identical to those for suspensions in pure water. At a high concentration of 10 mM, the MBSL intensity was similar to that of the pure water suspension and the destruction rate was slightly higher.

Fig. 10.

Relative MBSL intensity and destruction rate of microcapsules (3–5 µm) after 30 min irradiation in SDS aqueous solutions at 430 kHz. The arrows on the vertical axes show the MBSL intensity (blue) and the destruction rate (red) in pure water.

Fig. 11 shows that the destruction rate of the 1–2 μm microcapsules in 2 mM SDS aqueous solution was higher than that in pure water, whereas the destruction rate of the 3–5 μm microcapsules in 2 mM SDS aqueous solution was lower than that in pure water (results not shown).

Fig. 11.

Destruction rate of microcapsules (1–2 μm in diameter) after 30 min irradiation in SDS aqueous solution at 430 kHz.

4.2. Discussion

4.2.1. Effect of SDS addition

The bubble activity that contributed to microcapsule destruction was examined based on the effect of the SDS concentration on the MBSL intensity and microcapsule destruction rate (Fig. 10). The SL intensity increased in a low-concentration SDS aqueous solution because the number of bubbles causing Rayleigh contraction, which contributes to light emission, is increased by inhibiting the coalescence of bubbles during the bubble growth stage [25], [26], [27]. SDS is a surfactant, and thus contains hydrophilic and hydrophobic moieties. In solution, the Na cation dissociates from the polar headgroup of SDS and the SDS anions are adsorbed on the bubbles, giving the bubbles a negative charge, which prevents the bubbles from coalescing because of the electrostatic repulsive force. These effects suggest that the bubbles vibrate vigorously while maintaining the size that causes Rayleigh contraction. In Section 3, mechanical resonance was proposed as a cause of microcapsule destruction. The vibration is excited when the cavitation bubble oscillates linearly at the resonance size. Therefore, although the SL intensity in 2 mM SDS was higher than that in pure water, the microcapsule destruction rate was lower in 2 mM SDS (Fig. 10). The suspensions containing 0.1 and 0.01 mM SDS had similar MBSL intensities and destruction rates to the pure water suspension, suggesting that the SDS concentration was too low for the surfactant to have an effect. In contrast, at high SDS concentrations, excess SDS molecules decreased the electrostatic repulsion between bubbles, allowing bubbles to coalesce and reach or exceed the resonance diameter. Therefore, although the luminescence intensity decreased, the destruction rate was the same as that in the pure water suspension, and bubbles that exhibit SL may not be effective for destroying 3–5 μm microcapsules. Cavitation bubbles include those that exhibit stable linear oscillation, which are larger than the resonant bubble size, and active bubbles that cause Rayleigh contraction and emit light, which are smaller than the resonant bubble size. Small bubbles, such as SL bubbles, may not contribute to the destruction of 3–5 μm microcapsules.

4.2.2. Destruction factors

For 3–5 μm microcapsules, bubbles with stable linear oscillations may contribute to microcapsule destruction rather than active SL bubbles. However, for 1–2 μm microcapsules (Fig. 11), the microcapsule destruction rate increased despite the high SL emission intensity because small SL bubbles, which cause Rayleigh contraction, were involved in the destruction. The size of the bubbles that destroy microcapsules may depend on the relationship between the bubble size and the microcapsule size. We considered the cause of destruction based on the simulation of the microcapsule size and its mechanical resonance frequency (Fig. 8). The elastic modulus of the melamine resin shell of the microcapsules was several hundred megapascals, and the measured value of 200 MPa was used in the simulation as the elastic modulus of the microcapsules. The mechanical resonance frequency of the 1–2 μm microcapsules was calculated as > 10 MHz, which was substantially different from the frequency we used, and thus it is unlikely that the 1–2 μm microcapsules were destroyed by mechanical resonance. Fig. 12 shows an SEM image of 1–2 μm microcapsules ultrasonicated at 430 kHz for 30 min in 2 mM SDS. Several microcapsules showed concave damage and holes rather than rupturing.

Fig. 12.

SEM image of microcapsules (1–2 μm) after 30 min irradiation in SDS aqueous solution at 430 kHz.

The calculations and SEM image suggest that the microcapsules were destroyed by local force rather than mechanical resonance. We examined whether the microcapsule was directly destroyed by the shear stress caused by bubble vibration acting as the local force. The shear stress, σ [Pa], can be estimated by [37]

$$\sigma =\eta \frac{\text{d}V}{\text{d}x}$$ (4.2.2.1)

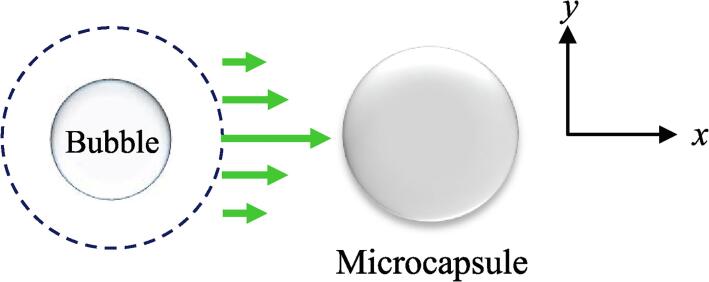
where σ [Pa·s] is the viscosity of the solution around the bubble, V is the bubble wall velocity, and dV/dx is the velocity gradient. V is obtained by calculating the vibration amplitude of a bubble from the Keller-Miksis equation [38] and differentiating it. Eq. (4.2.2.1) shows that the shear stress of the bubble vibration is proportional to the gradient of the vibration velocity of the bubble wall. The shear stress is generated near cavitation bubbles that exhibit respiratory oscillation. As shown in Fig. 13, the velocity component of the bubble vibration becomes maximum and minimum at the point closest to the microcapsule and the point separated by the radius of the bubble in the y-direction, respectively. This velocity gradient is transmitted to the microcapsule as stress through the viscosity of the liquid. Microcapsules larger than the bubbles can make the most of the velocity gradient for the shear stress to effectively function locally. Few bubbles grow to a size larger than the resonance diameter for 430 kHz in the 2 mM SDS aqueous solution. Bubbles that apply shear stress locally to the microcapsule and contribute to the microcapsule destruction are smaller than or equal to the size of the microcapsule, and thus small bubbles in the SDS aqueous solution increased the destruction rate of the 1–2 μm microcapsules.

Fig. 13.

Schematic of shear stress applied to microcapsules.

Therefore, microcapsule destruction is caused by the mechanical resonance described in Section 3 and the local force applied to the microcapsules by shear stress from the physical action of the cavitation bubbles.

5. Conclusion

We proposed two mechanisms for the ultrasonic destruction of microcapsules in water. In one, microcapsules are ruptured by mechanical resonance, and in the other, holes are caused by bubbles applying shear stress locally to the microcapsules. For polydisperse microcapsules (Section 3), the particle size of the microcapsules that were destroyed depended on the frequency. It may be possible that the resonance frequency decreases according to the number density of microcapsules. However, based on the SEM images and particle size distributions of the broken microcapsules, the oscillation analysis using the shell model, and the analysis of the change rate of the surface area of the shell, the polydisperse microcapsules were ruptured by mechanical resonance. In contrast, the 3–5 and 1–2 μm microcapsules showed concave damage and holes rather than rupturing (Section 4). The MBSL intensities and microcapsule destruction rates in surfactant solution depended on the microcapsule size. These results suggested that the relationship between the microcapsule size and bubble size is important. The damage to the microcapsules indicated that sheer stress was applied to the microcapsule locally.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.