The interaction of shockwaves with a vapour bubble in boiling histotripsy: The shock scattering effect

Highlights

• •2D nonlinear wave propagation with a bubble at the HIFU focus is simulated.
• •Constructive interference of a backscattered wave with incoming shockwaves appears.
• •Shock scattering effect is the mechanism for the formation of a cavitation cloud.

Abstract

Boiling histotripsy is a High Intensity Focused Ultrasound (HIFU) technique which uses a number of short pulses with high acoustic pressures at the HIFU focus to induce mechanical tissue fractionation. In boiling histotripsy, two different types of acoustic cavitation contribute towards mechanical tissue destruction: a boiling vapour bubble and cavitation clouds. An understanding of the mechanisms underpinning these phenomena and their dynamics is therefore paramount to predicting and controlling the overall size of a lesion produced for a given boiling histotripsy exposure condition. A number of studies have shown the effects of shockwave heating in generating a boiling bubble at the HIFU focus and have studied its dynamics under boiling histotripsy insonation. However, not much is known about the subsequent production of cavitation clouds that form between the HIFU transducer and the boiling bubble. The main objective of the present study is to examine what causes this bubble cluster formation after the generation of a boiling vapour bubble. A numerical simulation of 2D nonlinear wave propagation with the presence of a bubble at the focus of a HIFU field was performed using the k-Wave MATLAB toolbox for time domain ultrasound simulations, which numerically solves the generalised Westervelt equation. The numerical results clearly demonstrate the appearance of the constructive interference of a backscattered shockwave by a bubble with incoming incident shockwaves. This interaction (i.e., the reflected and inverted peak positive phase from the bubble with the incoming incident rarefactional phase) can eventually induce a greater peak negative pressure field compared to that without the bubble at the HIFU focus. In addition, the backscattered peak negative pressure magnitude gradually increased from 17.4 MPa to 31.6 MPa when increasing the bubble size from 0.2 mm to 1.5 mm. The latter value is above the intrinsic cavitation threshold of –28 MPa in soft tissue. Our results suggest that the formation of a cavitation cloud in boiling histotripsy is a threshold effect which primarily depends (a) the size and location of a boiling bubble, and (b) the sum of the incident field and that scattered by a bubble.

1. Introduction

Boiling histotripsy is a High Intensity Focused Ultrasound (HIFU) technique that employs a number of millisecond long HIFU pulses with high peak positive P₊ and negative P_- pressures at the HIFU focus (P₊ > 40 MPa and P_- < 10 – 15 MPa). This results in mechanical tissue fractionation without causing any significant thermal damage. Acoustic cavitation generated during boiling histotripsy exposure is the main mechanism for tissue fractionation [1], [2], [3]. A number of ex- and in vivo boiling histotripsy studies have clearly demonstrated that a well-defined lesion that contains complete fragmentation of soft tissue or acellular debris can be produced in the kidney, liver, heart and cardiac muscle [2], [3], [4], [5], [6], [7].

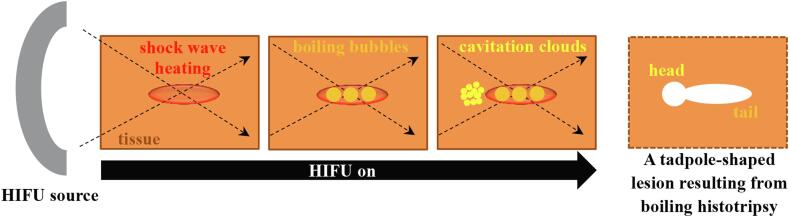
Contrary to a symmetric “cigar”-shaped thermally ablated lesion induced by traditional HIFU thermal ablation, boiling histotripsy produces a tadpole shaped lesion, consisting of a head and a tail with the head located towards the HIFU transducer [8]. The principle mechanisms behind this particular lesion shape formation, as opposed to a “cigar” shape, are thought to be due to the presence of boiling vapour bubbles and of inertial cavitation clouds during boiling histotripsy exposure [9]. Mechanisms of boiling histotripsy have been extensively investigated over the past 10 years. Nonlinear shocked waves with high acoustic pressure amplitudes induced at the HIFU focus in soft tissue can increase tissue temperature to boiling in a few milliseconds via shock wave heating effect [1], [2]. The interaction of this localised tissue heating with the incoming acoustic waves can then lead to the generation of a boiling vapour bubble at the HIFU focus [10], which expands to around a millimetre in size through rectified growth behaviour [11]. This growth is thought to be due to the combination of the asymmetry in a nonlinear shocked wave and water vapour that transports into the bubble [12], [13]. The extent of this growing bubble at the HIFU focus is, however, likely to be limited to the localised shockwave heated zone because of the large temperature gradient across the edge of the heated region [13]. Further interaction of this enlarged boiling bubble with incoming incident shockwaves can then induce inertial cavitation clouds that form in front of the boiling bubble, progressing towards the HIFU source until it is switched off [9]. The shear stresses produced around an oscillating boiling bubble and emissions of micro jetting and shockwaves resulting from violent bubble collapses involved in inertial cavitation clouds can tear off soft tissue [2], [11]. This leads to the formations of the tail and subsequently the head of a boiling histotripsy lesion (see Fig. 1). Because these two different types of bubble activity appear during boiling histotripsy exposure (boiling bubble and cavitation clouds), the nature of the resulting mechanical damage in cellular structures around the tail and the head of the lesion are also distinct from one another. For instance, it has been reported that the margins of the tail of a boiling histotripsy lesion produced in liver in vivo are sharply demarcated with smooth boundaries whereas broken hepatocyte plates with ragged boundaries are observed around the head of a boiling histotripsy lesion [11].

Fig. 1.

A schematic diagram illustrating the production of a tadpole-shaped lesion due to the formation of boiling bubbles and cavitation clouds in boiling histotripsy.

Whilst a number of studies have shown the effects of shockwave heating in creating a boiling bubble at the HIFU focus and have studied its rectified growth behaviour in soft tissue during the course of boiling histotripsy exposure [1], [2], [9], [11], [12], [13], little is known about the subsequent formation of cavitation clouds. In fact, it is of paramount importance to understand the generation of this bubble cluster in order to predict as well as to control the overall size of a lesion induced under a given boiling histotripsy exposure condition. In our previous study [9], we hypothesised that (a) the interaction of incoming incident shockwaves with a boiling vapour bubble would lead to the formation of cavitation clouds and (b) the extent of the head of a boiling histotripsy lesion would be primarily dependent upon the pressure magnitude of a backscattered acoustic field by a bubble. To support our hypothesis, the present study aims to investigate what causes the subsequent bubble cluster formation in boiling histotripsy. A numerical simulation of nonlinear wave propagation with the presence of a scatterer (i.e. a bubble) at the HIFU focus in a heterogeneous medium is performed. A qualitative analysis is conducted in order to capture basic features of the interactions of a shockwave with a bubble.

2. Numerical methods

High speed camera experimental results of bubble dynamics induced in a liver tissue phantom were reported in our previous boiling histotripsy studies [9], [11]. These results clearly showed the subsequent formation of a cavitation cloud in front of a primary boiling vapour bubble at the HIFU focus, resulting in the production of the head of a boiling histotripsy lesion. To gain further insight into the mechanisms behind the observed phenomena, a numerical study of the interaction of a shockwave with a vapour bubble immersed in a liver tissue phantom was carried out. The simulations were conducted using the open source k-Wave v1.2 MATLAB toolbox. k-Wave numerically solves the generalised Westervelt equation which accounts for heterogeneities in the ambient mass density, material nonlinearity (second-order nonlinearity), and power law absorption and dispersion [14], [15], [16]. The experimental validation of k-Wave has been performed for nonlinear wave propagation in a homogenous medium [17] as well as in a heterogeneous medium with simple geometric scatterers such as rectangular and wedge shaped olive oils or glycerol filled phantoms [18], [19]. The generalised Westervelt equation describing nonlinear wave propagation in heterogeneous media has the following form [20]

$${\mathrm{\nabla }}^2{p}_a-\frac{1}{c_0^2}\frac{{\partial }^2{p}_a}{\partial t^2}-\frac{1}{{\rho }_0}\mathrm{\nabla }{\rho }_0·\mathrm{\nabla }{p}_a+\frac{\beta }{{\rho }_0{c}_0^4}\frac{{\partial }^2{p}_a^2}{\partial t^2}+\left(\tau \frac{\partial }{\partial t}{\left(-{\mathrm{\nabla }}^2\right)}^{y/2}+\eta {\left(-{\mathrm{\nabla }}^2\right)}^{\left(y+2\right)/2}\right)p_a=0$$ (1)

where $p_a$ is the acoustic pressure, $c_0$ is the speed of sound in the medium, ${\rho }_0$ is the density of the medium, t is time, β = (1 + B/2A) is the coefficient of nonlinearity and B/A is the nonlinear parameter of the medium. A and B are the coefficients of the first and second order terms of the Taylor series expansion of the pressure-density relation. τ and η are respectively the absorption and dispersion proportionality coefficients. y is the material dependent power law exponent. To solve the governing partial differential equation (1), k-Wave uses the k-space pseudospectral method [21] where the Fourier collocation spectral method is used to compute spatial gradients. Compared to other available finite difference and finite element methods, the k-space pseudospectral method theoretically allows for much coarser grid spacings and larger time steps for the same degree of accuracy [17]. A detailed description of the k-Wave toolbox can be found in [16]. Simulating 3D nonlinear wave propagation in heterogeneous media is costly in terms of both memory consumption and computational time. For instance, the numerical 3D simulation of 1 MHz nonlinear wave propagation up to the 40^th harmonic (i.e., 40 MHz) requires at least 2¹² × 2¹² × 2¹² grid points (total of 6.872 × 10¹⁰ points) with a computational domain size of 75 × 75 × 75 mm, using a discretisation of two points per wavelength (PPW). Moreover, significant wave distortion in soft tissue can lead to the formation of a shock wavefront at the HIFU focus which contains tens of higher multiple harmonics of the fundamental frequency [1]. A larger number of PPW is, therefore, needed to resolve a steep shock wave front where the pressure drastically increases over a very short time (i.e. of order of nanoseconds) [22]. In addition, the Courant-Friedrichs-Lewy number (CFL ≡ c₀Δt/Δx), which is defined as the ratio of the distance a wave can travel in one time step Δt to the grid spacing Δx [17], also needs to be small enough to achieve sufficient accuracy (i.e., CFL ≤ c₀/c_max where c_max is the maximum speed of sound in the medium). All the aforementioned factors will eventually increase computational overheads in terms of run times and memory consumption. To reduce computational time while achieving sufficient accuracy and capturing basic features of the interaction of a nonlinear wave with a bubble, in the present study, we performed 2D simulation of nonlinear wave propagation in a heterogeneous medium. For simplicity, a vapour bubble at the HIFU focus was modelled as a stationary 2D infinite cylinder whose acoustic properties are equal to those of water vapour. Furthermore, the effects of acoustic emissions resulting from bubble oscillations under HIFU exposure on wave propagation were also not accounted for in the simulations.

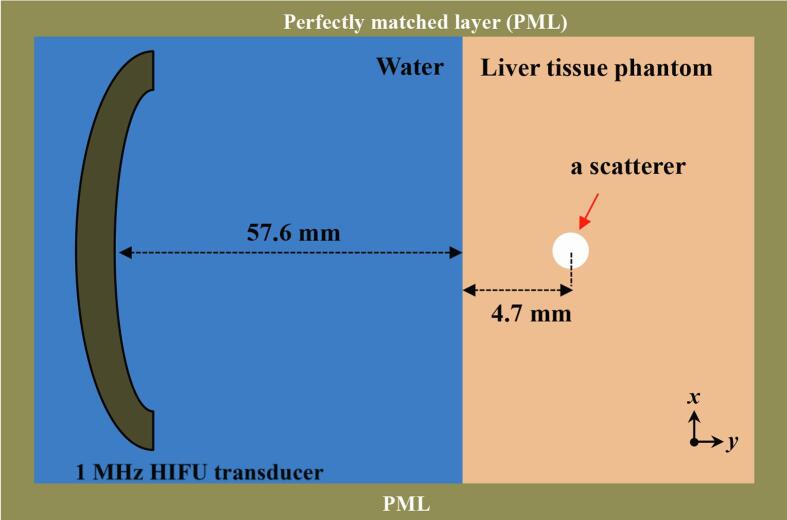
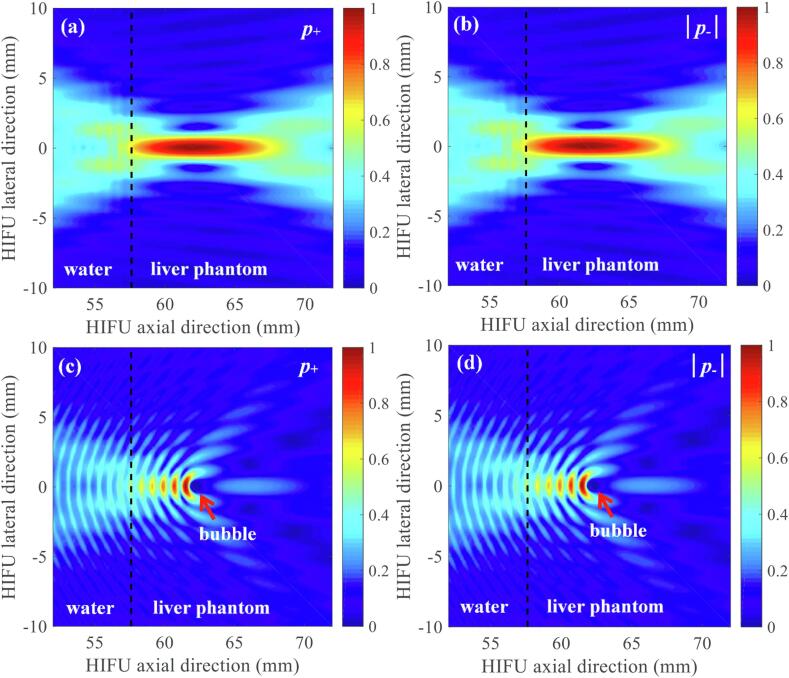
A schematic diagram illustrating the geometrical model used in the simulations performed is shown in Fig. 2. A 1.0 MHz single element bowl-shaped HIFU transducer with an aperture size of 64 mm and a radius of curvature of 62.6 mm was considered. This modelled HIFU source has the same geometry as the H-series HIFU transducers from Sonic Concepts (Bothell, WA, USA). The H-series transducers have been widely used in boiling histotripsy experiments [2], [6], [9], [11], [13]. In the simulations, 1 MHz HIFU waves propagated through a layer of water followed by a liver tissue phantom layer. A scatterer in the form of a vapour bubble was located 4.7 mm beyond the water-liver tissue phantom interface at the HIFU focus (i.e. at 62.3 mm in the axial direction), as shown in Fig. 2. The total grid size used was 2¹³ × 2¹³ points with a computational domain size of 75.51 × 75.51 mm including a perfectly matched layer (PML) of 20 × 20 grid points on each side of the domain. 160 PPW (nonlinear propagation up to the 67^th harmonic of the fundamental frequency, see the convergence test shown in Fig. 4, Fig. 5) and a CFL number of 0.05 with a temporal step size Δt of 0.3 ns and a grid spacing (Δx and Δy) of 9.26 μm in the axial and lateral directions were used in the simulation. The physical properties used in the simulations are listed in Table 1. All simulations were performed on a desktop PC with 3.6 GHz CPU (i7-9700 K), 16 GB of RAM and NVIDIA GeForce RTX 2080 Ti (11 GB) GPU. Each simulation took around 13 hours to complete. Fig. 3 depicts an example showing simulated acoustic fields with and without the presence of a bubble under linear propagation conditions using k-Wave as implemented in the present study. The axial and lateral full width half maxima of the pressure field of the HIFU source were, respectively, 12.27 mm and 1.72 mm.

Fig. 2.

A geometrical 2D model used in the simulation performed in the present study (figure not to scale).

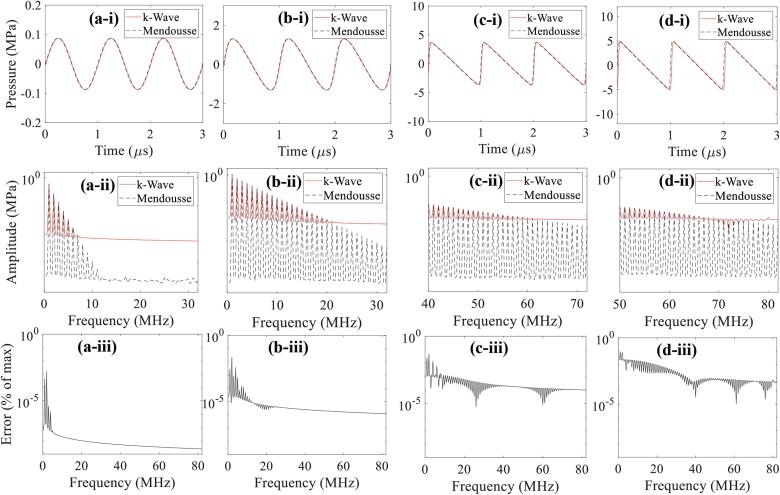
Fig. 4.

1D convergence test results of the propagation of plane progressive waves in the liver tissue phantom. Images a-i, b-i, c-i and d-i show the numerical (k-Wave, red solid line) and theoretical (Mendousse, black dashed line) results of the wave signal in time domain with an input source pressure of 0.1 MPa, 1.5 MPa, 5.0 MPa and 15 MPa, respectively. Corresponding continuous frequency spectra (a-ii, b-ii, c-ii, d-ii) and error as a percentage of the maximum amplitude (a-iii, b-iii, c-iii, d-iii) are depicted in the second and the last rows. 160 PPW and a CFL number of 0.05 were used.

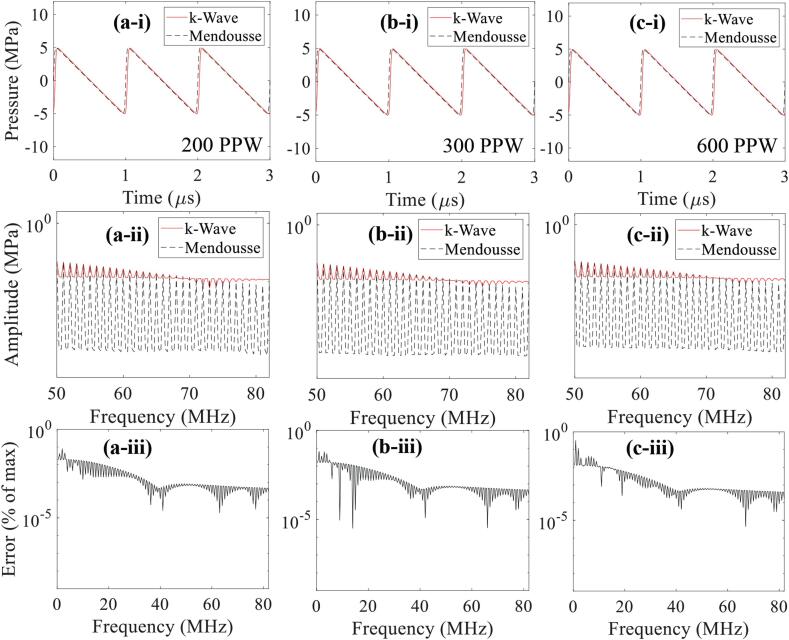
Fig. 5.

1D convergence test results of the generation of harmonics with (a) 200, (b) 300 and (c) 600 PPW. Figures in the first row show the time domain wave signals (a-i, b-i, c-i) whereas images in the second and the third rows represent corresponding continuous frequency spectra (a-ii, b-ii, c-ii) and error as a percentage of the maximum amplitude (a-iii, b-iii, c-iii), respectively. An input source pressure of 15 MPa and a CFL number of 0.05 were used. The maximum supported frequencies in k-Wave are 100, 150 and 300 MHz at 200, 300 and 600 PPW.

Table 1.

Physical properties used in the simulations.

	Water[17]	Liver tissue phantom[2], [24]	Watervapour bubble	Units
Speed of sound	1482	1544	477.5 [25]	m s−1
Density	1000	1044	0.598 [26]	kg m−3
Attenuation coefficient	0.217	15	164* [27]	dB m−1 MHz-y
Nonlinear parameter (B/A)	5	6	0.4* [28]	–
Power law exponent (y)	2	0.93	2#	–

*obtained for air. ^#assumed to equal to water.

Fig. 3.

Normalised simulated 2D spatial distribution of acoustic pressure fields without (a, b) and with (c, d) the presence of a bubble at the HIFU focus under linear propagation conditions. (a) and (c) are the simulated positive pressure fields p₊ whereas (b) and (d) are the magnitude of the computed negative pressure fields |p_-|. A bubble with a radius of 386 μm is indicated by an arrow in (c) and (d). The 1.0 MHz HIFU beam propagates from left to right. The simulations were performed over t = 60 μs. A bubble was modelled as a stationary 2D infinite cylinder.

Lastly, the pressure amplitude of an input sinusoidal signal used in the simulations gradually increased until a well-defined nonlinear shocked wave with P₊ ≥ 40 MPa and P_- ≤ 8 – 15 MPa appeared in the absence of a bubble at the HIFU focus. In this work, a shock wave is defined as a strongly distorted nonlinear wave with a very rapid rise time (<50 ns), P₊ ≥ 35 MPa and P_- of about 10 MPa [23].

To investigate the interaction of incident shockwaves with a bubble, it is crucially important to accurately model the formation of a shock wave front at the HIFU focus that contains tens of higher harmonics of the fundamental frequency. In addition, because of the large acoustic impedance mismatch at the liver tissue phantom-bubble interface, most of the higher frequency components would likely be reflected back to the HIFU source from the bubble, generating the backscattered acoustic field. In this study, a 1D convergence test was, therefore, carried to examine how well k-Wave could model 1 MHz nonlinear wave propagation with 160 PPW and a CFL number of 0.05. To do this, one of k-Wave’s given examples, example_na_modelling_nonlinearity.m, which describes the characteristics of the nonlinearity encapsulated by the first-order k-Wave simulation functions, was employed to simulate the propagation of plane progressive waves in the liver tissue phantom. In this test set-up, an input source pressure gradually increased until the shape of the time domain wave signal changed from a sine wave to an ‘N’-like wave. These 1D simulations results were then compared with the series solution given by Mendousse [29], which are shown in Fig. 4. In all cases, there is a good agreement between the theoretical and numerical results with a maximum error of 0.09% appearing at the fundamental frequency (1 MHz). With 160 PPW, the maximum supported frequency in k-Wave is 80 MHz (two points per wavelength at the highest generated harmonic). However, at this grid density, k-Wave appeared unable to resolve the harmonic content beyond the 67^th harmonic (67 MHz) (Fig. 4d-ii), relative to the Mendousse solution.

Our numerical analysis of the interaction of 1 MHz nonlinear wave with a bubble is, therefore, likely to be limited to a maximum frequency of 67 MHz. This particularly applies to the backscattered field by a bubble.

3. Results

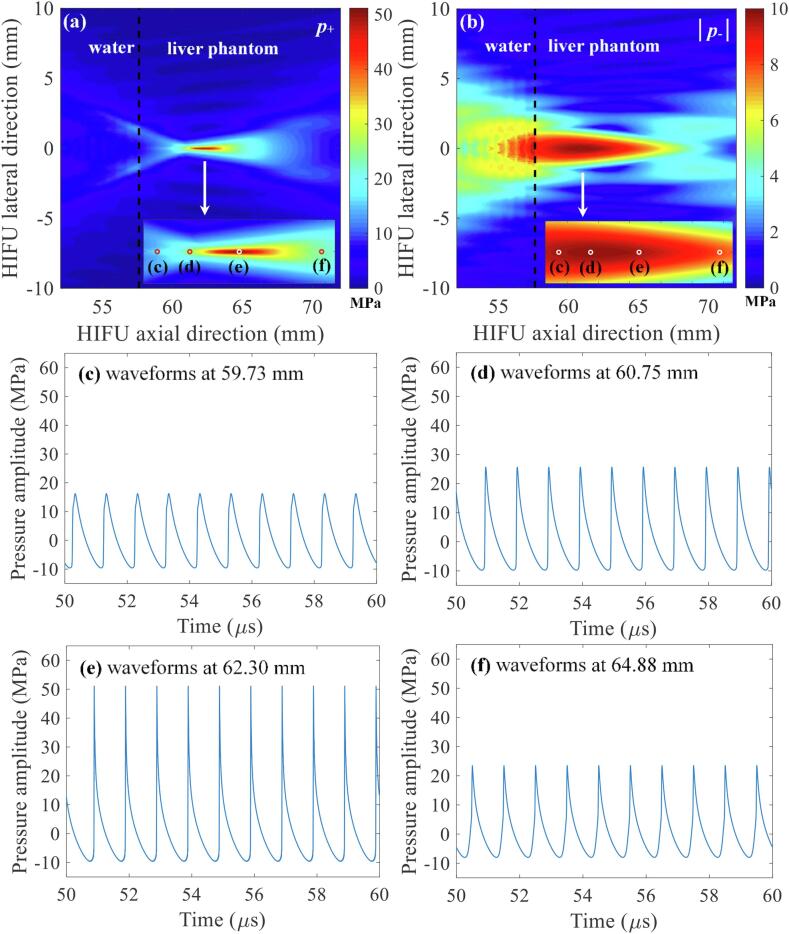
In the present study, a numerical simulation was performed to investigate the interaction of shockwaves with a bubble at the HIFU focus in a viscoelastic medium (i.e., liver tissue phantom) during the course of boiling histotripsy exposure. For simplicity and to capture the essential feature of the interaction of a shockwave and a bubble, a bubble was modelled as a non-translational 2D infinite cylinder whose properties are equal to those of water vapour. This 2D cylinder is hereafter referred to as a bubble. Fig. 6 shows simulated 2D spatial distributions of nonlinear acoustic fields and 1D nonlinear waveforms at a given distance in the HIFU axial direction in the absence of a bubble at the HIFU focus. A shockwave with P₊ of 51.2 MPa and P_- of – 9.8 MPa can be obtained from the k-Wave simulations (Fig. 6e). In contrast with the linear propagation conditions (Fig. 3a and b), the computed positive and negative pressure fields are no longer the same (Fig. 6a and b). This is because of the distortion of an initially harmonic acoustic waveform due to tissue nonlinearity, which leads to the asymmetry in the compressional and rarefactional pressure phases. As can be observed in Fig. 6e, the asymmetry is greatest at the HIFU focus where nonlinear effects are the strongest [1].

Fig. 6.

Simulated acoustic pressure fields in the absence of a vapour bubble at the HIFU focus under nonlinear propagation conditions. (a) and (b) are the simulated 2D spatial distributions of positive p₊ and negative |p_-| pressure fields. Images (c) to (f) respectively represent the waveforms at 59.73, 60.75, 62.30 and 64.88 mm in the HIFU axial direction. The 1.0 MHz HIFU beam with P₊ of 51.2 MPa and P_- of – 9.8 MPa propagates from left to right. The simulations were performed over t = 60 μs.

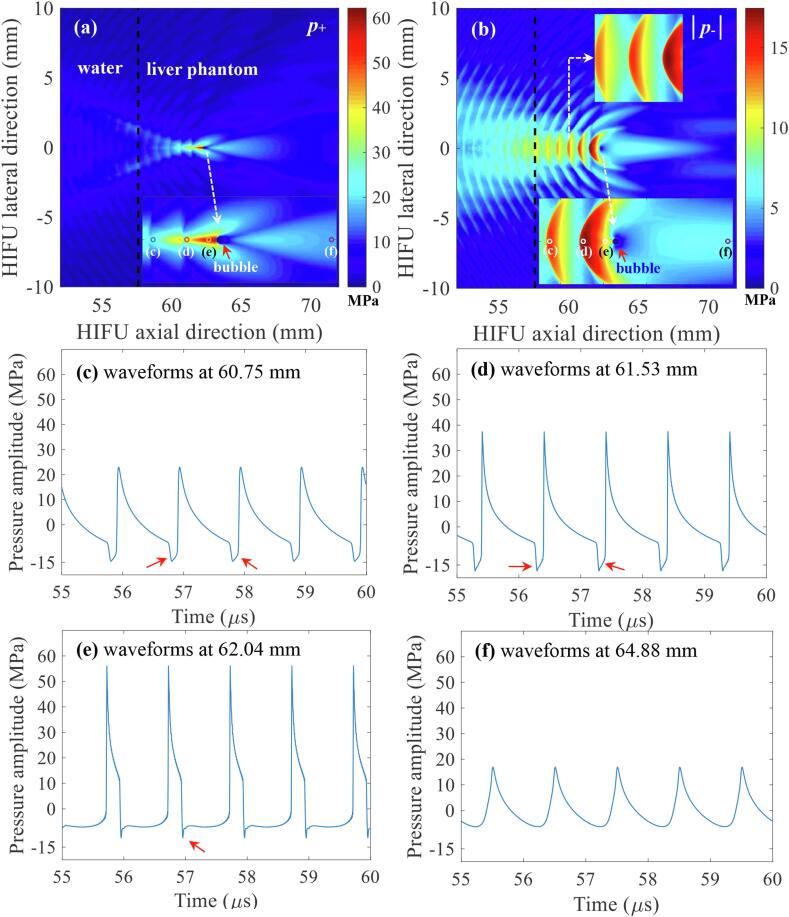
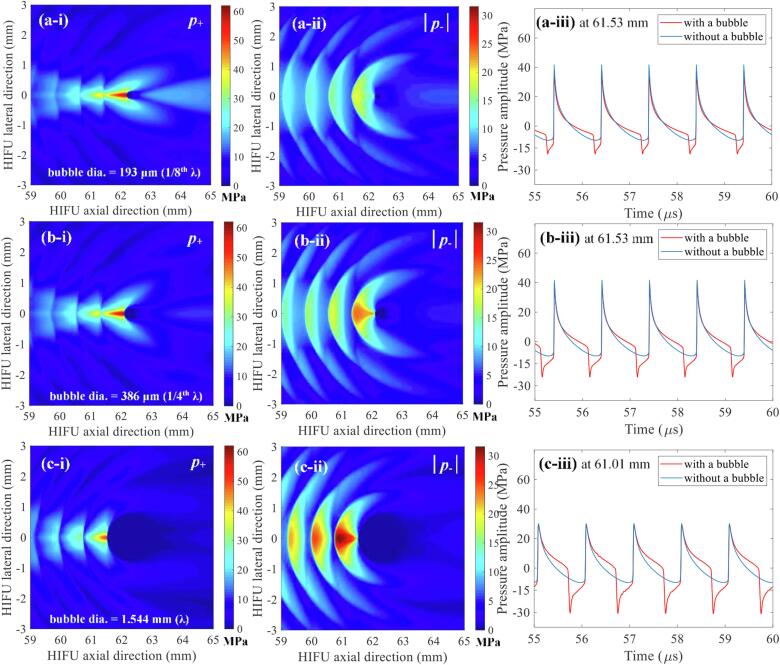
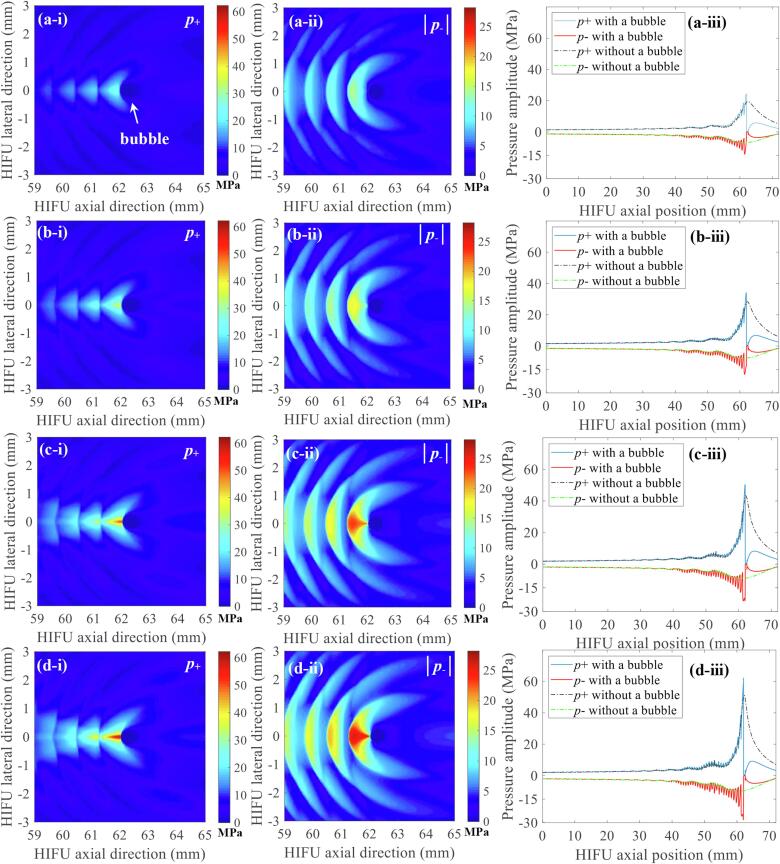
After the confirmation of the presence of a shockwave at the HIFU focus in the absence of a bubble, nonlinear acoustic fields scattered by a bubble were then computed with the same set of input parameters which were used to obtain Fig. 6 (i.e., P₊ of 51.2 and P_- of – 9.8 MPa). Since the acoustic cavitation threshold is primarily dependent on the peak negative pressure at a given driving frequency [12], the changes in the magnitude of negative pressure fields as a function of changes in the bubble size were analysed. The diameter of the bubble was varied from 154 μm (1/10^th of the wavelength λ at 1 MHz) to 1.544 mm (equal to λ). Fig. 7 shows the simulated 1 MHz nonlinear acoustic fields around a 154 μm-sized bubble. Interestingly, strong negative pressure fields between the HIFU transducer and the bubble are clearly observed with (a) the peak negative pressure of P_- = – 17.4 MPa (Fig. 7d) and (b) the presence of the constructive interference of the backscattered shockwave by the bubble with the incoming incident shockwaves (indicated by the red arrows in Fig. 7c to e). The highest negative pressure magnitude appears at 61.56 mm along the axial direction, in front of the bubble, and the backscattered pressure amplitudes gradually decrease towards the HIFU transducer. Furthermore, the peak negative pressure P_- rises from – 17.4 to – 31.6 MPa as the bubble size increases or becomes close to the wavelength of 1.544 mm (Fig. 8). Partially shielded acoustic pressure fields are observed behind a bubble in all the simulation cases (Fig. 7a and b, and Fig. 8a-i,-ii, b-i, -ii, and c-i, -ii).

Fig. 7.

Simulated acoustic pressure fields in the presence of a vapour bubble at the HIFU focus. (a) and (b) are the simulated 2D spatial distributions of positive p₊ and negative |p_-| pressure fields. Images (c) to (f) respectively represent the waveforms at 60.75, 61.53, 62.04 and 64.88 mm in the HIFU axial direction. The presence of the constructive interference of the backscattered shockwaves by the bubble with the incoming incident shockwaves is indicated by the red arrows in (c), (d) and (e). The 1.0 MHz HIFU beam with P₊ of 51.2 MPa and P_- of – 9.8 MPa propagates from left to right. The diameter of the bubble used in the simulations was 154 μm (1/10^thλ). The simulations were performed over t = 60 μs.

Fig. 8.

The effects of the size of a bubble on the pressure amplitude of the backscattered acoustic fields. Images in the left column (a-i, b-i, c-i) represent the 2D spatial distribution of positive pressure fields p₊ whereas those in the middle column (a-ii, b-ii, c-ii) indicate 2D negative pressure fields |p_-|. Figures in the right column (a-iii, b-iii, c-iii) depict 1D waveforms with (red lines) or without (blue lines) a bubble at a given position in the HIFU axial direction (61.53 and 61.01 mm). The bubble size was varied as (a) 193 (1/8^th of the wavelength), (b) 386 (1/4^th of the wavelength) and (c) 1544 μm (equals to the wavelength). In the simulations, the bubble was exposed to 1.0 MHz nonlinear shocked waves with peak positive and negative pressures of P₊ = 51.2 MPa and P_- = – 9.8 MPa at the HIFU focus. The simulations were performed over t = 60 μs. The HIFU beam propagates from left to right.

An additional calculation was performed in order to investigate the effects of the changes in the peak positive and negative pressure amplitudes of incident shockwaves (P_{+, incident} and P_{-, incident}) on the peak negative pressure magnitude of the acoustic fields backscattered by a bubble (P_{-, backscatter}). A bubble with a diameter of 515 μm (1/3^rd of the wavelength) was exposed to 1.0 MHz nonlinear shocked waves under four different exposure conditions: (1) P_{+, incident} of 19.5; P_{-, incident} of – 6.9 MPa, (2) P_{+, incident} of 28.3; P_{-, incident} of – 7.8 MPa, (3) P_{+, incident} of 43.3; P_{-, incident} of – 9.0 MPa, and (4) P_{+, incident} of 51.2, P_{-, incident} of – 9.8 MPa at the HIFU focus in the absence of a bubble. Fig. 9 depicts the simulated acoustic fields around the bubble at a given P_{+, incident} and P_{-, incident}. Overall, the peak negative pressure field generated between the HIFU source and the bubble increases with increasing pressure amplitudes of the incident shockwaves. Furthermore, it can be observed that the P_{+, incident} has a great impact on the P_{-, backscatter}. The peak negative pressure of the backscattered acoustic field by the bubble under P_{+, incident} = 51.2 and P_{-, incident} = – 9.8 MPa is, for instance, 5 MPa greater than that obtained with P_{+, incident} = 43.3 and P_{-, incident} = – 9.0 MPa (Fig. 9b and c, Table 2). In this comparison, the differences in P_{+, incident} and P_{-, incident} are 7.9 and 0.8 MPa, respectively. This is summarised in Table 2.

Fig. 9.

The effects of the changes in the pressure amplitudes of incident shockwaves (P_+,incident, P_-,incident) on backscattered acoustic fields by a bubble. Exposure conditions are as follows: (a) P_+,incident = 19.5 MPa; P_-,incident = – 6.9 MPa. (b) P_+,incident = 28.3 MPa; P_-,incident = – 7.8 MPa. (c) P_+,incident = 43.3 MPa; P_-,incident = – 9.0 MPa. (d) P_+,incident = 51.2 MPa; P_-,incident = – 9.8 MPa. Images in the left column (a-i, b-i, c-i, d-i) represent the 2D spatial distribution of positive pressure fields p₊ whereas those in the middle column (a-ii, b-ii, c-ii, d-ii) indicate 2D negative pressure fields |p_-|. Figures in the right column (a-iii, b-iii, c-iii, d-iii) depict the simulated 1D HIFU beam profile along the axis with or without the presence of a bubble at the HIFU focus. The bubble size used in the simulation was 515 μm (1/3^rd of the wavelength). The simulations were performed over t = 60 μs. The HIFU beam propagates from left to right.

Table 2.

The effects of the changes in the pressure amplitudes of incident shockwaves on the peak negative pressure magnitude of the backscattered acoustic fields by a bubble with a diameter of 515 μm (1/3^rd of the wavelength at 1 MHz).

Peak pressures of the incident wave* [MPa]		Peak negative pressure amplitude of the backscattered acoustic field P-, backscatter [MPa]
P+,incident	P−,incident
19.5	−6.9	−14.28
28.3	−7.8	−18.17
43.3	−9.0	−23.32
51.2	−9.8	−28.17

*Values simulated in the absence of a bubble.

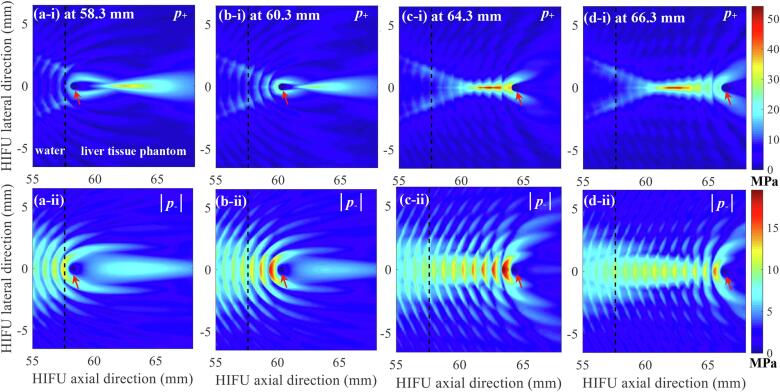
Fig. 10 shows the effects of the changes in the location of a bubble on backscattered acoustic fields in boiling histotripsy. In the simulations, the size of a bubble (i.e., 515 μm) as well as the exposure condition (P_{+, incident} of 51.2, P_{-, incident} of – 9.8 MPa) were kept constant, whilst the position of the bubble was varied as 58.3, 60.3, 64.3 or 66.3 mm along the HIFU axial axis. Both the peak positive and negative pressure magnitudes of the acoustic fields scattered by the bubble gradually increase as the bubble moves towards the HIFU focus.

Fig. 10.

The effects of the changes in the location of a bubble on backscattered acoustic fields in boiling histotripsy. Images on the first row (a, b, c and d-i) respectively represent the computed 2D spatial distributions of positive pressure fields p₊ with the presence of a bubble at 58.3, 60.3, 64.3 and 66.3 mm along the HIFU axial axis. The corresponding simulated 2D spatial distributions of negative pressure fields |p_-| are shown in the second row (a, b, c and d-ii). In the simulations, the size of a bubble was kept constant (515 μm). The 1.0 MHz HIFU beam with P₊ of 51.2 MPa and P_- of – 9.8 MPa propagates from left to right. The red arrows indicate the bubble.

4. Discussions

Boiling histotripsy is a promising HIFU technique which can be used to mechanically fractionate solid tumours. Mechanical damage in the shape of a tadpole (i.e., a head and a tail) is typically observed at the HIFU focus following boiling histotripsy treatment (Fig. 1) [6], [8], [9]. A number of ex- and in vivo studies have clearly shown the effects of boiling histotripsy in removing target tissue at the HIFU focus. However, studies of the control and prediction of the shape and size of a boiling histotripsy lesion for pre-treatment planning have not yet been performed. This is likely to be due to a limited understanding of the mechanisms underpinning the lesion generation during boiling histotripsy exposure, particularly the formation of the head. Our previous works [9], [11] have clearly demonstrated that the tail of a boiling histotripsy lesion is formed by shear stresses induced around an oscillating boiling bubble within a localised heated region, whereas the subsequent formation of cavitation clouds and their violent collapses are likely to be responsible for the production of the head of a boiling histotripsy lesion. In [9], [30], we hypothesised that:

• (a)a cavitation cluster formed between the HIFU transducer and a boiling vapour bubble is likely to be due to the constructive interaction of a shockwave scattered by a bubble with the incoming incident shockwaves;
• (b)the magnitude of the backscattered acoustic pressure field may determine the formation of and the site of bubble clouds during boiling histotripsy exposure.

To support our hypothesis, in this study, a numerical simulation of a 1.0 MHz HIFU field in the presence of a bubble at its focus was carried out. The k-Wave MATLAB toolbox was used, which numerically solves a system of first-order coupled equations (equivalent to the generalised Westervelt equation). A qualitative analysis was conducted to understand basic features of the interactions of a nonlinear wave with a bubble during boiling histotripsy exposure. k-Wave has been previously used in a number of studies to simulate nonlinear wave propagation through multiple tissue layers such as skin, muscle, strong scatterer such as ribs, kidney and blood vessels [31], [32]. It is, however, worth noting that it has neither been experimentally validated for fully capturing a strongly distorted nonlinear wave in heterogeneous media, nor for propagation through high contrast materials. A very large number of PPW and small CFL number are essentially necessary in order to model these, which substantially increase memory requirements and computational time.

A number of studies have investigated the interaction between a shockwave and a single bubble both numerically and experimentally in the field of extracorporeal shockwave lithotripsy (ESWL) [38], [39], [40], [41], [42]. ESWL is the most common treatment for breaking down kidney stones. Though P₊ and P_- used in boiling histotripsy are comparable to those in the shockwaves used in ESWL, a lithotripter pulse which consists of a single cycle shock wave at the focus is typically delivered at rates of 0.5 to 2 Hz [40], whereas a boiling histotripsy pulse with tens of thousands of shockwave cycles at the HIFU focus is fired at around 1 Hz to induce mechanical tissue damage. Therefore, most ESWL studies performed have focused on the investigation of the impact of a single shock wave pulse of very high pressure amplitude (30 to 100 MPa) on a bubble (e.g., changes of bubble wall motions). In contrast, in the present study, we have extensively investigated, for the first time, the interference of incoming incident shockwaves with backscattered acoustic fields by a bubble in order to understand the subsequent formation of cavitation clouds in boiling histotripsy.

4.1. Interaction of an incident shockwave with a bubble

Canney et al [1] experimentally observed acoustic emissions from a shock wave heating-induced boiling bubble in a tissue phantom, using an optical camera and a passive cavitation detection (PCD) system. When a millimetre-sized boiling bubble formed at the HIFU focus, a significant increase in the PCD voltage together with a sudden occurrence of higher order multiple harmonic components of the fundamental frequency in the spectrogram was observed. The authors speculated that these sudden changes, along with the formation of a boiling bubble, were likely to be due to the reflection of the incident shockwaves from the bubble. This reflection is due to the large acoustic impedance mismatch at the interface of the external medium and the gas and water vapour bubble, according to the authors. The numerical results depicted in Fig. 7, Fig. 8, Fig. 9 clearly show the presence of scattering of the incident shock waves by the vapour bubble. In addition, the constructive and destructive interactions of the scattered field by the bubble with the incoming incident shock waves were also observed. This results in the generation of localised peak negative pressures in the form of a layered structure separated by about 0.8 mm (about half of the wavelength at 1 MHz). The peak negative pressure magnitude between the acoustic fields simulated with and without the presence of a bubble at the HIFU focus were compared. Interestingly, the peak negative pressure magnitude of the backscattered field P_{-, backscatter} appeared to be higher than that in the absence of a bubble at the HIFU focus P_- (Fig. 6b and 7b). For instance, P_- is –9.8 MPa whilst P_{-, backscatter} is –31.36 MPa (a 3.2-fold increase, see Fig. 8c-ii). The increase in the peak negative pressure magnitude must therefore be attributable to the interaction of the acoustic field scattered by the bubble with incoming incident shockwaves. This interference has been experimentally examined in [33] where it was observed that bubble clouds began to form after a shockwave impinged on a bubble in a gel phantom. The authors speculated that the reflection and inversion of the peak positive pressure from the surface of the bubble interacted with the incoming incident rarefactional phase, producing a greater peak negative pressure field than in the absence of the bubble. This is known as the shock scattering effect [33] which is the main mechanism of cavitation cloud histotripsy where a dense cavitation cluster induced by this shock scattering effect mechanically destructs soft tissue. This shock scattering effect was also observed in our numerical results shown in Fig. 7c to e, Fig. 8a-iii, b-iii, c-iii and Fig. 9a-iii, b-iii, c-iii, d-iii. The shock scattering effect increases with the size of a bubble (Fig. 8), the relative distance between the HIFU focus and a bubble (Fig. 10) and the magnitude of the peak positive phase of an incident shockwave (Fig. 9 and Table 2).

4.2. Mechanisms of the formation of cavitation clouds in boiling histotripsy

Maxwell et al [34] and Lin et al [35] reported that the cavitation cloud’s intrinsic threshold is around –28 MPa for most soft tissues. This is the lowest rarefaction pressure at which a dense bubble cloud is almost certain to appear. In the present study, it was observed that the peak negative pressure amplitude of the backscattered waves by a bubble gradually increased from –17.4 MPa to –31.6 MPa as the bubble size increased (Fig. 8c), which is above the pressure threshold for cavitation clouds. These numerical results can explain our previous high speed camera experimental observations of bubble dynamics during boiling histotripsy [9], [11], [30], where a cavitation cluster did not appear immediately after the formation of a boiling vapour bubble at the HIFU focus, but was rather observed when boiling bubble size increased beyond a certain value (e.g. 480 μm).

Our numerical results suggest that cavitation clouds can migrate in the direction of the HIFU transducer (i.e. the direction opposite to wave propagation) during the course of boiling histotripsy exposure because of the shock scattering effect (Fig. 7b). The reduction of pressure amplitudes of backscattered fields due to tissue attenuation (Fig. 7b and Fig. 8a-ii, b-ii and c-ii) would, however, limit this axial bubble cloud’s growth. For instance, bubble clouds would stop progressing when a backscattered acoustic pressure is below the cavitation cloud’s intrinsic threshold [9].

4.3. Prediction of the size of a lesion produced by boiling histotripsy

The prediction of the shape and size of a boiling histotripsy lesion in soft tissue under a given HIFU exposure condition would be of much interest to pre-treatment planning. The numerical results presented in this study (Fig. 7, Fig. 8, Fig. 9) together with [9], [11], [30] suggest that the dimensions of the tail and the head of a boiling histotripsy lesion are dependent on the extent of a localised shockwave heated region and the pressure magnitude of a backscattered acoustic field by a boiling bubble, respectively.

To predict the size of a boiling histotripsy lesion, a numerical model capable of dealing with scattering by localised heterogeneities is essentially required for simulating acoustic and temperature fields in the presence of a bubble in soft tissue. This is mainly because a bubble highly reflects and scatters an incident ultrasonic field (Fig. 7, Fig. 8), whereby the heat deposition around a bubble is to be altered. For acoustic simulations, the full wave Westervelt equation can possibly be employed to obtain the spatial distribution of nonlinear acoustic fields around a vapour bubble in soft tissue. The bio-heat transfer equation, which accounts for the effects of heat diffusion, blood perfusion and heat deposition [36], could then subsequently be used in order to simulate the spatio-temporal distribution of the temperature field. These aforementioned numerical approaches could predict the changes in the extent of a heated region where a boiling vapour bubble is likely to form as a function of time. Along with this, bubble dynamics simulations as developed and performed in [11], [13] may also be useful for predicting how much tissue volume can potentially be destroyed within the heated zone.

Lastly, the size of the head of a boiling histotripsy lesion could possibly be predicted by generating a contour plot of a simulated backscattered field by a boiling bubble where the contour lines are equal to or above the cavitation cloud’s intrinsic threshold. This contour plot would indicate the potential site where cavitation clouds are likely to be induced. It has been demonstrated that acoustic pressure is the main component which triggers bubble nucleation in boiling histotripsy. However, HIFU heat deposition can also facilitate nucleation by reducing nucleation pressure thresholds [10]. In boiling histotripsy, shock wave heating increases tissue temperature, thereby decreasing the pressure threshold for cavitation clouds with time. Vlaisavljevich et al [37] have shown that the cavitation cloud’s intrinsic threshold reduces from –29.8 MPa at 10 °C to –14.9 MPa at 90 °C. This temperature- and pressure- dependent cavitation threshold should therefore be accounted for. For instance, modified classical nucleation theory developed in [10], which predicts preferential bubble nucleation sites at a given acoustic pressure and temperature during HIFU exposure, could be employed. Future work will be focused on the prediction of the overall size of a tadpole shaped lesion resulting from a given boiling histotripsy exposure condition.

5. Conclusions

In this work, the interactions of a shock wave with a vapour bubble during boiling histotripsy were numerically investigated. To the best of our knowledge, this is the first study reporting the mechanism underpinning the formation of cavitation clouds in boiling histotripsy. Our results clearly demonstrate the interference of a scattered shockwave by a bubble with an incoming incident shockwave, particularly in the rarefactional phase. This can induce a greater peak negative pressure field compared to that in the absence of a bubble at the HIFU focus. In addition, the backscattered pressure amplitude gradually increases with increasing bubble size, and it can go beyond the intrinsic cavitation threshold of –28 MPa. These results reveal that the shock scattering effect is likely to be the principle mechanism responsible for the subsequent formation of cavitation clouds after the production of a primary boiling vapour bubble at the HIFU focus during the course of boiling histotripsy. Our numerical results suggest that the formation of cavitation clouds in boiling histotripsy is a threshold effect which primarily depends on the size and location of a boiling bubble and the sum of the incident and scattered pressure from a bubble.

6. Author statement

We confirm that all named authors have agreed to the submission of this manuscript, and that they have sufficiently participated in the study to be named as authors. All co-authors have reviewed and agreed with the contents of the manuscript and there are no conflicts of interest to report. We certify that the submission is original work and is not under review at any other journal.

CRediT authorship contribution statement

Ki Joo Pahk: Conceptualization, Methodology, Investigation, Formal analysis, Data curation, Validation, Visualization, Writing - original draft, Writing - review & editing, Funding acquisition, Supervision. Sunho Lee: Methodology. Pierre Gélat: Investigation, Formal analysis, Writing - review & editing. Matheus Oliveira de Andrade: Formal analysis. Nader Saffari: Investigation, Formal analysis, Writing - review & editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following are the Supplementary data to this article: