Enhancement of heat transfer in forced convection by using dual low-high frequency ultrasound

Highlights

• •Thermal and hydrodynamic effect of combined low-and-high-frequency sonication is studied.
• •PIV and Sonochemiluminescence are carried out for characterization of ultrasound effects.
• •Thermal, hydrodynamic and cavitational results are analyzed in combination.
• •Synergetic effect of low and high frequency is highlighted.

Abstract

Combined sonication with dual-frequency ultrasound has been investigated to enhance heat transfer in forced convection. The test section used for this study consists of a channel with, on one hand, heating blocks normal to the water flow, equipped with thermocouples, and, on the other hand, two ultrasonic emitters. One is facing the heating blocks, thus the ultrasonic field is perpendicular, and the second ultrasonic field is collinear to the water flow. Two types of ultrasonic waves were used: low-frequency ultrasound (25 kHz) to generate mainly acoustic cavitation and high-frequency ultrasound (2 MHz) well-known to induce Eckart’s acoustic streaming. A thermal approach was conducted to investigate heat transfer enhancement in the presence of ultrasound. This approach was completed with PIV measurements to assess the hydrodynamic behavior modifications under ultrasound. Sonochemiluminescence experiments were performed to account for the presence and the location of acoustic cavitation within the water flow. The results have shown a synergetic effect using combined low-and-high-frequency sonication. Enhancement of heat transfer is related to greater induced turbulence within the water flow by comparison with single-frequency sonication. However, the ultrasonically-induced turbulence is not homogeneously distributed within the water flow and the synergy effect on heat transfer enhancement depends mainly on the generation of turbulence along the heating wall. For the optimal configuration of dual-frequency sonication used in this work, a local heat transfer enhancement factor up to 366% was observed and Turbulent Kinetic Energy was enhanced by up to 84% when compared to silent regime.

1. Introduction

The efficiency of ultrasound to enhance heat transfer has been widely demonstrated, whether in natural convection [1], [2], [3] or in forced convection [4], [5], [6]. It has led to applicative research for heat exchangers [7], [8], reactors [9] or heat pipe [10]. However, the effects induced by ultrasound strongly depend on the frequency used.

Hydrodynamically, two major phenomena can be observed, which are acoustic cavitation and acoustic streaming. Acoustic cavitation is the process of bubble creation, expansion and collapse, induced by waves pressure variation. When these bubbles collapse, they generate intense local hydrodynamic effects, with micro-jets at very high speed, and shock waves, that might result in the collapse of other bubbles around [11]. This phenomenon is mainly observed with wave frequencies ranging from 20 kHz to a few hundred kHz, which are usually qualified as low-frequency ultrasound. Considering that the cavitation bubble size is inversely proportional to the resonance frequency, low-frequency ultrasound generates bigger bubbles than high-frequency ultrasound. Acoustic cavitation has been quite well investigated to enhance heat transfer [2], [12], [13]. Indeed, when the process occurs close to a heating surface, it may disturb the thermal boundary layer, and therefore enhance heat transfer between this heating surface and the fluid [2].

On the other hand, ultrasound can generate acoustic streaming, which induces recirculating flows. While different types of acoustic streaming may occur according to different initial conditions, this study mostly focuses on Eckart’s acoustic streaming. It is generated by the dissipation and attenuation of acoustic wave energy caused by liquid absorption. It induces a pressure gradient within the fluid and thus fluid movement in the same direction as the acoustic field [14]. The ability of high-frequency ultrasound to generate intense Eckart’s acoustic streaming has been well-studied [15] and thus can increase turbulence within a flow and thereby enhancing heat transfer [16], [17].

Recent work has compared the effect of the ultrasound frequency on heat transfer enhancement in forced convection [18]. This study has clearly demonstrated that turbulence induced by low-frequency ultrasound tends to intensify with fluid velocity and thus increasing heat transfer enhancement. On the other hand, the enhancement of turbulence and heat transfer generated by high-frequency ultrasound is attenuated as the fluid velocity increases.

It is also relevant to mention that the influence of ultrasound on heat transfer also depends on the orientation of the acoustic field regarding the heat source. Indeed, Yukawa et al. [1], have investigated the evolution of heat transfer enhancement in natural convection for different incidence angles of a heating plate (from horizontal to vertical) with an upward ultrasonic field. The enhancement by ultrasound is greater when the heating plate is facing the ultrasonic field (horizontal) even though it is the worst angle for natural convective heat transfer.

Most studies about heat transfer enhancement by ultrasound only refer to the use of a single ultrasonic field although several works involving dual-frequency devices have been performed for sonochemical applications. For example, Iernetti et al. [19] have demonstrated that acoustic cavitation effects produced by 700 kHz ultrasound could be enhanced by orthogonal low-frequency ultrasound pulses, which was later confirmed by Ciuti et al. [20], [21]. Indeed, as cavitation bubbles are driven by low-frequency ultrasound collapse, they break down into smaller fragments that can be suitable cavitation nuclei for a higher frequency ultrasonic field. Moreover, combined ultrasonic fields with multiple frequencies could cause cavitation over a wider range of cavitation bubble radii, as the bubble size depends on the frequency. Feng et al. [22] have shown that the combination of dual-frequency ultrasound is at the origin of a synergetic effect on cavitation. Indeed, the combined ultrasound irradiation induces a more intense cavitation activity than the algebraic sum of individual irradiation. Other studies have confirmed this idea [23], and have also shown that the use of dual-frequency ultrasound with sources of half the power would generate more cavitation than single-frequency ultrasound with double the power [24]. However, it seems that the emitters’ position has an influence on this synergy of ultrasonic fields for cavitation activity in the case where emitters are collinear to each other, as demonstrated by Rahimi et al. [25].

Besides this, similar phenomena of cavitation enhancement can be observed, when forced fluid flow is associated with acoustic cavitation. Several studies have investigated this subject [26], [27], [28], [29], usually showing an enhancement of sonochemical activity for low-frequency ultrasound in fluid flow. More recently, Reuter et al. [30] have shown that a submerged jet injected in a low-frequency ultrasonic field induces a drastic increase of cavitation bubbles density in the jet zone thus enhancing the cavitation activity. Hatanaka et al. [27] have concluded that fluid flow could prevent cavitation bubbles from coalescing and clustering by weakening the secondary Bjerknes force responsible for the mutual attraction between bubbles. Therefore, the fluid flow could enhance sonochemical activity produced by acoustic cavitation.

Considering the effects on cavitation activity induced by dual-frequency ultrasound combination, it could be of great interest to assess heat transfer enhancement in this way. However, only a single work has reported the influence of a sound field (14 kHz) combined with an ultrasonic field (474 kHz) on a heat pipe to enhance heat transfer [31]. These results have shown that the heat pipe performances on heat transfer capacity are improved with dual-frequency sonication compared to single-frequency sonication. This study has revealed that the combination of ultrasonic fields results in a synergetic effect on heat transfer improvement.

While the literature is scarce about the influence of dual-frequency ultrasound on heat transfer, ultrasound has clearly shown its ability to enhance heat transfer, through different phenomena according to its frequency. Moreover, dual-frequency sonication usually leads to enhanced ultrasonically-induced effects. Accordingly, the present study is an investigation of dual low-high frequency ultrasound influence on heat transfer in forced convection and is supported by an analysis of the flow hydrodynamics in these conditions.

For this purpose, an experimental setup equipped with a heating wall and emitters of low (25 kHz) and high (2 MHz) frequency has been designed. Thermal analysis is proceeded to quantify heat transfer enhancement in the presence of ultrasound while a hydrodynamic phenomenological investigation is led with Particle Image Velocimetry. In addition, sonochemiluminescence is used here as a tool to visualize the presence and the location of acoustic cavitation. The combination of these three different approaches allows investigating the possible mechanisms underlying the obtained results.

2. Materials and methods

2.1. Test section presentation

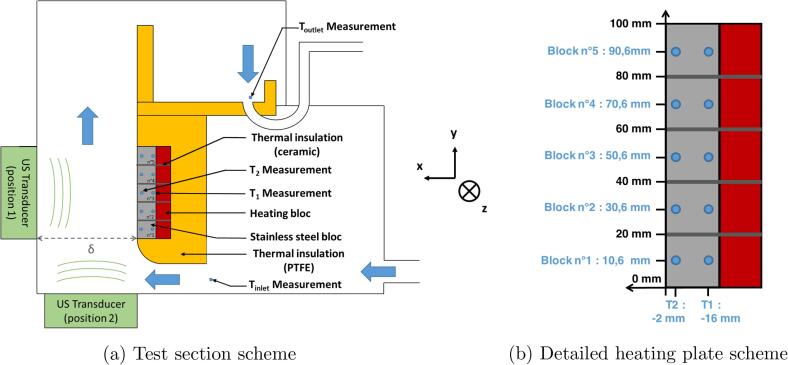
The test section used in this work was initially designed to investigate the effect of ultrasound on heat transfer in forced convection [17]. For this purpose, the fluid flows throughout a channel, composed of a heating wall on one hand and of two ultrasonic emitters on the other hand. The heating wall consists of five imposed-flux heating blocks, thermally insulated from each other’s as shown in Fig. 1b. Each heating block is equipped with thermocouples in order to determine local convective heat transfer coefficients. The set-up enables two locations for ultrasonic emitters: one faces the heating blocks while the second is located at the bottom of the test section close to the fluid inlet. This test section is presented in Fig. 1a. The fluid enters horizontally in the test section and then undergoes a 90° direction change. It then flows vertically along the rectangular channel to finally exit in the upper part of the test section.

Fig. 1.

Test section design.

Regarding the emitters’ location, the first emitter (position 1) faces the heating wall with a gap of 140 mm (x-axis) defined as $\delta$. The waves are thus emitted perpendicularly to the water flow. The second emitter (position 2) is at the origin of waves emitted collinearly to the flow in the channel (y-axis). Therefore, it is possible to study the influence of ultrasound according to the frequency and the direction of the emitted waves with respect to the water flow and to combine two ultrasonic fields orthogonally operating at low and high frequency respectively. It has to be noted that the distance between the heating wall and the emitter in position 1 was imposed by the space required for the emitter to be in position 2, and thus to combine two ultrasonic fields.

As detailed in Fig. 1b, the heating wall is composed of five independent heating blocks of 19 mm (y-axis) x 18 mm (x-axis) x 90 mm (z-axis) made of stainless steel with a thermal conductivity of ${\lambda }_s$ = 15 W.m⁻¹.K⁻¹. The heating wall is insulated with PTFE (${\lambda }_{\mathit{PTFE}}$ = 0,25 W.m⁻¹.K⁻¹) and is represented in yellow on Fig. 1. Moreover, the heating blocks are separated from each other by a 1 mm-thick ceramic thermal insulation (${\mathrm{Macor}}^{\copyright },{\lambda }_{\mathit{Macor}}$ = 1.46 W.m⁻¹.K⁻¹) represented in dark gray on Fig. 1. The thermal insulation ensures a unidirectional heat flux within each block, according to x-axis. Thermocouples are located on both sides of each heating block (in the middle of the block, according to z-axis), wall-side (T₁) and channel-side (T₂), as depicted on Fig. 1b. The liquid temperature is measured at the inlet (T_inlet) and outlet (T_outlet) of the test section. These temperature measurements allow calculating local heat transfer coefficients as detailed in paragraph 3.3. The total power supplied to the heating wall (named P_th) is equal to 450 W and is assumed to be equally distributed on the 5 heating blocks.

Regarding the global dimensions of the test section, the heating wall is 100 mm long (y-axis), the channel is 174 mm large (z-axis), defined as L later, and its hydraulic diameter D_h is 0,155 m, defined as follows:

$$D_h=\frac{4\times (L\times \delta )}{2\times L+2\times \delta }$$ (1)

This test section is part of an overall test bench allowing the control and measurement of the liquid flow rate, using a regulation valve and a flowmeter Krohne Waterflux 3100 W. The fluid circulates within the circuit using a pump Iwaki MX 251 CV5-E. The fluid temperature at the inlet of the test section is also regulated by using an external plate heat exchanger where temperature-controlled water from an external cooling system circulates.

The flow characteristics for every test are kept constant and are detailed in Table 1.

Table 1.

Flow characteristics.

Fluid	Inlet temperature [°C]	Velocity [m.s−1]	Reynolds number	Prandtl number
Water	20	6.6 × 10−3	1018	6,97

The flow regime is characterized by the Reynolds number. Taking into account the physical properties of the water, Reynolds number is here equal to 1018 meaning that the flow regime is considered as laminar. The Reynolds number is function of the fluid velocity V [m.s⁻¹], the hydraulic diameter D_h [m], and the physical properties of the fluid such as the density $\rho$ [998 kg.m⁻³] and the dynamic viscosity of the fluid $\mu$ [1 × 10⁻³ Pa.s]. It is defined as below:

$$\mathit{Re}=\frac{\rho \times V\times D_h}{\mu }$$ (2)

Laminar flow regime is chosen for this study since previous works have clearly shown that heat transfer enhancement induced by ultrasound is more important at this regime [7]. However, the flow regime cannot be theoretically considered as perfectly laminar due to perturbations of the flow velocity, owing to the shape of the test section and to change of direction of the liquid flow. This effect occurs in both experimental configurations (with and without ultrasound). Therefore, this work is a comparative approach between thermal and hydrodynamic results obtained with and without ultrasound.

Besides this, to characterize the speed of thermal and hydrodynamic phenomena in fluid, the Prandtl number is used. It is defined as the ratio of momentum diffusivity to thermal diffusivity, given as:

$$\mathit{Pr}=\frac{\mu /\rho }{\lambda /(\mathit{Cp}\times \rho )}=\frac{\mu \times \mathit{Cp}}{\lambda }$$ (3)

Here, Cp [4185 J.kg⁻¹.K⁻¹] is the thermal capacity, and $\lambda$ [0,6 W.m⁻¹.K⁻¹] is the thermal conductivity of the fluid. All the physical properties are calculated for water at T_inlet = 20 °C. For water, the Prandtl number is higher than 1 which means that momentum dissipates faster than heat through the fluid and thus the velocity profile will strongly influence the temperature profile. Consequently, disturbing the velocity profile using ultrasound seems relevant in order to intensify convective heat transfer.

2.2. Characterization of ultrasound emitters and experimental configurations

In this study, two different ultrasonic frequencies are chosen, 25 kHz, which refers to low-frequency ultrasound (LF) and 2 MHz that corresponds to high-frequency ultrasound (HF). Using a single ultrasonic emitter will first allow the comparison between specific effects induced by each ultrasonic frequency. In addition, the influence of the ultrasonic field direction with respect to the water flow can be thus analyzed. Finally, the effects induced by the combination of dual low-and-high-frequency ultrasound will be investigated.

The 25 kHz ultrasonic emitter (provided by Sinaptec, France) and the 2 MHz ultrasonic emitter (provided by Sonosys, Germany) are both 160 × 160 mm², and have an active surface of 100 × 100 mm² located at the center. However, they present differences regarding the locations of their respective piezoelectric ceramics. The 25 kHz emitter is composed of four round ceramics of 45 mm diameter equally distributed on the active surface while the piezoelectric ceramics of the 2 MHz emitter are divided into eight rectangular ceramics over the active surface. Each emitter has been characterized in order to identify its induced effects. The characterization method used has been previously described in [17]. With the 25 kHz emitter, the aluminum foil test has displayed the presence of intense acoustic cavitation with strong mechanical effects. Indeed, when the aluminum foil undergoes 25 kHz ultrasound, it erodes quickly after only a few seconds. On the other hand, 2 MHz ultrasound generates strong convective acoustic streaming but no mechanical cavitation has been observed with aluminum foil test. Furthermore, the acoustic power, defined as P_US, has been determined by the usual calorimetric method and thus corresponds to the acoustic power dissipated as heat by ultrasonic transducers. Therefore, the same supplied estimated power is used for both emitters in all experiments.

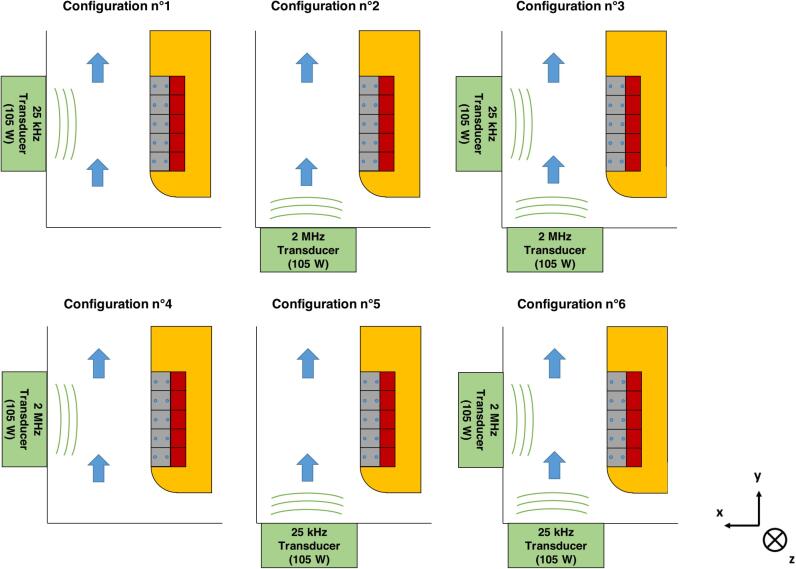
As explained in the test section presentation, ultrasound can be emitted in two directions, either perpendicularly (position 1) or collinearly (position 2) to the water flow as indicated in Fig. 1. P_US is equal to 105 W for both low and high frequency emitters. Moreover, it is possible to combine two ultrasonic fields (the total power is thus doubled: 105 W for LF emitter (25 kHz) + 105 W for HF emitter (2 MHz)). Thereby, it results in six possible experimental configurations with ultrasound (four single-frequency, that is to say configurations n°1, 2, 4 and 5 + two dual-frequency, that is to say configurations n°3 and 6) as detailed in Table 2 and illustrated on Fig. 2.

Table 2.

Tested experimental configurations.

Configuration n°		1	2	3	4	5	6
position 1	f	25 kHz	25 kHz	25 kHz	2 MHz	2 MHz	2 MHz
	$P_{\mathit{US}}$	105 W	0 W	105 W	105 W	0 W	105 W
position 2	f	2 MHz	2 MHz	2 MHz	25 kHz	25 kHz	25 kHz
	$P_{\mathit{US}}$	0 W	105 W	105 W	0 W	105 W	105 W

Fig. 2.

Scheme of the six experimental configurations.

2.3. Determination of the local heat transfer coefficient

As part of this study, the influence on heat transfer for the above 6 ultrasound configurations has been investigated. The purpose is then to evaluate the influence of each ultrasonic field configuration on convective heat transfer from heating wall to water using temperature measurements. The test starts when the heating blocks temperatures in silent regime are stable, that is to say in steady-state. As soon as sonication starts, wall temperatures drop displaying that convective heat transfer increases. However, while more heat is transferred to the fluid, the fluid temperature does not increase noticeably (about 0.1 °C) because of the large flow rate. The sonication keeps going until the wall temperatures are stable again, which completes the test. To ensure the results’ repeatability, every temperature measurement is run six times, and the error bars are thus the standard deviation.

As mentioned previously, the measured temperatures by thermocouples located on each side of the heating blocks allow calculating the mono-dimensional heat flux (here along x-axis), between the two points of measurement as:

$$\mathrm{\Phi }=\frac{{\lambda }_s}{e_{T_1-T_2}}\times S\times (T_1-T_2)$$ (4)

where $\mathrm{\Phi }$, ${\mathit{eT}}_1-T_2$ and S are respectively the heat power which crosses each block, the distance between thermocouple that measures T₁ and thermocouple that measures T₂ and the heating surface of one block in contact with the fluid. The wall temperature T_w is then given by the following formula, as the heat flux is considered to remain unidirectional and constant:

$$T_w=T_1-\frac{\mathrm{\Phi }\times e_{T_1-T_w}}{{\lambda }_s\times S}$$ (5)

The variation of water temperature between the test section inlet and outlet can be determined with the following equation:

$$\mathrm{\Delta }{T}_{\mathit{fluid}}=T_{\mathit{inlet}}-T_{\mathit{outlet}}=\frac{{\mathrm{\Phi }}_{\mathit{tot}}+P_{\mathit{US}}}{\dot{m}\times \mathit{Cp}}$$ (6)

${\mathrm{\Phi }}_{\mathit{tot}}$ is here the total heat power supplied to water by the five blocks. However, the sum of ${\mathrm{\Phi }}_{\mathit{tot}}$ and P_us is low compared to the fluid flowrate $\dot{m}$ multiplied by the fluid heat capacity Cp (see Eq. (6)). The temperature variation is therefore negligible without ultrasound (ΔT_in−out$\approx$ 0.6°C) and barely increase when ultrasound are turned on (+0.1°C, as mentioned before). The fluid temperature is thus defined as the average between T_inlet and T_outlet and is assumed to be constant during the process.

Convective heat transfer coefficient h [W.m⁻².K⁻¹] can then be calculated with T_fluid as the fluid temperature:

$$h=\frac{\mathrm{\Phi }}{S\times (T_w-T_{\mathit{fluid}})}$$ (7)

Finally, heat transfer enhancement by ultrasound is quantified by a factor called HTEF (Heat Transfer Enhancement Factor), which is function of heat transfer coefficients in silent regime h_silent and under ultrasound h_us:

$$\mathit{HTEF}=\frac{h_{\mathit{us}}-h_{\mathit{silent}}}{h_{\mathit{silent}}}$$ (8)

2.4. Particle image velocimetry set-up

To get a better understanding of the effects of ultrasound on heat transfer, it is also necessary to understand its influence on hydrodynamics. Particle Image Velocimetry (PIV) is a technique often employed to study acoustically-induced modifications of liquid flow patterns [32], [33], [34]. PIV is an optical method based on particle group trajectory tracking to measure instantaneous velocity field. First, the fluid is seeded with particles that are illuminated by a laser sheet. The movement of seeding particles is then recorded by a camera and it is thereby possible to measure the displacement of particles group between two images within an interrogation window. The time laps between images is fixed, which gives the velocity for each interrogation window of the measuring field and thus an instantaneous velocity field [35]. Here, a two-dimensional two-component device has been used. The laser is a Nd-Yag (provided by Dantec Dynamics) with two cavities which generate 200 mJ. The camera is an ImagerProX2M (provided by LaVision), with a 1600x1200-pixel resolution. The recording is carried out in double-frame, meaning that a doublet of images is shot with a given $\delta$t (between 5000 $\mathrm{\mu }$s and 12,000 $\mathrm{\mu }$s, depending on the configuration) between two images. The $\delta$t is adjusted for an average particle displacement of 8 pixels between 2 frames. The processing will then calculate the instantaneous velocity field from this frame doublet. The camera and the laser are synchronized with a trigger rate of 14,77 Hz. For 2500 frames doublet, the recording thus takes about 3 min. The measuring field is 140 mm (x-axis) by 185 mm (y-axis). This measuring field allows analyzing the flow along the heating blocks as well as a part of the section upstream and downstream. However, it does not cover the total flow section down to the emitter in position 2 and thus a part of the section is not visible (the hidden section corresponds to the distance between the emitter in position 2 and the bottom of the measuring field, which is 40 mm long (y-axis)).

The post-processing is made with Davis software (provided by LaVision). First, the average velocity field is calculated from 2500 instantaneous velocity fields. It allows then determining the TKE (Turbulent Kinetic Energy) [m².s⁻²] within the studied field in order to analyze the turbulence within the flow. The Turbulent Kinetic Energy is calculated as following [36]:

$$\mathit{TKE}=\frac{3}{4}\times {\sqrt{\frac{{\displaystyle \sum _{i=1}^N}{(V_i-V_{\mathit{avg}})}^2}{N-1}}}^2$$ (9)

where V_i is the measured instantaneous fluid velocity and V_avg is the average fluid velocity, here calculated over 2500 measured instantaneous fluid velocities. To assess the effect of ultrasound on turbulence, a TKE factor TKE EF is calculated similarly to the HTEF with the TKE in silent regime TKE_silent and under ultrasound TKE_us:

$$\mathit{TKEEF}=\frac{{\mathit{TKE}}_{\mathit{us}}-{\mathit{TKE}}_{\mathit{silent}}}{{\mathit{TKE}}_{\mathit{silent}}}$$ (10)

2.5. Sonochemiluminescence

When acoustic cavitation is generated in aqueous solutions, it produces free radicals ${\mathrm{H}}_{·}$ and ${\mathrm{OH}}_{·}$ from the thermal decomposition of water vapor within cavitation bubbles [37] according to the water sonolysis reaction:

$$H_{2}O\stackrel{)))}{\to }{H}^{·}+{\mathit{OH}}^{·}$$ (11)

To visualize the spatial acoustic cavitation distribution generated by ultrasound within the channel, the method based on the chemiluminescence of luminol described by Renaudin et al. [38] has been used. A luminol solution (3-aminophtalhydrazide, 1 mol.m⁻³) is used in aqueous solution at pH 10.7. The reaction of luminol with ${\mathrm{OH}}_{·}$ radicals generated by ultrasound produces a characteristic blue light. It is then possible to observe and photograph the cavitation repartition within the fluid. Here, the same camera ImagerProX2M (provided by LaVision) is used. The camera is set to record individual photography, with an exposure time of 60 s. The measuring field is the same as for PIV (140 mm (x-axis) by 185 mm (y-axis)). The images are then processed to scale the intensity of light generated by cavitation bubbles.

3. Results and discussion

3.1. Preliminary results under silent conditions

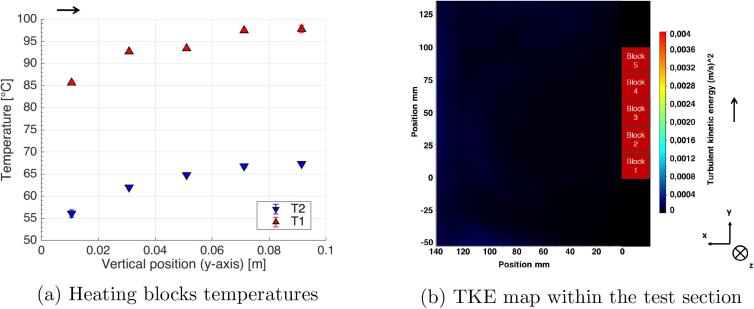
Within a flow, convective heat transfer tends to decrease with the thermal boundary layer growth along the heated wall to reach the point at which the exchange surface temperature remains constant under imposed flux heated wall conditions. From this point, the flow is considered to be thermally developed. The Fig. 3a shows the evolution of blocks temperatures along the heating wall without ultrasound. The water flows along the y-axis, represented by the horizontal black arrow. The vertical position corresponds here to the position on the heating wall. Here, the temperature of the heating wall reaches a maximum around block 4 (y = 0.07 m) and 5 (y = 0.09 m).

Fig. 3.

Temperature profile (a) and Turbulent Kinetic Energy (b) in silent conditions.

The Fig. 3b shows the TKE map within the test section without ultrasound. The water flows upward, represented by the vertical black arrow, following y-axis. Even though the specific geometry of the test section induces inlet effects and a flow that is not perfectly uni-directional, barely any turbulence is observed here, which is in good agreement with the flow laminar regime. This preliminary observation makes by consequence the PIV technique relevant.

3.2. Influence of low-frequency ultrasound on convective heat transfer

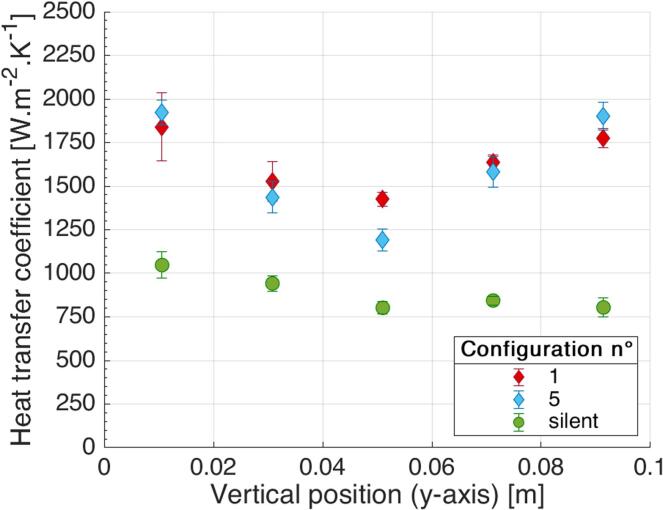
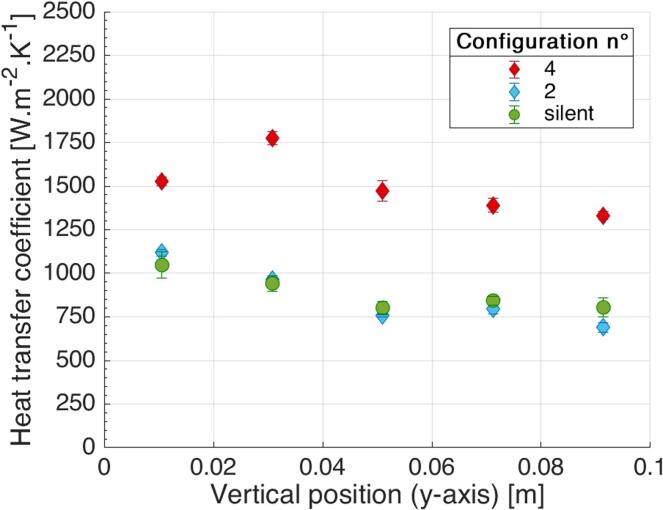
The Fig. 4 displays the influence of 25 kHz ultrasound on heat transfer coefficient h when the ultrasonic field is perpendicular (configuration n°1) or collinear (configuration n°5) to the water flow. These results are compared to heat transfer coefficients in silent regime with respect to the position along the heating wall. First, as expected, heat transfer in silent regime follows a decreasing trend to reach a minimum at block 5 due to thermal establishment. On the other hand, heat transfer is significantly enhanced by the presence of 25 kHz ultrasound as heat transfer coefficients are higher under ultrasound than in silent regime, regardless of the emitter position. Indeed, the spatial evolution of heat transfer is alike for both configurations. Heat transfer coefficients for configuration n°1 and n°5 are in the same order of magnitude, ranging from 1250 and 2000 W.m⁻².K⁻¹. However, the heat transfer under ultrasound does not decrease along the wall as the heat transfer under silent regime, and shows two maximums at block 1 and block 5.

Fig. 4.

Influence of low-frequency ultrasound on heat transfer coefficients along heating wall (f = 25 kHz, P_US = 105 W).

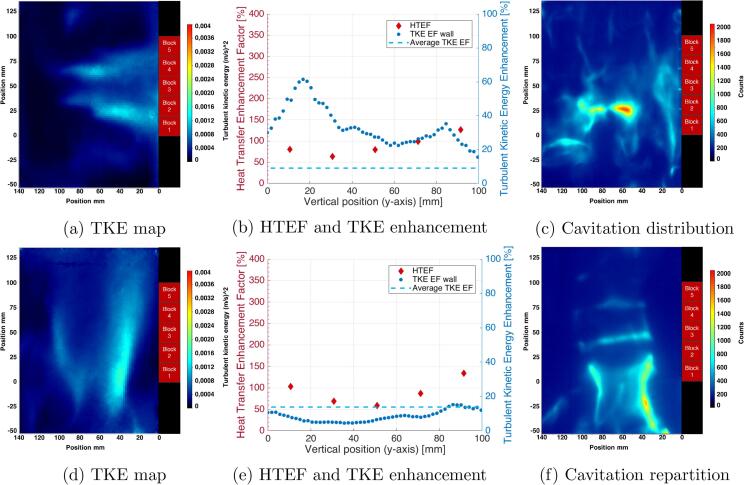
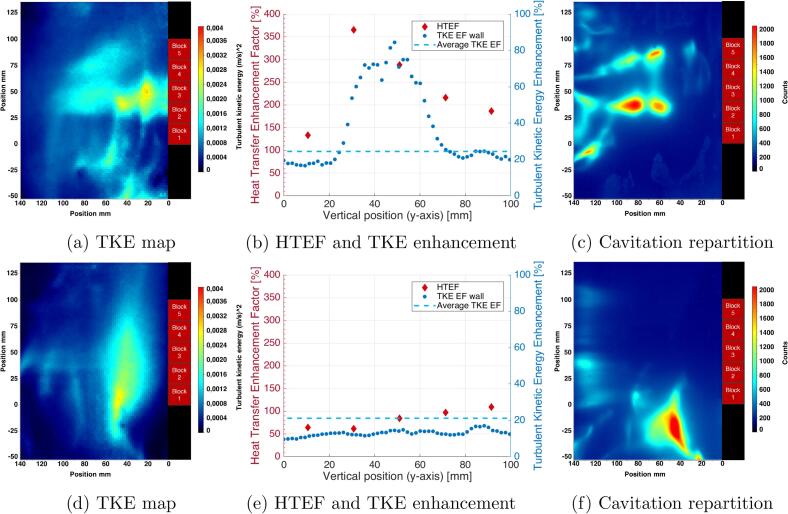
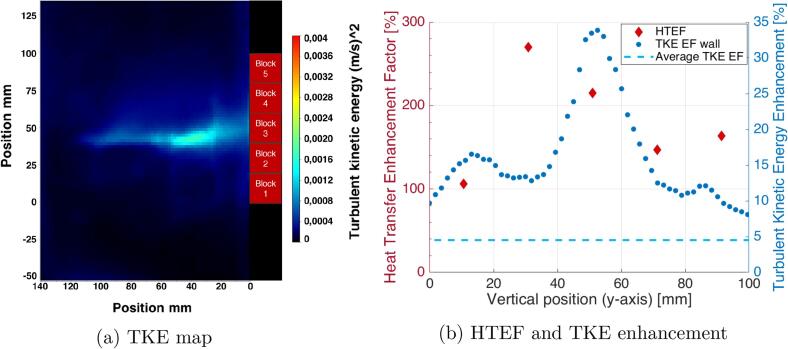
This spatial evolution of heat transfer under ultrasound along the heating wall can be explained by different factors. The heat transfer results are thus associated with PIV measurement and sonochemiluminescence experiments as presented in Fig. 5. Firstly, Turbulent Kinetic Energy within the measuring field under ultrasound is mapped to visualize the turbulence distribution within the water flow. Secondly, the enhancement factors for heat transfer and TKE are plotted together. The TKE Enhancement Factor along the heating wall are plotted with blue dots, and the dashed line corresponds to the TKE Enhancement Factor averaged within the overall PIV measuring field. Finally, the cavitation distribution is displayed by sonochemiluminescence pictures.

Fig. 5.

(a), (b), (c): Results for configuration n°1 (f = 25 kHz, perpendicular to the water flow, P_US = 105 W)// (d), (e), (f): Results for configuration n°5 (f = 25 kHz, collinear to the water flow, P_US = 105 W).

As it can be seen in Fig. 5a and d, depicting the turbulent kinetic energy map within the channel, the turbulence is mainly located on 2 areas, both when the 25 kHz ultrasonic field is perpendicular or collinear to the water flow. When the ultrasonic field is perpendicular to the water flow (Fig. 5a), these areas of turbulence are located close to the heating wall. Indeed, as it can be seen on Fig. 5b, the average TKE Enhancement Factor within the measuring field is equal to 9%, while the TKE Enhancement Factor along the wall is always greater with two peaks on block 1 (61%) and block 5 (35%) respectively. Since the TKE EF along the wall is always greater than the average TKE EF, it is most probably that the heat transfer enhancement is caused here by the turbulence generated along the heating wall since the HTEF and TKE Enhancement Factor along the wall have similar trends.

On the other hand, when the 25 kHz ultrasonic field is collinear to the water flow, the areas of turbulence are mainly located within the bulk of the water flow (Fig. 5d). In this configuration the average TKE enhancement factor is 14% (Fig. 5e). However, the TKE enhancement along the heating wall is lower than the average TKE Enhancement Factor except around block 1 and 5 where it reaches similar level. Therefore, the global enhancement of TKE within the water flow, associated with local TKE enhancement on block 1 and 5 induce a HTEF evolution along the heating wall similar to the configuration n°1.

The acoustic cavitation is undoubtedly at the origin of this turbulence as the cavitation distribution on the Fig. 5c and f are very similar to the turbulence distribution on the Fig. 5a and d respectively. This repartition can be explained by the location of piezoelectric transducers in the ultrasonic emitter as mentioned in Section 2.2.

3.3. Influence of high-frequency ultrasound on convective heat transfer

Heat transfer coefficients in the presence of 2 MHz ultrasound (configuration n°2 and n°4) can be compared with those of silent regime on Fig. 6. When the high-frequency ultrasonic field is perpendicular to the water flow (configuration n°4), heat transfer coefficients along the heating wall are higher than in silent regime. Moreover, they mostly follow the same decreasing trend along the heating wall than in silent regime except for the block 1. Since it is located at the starting point of the intersection between the water flow and the ultrasonic field, ultrasound probably has less influence at this point. Beside this, when the high-frequency ultrasonic field is collinear to the water flow (configuration n°2), there is no significant influence on convective heat transfer. Indeed, heat transfer coefficients are similar to those obtained in silent regime, demonstrating that the convective heat transfer is not affected by the presence of 2 MHz ultrasound in this specific configuration.

Fig. 6.

Influence of high-frequency ultrasound on heat transfer coefficients along heating wall (f = 2 MHz, P_US = 105 W).

Comparison can also be made between results observed in configuration n°4 and results of experimental configurations n°1 and 5 (Fig. 4). Heat transfer coefficients here are in the same order of magnitude (between 1300 and 1750 W.m⁻².K⁻¹), while their distribution along the heating wall is different owing to hydrodynamic effects induced by each ultrasonic frequency.

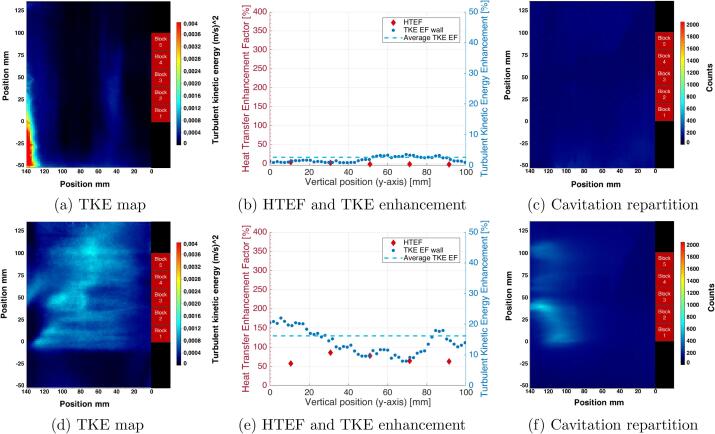
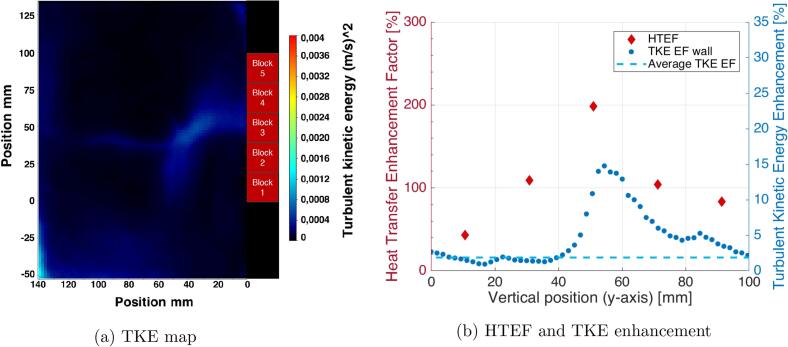
The Fig. 7a depicts that almost no significant turbulence is generated within the water flow when the HF ultrasonic field is collinear to the water flow and thus the HTEF correlates well with the TKE Enhancement Factor (see Fig. 7b). The collinearity of the ultrasonic field with the water flow seems to generate no additional turbulence within the fluid since the acoustically-induced streaming does not shear the mean flow. Moreover, Fig. 7c shows no cavitation visible on this area of the test section.

Fig. 7.

(a), (b), (c): Results for configuration n°2 (f = 2 MHz, collinear to the water flow, P_US = 105 W)// (d), (e), (f): Results for configuration n°4 (f = 2 MHz, perpendicular to the water flow, P_US = 105 W).

Nonetheless, when the ultrasonic field is perpendicular to the water flow, strong turbulence is generated within the water flow as shown in Fig. 7d. It produces global turbulence, with an average TKE Enhancement Factor of 16%, mixing the bulk and the boundary layer and thus enhancing convective heat transfer. Indeed, the HTEF and the TKE Enhancement Factor along the wall on Fig. 7e correlate reasonably well.

Given that almost no cavitation is generated here by high-frequency ultrasound (Fig. 7c and f), the turbulence is then clearly caused by Eckart’s acoustic streaming, as reported in previous work by Bulliard et al. [17]. This work also demonstrates an increase in the turbulence rate and a sharp change of the water flow direction induced by high-frequency ultrasound.

However, unlike low-frequency ultrasound, the ultrasonic field direction has a strong influence with high-frequency ultrasound to the point that in the case where high-frequency ultrasonic field and water flow are collinear, heat transfer is not improved despite the presence of ultrasound. Considering the strong influence of ultrasound on heat transfer regardless of the acoustically-induced effects depending on the wave frequency, it seems therefore interesting to combine two ultrasonic fields of low and high frequency.

3.4. Influence of combined dual low-high frequency ultrasound on convective heat transfer

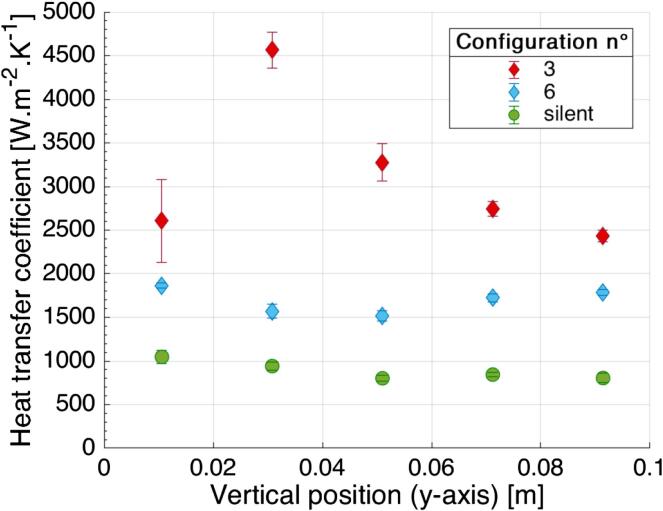
3.4.1. Comparison between configurations n°3 and n°6

The effects of two combined ultrasonic fields on heat transfer are presented in Fig. 8. For both configurations n°3 and n°6, heat transfer coefficients are higher than in silent regime clearly showing that convective heat transfer is enhanced by dual-frequency sonication. In configuration n°3, heat transfer coefficients are considerably higher than in silent regime. The evolution of the heat transfer coefficient along the heating wall reaches a maximum on block 2, with a heat transfer coefficient of about 4550 W.m⁻².K⁻¹, followed by a decreasing trend. On the other hand, heat transfer coefficients in configuration n°6 range from 1500 to 1900 W.m⁻².K⁻¹ and stays lower than in configuration n°3, no matter the block.

Fig. 8.

Influence of dual low-high frequency ultrasound on heat transfer coefficient (f = 25 kHz, P_US = 105 W + f = 2 MHz, P_US = 105 W).

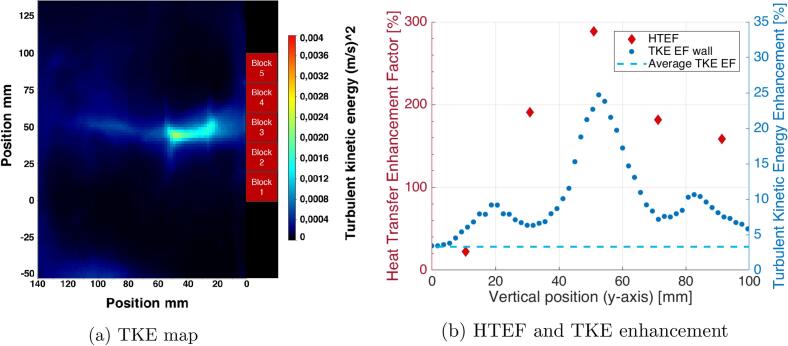
The Fig. 9a and d show that the turbulence is strong within the water flow, reaching similar level of TKE of about 0,025 m⁻².s⁻² in some areas for both configurations. Nonetheless, it is worth mentioning that the turbulence distribution is not homogeneous and rather confined to specific areas. For configuration n°6 (see Fig. 9d), this turbulence is mainly located in the bulk of the flow similarly to Fig. 5d. For configuration n°3 (see Fig. 9a), the combination induces strong turbulence within the water flow and along the heating wall, mostly on blocks 2 and 3.

Fig. 9.

(a), (b), (c): Results for configuration n°3 (f = 25 kHz, perpendicular to the water flow, P_US = 105 W + f = 2 MHz, collinear, P_US = 105 W) // (d), (e), (f): Results for configuration n°6 (f = 2 MHz, perpendicular to the water flow, P_US = 105 W + f = 25 kHz, collinear, P_US = 105 W).

The analysis of the Fig. 9e shows that the turbulence generated by ultrasound is mainly located within the bulk with an average TKE enhancement factor of 21%, which is always higher than the TKE enhancement factor along the heating wall. Indeed, the turbulence along the wall in configuration n°6 is roughly equivalent to the turbulence in configuration n°5, when the single 25 kHz emitter only generates ultrasonic field collinearly to the water flow as shown in Fig. 5e. Therefore, it has a limited impact on the heating blocks and HTEF in configuration n°6 reach a similar level to HTEF with a single 25 kHz ultrasonic field.

On the other side, the Fig. 9b for configuration n°3, shows a strong TKE enhancement along the wall mainly located on blocks 2 and 3 where it reaches up to 84%, and an average TKE enhancement factor of 24%. This is in good agreement with the spatial evolution of HTEF along the wall as it reaches a peak at block 2 and then decreases.

Compared to configuration n°6, it shows that for a similar average TKE enhancement factor, the HTEF is higher in configuration n°3 because the turbulence generated is mostly located close to the heating wall and therefore induces a greater disturbance of the boundary layer.

Moreover, the cavitation displayed on Fig. 9c and f is more intense than that observed with single-frequency ultrasound (see Fig. 5c and f). These results seem to be in good agreement with the conclusion of Ciuti et al. [21] about dual-frequency sonication, who explain that small exploded bubbles generated by low-frequency ultrasound could be used by high-frequency ultrasound as cavitation nuclei, resulting in an enhanced cavitation intensity. Besides this, since high-frequency ultrasound induces intense streaming that can be regarded as liquid flow, the combination of low-and-high-frequency ultrasound could be here considered similarly to the sonication of a jet as investigated by Reuter et al. [30], whose work clearly demonstrates that such a combination results in a significant enhancement of cavitation.

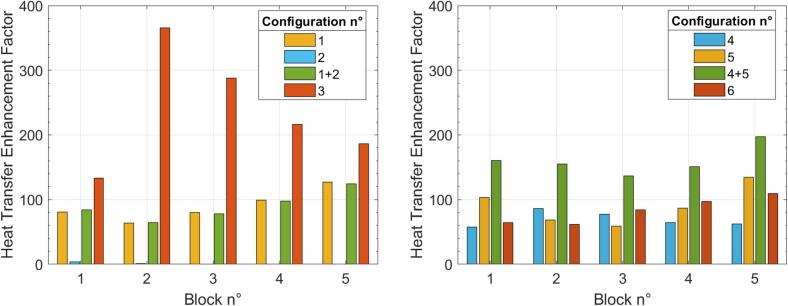
Assessment of the heat transfer enhancement for each experimental configuration can be made by the HTEF, as given on Fig. 10. For single frequency configuration, the HTEF reaches a similar level in both low-frequency configurations n°1 (left figure, yellow bar) and n°5 (right figure, yellow bar), with a maximum on block 5 of 127% and 134% respectively and both an average HTEF of 90%. For high-frequency configuration, the configuration n°2 (left figure, blue bar) presents no interest for heat transfer enhancement, as the HTEF is almost equal to 0 on every block. For the configuration n°4 (right figure, blue bar) on the other hand, the HTEF is almost constant along the blocks with an average HTEF of 70% and a maximum on block 2 of 86%.

Fig. 10.

Heat Transfer Enhancement Factor for each configuration.

For dual-frequency configuration, the HTEF for the configuration n°3 (left figure, red bar) is significantly higher than the algebraic sum of individual HTEF obtained for configurations n°1 and n°2 represented here by the green bar “1 + 2”, whatever the block. On average, The HTEF in configuration n°3 is 238%, compared to the average HTEF of 90% for the algebraic sum of HTEF. Moreover, the results for configuration n°3 highlights a major influence on block 2 and 3, as the HTEF reaches 366% and 288% respectively compared to the 65% and 78% on block 2 and 3 for the algebraic sum of configuration n°1 and n°2. Therefore, the enhancement induced by combined dual low-high frequency orthogonal ultrasound can be considered as resulting from a synergetic effect. On the other hand, the HTEF for the configuration n°6 (right figure, red bar) is lower than the algebraic sum of configurations n°4 and n°5, represented here by the green bar “4 + 5”. In this case, the HTEF is similar to the HTEF obtained with configuration n°4 or n°5 involving a single ultrasound emitter, illustrating that the combination brings almost no benefits in terms of heat transfer enhancement in this configuration. Consequently, these results demonstrate that the effects on heat transfer induced by ultrasound at different frequencies do not add to each other. The combination can generate intense heat transfer enhancement, stronger than the sum of the individual contributions. However, this enhancement strongly depends on the respective position of the emitters and thus on the direction of the ultrasonic waves with respect to the heating wall. As illustrated in this study, the configurations that induce disturbance of the thermal boundary layer have to be favored.

3.4.2. Influence of the ultrasonic power distribution

To understand the influence of each ultrasonic field in the optimized dual-frequency configuration and to ensure that the effects of the combination are not directly attributed to the increase of the total supplied ultrasonic power, combination tests are also conducted at constant total power (105 W). Experiments are then performed for different power distributions per emitter in configuration n°3, which is the most interesting for heat transfer enhancement, as demonstrated in Fig. 10. Three different power ratios are tested in this optimal configuration where low-frequency (25 kHz/ LF) ultrasonic field is perpendicular to the water flow and high-frequency (2 MHz/ HF) ultrasonic field is collinear to the water flow. The different proportions of power are respectively 30%LF-70%HF; 50%LF-50%HF and 70%LF-30%HF, for a total of 105 W. When adding configurations 1 (100% LF-0% HF) and 2 (0% LF-100% HF), it gives a total of five different power distributions with a total power kept constant and equal to 105 W (see in Table 3).

Table 3.

Power distribution per emitter.

Configuration n°	2	3a	3b	3c	1
Power ratio (%)	0–100	30–70	50–50	70–30	100–0
25 kHz (position 1)	0 W	31.5 W	52.5 W	73.5 W	105 W
2 MHz (position 2)	105 W	73.5 W	52.5 W	31.5 W	0 W

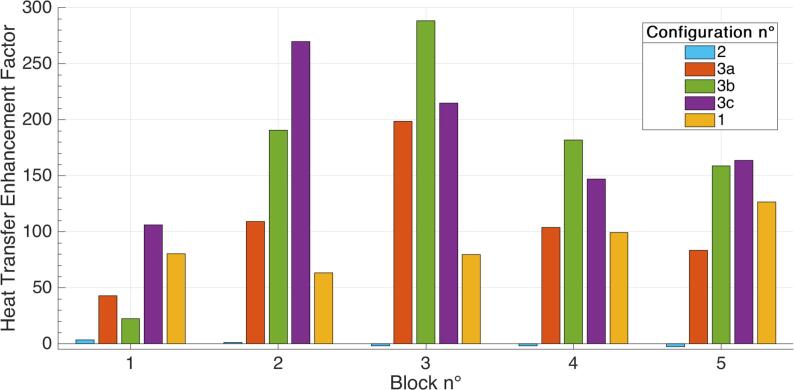
Fig. 11, Fig. 12, Fig. 13 display the turbulent kinetic energy map within the water flow and the TKE enhancement factor (average and along the wall) coupled with the HTEF with respect to the position along the heating wall. As expected, with a lower total power generated by emitters, the induced turbulence is also lower within the water flow. However, as the 25 kHz ultrasonic field is facing the heating wall, there is still important turbulence close to the heating blocks and thus the HTEF reaches a significant level. For instance, in the configuration n°3b and n°3c, the maximum HTEF reaches 288% and 270% respectively. Furthermore, the turbulence distribution along the wall seems to adopt a similar pattern for every power proportion used, with a global low TKE along the first and lasts blocks and a peak on the second and third blocks, which also correlates with the HTEF. Nonetheless, the turbulence tends to increase globally, respectively with the increase of power supplied to the low-frequency emitter. In addition to that, the peak seems to rather impact the first blocks with the decrease of power emitted by the high-frequency emitter, as if the acoustic streaming generated by high-frequency ultrasound was pushing up the turbulence in the bulk of the water flow. Therefore, increasing 25 kHz ultrasonic power seems to have a significant localized impact on the thermal boundary layer resulting in an increased heat transfer while 2 MHz ultrasonic power seems to have a more relevant effect on the location of the turbulence generated due to convective motions induced at a macroscopic scale in the fluid flowing along the channel.

Fig. 11.

Results for configuration n°3a (f = 25 kHz, perpendicular to the water flow, P_US = 31.5 W + f = 2 MHz, collinear, P_US = 73.5 W).

Fig. 12.

Results for configuration n°3b (f = 25 kHz, perpendicular to the water flow, P_US = 52.5 W + f = 2 MHz, collinear, P_US = 52.5 W).

Fig. 13.

Results for configuration n°3b (f = 25 kHz, perpendicular to the water flow, P_US = 73.5 W + f = 2 MHz, collinear, P_US = 31.5 W).

Finally, the HTEF for each ultrasonic power proportion are presented on Fig. 14. It shows clearly that the synergetic effect induced by combined dual low-high frequency orthogonal ultrasound is not due to the total supplied ultrasonic power. Indeed, as almost every HTEF for each power proportion of the dual-frequency configuration (configurations n°3a (orange), 3b (green) and 3c (purple)) are higher than those of the single frequency configuration (configurations n°1 (yellow) and 2 (blue)) although the supplied ultrasonic power is the same. However, it has to be said that most of this synergetic effect seems to have a rather localized effect on heat transfer, here mainly on block 2 and 3, as the HTEF decreases along the wall, to reach a slightly superior level than with single frequency at block 5.

Fig. 14.

Heat Transfer Enhancement Factor for each power distribution per emitter, total power is constant P_US = 105 W.

4. Conclusion

This study aimed to investigate the influence of dual low-high frequency ultrasound on heat transfer in forced convection. For this purpose, an experimental setup equipped with a heating wall and emitters of low (25 kHz) and high (2 MHz) frequency was designed. A thermal analysis was proceeded to quantify heat transfer enhancement while a hydrodynamic phenomenological investigation was led with Particle Image Velocimetry. In addition, sonochemiluminescence was used as a useful tool for qualitative detection of cavitation.

This study has shown that for convective heat transfer enhanced by ultrasound, the direction of the ultrasonic field may have a great influence depending on the wave frequency used. Sonication with low-frequency ultrasound (25 kHz) produces mainly acoustic cavitation that generates turbulence within the water flow resulting in heat transfer enhancement. The enhancement is quantified by a Heat Transfer Enhancement Factor, which reaches an average of 90% similarly whether the ultrasonic field is perpendicular (configuration n°1) or collinear (configuration n°5) to the water flow. One might here consider that whatever the emitter position, cavitation bubbles are generated close to the heating wall and their implosion is at the origin of the heat transfer enhancement that is observed for both single 25 kHz ultrasound experimental configurations.

Sonication with high-frequency ultrasound (2 MHz) results mainly in an Eckart’s acoustic streaming occurring at a macroscopic scale. When the ultrasonic field is perpendicular to the water flow (configuration n°4), the induced convective acoustic streaming is at the origin of turbulence within the liquid that impacts directly the heating wall surface, resulting in a HTEF of 70% in average. However, when the acoustic streaming is collinear to the water flow (configuration n°2), it has no significant effect on turbulence close to the heating wall and thus the heat transfer is not enhanced since the acoustically-induced streaming does not shear the mean flow.

In this work, the use of combined low-and-high-ultrasonic fields has demonstrated that the optimized combination results in a stronger enhancement of the cavitation intensity and thereby turbulence within the water flow than with single sonication. However, since the turbulence generated by the ultrasonic field combination is not homogeneously distributed within the water flow, the optimization to enhance heat transfer depends on the generation of turbulence close to the heating wall and thus on the location of the emitters.

The combined sonication using two ultrasonic fields in the optimal configuration (configuration n°3) results in a maximum local HTEF of 366%, and an average HTEF of 238%, which is greater than the algebraic sum of HTEF obtained with single-frequency sonications. The possible mechanisms of the observed synergy effect might be due to the improvement of cavitational effects induced by low-frequency ultrasound when associated with acoustic streaming induced by high-frequency ultrasound. Furthermore, it was demonstrated that the synergetic effect on heat transfer enhancement for combined sonication cannot be attributed to the total ultrasonic power.

Such combinations could be a promising and innovative way for heat transfer enhancement and could result in new possibilities for the optimization of ultrasonically-assisted heat exchangers.

CRediT authorship contribution statement

Christophe Poncet: Methodology, Formal analysis, Investigation, Data curation, Writing - original draft, Visualization. Sébastien Ferrouillat: Conceptualization, Methodology, Validation, Writing - review & editing. Laure Vignal: Resources, Writing - review & editing. Alain Memponteil: Writing - review & editing. Odin Bulliard-Sauret: Conceptualization, Writing - review & editing. Nicolas Gondrexon: Conceptualization, Methodology, Validation, Resources, Writing - review & editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following are the Supplementary data to this article: