Mechanisms of the negative potential associated with Leão’s spreading depolarization: A history of brain electrogenesis

Abstract

Spreading depolarization (SD) is a self-propagated wave that provokes transient disorder of numerous cell and tissue functions, and that may kill neurons in metabolically compromised tissue. We examined the mechanisms underlying the main hallmark of SD, a giant extracellular potential (ΔV_o) for which multiple electromotive forces have been proposed. The end-point is that neurons and not glia, dendritic channels and not spatial currents, and increased sodium conductance rather than potassium gradients, appear to be the main actors in the generation of the negative ΔV_o. Neuronal currents are established by two mechanisms, a voltage independent dendritic current, and the differential polarization along the neuron membranes. Notably, despite of a marked drop of ion gradients, these evolve significantly during SD, and yet the membrane potential remains clamped at zero no matter how much inward current is present. There may be substantial inward current or none in function of the evolving portion of the neuron dendrites with SD-activated channels. We propose that the ΔV_o promotes swelling-induced dendritic damage. Understanding SD electrogenesis requires all elements relevant for membrane potential, action currents, field potentials and volume conduction to be jointly considered, and it has already encouraged the search for new targets to limit SD-related pathology.

Spreading depolarization: A history of brain electrogenesis

Spreading depolarization (SD) is a wave of cellular depolarization that lasts at least tens of seconds and that propagates slowly through nervous tissue (1–3 mm/min).¹ SD produces mild, reversible dendritic dysfunction in a healthy brain,^2–4 yet it has an important clinical repercussion due to its relationship to migraine aura or its lethal effects in metabolically compromised tissue.⁵ As such, SD waves sweep across ischemic tissue when this is still alive, leaving a trail of dying neurons that ultimately triggers irreversible neurological sequelae.^6–9

Classically viewed as a wave phenomenon, SD has many properties in common with spikes in individual neurons, and in particular with dendritic spikes, such as its all-or-nothing nature (albeit with some graded features), membrane depolarization, activation of dendritic channels, site-specific waveform, and refractoriness, whereas it has a distinctive feature as is the substantial translocation of ions between neurons and the extracellular space (ES). Altogether, SD conveys many changes in cell and tissue functions over multiple timescales, including the electrical excitability of neurons, the ion homeostasis, and the energy metabolism, making of it one of the most challenging biophysical puzzles faced by modern neuroscience.¹⁰ Curiously, some of the main features of SD have been poorly explored, despite being used widely. This is the case for the main hallmark of SD, a large (10–40 mV) sustained (DC-like) negative shift in the extracellular potential (ΔV_o),¹¹ the largest electric signal in the brain and the topic of this review (Figure 1(a)). Multiple sources of extracellular current have been proposed to explain this field potential (FP), and some of the theories that we will discuss below have evolved over the years to incorporate new findings. Possibly, the concomitant changes of ion concentrations that ultimately define the electromotive forces (EMFs) in the brain make SD to depart from standard electrogenesis, and place it at the top of complex bioelectrical phenomena.

Figure 1.

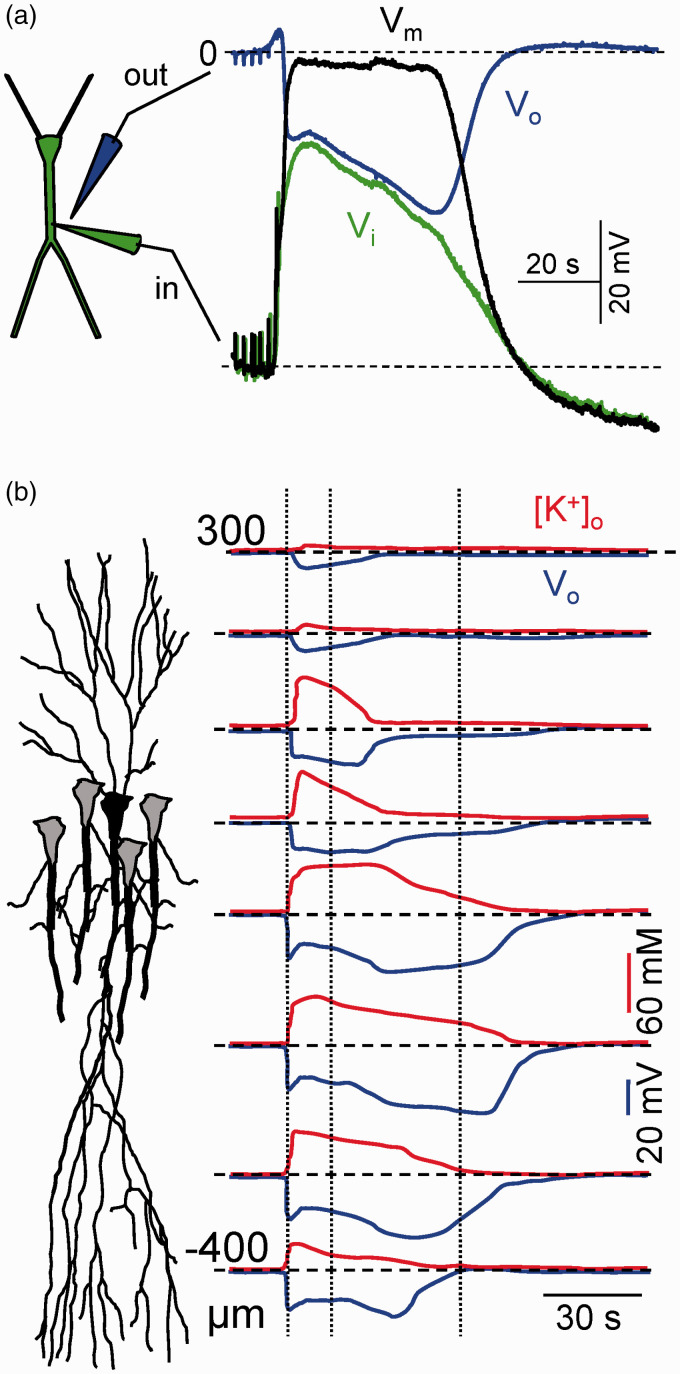
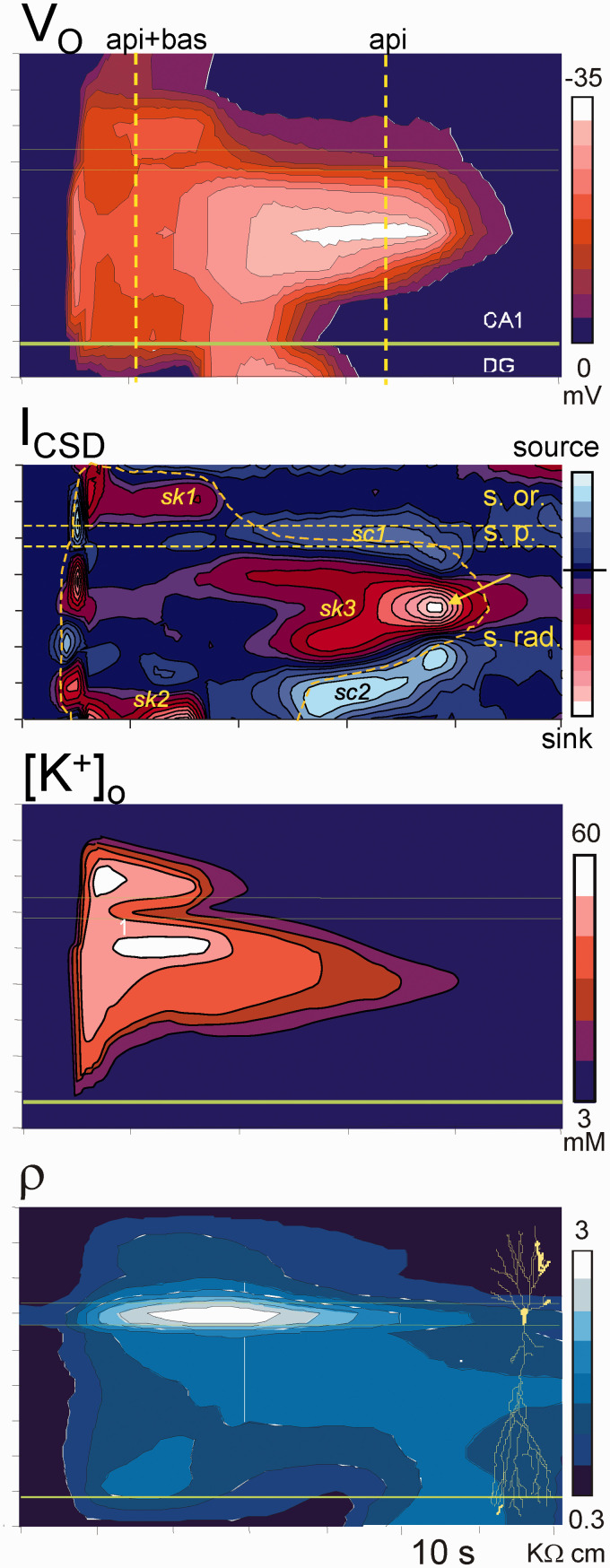
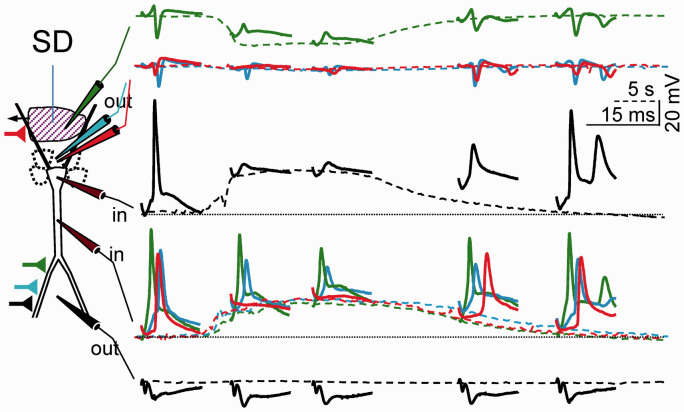
Main features of SD. (a) Simultaneous extra (V_o) and intracellular recording (V_i) in the main apical dendritic shaft of a pyramidal cell in the CA1 region, and the transmembrane potential (V_m). Note the balanced drift of V_i and V_o. Modified from Canals et al.⁵⁰ (b) Spatiotemporal display of the negative ΔV_o and [K⁺]_o along the CA1 strata. Note the strata-specific stereotypic changes and the continuous reduction of [K⁺]_o from the initial peak. SD is always shorter in the basal dendritic tree. The late phase occupies a narrow band in the apical dendrites. Reproduced from Herreras and Somjen.²¹

A brief historical context

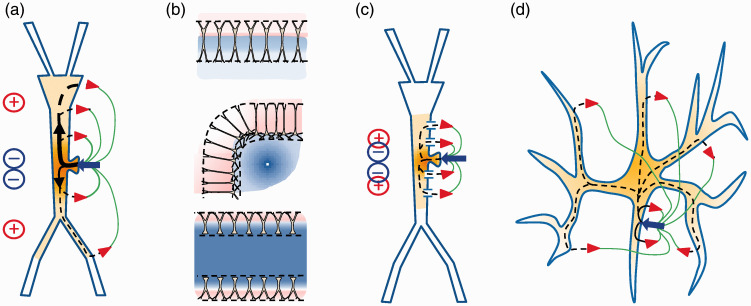
The fundamentals of bio-electrogenesis were discovered and assembled over the last century, and too often their understanding was delayed with respect to SD research. We shall first deal with data and theories involving the generation of currents across cell membranes, but also the elements participating in the establishment of the membrane potential (V_m) (ion gradients, channels and pumps), as well as the spread of FPs beyond the site of the sources (volume-conduction) are important and will be presented later in the text. The formalism establishing the behavior of electric currents and potentials inside neurons culminated in the 50s with the core conductor theory,¹² whereas their behavior in the ES is described by the volume conductor theory.¹³,¹⁴ Thus, the electrical current inside cells circulates down the V_m gradient, while it does in the opposite direction on the outside, forming loops of current that traverse the membrane in and out (Figure 2(a); current sources and sinks). The potentials generated by these currents spread and mix in the ES, and reach far from the cellular sources according to their spatial geometry and charge density (Figure 2(b)).¹⁵,¹⁶ This global framework lacked important elements that were acquired decades after SD was first reported, such as the presence and heterogeneous distribution of channels along the somatodendritic membranes, and the impact this has on the distribution of currents inside and outside the neurons (Figure 2(c)), i.e. whether inward and outward currents sum or cancel in the ES (Figure 2(c) and (d)).^16–18

Figure 2.

Some basic features of electrogenesis linking currents in single neurons and field potentials in the extracellular space. (a) Neuronal currents form transmembrane loops with intra and extracellular parts. An exemplary inward current (blue arrow) depolarizes the membrane and spreads the electric charge in the inside down the V_m gradient. Inward and outward currents (red arrowheads) form dipoles of current outside that generate positive and negative FPs. (b) The cytoarchitecture of the neurons and aggregates produces a variety of spatial distributions of the compound FPs, which reach beyond the sources through volume conduction. Reproduced from Herreras.¹⁶ (c) The presence of open channels in neuron segments greatly modifies the path of currents generated by other channels, hence the external dipoles and FPs as well. (d) The cell geometry has a critical impact on the spatial distribution of external dipoles. The distribution of currents inside polymorphic cells produces an effective cancellation of inward and outward currents outside that prevents the generation of FPs.

Before the 1960s, neurons were virtually viewed as universal generators of the FPs, also for the SD-related ΔV_o, yet it was still poorly understood how electrogenesis in single cells could be scaled-up to population potentials, which made this view fragile. Thus, the initial intracellular data showing complete depolarization of the neuronal soma during the passage of SD, along with the foundational discovery of neuron silencing appeared to rule out neuronal EMFs. The prevailing exploration into epileptogenesis and ion homeostasis from the 1960s to 1980s meant that neurons were given a less prominent role, and they were viewed more as passive suppliers of excitatory agents that promote the spatial spread of this phenomenon. This epoch saw the uprising of theories regarding the possible glial-mediated generation of sustained potentials. It should be remembered that by the time the ΔV_o of SD was first reported the volume conductor theory was in its infancy and its formal link to the cable model for single cells did not appear until the late 60s.¹⁹ Furthermore, the difficulties in gaining experimental access to dendrites that, let’s not forget, provide the bulk of extracellular current to the ES, delayed establishing the quantitative links between single cell electrogenesis and population potentials. This objective had to wait until computational capabilities allowed realistic simulation of morphologically detailed neurons and cell aggregates at the wake of this century.²⁰ Meanwhile, early theories on SD have imprinted a clear mark on the literature that persists to this day. It should therefore be of no surprise to some readers to find that a good deal of the data, although related to, are not strictly relevant to electrogenesis, and some of the relationships proposed admit more explanations than have formerly been contemplated.

Early research on the mechanisms underlying SD attempted to explain the astonishing macroscopic features of this phenomenon, such as the slow spatial spread and the strong rise of [K⁺]_o. These aspects are not reviewed here but they will be referred to when required. Indeed, the roughly mirroring changes of V_o and K_o (Figure 1(b)) during SD influenced many researchers, who inferred a causal relation between them that ultimately turned out not to be fully justified. Meanwhile, other no less remarkable changes were treated as side effects and their exploration was ignored for decades, including the also impressive changes in [Na⁺]_o and [Ca²⁺]_o. Although these were soon considered as promoters of cell damage, their role in the electrophysiology of SD was not sufficiently valued until the discovery of an SD-specific dendritic current.

Main features of the V_o shift associated to SD

The main (negative) phase of the ΔV_o lasts 20–50 s in metabolically intact tissue, and it engulfs a large volume of tissue that contains thousands of neural cells. It is preceded and followed by smaller short and long positive potentials, respectively, which vary notably in different structures and conditions. Such generic waveform adopts layer-specific shape in structures with simple cytoarchitecture, such as the monolayered CA1 region of the hippocampus (Figure 1(b)), which indicates anatomical constraints of the EMF supplying the current to the ES.²¹ The negative potential initiates by a fast peak that is followed by a sustained (main) phase. The latter generally expands by repetition, and it can be modulated by multiple agents and treatments, such as those interfering with energy availability, and some membrane channels and receptors.¹⁰ The well maintained set of altered cell and tissue functions during SD in different structures indicates that it is a unique type of global reaction, although there is little consensus regarding the order and relative importance of these changes.

Scope of this review

The pioneers in the study of SD suggested it is a multiphasic phenomenon. Indeed, the negative ΔV_o is neither the first nor the last event. Rather, it is heralded by a number of prodromals that develop over a few millimeters and several seconds ahead of the ΔV_o wavefront,²² and it is followed by a number of other events over a timescale of seconds to hours. Consequently, the ΔV_o is only part of the global reaction, and though the cells or cell elements contained within its spatial boundaries must provide the EMF, others may be involved in other aspects of the reaction that extend over different areas and periods.²³ The fact that the SD moves in space together with the non-linear relationships between many of the altered variables hampers determining the sequence of events. Conveniently, since the electrogenesis of FPs in the ES is nearly instantaneous, the anatomical sources can be tracked by establishing the location, geometry and density of the current sources,¹⁴,²⁴,²⁵ rather than from a temporal sequence of their many contributing elements that are strongly interdependent. Further on, the mechanisms that promote the spatial spread are not strictly relevant for the generation of the ΔV_o during the main SD phase, whose changes are slow enough to allow its stationary treatment. Rather than an exhaustive review of the literature, our aim is to focus on the experiments that link single cell electrogenesis to the build-up of the negative ΔV_o. However, different theories have dominated over the past half a century, and some still remain popular due to their linkage to epilepsy, potassium homeostasis and excitotoxicity. We will therefore follow a certain chronological order, and the examination of the different sources of current proposed over the years will be completed with remarks according to modern electrogenesis. Due to limitations of space, we refer the readers to authoritative reviews on other aspects of SD and those that address its clinical repercussions.⁷,⁹,¹⁰,^26–31

The hypotheses of glial currents

Elevation of [K⁺]_o, glial depolarization and development of sustained potentials in the ES have been widely reported in physiological events, as well as during epilepsy and SD.³²,³³ The relation between these events was once undisputed, but the scenario complicated as the techniques evolved. Indeed, glia may depolarize by a number of agents and, in turn, depolarized glia may provide feedback onto neurons through a number of mechanisms, from potassium redistribution (so-called spatial buffer) to the release of gliotransmitters.^34–38 Here we are only concerned with the ability of glia to supply current to the ES during SD. In this context, the theory proposing glia as the current generator during SD largely overlaps with that proposed for the generation of small amplitude sustained potentials during repetitive neuronal activity and epilepsy.³⁹ In this, the clearance of extracellular potassium into astrocytes was viewed as the critical event. Notably, more recent data from the hippocampus challenged this role of glia and potassium, and proposed that neurons also generate this type of potassium-induced potentials.^40–42 While further experiments will be required to clarify if cell type-specific mechanisms activate in different structures, we limit the following analysis to the postulated role of glia in the ΔV_o of SD. Information on glial excitability and electrophysiology, and regarding the participation of glia in other phenomena associated to SD can be found elsewhere.⁵,^43–47

Parallel changes of glial depolarization and extracellular potassium

Three main lines of evidence have been used to claim a role of glia on SD. A first one relies heavily on the concurrent changes of some cellular and population features. Thus, intracellular studies showed that glial depolarization during SD closely mirrors the increases in [K⁺]_o and the V_o negativity in the cortex, whereas that in neurons displayed temporal deviations with respect to these parameters, and some neurons even seemed not to enter SD at all.⁴⁸ However, the importance of this temporal relationship has been largely overstated, since SD runs preferentially through the superficial layers and it spares partially or completely the different cortical cell types variably extending across the cortical width.⁴⁹ In fact, such lags of neuronal depolarization have not been replicated in the monolayered hippocampus. Instead, hippocampal neurons may exhibit multiphasic depolarization depending on the dendritic strata seized by SD.⁵⁰ Thus, astrocyte depolarization reflects the changes in transmembrane K⁺ gradients after events in neurons provoke the rise of [K⁺]_o. Note that the timing of such events is important to elucidate the mechanisms of SD ignition and spread, yet not for the build-up of the ΔV_o during the main phase, since this is an instantaneous reflection of ES currents that have multiple and varying sources over the SD span (see below). In fact, there are several events that herald the ion and potential changes in which both glia and neurons participate.²²,⁴⁴

Spatial buffer and syphoning

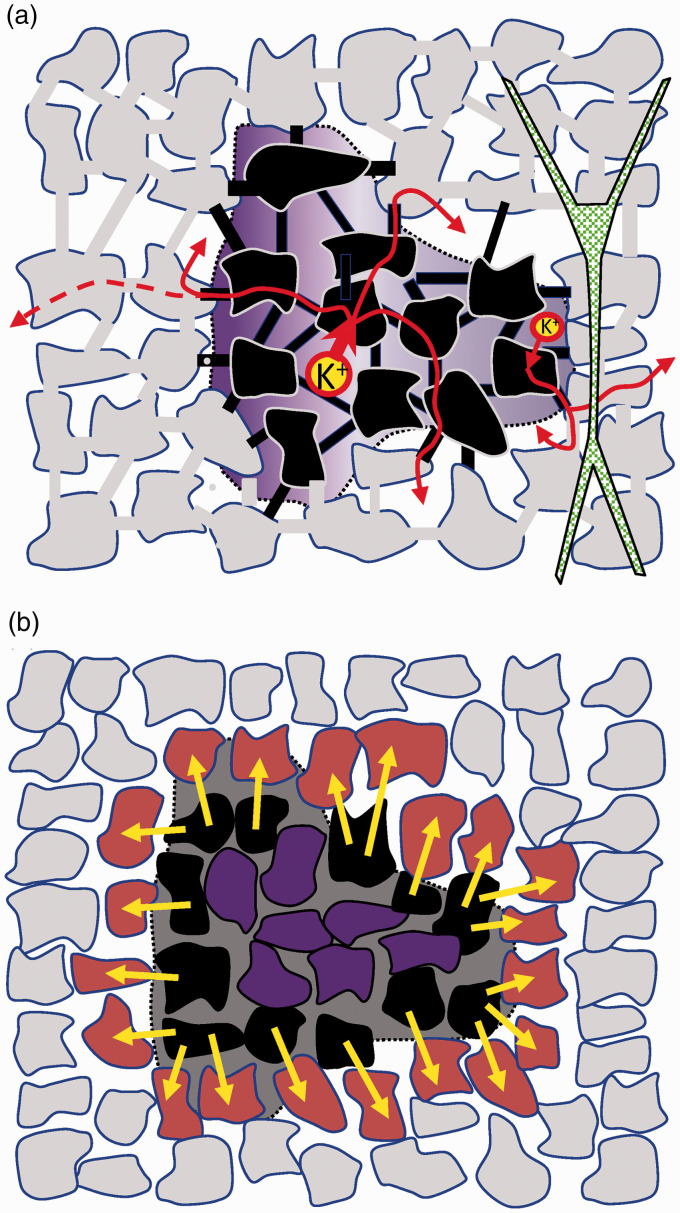
A second line of support came from the well-known assembly of astrocytes into a functional syncytium and the role of this in regulating [K⁺]_o.⁵,³⁵,⁵¹ Astrocytes are electrically contiguous through gap junctions (GJs), which enable the passage of ions and small molecules.⁵²,⁵³ In conditions of intense neuron activity, such as repetitive stimulation or seizures, the [K⁺]_o reaches a ceiling of ∼10–12 mM, which is mirrored by a small (1–4 mV), negative extracellular potential.⁵⁴,⁵⁵ An influential hypothesis maintains that regional depolarization of the syncytium in the high K⁺ zone promotes current flow from depolarized glia that returns to the ES through distant astrocytes. In this process, K⁺ is cleared from the ES into glia (spatial buffer) and the net loss of positive charge (a sink of current) would lead to the negative FP (see Figure 3(a)). This eye-catching mechanism received widespread attention in past decades, as is still the case.⁵⁶ The increase in intra-glial potassium has been documented,⁵⁷,⁵⁸ whereas evidence for its redistribution at more distant sites within the cortical parenchyma is less clear.

Figure 3.

Glial theories for the production of sustained FPs during SD. (a) Spatial buffer currents. This hypothesis relies on the selective uptake of K⁺ ions by astrocytes impelled by depolarization in parts of the astrocytic syncytium (black cells). The purple shadow represents the spatial coverage of the negative ΔV_o during an SD wave along the CA1 layers. Note that the opposite trend of the V_o and K_o in different phases of the wave constitutes a challenge for the theory of spatial currents. (b) Closed-sheet glial hypothesis. Homogeneous depolarization of astrocytes (purple cells) inside a large zone encroached by elevated [K⁺]_o cannot generate currents, but pairs of astrocytes connected through gap junctions in the outer rim (black and brown) can (see text for details).

Some researchers suggested that a similar mechanism may also account for the ΔV_o during SD. However, it has been argued that the reduced space constant of glial cells would limit the extension of current across the syncytium.⁵⁹ Detailed mathematical models do indeed show this to be a serious handicap to transport K⁺ over distances above a few tens of microns.⁶⁰,⁶¹ Importantly, there are other glial mechanisms known to uptake the excess potassium that are not linked to the generation of extracellular currents.⁶² Although modern data suggest a minor share of the spatial buffer on the clearing of excess K⁺, these studies have only marginally addressed the generation of sustained potentials and less so, the SD-associated V_o.^63–67

It should be noted that as far as it concerns to the capacity of glia to supply electrical current to the ES, the depolarizing agent is not much relevant, as only partial depolarization of the syncytium is required to establish current flow. Thus, depolarization can also be achieved by other agents known to increase during SD, such as glutamate, acetylcholine and GABA.^68–70 In fact, an alternative hypothesis proposed that glutamate and not K⁺ provokes depolarization in the SD-area and even that these two excitatory influences might act in synergy.³⁹,⁷¹ From the electric point of view, the depolarizing agent and the ion species carrying the charge are irrelevant. In fact, regardless of whether potassium is involved or not, the astrocytes that are engulfed in the SD-seized area undergo a uniform homogeneous depolarization, and hence they cannot generate transmembrane currents (see Figure 3(b) and below).

One particular case of interest is that of the elongated Müller glial cells in the retina. K⁺-induced depolarization of these cells during SD was proposed to promote a longitudinal current flow that performs analogous functions to the cortical astrocytes (i.e.: the removal of the excess K⁺ released from ganglion and amacrine cells, and its transport toward the vitreous humor).⁷² This is known as potassium syphoning and it differs from spatial buffering in that currents are generated across individual cells.⁷³ While the transcellular transport of K⁺ in these cells has been well documented,⁷³,⁷⁴ the quantitative contribution to the SD-associated ΔV_o and the reasons proposed to exclude retinal neurons are less straightforward. A contribution of neurons was deemed unlikely based on the inactivation of the soma and/or the loss of the response to light by some neuronal subtypes.⁷⁵ However, this argument is weak since somatic recordings are not capable of determining the ability of their electrically distant dendrites to generate currents.¹⁸,⁵⁰ In fact, the multilayered retina contains some elongated neurons known to underlie the generation of several physiological FPs.⁷⁶,⁷⁷ Also, the possible participation of Müller cells in the SD-associated ΔV_o does not validate the K⁺-mediated syncytial hypothesis in the cortex. Thus, whereas both propose the clearing of K⁺ from the ES as the EMF, the strength of the EMF and the current flow strictly depend on the V-gradients inside a cell or a syncytium, that is, on structure-specific geometry of the participating elements. Consequently, the possible contribution of Müller cells to the ΔV_o is due to their geometry, and not their capacity to remove and transport potassium out of the ES.

A novel closed-sheet glial hypothesis

As the spatial buffer hypothesis loses weight, it may be appropriate to consider other pathways of depolarization that, while still based on changes in [K⁺]_o, need not be related to its clearance from the interstitium. For instance, even if homogeneously depolarized astrocytes in SD-engulfed regions cannot act as current suppliers (they are isopotential), a current flow may still be established between pairs of connected astrocytes at the outer rim of the high K⁺ area, together making a two-layer shell of astrocytes where the inner one is more depolarized than the outer one (Figure 3(b)). The global spatial configuration constitutes a closed surface dipolar current generator (close-field),¹⁴ which in theory, at least, may support a uniform negative potential on the inside. This hypothesis finds experimental and computational support in the spatial distribution of FPs generated by extended neuronal populations arranged in a folded or curved architecture (Figure 2(b)). For instance, we reported that the synchronous activation of the C-shaped layer of radially oriented granule cells in the dentate gyrus conforms a curved dipolar sheet generator that promotes the clustering of volume-conducted currents in the inner part (the hilus), responsible for the giant FPs recorded in this region.⁷⁸ We also showed that the curved shape of the cortical mantle in small rodents is responsible for the remote recording of slow cortical waves with large amplitude over nearly the entire sub-cortical brain.⁷⁹ The extended spatial distribution of these FPs arises from a general physical principle of charge distribution in spherical conductors, which can be incarnated in different biological scenarios as closed generators, such as that formed by the lipid bilayer in single cells or in the multicellular arrangements we are dealing with here. The EMF would probably not be too strong given the tendency of GJ currents to reduce when the transcellular voltage gradient between connected astrocytes increases.⁸⁰ In addition, the small space constant of astrocytes plays against a major contribution, as it brings the charged layers closer together (provoking a small dipolar moment), which makes it highly dependent on the precise arrangement of the astrocytes at the outer limits of the SD. This mechanism has not been tested experimentally yet, which will be necessary to gain an idea of its quantitative possibilities.

Manipulating glia

A third line of evidence supporting glia came from pharmacological and genetic manipulations, such as the discovery of so-called Ca²⁺-waves in cultured astrocytes,⁸¹ or the arrest of SD propagation in slices and in vivo by GJ blockers.^82–84 Since Ca²⁺ enters neurons during SD,⁸⁵ the intracellular Ca²⁺ inherits the spatial dynamics of SD and behaves as a wave. The question that arises is whether astrocytic Ca²⁺ waves precede those in neurons.⁸⁶ While this issue is related to the mechanism of spread, the observations can also be extended to the identity of the sources of current in the ES during the main SD phase. Significantly, the deletion of glial connexin Cx43 does not prevent SD.⁸⁷ On the contrary, the speed of the waves increased and the susceptibility to initiate SD was also higher, but even more relevant, the amplitude of the V_o was barely affected, seemingly ruling the hypothesis of spatial glial currents driving this phenomenon.

Other manipulations aimed at dissociating neuronal and glial function by selectively reducing the electrogenic capabilities of the latter.⁵,⁸⁴ We established a region deprived of glial activity using a metabolic poison that is selectively taken up by these cells. Neurons maintain full excitability in the presence of this toxin while homeostatic glial functions were severely hampered (e.g. the clearing of excess potassium and the pH regulation). Also, the V_m of glial cells and their intracellular K⁺ content declined severely, both of which play against spatial currents. It was found that SD waves initiated outside the glial-impaired area could readily enter this zone, and they could even ignite spontaneously there, while the associated ΔV_o was dramatically expanded in this zone. We thus concluded that these cells are not the principal generators of the ΔV_o shift.

[K⁺]_O does not always match the ΔV_o

The claim of a causal relationship between the elevation of [K⁺]_o and the development of a ΔV_o relies heavily in their temporal coincidence, as witnessed in countless studies. The [K⁺]_o climbs to 30–60 mM and the maximum of the ΔV_o is reported to span the 10–40 mV range.¹⁰,²⁹,⁸⁵,⁸⁸ However, this overall coherence is not maintained over the span of individual SD waves. Thus, if we spare the initial seconds in which a notable lag between the changes in ion concentrations and V_o has been detected,⁸⁹,⁹⁰ it was found that while the V_o grows steadily for most of the main SD phase, the [K⁺]_o declines from its initial maximum. This phenomenon is best observed in the hippocampus where the changes of the V_o and [K⁺]_o are very stereotypic and layer dependent (Figure 1(b)).

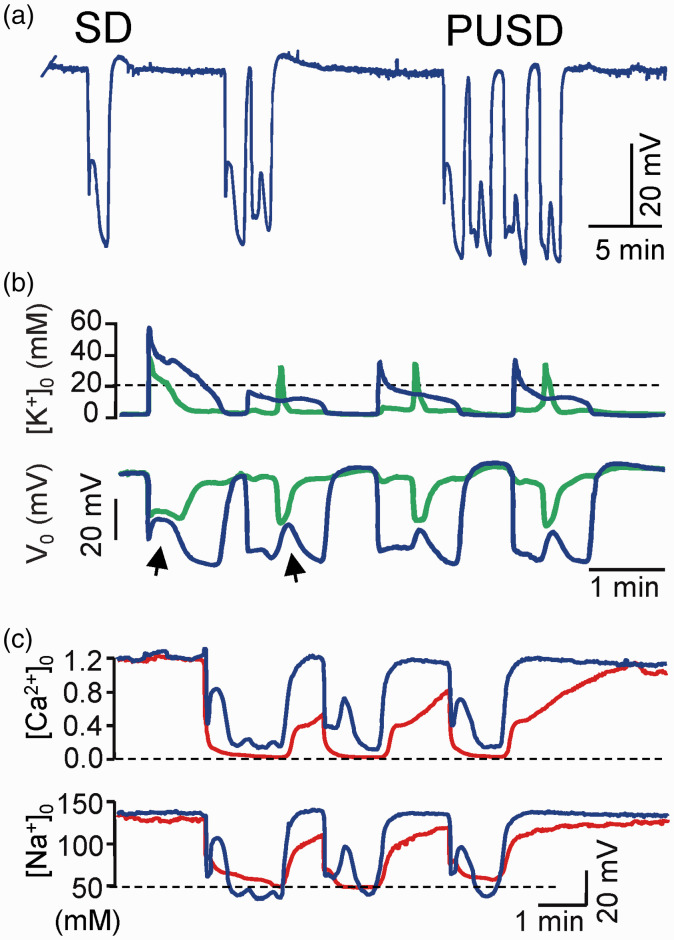
A selective reduction of the ΔV_o but not of the [K⁺]_o rise has been reported in the retina after barium blockade of K⁺ channels,⁹¹ although the absence of spatial data make these results difficult to interpret. More conclusive evidence comes from the evolving features of SD waves in the CA1 region. There, we reported a particular mode of rapidly queuing SD waves apparently skipping the refractory period (Figure 4(a)). We called these as prolonged unstable SDs (PUSDs).⁹⁰ During such state that can last up to 50 min, the SD restricts to a narrow band in the apical dendrites, with occasional eruptions of a short SD in the basal dendrites. To date, this phenomenon has only been described in the hippocampus of normoxic animals, although clusters of rapidly queuing SD waves with an apparent lack of refractoriness can also be observed at the periphery of brain infarcts or in metabolically compromised tissue, for example, during the evolution of brain infarcts both in animals and patients.⁸³,⁹² Strikingly, while the amplitude of the changes in V_o in the region of the apical dendrites does not vary (35–40 mV), the associated rise in [K⁺]_o is small after the first wave, reaching a plateau of about 10 mM in successive waves (Figure 4(b)). More notably, interstitial sodium and calcium both decrease to the same levels as in standard waves (Figure 4(c)), also dissociating from the variations in [K⁺]_o. Regardless of the reason why the [K⁺]_o does not rise after the leading wave in PUSDs, it is difficult to explain the maintenance of the V_o on the basis of spatial currents or any other mechanism that rely exclusively on transmembrane K⁺ gradients. Hence, these findings point to other ions and mechanisms, as will be discussed below.

Figure 4.

Prolonged unstable SD (PUSD) reveals important relationships. (a) PUSDs are rapidly queuing SD waves with apparent lack of refractoriness. (b) Most waves in PUSDs are restricted to a narrow apical band that matches the late phase of a standard wave (compare blue and green traces in apical and cell body layers, respectively). The occasional appearance of short SDs is the basal dendritic tree (arrows) brings together the respective FPs in the two layers, suggesting the mutual short-circuit of two domains of the same core conductors (see text for details). Note the small increase of [K⁺]_o in all but the first SD wave. (c) [Na⁺]_o and [Ca²⁺]_o drop to similar levels in all SD waves. Reproduced from Herreras and Somjen.²¹

Ion-diffusion currents

The earliest proposals for ion migration within the ES during SD arose from theories established to explain the slow spread of this wave through the tissue. Two of the characteristic features, the large increase of [K⁺]_o and the intense firing of neurons at the wave front,⁹³ were brought together in a theory where neuronal spiking at the wave front was proposed to produce the rise in [K⁺]_o, which in turn excited neighboring neurons into an excitation-diffusion cycle.⁹⁴ Although it was soon demonstrated that neuron firing is not required for the spread of SD,⁴⁸,⁹⁵ nor there is an elevation of [K⁺]_o ahead of the V_o shift,²⁴ the overall scheme survived by invoking additional sources of potassium and/or the synergistic action of other excitants (for a discussion of the mechanisms of SD spread see Somjen¹⁰). The claim that K⁺ migrates with the leading front of SD was based on the fact that externally applied electric fields may alter the velocity of the wave and also the amplitude of the ΔV_o.⁹⁴,⁹⁶ However, a wealth of data has shown that the SD spread, the velocity and the ΔV_o amplitude at a specific site are multifactorial,⁹⁷ and any relation to migrating ions should be considered with caution. Experimental evidence of the migration of ions in the interstitium in the presence of electric fields has been presented.⁹⁸ However, the argument is insufficient for SD as electrical fields also affect other ion species present in the interstitium, such as Na⁺, Ca²⁺ and Cl⁻, which also impact SD features.⁹⁹,¹⁰⁰ Likewise, it does not consider that the SD-core is a strongly negative field and if anything, it would be expected to attract K⁺ ions rather than promote their diffusion out of it. In addition, a number of other studies have shown varying effects of external polarizing fields, such as facilitated or hampered ignition, or layer-specific limitation of spread.¹⁰¹ As a speculative exercise, earlier we roughly estimated the diffusion potentials promoted by ES ion gradients between the SD core and outer regions, substituting the permeability terms in the Goldman equation with free ion mobility’s, which yielded 4.6 mV (SD region negative).² This value is low compared to the negative 30–40 mV reached at the SD core in the stratum radiatum of the CA1 region. Further speculation seems not justified given the experimental evidence indicating the ΔV_o amplitude is unrelated to the [K⁺]_o during PUSDs.

Neuronal currents

As mentioned initially, few researchers after the 1960s maintained the classic view that neurons were responsible for the ΔV_o during SD. The finding of near-complete depolarization in intrasomatic recordings of neurons may have played an instrumental role in this conceptual change as it is sufficient to account for the silencing of neurons during SD. In addition, the inactivation of afferent fibers may explain the disappearance of the EEG/LFPs and evoked responses, without invoking any specific change of dendritic electrogenesis, which let’s remember was not known at the time. The concomitant loss of membrane resistance (R_m) in somatic recordings also provided a plausible explanation for the so judged massive translocation of ions across neuron membranes. As described below, these arguments are insufficient as they failed to describe the functional state of dendrites during SD. Indeed, reported electric phenomena that evidenced neuronal electrogenesis in the cortex and the retina were generally neglected and judged as residual activity peripheral to the SD-affected tissue.⁴⁹,⁷⁵,¹⁰²

Site-specific waveforms and ΔV_o spatial profiles turn the focus back to dendrites

One piece of data that was not considered in sufficient detail at the time is the preferred passage of SD through the superficial cortical layers.¹¹,¹⁰³ This spatial pattern indicates a structural or functional specialization of the cellular elements in these layers, which are populated by astrocytes and dendrites of different neuron types. It became obvious that simpler structures will provide a more solid basis to investigate the anatomical correlates of the EMFs that generate the stereotypic ΔV_o profiles. As such, the ideal structure is the monolayered hippocampus, since its ordered architecture helps match the spatial profiles of FPs to the different neuronal elements with specialized electrogenic machinery.

An extensive analysis of the ΔV_o and ion profiles in the CA1 region permitted a spatiotemporal reconstruction of the complete ΔV_o and [K⁺]_o shells to be performed (Figure 5).²,²¹,⁹⁰ This analysis revealed sharp spatial borders of the negative ΔV_o and stereotypic time-dependent layer-specific variations that differed notably from those of potassium. Regarding the sources of the ΔV_o, we inferred the presence of two semi-independent current generators in basal and apical dendrites, as later confirmed through a current source density analysis.¹⁰⁴ Also, laminar analysis of tissue resistivity during SD shows a specific increase (ca. 4-fold) in the strata occupied by the SD negative core (Figure 5), which reduces the density of current required to values close to those of a fEPSP or a dendritic population spike in this region.¹⁰⁵

Figure 5.

Spatiotemporal reconstruction of the ΔV_o, population currents (ICSD), [K⁺]_o, and tissue resistivity (ρ). All but the latter belong to the same experiment. The profile of tissue resistivity served to correct for the population currents. An initial fast peak is followed by two phases of the ΔV_o characterized by different spatial coverage of the CA1. The first or main phase spans the two dendritic trees of pyramidal cells (api + bas), and the late phase restricts to mid portions of the apical tree (api). Sinks (sk) and sources (sc) of current show a peculiar spatiotemporal distribution. Inward currents (sinks) during the main phase appear only in the outer segments of distal dendrites, whereas there are no net currents in large portions along the pyramidal cell axis. Large inward currents arise at the late apical-only phase. Note discrepancies between V_o maxima and peaks of high [K⁺]_o. Horizontal lines mark the cell body layer. Modified from Makarova et al.¹⁰⁴

Importantly, the basal SD is shorter than the apical one, which provides a temporal mark that was instrumental some years later to understand the evolution of the V_m in the soma and apical dendrites of the same neurons (see below). The late apical-only phase of SD is restricted to a narrow dendritic band, it enlarges with repetition, and it may give way to the PUSDs. Positive excursions of the negative ΔV_o in the apical SD tightly matched the occurrence of basal SD, which indicated that the two generators were yoked together by low-resistance pathways that allowed them to short-circuit each other. This behavior is particularly evident during PUSDs (arrows in Figure 4(b)) in which basal SDs are occasional and unpredictable. The equalization of the ΔV_o in the two dendritic bands is only possible if the SD promotes strong inward currents in separate spatial domains of a single core conductor with elongated anatomy, such that the two domains (the basal and the apical dendritic trees) drain current to each other along a defined direction, i.e. along the main axis of pyramidal cells. This was confirmed by using detailed compartmental models of pyramidal cell aggregates (Figure 6).¹⁰⁵,¹⁰⁶ Had these two generators been incarnated by two glial syncytia in the two dendritic layers, their momentary coupling would not be expected to influence each other’s ΔV_o. Indeed, the reduced space constant of glia and the low resistance of GJs in all directions do not enable current drainage from sites beyond a few tens of microns, and currents would not be drained in a specific direction. These results were confirmed in a parallel study in the dentate gyrus, revealing a single surge of inward currents centered in the only dendritic tree of granule cells, whereas net outward currents appeared in the soma layer.⁴¹ Notably, inward currents are not found in the soma layers of the CA1 or dentate gyrus, consistent with the classic view of SD as an essentially dendritic phenomenon.

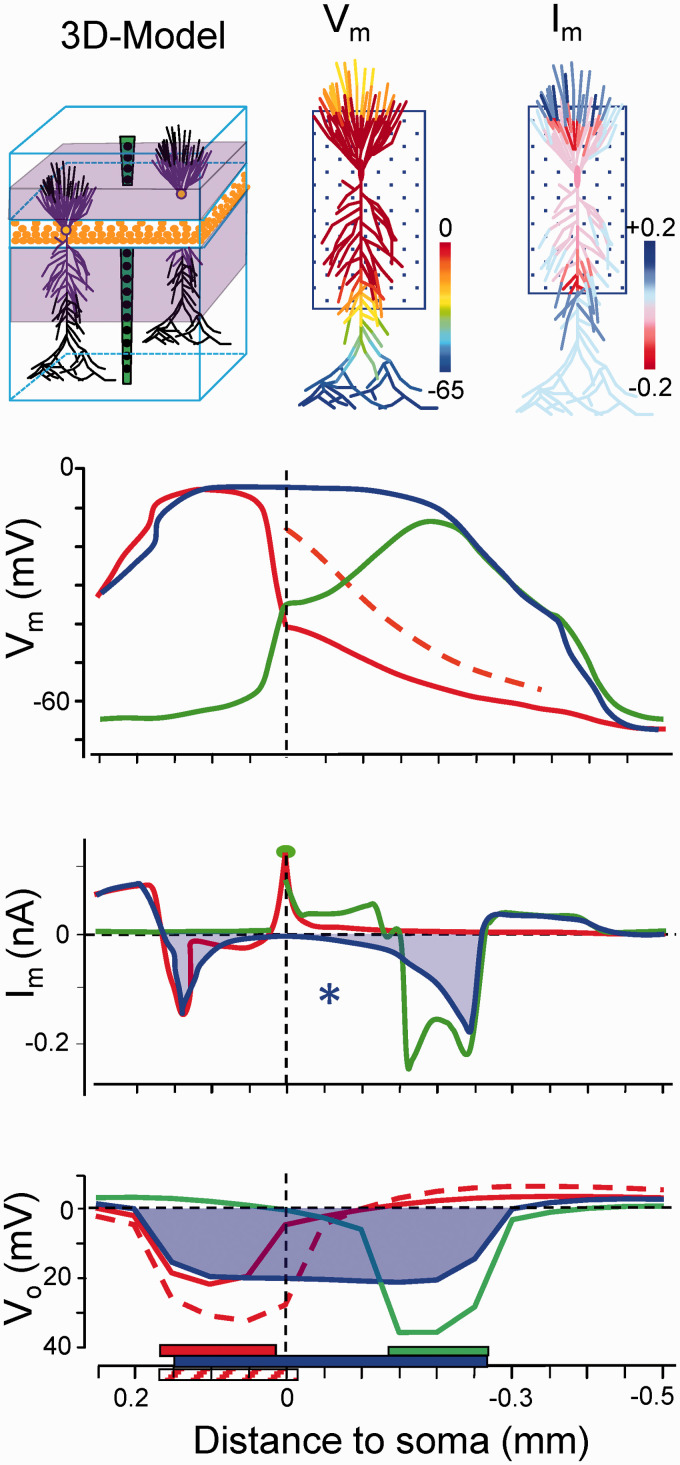
Figure 6.

Computational analysis of currents and potentials on individual pyramidal cells and the population aggregate in a model of the CA1 hippocampus. Experimental values of V_m and R_m in individual cells and ion gradients were implemented as SD conditions for all compartments contained within discrete somatodendritic bands (boxed areas in cell dummies and colored bars at the bottom). Note that net currents (I_m) are only generated at the outer rim of SD-activated compartments when the SD affects a wide portion of the neuron (blue traces), whereas net inward currents arise when it affects narrow dendritic bands (green and red traces). Paradoxically, the negative V_o spans the entire segment affected by SD despite the absence of currents in central membranes (asterisk). This V_o is volume conducted from the inward currents arising in the borders (see Makarova et al.¹⁰⁵ for expanded details).

Voltage clamp reveals V-independent currents during SD

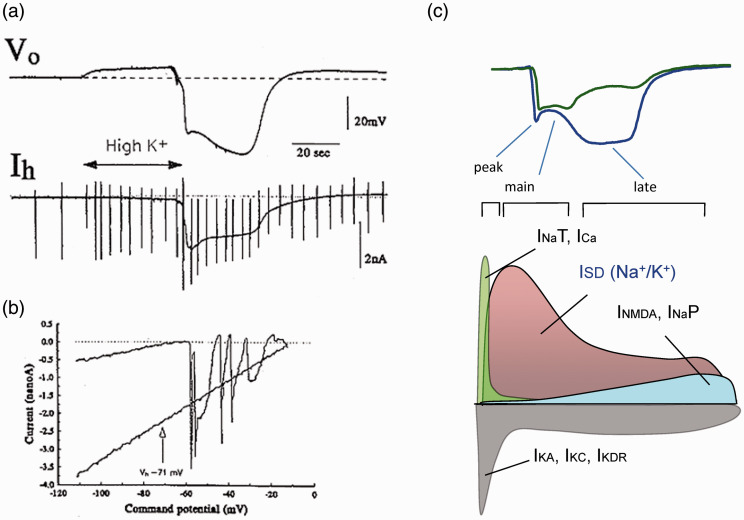
A key element that was not known at the time of the glia vs. neuron debate is the pervasive presence of membrane channels in dendrites. Hence, the possibility that active inward Na⁺ or Ca²⁺ dendritic currents might explain the depolarization of neurons was not yet an issue. Let’s remind this is not necessary in the spatial buffer hypothesis since depolarization is passive. The explosion of V-clamp studies in 1980–90s led to the exploration of the distribution and kinetic properties of different channels, which in the field of SD produced some very intriguing observations reported in a breakthrough paper by Somjen’s group.¹⁰⁷ A large V-independent current during the entire SD episode was reported in CA1 pyramidal cells but not in astrocytes, which was clearly discernible from standard V-dependent Na⁺ and Ca²⁺ depolarizing currents (Figure 7(a) and (b)). The near-zero equilibrium potential suggested a cation current, while the current-to-voltage relationship was not compatible with the kinetics of NMDAR-mediated currents. These receptors had generated much interest given that NMDAR blockers appeared to prevent SD.¹⁰⁸,¹⁰⁹ Since several details in those studies indicated that NMDARs were important to sustain a regular spread but only as a co-adjuvant extending the late phase of depolarization,⁹⁰,¹⁰⁶,¹¹⁰ the V-independent conductance in neurons acquired particular significance and inspired an important line of research to find out its identity.⁸³,⁸⁴,¹⁰⁰,¹⁰⁶,^111–122 Unfortunately, the main clinical objectives of reducing SD-related cell damage or migrainous pain make difficult to discriminate which of the interrelated SD phases and modulating conditions are being targeted by the different drugs or treatments. Ion channels and transporters in dendrites are candidates to move ions across membranes during SD. If we strictly refer to the period of negative ΔV_o, a number of channels can be ruled out. We previously suggested that the activation of some channels can set the conditions for others to open. For example, V-clamp data and biophysical modeling show that the different V-dependent and NMDAR glutamate channels drive time-evolving currents, according to their respective kinetics and the local V_m (see the proposed temporal scheme of the activated channels in Figure 7(c)).¹⁰⁶,¹⁰⁷,¹²³

Figure 7.

Voltage independent channels open during SD. (a) Experiment in vitro showing the large increase of holding current (I_h) in a pyramidal cell of the hippocampal CA1 region clamped at −71 mV. The SD wave was initiated by a small drop of high K⁺ in the CA3 region. The vertical strokes correspond to ramp voltage tests to probe the R_m. (b) I-V plots correspond to the cell’s response to ramp voltage commands in control (upper plot) and during SD. The control I/V plot shows current spikes presumably generated outside the clamped region, in the axon (Na⁺ mediated) and dendrites (Ca²⁺ mediated). The flat I/V plot during SD indicates these are no longer present, and the steeper slope indicates greatly increased input conductance. Reproduced with permission from Czéh et al.¹⁰⁷. (c) Proposed temporal sequence of the activated ion channels that provide the paths to move ions across membranes during SD. Middle and lower plots depict depolarizing and hyperpolarizing currents. I_SD is arbitrarily placed. The estimations are based on computer estimations from Makarova et al.¹⁰⁶.

Significant transmembrane ion gradients remain during SD

Consistent alterations of the interstitial ion content during SD have been described with ion-specific trajectories over the course of SD.²¹,⁸⁵,⁸⁹ The once thought massive translocation of ions has often been used in support of early views proposing the loss of membrane integrity and ion selectivity during SD that are untenable considering the size of the intra- and extracellular compartments (volume fraction). Thus, the volume fraction drops from 10 to 15% in control to about 4% during SD,¹²⁴,¹²⁵ which means that neurons give up a small amount of their K⁺ content, whereas a large reduction of Na⁺, Cl⁻ and Ca²⁺ raises little the internal concentrations. Most data in the literature refer to the peak values, which do not occur uniformly for the different ion species over the course of the SD (typically, the initial drop for K⁺ and the end values for Na⁺). Thus, ion gradients vary significantly over the course of SD and the different species follow independent trajectories (Figure 4), possibly by the different ion involvement and time course of the multiple mechanisms activated, such as potassium buffering, increased Na⁺ conductance, and cell volume regulation. The relevant point is that ion gradients during SD remain high enough as to maintain significant EMFs in neurons (e.g. in the main phase of SD in the hippocampus, K_i/K_o: 133/3.5 in control vs. 125/40 mM in SD-zone; Na_i/Na_o: 20/140 vs. 35/70 mM).¹⁰⁶,¹¹⁴ Note that the continuous drop of the [Na⁺]_o during the course of SD supports the increased Na⁺ conductance in neurons,¹⁰⁷ whereas the drop of [K⁺]_o is attributed to glial uptake.⁵⁷,⁵⁸ This in turn gives high significance to the fact that ion changes affect specific dendritic domains, whereas the portions of the neurons that are spared by SD still maintain intact ion gradients. Such regional ion gradients are critical to understand the EMFs during SD (see below).

The missing link: Intradendritic recordings show longitudinal potential gradients

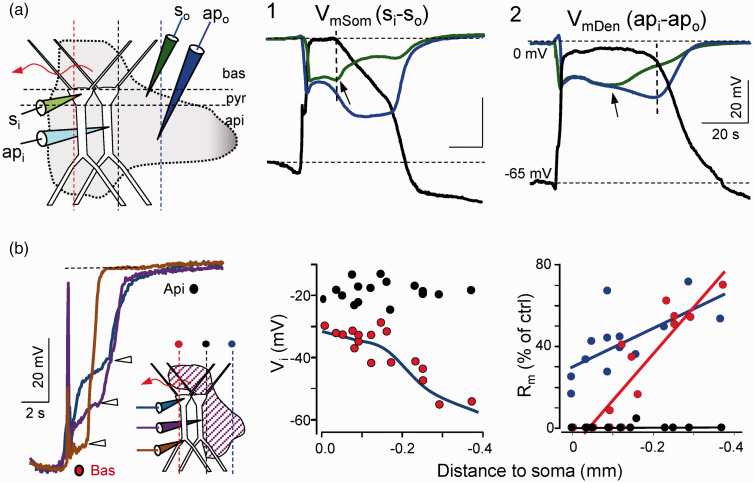
SD was always recognized as a dendritic phenomenon, yet evidence of the functional state of dendrites was incomplete. Patch-clamp studies identified numerous channel types endowing dendritic arbors with distinct active properties at different sites.¹⁷ In an attempt to determine where ion channels open in neurons during SD, we mapped the R_m and V_m along the somato-apical axis of pyramidal cells in the CA1 region by combining intradendritic and extracellular recordings.⁵⁰ We confirmed the full depolarization and the near total loss of the R_m at the soma and also, in the apical dendrites, yet only while the SD-associated ΔV_o was present in the corresponding dendritic strata (Figure 8(a)). Thus, when SD spreads in only one dendritic arbor, strong longitudinal gradients of V_m and R_m develop along the somatodendritic axis (Figure 8(b)). The spatiotemporal pattern of the R_m drop indicates that membrane channels open maximally at the wavefront in large portions of both dendritic trees and they close gradually in a centripetal manner, as later confirmed by realistic biophysical modeling.¹⁰⁶ Significantly, the opposite dendritic tree to that in which SD is can still generate evoked responses as it is only partially depolarized (Figure 9). The emerging view is that the negative ΔV_o and concomitant ionic changes in SD are tightly associated to the opening of specific channels in specific portions of dendrites, while other cell sites remain partially polarized and maintain high R_m. In conclusion and as first postulated by Leão himself, polarization gradients between different parts of neurons underlie the generation of the ΔV_o, at least in its main part.

Figure 8.

Longitudinal intracellular gradients of membrane potential (V_m) and resistance (R_m) during SD. (a) The V_m is fully depolarized only in neuron parts located in the strata that display the negative ΔV_o (vertical lines). (b) The shorter duration of the SD in the basal tree provides a temporal mark (arrows) to establish different phases according to which neuron elements are affected by SD: apical plus basal (so called the main phase: black dots), apical only (late phase: blue dots), and basal only (obtained by initiating SD waves in this dendritic tree: red dots). Population data show longitudinal gradients of depolarization and membrane résistance along the somatodendritic axis. Modified from Canals et al.⁵⁰

Figure 9.

Selective inactivation of the sections of neurons encroached within the extracellular negativity. Experiments are chosen when SD invaded only the basal tree and impalements are made in the soma or apical shaft as indicated. Orthodromic stimuli in different strata are marked by the colored synaptic buttons to the left. Note that somatodendritic action potentials and population spikes are abolished all throughout for basal stimuli but only in the basal dendrites for apical stimuli. Reproduced from Canals et al.⁵⁰

From neuron channels to field potentials

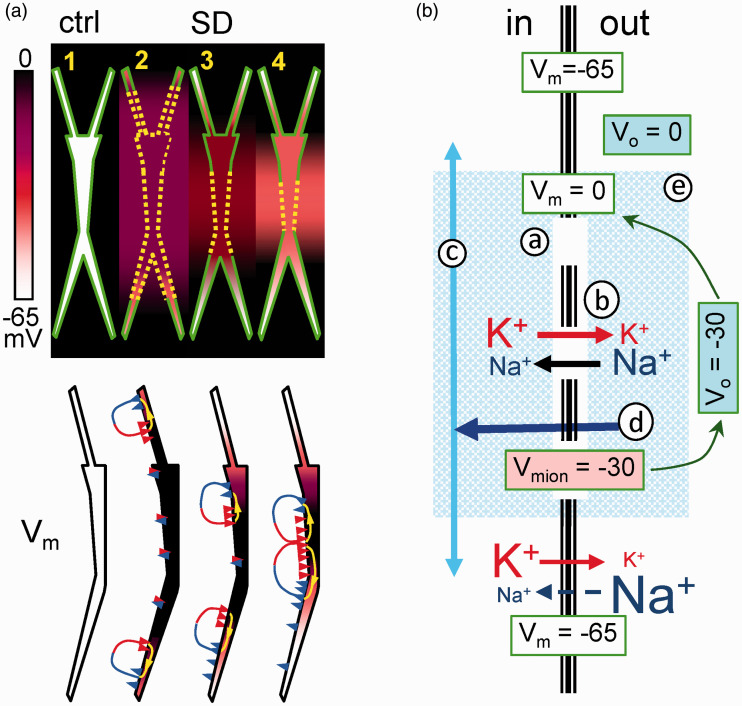
The only possibility to close the gap between single cell currents and extracellular FPs is through biophysical models of realistic cytoarchitecture. Figure 10(a) illustrates this for SD in the hippocampus based on a series of experimental and computational papers.⁵⁰,^104–106 The somatodendritic values of R_m and V_m are perhaps the most important, since they allow benchmarking the distributions of membrane channels in model units and the comparison of synthetic and real spatial profiles of the V_o and population currents in the aggregate. In experiments, we found that net inward currents are restricted to certain neuron sites and SD phases, never covering the entire anatomy of pyramidal cells (Figure 5). Contrary to intuitive expectations, when the negative shell of SD covered a long stretch of the neuron (ap+bas in Figure 5 and blue traces in Figure 6), the net inward current was only found at the outer borders, with no current evident in the middle portions. Indeed, this would be expected when a large stretch of an elongated neuron becomes isopotential, as found in intracellular studies (Figure 8). Therefore, an effect of SD-channels is to establish an electrical shunt of the membranes across which inward and outward currents can flow with ease (if they must), whereas little current escapes internally into SD-spared membranes to complete the loops of current. In this situation, the negative ΔV_o in middle apical sites is not contributed by local currents, but by volume-conduction of currents originated at the borders of SD-affected membranes. When the shorter basal SD ends, the apical one evolves to a narrowing dendritic portion, and thus, cancellation of the inward and outward currents in central segments lessens, causing net inward currents to appear. The emerging view is that a specific channel activates in dendritic membranes, although the longitudinal extent of the SD-affected membranes determines where and when net currents arise in the ES.

Figure 10.

(a) Schematic representation of the spatial distribution of V_i and V_o (upper scheme), and V_m and currents (lower dummies) in selected instants of SD. Dashed yellow lines indicate active SD membranes. Note that similar colors in and out of the neuron dummies indicate no transmembrane potential gradients (V_m=0). Paired blue and red arrowheads represent zones of zero net current (see text for details). Modified from Makarova et al.¹⁰⁴ (b) Schematic representation of the main actors during SD. The crucial event (1) is the opening of specific cation channels in a discrete portion of the membrane (hollow line). (2) Ions flow across, causing a moderate reduction of gradients that settle a local depolarized “resting” V_m (V_mion). (3) Since this segment is more depolarized, axial currents are created toward less depolarized zones (light blue arrows), causing a net inward current of equal magnitude across the shunted high-conductance membranes (dark blue arrow) (4). This current constitutes an extracellular sink responsible for the negative V_o that further depolarizes the membrane to its final near-zero value (5).

One neuron, two membranes: SD as a “frozen” dendritic spike

Although the conditions are changing during the span of SD, these are slow enough as to picture a remarkable biophysical scenario in which the electrochemical relationships amongst participating elements are easily observed. These are depicted in the scheme of Figure 10(b). Notably, the SD-active and SD-spared membranes both hold rather stable but distinct electrochemical gradients, which split individual neurons in anatomical segments with different but stable V_m. The mechanism of depolarization in SD segments seems paradoxical, as it is simultaneously active and passive. It is active, because as in standard synaptic potentials some channels open through which current flow across the SD-activated membranes; and it is passive because the different ion gradients establish neuron segments with different “resting” V_m, hence longitudinal (axial) gradients of depolarization that would not require channel opening to produce current flow (passive depolarization, as earlier proposed for syncytial currents or during externally applied fields). Therefore, the ΔV_o is dynamically contributed by two EMFs, each with varying share in different domains and SD phases. Volume-conducted currents dominate when SD-domains occupy a large extension of the neuron, whereas net inward current arises when the SD affects narrow dendritic portions in the apical tree. Note that only the latter imply net flow of charge across the membranes.

Is the SD-associated ΔV_o a Donnan potential?

At this point, we should remind of a remarkable coincidence as is that the V_i and V_o vary at a similar rate but in opposite directions over the span of SD (Figure 1(a)), making the V_m to appear clamped at ≈ 0 mV. Since the V_m is a joint function of ion gradients and permeabilities, we should find a hyperpolarizing influence to compensate for the larger ΔV_o in the late apical-only phase. The Na⁺ gradients reduce significantly during SD after the initial fast drop (Figure 4(c)), and there is also a notable recovery of K⁺ gradients, as inferred from the continuous reduction of the [K⁺]_o after the initial maximum (Figure 4(b)). According to the Goldman-Katz equation, both these changes move the V_i into a hyperpolarizing direction. It would thus seem that the reduction of [K⁺]_o is forced by the centripetal closure of SD channels in outer segments of the neuron anatomy as a necessary response to maintain the V_m clamped at zero following the surge of net inward current in dendritic regions in the late apical-only phase of SD.

An intriguing question is why the V_m stays close to zero in SD-affected membranes in a quasi-steady manner, whereas some ion species vary over the span of the SD and other sites of the same neurons maintain different V_m. Are all involved variables changing in a concerted manner to maintain a fix V_m? If so, what physical elements underlie this V_m? We earlier considered that the transmembrane ion fluxes during SD reflect the tendency to achieve a Donnan equilibrium in a situation when the permeability for small cations grows large and equalizes, and the pumps’ capacity to maintain/restore the ion gradients is exceeded.¹²⁶ Once the equilibrium is attained, we may not expect any net current across the membranes, whereas the V_m would approach a Donnan potential. The magnitude of such potential is unknown and it is thought to depend on the amount of intracellular impermeable charges that differ in different cell types. It is tempting to think that it is reflected by the ΔV_o attained in the neuron segments and SD phases when there is no net current across the membranes (≈15–20 mV during the main SD phase). In this line, the near zero V_m value would arise from the balance of such an hypothetical Donnan potential and an opposite potential generated by the still remaining neuronal currents. Let’s consider for instance the possibility that a single cell become entirely isopotential because of a uniform distribution of SD-activated currents. Would the ΔV_o disappear in the outside? Or rather, would the cell “see” SD-like ion gradients and a Donnan potential across its membranes? The sharp spatial drop of such a single-cell V_o as well as the immediate balance of ions in the interstitium would prevent the hypothetical single-cell extracellular changes to be detected. And yet, wouldn’t be the experimental ion concentrations and ΔV_o during SD a direct reflection of such equilibrium in a population sufficiently extended in the space as to avoid rapid equilibration with non-invaded regions? For the moment, the answers to these questions remain unanswered, at least until we can experimentally establish a situation in which volume-conducted and net inward currents can be ruled out as primary contributors.

The ΔV_o, ion gradients, swelling and dendritic damage: An hypothesis

The entry of water into the cells that is expected when moving toward a Donnan equilibrium appears to have a slower kinetics over the span of the ΔV_o than ion changes, as judged by the gradual increase of tissue resistivity (Figure 5). The paths for water entry and the release of osmotic particles may explain the different dynamics.¹¹³,¹²⁷,¹²⁸ Interestingly, the ion concentrations keep drifting over the course of the SD, albeit these are restricted to the narrow apical band in the late phase, whereas distal apical dendrites, somata and basal dendrites recover much faster. We propose that this spatiotemporal pattern underlies the structural and functional damage after repeated SDs that affects specifically these dendritic segments, and the ΔV_o plays some part in it. On one hand, dendritic beading produced by repetitive SD waves is prominent in the apical dendrites.³ On another hand, the apical dendrites lose the ability to initiate and propagate dendritic spikes after a focus of SD waves, whereas synaptic potentials and somato-axonic spikes are readily produced.² Such specific rundown of apical dendritic electrogenesis is more severe and lasts longer the more PUSDs develop, which let’s remember, run preferentially on this dendritic band. The amplitude of the local ΔV_o grows much larger in this dendritic domain and since it commands the V_i to keep the V_m clamped near zero and promotes the emergence of net inward current only in these membrane patches, it can be said to play a part on the additional ion transfer into them. The fact that V_o growth is the inevitable consequence of the spatial narrowing of SD-activated membranes along the axis of the neuron does not detract from the fact that it is the ultimate responsible for the additional entry of ions and water. Thus, if SD-activated channels remained widely distributed, the osmotic challenge could be smaller and might distribute over the entire cell thus facilitating functional recovery.

What is wrong in past theories and some questions that remain open

Some general notions have survived from the early theories on SD that are not compatible with our current understanding of unitary and population electrogenesis, and these should now be laid to rest. The most significant statements often found in contemporary SD literature and that appear to be unsubstantiated include: (1) neurons are inactivated, and hence they cannot generate any currents; (2) the R_m drops to zero, and hence the neuron’s membrane integrity is lost; (3) transmembrane ion gradients disappear; (4) the negative ΔV_o mirrors the [K⁺]_o, and hence this ion is essential to generate the ΔV_o. In addition, we have highlighted here some data regarding SD that have been neglected, undervalued or misjudged in an attempt to maintain potassium in a central role in nearly all aspects of SD, a perception born out of a time when single cell and population electrogenesis were immature. We have re-interpreted such observations to make them compatible with current biophysical tenets. The end-point is that neurons and not glia, dendritic channels and not spatial currents, and sodium rather than potassium, appear to be the main actors in the generation of the negative ΔV_o.

Our understanding of SD electrogenesis has advanced considerably, but it remains incomplete and a number of problems remain unanswered and will require careful study. For example, the mechanisms that promote the initial flow of ions across the membranes are still to be elucidated, and the nature of the SD-channels that prolong this state for tens of seconds must be identified, information that will aid the search for new therapeutic targets to limit the damage caused by cerebrovascular insults. It may be premature to think of modulating SD-channels without establishing their identity, yet the centripetal narrowing of SD-affected membranes is compatible with the shutdown of SD-channels through an intracellular wave of a metabolite, which may be worthy of further study. Also, since there may be several SD-channels, and they may be unevenly distributed in different types of dendrites, it is important to probe the intracellular content of the different ion species with subcellular precision. Finally, glia is undoubtedly related to SD, and thus it will be necessary to clarify if they play an ancillary role or a critical but subtle one that is as yet beyond our capacity for analysis.

Electrogenesis in the brain is a highly quantitative biophysical matter and therefore in a privileged position to find the true causal relationships among the many variables affected during SD. By defining their role in the production of the ΔV_o, we have the opportunity to look at their dynamic changes with renewed standpoints and, perhaps also, to the elusive mechanisms of propagation of a phenomenon that has intrigued and inspired several generations of researchers.

Funding

The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: This work was financed by the Spanish Ministry of Science, Innovation, and Universities (Grant SAF2016-80100-R), and The Russian Science Foundation (Grant 19-12-00394). OH is a member of the Cajal Blue Brain Project (C080020-09; the Spanish partner of the Blue Brain Project initiative from EPFL, Switzerland).

Declaration of conflicting interests

The author(s) declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.

ORCID iD

Oscar Herreras https://orcid.org/0000-0002-8210-3710