Forecasting of COVID-19 onset cases: a data-driven analysis in the early stage of delay

Abstract

The outbreak of COVID-19 has become a global public health event. Many researchers have proposed many epidemiological models to predict the outbreak trend of COVID-19, but all use confirmed cases to predict “onset cases.” In this article, a total of 5434 cases were collected from National Health Commission and other provincial Health Commission in China, spanning from 1 December 2019 to 23 February 2020. We studied the delayed distribution of patients from onset to be confirmed. The delay is divided into two stages, which takes about 15 days or even longer. Therefore, considering the right truncation of the data, we proposed a “predict-in-advance” method, used the number of “visiting hospital cases” to predict the number of “onset cases.” The results not only show that our prediction shortens the delay of the second stage, but also the predicted value of onset cases is quite close to the real value of onset cases, which can effectively predict the epidemic trend of sudden infectious diseases, and provide an important reference for the government to formulate control measures in advance.

Supplementary Information

The online version contains supplementary material available at 10.1007/s11356-020-11859-w.

Introduction

In 2020, a novel coronavirus disease (COVID-19) epidemic broke out in the world, triggering a major crisis in global life, health, safety, and economic and social order. It spread very fast, as of 11 July 2020, there have been 85487 cases of COVID-19 confirmed in mainland China, including 4648 deaths, and 80293 discharged, as well as 1403 confirmed cases in Hong Kong, 46 in Macao, and 451 in Taiwan. COVID-19 also outbreaks all around the world. To hundred thirty-two countries have been attacked by COVID-19, causing 48,463,852 people confirmed, 1,227,951 died by 6 November, 2020.

During the outbreak, besides medical research on COVID-19 (Wang et al. 2020; Zeng et al. 2020), researchers all around the world collected data, described demographics, exposure history, and disease progress of “confirmed cases,” summarized the disease characteristics (Wang and Wu 2018; Chen et al. 2020a, b; Backer et al. 2020; Nie et al. 2020), built mathematical models to analyze and simulate the trend of COVID (Guo et al. 2020; Riou and Althaus 2020; Liu et al. 2020; Wu et al. 2020; Kucharski et al. 2020; Wang et al. 2020), and proposed appropriate suggestions based on their research.

Based on the officially published COVID-19 disease data, domestic and international passenger transport data, and the potential impact of various public health interventions implemented since January 2020, many mathematical models were established to estimate the scale of the epidemic and to simulate the possible future spread of the epidemic (Guo et al. 2020; Riou and Althaus 2020; Liu et al. 2020; Shao and Shan 2020; Pan et al. 2020). All of their studies have shown that rapid diagnostics, isolation, and comprehensive interventions will have a significant impact on its future trends. A modified SIR model was applied to predict the actual number of infection cases and the specific burden of isolation ward and ICU (Ming et al. 2020). They demonstrated that without public health interventions, the actual number of infections could be much higher than reported. Based on vector error correction models (VECM), Berta et al. (2020) proposed a bivariate error connection model, forecasting ICU demand in real-time, which is important for public health manager to plan or adjust health care resources. Based on SEIR simulation, Ai (2020) predicted epidemic peak in Hubei will be within 28th January 2020 to 7th February 2020, up to 7000–9000 infectious cases in total. Hellewell et al. (2020) and other authors developed a stochastic transmission model to figure out if isolation and contact tracing are able to control onwards transmission from imported cases of COVID-19. They used the model to quantify the potential effectiveness of contact tracing and isolation of cases at controlling a severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2)-like pathogen, which showed that isolation and contact tracing were effective ways to reduce the number of the infected. Cintra and Fontinele (2020) applied a SEIRD model with age division to predict the infection, death curve, and future scenarios of relaxation of social isolation and introduction of vaccines. Based on several dynamic models validated during previous outbreaks, Roosa et al. (2020) proposed real-time short-term models to forecast cumulative number of confirmed cases 5, 10, 15 days ahead. Several regression analysis-based models have been applied to predict the epidemic final size and final time of the epidemic in Egypt (Amar et al. 2020; Almeshal et al. 2020). Alberti and Faranda (2020) applied logistic model and investigated the predictions of COVID-19 on the different phases, finding that there is a wider uncertainty during the first week of epidemic growth, and uncertainty was reduced when the epidemics peak is past, thus modelling of epidemic growth should be focused on specific stage of growth.

Basic reproductive number is a parameter highly relative to the spreading scale of an epidemic disease; different models were used to estimate the basic reproductive number (Read et al. 2020; Cao et al. 2020; Zhao et al. 2020). The authors fitted a deterministic SEIR model, and they estimated a basic reproductive number of 3.11 (95% CI 2.39–4.13) (Read et al. 2020). They suggest that 58–76% of transmissions must be prevented to stop increasing and spreading. Based on daily reported cases from China, Cao et al. (2020) estimated the effective reproduction number and concluded that COVID-19 had a higher effective reproduction number than SARS with a comparable fatality rate. Zhao et al. (2020) simulated the epidemic curve of the COVID-19 case series in mainland China from January 10 to January 24, 2020 and found that the average basic reproductive number of COVID-19 is between 2.24 and 3.58, which is obviously greater than 1, indicating that the COVID-19 may have led to an outbreak. Yoriyuki (2020) estimated the daily changes of reproducing number with a Bayesian model, and the model was applied to evaluate the effectiveness of public healthcare measures of “keep social distance.” The lack of COVID-19 tests inevitably leads to the under-reporting data and underestimation of real pandemic in the country; thus, Oliveira et al. (2020) proposed a SIR model with correction for under-reporting in a Bayesian framework, estimating the rate of case reported and reproductive rate in Brazil.

Based on the “visiting hospital cases” data, this paper analyzed the occurrence and development of the disease cases from the onset, diagnosis, confirmed, hospitalization, and rehabilitation. We applied a Bayesian Hierarchical model to nowcast the occurrence and spread of COVID-19. The early warning model provides an important basis for government departments to formulate prevention and control measures.

Nowcasting is defined as forecasting the very near future or the very recent past. Recently, it has been widely used in real-time monitoring the epidemics in public health (Donker et al. 2011; Krzyścin et al. 2018). “Confirming delay “is a problem that must not be neglected when forecasting the epidemic trend. Consider that a man is attacked by COVID-19 and shows symptoms of cough and fever, it always takes some days before he is confirmed and reported. Such kinds of delay may easily cover up the real trend of outbreak because the true number of infected patients is greater than the number reported, which is not benefit for the timely control of the disease outbreaks. The additional delays between onset date and reporting date in the public health surveillance database should not be ignored.

Lawless was the first one who estimated the number of occured but not reported events, and he developed an algorithm called “nowcasts” to correct for reporting delay (Lawless 1994). Hohle and Heide proposed a Bayesian nowcasting algorithm based on Lawless’s report, which is used to forecast daily number of “reported cases” (Hohle and Heiden 2014). There is a long delay from onset to “be confirmed”, which can be divided into two stages. Stage I is the visiting delay between “onset date” and “visiting hospital date”; stage II is confirmed delay between “visiting hospital date” and “confirmed date.” All papers mentioned above used “confirmed cases” to forecast the number of true “onset cases,” but the delay between onset and “be confirmed” is quite long, which will mask the real outbreak trend of the infectious disease.

In this paper, we take the occurred but not yet “confirmed cases” into account, and apply a Bayesian forecast model with truncation (BFMT) (Hohle and Heiden 2014; Wang et al. 2018) to predict the number of “onset cases,” which shorten the delay of stage II, and wins time. Based on the predicted disease outbreak trends, control measures can be taken in advance to prevent large-scale outbreaks.

This is of great significance for the control of epidemics.

Methods

Data source and exploratory data analysis

Our data, collected from National Health Commission and other provincial Health Commission, in China, spanning from 1 December 2019 to 23 February 2020. Table 1 shows examples of our collected data information. Each confirmed case consists of the city information, the sentinel hospital, the symptom “onset date” (the self-reported date when the patient was attacked by COVID-19), “visiting hospital date” (when the patients went to hospital for detection), and the “confirmed date” (when the patients was confirmed by doctors and reported). There is a substantial delay between “onset date” and the “confirmed date,” The reporting delay is divided into two stages. Stage I is the “visiting hospital delay” between the “onset date” and “visiting hospital date”; stage II is the delay between “visiting hospital date” and the “confirmed date.”

Table 1.

Example of the information collected for the data set

	Hospital information			Onset date	Visiting date	Confirmed date
	Province	City	Sentinel hospital
Case 1	Hubei	Wuhan	People’s Hospital of Wuhan University	2020-01-28	2020-02-03	2020-02-06
Case 2	Zhejiang	Hangzhou	Hangzhou Xixi Hospital	2020-01-31	2020-02-05	2020-02-13
Case 3	Guangdong	Guangzhou	The Eighth People’s Hospital of Guangzhou	2020-01-31	2020-02-11	2020-02-14
Case 4	Anhui	Hefei	Hefei Infectious Disease Hospital	2020-02-02	2020-02-07	2020-02-09

Generally, the monitoring on the COVID-19 can be performed on time series aggregated by the date of symptom onset and the date of being confirmed. Specifically, till 1 day, we define “confirmed cases” as the currently available counts of patients confirmed by doctors, and define “onset cases” as the real number of patients who is infected with COVID-19 and show some symptoms. The goal of nowcasting is to predict the true number of ”onset cases“ based on the number of people visiting the hospital, instead of using the number of “confirmed cases” to predict the number of “onset cases”, because there will be a delay from “visiting hospital” to “be confirmed”.

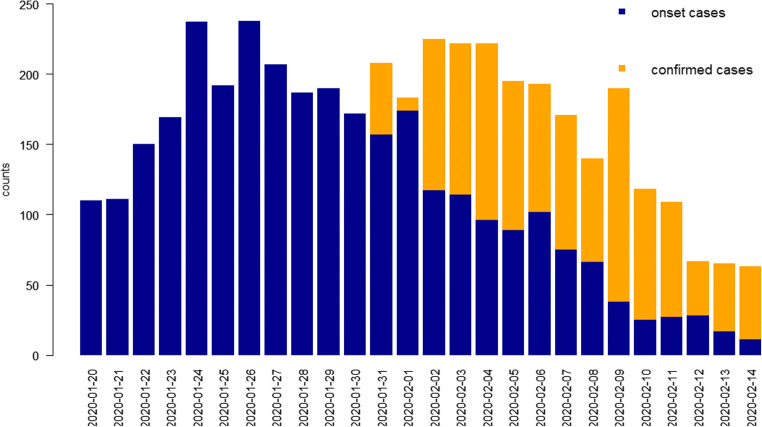
Figure 1 shows the daily counts of “confirmed cases” (yellow bar) and “onset cases” (blue bar); there is difference between the two kinds of data due to the delay. The histogram of “onset cases” is ahead of histogram of “confirmed cases.” As more “confirmed cases” data comes in, the number of “confirmed cases” (yellow bar) is getting closer to the number of “onset cases” (blue bar) in Fig. 1. Figure 1 clearly shows the distribution of delays from “visiting hospital” to “be confirmed”. This motivates us to use the data from “visiting hospital cases” to predict the number of “onset cases” in advance, and provide early warning to the public health system to take more time to take prevention and control measures, rather than waiting for the outbreak to occur and then control.

Fig. 1.

The blue bar denotes the daily number of “onset cases”, the yellow bar denotes the number of “confirmed cases” respectively, from 2020/01/20 to 2020/02/14

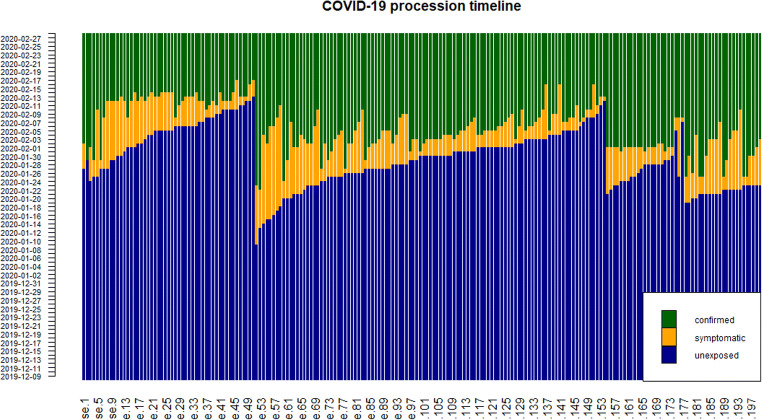
Figure 2 shows the procession timeline of 200 cases from unexposed to be attacked by COVID-19 and show symptoms such as cough and fever, then to be confirmed by doctors. The blue strips denote the state that patients have not unexposed to COVID-19, The yellow strips denote patients are infected but not confirmed, and they also demonstrate delay of stage I and stage II. The green strips denote that patients are confirmed. We can see from Fig. 2 that in the early days of the outbreak, there are quite long delays, but with government taking appropriate preventions and faster detection speed, the delays are dramatically shortened.

Fig. 2.

COVID-19 procession timeline

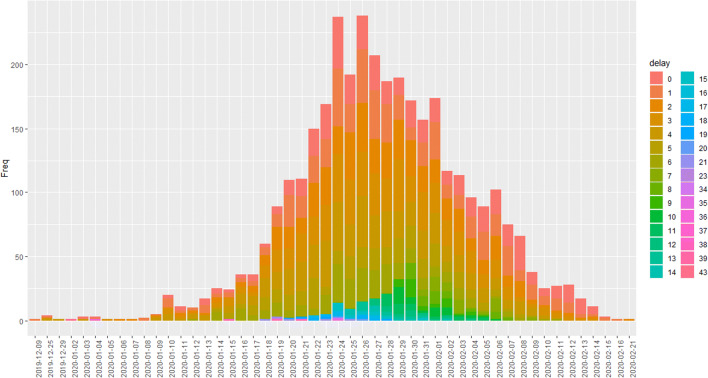
Figure 3 shows the distribution of “visiting delays” (in days) in stage I. It clearly shows that many patients went to the hospital within 1 week when they began to show symptoms of infection, and seldom have delays of more than 15 days. We assume the maximum delay occurs up to 7 days due to the 3σ principle. Note that the data will become less reliable and the information contained is not accurate when the delay becomes very large. We denotep_d,  d = 1, 2⋯7, as the observed proportion of the number of patients with delay d days to the total number of patients given a time span. Note that p₇ includes delay with days larger than or equal to 7 days, and $\sum _{d=1}^7{p}_d=1$.

Fig. 3.

Daily distribution of “visiting delays”

Notation and prediction of N_t

Here we set our study in a discrete time and set 1 day as a unit. We use the notation of (Lawless 1994) to describe variables we need for the prediction of the currently true number of patients in the presence of delay. n_{t, d} denotes the number of patients onset at time t but confirmed at time t + d, which means that n_{t, d} patients onset at time t are confirmed with a delay of d days. Let T be the current day or “now,” then t takes values on {0, ⋯, T}, and d takes values on {0, ⋯, D}. When the delay time d becomes very large, the data and the information it contains will become less reliable and less accurate. So one can assume that the maximum delay occurs up to D days, and patients confirmed with a delay larger than D are considered as with a delay of D days, which means patients with a delay larger than D days are included in the category of delay being “D days”. Note that when d > T − t, we could not know n_{t, d}, because at time T, the patients have not been confirmed and reported yet. So our data is the right-truncated type of data. Formally, we devote $N_{t,T}\triangleq N\left(t,T\right)={\sum }_{d=0}^{min\left(T-t,D\right)}{n}_{t,d}$ to be observed cases reported (those who are confirmed and reported) until time T. Thus with the limit of maximal delay, the true number of onset cases at time t, 0 ≤ t ≤ T, is

$$N_t\triangleq \sum _{d=0}^D{n}_{t,d}=\left\{\begin{array}{c}\stackrel{D}{\sum _{d=0}}{n}_{t,d},T-t\ge D,e.g.,\text{full data}\\ \stackrel{T-t}{\sum _{d=0}}{n}_{t,d}+\stackrel{D}{\sum _{d=T-t+1}}{n}_{t,d},T-t<D,e.g.,\text{truncate}d\mathit{\text{data}}\end{array}\right)$$

Note that for t larger than T − D, N_t is right-truncated. So we need to estimate the unobserved right-truncated N_t. N_t − N_{t, T} represents the cases which are onset but not yet visit hospital. Our goal is to estimate unobserved true number of infected patients. We apply BFMT module (Hohle and Heiden 2014; Wang et al. 2018) to forecast the daily total number of patients N_t. A convenient R package “surveillance” gives us great convenience (Salmon et al. 2018), details on the calculation of f(N_t∣ N_t,T) and on the sampling procedure from this posterior distribution could be found in Wang et al. (2018) and Salmon et al. (2018). We omit the details here.

Results and discussion

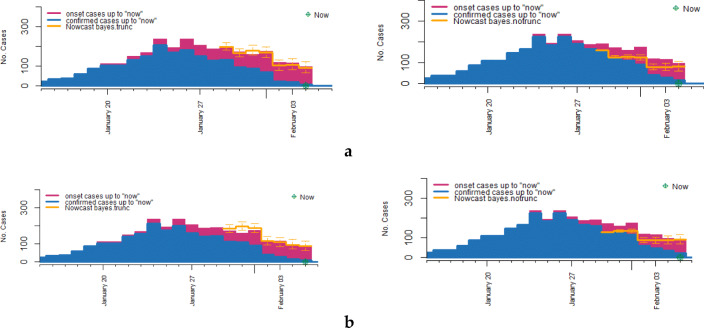
In this section, we compare BFMT method with Bayesian forecast model with no truction ( BFMnT) method which ignores the right truncation (Hohle and Heiden 2014). We take current time as 4 February and 5 February, then predict the number of occurred cases for 7 days on each current day. The nowcasting results are shown in Fig. 4 and in Table 2. Comparing the BFMT result of Fig. 4a (left) with the BFMnT result of Fig. 4a (right), we can see that the prediction for 29 January with BFMnT method is much lower than the true number, which underestimates the real situation of the epidemic, instead, the prediction for 29 January with BFMT method is very close to the true number of “onset cases.” Similarly, in Fig. 4b, we take current day as 5 February, we can see that the prediction for 30 January with BFMT method is more accurate than that with BFMnT method, the predicted number of “onset cases” with BFMnT method is lower than the true number of “onset cases.” In summary, the predicted result with BFMT method is significantly closer to the real situation than that with BFMnT method, and using BFMnT method underestimates the severity of the epidemic, which would make against the prevention and early warning of epidemic.

Fig. 4.

Nowcasting with BFMT method and BFMnT method respectively. a. The prediction for 7 days on 4 February with BFMT method (left) and BFMnT method (right) respectively. b The prediction for 7 days on 5 February with BFMT method (left) and BFMnT method (right) respectively

Table 2.

Let now = “2020-02-05,” prediction with BFMT method and BFMnT method

	Real onset cases	Predictions
		BFMT	BFMnT
2020-01-30	192	[186.4, 200.5]	[139.6, 141.5]
2020-01-31	184	[177.3, 201.1]	[159.7, 162.8]
2020-02-01	198	[194.2, 204.7]	[167.3, 173.4]
2020-02-02	123	[115.1, 134.4]	[105.3, 110.3]
2020-02-03	120	[104.9, 136.4]	[105.4, 137.2]

Taking the same current day as 4 February and 5 February, we use “BFMT” method and “BFMnT” method to nowcast the true number of “onset cases” for 7 days respectively, the results in Fig. 4 and Table 2 clearly show that when ignoring right truncation, prediction of N_t is much lower than the true number of “onset cases,” which means that using BFMnT method for prediction would underestimates the true number of “onset cases.” However, prediction with BFMT method is much closer to the real number of “onset cases,” although the predicted number is little higher than the true number of “onset cases.” Generally speaking, in epidemic predicting problem, overestimating the true number of patients is better than underestimating it. And we can see that using BFMT method lead to a small overestimation which is acceptable, and apparently BFMT method is far closer to the true number and accurately reflect the actual trend of the epidemic.

Conclusion

This article focused on a total of 5434 cases collected from National Health Commission and other provincial Health Commission in China, spanning from 1 December 2019 to 23 February 2020. These data contain detailed information, such as the date of onset, the date of visiting hospital, and the date of confirmed. We proposed the method “predict-in-advance” to predict the number of “onset cases” using the number of “visiting hospital cases,” rather than using the number of “confirmed cases,” which significantly reduced the forecast time.

Then, we conducted a statistical analysis of the 5434 cases, and studied the delay distribution of cases. We found that there were two stages of delay from the “onset cases” to “confirmed cases.” The stage I is the delay from the onset to the visit, which is the delay in the patient’s medical treatment. Because COVID-19 and cold symptoms are similar, many people do not pay attention in the early stages of the disease, fail to go to the hospital in time, and do not perform self-isolation, which may lead to early transmission. The stage II is the delay between the patient’s “visiting hospital” and “be confirmed.” The delay distribution at stage II is very complicated. The diagnosis report will be delayed due to the lack of understanding of COVID-19, the lack of medical resources, the shortage of kits, the efficiency of experiments, and the different definitions of confirmed cases in the early stages of the COVID-19.

In addition, many researchers use the number of patients confirmed in the hospital to predict the number of “onset cases.” The time from onset to be confirmed is very long, such that the number of “onset cases” cannot be accurately predicted in time.

In view of this, we proposed the method “predict-in-advance.” For instance, we only have the “visiting hospital cases” data till today, we could use the number of visiting patients to predict the “onset cases,” which may lead to a very small overestimation of the number of “onset cases,” but least not underestimate them. However, it makes the prediction ahead of days (the delay in stage II), which can greatly shorten the forecast period, detecting possible epidemic incidents in time.

Finally, since the number of “visiting hospital cases” is used to predict the number of “onset cases” that will be overestimated (at least not underestimated), we will also consider applying a compound Poisson model to solve the problem of overestimation of the number of “onset cases” in the future. Based on the above results, this study will provide a scientific basis for epidemic assessment and risk management. According to the outbreak trends predicted in advance, government departments can specify control measures in a timely manner, which is of great significance to prevent large-scale outbreaks of infectious diseases.

Authors’ contributions

W. X., L. Y., and J. J. participated in statistical modeling and study design. W. X. and L. Y. performed data analysis. All authors drafted the manuscript. All authors assisted in collecting data, provided critical review of the manuscript, and approved the final draft for publication.

Funding

This work is supported by the National Key Research and Development Program of China (No. 2019YFC1606003) and Research Foundation for Advanced Talents of Beijing Technology and Business University (No.19008020162).

Data availability

No

Compliance with ethical standards

Ethical approval

Not applicable. This article does not involve experiments, only data analysis, no ethical standards are required

Consent to participate

Not applicable. This article does not involve experiments, only data analysis; no ethical standards are required.

Consent to publish

Not applicable. This article does not involve experiments, only data analysis; no ethical standards are required.

Competing interests

The authors declare that they have no competing interests.