Abstract
In this work, a unified representation of all the time-varying dynamics is accomplished with a Lagrangian framework for analyzing Fisher-Rao regularized dynamical optimal mass transport (OMT) derived flows. While formally equivalent to the Eulerian based Schrödinger bridge OMT regularization scheme, the Fisher-Rao approach allows a simple and interpretable methodology for studying the flows of interest in the present work. The advantage of the proposed Lagrangian technique is that the time-varying particle trajectories and attributes are displayed in a single visualization. This provides a natural capability to identify and distinguish flows under different conditions. The Lagrangian analysis applied to the glymphatic system (brain waste removal pathway associated with Alzheimer's Disease) successfully captures known flows and distinguishes between flow patterns under two different anesthetics, providing deeper insights into altered states of waste drainage.
Keywords: Optimal mass transport, Glymphatic system, Fisher-Rao regularization
1. Introduction
The optimal mass transport problem (OMT) entails minimizing the transportation cost associated with redistributing one probability distribution to match another. The static OMT formulation has been applied to medical image processing and registration [9, 11, 12]. The dynamical version of OMT [1] opened up new possibilities for numerical solutions and extensions using tools from the field of fluid dynamics [3, 21]. In particular, the authors consider a regularization of the dynamical OMT formulation [1] for modeling apparent fluid flow in dynamic contrast enhanced MRI (DCE-MRI) images where a diffusion term has been added to the Euler equation [7, 8]. Contrast transport derived using earlier models without a diffusion term were vulnerable to noise in the data [23], making the inclusion of a diffusion term advantageous from both physical and numerical standpoints. Analysis of the resulting velocity fields is typically carried out in an Eulerian framework, i.e., flow properties are considered at specific locations for each time point as compared to the Lagrangian framework, which tracks specific particles as they move over time; see Figure 1.
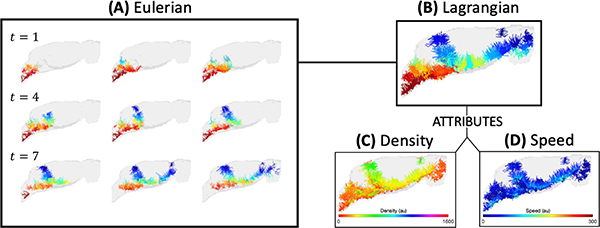
Fig. 1.
Eulerian and Lagrangian visualizations of flow dynamics. (A) For each time point, streamlines are computed at a fixed set of initial locations. Color is used to distinguish streamline clusters and time-varying flow behavior is observed by comparing streamlines across time. (B) Alternatively, temporal changes in particle trajectories are encompassed by pathlines and presented in a single image. Time-varying particle attributes associated with the pathlines, such as (C) density and (D) speed, exemplify the simplistic yet informative nature of our unified visualization framework.
The Lagrangian approach gives a useful alternative to the Eulerian scheme and has recently been presented in conjunction with the aforementioned regularized version of OMT [16]. The pipeline taken from this work has untapped practical applications for distinguishing elusive physiologically relevant flow patterns and so we adopt it in the present work to study the glymphatic system (GS) and brain waste drainage. In [16], the authors employ a regularized version of OMT by adding a diffusion term to the continuity equation in the Benamou-Brenier formulation of OMT [1]. It turns out that there are two equivalent ways to derive the Lagrangian coordinates of the optimal trajectories. The first is via a transformation of the advection-diffusion equation in the regularized problem, and the second by adding a Fisher-Rao information type term to the kinetic energy in the original dynamic formulation [4]. In the present work, we adopt the second method, i.e., Fisher-Rao regularization. We should note that employing Lagrangian coordinates derives improved visualizations of GS function in a time efficient display and also reveals new disparate dynamic waste drainage features in two different states of arousal that were previously difficult to discern.
Waste products are removed from the brain through the GS, a peri-vascular transit passage for cerebrospinal fluid (CSF) which facilitates mixing of CSF with interstitial fluid [14]. Impaired waste clearance due to glymphatic dysfunction has been associated with vascular dementia, Alzheimer's Disease (AD) [22] and sleep deprivation [24]. The GS accelerates waste clearance from the brain during slow wave sleep and with certain hypnotics when compared to other anesthetics and wakefulness [28]. A recent study showed that unconsciousness induced with dexmedetomidine and low dose isoflurane (DEXM+ISO) that mimics natural sleep enhances GS function to a greater extent when compared to deep anesthesia induced with isoflurane (ISO) [2]. These results suggest that hypnotic drugs that promote ǹatural' sleep might be superior to deeper states of sleep/anesthesia regarding preservation of sleep like GS function. Novel ways to improve or maintain GS function for general brain health is urgently needed and dependent on developing robust analysis tools to quantify its function.
The main contributions of this work are as follows:
We directly use the Fisher-Rao regularization of the energy functional in visualizing the flows, highlighting the framework's natural treatment of small diffusion values needed for studying the GS.
We successfully differentiate between GS flow patterns under two different anesthetics and provide additional new insights, in particular, to the relationship between GS flow and solute clearance via pathways outside of the brain.
2. Background
2.1. Regularized OMT
As alluded to above, the problem of optimal mass transport (OMT) is concerned with moving mass from one site to another so that minimal `work' is expended, and mass is preserved, see [26, 27] for a complete set of references. For our purposes with respect to medical images, we are interested in the dynamical OMT formulation due to Benamou and Brenier [1]. They proposed an alternative numerical solution by introducing time and solving a partial differential equation constrained space-time minimization problem. This formulation has the geometric interpretation of finding geodesics [20] between the given densities μ0 and μ1 in the space of probability densities and the trajectory of the transport is explicitly factored into the cost.
Explicit representation of the density's evolution suggests exciting capabilities for improved image registration techniques to account for dynamical aspects of physiological processes with additional aptitude for analyzing interesting time-varying phenomena. This is particularly powerful for medical applications where a complete physical model is often impractical to implement. We consider the following modified version of Benamou and Brenier's OMT formulation where a diffusion term is added in the continuity equation. The following regularized OMT problem over the normalized time interval t ϵ [0; 1] is used to motivate the Lagrangian framework for flow representation [16] that will be detailed in the next section:
| (1) |
| (2) |
| (3) |
where is the density interpolant between the given densities μ0 and μ1, assumed to have the same total mass over a bounded, connected subspace of , is the velocity and ϵ is the diffusivity. It is interesting to note that this may also be regarded as a reformulation of the Schrödinger bridge problem [4].
3. Lagrangian coordinates
Following [16], the optimal trajectory in Lagrangian coordinates for the regularized case is defined as follows. Let μmin and vmin denote the minimum arguments of the action (1) subject to (2). Define the augmented velocity
| (4) |
Noticing that
| (5) |
leads to the following conservation form of the constraint (2):
| (6) |
Analogous to [1], the Lagrangian coordinates of the flow X = X(t,x) corresponding to the minimizing velocity vmin is the solution of the differential equation
| (7) |
where according to (4),
3.1. Fisher-Rao regularization
It is very important to note that the regularized OMT problem is equivalent to a Fisher-Rao information theoretic regularization of OMT, which is very closely connected to the Sinkhorn approach [6], and is in fact a dynamic formulation of the Schrödinger bridge problem [4]. For small ϵ in the advection-diffusion equation above, Sinkhorn will become unstable, which is why one needs to employ a different approach in the medical imaging realm. We will therefore derive an equivalent Lagrangian formulation of regularized OMT via the Fisher-Rao regularized functional. We should note that there are a number of works demonstrating the well-known equivalence of Fisher-Rao and OMT joint interpolation functional and regularized OMT including [4, 18, 5, 19]. We briefly sketch the proof from these works to highlight some of the key steps of going from the regularized OMT problem to the Fisher-Rao regularized one. We refer the reader to the latter works for more details and insights into the methodology.
Following the notation of the previous section and references [4, 18, 5, 19], we claim that the problem defined by (1–3) is equivalent to
| (8) |
| (9) |
for time-varying densities and velocities where
| (10) |
Clearly, H(μ1||μ0) is a constant. Next, noting that
| (11) |
and
| (12) |
we just need to show that
| (13) |
to verify our claim. However, using integration by parts and the constraints (9) we see that
| (14) |
Finally,
| (15) |
since the total masses of μ1 and μ0 are equal.
Letting vmin denote the optimal vector field for (8–9), the Lagrangian coordinate solution is then exactly that given by (7) above. As previously noted, there are very fast algorithms for solving such entropic regularized versions of OMT for suficiently large ϵ [6]. Since we need to consider small ϵ values, we directly solve (8–9) based on the numerical scheme given in [25] where the initial and final densities μ0;μ1 are taken from the given DCE-MRIs.
3.2. Pathlines
In order to represent the characteristics of the flow over all time in one comprehensive figure, we use the Lagrangian framework to construct what are commonly known as pathlines. A pathline X(t;x) with initial position X(0;x) = x is given by (7) and traces the trajectory of an individual particle through-out the time interval. As detailed in [16], additional information such as %-signal from baseline is used to determine regions where flow is more likely to occur. Throughout this region of interest, p seeding points, denoted xl, are selected uniformly. Pathlines are then computed by integrating the augmented velocity (4) with initial positions xl. The speed ||v(t;X(t;xl)|| of each particle is simultaneously computed along each pathline, referred to as the speed pathline and denoted Xv = Xv(t;xl), by (tri)linearly interpolating the derived velocity field.
Next, in order to extract pathlines that are representative of the flow behavior in specific anatomical regions, we subsequently cluster the pathlines by proximity using the QuickBundles algorithm [10]. All computations were implemented in MATLAB and the Lagrangian analysis took approximately 1 minute to run for each of the 8 datasets (5 DEXM+ISO, 3 ISO) of resolution 128 × 128 × 128.
4. Discussion
While streamlines and pathlines are interchangeable for steady flows (i.e. time independent), the same cannot be said for unsteady flows (i.e. time dependent). A novel aspect of the dynamical OMT formulation [1] is its explicit description of the density's time-varying evolution, suggesting the need for Lagrangian analysis of this behavior. The Lagrangian approach provides an elegant framework to observe various attributes such as speed and density along the pathlines. Having a single representation for the history of a particle and its attributes across time lends itself to a natural means for differentiating between flows under different conditions. We show the capability of this framework as it pertains to the GS and waste drainage.
GS transport can be observed with DCE-MRI in combination with administration of para-magnetic contrast agents (e.g. DOTAREM) into the CSF [17]. However, supplementary analysis is required to extract and distinguish characteristics of the GS transport patterns and flow. Current techniques for quantifying GS transport include assessment of brain parenchymal solute uptake or clearance [14], kinetic analysis [17], and k-means cluster analysis [13, 15]. Kinetic analysis strategies provide a static `snapshoť of GS transport over 2–3 hours and provide global influx and efflux parameters however, regional information at the voxel level cannot be accurately derived due to heterogeneous transport kinetics across brain regions.
Here, we present a straightforward demonstration of the equivalence between the regularized dynamical OMT problem and the Fisher-Rao regularized variant in deriving the Lagrange coordinates associated with the flow. The Fisher-Rao perspective offers an accessible alternative methodology and deeper insight into the regularized OMT formulation as previously applied [16]. We apply the Lagrangian pipeline to measure GS function based on DCE-MRIs acquired in rats while under two different states of unconsciousness - `lighť sleep/hypnosis with DEXM+ISO versus `deep' sleep/anesthesia with ISO based on data from [2]. Specifically, we tested the Lagrangian OMT framework's ability to differentiate GS transport and solute drainage via pathways in the brain proper as well as along cranial effux routes between these two different states of arousal.
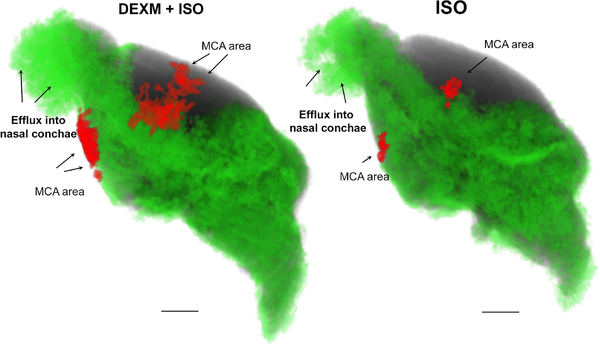
Clustered pathlines derived from the Lagrangian framework are shown in Figure 2. It is evident, based on the pathlines patterns observed in the rats under the two anesthetics, that GS transport function is different. With DEXM+ISO anesthesia, GS transport is accelerated (compared to ISO) as noted by the high density of pathlines extending into the parenchyma globally and along the middle cerebral artery (MCA). In contrast, the pathlines in rats anesthetized with ISO do not align with the MCA to the same extent and parenchymal uptake is also reduced in other areas including the midbrain and hippocampus. However, paradoxically, GS transport appears vigorous in the area of the olfactory bulb including solute efflux into the nasal conchae.
Fig. 2.
Comprehensive pathline visualization of 130 minutes of glymphatic transport of DOTA (Gd-Dota) in a rat anesthetized with DEXM+ISO (left) and ISO (right). The pathlines in green are derived from the entire brain and nasal conchae. Both rats exhibit pathlines in the nasal conchae, signifying that Gd-DOTA exited along the olfactory nerves via the cribriform plate to lymphatic vessels in the submucosa of the nasal cavities. Pathlines that follow the middle cerebral artery (MCA) are outlined in red. More pathlines are clearly evident in the rat anesthetized with DEXM+ISO than ISO anesthesia, confirming that GS transport is more efficient during DEXM+ISO anesthesia. Scale bar = 3mm.
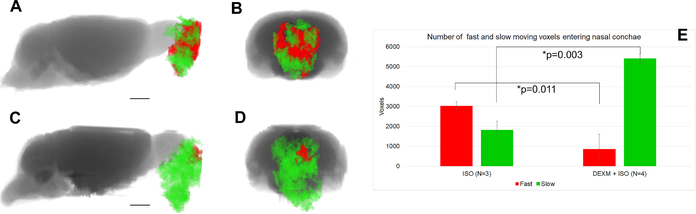
Figure 3 captures pathline speed (integrated over 130 minutes) through the GS in rats anesthetized with either DEXM+ISO or ISO. The speed pathlines associated with the whole brain are shown as a 3D volume rendered color-coded map. Higher and lower magnitudes of speed are represented by red and blue colors, respectively. More speed pathlines are apparent in the frontal part of the brain in the DEXM+ISO anesthetized rats compared to ISO. Paradoxically, in the ISO anesthetized state, pathline speed appears to be higher in the nasal conchae (arrows). In Figure 4, we have captured the faster (red) and slower (green) moving speed lines, given in arbitrary units (a.u.) in an ISO anesthetized rat (Figures 4A, B) compared to a DEXM+ISO anesthetized rat (Figures 4C, D). It is obvious that the proportion of faster moving particles in the clustered pathlines is higher in ISO than DEXM+ISO anesthetized rats, as confirmed via quantitative analysis (Figure 4E). These differences suggest that solute efflux to lymphatic vessels in the nasal conchae may be acting as an efflux `valve' in the setting of impaired fluid flow in ISO anesthesia.
Fig. 3.
Speed pathlines over 130 minutes of GS transport distinguishing flow behavior under two anesthetics, DEXM+ISO (top) and ISO (bottom).
Fig. 4.
Speed pathlines into the nasal conchae extracted from the GS speed `connec-tome' and divided up into fast (red) speed lines with speed magnitude > 0055 a.u. and slower (green) speed lines with speed magnitudes in the range of 0:001 – 0:050 a.u. (A, B) ISO anesthetized rats are characterized by rapid efflux of solute into the nasal cavity and (C, D) the vast majority of speed lines in the DEXM+ISO anesthetized rats are slower. (E) Proportion of voxels with fast moving solute. Data are mean ∓ SEM.
5. Conclusion and Future Work
We presented a Lagrangian representation of Fisher-Rao regularized OMT to represent time-varying dynamics and various attributes in a single visualization. The resultant framework was then used to capture known GS transport flow patterns and provide additional insights in distinguishing GS function under different anesthetic conditions in addition to clearance of solutes via the olfactory nerves and into the nasal conchae. In the future, we will use the computed particle attributes as features in machine learning algorithms to differentiate and classify various transport related flow patterns for diagnostic purposes.
Acknowledgements
This study was supported by AFOSR grants (FA9550-17-1-0435, FA9550-20-1-0029), a grant from National Institutes of Health (R01-AG048769, RF1-AG053991), MSK Cancer Center Support Grant/Core Grant (P30 CA008748), and a grant from Breast Cancer Research Foundation (BCRF-17-193).
References
- 1.Benamou JD and Brenier Y. A computational fluid mechanics solution to the monge-kantorovich mass transfer problem. Numerische Mathematik, 84:375–393, 2000. [Google Scholar]
- 2.Benveniste H, Lee H, Ding F, Sun Q, Al-Bizri E, Makaryus R, Probst S, Nedergaard M, Stein EA, and Lu H. Anesthesia with dexmedetomidine and low-dose isoflurane increases solute transport via the glymphatic pathway in rat brain when compared with high-dose isoflurane. Anesthesiology: The Journal of the American Society of Anesthesiologists, 127(6):976–988, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Buttazzo G, Jimenez C, and Oudet E. An optimization problem for mass transportation with congested dynamics. SIAM Journal on Control and Optimization, 48(3):1961–1976, 2009. [Google Scholar]
- 4.Chen Y, Georgiou TT, and Pavon M. On the relation between optimal transport and Schrödinger bridges: A stochastic control viewpoint. Journal of Optimization Theory and Applications, 169(2):671–691, 2016. [Google Scholar]
- 5.Chizat L, Peyre G, Schmitzer B, F-X. Vialard, Unbalanced optimal transport: dynamic and Kantorovich formulations. Journal of Functional Analysis, 274:30903123, 2018. [Google Scholar]
- 6.Cuturi M. Sinkhorn distances: Lightspeed computation of optimal transport. In Advances in neural information processing systems, pages 2292–2300, 2013. [Google Scholar]
- 7.Elkin R, Nadeem S, Haber E, Steklova K, Lee H, Benveniste HB, and Tannenbaum A. GlymphVis: Visualizing glymphatic transport pathways using regularized optimal transport. MICCAI 2018, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Elkin R, Nadeem S, LoCastro E, Paudyal R, Hatzoglou V, Lee NY, Shukla-Dave A, Deasy JO, and Tannenbaum A. Optimal mass transport kinetic modeling for head and neck DCE-MRI: Initial analysis. Magnetic resonance in medicine, 82(6):2314–2325, 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Feydy J, Charlier B, Vialard F, François X, G. Peyré Optimal transport for diffeomorphic registration MICCAI, 2017. [Google Scholar]
- 10.Garyfallidis E, Brett M, Correia MM, Williams GB, and Nimmo-Smith I. Quickbundles, a method for tractography simplification. Frontiers in Neuroscience, 6:175, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Gerber S, Niethammer M, Styner M, and Aylward S Exploratory population analysis with unbalanced optimal transport. In International Conference on Medical Image Computing and Computer-Assisted Intervention, pages 464–472,2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Haker S, Tannenbaum A, Zhu L, Angenent S. Optimal Mass Transport for Registration and Warping. International Journal of Computer Vision, 60(3):225–240, 2004. [Google Scholar]
- 13.Iliff JJ, Lee H, Yu M, Feng T, Logan J, Nedergaard M, and Benveniste H. Brain-wide pathway for waste clearance captured by contrast-enhanced mri. The Journal of clinical investigation, 123(3):1299–1309, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Iliff JJ, Wang M, Liao Y, Plogg BA, Peng W, Gundersen GA, Benveniste H, Vates GE, Deane R, Goldman SA, et al. A paravascular pathway facilitates csf flow through the brain parenchyma and the clearance of interstitial solutes, including amyloid β. Science translational medicine, 4(147):147ra111–147ra111, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Jiang Q, Zhang L, Ding G, Davoodi-Bojd E, Li Q, Li L, Sadry N, Nedergaard M, Chopp M, and Zhang Z. Impairment of the glymphatic system after diabetes. Journal of Cerebral Blood Flow & Metabolism, 37(4):1326–1337, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Koundal S, Elkin R, Nadeem S, Xue Y, Constantinou S, Sanggaard S, Liu X, Monte B, Xu F, Van Nostrand W, Nedergaard M, Lee H, Wardlaw J, Benveniste H, and Tannenbaum A. Optimal Mass Transport with Lagrangian Workflow Reveals Advective and Diffusion Driven Solute Transport in the Glymphatic System. Scientific Reports, 10(1):1–18,2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Lee H, Xie L, Yu M, Kang H, Feng T, Deane R, Logan J, Nedergaard M, and Benveniste H. The effect of body posture on brain glymphatic transport. Journal of Neuroscience, 35(31):11034–11044, 2015. s [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Li W, Yin P, and Osher S. Computations of optimal transport distance with Fisher information regularization. Journal of Optimization Theory and Applications, 75(3):1581–1595, 2018. [Google Scholar]
- 19.Liero M, Mielke A, and Savare G. Optimal transport in competition with reaction: the Hellinger-Kantorovich distance and geodesic curves. SIAM Journal Math. Analysis, 48(4):2869–2911, 2016. [Google Scholar]
- 20.Otto F. The geometry of dissipative evolution equations: the porous medium equation. Communications in Partial Differential Equations, 2001. [Google Scholar]
- 21.Papadakis N, Peyré G, and Oudet E. Optimal transport with proximal splitting. SIAM Journal on Imaging Sciences, 7(1):212–238, 2014. [Google Scholar]
- 22.Peng W, Achariyar TM, Li B, Liao Y, Mestre H, Hitomi E, Regan S, Kasper T, Peng S, Ding F, et al. Suppression of glymphatic fluid transport in a mouse model of alzheimer's disease. Neurobiology of disease, 93:215–225, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Ratner V, Gao Y, Lee H, Elkin R, Nedergaard M, Benveniste H, and Tannenbaum A. Cerebrospinal and interstitial fluid transport via the glymphatic pathway modeled by optimal mass transport. NeuroImage 152:530–537, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Shokri-Kojori E, Wang GJ, Wiers CE, Demiral SB, Guo M, Kim SW, Lindgren E, Ramirez V, Zehra A, Freeman C, et al. β-amyloid accumulation in the human brain after one night of sleep deprivation. Proceedings of the National Academy of Sciences, 115(17):4483–4488, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Steklova K and Haber E. Joint hydrogeophysical inversion: state estimation for seawater intrusion models in 3d. Computational Geosciences, 21(1):75–94, 2017. [Google Scholar]
- 26.Villani C. Topics in Optimal Transportation. Number 58 American Mathematical Soc., 2003. [Google Scholar]
- 27.Villani C. Optimal Transport: Old and New, volume 338 Springer Science & Business Media, 2008. [Google Scholar]
- 28.Xie L, Kang H, Xu Q, Chen MJ, Liao Y, Thiyagarajan M, O'Donnell J, Christensen DJ, Nicholson C, Iliff JJ, et al. Sleep drives metabolite clearance from the adult brain. science, 342(6156):373–377, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]