Differentiating axonal loss and demyelination in chronic MS lesions: A novel approach using single streamline diffusivity analysis

Samuel Klistorner; Michael H Barnett; Jakob Wasserthal; Con Yiannikas; Joshua Barton; John Parratt; Yuyi You; Stuart L Graham; Alexander Klistorner

doi:10.1371/journal.pone.0244766

. 2021 Jan 6;16(1):e0244766. doi: 10.1371/journal.pone.0244766

Differentiating axonal loss and demyelination in chronic MS lesions: A novel approach using single streamline diffusivity analysis

Samuel Klistorner ¹, Michael H Barnett ^2,³, Jakob Wasserthal ⁴, Con Yiannikas ⁵, Joshua Barton ², John Parratt ⁵, Yuyi You ^1,⁶, Stuart L Graham ⁶, Alexander Klistorner ^1,^6,^*

Editor: Fernando de Castro⁷

PMCID: PMC7787472 PMID: 33406139

Abstract

We describe a new single-streamline based approach to analyse diffusivity within chronic MS lesions. We used the proposed method to examine diffusivity profiles in 30 patients with relapsing multiple sclerosis and observed a significant increase of both RD and AD within the lesion core (0.38+/-0.09 μm²/ms and 0.30+/-0.12 μm²/ms respectively, p<0.0001 for both) that gradually and symmetrically diminished away from the lesion. T1-hypointensity derived axonal loss correlated highly with ΔAD (r = 0.82, p<0.0001), but moderately with ΔRD (r = 0.60, p<0.0001). Furthermore, the trendline of the ΔAD vs axonal loss intersected both axes at zero indicating close agreement between two measures in assessing the degree of axonal loss. Conversely, the trendline of the ΔRD function demonstrated a high positive value at the zero level of axonal loss, suggesting that even lesions with preserved axonal content exhibit a significant increase of RD. There was also a significant negative correlation between the level of preferential RD increase (ΔRD-ΔAD) in the lesion core and the degree of axonal damage (r = -0.62, p<0.001), indicating that ΔRD dominates in cases with milder axonal loss. Modelling diffusivity changes in the core of chronic MS lesions based on the direct proportionality of ΔAD with axonal loss and the proposed dual nature of ΔRD yielded results that were strikingly similar to the experimental data. Evaluation of lesions in a sizable cohort of MS patients using the proposed method supports the use of ΔAD as a marker of axonal loss; and the notion that demyelination and axonal loss independently contribute to the increase of RD in chronic MS lesions. The work highlights the importance of selecting appropriate patient cohorts for clinical trials of pro-remyelinating and neuroprotective therapeutics.

Introduction

Diffusion tensor imaging (DTI) is sensitive to the microstructural organisation of white matter tracts and has been suggested as a new promising tool that provides greater pathological specificity than conventional MRI, helping, therefore, to elucidate disease pathogenesis and monitor therapeutic efficacy. While axial diffusivity (AD) has been linked to axonal pathology, radial diffusivity (RD) has been suggested as a surrogate biomarker associated with the level of white matter myelination [1–3]. This is of particular importance since recent interest in the development of remyelinating therapies [4–6] has increased demand for reliable and standardized techniques capable of assessing remyelination in vivo.

The main advantages of the DTI technique are its simple single-shell protocol, relatively fast data acquisition and straightforward analysis. While more complex models [7–9] may help to better explain the observed experimental or clinical data [10], they require very high quality acquisition and measurements that may not be feasible in a clinical setting. Therefore, DTI remains the method of choice in clinical studies/trials, particularly when multiple sites are involved.

However, apart from intrinsic white matter properties, the alterations in DTI metrics can also be affected by the degree of fibre coherence. The majority of white matter voxels are characterized by extensive crossing, kissing, bending or fanning of fibers [11]. Therefore, apart from the limited area of white matter occupied by coherent fiber tracts, voxel-based analysis utilising DTI models does not adequately estimate orientationally-sensitive diffusivity measures, such as axial and radial diffusivity (AD and RD) [12, 13].

In order to isolate disease-related DTI changes from alterations related to fiber coherence the comparison of pathological tissue must be made with an area of the brain which displays similar fiber structure. Thus, attempts have been made to use symmetrical white matter areas of the opposite hemisphere to control for fiber non-homogeneity. This process, however, is challenging and require manual input. In addition, MS lesions frequently affect symmetrical (periventricular) parts of the brain.

An alternative approach utilising an analysis of fiber tract diffusivity profiles has recently been suggested [14–16]. Using this technique, profiles of various diffusivity measures (such as fractional anisotropy, mean, radial and axial diffusivity) of an individual coherent white matter fiber tract in a subject or group of subjects are constructed between the two regions of interest (ROIs) and compared to a similar fiber tract in a different group (for example, non-MS controls).

This approach has recently been extended by segmenting a single coherent tract into areas bound by seemingly similar pathological processes (such as MS lesions), which allows the separation of lesional fibers (i.e. fibers crossing the lesion) from non-lesional fibers of the same tract. Due to similar coherency of corresponding lesional and non-lesional fibers this technique facilitates within-subject comparison of diffusivity measures between normal and pathological tissue by providing “internal” reference [17].

However, MS lesions are rarely confined within a single (coherent) fiber tract. Rather, multiple crossing tracts frequently traverse individual lesions (or part thereof) in different directions; the presence of crossing fibers, therefore, similarly limits existing implementations of the profile-based technique. In addition, due to the irregular shape of MS lesions, the intra-lesional length of individual fibers can vary considerably, degrading the accuracy of diffusivity measurements inside and outside of lesions.

In an effort to expand this approach beyond the coherent fiber tracts we developed a new fully automated single-fiber based technique to analyse diffusivity alteration within MS lesions and its close surrounding. The method is based on computation of the difference (asymmetry) between the diffusivity profile of an individual streamline passing through the lesion of interest (“lesional fiber”) and the average diffusivity profiles of several adjacent and similarly oriented non-lesional streamlines of equal length and orientation, obtained from the same fiber tract (“non-lesional fibers”). Similar to previously described technique used in coherent fiber tracts, this method provides “internal” reference for diffusivity measure within MS lesions. In addition, this technique eliminates the ambiguity of the fiber-based analysis caused by irregular lesion shape. Furthermore, based on based on an observation that distribution of mean diffusivity in the brain white matter is relatively uniform (see S1 Fig), we developed an algorithm to minimise the residual effect of fiber non-coherency between corresponding voxels of lesional and non-lesional streamlines.

Using this technique, we estimated asymmetry profiles of axial and radial diffusivity (ΔAD and ΔRD) in the core and rim of individual lesions and in surrounding normal appearing white matter; and computed the personalised (subject-based) diffusivity profile in 30 patients with relapsing remitting MS (RRMS). In addition, we estimated the relative contribution of demyelination and axonal damage to the elevation of RD in chronic MS lesions.

Method

Standard protocol approvals, registrations, and patient consents

The study was approved by University of Sydney and Macquarie University Human Research Ethics Committees and followed the tenets of the Declaration of Helsinki. Written informed consent was obtained from all participants.

Subjects

Thirty consecutive patients with RRMS, defined according to the revised McDonald 2010 criteria, were enrolled [18].

MRI protocol

The following sequences were acquired using a 3T GE Discovery MR750 scanner (GE Medical Systems, Milwaukee, WI):

Pre- and post-contrast (gadolinium) Sagittal 3D T1
FLAIR CUBE
diffusion weighted MRI

Specific parameters are presented in S1 File.

MRI image pre-processing

The baseline T1-weighted imaging was realigned to AC-PC orientation in MrVista package (Stanford University). Diffusion MRI was corrected for motion, eddy-current distortion in FSL and EPI susceptibility distortion using blip-up/ blip-down sequences.

Subsequently, tensor reconstruction was performed in MrDiffusion (MrVista, Stanford University). Tensor images were then linearly co-registered to corresponding T1 AC-PC images.

Lesion identification and analysis

Individual lesions were identified on the co-registered T2 FLAIR images and semi-automatically segmented using JIM 7 software (Xinapse Systems, Essex, UK) by a trained analyst.

The core of the lesion was identified by shrinking the lesion mask in all directions by 1 voxel using the “eroding” function of JIM software. The rest of the lesion was assigned as the “rim” area. Only lesions measuring larger than 100 mm³ (i.e.100 voxels on T2 FLAIR image) were selected for analysis. Gadolinum (Gd)-enhancing lesions (detected in 2 patients) were excluded from the analysis.

The lesion mask was also applied to pre-contrast 3D-T1-weighted images to quantify lesion hypointensity. Since some lesional voxels (particularly in lesions with a high degree of tissue destruction) did not contain any traversing fibers, only voxels which intersected with lesional fibers (see below) were selected for T1-hypointensity calculation.

In order to reduce inter-subject variability, lesional T1-hypointensity was normalised by the intensity of NAWM, which was measured using two additional 5 mm ROIs placed in the NAWM of both hemispheres. In addition, the minimum intensity of CSF on T1-weighted images was measured by placing 2 mm ROIs inside anterior horns of lateral ventricles.

Identification of major fiber tracts

TractSeg algorithm was used to identify 72 anatomically well-defined tracts as described by Wasserthal and co-workers [19, 20]. TractSeg uses a fully convolutional neural network to directly segment these tracts, taking the fiber orientation distribution function (fODF) peaks as input. To generate tract-specific tractograms, TractSeg also generates so called tract orientation maps (TOMs) that can be used together with the tract segmentations to generate high-quality tractograms of 72 major tracts. For each tract, 2000 streamlines were generated.

TractSeg only generates binary tract masks, which, however, make it easy to generate streamlines since seeding for probabilistic tractography is produces within the mask and certain number of streamlines are generated for each tract. The TractSeg methodology through MS lesion is described in [20].

Single fiber-based lesional profile

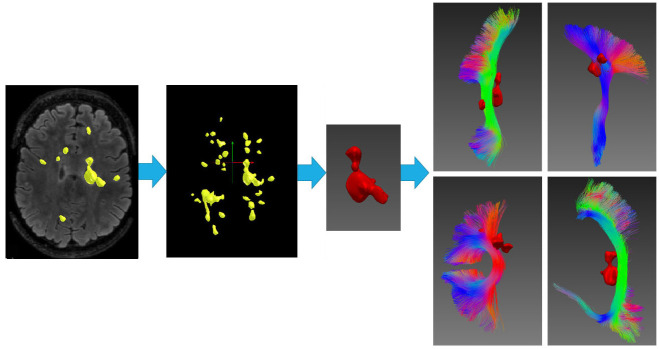
Each individual lesion was intersected with all 72 tracts and tracts overlapping with lesions were selected for analysis (Fig 1).

Each lesional streamline was analysed separately.

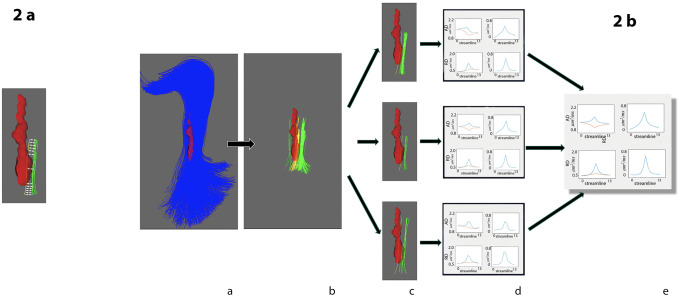
Firstly, the lesional streamline (“lesional fiber”) was limited to five mm on each side of the lesion and limiting ROIs perpendicular to lesion streamline were constructed. Then, a minimum of 5 adjacent streamlines not overlapping with any lesion (“non-lesional fibers”), but of similar length and orientation to the lesional fiber, were selected from the same fiber tract to be used as a “local reference” (Fig 2a) (lesional fibers which did not have corresponding non-lesional fibers were discarded). By using the same perpendicular ROIs to limit non-lesional fibers, the length of lesional/non-lesional fiber pairs included in the analysis was congruent. Similarly, proximity and parallel orientation of fiber pairs was achieved by ensuring that 90% of the voxels of each matched non-lesional fiber was constrained within a 5 mm diameter ‘tube’ with the lesional fiber at its central longitudinal axis. In order to avoid an effect of Wallerian degeneration, all fibers intersecting with more than 1 lesion were excluded from analysis. In addition, all fibers intersecting with the either the CSF (which was extended by 1 voxel) or grey matter mask were excluded.

Secondly, AD and RD diffusivity profiles were separately calculated for each lesional/non-lesional pair (see examples in Fig 2b, part c). Due to the typically irregular shape of MS lesions, the length of the “intra-lesional” component of lesional streamlines can vary substantially, resulting in length heterogeneity of constructed fiber pairs. Therefore, to standardise measurement of the diffusivity profile, all voxels of individual lesional fibers situated within the lesion core were averaged together to generate a single diffusivity value for the lesion core. Similarly, averaging was performed for corresponding voxels of matching non-lesional fibers to produce a single non-lesional reference diffusivity value. As a result, each lesional/non-lesional pair had length of 13 points (1 point representing lesion core plus 1 and 5 points on each side corresponding to lesion rim and extra-lesional part respectively) (Fig 2a). Examples of AD and RD diffusivity profiles for an individual lesional/non-lesional pair are presented in Fig 2b, part d, left column.

Thirdly, ΔAD and ΔRD profiles for each single fiber were computed by calculating the difference (asymmetry) between diffusivity measures along the selected individual lesional fiber and corresponding points of averaged diffusivity of the matching non-lesional fibres on a voxel-by-voxel basis (Fig 2b, part e, right column).

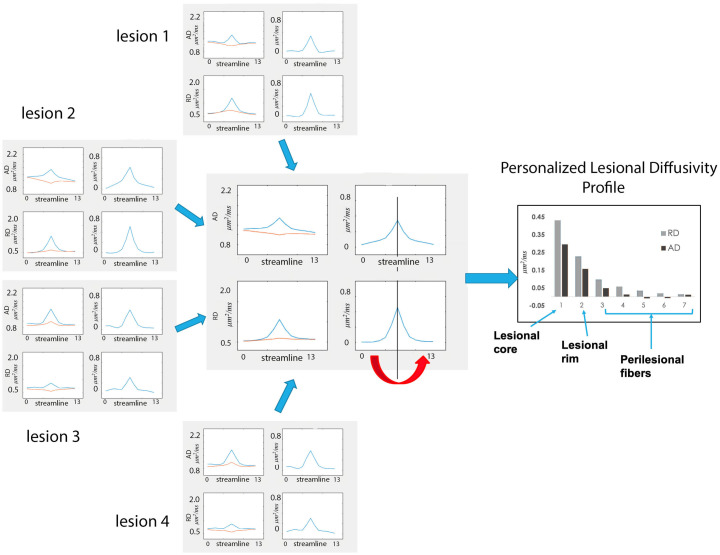
All single fiber profiles intersecting individual lesions were combined into AD and RD lesional, non-lesional and asymmetry (ΔAD and ΔRD) profiles for each lesion. Patient-wise diffusivity profiles were then computed as a weighted average of the diffusivity profiles of all individual lesions (Fig 3). The weighting (which was performed to adjust for difference in lesion size) was proportionally related to the total number of fibers in all the lesions. Since ΔAD and ΔRD profiles were highly symmetrical with respect to the lesion core, for the purpose of further analysis corresponding points of ΔAD and ΔRD profiles on both sides of the lesion were averaged together, producing a single value of ΔAD and ΔRD for points equally removed from the lesion core (so called Personalized Lesional Diffusivity (PLD) Profile) (Fig 3).

Fig 3 — Diffusivity profiles of individual lesions are averaged to produce a patient-specific profile. Corresponding points of the left and right parts of the asymmetry profile are averaged together (red arrow), producing a single value of ΔAD and ΔRD for points equally removed from the lesion core (Personalized Lesional Diffusivity (PLD) Profile-see graph on the right). Vertical axis—μm²/ms.

Control for crossing fibers

MD represents direction-insensitive measure of the total fiber membrane density [21]) and, as a result, remained relatively uniform across the entire white matter in normal brain tissue (see S1a Fig). Conversely, AD and RD, in accordance with their nature, are strongly dependant on fiber coherence. As mentioned above, this represents a serious impediment to the measurement of pathology-related AD and RD changes. However, several features of the proposed technique might minimise the effect of crossing fibers.

Thus, corresponding voxels, which are used to analyse asymmetry of lesional and matching non-lesional fibers of each individual fiber tract have, by definition, at least one common set of fiber bundles, reducing, therefore, potential difference in fiber orientation between the two. In addition, owing to the close proximity of lesional and matching non-lesional fibers the effect of crossing fibers on diffusivity of the corresponding pair of voxels is likely to be similar and, hence, minimized when the difference between the two (i.e. asymmetry) is calculated. Furthermore, adding together large numbers of individual lesional/non-lesional pairs of fibers belonging to different fiber tracts and, therefore, crossing corresponding voxels in different directions is also likely to average out the effect of crossing fibers, at least to some extent.

It is, however, still possible that crossing fibers from other tracts may partially or fully intersect one group of voxels, but not another (for instance, intersect only voxels which belong to lesional fibers, but not voxels associated with non-lesional fibers). This will result in significant change of AD and RD values in voxels containing additional crossing fibers, “contaminating”, therefore, the measurement of tissue damage.

The direction of AD and RD change in such a case, however, is expected to be opposite. Thus, presence of additional crossing fibers will result in reduction of the fiber coherence within the voxel, which will cause decrease of diffusivity along the main axis (i.e. reduction of AD) and increase of diffusivity in other directions (i.e. rise of RD) compare to corresponding voxel not affected by the crossing fibers. To validate this assumption, we examined association between AD and RD in individual voxels of normal white matter, which indeed demonstrated strong negative relationship (r = 0.85, p<0.001, see S1a and S1b Fig).

Furthermore, while MD is typically elevated in MS lesions due to increased amount of interstitial fluid and reduction of axonal membranes and myelin caused by axonal loss, comparable level of MD between corresponding voxels which belong to lesional and non-lesional streamlines outside the lesion would indicates similar degree of tissue preservation, suggesting that all relative changes of AD and RD in those voxels are due to variations in fiber coherency (i.e. crossing fibers).

This reasoning was used to detect and minimise the potential effect of crossing fibers on AD and RD in corresponding voxels of lesional and non-lesional streamlines by using custom-designed algorithm implemented in Phyton (see S1 File).

Statistical analysis

Statistical analysis was performed using SPSS 22.0 (SPSS, Chicago, IL, USA). Pearson correlation coefficient was used to measure statistical dependence between two numerical variables. P < 0.05 was considered statistically significant. Comparisons between groups were made using Student t-test. Shapiro-Wilk test was used to test for normal distribution.

Results

Diffusivity profile of chronic MS lesions

Single fiber-based diffusivity analysis was performed in 30 RRMS patients (age: 43.6+/-9.9 years, EDSS: 1.4+/-1.2, disease duration: 5.3+/-3.5 years, m/f ratio: 11/19). In total 314 lesions (average lesion volume 760 mm²) were analysed.

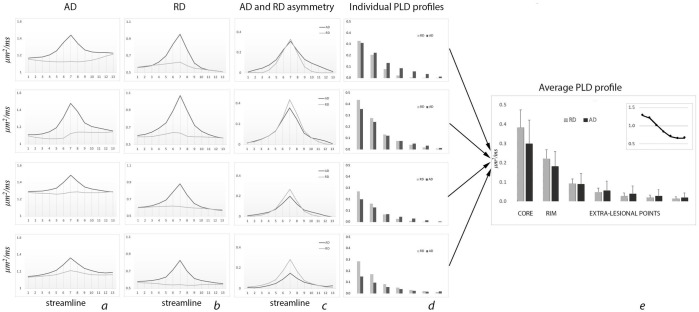
Examples of patient-based diffusivity profiles and the averaged (across all patients) diffusivity profile are shown in Fig 4. Average number of fibers per lesional voxel was 82+/-71. Columns a and b display typical examples of lesional and non-lesional AD (column a) and RD (column b) profiles, while columns c shows AD and RD asymmetry profiles (ΔAD and ΔRD). Individual PLD profiles presented in column d.

Patient-based diffusivity profiles of lesional fibers demonstrated a significant increase of both RD and AD in the lesion core compared to non-lesional fibers (average ΔRD and ΔAD 0.38+/-0.09 μm²/ms and 0.30+/-0.12 μm²/ms, p<0.0001 for both) that gradually and symmetrically (on both sides) diminished away from the lesion, in some patients almost reaching the level of diffusivity in non-lesional fibers (Table 1). However, both RD and AD of lesional fibers outside the lesion remained significantly higher than diffusivity measures in the corresponding points of non-lesional fibers (paired t-test, p<0.0001 for all points). There was a high correlation (r = 0.67, p<0.001) between relative asymmetry of AD within and outside of lesions (lesion core vs average of 2 most remote extra-lesional points). However, the correlation of lesional ΔRD with RD asymmetry outside of lesion was not significant (p = 0.07).

Table 1. Averaged diffusivity values (mean (SD)) in lesion core, rim and extra-lesional part of lesional fibers and in corresponding voxels of matching non-lesional fibers.

(units-μm²/ms).

	Core	Rim	Extra-lesional part (distance from lesion)
			1 mm	2 mm	3 mm	4 mm	5 mm
AD lesion fibers	1.52 (0.14)	1.40 (0.09)	1.3 (0.08)	1.27 (0.08)	1.26 (0.08)	1.25 (0.07)	1.24 (0.07)
AD non-lesion fibers	1.22 (0.08)	1.22 (0.07)	1.21 (0.07)	1.22 (0.07)	1.22 (0.06)	1.22 (0.06)	1.22 (0.06)
RD lesion fibers	1.0 (0.12)	0.82 (0.06)	0.68 (0.05)	0.63 (0.05)	0.61 (0.05)	0.59 (0.05)	0.59 (0.05)
RD non-lesion fibers	0.61 (0.05)	0.60 (0.05)	0.59 (0.05)	0.59 (0.05)	0.58 (0.05)	0.58 (0.05)	0.57 (0.04)

Open in a new tab

The relative magnitude of ΔAD and ΔRD varied considerably along the PLD profile. While inside the lesion (both in the core and in the rim) averaged ΔRD was larger than ΔAD, this relationship was reversed in the extra-lesional part of PLD profile, where ΔAD dominated. This is demonstrated in Fig 4e (see Insert), which shows ΔAD/ΔRD ratio at different points along the PLD profile.

Relationship between T1 hypointensity and diffusivity profile in the core of chronic MS lesions

Previous studies have demonstrated that the degree of hypointensity on T1-weighted MR images (T1 hypointensity) reflects the severity of axonal loss in MS lesions [22, 23]. Therefore, we used T1 hypointensity to estimate the degree of axonal damage in chronic lesions. Overall, 33% of all lesional voxels contained at least one streamline and were used to analyse T1-hypointensity. Normalized (by NAWM) reduction of intensity of the T1 signal was significantly more prominent (by 26.8%) in voxels used for the analysis compared to the rest of the lesion (reduction of T1 intensity 592 and 751 units respectively, p<0.001, paired t-test), indicating that voxels with better axonal preservation have higher chance of containing tractography streamlines and, therefore, are preferentially selected for single fiber-based analysis. This was also supported by the significant negative correlation between the proportion of analysed voxels in each lesion and lesion T1 hypointensity (r = -0.53, p = 0.002).

Based on assumptions that NAWM represents intact (i.e. no axonal loss) brain tissue (average T1 intensity value of NAWM was 3326 units), while CSF characterises brain tissue totally devoid of axons (average value of minimum T1 intensity of CSF = 863 units) and the intensity of T1 signal is inversely proportional to the degree of axonal loss, we estimated the percentage of patient-wise tissue loss. According to this calculation, the loss of axonal tissue in the lesion core ranged between 22% and 66% (average 36.1+/-11.6%).

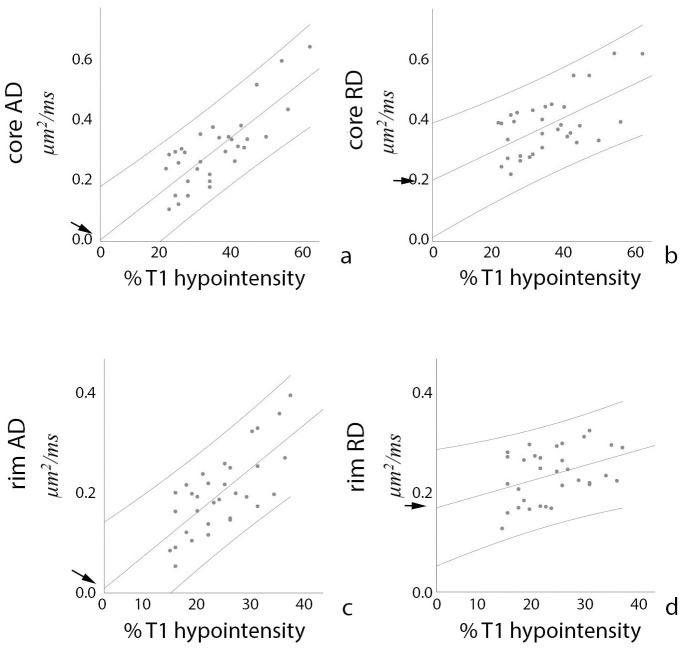
In order to examine a link between axonal loss and an increase of parallel and perpendicular diffusivity measures derived using the single-fiber approach, patient-based correlation between degree of axonal loss (as defined above) and ΔAD and ΔRD in the core and the rim of chronic lesions was performed. The analysis of lesion core revealed a high degree of correlation between increase in AD and axonal loss in corresponding voxels (r = 0.82, p<0.0001). While increase in RD in the lesion core was also significantly associated with loss of T1 signal, the correlation was moderate (r = 0.60, p<0.0001). The slope of ΔAD correlation with axonal loss was considerably steeper than the slope of ΔRD (0.0034 vs 0.0021).

Furthermore, the trendline of the ΔAD vs T1-hypointensity derived axonal loss function intersected both axes at zero, indicating close agreement between two measures in assessing the axonal loss (Fig 5a, arrow). Conversely, the trendline of the ΔRD function demonstrated high positive value (0.20 μm²/ms) (Fig 5b, arrow) at zero axonal loss. The presence of a significant residual value of ΔRD suggests that even lesions with preserved axonal content (i.e. T1-isointense lesions) exhibit a significant increase in RD.

Fig 5 — Arrows point at intersection between diffusivity increase and “zero” axonal loss (p values are noted a text). Vertical axis—μm²/ms, Horizontal axis—% of T1 hypointensity-derived axonal loss.

In agreement with previous reports, diffusivity was lower in the lesion rim than the lesion core (Table 1). The degree of axonal loss (as determine by T1-hypointensity) in the voxels corresponding to the rim area was also reduced compared with the lesion core (21.2+/-6.0%, range 13–34%). Correlation between T1 hypointensity-derived axonal loss and ΔAD, however, remained high (r = 0.73, p<0.0001). The trendline of the correlation function demonstrated a similar slope to the lesion core (0.0035) and intersected with the zero value of the horizontal (T1-hypointensity derived axonal loss) axis very close to zero value of ΔAD (-0.004 μm²/ms) (Fig 5c), again indicating close agreement between T1 signal and ΔAD as a measure of axonal damage. Conversely, ΔRD was only weakly correlated with T1 signal (r = 0.39, p = 0.026) showing flatter slope of the correlation curve compare to the correlation in the lesion core (0.0013). However, intersection of the ΔRD trendline with zero value of the axonal loss axis still demonstrated significant residual value of ΔRD (0.15 μm²/ms) (Fig 5d).

By further examining changes of AD and RD in the lesional core of individual patients, we observed considerable variation in both the magnitude of diffusivity increase (reflected in a relatively large standard deviation, Fig 4d), and the relationship between ΔAD and ΔRD. Thus, in some patients ΔRD in the lesional core was significantly larger than ΔAD (see, for example Fig 4, bottom row), while in other patients a similar increase of parallel and perpendicular diffusivities was noted (Fig 4, top row). Therefore, we examined how the difference between the change of radial and axial diffusivities (ΔRD-ΔAD) is related to the degree of axonal loss. The result, shown in Fig 6, demonstrates significant negative correlation between the level of preferential RD increase and the degree of (T1 hypointensity-derived) axonal destruction (r = -0.62, p<0.001), indicating that ΔRD dominates in cases with milder axonal loss (where majority of axons still survive, but remain demyelinated), but ΔAD and ΔRD approach parity as axonal damage advances.

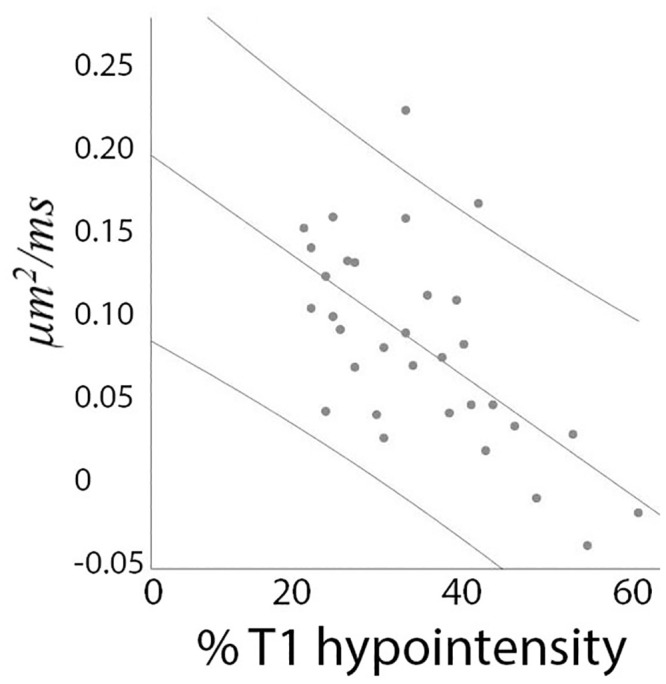
Fig 6 — Vertical axis—μm²/ms, Horizontal axis—% of T1 hypointensity-derived axonal loss.

Modelling effects of axonal loss and demyelination on diffusivity in the lesion core

Our previous work suggests that, in highly coherent fiber tracts, ΔAD within chronic MS lesions reflects axonal loss, while ΔRD is related to both axonal loss and demyelination in survived axons [24]. Since the current approach substantially minimizes the effect of crossing fibers, we hypothesized that diffusion modelling within coherent fiber tracts can be extended to lesions involving any region of the brain. In the current study, we found a high degree of correlation between T1 hypointensity-defined axonal loss and ΔAD and congruence of the “zero” value of both measures (based on trendline projection), supporting the close relationship between increase in AD and the degree of axonal destruction. Conversely, we found only a moderate correlation of T1 hypointensity with ΔRD and a lesser slope of the correlation curve, indicating that factors not directly associated with axonal degeneration in part drive the increase in perpendicular diffusivity observed in chronic MS lesions (see comparison of ΔAD and ΔRD trendlines in Fig 7a). Furthermore, the high residual value of ΔRD at “zero” axonal loss level and a preferential increase of RD in patients with mild axonal loss (which gradually diminishes as axonal loss advances), suggest that neurodegeneration and non-axonal loss related factors have opposing effects on ΔRD. A declining impact of non-axonal loss related factors on ΔRD as axonal damage become more prominent implicates loss of the myelin sheath in survived (i.e. existing) axons, since the impact of demyelination (which is known to increase RD) is expected to be largest in lesions with relatively well-preserved axons. However, since the number of (demyelinated) axons decline as axonal loss progresses the contribution of demyelination to ΔRD is also expected to decrease proportionally with attrition of demyelinated axons. It is therefore plausible to assume that the increase of RD in chronic MS lesions is driven by the combination of two independent factors: loss of axons and loss of myelin sheath in survived axons. Following this logic, we modelled the relationship between axonal loss, demyelination and changes in AD and RD to evaluate how well our assumption explains the real data.

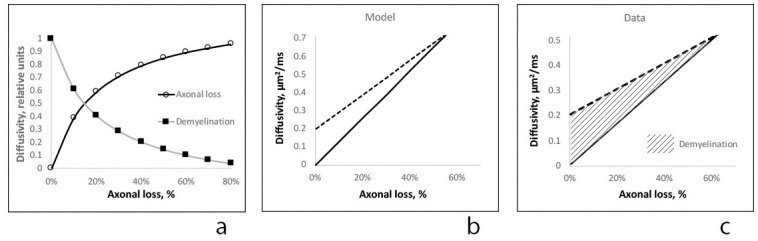
Fig 7 — a. Relative contribution of demyelination-related ΔRD^dem (black squares) and axonal loss-related ΔRD^ax (circles) to radial diffusivity increase in core of MS lesions. Vertical axis -relative units, Horizontal axis—T1 hypointensity-derived axonal loss. b. Modeling of ΔRD (dash line) and ΔAD (solid line) vs axonal loss. Vertical axis—μm²/ms, Horizontal axis—% of T1 hypointensity-derived axonal loss. c. Trendlines of ΔRD (dash line) and ΔAD (solid line) vs axonal loss (lesion core). Stripe area represents potential contribution of demyelination to ΔRD. Vertical axis—μm²/ms, Horizontal axis—% of T1 hypointensity-derived axonal loss.

Based on replacement of lost axonal tissue by extra-cellular water, we previously estimated the increase in axial diffusivity (ΔAD) in chronic MS lesions [24]. Namely,

Δ AD = {(1 - f) x {AD}^{normal tissue}) + (f x {AD}^{ax loss})} - {AD}^{normal tissue}

Where:

"f" volume fraction (%) of axonal loss

“1 –f” volume fraction of normal tissue

AD^{normal tissue} average AD in non-lesional fibers (1.22 μm²/ms)

AD^{ax loss} AD in lesion with complete axonal loss (2.5 μm²/ms)

Increase in radial diffusivity was modelled as a sum of demyelination-related ΔRD^dem and axonal loss-related ΔRD^ax changes:

Δ RD = Δ {RD}^{d e m} + Δ {RD}^{ax}

Assuming that in hypothetical lesions with fully preserved axons, the increase of RD is entirely driven by demyelination, the intersection of the ΔRD trendline with the zero value of the (horizontal) axonal loss axis (Fig 5b) was used to identify the value of demyelination-related increase of RD (ΔRD^dem), which was equal to 0.2 μm²/ms. (This was similar to previously reported demyelination-related increase of RD in highly coherent tracts, such as optic radiation (0.23 μm²/ms)) [24]. Therefore, demyelination-related increase of RD was calculated as follows:

Δ {RD}^{dem} = (0.20 x (“ 1 - f ”))

Axonal loss-related ΔRD^ax was calculated as a replacement of lost axonal tissue by extra-cellular water:

Δ {RD}^{ax} = {(1 - f) x {RD}^{normal tissue}) + (f x {RD}^{ax loss})} - {RD}^{normal tissue}

Where:

RD^{normal tissue} average AD in non-lesional fibers (0.59 μm²/ms)

RD^{ax loss} RD in lesion with complete axonal loss (1.7 μm²/ms)

We previously reported that in chronic MS lesions situated within highly coherent fiber tracts the maximum AD and RD values do not exceed 2.5 μm²/ms and 1.7 μm²/ms respectively [24], indicating some degree of diffusion restriction and residual anisotropy even in severely damaged white matter, which was attributed to lesional gliosis and axonal tortuosity [8–10, 25]. Therefore, those values were used in the current modelling, presented in Fig 7.

The relative contribution of two opposing processes, increasing ΔRD^ax and decreasing ΔRD^dem, to ΔRD is plotted in Fig 7a, highlighting the leading contribution of demyelination to ΔRD in lesions with minimal axonal loss, which rapidly diminishes as axonal loss progresses. Fig 7b demonstrates the predicted slopes of ΔRD and ΔAD vs axonal loss. While the increase in RD is larger at low levels of axonal loss, ΔRD and ΔAD become equal as axonal degeneration advances. Note that the similarity of the relationship of ΔRD and ΔAD slopes between the model and experimental data (ΔRD and ΔAD trendlines of lesion core data are presented in Fig 7c).

Discussion

While DTI was suggested as a potential in-vivo biomarker of axonal loss and demyelination in MS more than a decade ago, its practical application, including use in clinical trials, is limited by inherent dependency on fiber coherency and complexity of the underlying brain structure.

In the current work, we describe a novel approach to analyse diffusivity in chronic MS lesions, based on a computation of a difference (asymmetry) between diffusion properties of a single lesional streamline and corresponding points in neighbouring non-lesional streamlines of similar length and orientation selected from the same fiber tract.

The proposed approach was designed to minimise the impact of crossing fibers on the inter-voxel variability of orientation-selective diffusivity measures and to eliminate the confounding effect of irregular MS lesion morphology, thereby improving the detection of pathology-specific DTI changes in MS lesions.

We observed a parallel change in lesional and matching non-lesional AD and RD profiles external to the lesion, as seen in individual examples (Fig 4); and symmetrical (on either side of the core) alteration in RD and AD (Fig 4, column c), supporting our proposition that single fiber-based technique can potentially extend the application of diffusivity profile analysis beyond coherent fiber tracts, which, we believe, is facilitated by the close proximity of corresponding lesional and non-lesional voxels, contribution of parallel fibers from at least one common fiber tract, averaging of a large number of differently oriented pairs of lesional/non-lesional fibers for each set of corresponding voxels and normalisation algorithm.

While the analysis of lesional vs non-lesional fibers is performed on a voxel-based basis and, therefore includes contribution from all fibers crossing the voxel in different directions (i.e. diffusivity of the entire voxel which belongs to the particular point of the lesional fiber is compared to the diffusivity of the entire voxel which belongs to the corresponding point of the non-lesional fiber), the advantage of the proposed technique is that it provides a true “local” reference for the measurement of pathology-related diffusivity changes inside MS lesions and in its immediate surrounding.

The single fiber-based approach also obviates the confounding effect of irregular lesion morphology on traditional tract-based analyses. Due to the typically irregular shape of MS lesions, the length of the “intra-lesional” component of individual streamlines can vary substantially. Therefore, averaging of all lesional fibers (even within single fiber tract) and comparison with averaged non-lesional fibers, as is typically implemented in tract-based analysis, will inevitably result in significant distortion of the lesional diffusivity profile. Since each lesional streamline is individually matched to non-lesional fibers of similar length in the approach proposed here, the “intra-lesional” part each lesional fiber is identified independently and asymmetry analysis of each individual lesional/non-lesional pair performed prior to averaging. As a result, only corresponding parts of the asymmetry profile are averaged, eliminating the effect of irregular lesion shape on calculation of the diffusivity profile.

We used the single fiber-based approach to examine orientation-sensitive diffusivity measures (AD and RD) in chronic white matter lesions of MS patients. Our analysis revealed a substantial increase of both AD and RD in the lesion core, which diminished towards the lesion rim. While small, altered diffusivity remained significant even in the extra-lesional component of lesional fibers. Considerable variability of the increase of lesional diffusivity was observed between patients, although the magnitude of ΔRD was typically larger. Parallel and perpendicular diffusivities also demonstrated different behaviour in relation to axonal loss. In particular, there was high degree of correlation between increased axial diffusivity and T1 hypointensity-based measures of tissue destruction in the lesion core, suggesting a strong association between ΔAD and axonal loss. Furthermore, the trendline of the correlation function intersected both axes at zero, reinforcing the notion that both measures reflect similar underlying patho-mechanisms. Since T1-hypointensity is linked to the degree of axonal destruction, it is reasonable to assume that ΔAD derived using the single fiber-based approach is also strongly associated with axonal loss in MS lesions.

The correlation of ΔRD with T1-hypointensity in the lesion core, however, was only moderate. Moreover, contrary to AD, the trendline of the ΔRD correlation function had a flatter slope and intersected zero on the horizontal (T1-hypointensity) axis at a relatively high positive value of ΔRD. In addition, a relatively larger increase of RD (ΔRD-ΔAD) in the lesional core was found to be inversely associated with the degree of T1 hypointensity, indicating that magnitude of ΔRD is higher in cases with milder axonal loss, but ΔAD and ΔRD approach parity as axonal damage advances.

Taken together, our results strongly support a direct link between the increase of axial diffusivity derived using the single fiber-based technique and the degree of axonal destruction. More importantly, the findings support the notion that the increase of RD in chronic MS lesions is driven by the combination of two factors: axonal destruction and loss of myelin sheath in survived axons. While the effect of demyelination dominates in cases of mild axonal destruction (where majority of axons still survive, but remain demyelinated), neurodegeneration is a primary cause of RD increase in more destructive lesions.

Modelling diffusivity changes in the core of chronic MS lesions based on the direct proportionality of ΔAD with axonal loss and the proposed dual nature of ΔRD yielded results that were strikingly similar to the experimental data. The difference in magnitude of the diffusivity increase between the model and the experimental data, noticeable at the high end of the axonal loss scale, is likely to be related to the restricting effect of glial fibers on the diffusion of water molecules [8, 25], which are particularly dense in severely damaged tissue.

The proposed single fiber-based technique preserves the advantage of the fiber-based approach by estimating the diffusivity only in parts of the lesion characterised by relative sparing of axons. Contrary to ROI-based analysis (where all lesional voxels are combined together), single-fiber analysis is “biased” towards the voxels with better axonal preservation since they have relatively high anisotropy and, therefore, a greater chance of containing tractography streamlines. Conversely, voxels with a high degree of axonal loss, which typically exhibit more isotropic diffusivity, are less likely to be included in the current analysis. This is supported by the significantly greater T1 signal in voxels selected for single fiber-based analysis relative to the remaining lesional voxels and a significant negative correlation between the proportion of analysed voxels and whole lesion T1 hypointensity. As a result, the single fiber-based method minimizes the “diluting” effect of existing tissue loss on longitudinal monitoring of orientation-sensitive diffusivity measures such as RD. This is particularly applicable to measurement of remyelination in MS lesions, where remyelination-induced change of diffusivity can only occur in survived (existing) axons.

We recently reported an elevation of AD in the distal part of the lesional fibers in highly coherent fiber tracts (optic radiation) [17]. The distribution of the observed increase in AD suggested that it may be related to the extent of the axonal transection within the lesion and the subsequent loss of a distal part of connected axons caused by Wallerian Degeneration (WD). In concordance with these findings, we observed a highly significant correlation of ΔAD (but not ΔRD) between the lesion core and the extra-lesional part of the lesional fibers and a preferential increase of AD in lesional fibers outside the lesion in the current study, supporting ΔAD as a potential biomarker of WD, even outside of highly coherent fiber tracts.

Finally, while changes of diffusivity in the lesion rim demonstrated similar trends, the relative increase of both AD and RD was smaller compared to the lesion core. We also observed a higher degree of variability of ΔRD unrelated to axonal loss (as indicated by a weaker correlation with T1 signal) and lower value of ΔRD at the intersection of the trendline with “zero” on the T1 hypointensity axis. Differences from the lesion core are likely be related to less severe axonal loss and a variable degree of remyelination between patients, both characteristic features of the lesion edge. This may render the lesion rim a better target for monitoring subtle changes of treatment-induced myelination in clinical trials [26].

The single fiber-based method has some limitations. While the proposed approach is beneficial for longitudinal analysis of changes affecting survived axons (such as remyelination), voxel-based analysis may be more suited for measurement of tissue loss in cross-sectional comparison studies, especially when axonal loss is severe. Another limitation is related to potential partial voluming effect caused by resampling of DTI images.

Monitoring remyelination using this technique is also limited to lesions with relatively well-preserved axons, since in cases where neurodegeneration exceeds 30–40% ΔRD is mainly driven by axonal loss and the contribution of demyelination becomes negligible. This limitation is probably applicable to all diffusion-based studies of remyelination.

In addition, due to strict constraints imposed by the technique on the location of non-lesional fibers (such as specific distance from the analysed single streamline), more centrally located voxels in large lesions are less likely to be included in analysis.

Supporting information

S1 Fig. MD, AD and RD values in normal white matter.

a. Diffusivity values in 200 individual voxels randomly selected in brain’s white matter of normal subject. While AR and RD vary significantly (Coefficient of variability: AD-21%, RD-26%) and in opposite directions, MD remains relatively constant (Coefficient of variability: MD-7%). RD values multiplied by 2. b. Correlation between AD and RD in individual voxels randomly selected in brain white matter of normal subject (r = 0.85, p<0.001).

(DOCX)

Click here for additional data file.^{(127.7KB, docx)}

S2 Fig. MD-based normalisation.

a. Left column demonstrates original AD and RD profiles of lesional (blue) and non-lesional (red) fibers. Blue arrow indicates linear fitting of lesional fiber. Red arrow indicates linear fitting of non-lesional fibers. Horizontal axis: points along the fibers. Point 7 indicates lesion. Vertical axis: μm²/ms. b. Slopes of ΔAD, ΔRD and ΔMD in individual lesional/non-lesional pair.

(DOCX)

Click here for additional data file.^{(122.7KB, docx)}

S1 File

(DOCX)

Click here for additional data file.^{(14.8KB, docx)}

Data Availability

There are ethical restrictions on sharing the data set, which contains potentially sensitive patient information. However, other researchers may send data access requests to the Macquarie University Human Ethics Committee (human.ethics@mq.edu.au).

Funding Statement

AK-National Multiple Sclerosis Society (NMSS), Novartis Save Neuron Grant, Sydney Eye Hospital foundation grant and Sydney University Medical foundation. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

References

1.Song S.-K. et al. , “Demyelination increases radial diffusivity in corpus callosum of mouse brain.,” Neuroimage, vol. 26, no. 1, pp. 132–40, May 2005. 10.1016/j.neuroimage.2005.01.028 [DOI] [PubMed] [Google Scholar]
2.Klawiter E. C. et al. , “Radial diffusivity predicts demyelination in ex vivo multiple sclerosis spinal cords,” Neuroimage, vol. 55, pp. 1454–1460, 2011. 10.1016/j.neuroimage.2011.01.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
3.Janve V. a et al. , “The radial diffusivity and magnetization transfer pool size ratio are sensitive markers for demyelination in a rat model of type III multiple sclerosis (MS) lesions.,” Neuroimage, vol. 74, pp. 298–305, July 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
4.Cadavid D. et al. , “Safety and efficacy of opicinumab in acute optic neuritis (RENEW): a randomised, placebo-controlled, phase 2 trial,” Lancet Neurol., vol. 16, no. 3, pp. 189–199, 2017. 10.1016/S1474-4422(16)30377-5 [DOI] [PubMed] [Google Scholar]
5.Green A. J. et al. , “Clemastine fumarate as a remyelinating therapy for multiple sclerosis (ReBUILD): a randomised, controlled, double-blind, crossover trial,” Lancet, vol. 390, pp. 2481–89, 2017. 10.1016/S0140-6736(17)32346-2 [DOI] [PubMed] [Google Scholar]
6.Klistorner A., Chai Y., Leocani L., Albrecht P., Aktas O., and Butzkueven H., “Assessment of Opicinumab in Acute Optic Neuritis Using Multifocal Visual Evoked Potential,” CNS Drugs, vol. online fir, 2018. 10.1007/s40263-018-0575-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
7.Wang Y. et al. , “Differentiation and quantification of inflammation, demyelination and axon injury or loss in multiple sclerosis.,” Brain, vol. 138, no. Pt 5, pp. 1223–38, May 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
8.Zhang H., Schneider T., Wheeler-kingshott C. A., and Alexander D. C., “NODDI: practical in vivo neurite orientation dispersion and density imaging of the human brain,” Neuroimage, vol. 61, pp. 1000–1016, 2012. 10.1016/j.neuroimage.2012.03.072 [DOI] [PubMed] [Google Scholar]
9.Assaf Y., Freidlin R. Z., Rohde G. K., and Basser P. J., “New Modeling and Experimental Framework to Characterize Hindered and Restricted Water Diffusion in,” vol. 978, pp. 965–978, 2004. [DOI] [PubMed] [Google Scholar]
10.Panagiotaki E., Schneider T., Siow B., Hall M. G., Lythgoe M. F., and Alexander D. C., “Compartment models of the diffusion MR signal in brain white matter: A taxonomy and comparison,” Neuroimage, vol. 59, no. 3, pp. 2241–2254, 2012. 10.1016/j.neuroimage.2011.09.081 [DOI] [PubMed] [Google Scholar]
11.Jeurissen B., Leemans A., Tournier J., Jones D. K., and Sijbers J., “Investigating the Prevalence of Complex Fiber Configurations in White Matter Tissue with Diffusion Magnetic Resonance Imaging,” Hum. Brain Map, vol. 2766, pp. 2747–2766, 2013. 10.1002/hbm.22099 [DOI] [PMC free article] [PubMed] [Google Scholar]
12.Taipel S. et al. , “Fractional Anisotropy Changes in Alzheimer’s Disease Depend on the Underlying Fiber Tract Architecture: A Multiparametric DTI Study using Joint Independent Component Analysis,” J. Alzheimer’s Dis., vol. 41, pp. 69–83, 2014. [DOI] [PubMed] [Google Scholar]
13.Wheeler-Kingshott C. A. M. and Cercignani M., “About ‘Axial’ and ‘Radial’ Diffusivities.,” Mag Res Med, vol. 61, pp. 1255–1260, 2009. [DOI] [PubMed] [Google Scholar]
14.Jones D. K. et al. , “A diffusion tensor magnetic resonance imaging study of frontal cortex connections in very-late-onset schizophrenia-like psychosis,” Am. J. Geriatr. Psychiatry, vol. 13, no. 12, pp. 1092–1099, 2005. 10.1176/appi.ajgp.13.12.1092 [DOI] [PubMed] [Google Scholar]
15.Yeatman J. D., Dougherty R. F., Myall N. J., Wandell B. a, and Feldman H. M., “Tract profiles of white matter properties: automating fiber-tract quantification.,” PLoS One, vol. 7, no. 11, p. e49790, January 2012. 10.1371/journal.pone.0049790 [DOI] [PMC free article] [PubMed] [Google Scholar]
16.Reich D. S., Smith S. A., Gordon-Lipkin E. M., Ozturk A., Caffo B. S., and Balcer L. J., C. P.A., “Damage to optic radiation in multiple sclerosis is associated with retinal injury and visual disability.,” Arch neurol, vol. 66, pp. 998–1006, 2009. 10.1001/archneurol.2009.107 [DOI] [PMC free article] [PubMed] [Google Scholar]
17.Klistorner A. et al. , “Decoding diffusivity in multiple sclerosis: Analysis of optic radiation lesional and non-lesional white matter,” PLoS One, vol. 10, no. 3, 2015. 10.1371/journal.pone.0122114 [DOI] [PMC free article] [PubMed] [Google Scholar]
18.Polman C. H. et al. , “Diagnostic criteria for multiple sclerosis: 2010 revisions to the McDonald criteria.,” Ann. Neurol., vol. 69, no. 2, pp. 292–302, February 2011. 10.1002/ana.22366 [DOI] [PMC free article] [PubMed] [Google Scholar]
19.Wasserthal J., Neher P., and Maier-hein K. H., “TractSeg—Fast and accurate white matter tract segmentation,” Neuroimage, vol. 183, no. June, pp. 239–253, 2018. [DOI] [PubMed] [Google Scholar]
20.Wasserthal J., Neher P., and Maier-hein K. H., “Combined tract segmentation and orientation mapping for bundle-specific tractography,” no. Mic, 2019. 10.1016/j.media.2019.101559 [DOI] [PubMed] [Google Scholar]
21.Sepehrband F. et al. , “Brain tissue compartment density estimated using diffusion-weighted MRI yields tissue parameters consistent with histology,” Hum. Brain Mapp., vol. 36, no. 9, pp. 3687–3702, 2015. 10.1002/hbm.22872 [DOI] [PMC free article] [PubMed] [Google Scholar]
22.van Walderveen A. A. A. et al. , “Histopathologic correlate of hypointense lesions on Tl-weighted spin-echo lesions in multiple sclerosis MRI,” Neurology, vol. 50, pp. 1282–1288, 1998. [DOI] [PubMed] [Google Scholar]
23.Brex P. a et al. , “Lesion heterogeneity in multiple sclerosis: a study of the relations between appearances on T1 weighted images, T1 relaxation times, and metabolite concentrations.,” J. Neurol. Neurosurg. Psychiatry, vol. 68, no. 5, pp. 627–32, 2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
24.Klistorner A. et al. , “Diffusivity in the core of chronic multiple sclerosis lesions,” PLoS One, vol. 13, no. 4, 2018. 10.1371/journal.pone.0194142 [DOI] [PMC free article] [PubMed] [Google Scholar]
25.Budde M. D., Janes L., Gold E., Turtzo L. C., and Frank J. A., “The contribution of gliosis to diffusion tensor anisotropy and tractography following traumatic brain injury: validation in the rat using Fourier analysis of stained tissue sections.,” Brain, vol. 134, no. Pt 8, pp. 2248–60, August 2011. 10.1093/brain/awr161 [DOI] [PMC free article] [PubMed] [Google Scholar]
26.Klistorner A. et al. , “Diffusivity in multiple sclerosis lesions: At the cutting edge?,” NeuroImage Clin., vol. 12, pp. 219–226, 2016. 10.1016/j.nicl.2016.07.003 [DOI] [PMC free article] [PubMed] [Google Scholar]

PLoS One. doi: 10.1371/journal.pone.0244766.r001

Decision Letter 0

Fernando de Castro

5 Nov 2020

PONE-D-20-27494

Differentiating axonal loss and demyelination in chronic MS lesions: a novel approach using single streamline diffusivity analysis.

PLOS ONE

Dear Dr. Klistorner,

Thank you for submitting your manuscript to PLOS ONE. After careful consideration, we feel that it has merit but does not fully meet PLOS ONE’s publication criteria as it currently stands. Therefore, we invite you to submit a revised version of the manuscript that addresses the points raised during the review process. Both expert reviewers found important concerns to be addressed, mainly regarding description of Methods and protocols, as well as in the quality and organization of figures.

Please submit your revised manuscript by Dec 20 2020 11:59PM. If you will need more time than this to complete your revisions, please reply to this message or contact the journal office at plosone@plos.org. When you're ready to submit your revision, log on to https://www.editorialmanager.com/pone/ and select the 'Submissions Needing Revision' folder to locate your manuscript file.

Please include the following items when submitting your revised manuscript:

A rebuttal letter that responds to each point raised by the academic editor and reviewer(s). You should upload this letter as a separate file labeled 'Response to Reviewers'.
A marked-up copy of your manuscript that highlights changes made to the original version. You should upload this as a separate file labeled 'Revised Manuscript with Track Changes'.
An unmarked version of your revised paper without tracked changes. You should upload this as a separate file labeled 'Manuscript'.

If you would like to make changes to your financial disclosure, please include your updated statement in your cover letter. Guidelines for resubmitting your figure files are available below the reviewer comments at the end of this letter.

If applicable, we recommend that you deposit your laboratory protocols in protocols.io to enhance the reproducibility of your results. Protocols.io assigns your protocol its own identifier (DOI) so that it can be cited independently in the future. For instructions see: http://journals.plos.org/plosone/s/submission-guidelines#loc-laboratory-protocols

We look forward to receiving your revised manuscript.

Kind regards,

Fernando de Castro

Academic Editor

PLOS ONE

Journal Requirements:

When submitting your revision, we need you to address these additional requirements.

1. Please ensure that your manuscript meets PLOS ONE's style requirements, including those for file naming. The PLOS ONE style templates can be found at

https://journals.plos.org/plosone/s/file?id=wjVg/PLOSOne_formatting_sample_main_body.pdf and

https://journals.plos.org/plosone/s/file?id=ba62/PLOSOne_formatting_sample_title_authors_affiliations.pdf

2. We note that you have indicated that data from this study are available upon request. PLOS only allows data to be available upon request if there are legal or ethical restrictions on sharing data publicly. For information on unacceptable data access restrictions, please see http://journals.plos.org/plosone/s/data-availability#loc-unacceptable-data-access-restrictions.

* In your revised cover letter, please address the following prompts:

a) If there are ethical or legal restrictions on sharing a de-identified data set, please explain them in detail (e.g., data contain potentially identifying or sensitive patient information) and who has imposed them (e.g., an ethics committee). Please also provide contact information for a data access committee, ethics committee, or other institutional body to which data requests may be sent.

b) If there are no restrictions, please upload the minimal anonymized data set necessary to replicate your study findings as either Supporting Information files or to a stable, public repository and provide us with the relevant URLs, DOIs, or accession numbers. Please see http://www.bmj.com/content/340/bmj.c181.long for guidelines on how to de-identify and prepare clinical data for publication. For a list of acceptable repositories, please see http://journals.plos.org/plosone/s/data-availability#loc-recommended-repositories.

We will update your Data Availability statement on your behalf to reflect the information you provide.

3. Thank you for stating the following in the Financial Disclosure :

'AK-National Multiple Sclerosis Society (NMSS), Novartis Save Neuron Grant, Sydney Eye Hospital foundation grant and Sydney University Medical foundation.

We note that one or more of the authors have an affiliation to the commercial funders of this research study : 'Novartis'.

1. Please provide an amended Funding Statement declaring this commercial affiliation, as well as a statement regarding the Role of Funders in your study. If the funding organization did not play a role in the study design, data collection and analysis, decision to publish, or preparation of the manuscript and only provided financial support in the form of authors' salaries and/or research materials, please review your statements relating to the author contributions, and ensure you have specifically and accurately indicated the role(s) that these authors had in your study. You can update author roles in the Author Contributions section of the online submission form.

Please also include the following statement within your amended Funding Statement.

“The funder provided support in the form of salaries for authors [insert relevant initials], but did not have any additional role in the study design, data collection and analysis, decision to publish, or preparation of the manuscript. The specific roles of these authors are articulated in the ‘author contributions’ section.”

If your commercial affiliation did play a role in your study, please state and explain this role within your updated Funding Statement.

2. Please also provide an updated Competing Interests Statement declaring this commercial affiliation along with any other relevant declarations relating to employment, consultancy, patents, products in development, or marketed products, etc.

Within your Competing Interests Statement, please confirm that this commercial affiliation does not alter your adherence to all PLOS ONE policies on sharing data and materials by including the following statement: "This does not alter our adherence to PLOS ONE policies on sharing data and materials.” (as detailed online in our guide for authors http://journals.plos.org/plosone/s/competing-interests). If this adherence statement is not accurate and there are restrictions on sharing of data and/or materials, please state these. Please note that we cannot proceed with consideration of your article until this information has been declared.

* Please include both an updated Funding Statement and Competing Interests Statement in your cover letter. We will change the online submission form on your behalf.

Please know it is PLOS ONE policy for corresponding authors to declare, on behalf of all authors, all potential competing interests for the purposes of transparency. PLOS defines a competing interest as anything that interferes with, or could reasonably be perceived as interfering with, the full and objective presentation, peer review, editorial decision-making, or publication of research or non-research articles submitted to one of the journals. Competing interests can be financial or non-financial, professional, or personal. Competing interests can arise in relationship to an organization or another person. Please follow this link to our website for more details on competing interests: http://journals.plos.org/plosone/s/competing-interests

[Note: HTML markup is below. Please do not edit.]

Reviewers' comments:

Reviewer's Responses to Questions

Comments to the Author

1. Is the manuscript technically sound, and do the data support the conclusions?

The manuscript must describe a technically sound piece of scientific research with data that supports the conclusions. Experiments must have been conducted rigorously, with appropriate controls, replication, and sample sizes. The conclusions must be drawn appropriately based on the data presented.

Reviewer #1: Yes

Reviewer #2: Partly

**********

2. Has the statistical analysis been performed appropriately and rigorously?

Reviewer #1: Yes

Reviewer #2: I Don't Know

**********

3. Have the authors made all data underlying the findings in their manuscript fully available?

The PLOS Data policy requires authors to make all data underlying the findings described in their manuscript fully available without restriction, with rare exception (please refer to the Data Availability Statement in the manuscript PDF file). The data should be provided as part of the manuscript or its supporting information, or deposited to a public repository. For example, in addition to summary statistics, the data points behind means, medians and variance measures should be available. If there are restrictions on publicly sharing data—e.g. participant privacy or use of data from a third party—those must be specified.

Reviewer #1: Yes

Reviewer #2: Yes

**********

4. Is the manuscript presented in an intelligible fashion and written in standard English?

PLOS ONE does not copyedit accepted manuscripts, so the language in submitted articles must be clear, correct, and unambiguous. Any typographical or grammatical errors should be corrected at revision, so please note any specific errors here.

Reviewer #1: Yes

Reviewer #2: Yes

**********

5. Review Comments to the Author

Please use the space provided to explain your answers to the questions above. You may also include additional comments for the author, including concerns about dual publication, research ethics, or publication ethics. (Please upload your review as an attachment if it exceeds 20,000 characters)

Reviewer #1: In this study authors developed a new method for evaluating axonal damage inside MS lesion on brain MRI in 30 MS cases by using a single streamline diffusivity analysis. They found a significant increase of both axial and radial diffusivity and AD showed a very high correlation with T1 hypointensity. This article is a new addition to the contribution of the team to the application of DWI to the understanding on MS lesions and quantification of axonal loss. The team is very well experienced and recognized and this new method is highly valuable for improving our understanding about how MS damage the brain and for testing new neuroprotective and remyelinating therapies.

Comments

1. Methods: indicates the number of voxels that 100 mm3 represent in this specific scanner. Explain how TractSeg algorithm solved the interruption of the tract within the lesions to provide the reconstruction of the tract. Authors explained that they use reference fibbers, but the algorithm should make use of a statistical or probability analysis to approach the fibbers within the lesion. Or it was always required a 100% match with the reference fibber? Indicate how many fibbers on average were present in the DWI voxels.

2. Can you provide the DTI protocol? I was unable to find it in the supplementary material

3. Figures are of low resolution (specially the insets with the graphs). Please, provide high quality figures

4. Figure 5 and 6: provide legends to the X and Y axis as indicated in the figure legend

Reviewer #2: The authors attempt to develop a single-streamlined approach to analyze diffusivity within chronic MS lesions. While the method seems potentially promising there are too many issues with the presentation and interpretation of the data to know if this method is sound.

Major issues:

• In the second last paragraph of the introduction, the authors state, “based on an assumption of uniform mean diffusivity of the brain white matter,” Why is that assumption valid?

• The authors state in the methods section about the MR parameters that “Specific parameters are presented in Supplementary material.” I do not see these parameters in the supplemental material. The administration of Gd can change metrics so I also expected to see the order in which the images were collected and that is not there either.

• Axis labels on the graphs in Figure 2 are necessary. What is the x-axis? What do the blue and the orange lines mean? The titles of the graph should be the y-axis labels. Is difference AD the delta-AD written in the manuscript? The authors should use consistent notation. In Figure 4 they seem to call this AD and RD asymmetry. Consistency is necessary. Labelling also applies to Figure 3-7.

• The bar graph in Figure 3 is also very confusing. Do the bars not represent Delta-RD and Delta-AD? If they do, then the legend needs to be changed. If they do not, a much better explanation of what is in the graph needs to be made. Using blue and orange is also VERY confusing. In the other graphs in Figure 3 and in the graphs in Figure 2, blue is meant to represent the lesion while orange is meant to represent the non-lesion tracks. Yet in the bar graph in Figure 3, blue and orange mean something else. The colors need to be changed for consistency. I am also unclear if I understand things correctly. Do only 2 voxels worth of data go into the lines in 2-7? Are data from a whole lesion core (line 1) really comparable with data from a single voxel ring around the lesion? It seems like the statistics would be poor for the analysis outside the lesion core. The lesion rim likely suffers inhomogeneously from partial voluming effects. Is that considered in the analysis?

• The author’s explanation of their new change in the way data are analyzed normalizing the differences as done in Figure 2 of the supplement is interesting but not convincing. What other factors can result in a change in RD and AD but not MD and have the authors checked to see if those effects are seen in their work and how they would affect their work. For example, some work has been done indicating axon diameter changes in different area of the brain. I would think that could result in a consistent MD but a change in AD and RD. From what the authors have written, they appear to have assumed that the changes they see are from crossing fibers and not from some other means. I need to be convinced they are not from other means or that these other means are irrelevant.

• Figure 4 switches the color scheme for Figure e. a-d had AD dark and RD light and Figure e has RD dark and AD light. Consistency is needed.

• Table 1: what are the uncertainties in the numbers in the table?

Minor issues:

• Very minor English mistakes can be found throughout the manuscript (for example “this represent”. A quick read though to fix these mistake should be done.

• Page 9 of the document, paragraph 4, the authors refer to “normal” cohorts. I believe the disease societies are asking scientists to stop using these terms and rather use terms such as “non-MS” cohorts.

**********

6. PLOS authors have the option to publish the peer review history of their article (what does this mean?). If published, this will include your full peer review and any attached files.

If you choose “no”, your identity will remain anonymous but your review may still be made public.

Do you want your identity to be public for this peer review? For information about this choice, including consent withdrawal, please see our Privacy Policy.

Reviewer #1: Yes: Pablo Villoslada

Reviewer #2: No

[NOTE: If reviewer comments were submitted as an attachment file, they will be attached to this email and accessible via the submission site. Please log into your account, locate the manuscript record, and check for the action link "View Attachments". If this link does not appear, there are no attachment files.]

While revising your submission, please upload your figure files to the Preflight Analysis and Conversion Engine (PACE) digital diagnostic tool, https://pacev2.apexcovantage.com/. PACE helps ensure that figures meet PLOS requirements. To use PACE, you must first register as a user. Registration is free. Then, login and navigate to the UPLOAD tab, where you will find detailed instructions on how to use the tool. If you encounter any issues or have any questions when using PACE, please email PLOS at figures@plos.org. Please note that Supporting Information files do not need this step.

PLoS One. 2021 Jan 6;16(1):e0244766. doi: 10.1371/journal.pone.0244766.r002

Author response to Decision Letter 0

23 Nov 2020

Please find response to reviewers’ comments below.

RReviewer #1: In this study authors developed a new method for evaluating axonal damage inside MS lesion on brain MRI in 30 MS cases by using a single streamline diffusivity analysis. They found a significant increase of both axial and radial diffusivity and AD showed a very high correlation with T1 hypointensity. This article is a new addition to the contribution of the team to the application of DWI to the understanding on MS lesions and quantification of axonal loss. The team is very well experienced and recognized and this new method is highly valuable for improving our understanding about how MS damage the brain and for testing new neuroprotective and remyelinating therapies.

Comments

Q 1. Methods: indicates the number of voxels that 100 mm3 represent in this specific scanner. Explain how TractSeg algorithm solved the interruption of the tract within the lesions to provide the reconstruction of the tract. Authors explained that they use reference fibbers, but the algorithm should make use of a statistical or probability analysis to approach the fibbers within the lesion. Or it was always required a 100% match with the reference fibber? Indicate how many fibbers on average were present in the DWI voxels.

A. 100 mm3 represent 100 voxels on T2 FLAIR image. Now added to Method section.

TractSeg only generates binary tract masks, which, however, makes it easy to generate streamlines since seeding for probabilistic tractography is produces within the mask and certain number (2000) of streamlines are required for each tract. The TractSeg methodology through MS lesion is described in 1. This is now added in Method section

Reference fiber was always required. Lesional fibers which did not have matching reference “non-lesional” fibers were not included in analisys.

Average number of fibers per lesional voxel: 82+/-71 (added to Result section.)

Q. 2. Can you provide the DTI protocol? I was unable to find it in the supplementary material

A. Sorry MRI protocol was not included. Added now in Suppl material.

Q. 3. Figures are of low resolution (specially the insets with the graphs). Please, provide high quality figures

A.All figures are now 300p resolution.

Figures 2b, 3, 5 are improved

Q 4. Figure 5 and 6: provide legends to the X and Y axis as indicated in the figure legend

A.Legend for fig 5 and 6 are now provided

Major issues:

Q • In the second last paragraph of the introduction, the authors state, “based on an assumption of uniform mean diffusivity of the brain white matter,” Why is that assumption valid?

A.This assumption is based on our extensive experience of observing Mean Diffusivity images, which generally look homogeneous (contrary to AD or RD maps). This is further quantified in Supplementary material, (see Suppl Fig 1 which demonstrated very low variability of MD values across white matter-coef of variability 7%). However, we agree with reviewer that presenting this as an assumption is not justified. Therefore, sentence is modified as follow ”…based on an observation that distribution of mean diffusivity in the brain white matter is relatively uniform (see Suppl material, Fig.1)”

Q • The authors state in the methods section about the MR parameters that “Specific parameters are presented in Supplementary material.” I do not see these parameters in the supplemental material. The administration of Gd can change metrics so I also expected to see the order in which the images were collected and that is not there either.

A.Sorry, MRI protocol was not included. Added now in Suppl material. Order of image acquisition is also added.

Q • Axis labels on the graphs in Figure 2 are necessary. What is the x-axis? What do the blue and the orange lines mean? The titles of the graph should be the y-axis labels. Is difference AD the delta-AD written in the manuscript? The authors should use consistent notation. In Figure 4 they seem to call this AD and RD asymmetry. Consistency is necessary. Labelling also applies to Figure 3-7.

A.We thank reviewer for the suggestion. Labels are added to Fig.2 In addition, following description is added to figure legend “Right column shows absolute values (blue-diffusivity profile of lesional fibers, red- diffusivity profile of non-lesional fibers. Left column shows asymmetry between lesional and non-lesional fibers”, i.e. delta AD or RD”.

As suggested, “difference” changed to “asymmetry”, for consistency.

Fig. 3-7 modified as suggested.

Q • The bar graph in Figure 3 is also very confusing. Do the bars not represent Delta-RD and Delta-AD? If they do, then the legend needs to be changed. If they do not, a much better explanation of what is in the graph needs to be made. Using blue and orange is also VERY confusing. In the other graphs in

A.Reviewer is correct, bars in Fig. 3 represent Delta-RD and Delta-AD. This is explained in Method section: “�AD and �RD for points equally removed from the lesion core called Personalized Lesional Diffusivity”.

Q Figure 3 and in the graphs in Figure 2, blue is meant to represent the lesion while orange is meant to represent the non-lesion tracks. Yet in the bar graph in Figure 3, blue and orange mean something else. The colors need to be changed for consistency.

A.We thank reviewer for the suggestion. Colours corrected.

Q I am also unclear if I understand things correctly. Do only 2 voxels worth of data go into the lines in 2-7? Are data from a whole lesion core (line 1) really comparable with data from a single voxel ring around the lesion? It seems like the statistics would be poor for the analysis outside the lesion core. The lesion rim likely suffers inhomogeneously from partial voluming effects. Is that considered in the analysis?

A.Reviewer is correct in assuming that only 2 voxels are considered for each point between 2 and 7. However, those 2 points applied to SINGLE lesional fiber profile and it is compared to core voxels of SINGLE fiber (which can be anything from 1 to many, depending on size of the lesion). To calculate Personalised Lesional Profile presented in Fig 3But many single fiber profiles (often hundreds) are used. Therefore, statistics for the comparison between core and other layer is sound. Partial volume effect was not considered in the analysis, which is now added to study limitations.

Q • The author’s explanation of their new change in the way data are analyzed normalizing the differences as done in Figure 2 of the supplement is interesting but not convincing. What other factors can result in a change in RD and AD but not MD and have the authors checked to see if those effects are seen in their work and how they would affect their work. For example, some work has been done indicating axon diameter changes in different area of the brain. I would think that could result in a consistent MD but a change in AD and RD. From what the authors have written, they appear to have assumed that the changes they see are from crossing fibers and not from some other means. I need to be convinced they are not from other means or that these other means are irrelevant.

A.We thank reviewer for the comment. There are indeed some publications suggesting variation of axonal diameter in different parts of the brain However, since our analysis is based on the difference between lesional and neighbouring non-lesional fibers, we believe that this factor is not likely to play significant role in opposite change of AD and RD, used for normalisation. Apart from variability of axonal diameter, mentioned by the reviewer, we cannot think of any other reason for observed phenomenon of stable MD and opposite change of RD and AD except for crossing fibers.

Q • Figure 4 switches the color scheme for Figure e. a-d had AD dark and RD light and Figure e has RD dark and AD light. Consistency is needed.

A.We thank reviewer for the suggestion. Colours corrected.

Changed as suggested.

Q • Table 1: what are the uncertainties in the numbers in the table?

A.Standard Deviation in presented in brackets

Minor issues:

Q • Very minor English mistakes can be found throughout the manuscript (for example “this represent”. A quick read though to fix these mistake should be done.

A.We thank reviewer for the suggestion. Corrected.

Q • Page 9 of the document, paragraph 4, the authors refer to “normal” cohorts. I believe the disease societies are asking scientists to stop using these terms and rather use terms such as “non-MS” cohorts.

A.We thank reviewer for the suggestion. Corrected as suggested.

Attachment

Submitted filename: reply to reviewers.docx

Click here for additional data file.^{(23KB, docx)}

PLoS One. doi: 10.1371/journal.pone.0244766.r003

Decision Letter 1

Fernando de Castro

8 Dec 2020

PONE-D-20-27494R1

Differentiating axonal loss and demyelination in chronic MS lesions: a novel approach using single streamline diffusivity analysis.

PLOS ONE

Dear Dr. Klistorner,

Thank you for submitting your manuscript to PLOS ONE. After careful consideration, we feel that it has merit but does not fully meet PLOS ONE’s publication criteria as it currently stands. Therefore, we invite you to submit a revised version of the manuscript that addresses the points raised during the review process. The very minor changes suggested by expert reviewer #2 are related to some overstatements in the text, as well as apparent confessions, between the title of figures and the axes in plots. Please, revise them and send them back to us for their final approval.

Please submit your revised manuscript by Jan 22 2021 11:59PM. If you will need more time than this to complete your revisions, please reply to this message or contact the journal office at plosone@plos.org. When you're ready to submit your revision, log on to https://www.editorialmanager.com/pone/ and select the 'Submissions Needing Revision' folder to locate your manuscript file.

Please include the following items when submitting your revised manuscript:

A rebuttal letter that responds to each point raised by the academic editor and reviewer(s). You should upload this letter as a separate file labeled 'Response to Reviewers'.
A marked-up copy of your manuscript that highlights changes made to the original version. You should upload this as a separate file labeled 'Revised Manuscript with Track Changes'.
An unmarked version of your revised paper without tracked changes. You should upload this as a separate file labeled 'Manuscript'.

We look forward to receiving your revised manuscript.

Kind regards,

Fernando de Castro

Academic Editor

PLOS ONE

[Note: HTML markup is below. Please do not edit.]

Reviewers' comments:

Reviewer's Responses to Questions

Comments to the Author

1. If the authors have adequately addressed your comments raised in a previous round of review and you feel that this manuscript is now acceptable for publication, you may indicate that here to bypass the “Comments to the Author” section, enter your conflict of interest statement in the “Confidential to Editor” section, and submit your "Accept" recommendation.

Reviewer #1: All comments have been addressed

Reviewer #2: (No Response)

**********

2. Is the manuscript technically sound, and do the data support the conclusions?

Reviewer #1: Yes

Reviewer #2: Yes

**********

3. Has the statistical analysis been performed appropriately and rigorously?

Reviewer #1: Yes

Reviewer #2: I Don't Know

**********

4. Have the authors made all data underlying the findings in their manuscript fully available?

Reviewer #1: Yes

Reviewer #2: Yes

**********

5. Is the manuscript presented in an intelligible fashion and written in standard English?

Reviewer #1: Yes

Reviewer #2: Yes

**********

6. Review Comments to the Author

Reviewer #1: Authors have addressed properly all my comments and doubts. The figures are now of good quality and the labels have been added to the axis

Reviewer #2: The authors have made substantive changes to the manuscript so that their work has become much clearer. I have two issues, which I believe can easily be corrected, with the manuscript as it stands.

1. The authors have a whole bunch of metrics which have been shown in their studies, or in others, to correlate with various pathologies. Yet, the authors do not do the correlations themselves with the people in this study. The manuscript itself does an excellent job not overstating what was done. The abstract, on the other hand, does overstate what was done which can be dangerous as the abstract is often the only part of a manuscript that is read by researchers who are looking for some trick to describe their own data. Thus, I suggest changing the overreaching statement “Our result demonstrates close association between an increase of AD and the degree of axonal loss and support the notion that the increase of RD in chronic MS lesions is driven by the combination of two factors: axonal destruction and loss of myelin sheaths in survived axons. While the effect of demyelination dominates in cases of mild axonal loss, neurodegeneration is a primary cause of increased RD in more destructive lesions. These finding highlight the importance of selecting appropriate patient cohorts for clinical trials of pro-remyelinating and neuroprotective therapeutics.” to something more accurate. The summary the authors wrote at the end of the manuscript has a nice statement that could be used instead, “Evaluation of lesions in a sizable cohort of MS patients using the proposed method supports the use of �AD as a marker of axonal loss; and the notion that demyelination and axonal loss independently contribute to the increase of RD in chronic MS lesions.”

2. Once again the plots, while much more clear, are not in the standard format for plots. The authors seem to be confusing the title of the plot with what should be on the y-axis. This is true for almost every plot in the figures presented. To make things clear, I will explain what I mean using just the top graph of Figure 2b. There should be no title. The y-axis should be labelled AD (µm2/ms). The x-axis is labelled sufficiently with streamline.

**********

7. PLOS authors have the option to publish the peer review history of their article (what does this mean?). If published, this will include your full peer review and any attached files.

If you choose “no”, your identity will remain anonymous but your review may still be made public.

Do you want your identity to be public for this peer review? For information about this choice, including consent withdrawal, please see our Privacy Policy.

Reviewer #1: Yes: Pablo Villoslada

Reviewer #2: No

PLoS One. 2021 Jan 6;16(1):e0244766. doi: 10.1371/journal.pone.0244766.r004

Author response to Decision Letter 1

9 Dec 2020

Reviewer #1: Authors have addressed properly all my comments and doubts.

Q1. The authors have a whole bunch of metrics which have been shown in their studies, or in others, to correlate with various pathologies. Yet, the authors do not do the correlations themselves with the people in this study. The manuscript itself does an excellent job not overstating what was done. The abstract, on the other hand, does overstate what was done which can be dangerous as the abstract is often the only part of a manuscript that is read by researchers who are looking for some trick to describe their own data. Thus, I suggest changing the overreaching statement “Our result demonstrates close association between an increase of AD and the degree of axonal loss and support the notion that the increase of RD in chronic MS lesions is driven by the combination of two factors: axonal destruction and loss of myelin sheaths in survived axons. While the effect of demyelination dominates in cases of mild axonal loss, neurodegeneration is a primary cause of increased RD in more destructive lesions. These finding highlight the importance of selecting appropriate patient cohorts for clinical trials of pro-remyelinating and neuroprotective therapeutics.” to something more accurate. The summary the authors wrote at the end of the manuscript has a nice statement that could be used instead, “Evaluation of lesions in a sizable cohort of MS patients using the proposed method supports the use of �AD as a marker of axonal loss; and the notion that demyelination and axonal loss independently contribute to the increase of RD in chronic MS lesions.”

A1. Follow reviewer suggestion the last paragraph was removed from Abstract and replaced with following :” Evaluation of lesions in a sizable cohort of MS patients using the proposed method supports the use of �AD as a marker of axonal loss; and the notion that demyelination and axonal loss independently contribute to the increase of RD in chronic MS lesions”.

All plots are modified as suggested.

Attachment

Submitted filename: reply to reviewers 2.docx

Click here for additional data file.^{(17.6KB, docx)}

PLoS One. doi: 10.1371/journal.pone.0244766.r005

Decision Letter 2

Fernando de Castro

16 Dec 2020

Differentiating axonal loss and demyelination in chronic MS lesions: a novel approach using single streamline diffusivity analysis.

PONE-D-20-27494R2

Dear Dr. Klistorner,

We’re pleased to inform you that your manuscript has been judged scientifically suitable for publication and will be formally accepted for publication once it meets all outstanding technical requirements.

Within one week, you’ll receive an e-mail detailing the required amendments. When these have been addressed, you’ll receive a formal acceptance letter and your manuscript will be scheduled for publication.

An invoice for payment will follow shortly after the formal acceptance. To ensure an efficient process, please log into Editorial Manager at http://www.editorialmanager.com/pone/, click the 'Update My Information' link at the top of the page, and double check that your user information is up-to-date. If you have any billing related questions, please contact our Author Billing department directly at authorbilling@plos.org.

If your institution or institutions have a press office, please notify them about your upcoming paper to help maximize its impact. If they’ll be preparing press materials, please inform our press team as soon as possible -- no later than 48 hours after receiving the formal acceptance. Your manuscript will remain under strict press embargo until 2 pm Eastern Time on the date of publication. For more information, please contact onepress@plos.org.

Kind regards,

Fernando de Castro

Academic Editor

PLOS ONE

Additional Editor Comments (optional):

Reviewers' comments:

Reviewer's Responses to Questions

Comments to the Author

Reviewer #2: All comments have been addressed

**********

2. Is the manuscript technically sound, and do the data support the conclusions?

Reviewer #2: (No Response)

**********

3. Has the statistical analysis been performed appropriately and rigorously?

Reviewer #2: (No Response)

**********

4. Have the authors made all data underlying the findings in their manuscript fully available?

Reviewer #2: (No Response)

**********

5. Is the manuscript presented in an intelligible fashion and written in standard English?

Reviewer #2: (No Response)

**********

6. Review Comments to the Author

Reviewer #2: (No Response)

**********

7. PLOS authors have the option to publish the peer review history of their article (what does this mean?). If published, this will include your full peer review and any attached files.

If you choose “no”, your identity will remain anonymous but your review may still be made public.

Do you want your identity to be public for this peer review? For information about this choice, including consent withdrawal, please see our Privacy Policy.

Reviewer #2: No

PLoS One. doi: 10.1371/journal.pone.0244766.r006

Acceptance letter

Fernando de Castro

21 Dec 2020

PONE-D-20-27494R2

Differentiating axonal loss and demyelination in chronic MS lesions: a novel approach using single streamline diffusivity analysis.

Dear Dr. Klistorner:

I'm pleased to inform you that your manuscript has been deemed suitable for publication in PLOS ONE. Congratulations! Your manuscript is now with our production department.

If your institution or institutions have a press office, please let them know about your upcoming paper now to help maximize its impact. If they'll be preparing press materials, please inform our press team within the next 48 hours. Your manuscript will remain under strict press embargo until 2 pm Eastern Time on the date of publication. For more information please contact onepress@plos.org.

If we can help with anything else, please email us at plosone@plos.org.

Thank you for submitting your work to PLOS ONE and supporting open access.

Kind regards,

PLOS ONE Editorial Office Staff

on behalf of

Dr. Fernando de Castro

Academic Editor

PLOS ONE

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

S1 Fig. MD, AD and RD values in normal white matter.

(DOCX)

Click here for additional data file.^{(127.7KB, docx)}

S2 Fig. MD-based normalisation.

(DOCX)

Click here for additional data file.^{(122.7KB, docx)}

S1 File

(DOCX)

Click here for additional data file.^{(14.8KB, docx)}

Attachment

Submitted filename: reply to reviewers.docx

Click here for additional data file.^{(23KB, docx)}

Attachment

Submitted filename: reply to reviewers 2.docx

Click here for additional data file.^{(17.6KB, docx)}

Data Availability Statement

[pone.0244766.ref001] 1.Song S.-K. et al. , “Demyelination increases radial diffusivity in corpus callosum of mouse brain.,” Neuroimage, vol. 26, no. 1, pp. 132–40, May 2005. 10.1016/j.neuroimage.2005.01.028 [DOI] [PubMed] [Google Scholar]

[pone.0244766.ref002] 2.Klawiter E. C. et al. , “Radial diffusivity predicts demyelination in ex vivo multiple sclerosis spinal cords,” Neuroimage, vol. 55, pp. 1454–1460, 2011. 10.1016/j.neuroimage.2011.01.007 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0244766.ref003] 3.Janve V. a et al. , “The radial diffusivity and magnetization transfer pool size ratio are sensitive markers for demyelination in a rat model of type III multiple sclerosis (MS) lesions.,” Neuroimage, vol. 74, pp. 298–305, July 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0244766.ref004] 4.Cadavid D. et al. , “Safety and efficacy of opicinumab in acute optic neuritis (RENEW): a randomised, placebo-controlled, phase 2 trial,” Lancet Neurol., vol. 16, no. 3, pp. 189–199, 2017. 10.1016/S1474-4422(16)30377-5 [DOI] [PubMed] [Google Scholar]

[pone.0244766.ref005] 5.Green A. J. et al. , “Clemastine fumarate as a remyelinating therapy for multiple sclerosis (ReBUILD): a randomised, controlled, double-blind, crossover trial,” Lancet, vol. 390, pp. 2481–89, 2017. 10.1016/S0140-6736(17)32346-2 [DOI] [PubMed] [Google Scholar]

[pone.0244766.ref006] 6.Klistorner A., Chai Y., Leocani L., Albrecht P., Aktas O., and Butzkueven H., “Assessment of Opicinumab in Acute Optic Neuritis Using Multifocal Visual Evoked Potential,” CNS Drugs, vol. online fir, 2018. 10.1007/s40263-018-0575-8 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0244766.ref007] 7.Wang Y. et al. , “Differentiation and quantification of inflammation, demyelination and axon injury or loss in multiple sclerosis.,” Brain, vol. 138, no. Pt 5, pp. 1223–38, May 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0244766.ref008] 8.Zhang H., Schneider T., Wheeler-kingshott C. A., and Alexander D. C., “NODDI: practical in vivo neurite orientation dispersion and density imaging of the human brain,” Neuroimage, vol. 61, pp. 1000–1016, 2012. 10.1016/j.neuroimage.2012.03.072 [DOI] [PubMed] [Google Scholar]

[pone.0244766.ref009] 9.Assaf Y., Freidlin R. Z., Rohde G. K., and Basser P. J., “New Modeling and Experimental Framework to Characterize Hindered and Restricted Water Diffusion in,” vol. 978, pp. 965–978, 2004. [DOI] [PubMed] [Google Scholar]

[pone.0244766.ref010] 10.Panagiotaki E., Schneider T., Siow B., Hall M. G., Lythgoe M. F., and Alexander D. C., “Compartment models of the diffusion MR signal in brain white matter: A taxonomy and comparison,” Neuroimage, vol. 59, no. 3, pp. 2241–2254, 2012. 10.1016/j.neuroimage.2011.09.081 [DOI] [PubMed] [Google Scholar]

[pone.0244766.ref011] 11.Jeurissen B., Leemans A., Tournier J., Jones D. K., and Sijbers J., “Investigating the Prevalence of Complex Fiber Configurations in White Matter Tissue with Diffusion Magnetic Resonance Imaging,” Hum. Brain Map, vol. 2766, pp. 2747–2766, 2013. 10.1002/hbm.22099 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0244766.ref012] 12.Taipel S. et al. , “Fractional Anisotropy Changes in Alzheimer’s Disease Depend on the Underlying Fiber Tract Architecture: A Multiparametric DTI Study using Joint Independent Component Analysis,” J. Alzheimer’s Dis., vol. 41, pp. 69–83, 2014. [DOI] [PubMed] [Google Scholar]

[pone.0244766.ref013] 13.Wheeler-Kingshott C. A. M. and Cercignani M., “About ‘Axial’ and ‘Radial’ Diffusivities.,” Mag Res Med, vol. 61, pp. 1255–1260, 2009. [DOI] [PubMed] [Google Scholar]

[pone.0244766.ref014] 14.Jones D. K. et al. , “A diffusion tensor magnetic resonance imaging study of frontal cortex connections in very-late-onset schizophrenia-like psychosis,” Am. J. Geriatr. Psychiatry, vol. 13, no. 12, pp. 1092–1099, 2005. 10.1176/appi.ajgp.13.12.1092 [DOI] [PubMed] [Google Scholar]

[pone.0244766.ref015] 15.Yeatman J. D., Dougherty R. F., Myall N. J., Wandell B. a, and Feldman H. M., “Tract profiles of white matter properties: automating fiber-tract quantification.,” PLoS One, vol. 7, no. 11, p. e49790, January 2012. 10.1371/journal.pone.0049790 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0244766.ref016] 16.Reich D. S., Smith S. A., Gordon-Lipkin E. M., Ozturk A., Caffo B. S., and Balcer L. J., C. P.A., “Damage to optic radiation in multiple sclerosis is associated with retinal injury and visual disability.,” Arch neurol, vol. 66, pp. 998–1006, 2009. 10.1001/archneurol.2009.107 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0244766.ref017] 17.Klistorner A. et al. , “Decoding diffusivity in multiple sclerosis: Analysis of optic radiation lesional and non-lesional white matter,” PLoS One, vol. 10, no. 3, 2015. 10.1371/journal.pone.0122114 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0244766.ref018] 18.Polman C. H. et al. , “Diagnostic criteria for multiple sclerosis: 2010 revisions to the McDonald criteria.,” Ann. Neurol., vol. 69, no. 2, pp. 292–302, February 2011. 10.1002/ana.22366 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0244766.ref019] 19.Wasserthal J., Neher P., and Maier-hein K. H., “TractSeg—Fast and accurate white matter tract segmentation,” Neuroimage, vol. 183, no. June, pp. 239–253, 2018. [DOI] [PubMed] [Google Scholar]

[pone.0244766.ref020] 20.Wasserthal J., Neher P., and Maier-hein K. H., “Combined tract segmentation and orientation mapping for bundle-specific tractography,” no. Mic, 2019. 10.1016/j.media.2019.101559 [DOI] [PubMed] [Google Scholar]

[pone.0244766.ref021] 21.Sepehrband F. et al. , “Brain tissue compartment density estimated using diffusion-weighted MRI yields tissue parameters consistent with histology,” Hum. Brain Mapp., vol. 36, no. 9, pp. 3687–3702, 2015. 10.1002/hbm.22872 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0244766.ref022] 22.van Walderveen A. A. A. et al. , “Histopathologic correlate of hypointense lesions on Tl-weighted spin-echo lesions in multiple sclerosis MRI,” Neurology, vol. 50, pp. 1282–1288, 1998. [DOI] [PubMed] [Google Scholar]

[pone.0244766.ref023] 23.Brex P. a et al. , “Lesion heterogeneity in multiple sclerosis: a study of the relations between appearances on T1 weighted images, T1 relaxation times, and metabolite concentrations.,” J. Neurol. Neurosurg. Psychiatry, vol. 68, no. 5, pp. 627–32, 2000. [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0244766.ref024] 24.Klistorner A. et al. , “Diffusivity in the core of chronic multiple sclerosis lesions,” PLoS One, vol. 13, no. 4, 2018. 10.1371/journal.pone.0194142 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0244766.ref025] 25.Budde M. D., Janes L., Gold E., Turtzo L. C., and Frank J. A., “The contribution of gliosis to diffusion tensor anisotropy and tractography following traumatic brain injury: validation in the rat using Fourier analysis of stained tissue sections.,” Brain, vol. 134, no. Pt 8, pp. 2248–60, August 2011. 10.1093/brain/awr161 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0244766.ref026] 26.Klistorner A. et al. , “Diffusivity in multiple sclerosis lesions: At the cutting edge?,” NeuroImage Clin., vol. 12, pp. 219–226, 2016. 10.1016/j.nicl.2016.07.003 [DOI] [PMC free article] [PubMed] [Google Scholar]

PERMALINK

Differentiating axonal loss and demyelination in chronic MS lesions: A novel approach using single streamline diffusivity analysis

Samuel Klistorner

Michael H Barnett

Jakob Wasserthal

Con Yiannikas

Joshua Barton

John Parratt

Yuyi You

Stuart L Graham

Alexander Klistorner

Roles

Abstract

Introduction

Method

Standard protocol approvals, registrations, and patient consents

Subjects

MRI protocol

MRI image pre-processing

Lesion identification and analysis

Identification of major fiber tracts

Single fiber-based lesional profile

Fig 1. Selection of fiber tracts.

Fig 2. Constructing single fiber tract diffusivity profile of individual lesion.

Fig 3. Computation of personalized lesional diffusivity profile.

Control for crossing fibers

Statistical analysis

Results

Diffusivity profile of chronic MS lesions

Fig 4. PLD profile.

Table 1. Averaged diffusivity values (mean (SD)) in lesion core, rim and extra-lesional part of lesional fibers and in corresponding voxels of matching non-lesional fibers.

Relationship between T1 hypointensity and diffusivity profile in the core of chronic MS lesions

Fig 5. Correlations between diffusivity increase (vertical axis) and T1 hypointensity-derived axonal loss (horizontal axis).

Fig 6. Correlation between ΔRD-ΔAD (vertical axis) and T1 hypointensity-derived axonal loss (horizontal axis).

Modelling effects of axonal loss and demyelination on diffusivity in the lesion core

Fig 7. Results of diffusivity modelling.

Discussion

Supporting information

Data Availability

Funding Statement

References

Decision Letter 0

Fernando de Castro

Roles

Author response to Decision Letter 0

Decision Letter 1

Fernando de Castro

Roles

Author response to Decision Letter 1

Decision Letter 2

Fernando de Castro

Roles

Acceptance letter

Fernando de Castro

Roles

Associated Data

Supplementary Materials

Data Availability Statement

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases