A Flexible Framework for Nonparametric Graphical Modeling that Accommodates Machine Learning

Abstract

Graphical modeling has been broadly useful for exploring the dependence structure among features in a dataset. However, the strength of graphical modeling hinges on our ability to encode and estimate conditional dependencies. In particular, commonly used measures such as partial correlation are only meaningful under strongly parametric (in this case, multivariate Gaussian) assumptions. These assumptions are unverifiable, and there is often little reason to believe they hold in practice. In this paper, we instead consider 3 nonparametric measures of conditional dependence. These measures are meaningful without structural assumptions on the multivariate distribution of the data. In addition, we show that for 2 of these measures there are simple, strong plug-in estimators that require only the estimation of a conditional mean. These plug-in estimators (1) are asymptotically linear and non-parametrically efficient, (2) allow incorporation of flexible machine learning techniques for conditional mean estimation, and (3) enable the construction of valid Wald-type confidence intervals. In addition, by leveraging the influence function of these estimators, one can obtain intervals with simultaneous coverage guarantees for all pairs of features.

1. Introduction

With the development of new high-throughput measurement technologies in biotechnology, engineering, and elsewhere, it is increasingly common to measure a number of features on each of a collection of people/objects without a strong apriori understanding on the interplay between these features. It is fundamental to developing science that we learn these relationships. For example, understanding co-expression of genes (Stuart et al., 2003; Ben-Dor et al., 1999; Ma et al., 2007; Chu et al., 2009) is foundational to biology; identifying regulatory networks (Hartemink et al., 2000) can help us understand cell differentiation (Huang & Ingber, 2000; Boyer et al., 2005), and identify targets for treatment of disease (Csermely et al., 2005; Berger & Iyengar, 2009); and among many other applications.

The relationships between features can be evaluated and expressed using Graphical Modeling: Here we use a graph G = (V, E, W), where V = {1, …, p} (p > 2) indexes a set of nodes {V_i}_i∈V representing the features, E = {e_i,j} is a set of edges corresponding to dependence between adjacent nodes, and W = {w_i,j} is a collection of weights expressing the strength of each edge. In defining these edges and weights, one must decide on a measure of association/dependence. Covariance and correlation are two commonly-used measures for the dependence between two variables in multivariate analysis (Anderson et al., 1958; Székely et al., 2007; Samuel et al., 2001; Langfelder & Horvath, 2008; Choi et al., 2010; Zager & Verghese, 2008).

However, one is often interested in a more causally-motivated parameter: In particular, when using correlation, features can easily be connected due to indirect effects (Bedford & Cooke, 2002). For example, two “connected” features may be mechanistically tied to a third feature, and otherwise completely unrelated. These are often not the edges we wish to discover. One is often more interested in a conditional measure: For two features Y and Z, conditional on fixing all other features $X={\left\{V_k\right\}}_{k=1}^p-\left\{Y,Z\right\}$, we aim to assess if there an association between Y and Z. Previous work has attempted to address this using partial correlation (De La Fuente et al., 2004; Baba et al., 2004). Rather than connecting features with non-zero correlation, instead features with non-zero entries in the precision matrix are connected. This corresponds to assessing the conditional dependence when all of the features considered have a joint Gaussian distribution (Yuan & Lin, 2007; Friedman et al., 2008). In practice, that is rarely, if ever, the case, and edges may correspond to scientific quantities of little interest.

In this work, we address this issue: We consider a more general form of conditional dependence that reduces to the partial correlation when all features are Gaussian. This dependence measure admits a straightforward, natural, and efficient estimator, that facilitates the use of general machine learning methods in estimating dependence. In addition, these estimators allow us to construct asymptotically-valid confidence intervals and run hypothesis tests (while accounting for multiple testing, when evaluating all edges in a graph).

The dependence measure that we primarily consider, which we term the scaled expected conditional covariance is

$${\Psi }_{Y,Z}=\frac{\text{E}\left[\mathrm{Cov}\left(Y,Z|X\right)\right]}{\sqrt{\text{E}\left[\mathrm{Var}\left(Y|X\right)\right]}\sqrt{\text{E}\left[\mathrm{Var}\left(Z|X\right)\right]}}.$$ (1)

Here, Cov(Y, Z|X) is the conditional covariance of Y and Z given X, and Var(Y|X) is the conditional variance of Y given X. This parameter is just a functional that maps the joint distribution of X, Y, and Z to a real number. In contrast to parameters from classical statistics, e.g. coefficients in a linear model, Ψ_Y,Z is model agnostic, and does not implicitly assume any functional form on the relationships between our variables. This parameter summarizes the average degree of association between our features: This summarization using the average has two advantageous attributes: 1) It provides a single summary of dependence between features; and 2) Averages can be estimated at better rates than local quantities (Bickel et al., 1993). These issues dissuade us from directly using a local quantity such as Cov(Y, Z|X).

Later, we will further show that estimating these average dependence measures, such as (1), primarily (and in some cases only) relies on the estimation of a conditional mean. This reduces the problem of testing/evaluating conditional dependence to a canonical prediction problem, which allows us to naturally incorporate flexible machine learning techniques, such as generalized additive models (Hastie, 2017), local polynomial regression (Seifert & Gasser, 2004), random forests (Liaw et al., 2002) etc., and make inference even when X is high-dimensional (Tibshirani, 1996; Meinshausen et al., 2006).

2. Related Work

Related work falls in two categories: The first does not directly estimate a parameter encoding dependence, but rather just tests a null hypothesis of conditional independence. This is the strategy generally taken with Gaussian graphical models (Wermuth & Lauritzen, 1990; Toh & Horimoto, 2002; Uhler, 2017), where the graph structure is encoded by the precision matrix. This idea was extended by (Liu et al., 2012) and (Barber et al., 2018) to transelliptical graphical model where nonparametric rank-based regularization estimators were used for estimating the latent inverse covariance matrix. Although, these approaches generalize the estimation to non-Gaussian setting and accommodate for high-dimensional data. They still assume specific underlying model structures.

The other approach evaluates the degree of dependence through estimation of a target parameter: (Douglas et al., 1998) measured the local dependence of pairs via a conditional covariance function by monotonically transforming the conditioning function to a total score. (Bedford & Cooke, 2002) weakened the concept of conditional independence and applied the conditional correlation coefficient to account for the dependence structure. (Fukumizu et al., 2004; Gretton et al., 2005; Sun et al., 2007; Fukumizu et al., 2008) consider a more general nonparametric characterization of conditional independence using covariance operators on reproducing kernel Hilbert spaces (RKHS) to capture nonlinear dependence. However, in these cases, a local parameter was used: These conditional dependence measures depend on the value taken by conditioning variables. This parameter thus cannot be used as a summary measure.

Summary measures of conditional dependence which i) do not make parametric assumptions on the model; and ii) adjust for other covariates have been proposed in regression setting. The most canonical of such measures is the average treatment effect ∫ E[Y|X = x, Z = 1] − E[Y|X = x, Z = 0]dP(x) (Becker et al., 2002), which has been extensively discussed in the semiparametric context (Van Der Laan & Rubin, 2006; Kennedy, 2016). But this measure is limited to evaluating association with a binary treatment. Approaches that attempt to use this with a continuous treatment are often either adhoc, or result in a local measure (Hirano & Imbens, 2004; Hill, 2011; Kennedy et al., 2017).

There exist methodologies which give omnibus measures of departure from conditional independence. For example, Zhang et al., 2012 and Wang et al., 2015 used kernels and characteristic functions respectively to average over some functions of the conditioning variables. These methods have the potential advantage that they use an omnibus test and thus do not have to prespecify a particular direction to consider for departures from conditional independence. This advantage however is tied to their restriction: they need to specify very specific methods of “regressing out the conditioning variables”, such as using RKHS regression or local averaging. This may be inappropriate when confounders are high-dimensional or with heterogeneous types. In addition, tuning of hyperparameters in these methods can be difficult. The theoretically optimal bandwidth pointed out in the paper can be hardly achievable by any sort of split sample validation criterion, such as minimizing MSE.

There are other methods which use resampling strategies to modify the original data, in an attempt to construct a pseudo-dataset where the indicated features are conditionally independent, Doran et al., 2014 cleverly uses a restricted set of permutations that fix something akin to a sufficient dimension reduction of the conditioning variables. This approach works well in some scenarios, however with high dimensional features, for example, it may be infeasible to effectively select such a dimension reduction, which would result in a procedure more akin to a marginal, rather than conditional independence testing. Sen et al., 2017 uses a bootstrap to construct pseudo-conditionally-independent data. It then attempts to differentiate between the original data, and this new pseudo-data. Failure to differentiate suggests that the original data was conditionally independent. This methodology does allow ML-based tools to be used in constructing the classifier, however it still hinges on our ability to construct conditionally independent pseudo-data.

Newey & Robins, 2018 recently discussed expected conditional covariance (one of the 3 measures in this manuscript) as a summary of dependence in low-dimensional partially-linear additive regression. Their estimator is similarly a plug-in, however they discuss only a very particular strategy (which does not leverage Machine Learning techniques) of estimating the requisite conditional mean functions. In contrast, we decouple estimation of the conditional mean from evaluation of the expected conditional covariance. As such, in Section 4, we show that a wide array of ML-based predictive modeling techniques might be used in building those predictive functions for the conditional mean, and then leveraged in estimation of the expected conditional covariance.

3. Average Conditional Dependence Measures

Let $O=(Y,Z,X)\in {\mathbb{R}}^p$ denote a random vector drawn from some joint distribution $P\in \mathcal{M}$, where $\mathcal{M}$ is an unrestricted model space. Here, we have $Y\in \mathbb{R}$, $Z\in \mathbb{R}$, and $X\in {\mathbb{R}}^{p-2}$. For ease of notation, we have identified Y and Z as a pair of features of interest, and are aiming to evaluate the dependence between Y and Z conditional on X. However, we eventually plan to evaluate this dependence between all pairs of variables.

For simplicity, we denote the conditional means and the conditional variances with respect to distribution P as μ_P,Y(x) = E_P(Y|X = x) and ${\sigma }_{P,Y}^2\left(x\right)={\mathrm{Var}}_P\left(Y|X=x\right).$ Our first measure of dependence, previously mentioned in Section 1, is the expected conditional covariance

$$\begin{gathered} {\Psi }_1\left(P\right)={\text{E}}_P\left[{\mathrm{Cov}}_P\left(Y,Z|X\right)\right] \\ =\int \left(y-{\mu }_{P,Y}\left(x\right)\right)\left(z-{\mu }_{P,Z}\left(x\right)\right)dP\left(o\right), \end{gathered}$$ (2)

We define our second measure similarly, as the expected conditional correlation

$$\begin{gathered} {\Psi }_2\left(P\right)={\text{E}}_P\left[{\mathrm{Corr}}_P\left(Y,Z|X\right)\right] \\ =\int \frac{{\mathrm{Cov}}_P\left(Y,Z|X=x\right)}{\sqrt{{\sigma }_{P,Y}^2\left(x\right){\sigma }_{P,Z}^2\left(x\right)}}dP\left(x\right). \end{gathered}$$ (3)

Ψ₁ and Ψ₂ are the averaged conditional analogs to covariance and correlation. By averaging these conditional associations, these measures provide a global, instead of local, assessment of dependence.

In graphical modeling, as we are evaluating dependence between multiple pairs of features, it is important to use a standardized measure of association. Non-zero values of Ψ₁ will vary according to the scale of our variables. In contrast, Ψ₂ is standardized. Unfortunately, while Ψ₂ appears to be a very natural quantity, it ends up being somewhat difficult to estimate (this is further discussed in Section 4). In light of this, we propose a third, alternative standardized measure of dependence which we term the scaled expected conditional covariance

$${\Psi }_3\left(P\right)=\frac{{\Psi }_1\left(P\right)}{\sqrt{V_Y\left(P\right)V_Z\left(P\right)}},$$ (4)

where $V_Y\left(P\right)={\text{E}}_P[{\sigma }_{P,Y}^2\left(X\right)]$ and $V_Z\left(P\right)={\text{E}}_P[{\sigma }_{P,Z}^2\left(X\right)]$. Ψ₃ is constructed by scaling the expected conditional covariance with the square root of the products of the two expected conditional variances. This is analogous to how correlation is formed from covariance (only, in this case we average before taking our quotient). Indeed, it is simple to show that Ψ₃ is scale invariant, and furthermore takes on values in [−1, 1].

Though Ψ₃ is perhaps less natural than Ψ₂, it turns out to be much easier to estimate from data. This makes intuitive sense as Ψ₂ contains positive local quantities in the denominator (the conditional standard deviations), where Ψ₃ contains only global quantities in the denominator. Estimating local quantities is more difficult, and instability of those estimates in the denominator (in particular if they are near 0) will result in instability of the estimator of Ψ₂. More specifically, our theory takes advantage of the fact that V_Y(P) = E_P[Cov_P(Y, Y|X)], and that the standard delta-method can be applied to a ratio of efficient estimators in the case of Ψ₃ (Oehlert, 1992).

3.1. Higher Order Dependence

In this Section we discuss the relationship of our parameters to the conditional dependence/independence of features. In particular, we know that, without modification, covariance only encodes linear dependence. Unless variables are jointly Gaussian, linear independence does not imply independence (Hyvärinen et al., 2001). However, general dependence can be evaluated using higher-order moments (or equivalently covariance of derived features) (Fukumizu et al., 2008; Gretton et al., 2005). Using similar ideas, we relate our dependence measures to non-linear association.

Consider two pre-specified functions ${\varphi }_1:\mathbb{R}\to {\mathbb{R}}^{p_1}$ and ${\varphi }_2:\mathbb{R}\to {\mathbb{R}}^{p_2}$ and assume that both functions are conditionally integrable: E[ϕ₁(Y)|X] < ∞, E[ϕ₂(Z)|X] < ∞. Further consider a non-negative weight function w(x). Then, the (ϕ₁, ϕ₂, w)-expected conditional covariance is defined as

$${\Psi }_1^{{\varphi }_1,{\varphi }_2,w}\left(P\right)={\text{E}}_P\left[w\left(x\right){\mathrm{Cov}}_P\left({\varphi }_1\left(Y\right),{\varphi }_2\left(Z\right)|X\right)\right].$$ (5)

One can similarly extend Ψ₂(P) and Ψ₃(P) by replacing Y and Z with ϕ₁(Y) and ϕ₂(Z). Theoretically, estimating ${\Psi }_1^{{\varphi }_1,{\varphi }_2,w}\left(P\right)$ is essentially the same as estimating Ψ₁(P) since ϕ₁(Y) is nothing more than a random variable. But conceptually, this simple transformation in (5) allows us assess higher order conditional dependence structure between Y and Z. In many cases, w(x) will be taken to be 1, however it is required to characterize necessary and sufficient conditions for conditional independence.

3.2. Conditional Independence Testing

Using this idea of higher order dependence, we can develop necessary and sufficient conditions for conditional independence between Y and Z conditional on X. In particular, We consider (ϕ₁, ϕ₂, w)-expected conditional covariance, for $w\left(X\right)=\mathbb{1}\left\{X\in S_x\right\},{\varphi }_1\left(Y\right)=\mathbb{1}\left\{Y\in S_y\right\},$ and ${\varphi }_2\left(Z\right)=\mathbb{1}\left\{Z\in S_z\right\}$ for arbitrary sets S_x, S_y, and S_z. In this case, we see that (ϕ₁, ϕ₂, w)-expected conditional covariance equal to 0 is equivalent to P(Y ∈ S_y, Z ∈ S_z|X ∈ S_x) = P(Y ∈ S_y|X ∈ S_x)P(Z ∈ S_z|X ∈ S_x). This gives us a simple necessary and sufficient condition for conditional independence

Proposition 1 Random variables Y and Z are independent conditional on X iff for every ϕ₁, ϕ₂ and w in ℓ₂(P)¹, for which ${\Psi }_1^{{\varphi }_1,{\varphi }_2,w}\left(P\right)$ is defined and finite, we have ${\Psi }_1^{{\varphi }_1,{\varphi }_2,w}\left(P\right)=0$.

Comprehensively testing for conditional independence via Proposition 1 is generally intractable as one would have to consider all possible w, ϕ₁, and ϕ₂. This is unsurprising: General conditional dependence is extremely difficult to evaluate — in practice impossible with any reasonable quantity of data in moderate to high dimensions. In practice, we instead choose a few test functions (ϕ₁ and ϕ₂) to use, and just evaluate conditional dependence in those directions (finding conditional associations in any of those directions does imply that our features are not conditionally independent). This same idea is employed with Gaussian graphical modeling; only there, conditional dependence is completely characterized by linear conditional dependence. Additionally, in the joint Gaussian setting local and global dependence are equivalent (the conditional covariance between two features in a joint gaussian model cannot vary with the values of the other features).

In the rest of this manuscript, we just consider ϕ₁(y) = y, ϕ₂(z) = z, and w(x) = 1, returning to our original measures. While these measures cannot conclusively show that a pair of features are conditionally independent, if any of Ψ₁, Ψ₂ or Ψ₃ are non-zero, that does allow us to conclude that those features are conditionally dependent.

4. Estimating the Parameters

Suppose that we observe n i.i.d samples ${\left\{o_i\right\}}_{i=1}^n={\left\{y_i,z_i,x_i\right\}}_{i=1}^n$ from an unknown distribution $P\in \mathcal{M}$ where $\mathcal{M}$ is a nonparametric model space. Our goal is to estimate the three well-defined global measures Ψ_i, i = 1, 2, 3 for conditional dependence. Before we discuss specific estimation of these 3 measures, we note that all 3 will require estimation of the intermediate quantities μ_P,Y(x) = E_P[Y|X] and μ_P,Z(x) = E_P[Z|X]. Estimating these conditional means is precisely the goal of most predictive modeling techniques. In the case that Y or Z is continuous, regression techniques can be used; If they are binary, then probabilistic classification methods might be used (eg. penalized regression, neural network, tree-based methods like random forests or boosted trees, etc…). In the following discussion we will often leverage predictive models ${\widehat{\mu }}_Y\left(x\right)$ and ${\widehat{\mu }}_Z\left(x\right),$ and care must be taken in estimating these models (using various statistical/machine learning tools, with proper selection of tuning parameters via split-sample validation, etc…). There is an enormous literature on building such models that we cannot hope to engage with here. However, we note that our ability to leverage these ideas in evaluating dependence is a strong asset for our method. Our asymptotic results will tend to rely on the following assumption:

Assumption 1 Suppose we have n observations o_i = (x_i, y_i, z_i), i = 1, …, n drawn iid from some distribution P. Let ${\widehat{\mu }}_Y$ and ${\widehat{\mu }}_Z$ be estimators of μ_P,Y, μ_P,Z based on those observations. We assume that those estimators each fall in a P-Donsker Class (Van der Vaart, 2000), and further that

$$\int {\left[{\widehat{\mu }}_Y\left(x\right)-{\mu }_{P,Y}\left(x\right)\right]}^{2}dP\left(x\right)=o_p\left(n^{-1/2}\right),$$

$$\int {\left[{\widehat{\mu }}_Z\left(x\right)-{\mu }_{P,Z}\left(x\right)\right]}^{2}dP\left(x\right)=o_p\left(n^{-1/2}\right).$$

This is just saying that our predictive models converge to the truth sufficiently fast. For correctly specified low/moderate dimensional parametric models (eg. linear/logistic regression) this will be satisfied (in fact the rate is actually O_p (n⁻¹)). This will also be the case for various nonparametric and high dimensional methods under fairly general assumptions including the Lasso (Tibshirani, 1996), additive models (Sadhanala & Tibshirani, 2017), and neural network models (Bach, 2017).

From here we can consider estimating our dependence measures. We begin with the expected conditional covariance Ψ₁(P). In this case we propose a natural plug-in estimator:

$${\widehat{\Psi }}_1\equiv \frac{1}{n}\sum _{i=1}^n\left[y_i-{\widehat{\mu }}_Y\left(x_i\right)\right]\left[z_i-{\widehat{\mu }}_Z\left(x_i\right)\right],$$ (6)

in which we use our predictive models ${\widehat{\mu }}_Y$ and ${\widehat{\mu }}_Z$. As discussed in the next theorem this estimator is quite well-behaved.

Theorem 1 Suppose Assumption 1 holds for ${\widehat{\mu }}_Y$ and ${\widehat{\mu }}_Z$. Then the plug-in estimator ${\widehat{\Psi }}_1$ is $\sqrt{n}-\mathit{consistent}$, asymptotically linear, and nonparametrically efficient with influence function $D_P^{\left(1\right)}\left(o_i\right)=\left(y_i-{\mu }_{P,Y}\left(x_i\right)\right)\left(z_i-{\mu }_{P,Z}\left(x_i\right)\right)-{\Psi }_1\left(P\right)$. This additionally implies that ${\widehat{\Psi }}_1$ is asymptotically normal:

$$\sqrt{n}\left[{\widehat{\Psi }}_1-{\Psi }_1\left(P\right)\right]{\to }_{d}N\left[0,{\sigma }_1^2\left(P\right)\right],$$ (7)

where ${\sigma }_1^2\left(P\right)=\int {\left[D_P^{\left(1\right)}\left(o\right)\right]}^{2}dP\left(o\right)$.

It is straightforward to obtain a consistent estimator of the asymptotic variance ${\sigma }_1^2\left(P\right),$ which is ${\widehat{\sigma }}_1^2=\frac{1}{n}{{\sum }_{i=1}^n\left(\left[y_i-{\widehat{\mu }}_Y\left(x_i\right)\right]\left[z_i-{\widehat{\mu }}_Z\left(x_i\right)\right]-{\widehat{\Psi }}_1\right)}^2$. This can be used with asymptotic-normality to form confidence intervals for Ψ₁ with asymptotically correct coverage. In addition, we should note that, so long as Assumption 1 holds, the plug-in estimator ${\widehat{\Psi }}_1$ has the same first-order behaviour (rate and variance), as the plug-in estimator with μ_P,Y and μ_P,Z known (which is first-order optimal in that case). This means that, under Assumption 1, there is no asymptotic cost to estimating the predictive models. These results can be shown by simple calculation (see supplementary materials).

We will postpone a discussion of estimating Ψ₂, and first discuss estimation of Ψ₃. We use a similar plug-in for Ψ₃: ${\widehat{\Psi }}_3=\frac{{\widehat{\Psi }}_1}{\sqrt{{\widehat{V}}_Y{\widehat{V}}_Z}},$ where ${\widehat{V}}_Y=\frac{1}{n}{{\sum }_{i=1}^n\left(y_i-{\widehat{\mu }}_Y\left(x_i\right)\right)}^2$ and ${\widehat{V}}_Z=\frac{1}{n}{{\sum }_{i=1}^n\left(z_i-{\widehat{\mu }}_Z\left(x_i\right)\right)}^2$. Using a similar direct calculation, we can show that ${\widehat{V}}_Y$ and ${\widehat{V}}_Z$ are asymptotically linear and efficient estimates of V_Y(P) and V_Z(P). Thus, by applying the delta-method we get the following result

Theorem 2 Suppose Assumption 1 holds for ${\widehat{\mu }}_Y$ and ${\widehat{\mu }}_Z$. Then the plug-in estimator ${\widehat{\Psi }}_3$ is $\sqrt{n}-\mathit{consistent}$, asymptotically linear, and nonparametrically efficient with influence function $D_P^{\left(3\right)}\left(o_i\right)=\frac{\left(y_i-{\mu }_{P,Y}\left(x_i\right)\right)\left(z_i-{\mu }_{P,Z}\left(x_i\right)\right)}{\sqrt{V_Y\left(P\right)V_Z\left(P\right)}}-{\Psi }_3\left(P\right)\left[\frac{{\left(y_i-{\mu }_{P,Y}\left(x_i\right)\right)}^2}{2V_Y\left(P\right)}+\frac{{\left(z_i-{\mu }_{P,Z}\left(x_i\right)\right)}^2}{2V_Z\left(P\right)}\right]$, This additionally implies that ${\widehat{\Psi }}_3$ is asymptotically normal:

$$\sqrt{n}\left[{\widehat{\Psi }}_3-{\Psi }_3\left(P\right)\right]{\to }_{d}N\left[0,{\sigma }_3^2\left(P\right)\right],$$ (8)

where ${\sigma }_3^2\left(P\right)=\int {\left[D_P^{\left(3\right)}\left(o\right)\right]}^{2}dP\left(o\right)$.

We can similarly use a consistent estimate of ${\sigma }_3^2(P)$, and combine that with asymptotic normality to build a confidence interval for Ψ₃. This again has the same efficiency as the optimal estimator with μ_P,Y and μ_P,Z known.

Building an estimator for Ψ₂(P) is a bit more complicated. Here, we must analyze the canonical gradient of Ψ₂(P) under a nonparametric model. This informs us about the low-order terms in a von-mises expansion, and allows us to calculate the so-called “one-step” correction needed to update our plug-in estimator to construct an efficient estimator (Bickel et al., 1993). In order to follow this path, we also need estimators of Cov(Y, Z|X = x), ${\sigma }_Y^2\left(x\right),$ and ${\sigma }_Z^2\left(x\right)$. We will denote such estimators by $\widehat{\mathrm{Cov}}\left(Y,Z|X=x\right),{\widehat{\sigma }}_Y^2\left(x\right),$ and ${\widehat{\sigma }}_Z^2\left(x\right)$. Coming up with strong estimators for these intermediate quantities is a significant hurdle in estimating Ψ₂ well, and a major reason why we instead propose Ψ₃ as a standardized measure of conditional dependence.

Based on all of this, the estimator we propose for Ψ₂(P) is ${\widehat{\Psi }}_2={\tilde{\Psi }}_2+\frac{1}{n}{\sum }_{i=1}^n{\tilde{D}}^{\left(2\right)}\left(o_i\right)$, where ${\tilde{\Psi }}_2$ is a naive estimator of form

$${\tilde{\Psi }}_2=\frac{1}{n}\sum _{i=1}^n\left\{\frac{\left(y_i-{\widehat{\mu }}_Y\left(x_i\right)\right)\left(z_i-{\widehat{\mu }}_Z\left(x_i\right)\right)}{\sqrt{{\widehat{\sigma }}_Y^2\left(x_i\right){\widehat{\sigma }}_Z^2\left(x_i\right)}}\right\}$$ (9)

and

$${\tilde{D}}^{\left(2\right)}\left(o_i\right)=\left[\frac{\widehat{\mathrm{Cov}}\left(Y,Z|X=x_i\right)}{\sqrt{{\widehat{\sigma }}_Y^2\left(x_i\right){\widehat{\sigma }}_Z^2\left(x_i\right)}}\right]\times \left[\frac{{\left(y_i-{\widehat{\mu }}_Y\left(x_i\right)\right)}^2}{2{\widehat{\sigma }}_Y^2\left(x_i\right)}+\frac{{\left(z_i-{\widehat{\mu }}_Z\left(x_i\right)\right)}^2}{2{\widehat{\sigma }}_Z^2\left(x_i\right)}-1\right]$$ (10)

Here D⁽²⁾ is the canonical gradient (or equivalently the efficient influence function) of Ψ₂(P) in the nonparametric model-class.

Standard theory for such one-step estimators gives us the following result:

Theorem 3 Suppose ${\widehat{\mu }}_Y(x)$, ${\widehat{\mu }}_Z(x)$ satisfy Assumption 1, and similarly estimators Cov(Y, Z|X = x), ${\sigma }_Y^2\left(x\right)$, and ${\sigma }_Z^2\left(x\right)$ are also from P-Donsker classes, and converge to the truth at that same n^−1/2 rate in squared error loss. Then the estimator ${\widehat{\Psi }}_2$ is $\sqrt{n}-\mathit{consistent}$, asymptotically linear, and nonparametrically efficient with influence function $D_P^{(2)}(o)$ defined in (10), This additionally implies that ${\widehat{\Psi }}_2$ is asymptotically normal:

$$\sqrt{n}\left[{\widehat{\Psi }}_2-{\Psi }_2\left(P\right)\right]{\to }_{d}N\left[0,{\sigma }_2^2\left(P\right)\right],$$ (11)

where ${\sigma }_2^2\left(P\right)=\int {\left[D_P^{\left(2\right)}\left(o\right)\right]}^{2}dP\left(o\right)$.

Theorem 3 has requirements on convergence of additional intermediate quantities (conditional covariances and conditional variances). In practice, even in simple scenarios ${\widehat{\Psi }}_2$ performs much more poorly than ${\widehat{\Psi }}_1$ and ${\widehat{\Psi }}_3$. The theoretical route we took to derive this “efficient” estimator, could also have been applied for Ψ₁ and Ψ₂ to construct efficient estimators. It turns out, that in those cases, we would have ended up with precisely the plugins ${\widehat{\Psi }}_1$ and ${\widehat{\Psi }}_2$ from such constructions (however, one can more easily show efficiency of those estimators from direct calculation).

4.1. Double Robustness of ${\widehat{\Psi }}_1$

In Assumption 1, we give separate convergence rates bounds for each predictive model. In fact, for the result of Theorem 1 we only require that $R_1\left({\widehat{P}}_n,P\right)\equiv \int \left[{\widehat{\mu }}_Y\left(x\right)-{\mu }_{P,Y}\left(x\right)\right]\left[{\widehat{\mu }}_Z\left(x\right)-{\mu }_{P,Z}\left(x\right)\right]dP\left(x\right)=O_P\left(n^{-1/2}\right)$. In particular, this is precisely the second-order term from an asymptotic expansion of our estimator. Using this, we can directly show that our estimator ${\widehat{\Psi }}_1$ is doubly robust in that

• ${\widehat{\Psi }}_1$ is consistent if either one of ${\widehat{\mu }}_Y\left(x\right)$ and ${\widehat{\mu }}_Z\left(x\right)$ is consistent, and in a P-Glivenko-Cantelli Class. (and thus $R_1\left({\widehat{P}}_n,P\right)=o_P\left(1\right)$)

• ${\widehat{\Psi }}_1$ is efficient if ${\widehat{\mu }}_Y\left(x\right)$ and ${\widehat{\mu }}_Z\left(x\right)$ converge sufficiently fast that $R_1\left({\widehat{P}}_n,P\right)=o_P\left(n^{-1/2}\right)$.

This indicates additional robustness of ${\widehat{\Psi }}_1$ to model misspecification (Scharfstein et al., 1999; Van der Laan et al., 2003). Even if one of ${\widehat{\mu }}_Z$ and ${\widehat{\mu }}_Y$ is inconsistent, ${\widehat{\Psi }}_1$ will still remain consistent as long as the other one is consistent. Unfortunately, neither the expected conditional correlation, nor the scaled expected conditional covariance estimators are double-robust. In particular, the scaled expected conditional covariance has second-order remainder terms associated with estimating each expected conditional variance which separately involve convergence of ${\widehat{\mu }}_Y(x)$ and ${\widehat{\mu }}_Z(x)$. See supplementary materials for details about remainder terms.

4.2. Suboptimal Estimators

To some degree, it is a happy coincidence that the estimators for Ψ₁ and Ψ₂ proposed in Section 4 are simple and turn out to be first-order optimal. Generally simple plug-in estimators will not even be rate optimal (and converge at a slower rate than n^−1/2). For example, one might consider an alternative representation of Ψ₁(P) = E_P[E_P(Y Z|X) − E_P(Y|X) E_P(Z|X)], and thus consider estimating Ψ₁(P) by

$${\widehat{\Psi }}_{1,naive}=\frac{1}{n}\sum _{i=1}^n\left[{\widehat{\mu }}_{YZ}\left(x_i\right)-{\widehat{\mu }}_Y\left(x_i\right){\widehat{\mu }}_Z\left(x_i\right)\right],$$ (12)

where ${\widehat{\mu }}_{YZ}\left(x_i\right)$ is an estimator of E_P (Y Z|X). If ${\widehat{\mu }}_Y$ and ${\widehat{\mu }}_Z$ do not converge at a parametric rate (of n⁻¹ in MSE)– when using ML-based estimates they generally will not– ${\widehat{\Psi }}_{1,\mathit{naive}}$ will converge at slower than an n^−1/2 rate. One could similarly define a simple estimator of Ψ₂(P), ${\widehat{\Psi }}_{2,naive}=\frac{1}{n}{\sum }_{i=1}^n\frac{\widehat{\mathrm{Cov}}\left(Y,Z|x_i\right)}{\sqrt{{\widehat{\sigma }}_Y^2\left(x_i\right){\widehat{\sigma }}_Z^2\left(x_i\right)}}$. Unfortunately, as in the case of ${\widehat{\Psi }}_{1,naive}$, this estimator will not be efficient or even converge at a n^−1/2 rate.

4.3. Constructing Confidence Intervals

Constructing a confidence interval based on the so-called naive estimators, ${\widehat{\Psi }}_{1,\mathit{naive}}$ and ${\widehat{\Psi }}_{2,\mathit{naive}}$, is difficult. Due to the excess bias, they are, in general, not asymptotically linear, so confidence intervals based on Gaussian approximations are not possible. In addition, resampling methods including bootstrapping, are generally invalid in this context. Fortunately, ${\widehat{\Psi }}_1$, ${\widehat{\Psi }}_2$ and ${\widehat{\Psi }}_3$ do not suffer from these issues. As shown in Theorems 1-3, these centered estimators converge in distribution to mean-zero normal variables with asymptotic variance ${\sigma }_j^2\left(P\right)=\int {\left[D_P^{\left(j\right)}\left(o\right)\right]}^{2}dP\left(o\right)$ for j = 1, 2, 3. Thus, if we estimate our variances by

$${\widehat{\sigma }}_j^2=\frac{1}{n}\sum _{i=1}^n{\widehat{D}}^{\left(j\right)}{\left(o_i\right)}^2,$$ (13)

where ${\widehat{D}}^{(j)}$ is any consistent estimator of the influence function, we can form valid confidence intervals. Then, by leveraging asymptotic normality, we can construct a (1 − α)% Wald-type confidence interval for Ψ_j as

$$\left[{\widehat{\Psi }}_j-n^{-1/2}{q}_{1-\alpha /2}{\widehat{\sigma }}_j,{\widehat{\Psi }}_j+n^{-1/2}{q}_{1-\alpha /2}{\widehat{\sigma }}_j\right],$$ (14)

which has asymptotically correct coverage. q_α stands for the α-th quantile of a standard normal distribution.

Asymptotic linearity can be leveraged more broadly to give intervals for multiple pairs of features with correct simultaneous coverage. In particular, suppose we are in an asymptotic regime with p fixed and n growing. Consider 2 pairs of features (j₁, j₂), and (j₃, j₄) with j₁ ≠ j₂ and j₃ ≠ j₄, (this can be extended to any number of pairs). In this case, we consider estimation of $[{\Psi }_1^{j_1,j_2},{\Psi }_1^{j_3,j_4}{]}^{⊺}$, the expected conditional covariance of both pairs of features. Here, it is straightforward to show that under Assumption 1, we have

$$\sqrt{n}\left[\left(\begin{array}{c}{\widehat{\Psi }}_1^{j_1,j_2}\\ {\widehat{\Psi }}_1^{j_2,j_3}\end{array}\right)-\left(\begin{array}{c}{\Psi }_1^{j_1,j_2}\\ {\Psi }_1^{j_2,j_3}\end{array}\right)\right]\to N\left(0,\Sigma \right),$$

where Σ is defined based on expectations of products of influence functions for each estimator. This idea generalizes to arbitrary (but fixed) numbers of covariates, and can also be applied to estimation of Ψ₂, and Ψ₃. This joint normality can be combined with standard methods in multiple testing to construct confidence intervals with simultaneous coverage (Van der Laan, 2008).

4.4. Relationship to De-biased Lasso

In addition to graphical modeling, other meaningful measures can be obtained by slightly modifying Ψ₁. One measure of particular interest is

$$\Phi =\frac{\text{E}\left[\mathrm{Cov}\left(Y,Z|X\right)\right]}{\text{E}\left[\mathrm{Var}\left(Z|X\right)\right]}.$$ (15)

Φ is a nonparametric functional, that combines expected conditional variance and covariance (similar to Ψ₁). In fact, as with Ψ₁, we can use a simple plug-in estimator (with estimated conditional means constructed using any suitable machine learning technique) to estimate and make inference for Φ. If we further assume that we are working in a parametric space and the data (Y, Z, X) are generated from a linear model E[Y|Z, X] = γZ + βX, Φ is precisely the coefficient γ (Newey & Robins, 2018). In low dimensional problems γ is estimated efficiently by standard linear regression — in high dimensional problems it is common to use the Lasso (Tibshirani, 1996; O’Brien, 2016) with de-biasing to conduct inference (Sara et al.; Cun-Hui et al.). The work in this manuscript gives an alternative approach to estimation and inference. In particular, in the challenging case that the features are high-dimensional, the (theoretically optimal) plug-in estimator $\widehat{\Phi }$ is consistent and efficient (if the conditional mean estimates are sufficiently good). Under suitable conditions, the de-biased lasso will give an estimator with the same first order behavior when the design matrix is random (Geer, 2016). However, the de-biased lasso requires estimation of Σ⁻¹ (usually by node-wise regression) which our nonparametric approach does not. Thus, the results in this paper provide an alternative for obtaining the estimators and confidence intervals of regression coefficients for linear models with either low- or high-dimensional features.

5. Experiments

In this section, we assess the performance of the proposed (theoretically optimal) plug-in estimators of global dependence measures, in terms of the asymptotic performance, as well as their effectiveness in conditional independence testing and graph recovery. Here, we present the main results and provide additional results in supplementary materials.

5.1. Asymptotic Performance

We present the asymptotic properties of Ψ₁ by computing the empirical bias, variance, and coverage of 95% Wald-type confidence interval in the setting of low-, moderate, and high-dimensional features.

We start with a simple scenario, where the conditioning variable X is univariate:

$$Y=\sin \left(3X\right)+e_y,Z=\cos \left(2X\right)+e_z,$$ (16)

where X ~ Uniform(0,2) independent of $\overrightarrow{e}={\left(e_y,e_z\right)}^T\sim N\left[\left(\begin{array}{c}0\\ 0\end{array}\right),\left(\begin{array}{cc}1& -0.5\\ -0.5& 1\end{array}\right)\right]$.

Then, we consider a setting of high-dimensional features, where we generate Y and Z from a linear model:

$$Y=X{\beta }_y+e_y,Z=X{\beta }_z+e_z,$$ (17)

where X ~ N(0, I₅₀₀₀), ${\beta }_y=(\underset{10}{\underbrace{1,\dots ,1,}}\underset{4990}{\underbrace{0,\dots ,0}})$ and ${\beta }_z=(\underset{10}{\underbrace{-1,\dots ,-1,}}\underset{4990}{\underbrace{0,\dots ,0}})$. The error term $\overrightarrow{e}={\left(e_y,e_z\right)}^T$ is the same as in the low-dimensional case.

In both cases, the true values of Ψ₁ are −0.5. We generate random datasets of size n ∈ {500, 1000, 2000, …, 6000} and estimate Ψ₁ (we run 400 simulates for each sample size). The conditional means are estimated by local polynomial regression in the low-dimensional case and by lasso algorithm in the high-dimensional case. We compare our (theoretically optimal) plug-in estimator ${\widehat{\Psi }}_1$ to the naive estimators: ${\widehat{\Psi }}_{1,\mathit{naive}}$ in (12).

Figure 1 shows that, the empirical $\sqrt{n}-\mathrm{scaled}$ bias of our theoretically optimal plug-in estimator ${\widehat{\Psi }}_1$ goes toward zero with increasing sample size, which corresponds to our asymptotic result. This is not the case for the naive estimator. The confidence interval of ${\widehat{\Psi }}_1$ converges to the nominal 95% as sample size increases. As expected, due to excess bias, the bootstrap interval based on the “naive” estimators performs poorly (with coverage actually converging to 0). See supplementary materials for experiments of a moderate-dimensional case and the evaluation of Ψ₃.

Figure 1.

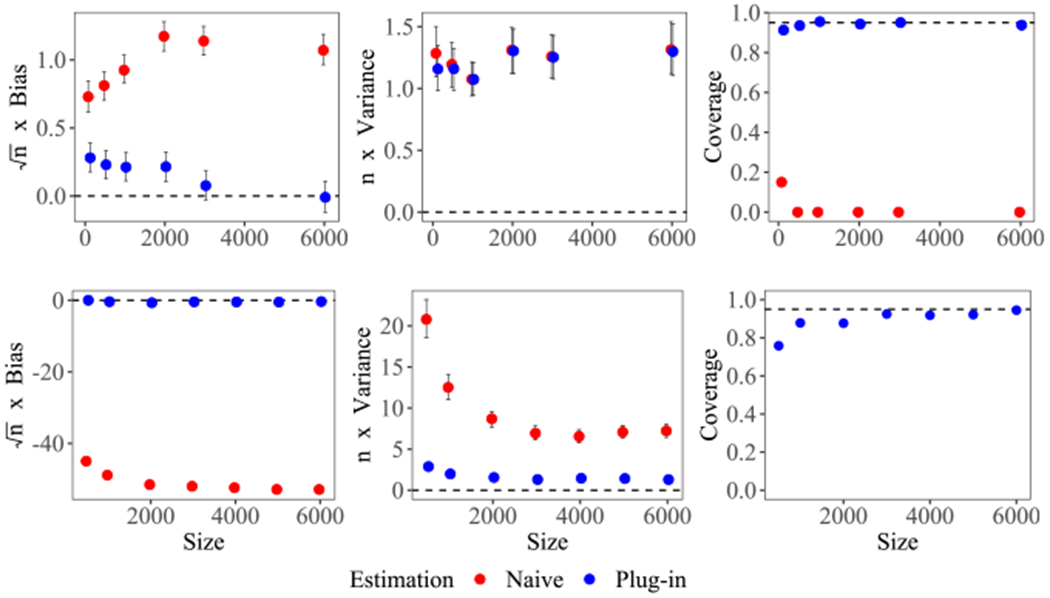
Empirical $\sqrt{n}–\mathrm{scaled}$ bias, Empirical n—scaled variance and empirical coverage of 95% confidence interval of ${\widehat{\Psi }}_1$ (blue) and ${\widehat{\Psi }}_{1,\mathit{naive}}$ (red) for the low-dimensional case (top) and the high-dimensional case(bottom). We only provide a bootstrap-based confidence interval for naive estimators in the low-dimensional case to show its failure.

5.2. Conditional Independence Testing.

We examine the probabilities of Type I error under Y ⫫ Z|X and the power under $Y\cancel{⫫}Z|X$. Here, we consider the scenarios where $X\in {\mathbb{R}}^1$ and $X\in {\mathbb{R}}^5$ respectively. We compare the test based on the scaled expected conditional covariance (SEcov), i.e. Ψ₃, with KCI-test (Zhang et al., 2012), CDI-test (Wang et al., 2015) and CCIT-test (Sen et al., 2017). The conditional means for Ψ₃ are estimated by local polynomial regression when $X\in {\mathbb{R}}^1$ and by random forest when $X\in {\mathbb{R}}^5$.

In the low-dimensional setting, we still use model (16) to generate the data (Y, Z, X). For type I error, we let $\mathrm{Cov}{\left(e_y,e_z\right)}^T=\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right)$ such that Y ⫫ Z|X. For power, we let $\mathrm{Cov}{\left(e_y,e_z\right)}^T=\left(\begin{array}{cc}1& -0.5\\ -0.5& 1\end{array}\right)$, such that $Y\cancel{⫫}Z|X$. In the moderate-dimensional setting, we use the same pattern as the Case1 in (Zhang et al., 2012) for comparison. Y and Z are generated by G(F(X) + E), $X\in {\mathbb{R}}^5$, where G and F are mixtures of linear, cubic, and tanh functions and are different for Y and Z. E is independent with both Y and Z. Under this mechanism, Y ⫫ Z|X holds. For $Y\cancel{⫫}Z|X$, we add errors cosh(e_y) to Y and $\cosh (e_z^2)$ to Z where e_y, e_z ~_iid N(0, 1).

Figure 2 shows that Ψ₃ is always capable of controlling type I errors and achieving a high power, regardless of the dimension of the conditioning set. However, this is not the case for other tests. When $X\in {\mathbb{R}}^1$, the power of KCI- and CDI-test gradually increases with increasing sample size. They can control type I errors at a relatively low level but not comparable to the performance of Ψ₃. When $X\in {\mathbb{R}}^5$, both kernel-based tests collapse. That is, they almost always reject the null hypothesis when Y ⫫ Z|X, and often fail to reject the null when $Y\cancel{⫫}Z|X$. The CCIT-test achieves a relatively high power but struggles to control type type-I errors in both low- and moderate-dimensional settings. In addition, the CDI test is much less efficient compared to the other three. With regard to computation, estimating Ψ₃ is the most efficient method for each fixed sample size, since it only requires the estimation of mean models.

Figure 2.

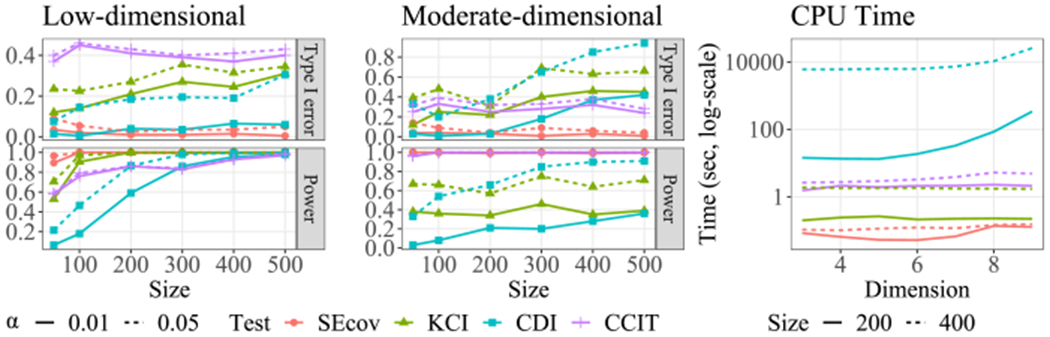
Left and middle: Type I error and power of three conditional independent testing methods for a low- and a moderate-dimensional case. Right: average CPU time taken by four tests. SEcov, KCI-test and CDI-test are all implemented in R. CCIT-test is implemented in Python.

5.3. Graph Recovery.

We now attempt to reconstruct the graph using SEcov, i.e. Ψ₃, with moderate dimensional features (the conditional means are estimated by random forest). We make comparison with Gaussian graphical model (GGM), and transelliptical graphical model (TGM) (Liu et al., 2012) where the CLIME estimator (Cai et al., 2011) using Kendall’s taus is employed. The graphs are generated from the following cases:

• Case1 (Gaussian): X ~ N₈(0, Σ).

• Case2 (Copulas): Z ~ N₈(0, Σ), U = Φ(Z), $X_i=f_i^{-1}\left(U_i\right)$ where $f_i^{-1}$ are quantile functions of Gamma(2, 1), Gamma(2, 1), Beta(2, 2), Beta(2, 2), t(5), t(5), Unif(0, 1), and Unif(0, 1) for i = 1, …, 8.

• Case3 (Transelliptical): X ~ TE₈(Σ, ξ; f). ξ ~ χ_p and f = {f₁, …, f₈} = {h₁, h₂, h₃, h₄, h₁, h₂, h₃, h₄}, where $h_1^{-1}\left(x\right)=\sqrt{\exp \left(x\right)},h_2^{-1}\left(x\right)=sign\left(x\right){\left|x\right|}^{1/2},h_3^{-1}\left(x\right)=x^3$, and $h_4^{-1}\left(x\right)=\Phi \left(x\right)$.

• Case4 (non-Gaussian, non-copulas, non-transelliptical): $X_1=X_2+X_3+X_4/2+\sin \left(X_5\right)+X_6^2+\exp \left(X_7\right)+X_8$ and X₂ = sin(X₇) + |X₈|, where X₃, …, X₈ ~_iid exp(2).

Figure 3 shows that, all three methods work extremely well only when the data is Gaussian distributed (Case1). When the data follows a copulas (Case2) or transelliptical distribution (Case3), both TGM method and Ψ₃ have a comparably great performance while GGM become much less effective due to the model misspecification. We note that, if the data has a highly skewed transelliptical distribution, Ψ₃ may work poorly and TGM remains valid. For Case 4 where the data is non-Gaussian, non-copulas, and non-transelliptical, GGM method totally collapses, which is almost equivalent to a coin flip. The effectiveness of TGM method is also compromised since it uses a misspecified model. On the contrary, Ψ₃ which does not depend on any model assumptions still presents a strong performance.

Figure 3.

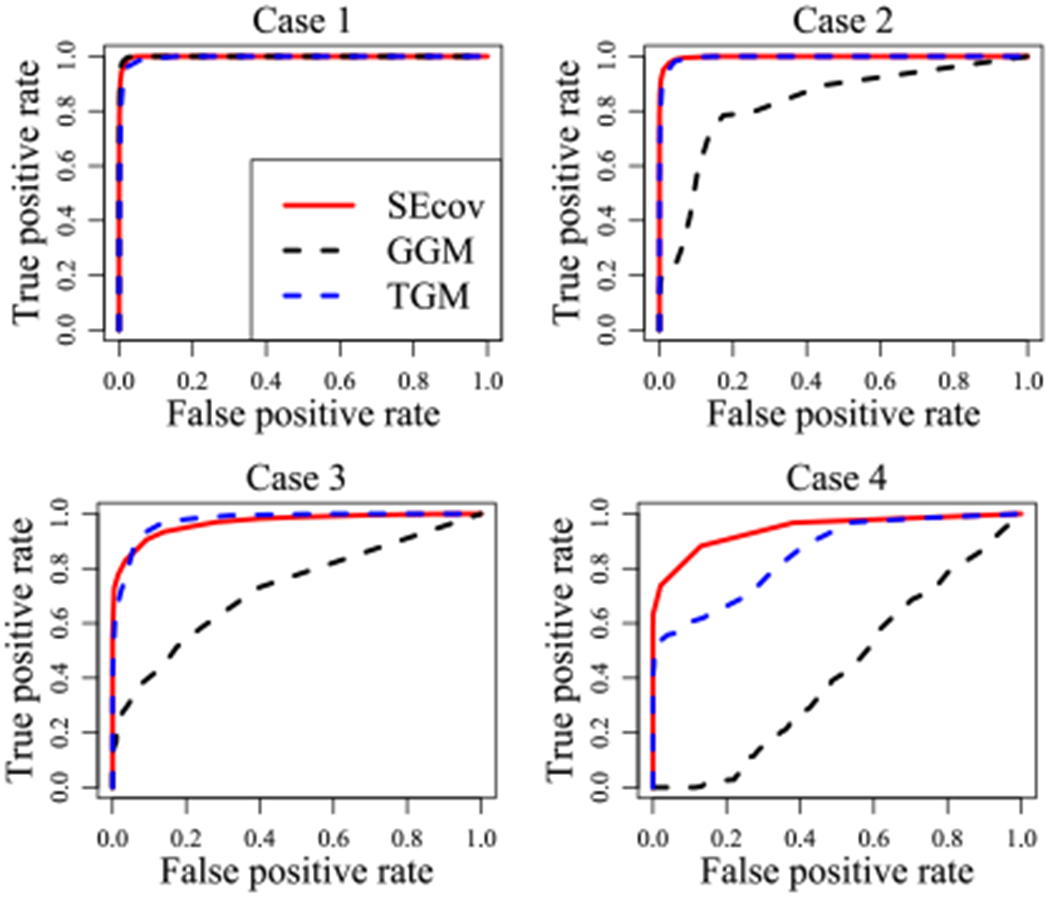
ROC curves of graph recovery for different methods in Case1-Case4. n = 400, p = 8.

6. Discussion

In this paper, we introduce three global measures for evaluating conditional dependence and reconstructing a conditional dependence graph. These measures are model-agnostic and we show that there exist natural and simple plug-in estimators that are asymptotically normal and efficient under mild conditions. Thus, we can construct Wald-type confidence intervals with asymptotically correct coverage. These tasks have proven difficult for existing graphical modeling methods.

One major strength of this work is in that the estimation of the proposed global measures only requires estimating two conditional mean models. Our framework allows us to use flexible machine learning tools for these estimates. Thus, the efficacy of our methodology is intimately connected to our ability to build a good predictive model: If we can build effective predictive models, our methodology can leverage that, and should do a good job evaluating conditional independence. This means, as the field’s ability to engage in predictive modeling grows, so will the scope of this methodology. For example, in the high-dimensional setting, one might use Lasso, or tree-based ensembles to regress out the conditioning variables. If the conditioning variables take form of images, or text documents, one could use deep-learning (with enough data) for that adjustment. The predictive methodology can and should be selected to fit the context.

People may concerned about the effectiveness of the proposed methodology in very high-dimensional settings, as it requires fitting ~ p² models. However, since each conditional mean is estimated independently, the dependence between every pair of features can be evaluated entirely in parallel. Additionally, one might also consider adopting some form of “pre-screening”. For example, one may apply a simpler method (with potential false positives) first to create a network with a super-set of edges and then deploy the methodology proposed in this manuscript to refine this to a more accurate graph.