Additivity of segregation cues in simulated cocktail-party listening

Abstract

An approach is borrowed from Measurement Theory [Krantz et al. (1971). Foundations of Measurement (Academic, New York), Vol. 1] to evaluate the interaction of voice fundamental frequency and spatial cues in the segregation of talkers in simulated cocktail-party listening. The goal is to find a mathematical expression whereby the combined effect of cues can be simply related to their individual effects. On each trial, the listener judged whether an interleaved sequence of four vowel triplets (heard over headphones) were spoken by the same (MMM) or different (FMF) talkers. The talkers had nominally different fundamental frequencies and spoke from nominally different locations (simulated using head-related transfer functions). Natural variation in these cues was simulated by adding a small, random perturbation to the nominal values independently for each vowel on each trial. Psychometric functions (PFs) relating d′ performance to the difference in nominal values were obtained for the cues presented individually and in combination. The results revealed a synergistic interaction of cues wherein the PFs for cues presented in combination exceeded the simple vector sum of the PFs for the cues presented individually. The results are discussed in terms of their implications for possible emergent properties of cues affecting performance in simulated cocktail-party listening.

I. INTRODUCTION

One's ability to attend to and follow the speech of one talker in the presence of one or more other talkers speaking at the same time is referred to as the cocktail party listening (CPL) effect. This term was coined by Cherry in his classic experiment investigating the perception of different speech streams presented simultaneously to the two ears.¹ Listeners regularly apply this skill in everyday social gatherings when they separate the voice of a conversation partner from a background of babble.

Since Cherry's early experiments, much research has been conducted to understand how we accomplish this difficult task and what factors play a significant role. Two acoustic cues that have been repeatedly identified as crucial in this literature are differences in the location of talkers and differences in the fundamental frequency (F0) of the talker voices. The effect of these cues has been well documented, but precisely how they might interact to influence perception when, as in natural situations they occur together, has not been widely investigated.^2,3 For those studies that have specifically addressed the question, the results have been mixed. Rennies et al. measured listening effort and speech intelligibility for conditions of masking in which voice F0 (gender) and location cues were presented individually and in combination. They found that a secondary cue provided little benefit in reducing listening effort or increasing speech intelligibility.⁴ Xia et al. obtained a similar result for the combination of voice F0 and spatial cues in a dual-task paradigm where the secondary task was visual tracking.⁵ Using magnetoencephalography (MEG), Du et al. measured cortical activity in response to voice F0 and spatial location individually and in combination during a concurrent vowel identification task.⁶ Unlike the study of Rennies et al., the two cues were made to be quite distinct (90-degrees spatial separation and one semitone difference in F0). For these conditions, the effect of the two cues on cortical activity was found to be additive. Darwin et al. investigated the individual and combined effect of voice F0 and timbre (vocal tract length) on co-modulation masking release (CMR).⁷ Their study differed fundamentally from the previous two in using timbre rather than location as a cue. Nonetheless, where the two cues individually were equated in effectiveness, they found CMR for the combination of the cues to be more than twice the CMR for either cue in isolation.

There are clearly many differences among these studies that could be responsible for the difference in results. Most notably, there were differences in the relative effectiveness of the individual cues and the initial performance level of listeners before the cues were combined. Where two cues differ substantially in effectiveness, the weaker cue might be expected to have little additional effect. Similarly, a cue that yields near asymptotic performance leaves little room for improvement with the addition of a second cue. These differences, in fact, may have been responsible for the failure in the Rennies et al. and Xia et al. studies to find a benefit for the second cue.

To characterize precisely the interaction of cues in CPL, it is necessary to measure the entire psychometric function relating the combined effect of cues to their individual effects at all levels of performance and, moreover, to equate the relative effectiveness of each cue in isolation so that one does not dominate. This was the tactic taken in the present study. The goal was to characterize mathematically the interaction of voice F0 and spatial separation on performance in a simulated CPL task. For this purpose, we borrowed an approach from measurement theory previously used to evaluate how two or more maskers combine.^8–15 (For a broader discussion of its historical application to psychophysical scaling see Ref. 16.) The approach involves no assumptions; it merely provides a means to find mathematical transformations, if they exist, wherein the combined effects of variables can be related to their individual effects by addition. Let d′(θ) and d′(F0) denote, respectively, the isolated effects of the location and voice F0 cues on d′ performance. We seek a transformation H that preserves a general form of additivity of these effects when the two cues are combined. That is,

$$\mathrm{H}[d\prime (\theta \circ \mathrm{F}0)\left]\hspace{0.17em}=\hspace{0.17em}\mathrm{H}\right[d\prime (\theta )\left]\hspace{0.17em}+\hspace{0.17em}\mathrm{H}\right[d\prime \left(\mathrm{F}0\right)],$$ (1)

where θ ∘ F0 denotes the experimental operation of combining the two cues. Now if there is no interaction and the cues affect performance independently of one another, then the combined effect of the cues would amount to the simple vector sum of their individual effects. The function H, in this case, would be a power-law function H(z) = z^p with exponent p = 2; d′(θ ∘ F0)² = d′(θ)² + d′(F0).² But, if there is an interaction, the combined effect would amount to something other than the vector sum, and H, if it exists, would indicate the exact form of the interaction that led to this result. For example, H(z)=log(z) would indicate a multiplicative interaction between cues such that the combined effect of the cues would be greater than the simple sum of their individual effects (a type of Gestalt perception where the perceived whole is greater than the sum of its parts). The same would be true for H(z) = z^p, p<2, but yielding a different form of the psychometric function.

II. METHODS

In a single-interval, forced-choice procedure, participants were asked to report whether a sequence of vowels were spoken by one or two alternating talkers. Immediate feedback was provided after each trial via a visual prompt. The stimulus was a series of four English vowel triplets presented over headphones to subjects seated in a double-walled sound attenuated booth. The triplets were synthesized using the matlab program “Vowel_Synthesis_GUI25” available on the matlab exchange. All vowels had a duration of 100 ms and were gated on and off with 5-ms cosine-squared ramps. Vowels were presented with a 100-ms, inter-triplet interval and were played at a 44 100-Hz sampling rate with 16-bit resolution using a RME Fireface UCX audio interface. The vowels were selected at random for each triplet from a set of 10 exemplars having equal probability of occurrence (IY, IH, EH, AE, AH, AA, AO, UH, UW, ER; according to APRABet vowel names).

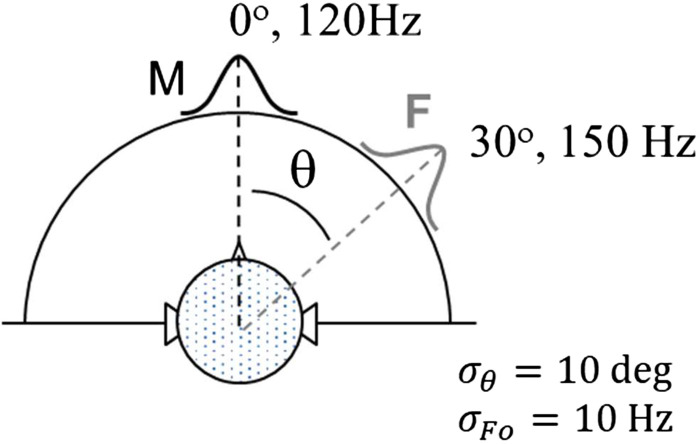
Talkers were distinguished by the F0 of their voice and their location on the azimuthal plane (θ) simulated using KEMAR (the Knowles Electronics Manikin for Acoustic Research) head-related transfer functions. Talker M (male) had a nominal F0 of 120 Hz and a nominal location θ of 0 degrees. Talker F (female) had a higher nominal F0, between 125 and 155 Hz, depending on the condition, and was located to the right of talker M. The differences (Δ) between the nominal values of F0 and θ for the two talkers were varied as independent variables across blocks of trials. For each trial within a block, a random perturbation with a standard deviation σ_θ=10 degrees for the spatial cue and σ_F0=10 Hz for the voice F0 cue was added to each vowel for each triplet. The variation was included to reflect the natural within-talker variation that occurs during speech. The ratio Δ/σ was equated for both cues across conditions. Figure 1 provides a depiction of the differences between the two talkers. When one talker was presented within a trial each stimulus triplet was spoken by talker M (MMM). When two talkers were presented, the first and last vowel of each triplet was spoken by talker F, and the second vowel was spoken by talker M (FMF). In both cases, the vowels were different for each triplet, but the first and last vowels within a triplet were always the same and always had the same perturbation in F0 and θ.

FIG. 1.

(Color online) Stimulus configuration of simulated cocktail-party listening task. See text for description.

To maximize the likelihood of measuring an interaction, if it exists, the effectiveness of each cue in isolation was equated before they were combined. This was done so that one or the other of the cues would not dominate performance. Our previous published work suggested that the effect of the F0 and spatial cues would be the same if the values of Δ/σ for these cues were selected to be the same.¹⁰ Indeed, this was found to be true for all subjects recruited for this study and so the two cues were equated in this way.

A. Conditions

For each condition, subjects completed eight blocks of 50 trials each and were encouraged to take breaks as needed in between blocks. There was a total of 21 different measurements grouped into three conditions: (1) “F0 Cue in Isolation,” mean difference in F0 of the talkers alone, (2) “Spatial Cue in Isolation,” mean difference in the location of the talkers alone, and (3) “Combined Cues,” mean differences in both cues simultaneously. When a mean difference occurred in one cue alone, the mean difference of the other cue was zero, but that cue continued to be perturbed from trial to trial as before. Subjects were run on the combined-cue condition first and on the remaining two conditions in random order. Within each condition there were seven measurements corresponding to different values of Δ for the cues. The value of Δ ranged from 5 to 35 units (in Hz for F0 and in degrees for θ) in five-unit increments.

B. Subjects

The subjects were six young, normal-hearing listeners (five females and one male, ages 18–26 yr) from the University of South Florida. They were paid for their participation in the study. Audiometric thresholds for all subjects were less than 25 dB hearing level (HL) at the audiometric frequencies of 250–8000 Hz. Some subjects had participated in earlier experiments involving very similar conditions, but all subjects received at least one block of training trials in each condition prior to data collection. Informed consent was obtained, and all procedures were followed in accordance with internal review board (IRB) approval.

III. RESULTS

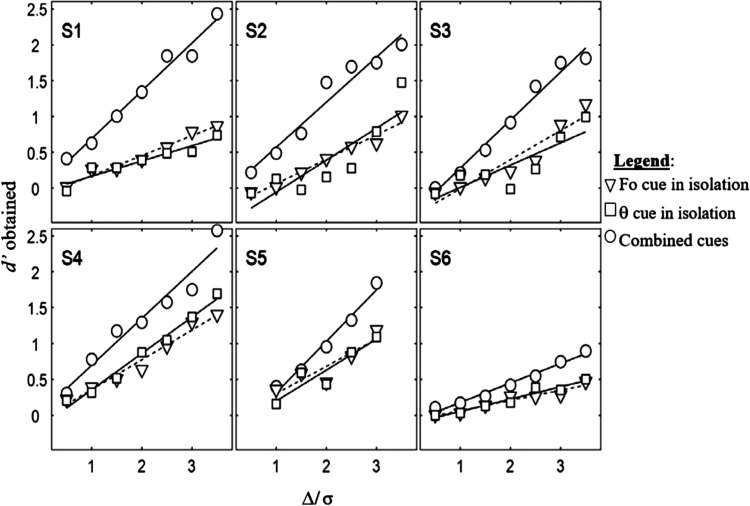
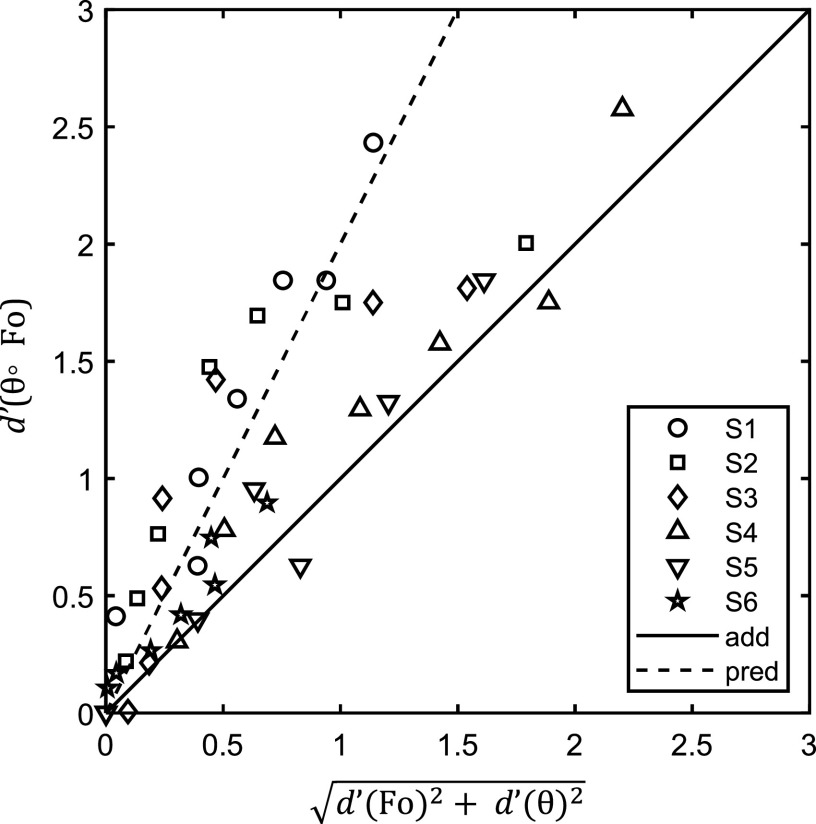
The results for each subject are given in separate panels in Fig. 2 where d′ performance is plotted as a function of Δ/σ for the cues in isolation (squares for the spatial cue, triangles for the voice F0 cue) and for both cues combined (circles). The curves drawn through the data are the results of a linear regression with least-squares criterion. The intercepts are close to 0 in each case, which is to be expected inasmuch as F0 and θ are the only cues for segregation (d′=0 at Δ/σ =0). There is wide variability among listeners in both overall performance level and the combined effect of the two cues. This degree of variability is quite typical for normal-hearing listeners participating in CPL studies, where performance sometimes varies from near chance to perfect levels across listeners.^17,18 The variability in the combined effect relative to the individual effects of the cues is made more evident in Fig. 3 where d′ for the combined cues for all subjects is plotted against the d′ predicted from the vector sum of the d′ values for the isolated cues. Data above the diagonal in this figure represent cases where the combined effect is greater than the vector sum; data falling on the diagonal represent cases where the combined effect is equal to the vector sum. The dashed line is a prediction described later in the discussion. For subject S6 the combined effect of the cues is given by the simple vector sum of their isolated effects, but for the remaining subjects the combined effect is greater than the vector sum by varying amounts. The results suggest that the cues are not processed independently in most cases, but rather interact such that the presence of one cue aids the processing of the other: a type of synergistic interaction among cues.

FIG. 2.

Performance in d′ for each listener (panels) is plotted as a function of Δ/ σ for F0 alone (triangles), θ alone (squares), and both cues combined (circles). Curves are the result of a linear regression on the data using the least-squares criterion.

FIG. 3.

d′ for the combined cues for all subjects (symbol type) is plotted against the d′ predicted from the vector sum of the d′ values for the isolated cues. Data above the diagonal represent cases where the combined effect of cues is greater than the vector sum of their isolated effects. The dashed line gives the prediction for the maximum effect of a model of object formation described in the discussion.

Returning to the original goal of the study, we can evaluate whether a simple mathematical expression exists to describe this interaction. From Fig. 2, the relation between the curves for isolated and combined cues can be expressed as

$$d\prime (\theta \circ F0)\approx \mathrm{\text{kd}}\prime (\theta ),$$ (2)

where k is the ratio of slopes (combined relative to individual) and d′ (θ) ≈ d′ (F0). Substituting in Eq. (1),

$$\mathrm{H}[\mathrm{k}d\prime (\theta )]\approx 2\mathrm{H}[d\prime (\theta )].$$ (3)

Eq. (3) is known as a Schroeder equation, and a solution is given by a power-law function H(z) = z^p, where p = log(2)/log(k).¹⁹ Rewriting Eq. (3), the relation between the combined and individual psychometric functions is given by

$$\hspace{0.17em}d\prime (\mathrm{\theta }\circ \mathrm{F}0)\approx 2^{1/\mathrm{p}}d\prime (\theta ).$$ (4)

We have thus shown in Eq. (4) that a simple mathematical expression does indeed exist to describe the interaction between the effects of voice F0 and spatial separation in this simulated CPL task. The magnitude of that interaction differs for different listeners, but in each case is described well by a single free parameter 0 < p ≤ 2.

IV. DISCUSSION

The results of this study reveal an apparent synergistic interaction between voice F0 and spatial cues wherein the benefit received from their combination exceeds the simple sum of the benefit received from each cue presented in isolation. The nature of this interaction is described by a more general form of additivity in which a power-law transformation is applied to the individual and combined effects of the cues prior to summation. Similar results have been reported in the literature on auditory masking.^11–13 Here the combined effect of two equally effective maskers is found to exceed the simple sum of the individual effects of the maskers, but is nonetheless well described by a power-law transformation that preserves the general form of additivity given by Eq. (1).^14,15,20 Of course the masking results represent a combination that has a detrimental rather than a facilitatory impact on listener performance, a reverse case of the relationship shown in this experiment. Other studies, as noted in the introduction, have reported a sub-additive interaction between cues.^4,5 Methodological distinctions, particularly the control of the relative effectiveness of the “F0 Cue in Isolation”/“Spatial Cue in Isolation” conditions could have been responsible for the difference in outcomes. Notably, the one study by Darwin et al., wherein the effectiveness of cues was equated before they were combined, obtained results consistent with the super-additive relation reported here.⁷ Measuring across a range of performance levels in d′, as done here, also controlled for potential ceiling effects on performance, which might have occurred in other studies.

It is tempting to speculate on the possible connection of the present results to the phenomena of auditory object formation. In the literature, auditory object formation has been defined as the perceptual grouping of sound components into a larger perceived single entity or whole—the whole being perceived to be greater than the sum of the perception of its individual parts.²¹ In this experiment these sound components would be the spatial position and F0 of the talkers and the larger entity (object) would be the perception of a distinct talker resulting from the combination of these components. Figure 4 provides an analogy from vision. Here the perception of a triangle on the right emerges only when the individual features on the left are combined. Such effects are most striking in visual examples, but it seems likely they influence auditory perception as well in a way that could serve to the listener's benefit in cocktail party listening situations.

FIG. 4.

The figure serves as a visual representation for how the spatial and voice F0 cues might work together in this experiment to help listeners segregate talkers through object formation (Ref. 22). The first two grouping of features on the left are analogous to the cues in isolation, and the third group on the right is analogous to their combination where a triangle appears as an emergent object that aids in the segregation from other objects.

We can use this idea to make a precise prediction for the form of the psychometric functions shown in Fig. 2. The proportional relation between d′ and Δ/σ given by the data suggests a simple model in which the failure to perceptually segregate the A and B vowel streams causes the listener to weigh some elements of the B stream in their decision. Let ΔA_j and ΔB_j be the mean values of Δ_j sampled for the A and B triplets on the jth trial, then the listener responds “two talkers” if and only if the weighted combination of ΔA_j and ΔB_j exceeds some decision criterion,

$$\text{Respond}\hspace{0.17em}“\text{two}\hspace{0.17em}\text{talkers}\text{'}\text{'}\hspace{0.17em}\text{iff}\hspace{0.17em}{\Delta }_{\mathrm{j}}=\hspace{0.17em}\mathrm{w}\Delta {\mathrm{A}}_{\mathrm{j}}+\hspace{0.17em}\left(1-\mathrm{w}\right)\Delta {\mathrm{B}}_{\mathrm{j}}>\hspace{0.17em}\text{criterion},$$ (5)

where 0.5 ≤ w ≤ 1 gives the relative weight on the two sequences. The prediction for the psychometric function is

$$d\prime =\hspace{0.17em}\mathrm{k}\{\mathrm{E}{\left[{\Delta }_{\mathrm{j}}\right|2\hspace{0.17em}\text{talkers}\left]\hspace{0.17em}-\hspace{0.17em}\mathrm{E}\right[{\Delta }_{\mathrm{j}}|1\hspace{0.17em}\text{talker}\left]\}/\mathrm{E}\right[\mathrm{V}({\Delta }_{\mathrm{j}})]}^{1/2}$$ (6)

where E[Δ_j] is the expected value Δ_j, V(Δ_j) is its variance, and k is a constant representing the effect on d′ of factors other than w. From Eq. (5), Δ_j is seen to be the sum of two normal random variables, wΔA_j and (1-w)ΔB_j. The expectation of Δ_j is thus given by the sum of the expectations of wΔA_j and (1-w)ΔB_j, and the variance by the sum of the variances of wΔA_j and (1-w)ΔB_j. Applying these operations, the numerator of Eq. (6) reduces to kwΔ and the denominator reduces to σ. Rewriting Eq. (6),

$$d\prime =\hspace{0.17em}\text{kw}\Delta /\sigma .$$ (7)

The form of the psychometric function given by Eq. (7) is precisely that of the obtained psychometric functions shown in Fig. 2, linear with w, representing the degree of perceptual segregation, now affecting the slope of the functions. The value of w ranges 0.5–1.0, no segregation to perfect segregation. Thus, the increase in segregation resulting from object formation can be expected to improve d′ performance for the combined cues by as much as a factor of 2 over that predicted by the vector sum of the individual effects of the cues. The dashed line of Fig. 3 shows the maximum improvement expected. Some points exceed the maximum, but this is to be expected given the variability in the estimates that go into the difference of d′s plotted here. Notwithstanding, the data as predicted fall roughly within the range between the maximum and the diagonal representing the vector sum of effects.

V. CONCLUSION

The results of this study reveal, as one might expect, that listeners perform better in cocktail-party listening when both voice F0 and spatial segregation cues are available than when whether either cue is presented in isolation. Of greater interest was that, for all but one listener, the improvement in performance exceeded what would be expected based on the simple vector sum of the individual effects of the two cues, suggesting a synergistic interaction of the cues. The improvement beyond expected moreover increased with increasing Δ/σ ratio of cues, representing the acoustic differences between talker voices. The results are consistent with a form of super-additivity of cues wherein additivity is preserved with a power-law transformation relating the combined to the individual effects of cues. Parallels are noted to the super-additive effects of masker combinations in masking studies and may be related to the perceptual process of object formation.