Abstract
New approach methodologies (NAMs) for chemical hazard assessment are often evaluated via comparison to animal studies; however, variability in animal study data limits NAM accuracy. The US EPA Toxicity Reference Database (ToxRefDB) enables consideration of variability in effect levels, including the lowest effect level (LEL) for a treatment-related effect and the lowest observable adverse effect level (LOAEL) defined by expert review, from subacute, subchronic, chronic, multi-generation reproductive, and developmental toxicity studies. The objectives of this work were to quantify the variance within systemic LEL and LOAEL values, defined as potency values for effects in adult or parental animals only, and to estimate the upper limit of NAM prediction accuracy. Multiple linear regression (MLR) and augmented cell means (ACM) models were used to quantify the total variance, and the fraction of variance in systemic LEL and LOAEL values explained by available study descriptors (e.g., administration route, study type). The MLR approach considered each study descriptor as an independent contributor to variance, whereas the ACM approach combined categorical descriptors into cells to define replicates. Using these approaches, total variance in systemic LEL and LOAEL values (in log10-mg/kg/day units) ranged from 0.74 to 0.92. Unexplained variance in LEL and LOAEL values, approximated by the residual mean square error (MSE), ranged from 0.20–0.39. Considering subchronic, chronic, or developmental study designs separately resulted in similar values. Based on the relationship between MSE and R-squared for goodness-of-fit, the maximal R-squared may approach 55 to 73% for a NAM-based predictive model of systemic toxicity using these data as reference. The root mean square error (RMSE) ranged from 0.47 to 0.63 log10-mg/kg/day, depending on dataset and regression approach, suggesting that a two-sided minimum prediction interval for systemic effect levels may have a width of 58 to 284-fold. These findings suggest quantitative considerations for building scientific confidence in NAM-based systemic toxicity predictions.
Keywords: uncertainty, variance, in vivo data, ToxRefDB, predictive models
Introduction1
Chemical safety assessments use in vivo toxicology studies for hazard identification and characterization, including derivation of points-of-departure (PODs). A POD is dose that marks the lower estimate for some response and may correspond to the no or lowest observable adverse effect level (NOAEL or LOAEL), or in some instances a modeled benchmark dose (BMD). The POD is used together with a set of uncertainty or assessment factors for calculating a reference dose (RfD) or derived no effect level (DNEL). However, the present and growing number of chemicals with little to no associated toxicity information (ECCC/HC, 2016; Judson et al., 2009; Judson et al., 2012) highlights the need to use in silico and in vitro approaches, termed new approach methodologies (NAMs) (USEPA, 2018) in hazard characterization to estimate PODs. In the United States, the Frank R. Lautenberg Chemical Safety for the 21st Century Act (Congress, 2016) mandates that vertebrate animal studies should be reduced or replaced to the “extent practicable and scientifically justified” in toxicity testing, while setting a standard that the NAMs need to provide “information of equivalent or better scientific quality and relevance.” In a memo, Directive to Prioritize Effects to Reduce Animal Testing, U.S. Environmental Protection Agency Administrator Andrew Wheeler reiterated these points and further specified goals of a 30% reduction in mammalian animal studies requested by 2025, with complete elimination of mammalian animal study requests by 2035 except in the case of exceptions at the discretion of the Administrator (Wheeler, 2019). Thus, although the need and legislative mandate to develop NAMs is clear, an obstacle to adoption of NAMs for use in regulatory toxicology is understanding the fit-for-purpose performance requirements (Casati et al., 2018; Kleinstreuer et al., 2017; Patlewicz et al., 2013; Rovida et al., 2015).
A number of efforts have been made to derive predicted systemic toxicity PODs for screening-level assessment when in vivo data are not available, and along with some of these efforts, quantification of the variability in the reference data has been reported to some extent. Two primary approaches available in the literature for prediction of a POD are (1) systematic read-across (Low et al., 2013; Shah et al., 2016), involving estimating a POD based on chemical structure similarity to a chemical with adequate hazard characterization, and (2) quantitative structure activity relationship (QSAR) prediction models for PODs based on chemical structural features associated with a training set of animal data (Hisaki et al., 2015; Mumtaz et al., 1995; Pizzo and Benfenati, 2016; Rupp et al., 2010; Toropov et al., 2015a; Toropova et al., 2015; Veselinović et al., 2016). One such predictive model, a multi-linear regression QSAR model of chronic oral rat lowest observable adverse effect level (LOAEL) values for approximately 400 chemicals, demonstrated a root mean square error (RMSE) of 0.73 log10(mg/kg/day), which was similar to the size of the variability in the training data, ± 0.64 log10(mg/kg/day), approximated as two times the mean standard deviation. These findings suggested that the error contributed by the predictive model itself was small, as the overall error in predictions approached the error in the reference data from different laboratories (Mazzatorta et al., 2008). In another study, artificial neural networks were used to model subchronic oral (RMSE = 0.111 log10(mg/kg/day)) and inhalation (RMSE = 0.133 log10(mg/kg/day)) no observable adverse effect levels (NOAELs) in rats for 120 chemicals (Dobchev et al., 2013). The Monte Carlo approach available in CORAL software has also been used in a number of cases to model subchronic oral rat NOAEL values, producing a spectrum of R-squared values from 0.46–0.71, suggesting that the inputs to these predictive models could only account for 50–70% of the variance in the reference data (Toropov et al., 2015b; Toropova et al., 2017; Veselinović et al., 2016). Another predictive NAM for systemic lowest effect levels (LELs) used a hybrid descriptor set, including in vitro bioactivity from ToxCast (Truong et al., 2017), physicochemical properties, and high-throughput toxicokinetic (httk) data (Pearce et al., 2017), to predict in vivo data collected from the US EPA Toxicity Reference database (ToxRefDB) (Martin et al., 2009b; Martin et al., 2009c) the Hazard Evaluation Support System database (HESS-DB), and the Cosmetics to Optimize Safety database (COSMOS-DB). Truong and colleagues (Truong et al., 2017) found that in developing a baseline expectation of predictive model performance, chemical and study-level information from the in vivo dataset accounted for 74% of the total variance in the prediction. It would be helpful to understand the sources of variance in the in vivo data used as a reference and in training, and to better quantify this variance and the contributions of chemical information and study-level descriptors (i.e., covariates). It is often difficult to understand how much variance in NAM-based predictions like these is due to the NAM approach because most reports on NAMs for POD prediction do not define and/or clearly report the variability or reproducibility in the in vivo training set data.
Indeed, the reproducibility of in vivo animal study results has been a continuing topic of interest in toxicology. A previous evaluation of the rodent carcinogenicity classifications from two different data sources demonstrated only 57% concordance (carcinogenic/non-carcinogenic), with seemingly strong influences of species and strain on the result and the reproducibility (Gottmann et al., 2001). An evaluation of an in vitro estrogen receptor pathway model (Browne et al., 2015) was dependent on comparison to available in vitro estrogen receptor activity data and in vivo rodent uterotrophic bioactivity data. Kleinstreuer and colleagues showed that even in high quality studies for the rodent uterotrophic bioactivity assay, concordance (causing uterine weight gain, yes or no) was only achieved 74% of the time for replicate uterotrophic assays (Kleinstreuer et al., 2015), suggesting that if those data were used as the standard for comparison, NAMs could not predict the results of the uterotrophic with greater concordance. The reproducibility of both quantitative and qualitative findings in animal studies is impacted by the variance contributed by experimental design parameters, biological variability, and other unknown factors. As such, documented study descriptors can only account for a portion of the variance between the potency values obtained between animal studies for a given chemical. Possible contributors to variability observed in POD values derived from different studies include but are not limited to: animal species and strain, study type and duration, study source and year, chemical and associated purity, route of administration, spacing and number of doses used, and sex of the animal. Additionally, there will be unknown contributors to variability, including biological variability; experimental design parameters typically not documented in the study report (Claassen and Huston, 2013), e.g. the gender of the animal handlers (Sorge et al., 2014), the composition of the feed (Jensen and Ritskes-Hoitinga, 2007), and intestinal microbiota (Ericsson et al., 2015; Weitekamp et al., 2019); or sources of systematic error from equipment or procedures. Thus, contributors to variability in POD values for an in vivo study include those that can be explained, i.e. study-level covariates captured in databases like ToxRefDB, and those that are unexplained due to lack of recorded information or understanding of how unknown factors may contribute to variability. While we might naively expect that chemical identity and study descriptors would completely explain the outcome of an in vivo toxicity study, the presence of any unknown factors (i.e., unexplained variance) in the derivation of the POD limits the accuracy of any prediction using NAMs.
Using performance comparisons to animal study data to develop scientific confidence in NAMs is necessarily limited by the uncertainty present in the animal study data: NAMs cannot predict animal data used as a reference with greater accuracy than the precision in replicate reference data (Casati et al., 2018). If the underlying animal data used to train a predictive NAM are variable or noisy, the accuracy of the predicted PODs will be limited by the training data variability. One needs to know how much of this lack of forward predictivity is due to a less than perfect predictive NAM, and how much is due to the noise in the training data. Answering this question may help judge whether a model has acceptable performance for its purpose (Casati et al., 2018). The variance in the training data defines the minimum variance associated with a NAM, with the likelihood that the NAM will contribute additional variance or uncertainty. Thus, if a component of building scientific confidence in NAMs involves a performance comparison to animal toxicity studies, an understanding of the quantitative variability in these reference data is needed to understand how much NAM uncertainty may be due to variability in the reference data, particularly if these data were used as training set data.
In the present work, statistical approaches were used to estimate the variance in LELs and LOAELs from in vivo studies of adult animals described in the publicly-available Toxicity Reference Database (ToxRefDB) version 2.0 (Watford et al., 2019). In doing so, we addressed two primary questions regarding these reference data for systemic effects: (1) for a given chemical, what is an estimate of a bound on accuracy for NAM prediction of systemic toxicity given the variability in effect levels from in vivo reference data; and, (2) what is an estimate of the upper limit on the performance of a NAM based on available reference data, i.e. what is the maximum amount of variance that a NAM can explain in this reference data set? Herein we estimate the size of a “minimum prediction interval,” i.e. the interval in which a new observation or model prediction would be expected to fall; this minimum prediction interval is based on variance estimates of systemic toxicity information in ToxRefDB, and does not reflect variance that would likely be contributed by a less than perfect NAM or predictive model. Importantly, this work sets a threshold on the accuracy expected from predictive modeling of systemic PODs and may help inform fit-for-purpose acceptance criteria for PODs derived from NAMs.
2. Methods
2.1. Overview of experimental approach
A reference of the statistical terms used in this work is provided in Table 1. In a first approach we used multi-linear regression (MLR) and robust linear regression (RLR) to estimate the total variance, and the amount explained by study descriptors (Figure 1), for 2724 study records of 563 chemicals (Figure 2). This analysis combined effects in adults across study types and assumed that study descriptors independently contributed to variance. In a second approach, referred to as an augmented cell means (ACM) approach, studies were grouped for variance estimation using a more stringent requirement for replication, defining “cells” of replication, such that replicate studies shared categorical descriptors (chemical, study type, species, sex, and administration method), accounting for potential interactions among these descriptors. The ACM approach reduced the dataset size from the MLR approach, but the ACM approach may better account for interactions among study descriptors and the imbalanced nature of the dataset (i.e., not all combinations of the study descriptors occur in the dataset and not all combinations occur with similar frequencies). The MLR and ACM approaches were further used on data subsets by study type. For all models, the variance left unexplained by study design descriptors was estimated by the mean square error (MSE), which represents the difference between the model predictions and the values being estimated, or residual variance. In modeling applications, the MSE limits the maximal coefficient of determination, or R2, which is the proportion of the variance in the data that can be accounted for using the descriptors available.
Table 1.
Statistics reference.
| Term | Concept | More detail found in |
|---|---|---|
| Accuracy | The degree to which a value matches the “true” value; in context, NAM accuracy to predict reference in vivo data cannot exceed the reference in vivo data accuracy for predicting itself. | NA |
| Explained variance | Amount of the total variance that can be explained by the regression model built using study descriptors, where the unexplained variance is approximated by MSE. | Methods Section 2.3.3 |
| Minimum prediction interval | A prediction interval is the possible range for a new value given some dataset and model with their own contributions to variance. The minimum prediction interval defined in this work is the possible range of a new value given the variance in the in vivo data available for training. Thus, only a perfect model could have a “minimum prediction interval” because all other models will contribute additional variance and width to the prediction interval. | Methods 2.3.7 |
| MSE, also known as the residual mean square error | MSE for the regression model is the residual sum of squares divided by the degrees of freedom for the regression model, where the residual sum of squares is equal to the sum of the squared difference between each empirical observation Yi and the predicted value for observation i (f(xi), and the degrees of freedom are equal to the number of observations, n, and the number of covariates (in this case, study descriptors). | Methods Section 2.3.3, 2.3.5., Equation 3 |
| % total variance explained | % total variance explained by study descriptors. In practice, this is the same as the coefficient of determination or R-squared. | Methods Section 2.3.3, Equation 4 |
| Predictive model | A model that is constructed for forward prediction of unavailable values, typically trained on reference data. | NA |
| Regression model | A statistical model of the existing data; seeks to explain variance in the current dataset rather than creating a forward prediction. | NA |
| RMSE, also known as residual root mean square error | RMSE is the square root of the MSE and gives a measure of the residual spread or standard deviation for the regression model, in the same units as the LEL and LOAEL values (whereas the total variance and MSE are unitless). For normally distributed residual values, 95% of residuals should fall between ±1.96*RMSE. In this work, RMSE is used to approximate what a minimum prediction interval might be for a prediction model using these data as a reference. | Methods 2.3.5 |
| R-squared or R2 (coefficient of determination) | The proportion of variance in a dependent variable that be explained by a regression model or independent variable. The maximum R2 for a model representing some data is limited by the percent of the total variance that is explained by the available regression model parameters (in this work, study descriptors). | Methods 2.3.5 |
| Total variance | Explained + Unexplained variance; the sum of the squared deviations of every observation from the sample mean divided by the degrees of freedom for the sample | Methods 2.3.3, Equations 1 and 2 |
| Uncertainty | When applied to reference in vivo data in this work, uncertainty might be quantified as a confidence interval for a mean value or perhaps the minimum prediction interval for a new predicted LEL or LOAEL value. | NA |
| Unexplained variance | The portion of the variance that is not explained by the regression model built using study descriptors. This is estimated as the MSE. | Methods 2.3.3, Equation 1 |
| Upper bound of performance | In reference to a predictive model; the limit on how precise a predictive model could be given the reference data used in training. In this work, the upper bound of performance includes the upper bound on an R2 for a model of these data and the maximum accuracy of a prediction model for systemic toxicity values (i.e., the minimum prediction interval). | NA |
| Variability | The spread or dispersion of some data. | NA |
This table explains statistical terms used in this work.
Figure 1. Variance estimation workflow for this study.

The variance estimation workflow for this study begins with ToxRefDB version 2.0. (A) outlines the workflow for more permissively defined study replicates to enable a larger dataset for consideration of variance coupled with MLR and RLR, whereas (B) outlines the workflow for more stringently defined study replicates using the ACM modeling approach. In (A), the full dataset requires that replicate LEL or LOAEL values come from adults only; systemic endpoints only; oral exposures only; and, exposures in mg/kg/day units. This full MLR and RLR dataset was then subset by study type. In (B), the same filtering criteria as in (A) were used, with the added requirement that study replicates be defined as “cells” by requiring categorical variables to be the same. This smaller full ACM dataset was also subset by study type. Variance calculations were executed on the full datasets and the subsets by study type.
Figure 2. Variance model for the toxicity dataset.
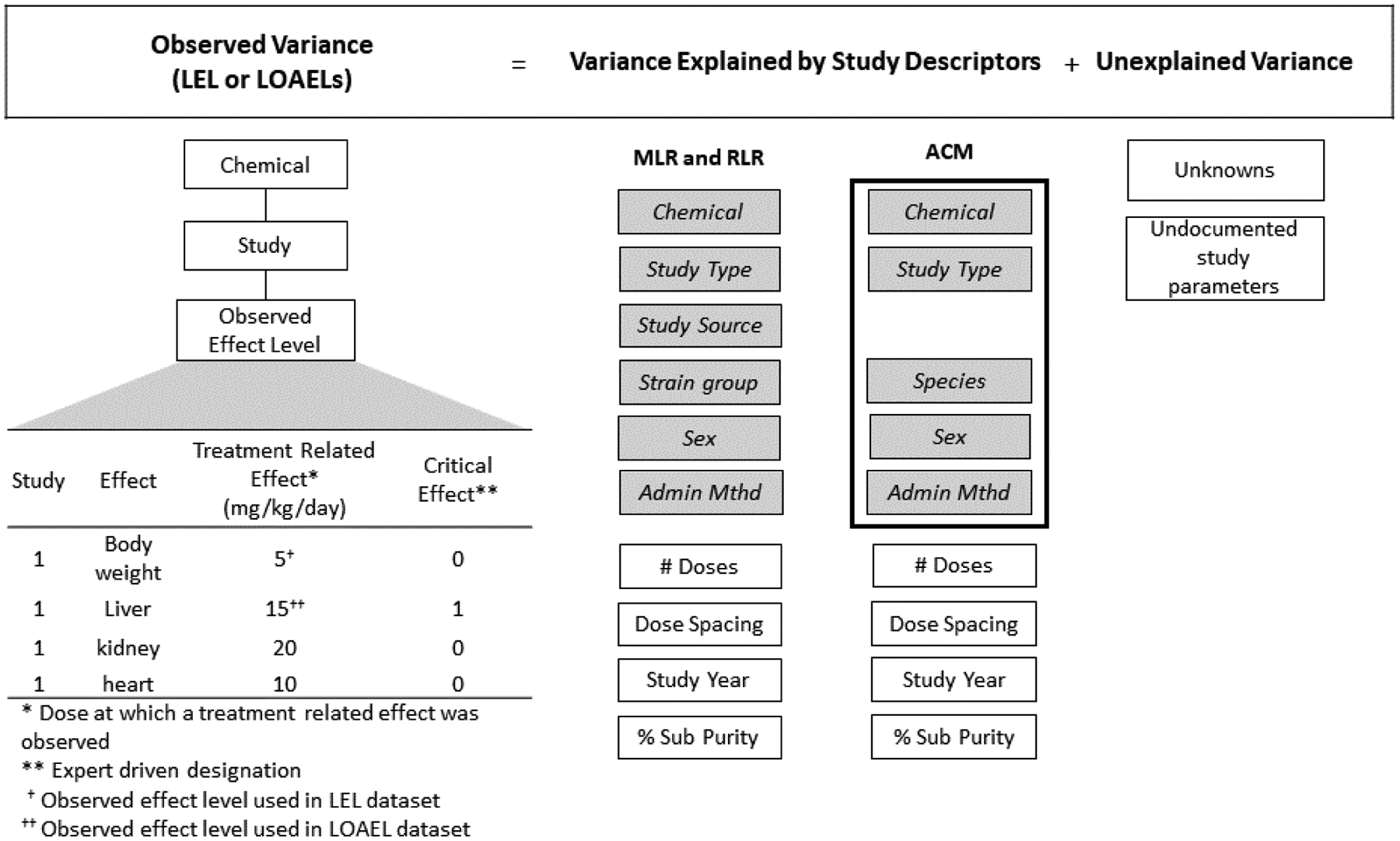
The observed variance in effect levels (LEL = lowest effect level; LOAEL = lowest observable adverse effect level) for a chemical across multiple studies is described as the sum of the explained variance (given by the variance in identified study parameters) and unexplained variance. The LEL is the lowest treatment-related effect observed for a given chemical in a study, and the LOAEL is defined by expert review as coinciding with the critical effect dose level from a given study. Multiple studies for a given chemical yield multiple LELs and LOAELs for computation of variance. MLR = multilinear regression; RLR = robust linear regression; ACM = augmented cell means; Adm. Method = administration method; % Sub Purity = % substance purity used in the study. The gray shaded study descriptor boxes are categorical variables, and the white study descriptor boxes are continuous variables. The box around five categorical study descriptors for the ACM indicates these were concatenated to a factor to define study replicates.
2.2. Database used
2.2.1. Data source
ToxRefDB version 2.0 was used as the data source for this work (USEPA, 2019; Watford et al., 2019); it contains information curated largely from studies conducted in accordance with or by specifications similar to the EPA Office of Chemical Safety and Pollution Prevention (OCSPP) 870 series Health Effects Test Guidelines, with records associated with 1142 chemicals and 5960 studies (including guideline and guideline-like studies) (Figure 1). The single largest source of these data was obtained via curation of reviews of registrant-submitted toxicity studies, known as data evaluation records (DERs), from the USEPA’s Office of Pesticide Programs (OPP) within the OCSPP, with additional data obtained from studies available from the National Toxicology Program, the pharmaceutical industry, and the publicly-available literature. The database includes information regarding the study design, the Health Effects 870 series guideline if applicable, chemical identity, treatment group parameters, and treatment-related effect levels, i.e. the doses at which an effect was significantly different from control (Martin et al., 2009a; Martin et al., 2009d). Additionally, study-level critical effects are curated within ToxRefDB (for records from OPP DERs and some expertly reviewed studies from other sources), which designate the LOAEL value at a study level.
To include the largest number of studies available with systemic LELs and LOAELs, we initially included data from five different study types to form the full datasets: chronic (CHR), subchronic (SUB), multi-generation reproductive (MGR), developmental (DEV), and sub-acute (SAC). Only observations in adult or first-generation treatment groups (F0) were used from the DEV and MGR studies. We also limited the dataset to include only study designs with an oral administration route, but placed no restrictions on administration methods, e.g. feed, capsule, gavage/intubation, or water were allowed if the dose unit was available as mg/kg/day. The limited number of studies available using other administration methods (e.g. intravenous, inhalation) prevented reasonable consideration of these administration methods. Only studies in which treatment-related effects were observed were included to ensure that an LEL level could be derived. Finally, the dataset was limited to studies that included mouse, rat, dog, or rabbit. This resulted in an initial full dataset that corresponded to 563 chemicals and 2724 study records (Figure 1A).
2.2.2. Effect level data
LELs were calculated here as the log10(mg/kg/day) of the lowest dose for which a statistically significant treatment-related target organ, clinical chemistry, or in-life observation (e.g. body weight, clinical signs) effect was observed in the study. In contrast, LOAEL values were defined by expert review to determine the critical effect level either as part of the hazard assessment process (reflected in study summaries obtained from US EPA DERs) or via similar weigh-of-evidence process developed for data curation of ToxRefDB v2.0 (Watford et al., 2019). A study LEL may equal a study LOAEL if the effect observed at the LEL was also deemed a critical effect. To preserve the number of studies for this analysis, if a critical effect was not identified for a given study, the LEL value for the study was used as the LOAEL (this was true for 11% of the full dataset, or 305 of the 2724 study records). Use of LOAELs as a second dataset was based on the hypothesis that use of these expert-informed values that reflect adversity might reduce the heterogeneity of the effect levels between studies for a given chemical. If the threshold for adverse effects was consistent for a chemical across studies, or between multiple iterations of a given chemical-study type pair in the database, then effect values would demonstrate a reduced total variance. The full dataset demonstrated 67% concordance of the LEL and LOAEL values (1830/2724 studies), including the ~11% of records where LOAEL was inferred as equal to the LEL. A complete list of endpoint categories, endpoint targets, and effects used in this analysis is provided in Supplemental File 1 Table 1 within the full dataset used for MLR and RLR.
2.3. Variance and regression approaches
2.3.1. Study descriptors
Ten study descriptors were used in MLR and RLR statistical modeling, including six categorical descriptors (chemical, study type, study source, strain group, sex, administration method) and four continuous descriptors (number of doses, dose spacing, study year, and substance purity) (Table 2, Figure 2). For the ACM statistical modeling, the categorical study descriptors chemical, study type, species, administration method, and sex were used; these were combined into a factor to define a study replicate. All study descriptors are summarized in Table 2. For the MLR and RLR, strain and species were combined into a single study descriptor termed strain group, defaulting to species only when strain was not available. Similarly, administration route and method were combined into a single study descriptor, defaulting to the administration route when method was unavailable. Dose spacing by study (i.e. log10-dose spacing) was calculated by averaging the distance between each test chemical dose (excluding the vehicle control). Dose spacing, study year, and substance purity were all centered about the mean, with missing values changed to the mean.
Table 2.
Study descriptors used in the MLR and ACM analyses.
| Study Descriptor | Conditions | Adjustments |
|---|---|---|
| Chemical | Identified using CASRN and chemical name | |
| Study Type | CHR, SUB, DEV, MGR, SAC | Only adults and parental animals were considered |
| Study Source | OPP, NTP, Pharma, Open Lit | Missing values were assigned value “unknown”; not used in the ACM models |
| Strain Group or Species | Species used: mouse, rat, dog, rabbit | The term “strain group” indicates that when strain was not specified, the species name was assigned. For MLR, since all data were used, strain group was used as a descriptor. For ACM, species was used as a descriptor to allow for more cells. |
| Sex | Male, Female, Male & Female | |
| Administration Method | Feed, Capsule, Gavage/Intubation, Oral, Water | NAs, “Not Reported,” and “Unassigned” were assigned the value “Oral” |
| Number of Dose Levels | Number of non-control, treatment related doses | |
| Dose Spacing | Average distance between each dose | Values were centered about the mean |
| Study Year | 1959 to 2012 | Values were centered about the mean; NAs changed to mean |
| % Substance Purity | 77% to 100% | Values were centered about the mean; NAs changed to mean |
Any adjustments, calculations, and conditional filters used are also indicated. CASRN = CAS registry number; CHR = chronic; SUB = subchronic; DEV = developmental; MGR = multigenerational reproduction; SAC = subacute; OPP = Office of Pesticide Programs data evaluation record as a source; OpenLit = open literature a source; NTP = National Toxicology Program as a source; Pharma = donated studies from the pharmaceutical industry.
2.3.2. Defining replicate studies for regression
This work requires defining replicate studies for consideration of the spread, or variance, in the LELs and LOAELs for a given chemical. Defining a replicate study for a given chemical is a challenge: in computational modeling, scientists might consider all effect level values associated with repeat dose adult systemic effects, regardless of study type and duration; yet, a reasonable hypothesis is that variance in systemic effect levels from replicate study types are influenced by the study type, and that study type and other study descriptors may not contribute independently to variance. For instance, because many of the study records reflect guideline adherent or guideline-like studies, study type may be confounded with species, sex, and administration method as the OCSPP Health Effects 870 series guidelines stipulate certain conditions to be followed. How replicate studies are defined is critical for understanding variance estimates for these effect level data; the desire to have a permissive definition of “replicate” and use the maximum dataset possible to avoid skewed variance estimates should be tempered by the desire to understand how specific study descriptors, or elements of study design, may impact the quantitative variance between studies. In this work, we approach this in two different ways: (1) by considering the amount of variance accounted for by study type and other study level descriptors in a multilinear regression model of the largest dataset possible; and (2) by using two main approaches to regression modeling of these systemic effect level data on large datasets and datasets subset by study type. Note that when we use the term “regression modeling,” this is a statistical model of existing data; we have not developed a predictive model to be used in a forward sense in this work. Different regression models were used to characterize the variance: MLR (Jobson, 2012) and RLR, and an ACM (UCLA) model. We chose to use methods that parameterize the datasets differently in order to balance the two divergent concerns introduced above: (1) the ability to maximize the dataset size in order to provide a general estimation of uncertainty around effect level values and reduce the impact of possible outliers or database errors; and, (2) the ability to account for possible interactions among the study descriptors and the resulting uncertainty created by the interactions (see Figures 1 and 2).
The MLR and RLR approaches estimate the contribution of study descriptors to the total variance of an effect level (LELs or LOAELs). If these ten study descriptors were sufficient to describe the studies, then the predictions from MLR or RLR would perfectly reproduce the observations (i.e., with all of the variance explained). The use of MLR and/or RLR allows for the inclusion of all chemicals in which at least two studies were available, maximizing the dataset size; however, MLR and RLR assume that study descriptors contribute independently to variance. Possible interactions among the study conditions, e.g. sex and study type or study type and species, can result in an overestimation of the total variance. In contrast, the ACM approach accounts for the possible interactions among the categorical study descriptors. Thus, the ACM model uses a more stringent definition of “replicate,” resulting in a significantly smaller dataset available. A “cell” in the ACM models is a unique combination of categorical study descriptors, i.e. a unique combination of chemical, species, study type, administration method, and sex. The resultant ACM model estimates variance using the cell as a factor and four-continuous study descriptors (dose spacing, number of doses, study year, and substance purity). Using both the MLR/RLR and ACM methods provide a thorough perspective on variance in effect level data in ToxRefDB.
2.3.3. Total, unexplained, and explained variance
The total variance estimates in LEL and LOAEL values were calculated and can be understood as the sum of explained and unexplained variance in the data (Figure 2), as described conceptually by Equation 1.
| Eq. 1 |
Variance is a statistical measure, defined by the average of the squared differences from the mean, that indicates the “spread” of a data set. Here, we reference sample variance for Equation 2: total variance, s2, is given as the sum of the squared deviations of every observation, xi, from the sample mean, , divided by the degrees of freedom for the sample (n observations minus 1).
| Eq. 2 |
MLR, RLR, and ACM modeling approaches were then employed to indicate the fraction of variance in the LEL or LOAEL values that could be explained by a model. The explained variance in LELs and LOAELs in ToxRefDB was quantified as the fraction of the total variance that was accounted for by ten reported study descriptors used in modeling: chemical identity, strain group, sex, study type, administration method, dose spacing, number of doses, study year, substance purity, and study source (Table 2).
The fraction of the variance that was unexplained by study parameters was quantified as the estimated residual mean square error (MSE) (Equation 3). In Equation 3, MSE is defined as the residual sum of squares divided by the degrees of freedom for the regression model, where the residual sum of squares is equal to the sum of the squared difference between each observed POD, Yi, and the predicted value for a given observation, (f(ri)), and the degrees of freedom are equal to the difference of the number of observations, N, and the number of covariates, p (in this case, study descriptors).
| Eq. 3 |
The unexplained variance could be derived from one or more sources, including any variance not explained by study descriptors, e.g. the unknown differences between specific laboratories that conducted these studies, unknown study conditions (Consulting and Huff, 1989; Sorge et al., 2014) or biological variability of the animals used (Leisenring and Ryan, 1992). The percent of the total variance that can be explained relates to the total variance and the MSE, as indicated in Equation 4. Equation 4 is based on the concept that total variance is equal to the sum of the explained and unexplained variance, with the unexplained variance within observations approximated as MSE. Thus, the percent explained variance is equal to the difference of the total variance and the computed MSE, divided by the total variance, and then all multiplied by 100 percent as given below.
| Eq. 4 |
2.3.4. MLR, RLR, and ACM approaches
The regression modeling using MLR, RLR, and ACM approaches to explain variance in the LEL and LOAEL values is generically presented in Equations 5a and 5b. Equations 5a and 5b are simplified representations of multilinear regression equations that typically take the mathematical form of y = intercept + beta coefficient1*variable1 + beta coefficient 2*variable2 + beta coefficient 3*variable3 + beta coefficientn*variablen; these simplified equations show that the LEL or LOAEL was predicted using a collection of study descriptors, with each of these descriptors multiplied by a beta coefficient, otherwise known as a regression weight or slope value. RLR was used for comparison with MLR because RLR may be more “robust” against outliers in the dataset and heteroscedasticity (i.e., errors that are not independent and distributed normally). The study descriptors used and general approach (Figure 2) are the same for the MLR and RLR approaches. For the ACM models, a factor of the chemical, strain, study type, and administration method was used rather than considering those descriptors as independent contributors to the LEL and LOAEL variance. To the extent that there are interactions between chemical, strain, study type, administration method, and sex, the MLR approach would overestimate the unexplained variance or MSE; however, using the ACM approach decreases the dataset size considerably due to the more stringent definition of replicates, and this might decrease the unexplained variance estimate (or MSE) because of a smaller dataset size. Thus, both approaches were used for comparison.
| Eq. 5a |
| Eq. 5b |
2.3.4.1. Details of MLR and RLR modeling
The MLR modeling was performed using R base package “stats” lm() function (R version 3.6.1) (see section of the Methods on software). All ten study descriptors used to fit the MLR model are listed in Table 2. For the full dataset, chemicals with only a single study were discarded to prevent self-identification in the modeling process. Study-level LEL or LOAEL values were used as the primary response variable in the model. The significance of each study descriptor as a coefficient in the MLR model of variance was determined using p-values (α = 0.05) from an analysis of variance (ANOVA).
The residuals of the MLR model for the full LEL and LOAEL datasets were evaluated using five standard diagnostic plots (1) Residuals vs. Fitted, (2) Normal Q-Q, (3) Scale-Location, (4) Cook’s Distance, and (5) Residual vs. Leverage. The Residual vs. Fitted plot was assessed for any patterns to detect non-linearity in the residuals; equal dispersion of points around the red dotted line in the Residual vs. Fitted plot indicates that the residuals are linear and that regression assumptions may be appropriate. The Normal Q-Q plot was used to assess if the residuals were normally distributed; points deviating from the dotted unity line indicate potential deviation from a normal distribution of residuals. The Scale-Location plot was inspected for homoscedasticity (equal variance) in the residuals; in this plot, a horizontal red line with randomly distributed points on the top and the bottom is a good indicator of homoscedasticity. The Cook’s distance plot was used to identify observations with larger Cook’s distance scores, i.e. outlier points that may be influential in the regression. The Residual vs. Leverage plot was used to further identify points that may be influential, with high leverage. Points with high Cook’s distance may also be visually identified from this plot; in particular, points that fall outside of the curved dotted red lines have high Cook’s distance values. Points with high Cook’s distance were alternatively identified empirically as points with a distance greater than 4/N-p-1, where N is the total number of observations, and p is the number of coefficients in the model. To assess the potential influence of high leverage points, high Cook’s distance points from the Residual vs. Leverage plot, high Cook’s distance points, and all potential outliers and influential points on the MLR model, four additional MLR models were built with: (1) high leverage data points removed; (2) high Cook’s distance points from the plot removed; (3) high Cook’s distance points removed; and (4) all potential outliers removed (excluding all points identified using 1 through 3).
The RLR model used the same input specifications as the MLR model. The R package MASS (version 7.3–51.1) was used (function rlm()) with the default Huber M-estimation method. RLR (Venables and Ripley, 2002) is less sensitive to outliers in the dataset than the ordinary least squares method employed using MLR. RLR down-weights outliers in the dataset, but prediction intervals will be wider than MLR. RLR was only used to evaluate the full dataset (Figure 1A).
To assist in full interpretation of the MLR model of the full dataset, nested models were developed in a leave-one-out (LOO) approach (2011) to evaluate the relative impact of each study parameter on the total variance. An analysis of variance (ANOVA) was used to compare between full and nested models to evaluate the significance of each study descriptor.
For a thorough comparison of the regression approaches, an MLR model was also built using the same input (10 study descriptors) as described previously but including only the subset of studies in the ACM full dataset, described further in section 2.3.3.2 and Figure 1B.
2.3.4.2. Details of ACM modeling
ACM modeling was also used to estimate the contribution of selected study descriptors to the variance in LEL and LOAEL values (Figure 2). The ACM used herein is a combination of a cell means model for categorical descriptors and an MLR model for quantitative descriptors; thus, we termed this an “augmented” cell means model. In the implementation of cell means used in this ACM model, a new factor is created in which the levels are a unique combination of the categorical covariates. The factor in the ACM models is comprised of a unique set of chemical identity, species, administration method, study type, and sex. Only cells with at least two records, i.e. two replicates, were preserved in the ACM dataset (Figure 1B).
The ACM dataset was manually reviewed in an effort to remove study records that may have been duplicative. Replicates for the cells in the ACM dataset usually occurred due to one or more of the following scenarios: (1) the replicates originated due to different companies registering the same chemical and conducting separate studies; (2) study data were available from registrant-submitted studies and the NTP; (3) studies from the open literature resembled a guideline for which a registrant-submitted study was available; (4) pilot or range-finding studies run non-concurrently with a full study (a large portion of DEV studies fit this scenario); (5) the same registrant replicated a study to improve N, available measures, or dose range tested, sometimes many years apart, likely to refine a risk assessment question; (6) different purities of chemical were used, and current chemical mappings would not distinguish these as separate chemicals; and, (7) chronic exposures of different durations (6 versus 12 months in dogs, or 12 versus 24 months in rodents) that were not run concurrently for some reason (interim and terminal sacrifices were not allowed as replicates because these would be concurrent). Studies and/or cells were removed to curate the ACM full dataset to remove instances such as: (1) errors in chemical mapping, e.g. grouping of a metabolite and a parent as one chemical or mixtures grouped with a single parent chemical; (2) duplicate records between regulatory authorities such as the Pesticide Management and Regulatory Agency and EPA summaries of the same original study; (3) duplicate records due to DER updates; (4) replication of legacy data extraction; (5) duplicate records due to consideration of carcinogenic and chronic effects from the same animal cohort in separate study summary documents; and, (6) other special cases, e.g. only a single dose was retested in a follow-up study or additional analysis of the same original study.
2.3.5. MSE, RMSE, and defining an upper limit of performance
The MSE, or approximation of variance unexplained by the study descriptors, is used to compute the residual root mean square error (RMSE). RMSE is the square root of the MSE and gives a measure of the residual spread or standard deviation for the regression model, in the same units as the LEL and LOAEL values (whereas the total variance and MSE are in units of (log10-mg/kg/day)2).
The MSE is also critical for computation of the maximum coefficient of determination, or R-squared, for a model of systemic effect levels. The R-squared value indicates the proportion of variance explained by the model. The general relationship (Equation 6) between R-squared and MSE enables estimation of an optimal R-squared value for this specific reference dataset. The R-squared provides one estimate of an upper limit of performance for a predictive NAM that would use the systemic toxicity data in ToxRefDB as a reference set. In practice, the R-squared estimate in this work is the same as the % of total variance explained, but R-squared is presented to enable discussion of this more common metric of predictive NAM performance.
| Eq. 6 |
2.3.6. Modeling data subsets by study type
As study type relates strongly to study duration and the kinds of animals used, it was important to evaluate the hypothesis that replicates of a single study type would demonstrate reduced variance and unexplained variance estimates. The full datasets for MLR and ACM modeling were subset by study type, using CHR, SUB, and DEV study types only due to the number of studies available (Figure 1). Total variance, MSE, RMSE, and the percent of variance explained were calculated for MLR and ACM models of CHR, SUB, and DEV data subsets as described above.
2.3.7. Calculating the minimum prediction interval width
A minimum prediction interval is calculated in this work to demonstrate the range for the smallest amount of spread that would be anticipated for a forward prediction model that were to use the reference data described herein for prediction of systemic toxicity. The minimum prediction interval width expected is defined by the variability in the in vivo data that could be used as a reference set, as only a “perfect” prediction model would fail to contribute additional variability to a new, predicted value. Minimum prediction intervals for a prediction model built on these reference in vivo data are derived in two ways: (1) by examining the empirical cumulative distribution of the MLR regression model residuals, and assuming that the 2.5th percentile and 97.5th percentile approximate a 95% confidence interval for the regression model residuals; and, (2) assuming a normal distribution of residuals from the regression models, such that the 2.5th and 97.5th percentiles of a normal distribution multiplied by the regression model RMSE give the lower and upper bounds of a minimum prediction interval (i.e., the minimum spread of residuals from a prediction model will be the spread of the residuals from the reference data). Using Equations 7a and 7b, the lower and upper bound predictions based on the empirical cumulative distribution of MLR regression model residuals are calculated. Using Equations 7c and 7d, the lower and upper bound predictions based on the RMSE and normally-distributed residuals are calculated. The 2.5th and 97.5th percentiles of a normal distribution (as given by the qnorm() function in Equations 7c and 7d) are roughly −1.96 and 1.96. As the LEL and LOAEL values are in log10-mg/kg/day units, Equations 7a–7d are formatted to provide prediction bounds in mg/kg/day units for easier interpretation by un-logging the upper and lower prediction bounds.
| Eq. 7a |
| Eq. 7b |
| Eq. 7c |
| Eq. 7d |
2.4. Software and data availability
All analyses were performed with open source R version 3.6.1 and RStudio version 1.2.1335. The datasets used for MLR and ACM modeling are available as Supplemental File 1 (Tables 1 and 2). All of the R code used for this analysis and to make the figures in this work is available as an R Markdown file (exported as html) for Supplemental File 2. The code and data are also available for download at: ftp://newftp.epa.gov/COMPTOX/CCTE_Publication_Data/BCTD_Publication_Data/Paul-Friedman/Variability_in_vivo_data.
Results
The MLR (and RLR) full dataset corresponded to 563 chemicals and 2724 study records (Figure 1). The ACM full dataset contained 133 unique cells, or unique factors comprised of chemical, study type, species, sex, and administration method, that corresponded to 96 chemicals and 278 study records. Thus, a stringent definition of study replicates as defined by the ACM modeling approach reduced the dataset available for modeling by about 83% in terms of chemicals and by about 90% in terms of study records (Figure 1). The full datasets were comprised of information from CHR, DEV, MGR, SAC, and SUB study types, with CHR and SUB studies comprising the vast majority (approximately 70 to 75% of the MLR and ACM datasets, respectively) (Supplemental Figures 1 and 2). Most of these studies were from experiments with rats, with dog, mouse, and rabbit studies represented as well. The potential for study type by strain group interactions in the MLR and RLR models is evident in that the study type is highly related to the species and strain of animal used; for example, DEV studies following 870 series Health Effects Guidelines would be conducted in rat or rabbit, whereas CHR studies would not include rabbits, and this is reflected in the available dataset.
First, we quantified the total variance, and the MSE, RMSE, and percent variance explained by each regression model (Table 3) for the full datasets available for systemic LEL and LOAEL values. Overall, the total variance in large datasets of LEL and LOAEL values ranged from 0.744 to 0.916 (in units of (log10-mg/kg/day)2). Though the ACM full cell dataset was significantly smaller than the datasets used for MLR and RLR modeling, the total variance for the ACM full cell dataset was 0.858 for LELs and 0.750 for LOAELs, compared to 0.838 to 0.916 for LEL values and 0.744 to 0.792 for LOAEL values with the MLR and RLR datasets, respectively. Regardless of the regression type (RLR, MLR, or ACM) and the associated datasets, the total variance was slightly lower for the LOAEL datasets (ranging from 0.744 to 0.792) when compared to the LEL datasets (0.838 to 0.916).
Table 3.
Variance estimation results for full datasets.
| Regression Type | Data | LEL | LOAEL | N | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Total Variance | MSE | RMSE | % exp. | Total Variance | MSE | RMSE | % exp. | |||
| RLR | full dataset | 0.916 | 0.359 | 0.599 | 60.8 | 0.792 | 0.266 | 0.516 | 66.4 | 2724 |
| MLR | full dataset | 0.916 | 0.347 | 0.589 | 62.1 | 0.792 | 0.258 | 0.508 | 67.4 | 2724 |
| MLR | high leverage points removed | 0.908 | 0.339 | 0.582 | 62.7 | 0.781 | 0.250 | 0.500 | 68.0 | 2709 |
| MLR | high Cooks distance plot points removed | 0.911 | 0.339 | 0.582 | 62.8 | 0.788 | 0.254 | 0.504 | 67.8 | 2721 |
| MLR | high Cooks distance points removed | 0.842 | 0.261 | 0.511 | 69.0 | 0.748 | 0.200 | 0.448 | 73.3 | 2614 |
| MLR | all potential outliers removed | 0.838 | 0.261 | 0.511 | 68.9 | 0.744 | 0.200 | 0.448 | 73.1 | 2603 |
| ACM | full cell dataset | 0.858 | 0.320 | 0.565 | 62.7 | 0.750 | 0.254 | 0.504 | 66.1 | 278 |
| MLR | full cell dataset | 0.858 | 0.387 | 0.622 | 54.9 | 0.750 | 0.312 | 0.559 | 58.4 | 278 |
Multiple regression types (RLR = robust linear regression; MLR = multilinear regression; ACM = augmented cell means) with different full datasets were used to build models of the available data for variance estimation. Total variance and MSE are in units of (log10(mg/kg/day))2, whereas RMSE is in log10(mg/kg/day) units just like the dataset. % exp = percent total variance explained. N = number of study records in the dataset.
Several different models were built on the full datasets for comparison and to understand the stability of the MSE and RMSE for these LEL and LOAEL datasets. RLR and MLR modeling on the full dataset returned similar results; the MSE for the RLR model was slightly higher (0.359) than the MSE for the MLR model (0.347), resulting in a slightly larger RMSE (0.599 for RLR versus 0.589 for MLR). Robust regression was used because it is believed to be less susceptible to outliers and highly influential points in the dataset. However, the results were very similar, and if anything suggested that the RLR model might explain less of the variance in effect level data, and as such only MLR modeling was used in subsequent experiments. The MLR modeling approach is potentially susceptible to outliers and influential points, and so a series of experimental trials in removing potential outliers and high leverage points were conducted based on an analysis of the MLR residuals (Figure 3), with the hypothesis that removing potential high leverage or highly influential points might enable a MLR model that explained more variance in the dataset. Fifteen high leverage points (from 2724 total) were identified in the LEL and LOAEL datasets using plots of the residuals vs. fitted values; these points were removed from the dataset before reanalysis with MLR, yielding slight decreased total variance, MSE, and RMSE and subsequent 2% increase in explained variance from approximately 61% to 63% explained (Table 3). Similarly, points with high Cook’s distance identified using a standard diagnostic plot of the residuals vs. fitted values (Figure 3) and points with high Cook’s distance identified empirically were removed to build MLR models; dropping the high Cook’s distance points removed about 4% of the total dataset, decreased the total variance to 0.842, and increased the explained variance the most (by about 8%) to approximately 69% explained. Removing all potential outlier, high leverage, and high Cook’s distance points achieved similar performance. Together, the MLR models for the full dataset, even with all potential outliers removed, resulted in a total variance approaching 0.84 to 0.92, with percent explained variance of 61–69%.
Figure 3. MLR Regression Diagnostic Plots.
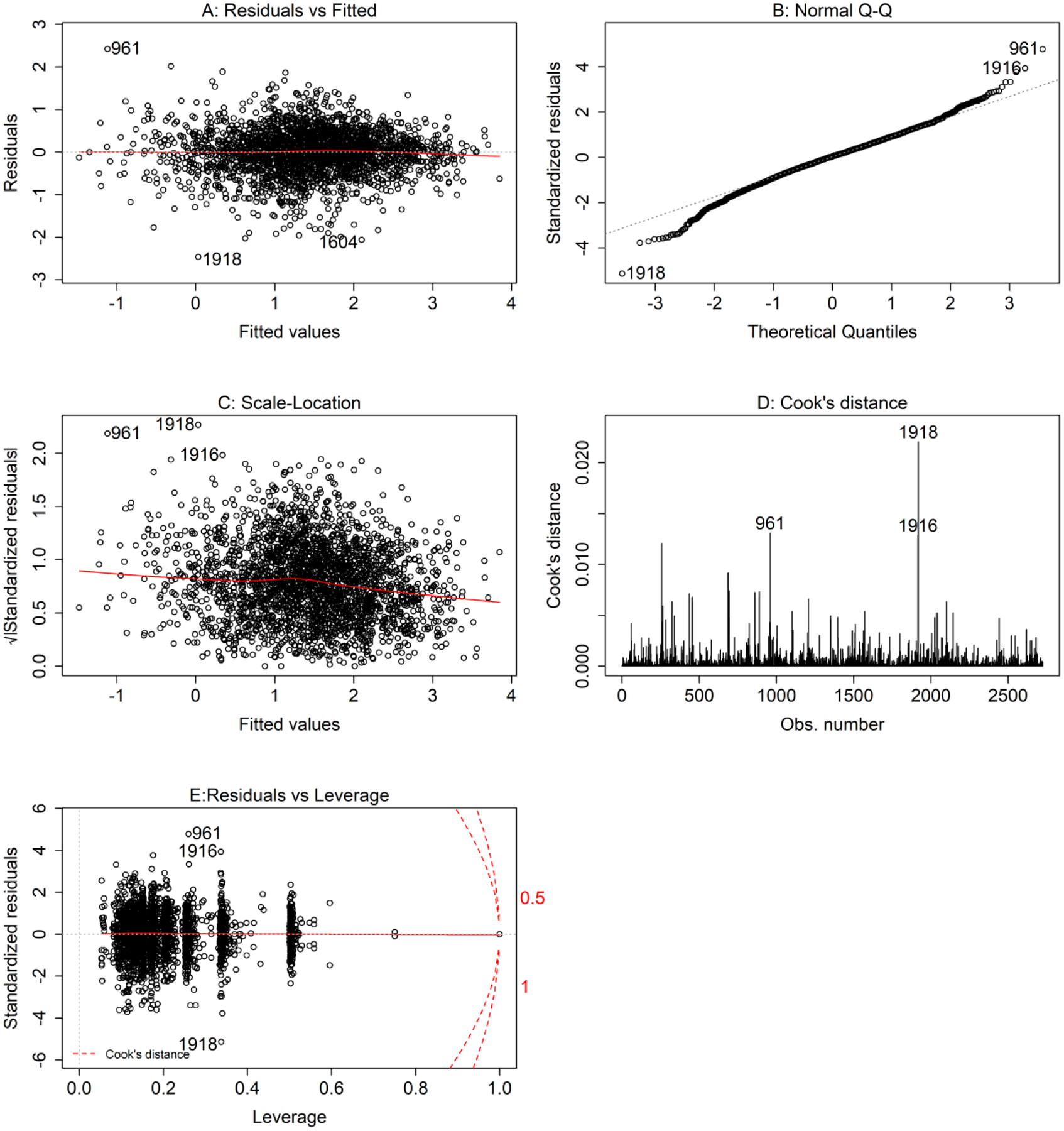
Standard diagnostic plots to evaluate the residuals for the MLR model of the full dataset. (A) is the Residuals vs Fitted plot; (B) is the Normal Q-Q plot; (C) is the Scale-Location plot; (D) is the Cook’s distance plot; (E) is the Residuals vs Leverage plot. Potential outliers are labeled by their observation number (961, 1916, 1918) in the dataset.
The standard diagnostic plots in Figure 3 further suggest that: (1) in Figure 3a, the residuals from the MLR model of the full dataset have a fairly linear pattern, based on a relatively equal dispersion of residuals over the fitted values; (2) in Figure 3b, the residuals are fairly normally distributed, based on alignment of most of the standardized residuals with the straight dotted line, with some deviation at the tails suggesting a slight long-tailed residual distribution; (3) in Figure 3c, the residuals appear spread well along the range of fitted values, based on a relatively straight red line; (4) in Figure 3d, that there were a few points with larger Cook’s distance (a metric of leverage and residual size); and, (5) in Figure 3e, that there may be a few suspected outliers, but that these points are not likely to be influential or extreme because no points fall to the outside of the curved dotted red lines. This work to examine the distribution of the residuals from the MLR of the full dataset support the use of assumptions that rely on normality, including assumptions such as approximating a minimum prediction interval using model RMSE.
An ACM model was also built using as much of the full dataset as possible, labeled as the full cell dataset. The full cell dataset was necessarily smaller than the full dataset because the “cell” in the ACM modeling approach required that chemical, study type, species, administration method, and sex were all identical for replicates. Though the dataset was approximately 10% of the size of the full dataset, the total variance, MSE, RMSE, and percent explained variance were very similar to the full dataset (Table 3). The total variances in the full cell dataset for LEL and LOAEL values were 0.858 and 0.750, respectively, compared to the full dataset with various MLR models, which demonstrated variances of 0.838 to 0.916 for LEL values and 0.744 to 0.792 for LOAEL values. The unexplained variance, as represented by MSE, was also similar; the MSE values for the ACM model of the full cell datasets were 0.320 and 0.254 for LEL and LOAEL values, respectively, compared to the MLR model MSE values of 0.261 to 0.359 for LEL values and 0.200 to 0.266 for LOAEL values. The RMSE values were also similar regardless of modeling approach for the full dataset and the full cell dataset. For completeness of comparison, an MLR model was built using the full cell dataset; as anticipated, the MLR model had higher MSE and RMSE values than the ACM model with the same data, which would result in a slightly wider estimate of a minimum prediction interval and a lower percent variance explained. Despite the small size of the full cell dataset, the MLR model values for this dataset are still within range of the other model results in Table 3. To the extent that there are interactions among the categorical study descriptors, such as study type and strain group, or study type and sex, the MLR model will overpredict the residual variance due to the assumption that these study descriptors independently and consistently contribute to variance, regardless of the chemical. However, the total variance, MSE, RMSE, and percent explained variance remained within a relatively small range regardless of the regression type and dataset used.
To better understand which study descriptors may have explained the greatest amount of variance in the MLR models, a leave-one-out approach for regression modeling was employed, meaning that MLR models were iteratively built and evaluated by ANOVA after removing one descriptor (Table 4). The MSE increased the most when chemical was removed from the MLR model, indicating that chemical explains more variance than any other descriptor; in fact, inclusion of chemical alone decreased the unexplained variance by nearly 50%. Strain group decreased the unexplained variance by about 6%, followed closely by study type which decreased unexplained variance by about 3%. Though administration method demonstrated a significant p-value by ANOVA (α = 0.05), the administration method may only have explained less than 1% of the explained variance. As administration method was constrained by an oral administration route, and nearly 65% of the full dataset was comprised of studies that used feed and 26% that used gavage; administration method may have been a less valuable study descriptor within this dataset and may have reflected the study types included. Similarly, dose spacing and dose number were also statistically significant covariates by p-value but explained only minute amounts of variance. Study year and substance purity were not significant covariates in the full MLR model.
Table 4.
Leave-one-out regression modeling.
| Model Parameters (Removed) | LEL | LOAEL | ||||
|---|---|---|---|---|---|---|
| MSE | % exp. | p-value | MSE | % exp. | p-value | |
| All | 0.347 | 62.1 | 0.258 | 67.4 | ||
| (Chemical) | 0.766 | 16.4 | 1.03e-229 | 0.683 | 13.8 | 9.86e-303 |
| (Strain group) | 0.401 | 56.2 | 4.57e-54 | 0.301 | 62.0 | 1.96e-58 |
| (Study type) | 0.371 | 59.5 | 2.69e-30 | 0.272 | 65.7 | 3.72e-25 |
| (Adm method) | 0.350 | 61.8 | 1.25e-03 | 0.258 | 67.4 | 5.90e-02 |
| (Dose spacing) | 0.350 | 61.8 | 2.27e-05 | 0.259 | 67.3 | 3.11e-03 |
| (Dose number) | 0.351 | 61.7 | 1.46e-06 | 0.258 | 67.4 | 6.65e-01 |
| (Study year) | 0.347 | 62.1 | 7.69e-01 | 0.258 | 67.4 | 5.08e-01 |
| (Substance purity) | 0.347 | 62.1 | 1.98e-01 | 0.258 | 67.4 | 4.94e-01 |
| (Study source) | 0.348 | 62.0 | 3.62e-02 | 0.259 | 67.3 | 8.06e-03 |
| (Sex) | 0.349 | 61.9 | 5.71e-04 | 0.258 | 67.4 | 3.79e-01 |
The full MLR dataset was used for leave-one-out regression modeling of LEL and LOAEL values. MSE (in units of (log10(mg/kg/day))2, estimate of unexplained variance) and the p-value for the covariate based on ANOVA for the MLR models are provided. The α was set to 0.05 for the ANOVA. % exp = percent total variance explained.
The full dataset and full cell dataset were then further partitioned by study type (Figure 2) for variance estimation (Table 4). The MLR data subsets by study type were still relatively large, whereas the ACM data subsets had only 28, 43, and 56 cells for the DEV, SUB, and CHR study types with 24–45 chemicals and 54–117 studies each, which may present a limitation for interpretation of the ACM subset models. Despite limitations in the number of studies available, the total variance, MSE, RMSE, and percent of variance explained were similar for the SUB and CHR study datasets (Table 4). Total variance for SUB and CHR datasets were similar for the MLR (0.879, 0.952) and ACM models (1.013, 0.887). The unexplained variance for these MLR and ACM models of SUB and CHR data, as estimated by MSE, were all similar, ranging from 0.301 to 0.395; this resulted in similar RMSE values as well, ranging from 0.549 to 0.629 log10(mg/kg/day). These RMSE values for the full datasets in Table 3 were in the same range (0.448–0.622) as these subsets for SUB and CHR. Ultimately, based on the total variance and MSE for these SUB and CHR models, the percent explained variance appeared to fall in the range of 55–70% (Table 5), just like the full datasets in Table 3.
Table 5.
Variance estimation results for subsets by study type.
| Regression Type | Data | LEL | LOAEL | N | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Total Variance | MSE | RMSE | % exp. | Total Variance | MSE | RMSE | % exp. | |||
| MLR | SUB | 0.879 | 0.350 | 0.591 | 60.2 | 0.782 | 0.277 | 0.527 | 65.0 | 705 |
| ACM | SUB | 1.013 | 0.301 | 0.549 | 70.3 | 0.904 | 0.250 | 0.500 | 72.4 | 92 |
| MLR | CHR | 0.952 | 0.352 | 0.593 | 63.1 | 0.795 | 0.252 | 0.502 | 68.4 | 1149 |
| ACM | CHR | 0.887 | 0.395 | 0.629 | 55.4 | 0.825 | 0.265 | 0.515 | 68.0 | 117 |
| MLR | DEV | 0.604 | 0.246 | 0.496 | 59.3 | 0.594 | 0.217 | 0.465 | 63.5 | 275 |
| ACM | DEV | 0.410 | 0.328 | 0.573 | 20.0 | 0.398 | 0.316 | 0.562 | 20.7 | 54 |
Two regression types (MLR = multilinear regression, ACM = augmented cell means) were used to build models using data subset by the study type (SUB = subchronic; CHR = chronic; DEV = developmental) for variance estimation. Total variance and MSE are in units of (log10(mg/kg/day))2, whereas RMSE is in log10(mg/kg/day) units just like the dataset. % exp = percent total variance explained. N = number of study records in the dataset.
The MLR model of the DEV subset demonstrated total variance, MSE, RMSE, and percent variance explained values similar to the MLR and ACM regression modeling of the full cell dataset and the SUB and CHR datasets. In contrast, the ACM model for the DEV subset suggests either something specific about the DEV subset, or that this subset of studies was too small to evaluate using this methodology. The ACM DEV model had an N=54 studies, the smallest of any dataset used in this analysis, and demonstrated reduced total variance. However, the ACM DEV model maintained an MSE of 0.328, similar to other datasets in this analysis, resulting in a high proportion of the total variance being unexplained (only 20% of the variance was explained) (Table 4). These findings may relate to a species difference for DEV studies; DEV study records were predominantly from rabbit (26/54 ACM subset) and rat (26/54 ACM subset) whereas CHR and SUB study records were from rats, mice, and dogs. All of the adults in the DEV studies, regardless of dataset, were necessarily female. And the chemical, which appears to explain the highest proportion of the explained variance, was largely unique to each ACM data subset: 4 chemicals were shared in the DEV and CHR subsets for ACM; 7 chemicals were shared between the DEV and SUB datasets; and, only 7 chemicals were shared between the SUB and CHR datasets for ACM. No chemical was present in all three ACM subsets. Thus, the difference in the total variance for the ACM model of the DEV data may related to any one or more of these issues with this smaller dataset. A visual of the LEL range for the ACM study type subsets is provided in Figure 4; in general, the range of LELs for the DEV studies do appear more constrained, suggesting another possibility: that inclusion of range-finder and subsequent full studies of the same chemical in a DEV study model as cell replicates in the ACM DEV subset may have contributed to a reduced variance for this study type. However, examining the median LOAEL values for SUB and CHR studies in dog, mouse, and rat bioassays (Figure 5) suggest that these data are linearly related, with plots of median SUB LOAEL value to median CHR LOAEL value demonstrating slopes of 0.67, 0.63, and 0.74. These results indicate that given the variability in SUB and CHR animal data, if the median values are compared, the CHR LOAEL may be approximately two-thirds to three-quarters of the SUB LOAEL value.
Figure 4. LEL range by study type in the ACM subsets.
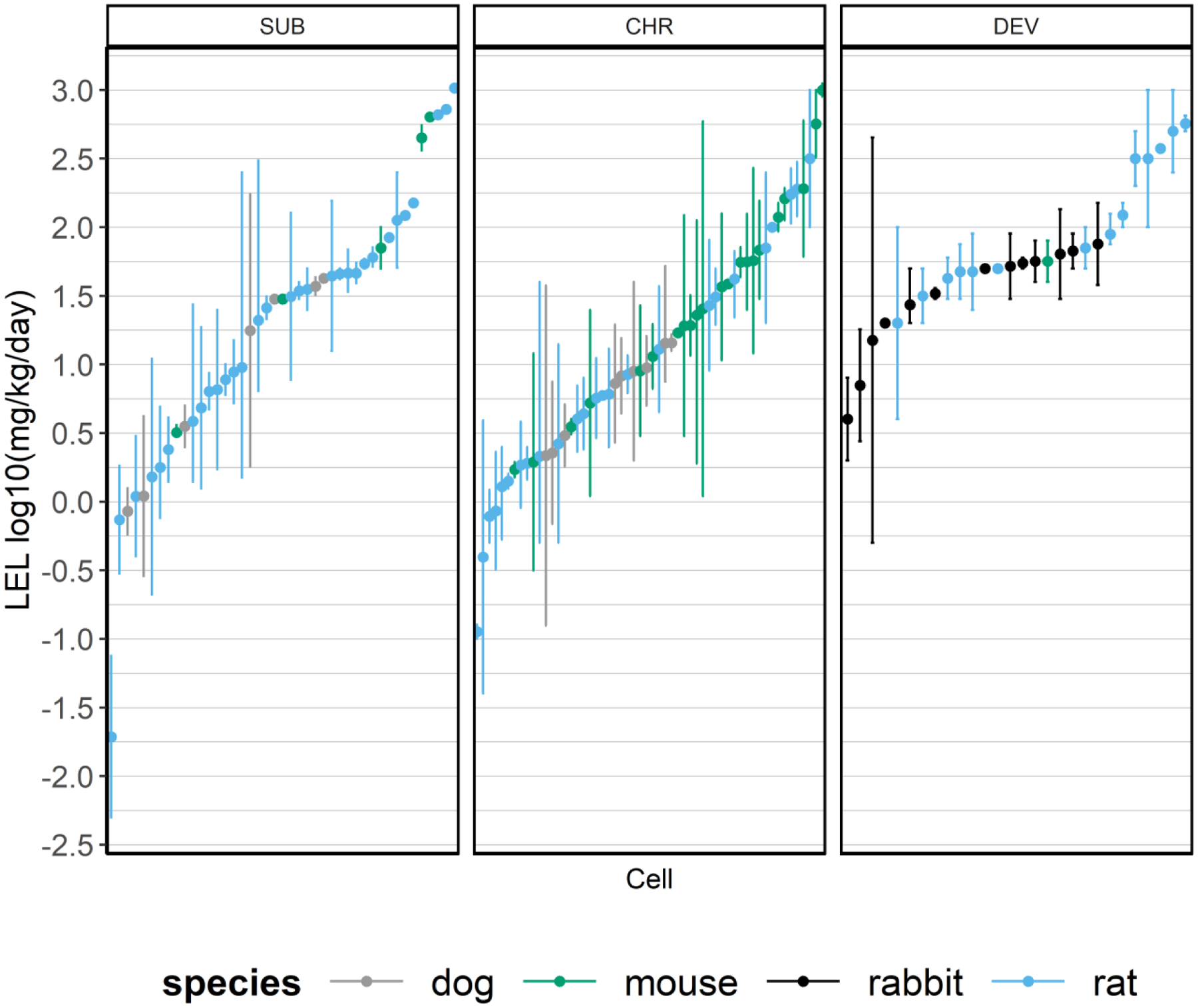
The LEL values are presented by study type in the ACM subsets (SUB, CHR, and DEV) are presented. The dot represents the LEL mean and the line shows the range from minimum to maximum for each cell of the respective ACM models. The cells are sorted by mean HED value, and the sort order and the chemicals reflected in the SUB, CHR, and DEV panels differ. Species is denoted by color, with gray = dog, green = mouse, black = rabbit, and blue = rat.
Figure 5. Chronic versus subchronic values by chemical in the ACM data subsets.
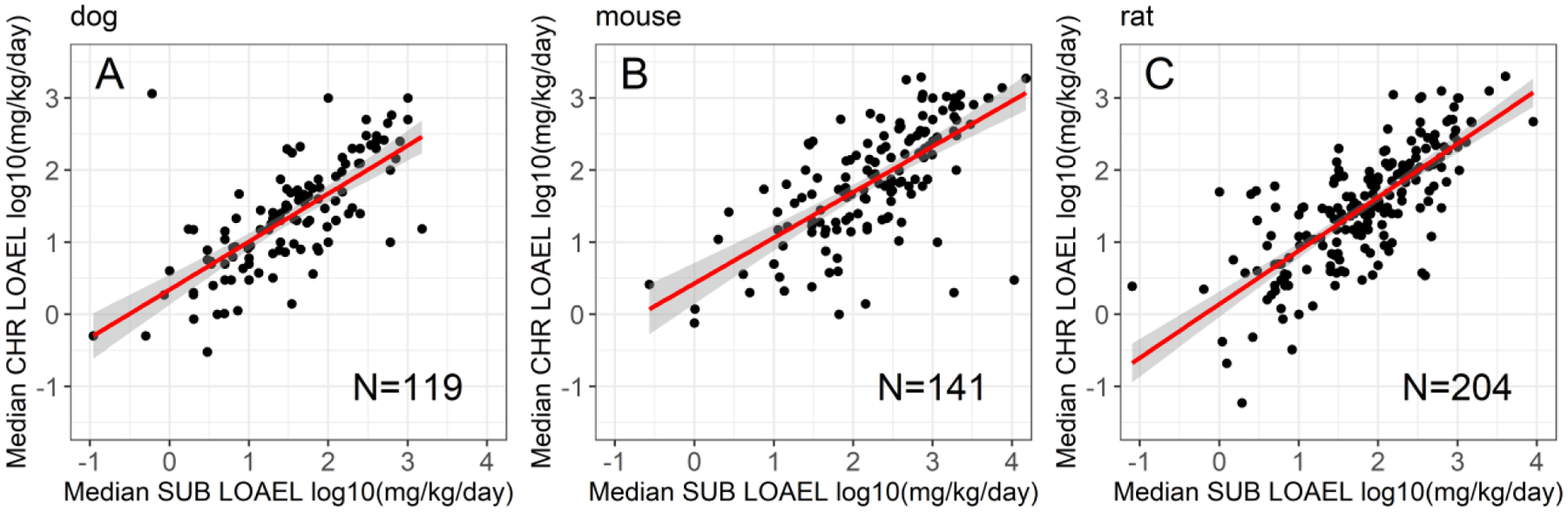
The median CHR LOAEL value plotted by the median SUB LOAEL value for (A) dog (N=119 chemicals), (B) mouse (N=141 chemicals), and (C) rat (N=204 chemicals). The slopes for the linear relationships demonstrated were 0.67, 0.63, and 0.74, with all three linear relationships demonstrating p < 0.05.
Based on variance estimation results, minimum prediction intervals for a new prediction model of systemic toxicity POD values were derived. A simple way to estimate a prediction interval in which 95% of new observations or predictions might be expected to fall is to multiply the regression model RMSE value by approximately ± 1.96 to obtain upper and lower bounds; however, like the multilinear regression approaches used in this work, this estimate is reliant upon the assumption that the regression model residuals are normally distributed. In Figure 3B, the Normal Q-Q plot suggests that the standardized residuals are fairly normally distributed, with deviation from the normality line for a small subset of points in the tails of the distribution beyond the 5th and 95th percentiles. An empirical cumulative distribution frequency (ECDF) of the MLR full dataset residuals demonstrated a fairly normal residual distribution (Figure 6) with somewhat elongated tails, as a normal distribution with equivalent mean and standard deviation (blue line) appears to lie almost directly on top of the empirical cumulative distribution of residuals from the MLR of the full LEL dataset (black line). The 2.5th and 97.5th percentiles of the empirical cumulative distribution of the MLR residuals are approximately −1.11 and 1.00 log10(mg/kg/day), respectively, with a mean of approximately zero and a standard deviation of 0.52. To evaluate the degree of any deviation from normality for the MLR LEL model residuals, beyond visual similarity to a normal distribution with the same mean and standard deviation, skewness, kurtosis, and a Kolmogorov-Smirnov test were used. The Kolmorogov-Smirnov nonparametric test was used to evaluate the equality of a normal distribution with the same sample size, mean, and standard deviation to the empirical cumulative distribution of the MLR LEL model residuals. The p-value on this test was 0.04728 and given an alpha = 0.05, this p-value indicates that the result was equivocal or borderline, with the possibility of an average difference (positive and negative) between residuals in the normal distribution and MLR LEL model residuals of approximately 0.04. The skewness of the MLR LEL model residual distribution was −0.25 and the excess kurtosis was 1.31. Given that the skewness is between −0.5 and 0.5, this suggests the model residual distribution is approximately symmetric. Given that the excess kurtosis is positive but less than 3, the MLR LEL model residual distribution appears leptokurtic (slightly heavy-tailed), as observed visually in the Normal Q-Q plot in Figure 3B and in Figure 6B, where the ordered normal distribution residuals are plotted against the ordered MLR LEL model residuals, with slight deviation of residuals from the unity line only at the extremes. Given that the distribution of residuals from the MLR full dataset model did not appear to deviate substantially from a normal distribution, minimum prediction intervals for a new POD value based on RMSE values from regression models in this work were derived using the assumption of normality.
Figure 6. ECDF for the residuals.
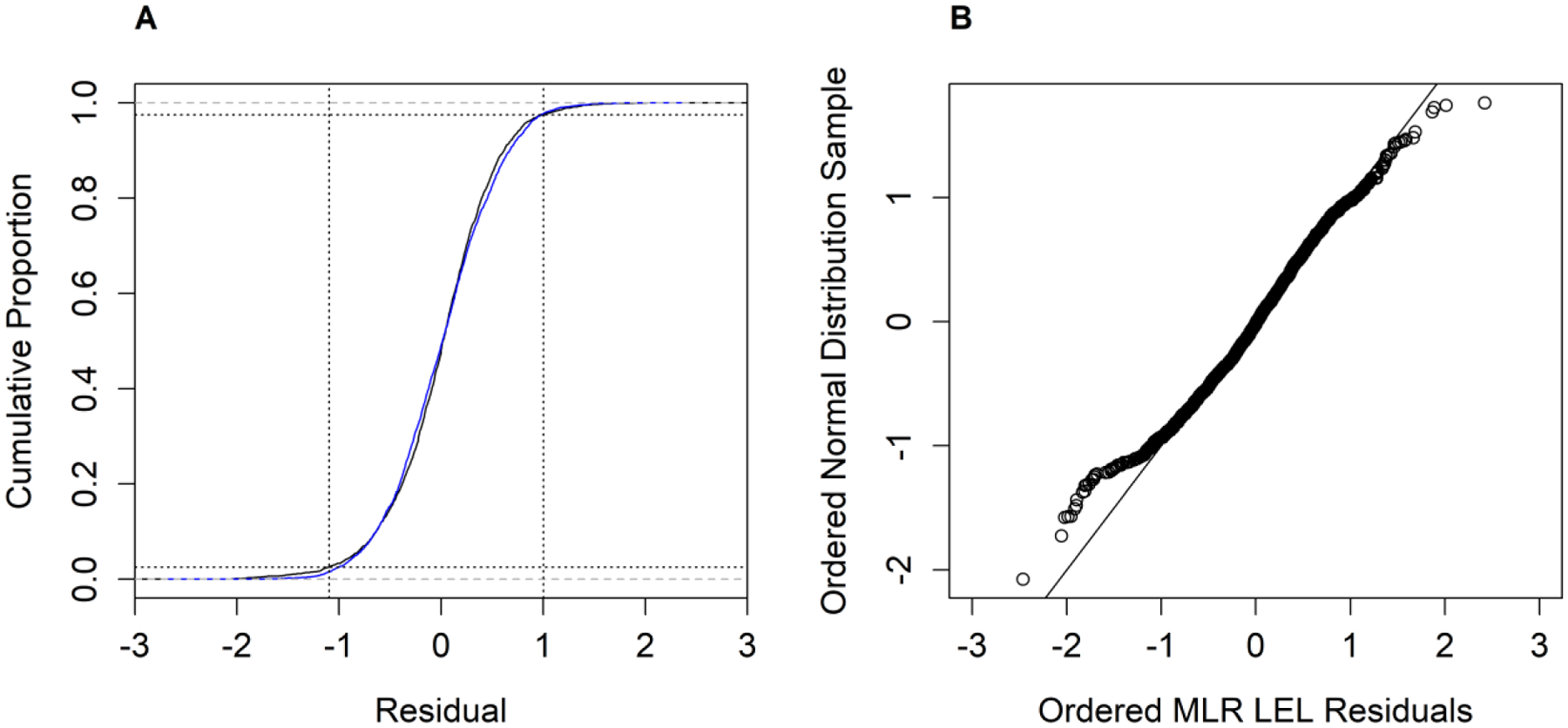
In (A), the ECDF of the MLR full LEL dataset model residuals (black) is plotted and compared to the ECDF of an equivalent sample size from a normal distribution (rnorm) with a mean (zero) and standard deviation (0.52) (blue). These distributions appear to lie on top of each other. In (B), a plot of the ordered normal distribution sample and the ordered MLR LEL model residuals demonstrate a fairly normal distribution of MLR LEL model residuals (with some deviation at the extremes suggesting long tails).
As the RMSE values for the regression models in this work ranged from 0.447 to 0.628, the minimum prediction interval for a new POD value, i.e. an LEL or LOAEL, is likely somewhere between 58- to 284-fold wide (Table 6, using Equations 7a–7d). The difference between the 2.5th and 97.5th quantiles from the ECDF of the residuals from the MLR model of the full LEL dataset is 126-fold; this means that the upper bound divided by the lower bound of a prediction is roughly 126. For “true” systemic toxicity effect values of 1, 10, and 100 mg/kg/day, this equates to a reasonable prediction range of 0.08–10, 0.8–100, and 8.0–1006 mg/kg/day, respectively. The RMSE values from every regression model in this work was then used to construct estimates of a minimum prediction interval for systemic toxicity LELs and/or LOAELs (Table 6).
Table 6.
Estimated prediction intervals by dataset.
| Regression Type | POD Type | Data | RMSE | Minimum Prediction Interval Width (fold = UB/LB) | 1 mkd LB | 1 mkd UB | 10 mkd LB | 10 mkd UB | 100 mkd LB | 100 mkd UB | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | ECDF of MLR model residuals | LEL | full dataset | NA | 126 | 0.08 | 10.06 | 0.80 | 100.60 | 7.98 | 1005.98 |
| 2 | ACM | LEL | CHR | 0.628 | 284 | 0.06 | 17.02 | 0.59 | 170.16 | 5.88 | 1701.6 |
| 3 | MLR | LEL | full cell dataset | 0.622 | 276 | 0.06 | 16.56 | 0.6 | 165.61 | 6.04 | 1656.14 |
| 4 | RR | LEL | full dataset | 0.599 | 213 | 0.07 | 14.93 | 0.67 | 149.29 | 6.7 | 1492.86 |
| 5 | MLR | LEL | CHR | 0.593 | 208 | 0.07 | 14.53 | 0.69 | 145.3 | 6.88 | 1452.98 |
| 6 | MLR | LEL | SUB | 0.592 | 207 | 0.07 | 14.46 | 0.69 | 144.64 | 6.91 | 1446.43 |
| 7 | MLR | LEL | full dataset | 0.589 | 204 | 0.07 | 14.27 | 0.7 | 142.7 | 7.01 | 1426.98 |
| 8 | MLR | LEL | high leverage points removed | 0.582 | 198 | 0.07 | 13.83 | 0.72 | 138.26 | 7.23 | 1382.61 |
| 9 | MLR | LEL | high Cooks distance plot points removed | 0.582 | 198 | 0.07 | 13.83 | 0.72 | 138.26 | 7.23 | 1382.61 |
| 10 | ACM | LEL | DEV | 0.573 | 166 | 0.08 | 13.28 | 0.75 | 132.76 | 7.53 | 1327.58 |
| 11 | ACM | LEL | full cell dataset | 0.566 | 161 | 0.08 | 12.86 | 0.78 | 128.63 | 7.77 | 1286.29 |
| 12 | ACM | LOAEL | DEV | 0.562 | 158 | 0.08 | 12.63 | 0.79 | 126.33 | 7.92 | 1263.28 |
| 13 | MLR | LOAEL | full cell dataset | 0.559 | 156 | 0.08 | 12.46 | 0.8 | 124.63 | 8.02 | 1246.29 |
| 14 | ACM | LEL | SUB | 0.549 | 149 | 0.08 | 11.91 | 0.84 | 119.13 | 8.39 | 1191.3 |
| 15 | MLR | LOAEL | SUB | 0.526 | 119 | 0.09 | 10.74 | 0.93 | 107.38 | 9.31 | 1073.84 |
| 16 | RR | LOAEL | full dataset | 0.516 | 103 | 0.1 | 10.26 | 0.97 | 102.65 | 9.74 | 1026.46 |
| 17 | ACM | LOAEL | CHR | 0.515 | 102 | 0.1 | 10.22 | 0.98 | 102.18 | 9.79 | 1021.84 |
| 18 | MLR | LEL | high Cooks distance points removed | 0.511 | 100 | 0.1 | 10.04 | 1 | 100.36 | 9.96 | 1003.56 |
| 19 | MLR | LEL | all potential outliers removed | 0.511 | 100 | 0.1 | 10.04 | 1 | 100.36 | 9.96 | 1003.56 |
| 20 | MLR | LOAEL | full dataset | 0.508 | 99 | 0.1 | 9.9 | 1.01 | 99.01 | 10.1 | 990.06 |
| 21 | MLR | LOAEL | high Cooks distance plot points removed | 0.504 | 97 | 0.1 | 9.72 | 1.03 | 97.23 | 10.28 | 972.35 |
| 22 | ACM | LOAEL | full cell dataset | 0.504 | 97 | 0.1 | 9.72 | 1.03 | 97.23 | 10.28 | 972.35 |
| 23 | MLR | LOAEL | CHR | 0.502 | 96 | 0.1 | 9.64 | 1.04 | 96.36 | 10.38 | 963.61 |
| 24 | MLR | LOAEL | high leverage points removed | 0.5 | 96 | 0.1 | 9.55 | 1.05 | 95.5 | 10.47 | 954.95 |
| 25 | ACM | LOAEL | SUB | 0.5 | 96 | 0.1 | 9.55 | 1.05 | 95.5 | 10.47 | 954.95 |
| 26 | MLR | LEL | DEV | 0.496 | 85 | 0.11 | 9.38 | 1.07 | 93.79 | 10.66 | 937.87 |
| 27 | MLR | LOAEL | DEV | 0.466 | 68 | 0.12 | 8.19 | 1.22 | 81.91 | 12.21 | 819.11 |
| 28 | MLR | LOAEL | high Cooks distance points removed | 0.447 | 58 | 0.13 | 7.52 | 1.33 | 75.18 | 13.3 | 751.8 |
| 29 | MLR | LOAEL | all potential outliers removed | 0.447 | 58 | 0.13 | 7.52 | 1.33 | 75.18 | 13.3 | 751.8 |
Three different estimates of prediction interval are used: the 2.5th to 97.5th percentiles from the ECDF of the MLR model for the full LEL dataset; the RMSE from the MLR model for the full LEL dataset; and, the MLR model for the full LEL dataset with all potential outliers removed. The minimum prediction interval width is the upper bound of the interval divided by the lower bound of the interval. For context, the lower and upper bounds of a prediction interval for 1, 10, and 100 mg/kg/day “true” POD values are shown. LB and UB = lower bound and upper bound, respectively; mkd = mg/kg/day.
Discussion
An open question in evaluating predictive models of systemic in vivo PODs has been the unknown variance within the in vivo reference data. This question has presented a challenge in evaluation of NAM model quality and ultimately, the utility of the model for regulatory applications such as prioritization or screening-level risk assessment. Herein we used regression models to evaluate study-to-study variability in LEL and LOAEL values via estimation of the total variance, the amount of this variance that can be explained by ten study descriptors, and the amount of variance left unexplained. The variance estimation and analysis reported here is for a large repeat dose in vivo toxicity dataset and may inform the anticipated best performance of any predictive model or NAM using these or similar data, setting a benchmark for how much variance may be inherent to these types of data, as well as an upper bound on the amount of variance that can be explained via modeling. Using multiple datasets and regression approaches, and despite large differences in sample size, this analysis suggests that 55 to 73% of the variance in systemic LEL or LOAEL values from repeat dose studies can be explained using the study descriptors (i.e., study metadata) in ToxRefDB version 2.0. Therefore, one measure of the upper limit of performance for a new predictive NAM of systemic toxicity, the R-squared value, would be unlikely to exceed 55–73%. Another significant finding of this work is estimation of the minimum prediction interval for systemic toxicity LELs and/or LOAEL values, based on the RMSE for regression models of the available dataset or an empirical cumulative distribution of the residuals from the MLR full LEL dataset model. A minimum prediction interval estimate is of interest for forward predictive modeling because it indicates the range that might be reasonable for a new POD estimate, whether from additional in vivo experiments or NAM-based experiments. Using the data in ToxRefDB version 2.0, the 95% minimum prediction interval of systemic LEL or LOAEL values is approximately 58- to 284-fold, suggesting that a perfect prediction model that does not contribute additional variance could predict in vivo LEL or LOAEL values within about 1.8 to 2.5 orders of magnitude on the log10(mg/kg/day) scale.
Multiple regression model approaches were undertaken in this work to understand the range of possible unexplained variance, or MSE, as well as the spread of the LEL and LOAEL values, or RMSE. The MLR and RLR approach relies on the assumption that study descriptors contribute independently and consistently to explained variance; this is reflected in the higher residual degrees of freedom for the MLR (and RLR) models, as the MLR (and RLR) model approach does not account for potential interactions between study descriptors that are known to exist, e.g. study type and strain group, or study type and sex. For instance, if no interaction among study parameters is assumed, the difference between strain group is the same regardless of the duration of exposure (i.e. SUB and CHR) or the chemical under study. This assumption is unlikely because toxicokinetics of chemical absorption, distribution, metabolism and excretion will vary by chemical, species, and duration (Haseman, 2000). Further, the studies included in this work were often conducted in accordance with Health Effects Test guidelines, and as such certain study types will use certain species of animals per these guidelines. Therefore, using the MLR model approach may underestimate the amount of variance that can be explained and may overstate the unexplained variance (MSE). Indeed, the MLR model results for the full cell dataset, the same dataset used for the full ACM models, demonstrated slightly higher MSE values (0.387 versus 0.320 for LEL values and 0.312 versus 0.254 for LOAEL values) and lower percent variance explained (55% versus 63% for LEL values and 58% versus 66% for LOAEL values). In the ACM model approach, the levels within a factor are evaluated individually. Every cell is a unique combination of all the categorical levels within the dataset, resulting in a more stringent definition of a study replicate. However, the tradeoff for the ACM model approach is that the dataset is much smaller, and typically this type of dataset curation is not possible for predictive modeling of training set information from hundreds to thousands of chemicals. Thus, a series of MLR and ACM models were built to understand the possible range of variance, unexplained variance, and explained variance values for systemic LEL and LOAEL values from repeat dose studies.
Across the datasets (LEL and LOAEL; full or with potential outliers removed) and modeling methods (MLR and ACM), the unexplained variance (MSE) varies within a relatively small range, with values spanning 0.2 to 0.39, and the percent of total variance explained varying from 55 to 73%. The total variance and unexplained variance were, in general, slightly lower for the LOAEL datasets than the LEL datasets, regardless of regression model type. It seems plausible that effects associated with adversity (LOAELs) might occur within a smaller range across studies than treatment-related effects (LELs) due to elimination of outliers or less biologically significant changes. Because LOAEL values require expert opinion, these values may not be available for all data sources and may have some inherent bias. Removing potential outliers in the full dataset based on evaluation of the residuals from the MLR model is complex; data trimming could eliminate “real” signal for the variance estimation, or simply just remove outliers that distort the distribution of residuals. Removing points with high Cook’s distance, a measure of leverage and residual size, from the full dataset changed the variance and MSE values for the MLR model more than reducing the dataset to 10% of its original size on the basis of the ACM evaluation (Table 3). Removing all potential outliers from the full dataset resulted in the highest percent explained variance (69% for LEL values and 73% for LOAEL values), and so it is likely the MLR models of the full dataset with all potential outliers removed represent the best case in terms of the amount of variance in these data that can be explained (i.e., an upper limit on an R-squared for a predictive model of systemic LEL and LOAEL values). Nonetheless, the similarity in the MSE across all analyses of the full datasets suggest that the unexplained variance is relatively stable across methods and datasets, and as a result, the RMSE and resultant prediction interval estimates are also relatively similar. Given the relative stability in total variance, MSE, RMSE, and percent explained variance across datasets and regression methodologies, the findings instill confidence in the range of values observed as being indicative of the variability that might be expected from this and similar datasets used as a reference for predictive models.
Combining the systemic LEL and LOAEL values across different study types led to a concern that perhaps the heterogeneity of the datasets used in both the MLR and ACM model approaches would result in a less informative variance estimation. Thus, the original full datasets for MLR and ACM modeling were partitioned into the three most prevalent study types available in this dataset: SUB, CHR, and DEV. These datasets, particularly for the ACM modeling approach, were much smaller than the full dataset and thus more susceptible to potential outliers. However, all but the ACM model of the DEV subset aligned well with the models of the full dataset in terms of variance, MSE, RMSE, and percent variance explained. The DEV subset of data was much smaller, particularly for the ACM analysis (this was the smallest dataset used in a regression model in this work). The DEV data subset may have demonstrated smaller variance, and a higher proportion of unexplained variance, due to the specific parameters of these data, including the species and sex used (mostly rats and rabbits, and all female, in contrast to SUB and CHR studies); due to the small data subset size and specific parameters of these data, the variance estimation using the DEV data subset may not fully represent the variance estimation for the total MLR or ACM datasets. These subset analyses increase the confidence in the variance estimation of the full datasets and demonstrated that grouping study types together, particularly for the SUB and CHR studies, is likely appropriate in the context of trying to predict an overall LEL or LOAEL for a chemical. Comparison of SUB to CHR median LOAEL values in this dataset further underscore that it is appropriate to group effect values from SUB and CHR together for regression modeling, as the difference between the SUB and CHR LOAEL values on average is less than the variance in SUB or CHR data. This is consistent with previous work that suggest that an assumption of a 10-fold difference between SUB and CHR LOAEL values is a protective assumption based on approximately the 98th percentile of the SUB/CHR ratio distribution (Hattis et al., 2002). The consistency in the observed MSE (0.217 to 0.395 for study type subsets versus 0.200 to 0.387 for full datasets) builds confidence in the estimates resulting from the analyses that have combined multiple study types, especially SUB and CHR data.
There are a number of limitations to the analysis performed in the current work, including constraints using the data available in the identified data source, ToxRefDB version 2.0; the spectrum of available study types is relatively narrow, and though the chemicals included represent a heterogeneous set, these chemicals only represent a fraction of the chemicals currently in commerce (Muir and Howard, 2006). Definition of a study, and thereby a study replicate, is also a source of uncertainty in this analysis. Although more data are always desirable, there are no other publicly accessible databases of in vivo toxicology studies performed in accordance with EPA guidelines that can match the size, scope, and curation level of ToxRefDB. The use of ToxRefDB also underscores the critical importance of how study descriptors are recorded for databases of these study data, and the need for clear and consistent documentation of study descriptors in order to identify and class the data correctly for predictive modeling use (Browne et al., 2015; Kleinstreuer et al., 2015). It could be that estimates of variability in in vivo data may change if the volume of in vivo data that are computationally-accessible, of high quality and accuracy, and highly curated, were increased.
In the classical definition of a POD, a NOAEL or lower bound on a benchmark dose (BMDL) are preferred as the starting point for derivation of an RfD using uncertainty factors; yet, this analysis employed LEL and LOAEL values to establish expectations regarding the prediction of a LEL or LOAEL. This is because the use of in vitro high-throughput screening data and other information to model in vivo hazard has focused on identifying a bioactive concentration in vitro, i.e. an in vitro LEL, and relating this to a relevant dose in vivo. The amount of uncertainty in NOAEL values and LOAEL values present some similar limitations, in that the effect size or effect severity at the NOAEL or LOAEL may not be equal between studies; indeed, these associated uncertainties have been described previously, with a call to denote uncertainty or likelihood of adversity from magnitude of adversity and from incidence of adversity (Chiu et al., 2018; Chiu and Slob, 2015; WHO/IPCS, 2014). In future work, it would be advantageous to use BMD and BMDL values (Davis et al., 2011; Wignall et al., 2014), rather than LOAEL values, in an effort to see if the total variance could be reduced as suggested by Chiu and colleagues (Chiu et al., 2018).
In 2014, the US Environmental Protection Agency (USEPA) hosted the ToxCast systemic Lowest Effect Level (LEL) Predictor Challenge (USEPA, 2014). The winning predictive model from this challenge aggregated ten machine learning models that used associative neural networks for prediction of LELs based on in silico descriptor sets for 2D and 3D chemical structure representations. With a test chemical set, this winning model performed with an RMSE of 1.08 log10(mg/kg/day) (Novotarskyi et al., 2016), which falls within the minimum prediction interval estimated from the variance quantified for the ToxRefDB considered in the present work (2.3 log10(mg/kg/day)) (Novotarskyi et al., 2016). The forward prediction models developed by Truong and colleagues to predict systemic LELs on a chemical-basis, using data extracted from ToxRefDB, and two other databases including Hazard Evaluation Support System and COSMOS databases, demonstrated RMSE values of approximately 0.73 log10-mg/kg/day and R-squared value of approximately 50%, depending on the sets of descriptors used (Truong et al., 2017); indeed, the “benchmark” model demonstrated that only 74% of the total variance could be explained using study-level covariates, placing an upper bound on the R-squared in roughly the same range as the data experiments reported herein. Thus, previous exercises using similar datasets appear to support the relatively large amount of variance in LEL and LOAEL values and that is unlikely that a predictive model could have explained more than 60–70% of the variance in reference, repeat-dose animal data.
A minimum prediction interval between 58- and 284-fold wide for systemic LEL or LOAEL values and an upper limit on R-squared of 0.55 to 0.73 for models of these LEL and LOAEL data together have important implications for refinement of NAM approaches. As indicated in Table 6, this means that doses of 0.08 to 10 mg/kg/day might be reasonable predictions of a “true” LEL or LOAEL of 1 mg/kg/day. For instance, refinements of in vitro to in vivo extrapolation methods to derive an in vivo dose equivalent based on in vitro bioactive concentrations (Honda et al., 2019; Wambaugh et al., 2018) may not be able to predict in vivo values with better accuracy than within 1–2 log10-mg/kg/day if the variability in the in vivo data is considered. A potential avenue for improving quantitative prediction of animal-based POD values may be to refine both the bioactivity data and the animal data used, confining the bioactivity data and in vivo data that were related biologically, i.e. via an adverse outcome pathway (Ankley and Edwards, 2018), and future work should explore this possibility.
The goals of this work were: to quantify the variance in a large database of study-level lowest effect level (LEL) and lowest observable adverse effect level (LOAEL) values for systemic effects in adult animals, thereby informing expectations regarding a reasonable range of POD values, or a minimum prediction intervals size, expected for NAM prediction of systemic toxicity; and further, to estimate the upper limit on predictive performance of NAMs for systemic toxicity, i.e. the amount of variance that can possibly be explained by a NAM or predictive model using these effect level data. Current practices for modeling in vivo data do not always include variance estimation of the reference data used for training and/or testing. When multiple effect values from multiple sources are presented for a chemical, the modeled values are chosen using knowledge of study descriptors and/or study quality, random sampling, or the minimum, mean, or median effect level for the chemical; this reduction in the reference data complexity obscures the variance in these data. Even when variance is estimated, it has typically been performed with a limited number of in vivo studies. The work described here represents a unique contribution to benchmarking model performance, as systemic effects from 2724 studies and 563 chemicals were available for the largest dataset used. This novel work illustrates the variance in ToxRefDB data, including the unexplained variance, and in doing so sets an upper limit on the anticipated R-squared for predictive modeling of systemic LELs using these data from ToxRefDB. Importantly, when evaluating predictive NAMs for systemic LELs or LOAELs, we now have the statistical information to inform understanding of their performance: for prediction of systemic LELs and LOAELs values (in ToxRefDB or similar datasets), the expectation should be that the R-squared approaches 0.5 to 0.7, and the accuracy of a predictive model should approach estimates within approximately 2 orders of magnitude on the log10(mg/kg/day) scale for excellent models, as limited by the underlying variance in systemic LEL or LOAEL values.
Importantly, assessment of the success of NAMs that predict systemic LEL or LOAEL values should include a refined expectation of the optimal model performance to account for variance in the reference data. A primary conclusion of this work is that refinement of NAMs to improve accuracy of NAM predictions of in vivo reference data may not be possible beyond values that are within 58- to 284-fold the “true” value. This does not eliminate the need to improve and use NAM predictions; rather, the use of NAM-based information in chemical safety assessment should emphasize NAM value for screening level chemical assessment beyond the accuracy of NAMs for prediction of in vivo data from animal models. Evaluating the negative and positive prediction value of NAMs for effects in animals, and more importantly for potential effects in humans, would inform NAM utility for chemical safety assessment. Finally, construction of NAM-based POD estimates that offer an equivalent level of public health protection as PODs produced by methods using animals may provide a bridge to major reduction in the use of animals as well as identification of cases in which animals may provide scientific value.
Supplementary Material
Supplemental File 1, Table 1: The full dataset used for MLR modeling.
Supplemental File 1, Table 2: The full dataset used for ACM modeling.
Supplemental File 2: HTML file of the Rmarkdown used to generate all of the data analysis and most figures in this work.
Supplemental File 3: Supplemental Figures 1 and 2 on the composition of the MLR full dataset and the ACM full cell dataset.
Highlights.
Variability in in vivo toxicity studies limits predictive accuracy of NAMs.
The US EPA Toxicity Reference Database includes repeat dose toxicity studies.
Total variance in systemic effect levels and the fraction explained were quantified.
Maximal R-squared for a predictive model of systemic effect levels may be 55 to 73%.
Estimated minimum prediction intervals for systemic effect levels were 58 to 284-fold.
Acknowledgements
The authors would like to acknowledge Dustin Kapraun, John Wambaugh, and Charles Wood (US EPA), and David Reif (North Carolina State University), for insightful comments on previous versions of this manuscript.
Funding
L.L.P. was supported by appointment to the Research Participation Program of the U.S. Environmental Protection Agency, Office of Research and Development, administered by the Oak Ridge Institute for Science and Education through an interagency agreement between the U.S. Department of Energy and the U.S. EPA.
Footnotes
Publisher's Disclaimer: Disclaimer: The United States Environmental Protection Agency (U.S. EPA) through its Office of Research and Development has subjected this article to Agency administrative review and approved it for publication. Mention of trade names or commercial products does not constitute endorsement for use. The views expressed in this article are those of the authors and do not necessarily represent the views or policies of the US EPA.
Abbreviations: Augmented cell means (ACM); Benchmark dose (BMD); chronic study (CHR); developmental study (DEV); lowest effect level (LEL); lowest observable adverse effect level (LOAEL); multi-linear regression (MLR); mean square error (MSE); new approach methodologies (NAMs); no observable adverse effect level (NOAEL); point-of-departure (POD); quantitative structure activity relationship (QSAR); Registration, Evaluation, Authorization, and Restriction of Chemicals (REACH); robust linear regression (RLR); root mean square error (RMSE); subchronic study (SUB); Toxicity Reference Database (ToxRefDB)
References
- CORAL-QSAR/QSPR. Istituto di Ricerche Farmacologiche Mario Negri, Milan, Italy. [Google Scholar]
- Leave-One-Out Error. In: Sammut C, Webb GI, (Eds.), Encyclopedia of Machine Learning. Springer, Boston, MA, 2011. [Google Scholar]
- Ankley GT, Edwards SW, 2018. The Adverse Outcome Pathway: A Multifaceted Framework Supporting 21(st) Century Toxicology. Curr Opin Toxicol. 9, 1–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Browne P, et al. , 2015. Screening Chemicals for Estrogen Receptor Bioactivity Using a Computational Model. Environ Sci Technol. 49, 8804–14. [DOI] [PubMed] [Google Scholar]
- Casati S, et al. , 2018. Standardisation of defined approaches for skin sensitisation testing to support regulatory use and international adoption: position of the International Cooperation on Alternative Test Methods. Arch Toxicol. 92, 611–617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chiu WA, et al. , 2018. Beyond the RfD: Broad Application of a Probabilistic Approach to Improve Chemical Dose-Response Assessments for Noncancer Effects. Environ Health Perspect. 126, 067009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chiu WA, Slob W, 2015. A Unified Probabilistic Framework for Dose-Response Assessment of Human Health Effects. Environ Health Perspect. 123, 1241–54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Claassen V, Huston JP, 2013. Neglected Factors in Pharmacology and Neuroscience Research: Biopharmaceutics, Animal Characteristics, Maintenance, Testing Conditions. Elsevier Science. [Google Scholar]
- Congress, U. S., FRANK R. LAUTENBERG CHEMICAL SAFETY FOR THE 21ST CENTURY ACT. In: Congress, (Ed.), H.R.2576, Vol. Public Law; 114–182, 2016. [Google Scholar]
- Consulting JKH, Huff J, 1989. Sources of Variability in Rodent Carcinogenicity Studies. Fundamental and Applied Toxicology. 12, 793–804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davis JA, et al. , 2011. Introduction to benchmark dose methods and U.S. EPA’s benchmark dose software (BMDS) version 2.1.1. Toxicol Appl Pharmacol. 254, 181–91. [DOI] [PubMed] [Google Scholar]
- Dobchev DA, et al. , 2013. Subchronic Oral and Inhalation Toxicities: a Challenging Attempt for Modeling and Prediction. Molecular Informatics. 32, 793–801. [DOI] [PubMed] [Google Scholar]
- ECCC/HC, Chemicals Management Plan (CMP) Science Committee Objectives Paper Meeting no. 5 - Integrating New Approach Methodologies within the CMP: Identifying Priorities for Risk Assessment, Existing Substances Risk Assessment Program, Vol. Retrieved from http://www.ec.gc.ca/ese-ees/default.asp?lang=En&n=172614CE-1. Government of Canada, Ottawa (ON), 2016. [Google Scholar]
- Ericsson AC, et al. , 2015. Effects of Vendor and Genetic Background on the Composition of the Fecal Microbiota of Inbred Mice. PLOS ONE. 10, e0116704. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gottmann E, et al. , 2001. Data quality in predictive toxicology: Reproducibility of rodent carcinogenicity experiments. Environmental Health Perspectives. 109, 509–514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haseman JK, 2000. Using the NTP database to assess the value of rodent carcinogenicity studies for determining human cancer risk. Drug Metab Rev. 32, 169–86. [DOI] [PubMed] [Google Scholar]
- Hattis D, et al. , 2002. A straw man proposal for a quantitative definition of the RfD. Drug Chem Toxicol. 25, 403–36. [DOI] [PubMed] [Google Scholar]
- Hisaki T, et al. , 2015. Development of QSAR models using artificial neural network analysis for risk assessment of repeated-dose, reproductive, and developmental toxicities of cosmetic ingredients. J Toxicol Sci. 40, 163–80. [DOI] [PubMed] [Google Scholar]
- Honda GS, et al. , 2019. Using the concordance of in vitro and in vivo data to evaluate extrapolation assumptions. PLoS One. 14, e0217564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jensen MN, Ritskes-Hoitinga M, 2007. How isoflavone levels in common rodent diets can interfere with the value of animal models and with experimental results. Laboratory Animals. 41, 1–18. [DOI] [PubMed] [Google Scholar]
- Jobson JD, 2012. Applied Multivariate Data Analysis: Regression and Experimental Design. Springer; New York. [Google Scholar]
- Judson R, et al. , 2009. The toxicity data landscape for environmental chemicals. Environmental Health Perspectives. 117, 685–695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Judson RS, et al. , 2012. Aggregating data for computational toxicology applications: The U.S. Environmental Protection Agency (EPA) Aggregated Computational Toxicology Resource (ACToR) System. Int J Mol Sci. 13, 1805–31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kleinstreuer NC, et al. , 2017. Development and Validation of a Computational Model for Androgen Receptor Activity. Chem Res Toxicol. 30, 946–964. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kleinstreuer NC, et al. , 2015. A Curated Database of Rodent Uterotrophic Bioactivity. Environmental Health Perspectives. 124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leisenring W, Ryan L, 1992. Statistical properties of the NOAEL. Regulatory Toxicology and Pharmacology. 15, 161–171. [DOI] [PubMed] [Google Scholar]
- Low Y, et al. , 2013. Integrative chemical-biological read-across approach for chemical hazard classification. Chem Res Toxicol. 26, 1199–208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin MT, et al. , 2009a. Profiling chemicals based on chronic toxicity results from the U.S. EPA ToxRef database. Environmental Health Perspectives. 117, 392–399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin MT, et al. , 2009b. Profiling chemicals based on chronic toxicity results from the U.S. EPA ToxRef Database. Environ Health Perspect. 117, 392–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin MT, et al. , 2009c. Profiling the reproductive toxicity of chemicals from multigeneration studies in the toxicity reference database. Toxicol Sci. 110, 181–90. [DOI] [PubMed] [Google Scholar]
- Martin MT, et al. , 2009d. Profiling the reproductive toxicity of chemicals from multigeneration studies in the toxicity reference database. Toxicological Sciences. 110, 181–190. [DOI] [PubMed] [Google Scholar]
- Mazzatorta P, et al. , 2008. Modeling Oral Rat Chronic Toxicity. Journal of Chemical Information and Modeling. 48, 1949–1954. [DOI] [PubMed] [Google Scholar]
- Muir DCG, Howard PH, 2006. Are There Other Persistent Organic Pollutants? A Challenge for Environmental Chemists. Environmental Science & Technology. 40, 7157–7166. [DOI] [PubMed] [Google Scholar]
- Mumtaz MM, et al. , 1995. Assessment of effect levels of chemicals from quantitative structure-activity relationship (QSAR) models. I. Chronic lowest-observed-adverse-effect level (LOAEL). Toxicol Lett. 79, 131–43. [DOI] [PubMed] [Google Scholar]
- Novotarskyi S, et al. , 2016. ToxCast EPA in Vitro to in Vivo Challenge: Insight into the Rank-I Model. Chemical Research in Toxicology. 29, 768–775. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patlewicz G, et al. , 2013. Use and validation of HT/HC assays to support 21st century toxicity evaluations. Regulatory Toxicology and Pharmacology. 65, 259–268. [DOI] [PubMed] [Google Scholar]
- Pearce RG, et al. , 2017. httk: R Package for High-Throughput Toxicokinetics. 2017. 79, 26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pizzo F, Benfenati E, 2016. In Silico Models for Repeated-Dose Toxicity (RDT): Prediction of the No Observed Adverse Effect Level (NOAEL) and Lowest Observed Adverse Effect Level (LOAEL) for Drugs in: Benfenati E, (Ed.), In Silico Methods for Predicting Drug Toxicity. Springer New York, New York, NY, pp. 163–176. [DOI] [PubMed] [Google Scholar]
- Rovida C, et al. , 2015. Integrated Testing Strategies (ITS) for safety assessment. Altex. 32, 25–40. [DOI] [PubMed] [Google Scholar]
- Rupp B, et al. , 2010. Chronic oral LOAEL prediction by using a commercially available computational QSAR tool. Arch Toxicol. 84, 681–8. [DOI] [PubMed] [Google Scholar]
- Shah I, et al. , 2016. Systematically evaluating read-across prediction and performance using a local validity approach characterized by chemical structure and bioactivity information. Regul Toxicol Pharmacol. 79, 12–24. [DOI] [PubMed] [Google Scholar]
- Sorge RE, et al. , 2014. Olfactory exposure to males, including men, causes stress and related analgesia in rodents. Nature Methods. 11, 629–632. [DOI] [PubMed] [Google Scholar]
- Toropov AA, et al. , 2015a. CORAL: model for no observed adverse effect level (NOAEL). Mol Divers. 19, 563–75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Toropov AA, et al. , 2015b. CORAL: model for no observed adverse effect level (NOAEL). Molecular diversity. 19, 563–75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Toropova AP, et al. , 2017. The application of new HARD-descriptor available from the CORAL software to building up NOAEL models. Food and Chemical Toxicology. [DOI] [PubMed] [Google Scholar]
- Toropova AP, et al. , 2015. QSAR as a random event: a case of NOAEL. Environ Sci Pollut Res Int. 22, 8264–71. [DOI] [PubMed] [Google Scholar]
- Truong L, et al. , 2017. Predicting in vivo effect levels for repeat-dose systemic toxicity using chemical, biological, kinetic and study covariates. Archives of Toxicology. [DOI] [PMC free article] [PubMed] [Google Scholar]
- UCLA, HOW CAN I TEST DIFFERENCES IN MEANS USING A CELL MEANS MODEL? In: Education I. f. D. R., (Ed.), Vol. 2018, https://stats.idre.ucla.edu/sas/faq/how-can-i-test-differences-in-means-using-a-cell-means-model/. [Google Scholar]
- USEPA, ToxCast Challenge | Topcoder and EPA. 2014.
- USEPA, Strategic Plan to Promote the Development and Implementation of Alternative Test Methods Within the TSCA Program. In: Prevention O. o. C. S. a. P., (Ed.), 2018. [Google Scholar]
- USEPA, ToxRefDB version 2.0. ftp://newftp.epa.gov/comptox/High_Throughput_Screening_Data/Animal_Tox_Data/current, 2019.
- Venables WN, Ripley BD, 2002. Modern Applied Statistics with S. Springer-Verlag; New York. [Google Scholar]
- Veselinović JB, et al. , 2016. The Monte Carlo technique as a tool to predict LOAEL. European Journal of Medicinal Chemistry. 116, 71–75. [DOI] [PubMed] [Google Scholar]
- Wambaugh JF, et al. , 2018. Evaluating In Vitro-In Vivo Extrapolation of Toxicokinetics. Toxicol Sci. 163, 152–169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watford S, et al. , 2019. ToxRefDB version 2.0: Improved utility for predictive and retrospective toxicology analyses. Reprod Toxicol. 89, 145–158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weitekamp CA, et al. , 2019. Triclosan-selected host-associated microbiota perform xenobiotic biotransformations in larval zebrafish. Toxicol Sci. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wheeler AR, Memorandum: Directive to Prioritize Efforts to Reduce Animal Testing. US Environmental Protection Agency, Washington, D.C., 2019. [Google Scholar]
- WHO/IPCS, Guidance Document on Evaluating and Expressing Uncertainty in Hazard Characerization. World Health Organization, Geneva, Switzerland, 2014. [Google Scholar]
- Wignall JA, et al. , 2014. Standardizing Benchmark Dose Calculations to Improve Science-Based Decisions in Human Health Assessments. 122, 499–505. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplemental File 1, Table 1: The full dataset used for MLR modeling.
Supplemental File 1, Table 2: The full dataset used for ACM modeling.
Supplemental File 2: HTML file of the Rmarkdown used to generate all of the data analysis and most figures in this work.
Supplemental File 3: Supplemental Figures 1 and 2 on the composition of the MLR full dataset and the ACM full cell dataset.
Data Availability Statement
All analyses were performed with open source R version 3.6.1 and RStudio version 1.2.1335. The datasets used for MLR and ACM modeling are available as Supplemental File 1 (Tables 1 and 2). All of the R code used for this analysis and to make the figures in this work is available as an R Markdown file (exported as html) for Supplemental File 2. The code and data are also available for download at: ftp://newftp.epa.gov/COMPTOX/CCTE_Publication_Data/BCTD_Publication_Data/Paul-Friedman/Variability_in_vivo_data.


