Abstract
The functions of the nasal cavity are very important for maintaining the internal environment of the lungs since the inner walls of the nasal cavity control the temperature and saturation of the inhaled air with water vapor until the nasopharynx is reached. In this paper, three-dimensional computational studies of airflow transport in the models of the nasal cavity were carried out for the usual inspiratory velocity in various environmental conditions. Three-dimensional numerical results are compared with experimental data and calculations of other authors. Numerical results show that during normal breathing, the human nose copes with heat and relative moisture metabolism in order to balance the intra-alveolar conditions. It is also shown in this paper that a normal nose can maintain balance even in extreme conditions, for example, in cold and hot weather. The nasal cavity accelerates heat transfer by narrowing the air passages and swirls from the nasal concha walls of the inner cavity.
Keywords: Air flow in the human respiratory system, Alveolar state, Heat transfer in the nasal cavity, Navier, Stokes equation, Finite volume method
Background
The human nasal cavity acts as an important component of the respiratory system with many vital functions, including heating, filtering, moisturizing the air flow and smell. These functions are based on transport phenomena, which depend on the nature of the air flow in the nasal structure.
After the first studies of nasal function [5, 12, 13, 43], it was clear that inhaling through the nasal cavity causes the incoming ambient air to become almost alveolar, then is completely saturated with water vapor and heated to a person’s body temperature by the time it reaches the pharynx. These results were confirmed in many studies that collected data on air temperature values from various places in the upper respiratory tract throughout the respiratory cycle. Nevertheless, in [32], it was noted that these statements are true for calm (uniform) breathing, and for some cases, at high speeds in the intrathoracic airways, it is necessary to carry out additional conditioning to fully prepare the inhaled air to alveolar conditions. However, the exact characteristics and distribution of transport phenomena are still unknown even for normal or healthy breathing.
Depending on the local Reynolds numbers (Re) for different structures of the nasal air flow, they can undergo various flow regimes (laminar, transitional and turbulent). The normal rate of respiration in the nasal cavity is seen as a laminar flow, which accelerates in certain places of the nose and turns into a transient flow, gradually turning into a turbulent flow due to a decrease in cross-sectional area [6]. In the paper [10], measurements were made using laser anemometry on a human nose model and found that the flow field is mainly laminar and the velocity profiles are almost parabolic in all cross sections.
Turbulent flow usually occurs at Re > 2000, but depending on the complexity of the airways, the transition to a turbulent regime can occur at lower values of the Re number (below the value of 2000). Turbulent flow leads to better mixing of heat and moisture, which contributes to the functions of the nasal cavity. For adults, airflow rates can vary from 80 to 200 ml/s with calm breathing and from 200 to 1000 ml/s during exercise [1, 37], with a Re range from a few hundred to several thousand. However, in [7] at flow rates of 115–170 ml/s, irregular flow in the nasal cavity was revealed, which makes the assumption of laminar flow controversial for calm breathing.
With the development of high-performance computing in recent years, many researchers have considered simulation using computational fluid dynamics (CFD) as an alternative approach to studying airflow in human respiratory systems. Compared to natural measurements, CFD modeling is advantageous for a detailed study of air flow in the nasal cavity model. However, an accurate airflow forecast requires careful selection of CFD models and rigorous testing. In papers [4, 26, 40], a laminar model is used to simulate airflow in the nasal cavity at relatively low speeds, when the kinetic energy of turbulence is insignificant.
In [14, 33, 34], modeling of unsteady two-dimensional and three-dimensional models is considered to study the transfer of air flow in the nasal cavity of a person and its general ability to condition air. The results of these works showed that the nose can effectively provide about 90% of the heat and water flows needed to condition the surrounding respiratory air, bringing it to alveolar conditions in various environmental conditions. A 3D anatomical copy of the human nose showed the best results and was able to provide 92% of the heat and 96% of the moisture needed to condition the inhaled air. However, it should be noted that in [33] two-dimensional geometry was considered as sections of the nasal cavity, and in [34] the three-dimensional model was constructed in a rough form and shaped like a trapezoid. It should be noted that during the simulation, simplifications in geometry can lead to uncertainties or inaccuracies in the numerical results compared with real nasal cavities.
The accuracy of the simulation strongly depends on the choice of the numerical method and rigorous verification with experimental data. Several tests of numerical CFD models of airflow in the human nasal cavity were performed, which compared the pressure drop in the nasal cavity and the static pressure on the walls of the nose [4, 31, 42]. More detailed comparisons of various characteristics were also made in [2, 3, 8, 45], however, these calculations were performed for not specified nasal cavities. Most of these previous studies have tested their models on a limited range of flow rates. In [28], the accuracy of various CFD models was estimated for modeling airflow velocities under various respiration conditions in the right nasal cavity, based on computed tomography (CT).
Some investigation in the past has been limited by the poor presentation of complex nasal geometry, lack of detailed airflow comparisons, and limited computing power. The high computational cost limits the use of detailed geometry; therefore, many authors conducted very limited studies for the simplified geometry of the human nasal cavity [27, 38, 41, 44].
There are a few numerical studies that consider heat and moisture transfer. So in the papers [29, 30], it is assumed that the walls of the nasal cavity representing the nasal mucosa have a constant temperature. In [36], air conditioning, heating and humidification of the air in the nasal cavity are considered. This paper presents experimental and computational results that were aimed at promoting modern physiological research and practical medicine related to the health of the respiratory system. Also [9, 35, 39, 41, 44] give estimates of the nose morphology in relation to anomalies and diseases using three-dimensional computational models by providing doctors with the understanding, necessary to make informed decisions regarding surgical interventions.
The aim of this work is to study the various properties of the flow as heating and moisturizing using computational methods on an anatomically accurate model of the nose. Detailed velocity analysis is presented and compared with data from the measurement [11] and computational data [28]. The abilities of the nasal cavity were studied: heating and moisturizing the air during normal breathing in different environmental conditions. To study the flow in the nasal cavity, the ANSYS Fluent was used.
Materials and methods
The mathematical model
To simulate the air flow in the nasal cavity, the basic equations for the conservation of mass, momentum, temperature and relative humidity are determined as follows:
| 1 |
| 2 |
| 3 |
| 4 |
where U is the velocity vector, t is the real time, P is the flow pressure, C is the concentration of water vapor, cр is the specific heat, D is the molecular diffusion coefficient, T is the temperature, ρ, ϑ and k are the density, kinematic viscosity and thermal conductivity, respectively.
The ANSYS Fluent was used to investigate the flow in the nasal cavity. For numerical study, second-order spatial discretization schemes for pressure and momentum were used. Thus, the real problem will be solved in a discrete form by applying the finite volume method. The SIMPLE algorithm was used to communicate between pressure and velocity. The SIMPLE algorithm can be represented as the following sequence of steps:
Representations of the initial pressure field P0 and set P∗ = P0, t = 0.
Definitions of the initial velocity field u0, v0, w0.
The solution of the equations of motion.
The solution of the equation for P' and P calculation by adding P' to P∗.
Using velocity correction formulas.
If there was ∣P ' ∣ little in all nodes of the computational grid, then it was assumed P0 = P, u0 = u, v0 = v, w0 = w, t = t + Δt. Otherwise, it was used the result P as P∗ and it was proceeded to stage 3.
If t < Tmax, then we have a return to step 3.
All details of applying this SIMPLE algorithm can be found in papers [15–25, 46].
Methods
Verification of the model
The full three-dimensional structure of the nasal cavity provides a very complex path of air passage. To provide comprehensive studies of the transport mechanisms of the nasal cavity, three-dimensional test problem has been done. For all calculations, it is assumed that the walls of the nasal cavity and nasal concha are motionlessly solid. The airflow in the nasal cavity is laminar and incompressible due to low speeds. The walls of the nasal cavity are considered to be completely saturated with water vapor and the temperature near the body due to the wet mucous layer reaches the vascular vessels of the nasal wall.
Three-dimensional numerical simulation
To bring the numerical results closer to the real problem, it will need to use three-dimensional models of the nasal cavity, since heating and humidification of the inhaled air strongly depends on the structure of the nasal cavity walls. Therefore, computational models should include more realistic three-dimensional geometry descriptions in order to determine the effect of complex geometry on various characteristics such as velocity, heat and mass transfer, and relative humidity.
In the paper [11], data from the measurements were made of the air flow in a nose prototype using a hot wire anemometer in a large-scale physical model of the nasal cavity, based on computed tomography of the right nasal cavity of a healthy man. In the measurements, various respiration rates were used, equivalent to 180 ml/s, 560 ml/s and 1100 ml/s in a real human nose, which corresponds to calm breathing, medium inhalation and intensive inhalation, respectively. Fig. 1 a, b displays the measurement setup and the relative position of the measurement sites on three slices, which were used to verify the obtained numerical values.
Fig. 1.
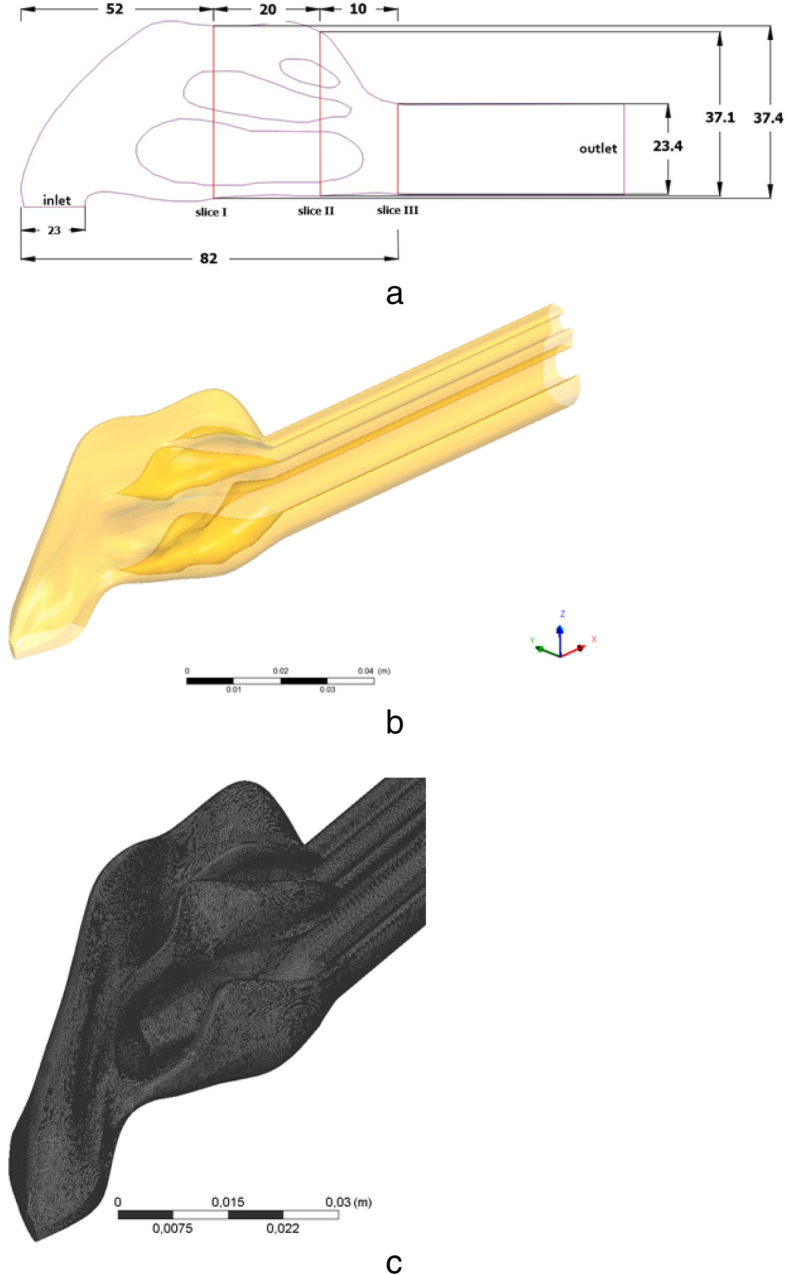
a-b Physical geometry of the studied area (all dimensions in mm), c the computational grid of a complex nasal cavity of a person.
The numerical model included the area from the front tip of the nose to the posterior end of the nasal concha. As displayed in Fig. 1a, b, the nasopharynx was expanded to fit the experimental setup.
The geometry of the human nasal cavity was created by aligning and processing 40 computed tomographic (CT) images of the respiratory tract of a healthy man. Using the AutoCAD software, intermediate geometric shapes of the nasal cavity were created that correspond to the average physical parameters of the human nasal cavity. From these idealized 2-D images (Fig. 2), a 3-D complex human nasal cavity was created. The locations of the anemometers in the study area are presented in Fig. 3.
Fig. 2.
The 2D digitized cross-sections of 40 computed tomographic (CT) images of the respiratory tract of a healthy man
Fig. 3.
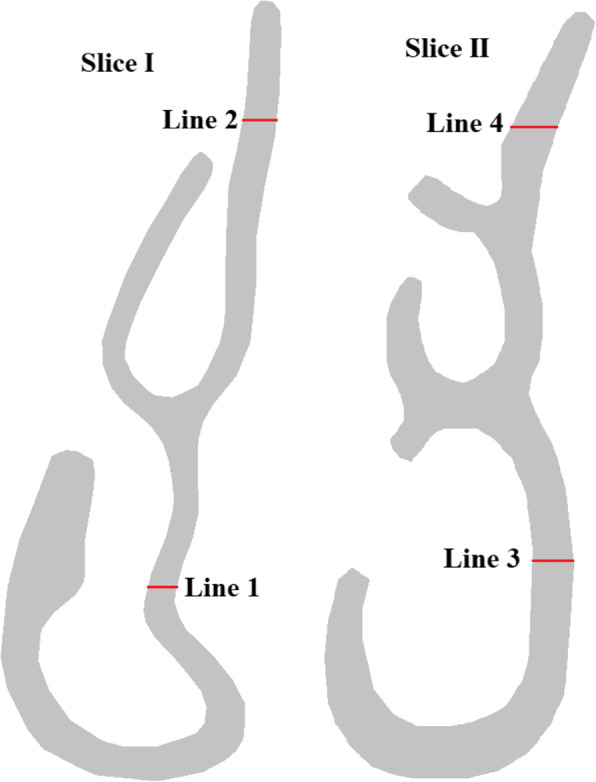
Location of lines 1–4 at slices 1 and 2
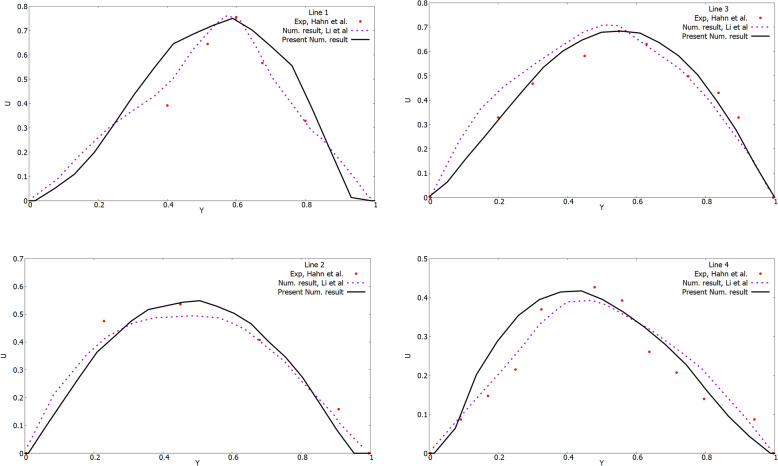
As can be seen from Fig. 3, in slices 1 and 2, 4 lines were located for measuring velocity at these points in the section. The computational grid of the studied area is presented in Fig. 1c. The final computational grid of the nasal cavity consisted of 6,876,463 elements (Fig. 1c). Comparisons of velocity profiles with measurement values [11] on lines 1–4 are presented in Fig. 4.
Fig. 4.
Comparison of the profiles of the horizontal velocity (U) component on lines 1–4 with the numerical results of other authors [28] and experimental data [11]
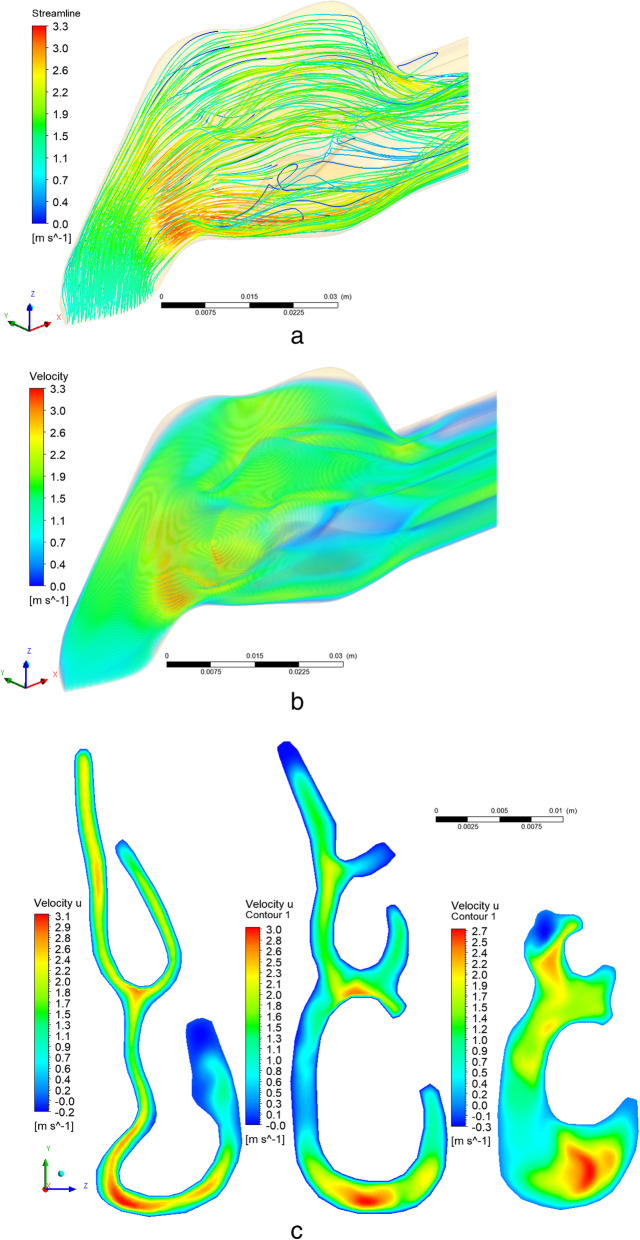
The velocity profiles were dimensionless by the value of the local maximum velocity. The X-axis for Y was dimensionless by the value of the local maximum distance. As shown in Fig. 4, the forecasts of the laminar model are in good agreement with measurement values [11]. The directions of the air flow in the nasal cavity and two-dimensional contours in sections 1–3 are shown in Figs. 5a, b and c. As expected, in the narrow channels of the nasal cavity the air flow accelerated and reached a maximum value of 3.33 m/s (Fig. 5a, b). It can be also noticed that due to the deep shells of the nasal cavity, vortices arise, which subsequently can well affect the heat and mass transfer. The two-dimensional velocity contours presented in Fig. 5c confirm the allegations of air flow acceleration due to the narrowing of the nasal concha and, as a result, the occurrence of vortices.
Fig. 5.
The longitudinal components of the air flow rate in the nasal cavity. a-b three-dimensional distributions of the longitudinal components of the air flow rate with the deposition of streamlines, c the two-dimensional contours of the longitudinal components of the velocity of the cross section 1–3
Despite some unevenness in the flow field profiles, it can be noted that the proposed model is in good agreement with the measurement values [11] under conditions of calm breathing. It can also be noted that the numerical results obtained show much closer values to the measurement data [11] than the obtained computational values in the paper [28]. However, the inaccuracies obtained in this work can be explained by the fact that the subtle features of the nasal cavity cannot be accurately measured due to the limited resolution of existing imaging methods. Accordingly, a model similar to the nasal cavity was developed (Fig. 1), in which the dimensions are taken from the averaged data on the human nasal cavities [11]. The model used allows us to comprehensively study a large number of the nasal cavity functions with respect to the structural components of the nasal cavity and the corresponding heat and mass transfer. It should be noted that in real conditions, the nose walls can be unequal or equal to the alveolar conditions, especially during exercise, and future models should clarify these assumptions.
Results
Numerical study of heating and moisturizing the air in the human nose
The air flow in the nasal cavity of a person plays an important role in many physiological functions of the nose, such as heating and moisturizing the flow of air and others. In this section, the proposed model is used to predict air flow and related transport phenomena in human nasal cavities.
It is assumed that the flow of heat and water vapor is released from the inside of the nasal mucosa. Normal respiration was chosen as a reference base, and then the effect of changes in ambient temperature was investigated. This study serves as the basis for a better understanding of transport phenomena in the nasal cavity (heat, mass), which are the main functions of the nose.
The studied area was identical to the second test problem of Fig. 1. It is believed that the walls of the nasal cavity are completely saturated with water vapor and due to the wet mucous layer and rich underlying vascular bed, the temperature values are close to body temperature. The temperature on the nose walls is taken equal to 37 °C, the humidity on the walls is taken 100%. Environmental conditions were taken as in paper [33], the temperature of the inhaled air is 25 °C and the relative humidity is 20%. Figure 6 shows the two-dimensional and three-dimensional distributions of the longitudinal components of the flow velocity for various sections (sections 1–3) with these conditions. From the obtained results, it can be noted that the global behavior of the air flow was not changed, but, however, the maximum longitudinal velocity increased to 3.47 m/s (Fig. 6a). The increase in maximum longitudinal velocity was affected by the conditions of heating and moisturizing on the walls of the nasal cavity. Figure e shows the process of heating inhaled air for various sections. From the results of Fig. 6e, it can be noticed that the inhaled air in section 3 is heated, and the air temperature is varying between 34 and 37 °C. The concentration of water vapor in the 3 section reaches the value of 0.66–0.99 (Fig. 6i). This structure of the nasal cavity increases the local rate of heat and moisture transfer due to the narrowing of the nasal channels for air. This constriction in the nasal cavities leads to the appearance of eddies downstream.
Fig. 6.
Two-dimensional and three-dimensional distributions of the longitudinal components of the flow rate for different environmental conditions: a-b at an ambient temperature of 25°C and humidity on the walls of the nasal cavity of 20% for different sections (sections 1-3). c-d at an ambient temperature of 5°C and humidity on the walls of the nasal cavity of 20% for different sections (sections 1-3). e-f at an ambient temperature of 5°C and humidity on the walls of the nasal cavity of 90% for different sections (sections 1-3). g-h at an ambient temperature of 40°C and humidity on the walls of the nasal cavity of 90% for different sections (sections 1-3). i-j at an ambient temperature of 25°C and humidity on the walls of the nasal cavity of 20% for different sections (sections 1-3). k-l at an ambient temperature of 5°C and humidity on the walls of the nasal cavity of 20% for different sections (sections 1-3). m-n at an ambient temperature of 5°C and humidity on the walls of the nasal cavity of 90% for different sections (sections 1-3). o-p at an ambient temperature of 40°C and humidity on the walls of the nasal cavity of 90% for different sections (sections 1-3). q-r at an ambient temperature of 25°C and humidity on the walls of the nasal cavity of 20% for different sections (sections 1-3). s-t at an ambient temperature of 5°C and humidity on the walls of the nasal cavity of 20% for different sections (sections 1-3). u-v at an ambient temperature of 5°C and humidity on the walls of the nasal cavity of 90% for different sections (sections 1-3). w-x at an ambient temperature of 40°C and humidity on the walls of the nasal cavity of 90% for different sections (sections 1-3).
To study the effect of respiration at various temperature and humidity environments, several simulations were carried out using the proposed model. Three modes were chosen for modeling heat and mass transfer in the nasal cavity for normal inspiration in extreme environments: at an ambient temperature of 40 °C and humidity on the walls of the nasal cavity 90%, at ambient temperature 5 °C and humidity on the walls of the nasal cavity 20%, ambient temperature 5 °C and humidity on the walls of the nasal cavity 90%. The velocity of air flow in the nasal cavity was used the same in all cases, however, the transfer process varies depending on the conditions. Figs. 6b, f, j show the simulation values at an ambient temperature of 5 °C and humidity on the walls of the nasal cavity of 20%. As shown in Fig. 6b, at a temperature of 5 °C and a humidity of 20%, the maximum velocity reached 3.56 m/s. The temperature of the inhaled air in section 3 ranges from 28 to 37 °C. However, it should be noted that a temperature of 28 °C occurs only in a small area, with an average temperature of 35 °C. As shown in Fig. 6j, inhaled air with a moisture content of 20% is moistened with water vapor from 0.62–0.99 until the nasopharynx is reached. In general, water vapor distributions are the same as the results from Fig. 6a.
Figure 6c shows the results of numerical modeling at an ambient temperature of inhaled air of 5 °C with humidity on the walls of the nasal cavity of 90%. The flow behavior at a temperature of 5 °C and a humidity of 90% is the same as the results of Fig. 6c. The results of Fig. 6 g and 6f are the same, since the conditions for the temperature of the inhaled air are the same. From the results of Fig. 6 k it can be seen that the concentration of inhaled air in section 3 is in the range 0.78–1.0. Figs. 6d, 6 h, 6 l show the results of numerical modeling at an ambient temperature of inhaled air of 40 °C with a nasal cavity humidity of 90%. At a temperature of inhaled air of 40 °C and with a humidity of 90%, the maximum flow velocity reaches a value of 3.4 m/s. The nasal cavity not only heats the inhaled air, but in some critical cases it can also cool. As shown in Fig. 6 h, inhaled air at 40 °C is cooled to body temperature. The concentration of inhaled air when passing through cross section 3 is 0.79–1.0, which is about an alveolar condition.
From the above results, it can be concluded that the nasal cavity balances the inhaled air with the internal conditions of the body with remarkable efficiency, and is almost independent of the surrounding air state. As a comparison, the influence of external conditions in Figs. 7 and 8 shows the temperature and concentration profiles on lines 1–4 from section 1–2 (Fig. 3). The X-axis for Y was dimensionless by the value of the local maximum distance. And the concentration on all the obtained numerical results is indicated as dimensionless, since it shows the mass fraction.
Fig. 7.
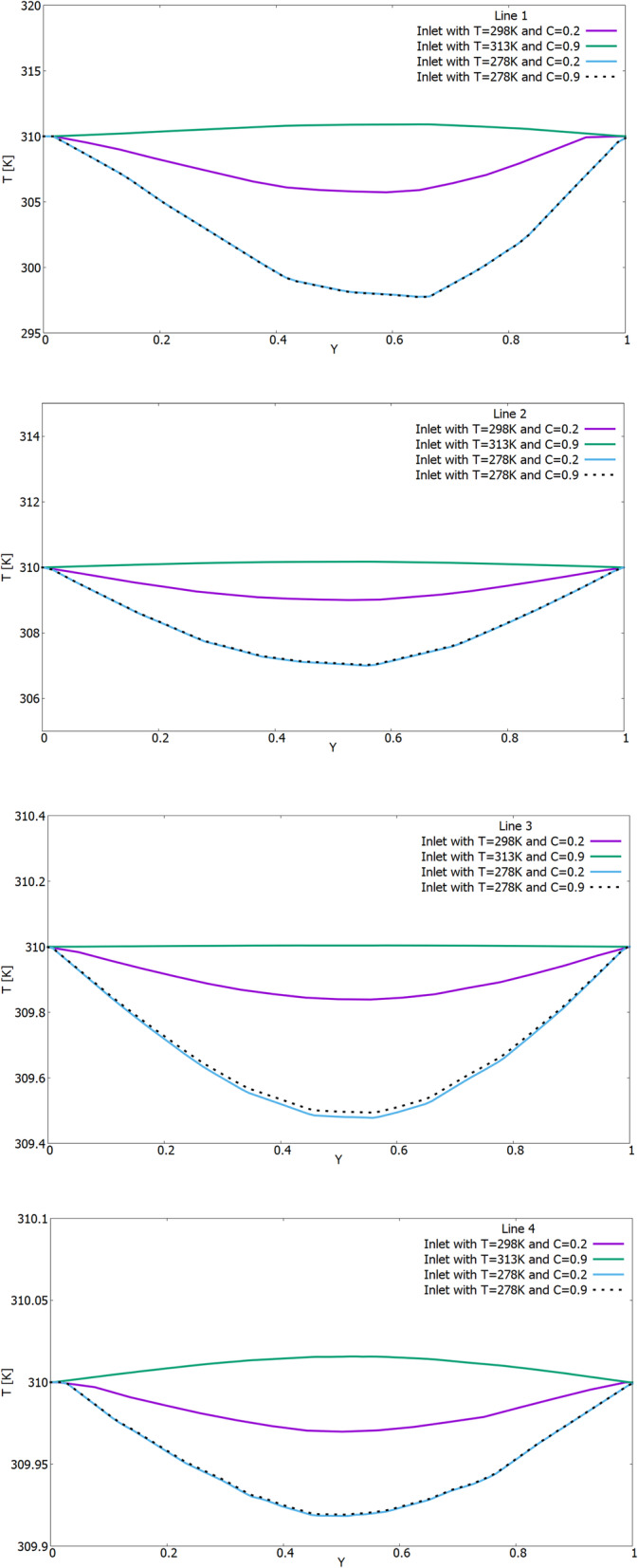
Comparison of temperature profiles (T) on lines 1–4 under different environmental conditions (for different ambient temperature and humidity on the walls of the nasal cavity: 1) 25 °C and 20%, 2) 5 °C and 20%, 3) 5 °C and 90%, 4) 40 °C and 90%)
Fig. 8.

Comparison of concentration profiles on lines 1–4 under different environmental conditions
The results of Fig. 7 show the difference in temperature distribution on measuring lines 1–4. In all the results, it can be seen that the temperature of the inhaled air tends to the conditions of the walls of the nasal cavity, that is, to the body temperature of 37 °C. As shown in Fig. 8, the concentration profiles on the measuring lines are the same under the same humidity conditions of the inhaled air. Like temperature values, the concentration of water vapor also tends to the conditions of the walls of the nasal cavity, that is, to a concentration equal to 1.0.
In this work, a realistic geometry of the human nasal cavity was used, but, however, it must be taken into account that this geometry is not universal since each person has his own structure of the nasal concha. However, the created three-dimensional geometry of the human nasal cavity can be of great benefit as a standard nasal replica for testing various conditions of ambient temperature, relative humidity and the rate of inhaled air flow.
Conclusion
This study is a comprehensive work on modeling the processes of heat and mass transfer in a 3D model of the human nasal cavity. The purpose of this study was to use the proposed computational model to investigate the dynamic ability of the nasal cavity to heat and moisten the inhaled air in the studied area, similar to the nose so that it is possible to comprehensively study the structural components.
Transport functions depend on accurate predictions of the airflow nature. Therefore, the numerical model is tested in an anatomically accurate computational model by comparing simulated velocity profiles with values from the measurement. The basic equations of the incompressible laminar air flow with constant viscosity and thermal conductivity are the continuity, Navier - Stokes, energy conservation and convection - diffusion equations.
The flow behavior during breathing varies depending on environmental conditions. Therefore, three-dimensional computational studies of transport phenomena in the nasal cavity were carried out under different environmental conditions. In all cases, the inhaled air was heated and moistened almost to the state of the nasal tissue before reaching the nasopharynx. Complex geometries increase the rate of local transfer of heat and moisture by improving mixing and maintaining thin boundary layers. A normal nose can withstand various extreme conditions. However, irregularities in the blood supply or wetting of the surface can reduce the flow rate of heat or moisture in the inhaled air. Further research will need to improve detailed descriptions of the heat transfer and humidification dynamics.
It should be noticed that for this study there are several limitations. The first limitation is the grid size since even most powerful computers cannot provide data from the numerical simulation for full three-dimensional cases with all details of the nasal cavity. The second limitation is the complexity of the implementation and analysis of experimental data from the tomographic images for the different nasal sinus. The third limitation is the tomographic apparatus, which gives only a limited number of images.
The proposed 3D model has the potential for use as geometric standard in future computational studies, as well as for use as a reference in diagnostics. The developed procedure can also be used to construct standard nose geometries for various identifiable groups in a larger population.
Acknowledgements
This work is supported by the grant from the Ministry of education and science of the Republic of Kazakhstan (AP08857306).
Authors’contributions
AI has made the conception and designs of the study, YZ, AA have made simulation, analysis and interpretation of data, AI has made modification and additional interpretation of data. The authors read and approved the final manuscript.
Abbreviations
- CFD
Computational fluid dynamics
- SIMPLE
Semi-Implicit Method for Pressure Linked Eqs.
- CT
Computed tomographic
- CAD
Computer-aided design
Funding
This research received no specific grant from any funding agency in the public, commercial or not-for-profit sectors.
Availability of data and materials
The datasets used and/or analyzed during the current study are available from the corresponding author on reasonable request.
Ethics approval and consent to participate
Not applicable.
Consent for publication
Not applicable.
Competing interests
The authors declare that there is no conflict of interests regarding the publication of this paper.
Footnotes
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Anderson, N.J., Cassidy, P.E., Janssen, L.L., Dengel, D.R., 2006. Peak inspiratory flows of adults exercising at light, moderate and heavy work loads. J.-Int. Soc. Respir Prot. 23, 53.
- 2.Ball C, Uddin M, Pollard A. High resolution turbulence modelling of airflow in an idealised human extra-thoracic airway. Comput Fluids. 2008;37:943–964. doi: 10.1016/j.compfluid.2007.07.021. [DOI] [Google Scholar]
- 3.Chen J, Gutmark E. Numerical investigation of airflow in an idealized human extra-thoracic airway: a comparison study. Biomech Model Mechanobiol. 2014;13:205–214. doi: 10.1007/s10237-013-0496-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Croce C, Fodil R, Durand M, Sbirlea-Apiou G, Caillibotte G, Papon J-F, Blondeau J-R, Coste A, Isabey D, Louis B. In vitro experiments and numerical simulations of airflow in realistic nasal airway geometry. Ann Biomed Eng. 2006;34:997–1007. doi: 10.1007/s10439-006-9094-8. [DOI] [PubMed] [Google Scholar]
- 5.Cole P. Some aspects of temperature, moisture and heat relationships in the upper respiratory tract. J Laryngol Otol. 1953;67:449–456. doi: 10.1017/S0022215100048908. [DOI] [PubMed] [Google Scholar]
- 6.Doorly D, Taylor D, Schroter R. Mechanics of airflow in the human nasal airways. Respir Physiol Neurobiol. 2008;163:100–110. doi: 10.1016/j.resp.2008.07.027. [DOI] [PubMed] [Google Scholar]
- 7.Doorly D, Taylor D, Franke P, Schroter R. Experimental investigation of nasal airflow. Proc Inst Mech Eng Part H. 2008;222:439–453. doi: 10.1243/09544119JEIM330. [DOI] [PubMed] [Google Scholar]
- 8.Doorly D, Taylor D, Gambaruto A, Schroter R, Tolley N. Nasal architecture: form and flow. Philos Trans R Soc Lond A: Math Phys Eng Sci. 2008;366:3225–3246. doi: 10.1098/rsta.2008.0083. [DOI] [PubMed] [Google Scholar]
- 9.Garcia GJM, Schroeter JD, Kimbell JS. Olfactory deposition of inhaled nanoparticles in humans. Inhal Toxicol. 2015;27:394–403. doi: 10.3109/08958378.2015.1066904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Girardin M, Bilgen E, Arbour P. Experimental study of velocity fields in a human nasal fossa by laser anemometry. Ann Otol Rhinol Laryngol. 1983;92:231–236. doi: 10.1177/000348948309200304. [DOI] [PubMed] [Google Scholar]
- 11.Hahn I, Scherer PW, Mozell MM. Velocity profiles measured for airflow through a large-scale model of the human nasal cavity. J Appl Physiol. 1993;75:2273–2287. doi: 10.1152/jappl.1993.75.5.2273. [DOI] [PubMed] [Google Scholar]
- 12.Hanna LM, Scherer PW. Measurement of local mass transfer coefficients in a cast model of the human upper respiratory tract. J Biomech Eng. 1986;108:12–18. doi: 10.1115/1.3138573. [DOI] [PubMed] [Google Scholar]
- 13.Ingelstedt S. Studies on conditioning of air in the respiratory tract. Acta Otolaryngol Suppl. 1956;131:1–80. [PubMed] [Google Scholar]
- 14.Issakhov A, Abylkassymova A. Application of parallel computing Technologies for Numerical Simulation of air transport in the human nasal cavity. Innovative computing, optimization and its applications. Stud Comput Intell. 2018;741:131–149. [Google Scholar]
- 15.Issakhov A., Bulgakov R., Zhandaulet Y. Numerical simulation of the dynamics of particle motion with different sizes. Eng Appl Comput Fluid Mech, 2019a, 13:1, 1–25.
- 16.Issakhov A, Bulgakov R, Zhandaulet Y. Numerical study of the dynamics of particles motion with different sizes from coal-based thermal power plant. Int J Nonlinear Sci Numerical Simul. 2019;20(2):223–241. doi: 10.1515/ijnsns-2018-0182. [DOI] [Google Scholar]
- 17.Issakhov A, Mashenkova A. Numerical study for the assessment of pollutant dispersion from a thermal power plant under the different temperature regimes. Int J Environ Sci Technol. 2019;16(10):6089–6112. doi: 10.1007/s13762-019-02211-y. [DOI] [Google Scholar]
- 18.Issakhov A., Zhandaulet Y. Numerical simulation of thermal pollution zones’ formations in the water environment from the activities of the power plant. Eng Appl Comput Fluid Mech, 2019a, 13:1, 279–299.
- 19.Issakhov A, Zhandaulet Y. Numerical study of Technogenic thermal pollution zones’ formations in the water environment from the activities of the power plant. Env Model Assess. 2019b; 10.1007/s10666-019-09668-8.
- 20.Issakhov A, Omarova P. Numerical simulation of pollutant dispersion in the residential areas with continuous grass barriers. Int J Environ Sci Technol. 2019; 10.1007/s13762-019-02517-x.
- 21.Issakhov A, Omarova P, As I. Numerical study of thermal influence to pollutant dispersion in the idealized urban street road. Air Qual Atmosphere Health. 2020;13:1045–1056. doi: 10.1007/s11869-020-00856-0. [DOI] [Google Scholar]
- 22.Issakhov A, Alimbek A, As I. A numerical study for the assessment of air pollutant dispersion with chemical reactions from a thermal power plant. Eng Appl Comput Fluid Mech. 2020;14(1):1035–1061. doi: 10.1080/19942060.2020.1800515. [DOI] [Google Scholar]
- 23.Issakhov A, Imanberdiyeva M. Numerical simulation of the movement of water surface of dam break flow by VOF methods for various obstacles. Int J Heat Mass Transf. 2019;136:1030–1051. doi: 10.1016/j.ijheatmasstransfer.2019.03.034. [DOI] [Google Scholar]
- 24.Issakhov A, Zhandaulet Y. Numerical study of dam break waves on movable beds for various forms of the obstacle by VOF method. Ocean Eng. 2020;209:107459. doi: 10.1016/j.oceaneng.2020.107459. [DOI] [Google Scholar]
- 25.Issakhov A, Zhandaulet Y, Abylkassymova A. Numerical simulation of the water surface movement with macroscopic particles on movable beds. Water Resour Manag. 2020;34(8):2291–2311. doi: 10.1007/s11269-020-02521-8. [DOI] [Google Scholar]
- 26.Keyhani K, Scherer P, Mozell M. Numerical simulation of airflow in the human nasal cavity. J Biomech Eng. 1995;117:429–441. doi: 10.1115/1.2794204. [DOI] [PubMed] [Google Scholar]
- 27.Lin C-L, Tawhai MH, McLennan G, Hoffman EA. Characteristics of the turbulent laryngeal jet and its effect on airflow in the human intra-thoracic airways. Respir Physiol Neurobiol. 2007;157:295–309. doi: 10.1016/j.resp.2007.02.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Li C, Jiang J, Dong H, Zhao K. Computational modeling and validation of human nasal airflow under various breathing conditions. J Biomech. 2017;64:59–68. doi: 10.1016/j.jbiomech.2017.08.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Lindemann J, Leiacker R, Rettinger G, Keck T. Nasal mucosal temperature during respiration. Clin Otolaryngol. 2002;27:135–139. doi: 10.1046/j.1365-2273.2002.00544.x. [DOI] [PubMed] [Google Scholar]
- 30.Lindemann J, Kühnemann S, Stehmer V, Leiacker R, Rettinger G, Keck T. Temperature and humidity profile of the anterior nasal airways of patients with nasal septal perforation. Rhinology. 2001;39:202–206. [PubMed] [Google Scholar]
- 31.Mylavarapu G, Murugappan S, Mihaescu M, Kalra M, Khosla S, Gutmark E. Validation of computational fluid dynamics methodology used for human upper airway flow simulations. J Biomech. 2009;42:1553–1559. doi: 10.1016/j.jbiomech.2009.03.035. [DOI] [PubMed] [Google Scholar]
- 32.McFadden ER. Respiratory heat and water exchange: physiological and clinical implications. J Appl Physiol. 1983;54:331–336. doi: 10.1152/jappl.1983.54.2.331. [DOI] [PubMed] [Google Scholar]
- 33.Naftali S, Schroter RC, Shiner R, Elad DJ. Transport Phenomena in the Human Nasal Cavity: A Computational Model. Ann Biomed Eng. 1998;26:831–839. doi: 10.1114/1.108. [DOI] [PubMed] [Google Scholar]
- 34.Naftali S, Rosenfeld M, Wolf M, Elad D. The air-conditioning capacity of the human nose. Ann Biomed Eng. 2005;33:545–553. doi: 10.1007/s10439-005-2513-4. [DOI] [PubMed] [Google Scholar]
- 35.Na Y, Chung KS, Chung SK, Kim SK. Effects of single-sided inferior turbinectomy on nasal function and airflow characteristics. Respir Physiol Neurobiol. 2012;180:289–297. doi: 10.1016/j.resp.2011.12.005. [DOI] [PubMed] [Google Scholar]
- 36.Pérez-Mota J, Solorio-Ordaz F, Cervantes-de Gortari J. Flow and air conditioning simulations of computer turbinectomized nose models. Med Biol Eng Comput. 2018;56(10):1899–1910. doi: 10.1007/s11517-018-1823-2. [DOI] [PubMed] [Google Scholar]
- 37.Rennie CE, Gouder KA, Taylor DJ, Tolley NS, Schroter RC, Doorly DJ. Nasal inspiratory flow: at rest and sniffing. Int Forum Allergy Rhinol. 2011;1:128–135. doi: 10.1002/alr.20021. [DOI] [PubMed] [Google Scholar]
- 38.Varghese SS, Frankel SH, Fischer PF. Direct numerical simulation of stenotic flows. Part 1. Steady flow JFluid Mech. 2007;582:253–280. doi: 10.1017/S0022112007005848. [DOI] [Google Scholar]
- 39.Vinchurkar S, De Backer L, Vos W, Van Holsbeke C, De Backer J, De Backer W. A case series on lung deposition analysis of inhaled medication using functional imaging based computational fluid dynamics in asthmatic patients: effect of upper airway morphology and comparison with in vivo data. Inhal Toxicol. 2012;24:81–88. doi: 10.3109/08958378.2011.644351. [DOI] [PubMed] [Google Scholar]
- 40.Wang T, Chen D, Wang P, Chen J, Deng J. Investigation on the nasal airflow characteristics of anterior nasal cavity stenosis. Braz J Med Biol Res. 2016;49. [DOI] [PMC free article] [PubMed]
- 41.Wang Y, Elghobashi S. On locating the obstruction in the upper airway via numerical simulation. Respir Physiol Neurobiol. 2014;193:1–10. doi: 10.1016/j.resp.2013.12.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Weinhold I, Mlynski G. Numerical simulation of airflow in the human nose. Eur. Arch. Oto-rhino-Laryngol. Head Neck. 2004;261:452–455. doi: 10.1007/s00405-003-0675-y. [DOI] [PubMed] [Google Scholar]
- 43.Webb P. Air temperatures in respiratory tracts of resting subjects. J Appl Physiol. 1951;4:378–382. doi: 10.1152/jappl.1951.4.5.378. [DOI] [PubMed] [Google Scholar]
- 44.Wang Y, Elghobashi S. On locating the obstruction in the upper airway via numerical simulation. Respir Physiol Neurobiol. 2014;193:1–10. doi: 10.1016/j.resp.2013.12.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Zhang Z, Kleinstreuer C. Laminar-to-turbulent fluid–nanoparticle dynamics simulations: model comparisons and nanoparticle-deposition applications. Int J Numer Methods Biomed Eng. 2011;27:1930–1950. doi: 10.1002/cnm.1447. [DOI] [Google Scholar]
- 46.Issakhov A, Alimbek A, Zhandaulet Y. The assessment of water pollution by chemical reaction products from the activities of industrial facilities: Numerical study. J Clean Prod. 2020:125239.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The datasets used and/or analyzed during the current study are available from the corresponding author on reasonable request.