Abstract.
Modeling vector-borne diseases is best conducted when heterogeneity among interacting biotic and abiotic processes is captured. However, the successful integration of these complex processes is difficult, hindered by a lack of understanding of how these relationships influence disease transmission across varying scales. West Nile virus (WNV) is the most important mosquito-borne disease in the United States. Vectored by Culex mosquitoes and maintained in the environment by avian hosts, the virus can spill over into humans and horses, sometimes causing severe neuroinvasive illness. Several modeling studies have evaluated drivers of WNV disease risk, but nearly all have done so at broad scales and have reported mixed results of the effects of common explanatory variables. As a result, fine-scale relationships with common explanatory variables, particularly climatic, socioeconomic, and human demographic, remain uncertain across varying spatial extents. Using an interdisciplinary approach and an ongoing 12-year study of the Chicago region, this study evaluated the factors explaining WNV disease risk at high spatiotemporal resolution, comparing the human WNV model and covariate performance across three increasing spatial extents: ultrafine, local, and county scales. Our results demonstrate that as spatial extent increased, model performance increased. In addition, only six of the 23 assessed covariates were included in best-fit models of at least two scales. These results suggest that the mechanisms driving WNV ecology are scale-dependent and covariate importance increases as extent decreases. These tools may be particularly helpful for public health, mosquito, and disease control personnel in predicting and preventing disease within local and fine-scale jurisdictions, before spillover occurs.
INTRODUCTION
In the United States, zoonotic vector-borne diseases, notorious for their ubiquitous, yet apparent low, ability to inflict disease to humans and animals for multiple years, have the ability to suddenly erupt into seasonal outbreaks.1 Abiotic factors, most notably those that are climatic (e.g., temperature, precipitation, and humidity), directly mediate the lifecycles of arthropod vectors, many of which are among the first species in an ecosystem to respond to seasonal changes.2–6 Medically important mosquitoes are affected differently by temperature and precipitation, and the responses are unique by species. For example, in the United States, Culex pipiens tend to thrive in temperate, wet urban environments,7,8 whereas Culex tarsalis tend to thrive in dry, hot rural environments.9,10 Depending on the vector species, under ideal abiotic conditions, the forces can provide conditions optimal for rapid population growth and development, biting opportunities, and pathogen amplification.6,11
These forces are often coupled with biotic factors that strongly influence local- and fine-scale dynamics of disease.12 For example, a given county may be predominantly wetland, a habitat conducive for mosquito breeding, but the true prevalence of mosquito abundance can differ drastically within particular, smaller regions. Impervious land (land which does not allow water to pass through) is commonplace throughout cities and towns and may affect the flow and drainage of water, creating artificially induced inundated and/or semi-permanent flooding events. In addition, expansions of cities, towns, and the connectivity of humans (e.g., roads) often create patches of natural habitat. These patches, or fragments, become disrupted pieces of the landscape, facilitating fine-scale differences in ecological systems. In the provided example, a predominant wetland county with human disturbances creates an increasingly complex, heterogeneous mixture of abiotic and biotic forces on mosquito vectors, directly affecting disease ecology that is measurable only at high resolutions.1,13,14
West Nile virus (WNV) is a mosquito-borne Flavivirus that infects a vast array of vertebrate hosts.15 In North America, it is predominantly transmitted from mosquitoes of the Culex genus, and the predominant Culex vector species differs by region.16 The enzootic cycle of WNV occurs when an infected mosquito takes a blood meal from an uninfected avian host, or when an uninfected mosquito takes a blood meal from an infected, and actively shedding, infected avian host.17,18 The susceptibility and infectiousness of an avian host vary by species, but birds from the family Corvidae and Turdidae are considered the most important for amplifying the disease.17–19 In the Midwestern United States, the enzootic cycle of WNV is predominately maintained by the mosquito vectors Cx. pipiens, Culex restuans, and Culex salinarius20–22 and occasionally can spill over to dead-end (hosts that are not capable of infecting subsequent biting mosquitoes) human and equine hosts.23 The most susceptible human hosts are those that are elderly and/or immunosuppressed.24,25 An estimated 75–80% of infected humans are asymptomatic, and of the remaining 20–25%, < 1% (or about 1 in 150 infected humans) will experience severe neuroinvasive disease.26 Cook and DuPage counties, encompassing the greater Chicago, IL metropolitan region, have been among the hardest hit with human WNV in the country, accounting for the second and nineteenth most human neuroinvasive cases since 2002, respectively.27 Since the introduction of WNV in 2002, hot spots for human WNV illness in Chicago have occurred in high–human density locations within Chicago city and in the northern and northwestern suburbs, infecting hundreds, despite differences in race, socioeconomic status, and other key demographics.28
Many studies have modeled WNV risk, often with mixed results of the effects (i.e., direction), seasonal timings, and magnitudes (i.e., effect sizes) of several commonly reported covariates. Previous studies have found that increased disease risk was positively correlated with human population density,29–31 whereas others have reported the opposite.32–34 Other studies have found a positive association with mosquito abundance and increased rainfall in winter months,35 whereas another reported a similar finding, but for late-season rainfall.34 Other studies have found no predictive power with increased precipitation in the Eastern United States36 or Ontario, Canada.37 However, increases in winter temperatures were often found to be positively associated with increases in mosquito abundance and/or human infection but were less clear in early and mid-seasons.30,31,38,39
Far fewer studies have investigated the effects of important factors on WNV disease risk at local scales (< 100 km2).13,40 Although there is no correct single scale to measure the entirety of a given disease,41–43 studies conducted at regional or landscape scales may overlook fine-scale processes affecting disease dynamics at local scales because heterogeneity within a landscape moderates the broad-scale consistency of such processes42,44,45 and are often not generalizable even within the regions where the studies take place.12 Focusing on covariate and model selection at a fine scale and then applying to broader scales will provide a better perspective and understanding of the heterogeneity of spatiotemporal processes that influence WNV disease ecology.13,46
Translating fine-scale ecological processes into digestible epidemiological analyses has been immensely difficult, requiring both the resources to gather data at high spatiotemporal resolution and computational hardware and technology to process such large data sets.13,47 These limitations often force researchers to choose between increasing extent and decreasing grain (or vice versa).42,48 However, in recent years, high-performance computer technology has become readily available and affordable.12 Combining elements of ecology, epidemiology, entomology, and spatial statistics, we use an existing and ongoing 12-year WNV data set of the Chicago region to evaluate the drivers of WNV eco-epidemiology at a high spatial and temporal resolution (30 m–1 km spatial × 1 week temporal resolution) across relatively large spatial extents. Specifically, we compared human WNV model and covariate performance across three increasing extents: 1) ultrafine-scale (UFS) subset of 55 study sites, 2) local scale of 1,019 sites, and 3) county scale of 5,345 sites. Pertaining to the ecology of disease, we hypothesize that as spatial scale increases (and thus, complexity in heterogeneity), the number of covariates increases, and the magnitude in effect of each covariate will decrease. We also hypothesize that as the extent of scale decreases, variances in WNV disease transmission will be better captured, as reflected by higher performing models.
METHODS
This project was approved by the Institutional Review Board of the University of Illinois at Urbana-Champaign, the Illinois Department of Public Health (IDPH), and the University of Illinois Biosafety Committee. Human case data were provided by the IDPH without any personal identifying information.
Definition, use, and terminology of scale.
Scale is defined as the spatial or temporal dimension of an object or process and consists of two components: grain and extent. Grain is the finest level of spatial/temporal resolution within a given data set, and extent is the domain of the study area. For purposes specific to this study, we define large scale as a study area with small extent containing more detail and small scale as a study area with large extent containing less detail. Fine scale and broad scale are synonymous with large and small scale, respectively, and can be used interchangeably.
Study sites.
The observational unit by which all models were evaluated consisted of 1 km–wide (0.65 km2) hexagon-shaped polygons. Hexagons were used for two notable reasons: 1) they are the most complex regular polygon that can continuously fill a 2-dimensional plane without gaps or overlap in configuration (less loss in orientation) and 2) the shape index (perimeter2/area) is more compact than most other shapes (e.g., square or rectangle), providing more accurate sampling.49 All models had the same spatial resolution (1 km width) and temporal grain (1 week), denoted by CDC epidemiological weeks (beginning on Sunday and ending on Saturday). These resolutions were the finest scale by which our research team could reliably collect data throughout our study sites because of limitations in data availability and revisit times.
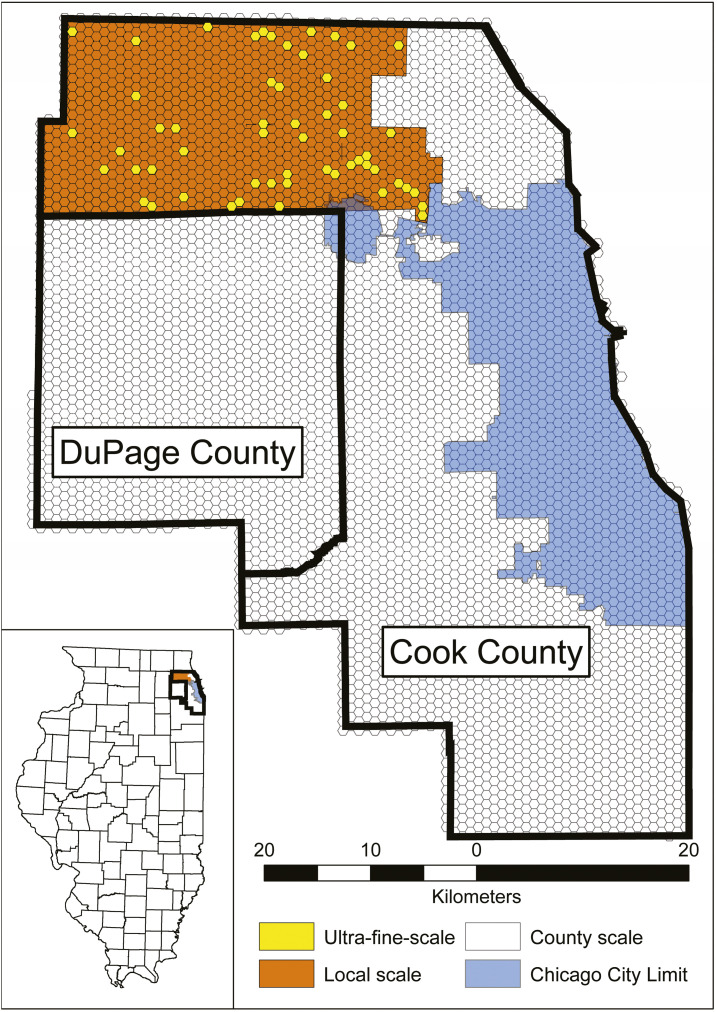
This study compared and evaluated the performance of each model and individual covariate across three study sites, varying in spatial extent: 1) 55 hexagons, 92.5 km2 (UFS); 2) 1,019 hexagons, 605.2 km2 (local scale); and 3) 5,345 hexagons, 3,471.7 km2 (county scale) (Figure 1).
Figure 1.
West Nile virus model comparison study area, displaying the Chicago city limit and the 1-km hexagonal grid observational units within Cook and DuPage counties. The models for the county, local, and ultrafine-scales (UFS) comprise all hexagons contained within both Cook and DuPage counties (n = 5,345), the hexagons bounded by the Northwest Mosquito Abatement District (indicated by the orange and yellow hexagons, n = 1,019), and the hexagons indicated in yellow (n = 55), respectively. This figure appears in color at www.ajtmh.org.
The UFS model, consisting of several individual field sites within each location, is the finest known spatial extent to evaluate WNV at weekly temporal resolutions.39 The 55 hexagons within the model have been selected across a spectrum of performance (ranging from extremely poor to extremely well-fit), based on strength of prediction, as indicated by the residual output from a previous Cook–DuPage WNV model.28 The decision to choose 55 hexagons is the maximum number of sites that our researchers could visit for 15 minutes each, weekly, over two field seasons (June–September 2018, 2019) while providing adequate spatial coverage as a subset of the Northwest Mosquito Abatement District (NWMAD).
The local scale is an area consisting of 1,019 hexagons. This region is an enclave of Cook county, encompassing the jurisdiction of one of the Chicago area’s four mosquito abatement agencies, the NWMAD. This local scale was chosen as study site because close collaboration from the NWMAD provided several advantages, including 1) access to high-quality and well-maintained longitudinal data sets; 2) permission to study and use equipment, if needed; 3) provision of important local information (e.g., areas that are flood- or mosquito-prone); 4) work toward a common goal to better understand and improve on the safety of public health as it pertains to local WNV dynamics.
The Cook–DuPage region, denoted as the county scale, comprises 5,345 hexagons and is the largest extent at which we evaluated human WNV illness. Despite its large two-county extent, the spatiotemporal resolution is still favorable for evaluating local–regional effects on WNV dynamics (1 km spatial grain × 1 week temporal resolution).
Model parameters.
Dependent variable: human illness.
Human WNV cases in Illinois were classified as either confirmed or probable, as reported to the IDPH by public health or licensed medical professionals by date of symptom onset (mandatory reporting of WNV cases is required in the state). The case definition for a confirmed case of arboviral encephalitis in Illinois is a clinically compatible illness that is laboratory confirmed at a public health laboratory. The laboratory criteria are a 4-fold or greater rise in serum antibody titer; or isolation of virus from, or demonstration of viral antigen in, tissue, blood, cerebrospinal fluid, or other body fluid; or specific IgM antibody in CSF. A probable case of arboviral encephalitis is a clinically compatible illness occurring during the season when arbovirus transmission is likely to occur and with the following supportive serology: a stable (2-fold or smaller change) elevated antibody titer to an arbovirus, for example, > 320 by hemagglutination inhibition, > 128 by complement fixation, > 256 by immunofluorescence, > 160 by neutralization, or a positive serologic result by enzyme immunoassay or IgM antibody capture enzyme-linked immunosorbent assay (MAC-ELISA).
We recognize that exposure to mosquito-borne disease occurs often and in many locations, and that confirming the moment an infected mosquito inoculates a human is nearly impossible. We assumed for this model that human cases were the result of exposure at their home addresses, and the latitude and longitude point locations of each human case were provided to the third decimal degree and aggregated to the hexagon level for analytical and display purposes. Any human case that occurred within a hexagon for a given week was converted into binary form (presence/absence of illness), controlling for human population, by week for each hexagon. Use of human case data was approved by the University of Illinois Institutional Review Board and the IDPH.
Independent variables.
The total number of independent variables available for each model varied by scale. The county, local, and UFSs had 40, 59, and 82 variables available, respectively (Table 1). Specific details pertaining to each independent variable’s processing and data source have been previously published.39
Table 1.
List of covariates available for analysis by scale study area.
| Covariate Information | Model Name | ||||||
| Designation | Description | Notation | Ultra-fine-scale | Local | County | ||
| Abiotic | Weather | Temperature | Average temperature current week | tempc | X | X | |
| Average temperature of one week before | templag1 | X | X | X | |||
| Average temperature of two weeks before | templag2 | X | X | X | |||
| Average temperature of three weeks before | templag3 | X | X | X | |||
| Average temperature of four weeks before | templag4 | X | X | X | |||
| Mean January temperature | Jantemp | X | X | X | |||
| Precipitation | Average precipitation current week | preci | X | X | |||
| Average precipitation of one week before | precilag1 | X | X | X | |||
| Average precipitation of two weeks before | precilag2 | X | X | X | |||
| Average precipitation of three weeks before | precilag3 | X | X | X | |||
| Average precipitation of four weeks before | precilag4 | X | X | X | |||
| Biotic | Environmental | Land Cover | Proportion of developed open space | dospct | X | X | X |
| Proportion of developed low intensity | dlipct | X | X | X | |||
| Proportion of developed medium intensity | dmipct | X | X | X | |||
| Proportion of developed high intensity | dhipct | X | X | X | |||
| Proportion of deciduous forests | dfpct | X | X | X | |||
| Proportion of evergreen forests | efpct | X | X | X | |||
| Proportion of mixed forests | mfpct | X | X | X | |||
| Proportion of barren land | blpct | X | X | X | |||
| Proportion of shrubs | shrubspct | X | X | X | |||
| Proportion of grassland | glandpct | X | X | X | |||
| Proportion of pasture | pasturepct | X | X | X | |||
| Proportion of cultivated land | clpct | X | X | X | |||
| Proportion of woody wetlands | wwpct | X | X | X | |||
| Proportion of herbaceous wetlands | hwpct | X | X | X | |||
| Proportion of total forest | ftotpct | X | X | ||||
| Proportion of total wetlands | wtotpct | X | X | ||||
| Proportion of open water | owpct | X | X | X | |||
| Normalized Difference Vegetation Index | NDVI | X | X | ||||
| Biological | Minimum Infection Rate (MIR) | MIR one week before | mirlag1 | X | X | X | |
| MIR two weeks before | mirlag2 | X | X | X | |||
| MIR three weeks before | mirlag3 | X | X | X | |||
| MIR four weeks before | mirlag4 | X | X | X | |||
| Average MIR current week | MIRmean | X | X | ||||
| Difference in weekly average MIR from 12-year average | MIRdiff | X | X | ||||
| Vector Index current week | Vector Index | X | X | ||||
| Vector Index one week before | VIlag1 | X | X | ||||
| Vector Index two weeks before | VIlag2 | X | X | ||||
| Mosquito Abundance | |||||||
| Vector Index three weeks before | VIlag3 | X | X | ||||
| Vector Index four weeks before | VIlag4 | X | X | ||||
| Light and gravid trap collection mean current week | Trap_Mean | X | X | ||||
| Light and gravid trap collection mean one week before | Trap_Meanlag1 | X | X | ||||
| Light and gravid trap collection mean two weeks before | Trap_Meanlag2 | X | X | ||||
| Light and gravid trap collection mean three weeks before | Trap_Meanlag3 | X | X | ||||
| Light and gravid trap collection mean four weeks before | Trap_Meanlag4 | X | X | ||||
| Mosquito Biting Rates (HLC) | Mosquitoes per visit | mosquitoes per visit | X | ||||
| Culex spp. per visit | Cx per visit | X | |||||
| Biotic | Anthropogenic | Socio-demographic | Percentage of White population | whitepct | X | X | X |
| Percentage of African American population | blackpct | X | X | X | |||
| Percentage of Asian population | asianpct | X | X | X | |||
| Percentage of Hispanic population | hispanicpct | X | X | X | |||
| Median household income | Income | X | X | X | |||
| Percentage of housing constructed before WWII | hpctpreww | X | X | X | |||
| Percentage of housing constructed post WWII (1945-1969) | hpctpostww | X | X | X | |||
| Percentage of housing constructed from 1970-1989 | hpct7089 | X | X | X | |||
| Percentage of housing constructed in 1990 or later | hpctpost90 | X | X | X | |||
| Land change & manipulation | Catch basin density | CB | X | X | |||
| Total area of building structures | bldg_footprint_area_total | X | |||||
| Average area of building structures | bldg_footprint_area_avg | X | |||||
| Total perimeter of building structures | Building_Footprint_peri_total | X | |||||
| Average perimeter of building structures | Building_Footprint_peri_avg | X | |||||
| Total area of residential lot | Residential_lot_area_total | X | |||||
| Average area of residential lot | Residential_lot_area_avg | X | |||||
| Total perimeter of residential lot | Residential_lot_peri_total | X | |||||
| Average perimeter of residential lot | Residential_lot_peri_avg | X | |||||
| Ratio of total building area by total lot area | total_bldg_area/total_lot_area | X | |||||
| Ratio of average building area by average lot area | avg_bldg_area/avg_lot_area | X | |||||
| Ratio of total building perimeter by total lot area | total_bldg_peri/total_lot_area | X | |||||
| Ratio of average building perimeter by average lot area | avg_bldg_peri/avg_lot_area | X | |||||
| Number of buildings | buildings | X | |||||
| Building density per mi.2 | bldg_density | X | |||||
| Number of residents per building | persons_per_bldg | X | |||||
| Human population | |||||||
| Total human population | totpop | X | X | X | |||
| Mean light pollution | lightpol | X | X | ||||
| Activity Observations | Senior Citizen Observations per visit | Senior_obs per visit | X | ||||
| Adults Observations per visist | Adults_obs per visit | X | |||||
| Children Observations per visit | Child_obs per visit | X | |||||
| Male Observations per visit | Male_obs per visit | X | |||||
| Female Observations per visit | Female_obs per visit | X | |||||
| Total Observations per visit | Total_obs per visit | X | |||||
| N/A | Other | Year | yr | X | X | X | |
| Hexagon Designation | hexid | X | X | X | |||
| Total Covariates Evaluated | 82 | 59 | 40 | ||||
Abiotic predictors.
Abiotic independent variables consisted of environmental (Multi-Resolution Land Characteristics (MRLC)50 National Land Cover Database) and weather (daily mean temperature and precipitation were acquired from the Parameter-elevation Regressions on Independent Slopes Model (PRISM)51 Climate Group [Oregon State University]) data. These were considered with 1-, 2-, 3-, and 4-week lags. Additional independent variables included catch basin (e.g., sewer) density and light pollution52,53 per hexagon. There were 29 variables available to both the UFS and local scale and 23 variables available to the county scale.
Biotic predictors.
All mosquito infection data were made available for all three scales and were provided by the IDPH, the state agency responsible for collecting and maintaining standardized mosquito collection and testing data. The vast majority of the tests used to identify the presence of WNV in mosquitoes were conducted via the rapid analyte measurement platform detection method, although some mosquito pools were also tested by real-time reverse transcriptase–PCR or VecTest. Mosquito infection data recorded between the epidemiological weeks 18–42 for each year between 2005 and 2016 were analyzed. Mosquito abundance data from a total of 59 traps (22 light and 37 gravid) were provided by the NWMAD and included in the models for the local and UFSs, but not the county scale because these data were not available for the entire county. As such, the vector index (VI), a factor of both mosquito infection and abundance, was calculated and made available for the local- and UFSs models. The following weekly mosquito infection indices were calculated by the following equations:
where = minimum infection rate (MIR), and a mosquito pool consisted of up to 50 female Culex mosquitoes that were collected by the same trap;
where and = estimated MIR.54
The mosquito infection indices were paired with each trap location that they were derived from, and interpolated across NWMAD via inverse distance weighting in a geographic information system, Environmental Systems Research Institute’s ESRI 2011, ArcGIS Desktop: Release 10.5.1., Redlands, CA. The average mosquito infection values were extracted for each hexagon using the zonal statistics tool in ArcGIS. These were also considered with 1-, 2-, 3-, and 4-week lags.
Total population and racial composition (white, African American, Hispanic, and Asian) at the census block level were extracted from the 2010 U.S. Census and converted to a percentage for each hexagon. The 2015 American Community Survey provided block level age of housing and income data that were aggregated by hexagon. The normalized difference vegetation index was processed from Landsat 7 and 8 bands for early, mid, and late summer periods from EarthExplorer55 and averaged by hexagon.
Statistical methods.
Model performance and comparisons.
The linear relationship between candidate covariates and the outcome (human WNV infection) for each model was initially screened by univariate linear regression analysis (cutoff P-value ≤ 0.20). Covariates that passed the initial univariate screening were then selected for the final model, a generalized linear regression personality, with a binomial distribution and logit link function, via forward selection, based on the lowest Bayesian information criterion (BIC) value achieved. Although assessed across the same temporal period (epidemiological weeks 18–42 from 2005 to 2016) and same spatial resolution (1-km hexagonal observation units), each of the three models corresponding to the three scales varied in spatial extent, resulting in increasing availability of data (Equation 1).
| (1a) |
| (1b) |
| (1c) |
where Y = weekly human WNV case probability for each hexagon between 2005 and 2016, β0 = intercept, and Xi = each of the WNV ecologically and/or epidemiologically relevant covariates made available for each scale (UFS = 82, local = 59, and county = 40 available covariates). Traditional performance metrics (e.g., Akaike Information Criterion [AIC] and BIC) are valid only for evaluating likelihood estimates across models that use the same data set. Therefore, this study evaluated the overall performance of each model by root mean square error (RMSE), an evaluation of the SD in residual values across each observation to the line of best fit. Receiver operating characteristic (ROC) curves were used to visualize each model’s overall performance, and area under the curve (AUC) values were calculated as secondary model performance indicators. All predictors were evaluated for multicollinearity and analyzed using the regression and fit model features, respectively, in JMP 14.2.0 (SAS Institute Inc., Cary, NC).
Human WNV illness risk maps (from 2005 to 2016), generated from the best-fit models at each scale, were created and compared for differences in magnitude in the probability of cumulative human cases. This process was conducted by first creating a raster layer for each included covariate per respective model. A raster layer visualizes data as a surface represented by a regular grid of pixels (each pixel represents 30 m). Using the raster calculator tool in ArcGIS, each included covariate’s estimate was input with its respective raster in a logistic regression (Equation 2), then transformed to create a probability map of human WNV cases (Equation 3).
| (2) |
| (3) |
Using the raster calculator again, the difference in probability “by pixel of the larger scale raster (either local or UFS) from the smaller scale raster (either county or local scale) was calculated (Equation 4).
| (4) |
where model C = best-fit model for county scale, model L = best-fit model for local scale, and model U = best-fit model for the UFS model.
Values greater than 1 indicate areas where the larger scale raster overestimated WNV risk, and values less than 1 indicate where the WNV risk was underestimated by the larger scale raster. To evaluate performance due to scale dependency, best-fit models from the smaller scales were also applied to larger scales, comparing BIC and ROC values with their original best-fit values.
Covariate performance and comparisons.
Individual covariate performance was evaluated within each respective scale’s best-fit model using the leave-one-covariate-out (LOCO) procedure.56 This method was chosen for the following reasons: 1) it is robust and not limited to linear models, 2) it emphasizes the importance of a variable in a model as it pertains to prediction, and 3) any algorithm can be used to measure the importance of the covariate and is computationally flexible.56 After each of the three scales’ respective best-fit models were chosen, the performance of each covariate was analyzed by removing it from the model and finding the difference in RMSE. Covariates removed with a percent difference in RMSE value extending further from zero in the positive direction indicated their increasing importance to the model, whereas a percent difference in RMSE value extending further from zero in the negative direction indicated decreasing importance to the model.
RESULTS
Descriptive statistics of each scale area.
Between 2005 and 2016, there were a total of 906 reported human cases in the Cook–DuPage study area. Within this region and time frame, the local scale study area consisted of 156 human cases (17.2%) with the UFS study contributing 46 human cases (5.1%).
Comparisons.
Models.
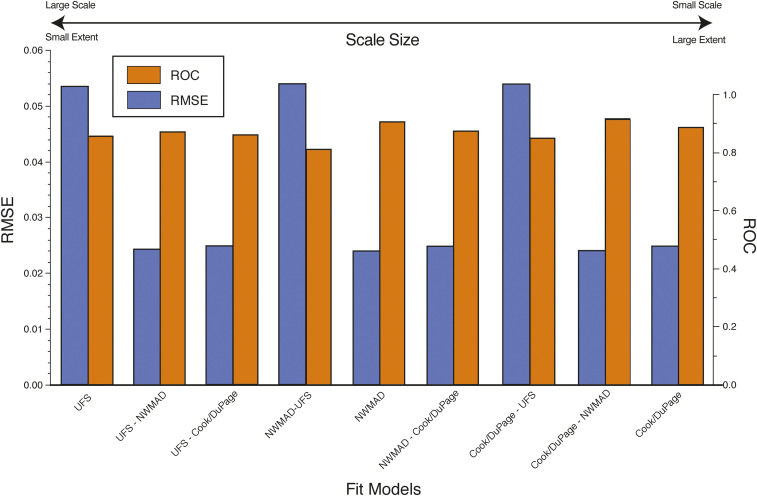
Best-fit models of county and local scales resulted in similarly small RMSE values (0.024872 and 0.023817, respectively), but more than doubled to 0.053571 in the final UFS model (Table 2). The final number of included covariates did not correlate with scale size, but the smallest scale (county level) did have the most covariates in the final model (n = 15). Applying best-fit models from one scale to another resulted in a general pattern of higher model performance as scale decreased (Figure 2). At all scales, the BIC score difference between the best-fit model and the next best-fit model was more than two.
Table 2.
Matrix of overall model performance and details of each model’s parameters. Values in bold indicate details of best-fit models for each respective scale. Remaining values are details of each scales’ best-fit model applied to the other two scales
| Scale applied to | |||||
|---|---|---|---|---|---|
| UFS | Local | County | |||
| Best model applied | UFS | P-value | < 0.0001 | < 0.0001 | < 0.0001 |
| No of covariates | 10 | 10 | 10 | ||
| (55) | BIC | 546.8 | 2067.5 | 13,547.8 | |
| ROC | 0.87 | 0.89 | 0.85 | ||
| RMSE | 0.053571 | 0.024347 | 0.024865 | ||
| Local | P-value | < 0.0001 | < 0.0001 | < 0.0001 | |
| No of covariates | 6 | 6 | 6 | ||
| (No of Hexagons) | (1,019) | BIC | 558.704 | 1987.63 | 13,222.1 |
| ROC | 0.82 | 0.91 | 0.87 | ||
| RMSE | 0.053883 | 0.023817 | 0.024867 | ||
| County | P-value | < 0.0001 | < 0.0001 | < 0.0001 | |
| No of covariates | 15 | 15 | 15 | ||
| (5,345) | BIC | 632.3 | 2079 | 13,161.8 | |
| ROC | 0.85 | 0.92 | 0.89 | ||
| RMSE | 0.053845 | 0.023812 | 0.024872 | ||
| Scale | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Covariate | UFS | Local | County | ||||||||
| Βn + 1 relationship, estimate, and P-value | |||||||||||
| Best model | UFS | β0 | − | 13.3857 | < 0.0001 | − | 16.2983 | < 0.0001 | − | 17.0640 | < 0.0001 |
| templag3 | + | 0.1623 | 0.0235 | + | 0.1680 | < 0.0001 | + | 0.1985 | < 0.0001 | ||
| templag4 | + | 0.2107 | 0.0026 | + | 0.2849 | < 0.0001 | + | 0.2589 | < 0.0001 | ||
| precilag1 | − | 0.0203 | 0.0428 | − | 0.0082 | 0.0442 | − | 0.0042 | 0.0028 | ||
| precilag2 | − | 0.0142 | 0.0885 | − | 0.0092 | 0.0194 | − | 0.0074 | < 0.0001 | ||
| precilag4 | − | 0.0189 | 0.0443 | − | 0.0152 | 0.0007 | − | 0.0076 | < 0.0001 | ||
| VIlag1* | − | 0.0037 | 0.5384 | + | 0.0026 | 0.0020 | + | 0.0044 | < 0.0001 | ||
| Asianpct | + | 0.0474 | 0.0239 | − | 0.0186 | 0.0497 | + | 0.0019 | 0.5906 | ||
| Dhipct | + | 0.0165 | 0.2297 | − | 0.0113 | 0.1198 | − | 0.0074 | 0.0004 | ||
| Mfpct | − | 4.6678 | 0.3461 | − | 0.6939 | 0.0214 | − | 0.2021 | < 0.0001 | ||
| Wwpct | − | 13.8269 | 0.9951 | − | 0.1784 | 0.0170 | − | 0.0463 | < 0.0001 | ||
| Local | β0 | − | 13.0397 | < 0.0001 | − | 18.2196 | < 0.0001 | − | 17.5333 | < 0.0001 | |
| templag3 | + | 0.1447 | 0.0381 | + | 0.1662 | < 0.0001 | + | 0.1828 | < 0.0001 | ||
| templag4 | + | 0.1767 | 0.0058 | + | 0.2445 | < 0.0001 | + | 0.2294 | < 0.0001 | ||
| MIRlag4 | + | 0.0103 | 0.0115 | + | 0.0090 | < 0.0001 | + | 0.0045 | < 0.0001 | ||
| Totpop | + | 0.0003 | 0.0663 | + | 0.0007 | < 0.0001 | + | 0.0003 | < 0.0001 | ||
| Jantemp | + | 0.0257 | 0.6356 | + | 0.1262 | < 0.0001 | + | 0.1288 | < 0.0001 | ||
| Dlipct | − | 0.0043 | 0.5512 | + | 0.0257 | < 0.0001 | + | 0.0208 | < 0.0001 | ||
| County | β0 | + | 31.0486 | 0.7583 | − | 27.0403 | 0.6323 | − | 33.4730 | 0.1189 | |
| Yr | − | 0.0213 | 0.6716 | + | 0.0046 | 0.8694 | + | 0.0082 | 0.4431 | ||
| templag2 | − | 0.0505 | 0.4964 | + | 0.0664 | 0.1115 | + | 0.0887 | < 0.0001 | ||
| templag3 | + | 0.1660 | 0.0299 | + | 0.1333 | 0.0020 | + | 0.1290 | < 0.0001 | ||
| templag4 | + | 0.1680 | 0.0144 | + | 0.2070 | < 0.0001 | + | 0.1840 | < 0.0001 | ||
| Jantemp | − | 0.0041 | 0.9451 | + | 0.1040 | 0.0031 | + | 0.1090 | < 0.0001 | ||
| mirlag1 | + | 0.0035 | 0.4715 | + | 0.0040 | 0.0710 | + | 0.0035 | < 0.0001 | ||
| mirlag2 | + | 0.0043 | 0.3715 | + | 0.0041 | 0.1368 | + | 0.0042 | < 0.0001 | ||
| mirlag3 | + | 0.0071 | 0.0517 | + | 0.0051 | 0.0601 | + | 0.0044 | < 0.0001 | ||
| mirlag4 | + | 0.0096 | 0.0309 | + | 0.0084 | < 0.0001 | + | 0.0045 | < 0.0001 | ||
| Totpop | + | 0.0001 | 0.5648 | + | 0.0005 | < 0.0001 | + | 0.0002 | < 0.0001 | ||
| Owpct | − | 0.0763 | 0.4064 | − | 0.0289 | 0.5398 | − | 0.0613 | 0.0005 | ||
| Dlipct | − | 0.0110 | 0.1962 | + | 0.0195 | < 0.0001 | + | 0.0168 | < 0.0001 | ||
| Dfpct | − | 0.0937 | 0.3387 | − | 0.1590 | 0.0452 | − | 0.0276 | 0.0096 | ||
| Glandpct | − | 0.0969 | 0.6389 | + | 0.0096 | 0.9184 | − | 0.0530 | 0.0392 | ||
| hpctpost90 | + | 0.0094 | 0.3838 | − | 0.0002 | 0.9689 | − | 0.0067 | 0.0035 | ||
UFS = ultrafine-scale.
Vector index and its associated lags were not available for the county-scale models. The next closest variable, MIR, was used as a proxy.
Figure 2.
Overall best-fit model performances for each of the three scales. In addition, the best-fit county (Cook/DuPage) and local Northwest Mosquito Abatement District (NWMAD) scale models were applied to the ultrafine-scale (UFS) model area (designated as larger scale model and smaller scale model, where “-” denotes “applied to”). The best-fit county scale was also applied to the local-scale model area. Models are ordered by scale size. This figure appears in color at www.ajtmh.org.
Covariates.
Overall, covariates included in the final model at any given scale tended to maintain their relationship (positive or negative), estimate values, and significance in regard to the independent variable (Table 2). In the UFS final model, the following covariates changed in their relationship, estimate, and/or significance when applied to the other two scales: VI 1-week lag, percentage of Asian population, and proportion of developed high intensity land cover. In the local-scale final model, only the covariate proportion of developed low-intensity land cover changed in relationship (changing from positive to negative) and significance (changing from strongly significant to nonsignificant) when applied to only the UFS area. When applied to the local scale, only two covariates included in the best-fit county model changed (proportion of land cover open water changed from nonsignificant to significant; proportion of land cover grassland changed from negative to positive and from significant to notsignificant). However, when applied to the UFS, there were numerous changes in relationships, estimates, and significances across most covariates.
Within each scale’s best-fit model, the overall importance (dependency) of included covariates increased with increasing scale (decreasing extent, Table 3). The indicator of covariate importance, the percent change in RMSE, ranged from 0.000643 to −0.000161 in the county scale, from 0.0001344 to −0.004954 in the local scale, and from 0.003043 to −0.000467 in the UFS, a range of 0.000804, 0.00050884, and 0.00351, respectively. Temperature 4-week lag was the most important covariate in the county and local scales and was the second most important covariate in the UFS. The most important covariate in the UFS was VI 1-week lag. Only the covariate, proportion of developed low-intensity land cover, in the local scale was notably non-important; all other negative covariate values were marginal.
Table 3.
Results of the leave-one-covariate-out performance method per respective scale’s best-fit model. The greater in magnitude of the percent change in RMSE indicates overall covariate importance (if positive) or unimportance (if negative) per each respective scale’s best-fit model. Covariates removed are provided in alphabetical order
| Covariate removed | Model | No of Scales included in | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| County | Local | Ultrafine-scale | ||||||||
| RMSE | % RMSE | Δ RMSE | RMSE | % RMSE | Δ RMSE | RMSE | % RMSE | Δ RMSE | ||
| None | 0.024872 | 1.000000 | 0.000000 | 0.023817 | 1.000000 | 0.000000 | 0.053571 | 1.000000 | 0.000000 | Not applicable |
| Asianpct | – | – | – | – | – | – | 0.053582 | 1.000205 | 0.000205 | 1 |
| dfpct | 0.024873 | 1.000040 | 0.000040 | – | – | – | – | – | – | 1 |
| dhipct | – | – | – | – | – | – | 0.053562 | 0.999,832 | −0.000168 | 1 |
| dlipct | 0.024876 | 1.000161 | 0.000161 | 0.023699 | 0.995,046 | −0.004954 | – | – | – | 2 |
| glandpct | 0.024873 | 1.000040 | 0.000040 | – | – | – | – | – | – | 1 |
| hpctpost90 | 0.024873 | 1.000040 | 0.000040 | – | – | – | – | – | – | 1 |
| Jantemp | 0.024879 | 1.000281 | 0.000281 | 0.023831 | 1.000588 | 0.000588 | – | – | – | 2 |
| mfpct | – | – | – | – | – | – | 0.053594 | 1.000429 | 0.000429 | 1 |
| MIRlag1 | 0.024873 | 1.000040 | 0.000040 | – | – | – | – | – | – | 1 |
| MIRlag2 | 0.024869 | 0.999,879 | −0.000121 | – | – | – | – | – | – | 1 |
| MIRlag3 | 0.024868 | 0.999,839 | −0.000161 | – | – | – | – | – | – | 1 |
| MIRlag4 | 0.024869 | 0.999,879 | −0.000121 | 0.023802 | 0.999,370 | −0.000630 | – | – | – | 2 |
| owpct | 0.024873 | 1.000040 | 0.000040 | – | – | – | – | – | – | 1 |
| precilag1 | – | – | – | – | – | – | 0.053546 | 0.999,533 | −0.000467 | 1 |
| precilag2 | – | – | – | – | – | – | 0.053604 | 1.000616 | 0.000616 | 1 |
| precilag4 | – | – | – | – | – | – | 0.053605 | 1.000635 | 0.000635 | 1 |
| templag2 | 0.024871 | 0.999,960 | −0.000040 | – | – | – | – | – | – | 1 |
| templag3 | 0.024877 | 1.000201 | 0.000201 | 0.023822 | 1.000210 | 0.000210 | 0.053605 | 1.000635 | 0.000635 | 3 |
| templag4 | 0.024888 | 1.000643 | 0.000643 | 0.023849 | 1.001344 | 0.001344 | 0.053608 | 1.000691 | 0.000691 | 3 |
| totpop | 0.024869 | 0.999,879 | −0.000121 | 0.023820 | 1.000126 | 0.000126 | – | – | – | 2 |
| VIlag1 | – | – | – | – | – | – | 0.053734 | 1.003043 | 0.003043 | 1 |
| wwpct | – | – | – | – | – | – | 0.053599 | 1.000523 | 0.000523 | 1 |
| Yr | 0.024873 | 1.000040 | 0.000040 | – | – | – | – | – | – | 1 |
RMSE = root mean square error.
Model predictions.
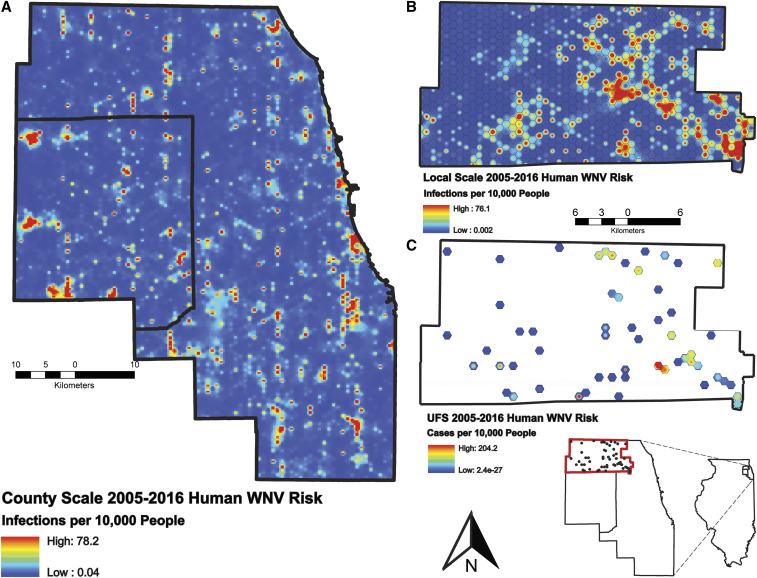
Risk maps displaying results (by pixel) of final models from 2005 to 2016 were created to display intensity of predicted human WNV illness by shades of red (Figure 3). The county-scale risk map displays several clusters of human risk, with the largest in western DuPage county (n = 3) and several along the Cook county Lake Michigan coast (n = 5). The local county risk map displays most human risk occurring in the eastern half of the study area, with two distinct, large clusters (one near the center and the other in the southeast corner). The UFS model predicted only one distinct, but high-intensity, cluster near the southeast corner of the study area.
Figure 3.
High-resolution human West Nile virus (WNV) risk maps for county (A), local (B), and ultrafine (B) scales. Values correspond to total infections per 10,000 people from 2005 to 2016. Each pixel is populated by the best-fit models for each respective scale. This figure appears in color at www.ajtmh.org.
DISCUSSION
Synthesis.
Even at the largest extent, the county level was assessed at a higher spatial and temporal resolution than most WNV studies. This study’s comparison provided insights into the processes of WNV disease dynamics, highlighting the changes across different scales.13 These change are most notable among the key similarities and differences between best-fit final models and the scale dependency of the covariates included within each. We found that as spatial scale increased, best-fit models decreased in explaining total variance, as defined by RMSE values. In addition, when evaluating covariates using the LOCO method, percent differences in RMSE increased as scale increased, suggesting that as spatial scale decreases, covariate importance increases. These findings align with other studies evaluating scale dependency of ecological processes and the traditionally hypothesized ecological mechanism that “factors should be most important at scales at which they vary the most because it will be difficult to find a statistically significant correlation when independent variables have low variance.”12,41 Final model selection should always be conducted using the most robust methods, but careful assessments must be made with very large-scale models because errors in prediction may be much greater than similar errors at smaller scales.
Despite having nine fewer covariates included its final model, as compared with the county model, the local scale’s overall RMSE was the lowest among all final models. Our initial hypothesis, claiming that as scale increased the number of covariates would also increase, was not supported by the local scale’s final model. Although no two scales can be explained by the exact same set of parameters, the local scale may be less heterogeneous across space than the larger county model. That being said, the UFS locations are located within the local scale and result in more included covariates (n = 10). Across all scales, only six (proportion of land cover developed low intensity, mean January temperature, MIR 4-week lag, temperature 3-week lag, temperature 4-week lag, and total human population) of the 23 total covariates (26.1%) assessed were included in two or more final models. Of these, only two (temperature 3-week lag and temperature 4-week lag, 8.7%) were included in all three scales’ final models. Percent difference in RMSE may be the most valid estimation for each covariate’s importance to a single model, but total frequency across models may provide the best indicator of its importance and robustness to WNV ecological processes.
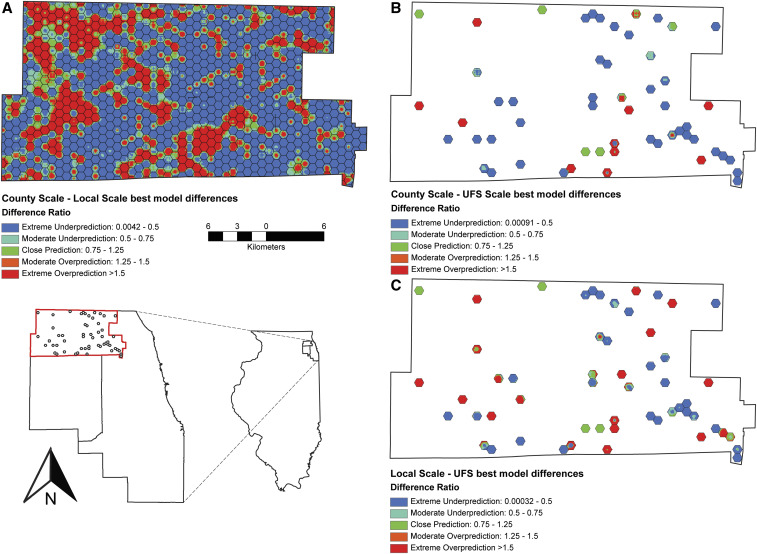
The best-fit model from all three scales performed very well, as indicated by the ROC AUC values. As scale decreased, clusters of disease risk increased in frequency, but decreased in area, resulting in a patchy distribution, a finding that aligns with bird distribution and increasing scale in another study.14 When overlaid, the best-fit model prediction of human WNV risk for each scale displayed similar clustering locations. Despite sharing the same location and containing mostly the same covariates, the predicted relationships have subtle, but critical, difference across scales. To visualize these differences, we calculated the percent difference in human WNV illness by pixel and categorized the values across a prediction performance scale (extreme underprediction to extreme overprediction, Figure 4). Although the extreme underprediction values never dropped below 0%, some extreme overprediction values exceed 150%. Despite being the most important human arboviral disease in North America, annual human cases are generally low. In addition, it is estimated that at least four of every five cases are not reported because most humans experience little to no symptoms.5 If reporting of actual disease incidence improved, extreme over- and underprediction events would likely reduce.
Figure 4.
Model comparisons, calculated as the difference between the best-fit larger scale model and the best-fit larger scale model, for county–local (A), county–ultrafine scale (UFS) (B), and local–UFS (C). This figure appears in color at www.ajtmh.org.
As observed in previous WNV models, covariates that were weather-specific were included in each of the final three models. In addition, of the 23 covariates included in any final model, only temperature 3-week lag and temperature 4-week lag were included in all three final models (the other 21 covariates were included in one or two models). In the upper midwest region of the United States, the 3- and 4-week temperature lags may be the most correlated to human WNV cases because of the length of time a mosquito requires to develop, acquire an infectious blood meal, bite a human, and have the human experience symptoms and be seen by a clinician for diagnosis.57–59 One- and 2-week temperature lags are likely too short of a time frame for all these events to occur.
Although only assessed in the local and UFS study regions, the VI was expected to be included in both final models. Only the 1-week lag was included in the UFS model, although as the single most important predictive factor. Instead, MIR 4-week lag was included in the local scale’s final model but was found to be among the weakest of the included covariates. High VI values, a combination of infection rates and mosquito abundance, likely require less lag time to be correlated to human WNV illness because of the likely advanced stage of the mosquitoes in the zoonotic infection cycle (mosquito–bird–mosquito–human). However, infection rates in mosquitoes, without abundance known, are more variable and can be associated with human WNV at any lag stage, as is observed in the county scale’s final model. Similar to 4-week temperature lags, MIRs with a 4-week lag may be the optimal period for the virus to have completed its enzootic transmission: mosquito–bird–mosquito, with ample time and opportunities to bite humans. Interestingly, mean January temperature was found to be positively associated with human WNV illness at the local and county scales. This relationship may be indicative of warmer winters that are providing mosquitoes with earlier emergence from diapause.60–62 These early emerging female mosquitoes may, in turn, increase the likelihood of earlier-than-expected enzootic cycles and, eventually, earlier season zoonotic cycles.
Understanding the ecological and epidemiological significance of human socioeconomic and demographic variables in regard to WNV is less intuitive. Of 33 anthropogeny-related covariates evaluated in this study, only the following three were included in at least one final model: percentage of Asian population, housing proportion built after 1990, and total human population (included in two models). For the UFS model, the percentage of the Asian population was found to be a positively significant predictor of human WNV infection. Given the small extent of the study area (55.1-km-wide hexagons), it is possible that a high proportion of the population that is of Asian descent resides in at least one of the high-risk WNV locations evaluated. Another possibility is that the Asian population in these locations may be confounding with disease incidence, resulting in a spurious correlation. In addition, the hexagons that were found to have the highest human WNV infection were found to contain many high-volume residential buildings (e.g., multi-level apartment buildings and condominiums) and may provide ample breeding and biting opportunities for Culex mosquitoes. In the county scale, housing built after 1990 was found to be a significantly negative predictor of human WNV illness. Newer houses have fewer areas that retain water and tend to be congregated in newer neighborhoods with improved drainage systems.63 In the Chicago area, newer houses are most likely found in the expanding suburbs, contain larger yards, and have lower human population densities than older houses. Increases in human population have been found to be a significantly positive predictor at the local and county scales. Higher human population densities provide increased opportunities for infected Culex mosquitoes to feed on humans, as opposed to the more preferred avian hosts.
Land cover was found to be a major predictor of human WNV, but the type of cover varied for each scale. Specific to the predominant Culex vector species in the Chicago area, Cx. pipiens, this species is associated with land cover that is largely human-derived; has a lot of development, little water and few wetlands; and is non-forested. In the county and UFS study areas, all land cover variables were negatively associated with human WNV risk, and all pertained to forest, grassland, or water/wetlands. However, at the local scale, proportion of land that was developed, low intensity, was found to be a significantly positive predictor of human WNV. In these locations, moderately spaced homes in suburban Chicago are integrated with numerous green spaces and wooded nature preserves. These conditions may provide an ideal balance of both avian hosts and human densities where persistent breeding and adequate feeding opportunities exist.
Limitations.
Evaluating the role of ecological processes in disease risk comes with many challenges. Realizing issues that may arise as spatial extent increases, most notably the modifiable area unit problem, this study attempted to reduce error when predicting human WNV illness by including data from very high spatial and temporal resolutions. Although many models are very well-constructed and perform well, environmental stochasticity and random processes can enhance response variability, particularly at large scales.64 Our results suggest that each scale has specific, but subtle, differences that explain the variability in WNV ecological processes. However, as the extent of our study increased (maintaining grain resolution), our models captured more unexplained variance. It is possible that at the largest scale (UFS), the sampling locations did not capture an adequate representation of that of the larger study area, resulting in higher RMSE values. However, it is expected that fine-scale ecological processes may have greater influence, and therefore importance, at small spatial extents. Another possible factor contributing to model differences by scale could simply be a factor of sample sizes. Data that are normally distributed will have greater opportunities to better capture model variance with increasing sample sizes. The county-scale model, as compared to the UFS model, contained 5,345 hexagons versus 55 hexagons, a factor of nearly 100. These results provide insights into the relationships that each individual covariate, as well as overall model performance, has across scales. Previous studies have highlighted the importance of evaluating ecological processing across multiple scales for these reasons.13,29,42,65
A large effort was placed on acquiring new ecology- and epidemiology-related factors associated with human WNV risk in our study areas. However, because of limited resources, in particular, the limited number of human researchers and availability for field collections, many covariates are point-specific and interpolated across the study areas. Keeping this limitation of sampling effort in mind, we attempted to maximize the number of field collections to as many as possible across a distribution that was representative of the entire study area, to reduce biases and inaccurate prediction values across space and time.43 Additional work stemming from this project can improve on these interpolation methods by focusing on field collections in regions where differences in model predictions are extremely over- or underpredicted (Figure 4).
Overall, our results provided insights into the behaviors of several key covariates with respect to human WNV risk across varying extents. That being said, we expected to see an increasing number of covariates in final models as extent increased. The local-scale model was expected to have between 11 and 14 covariates in its final model but ended up with 6, the fewest of any model. In addition, we expected that model error would be the smallest as extent became smaller. On the contrary, we found that the local model, with the fewest covariates included in the final model, had the lowest RMSE value, and the model with the smallest extent, UFS, had the greatest error. These values suggest that there are more regions that have less accurate predictions in the UFS model than the other models but do not infer this model is necessarily weaker or more poorly performing than the other two. It is possible that the covariates included in the local-scale model were optimized for local-scale analysis partly because most covariates were initially collected across the larger Cook and DuPage county regions or the UFS region. The local scale falls in between these two spectrums of extent and may incidentally become the best “size” to assess our data. However, it is more likely that imprecisions in the data (e.g., interpolations, averages, and choosing weekly instead of daily), applied within and across scales, all contribute to accumulating variance.66
Another potential issue that arises often in eco-epidemiology is the dilution effect.19,67 The dilution effect states that disease risk is limited or reduced because of an increase in biodiversity. Essentially, the more potential hosts or intermediate reservoirs in a given location, the less likely an individual will acquire a given zoonotic disease. The opposite phenomenon—the amplification effect—occurs when there is a lack of biodiversity, thus increasing disease risk.68,69 The greater Chicago area is the third most populated area in the United States, and the landscape has been severely altered by humans (swamp and grassland are now mostly pavement and built-up space). The northwest suburbs, which comprise nearly all of the local- and UFS study areas, have significantly more green spaces and natural areas. It is possible that species biodiversity is greater in these locations, as opposed to many other WNV “hot spots” throughout Chicago, and plays a role in reducing the number of human WNV cases.
Future directions.
Future studies should continue to evaluate processes of disease ecology across multiple scales and variable landscapes (rural versus urban, northern versus southern latitudes, built-up versus green space, etc.). As humans continue to burn fossil fuels, maintain our exponential population growth, and encroach into new habitats, understanding and predicting the future spread of infectious diseases are of paramount importance. There are numerous studies that attempt to evaluate vector-borne disease processes, but almost all occur across very small (e.g., multiple county or greater) scales. Although helpful with understanding overall disease ecology and trends across space, finer scale processes are rarely generalizable and can lead to potential bias and invalid statistical inferences.
Along with the increased emphasis for evaluating ecological processes across scales, more robust statistical methods need to be developed to quantitatively compare processes from models fit across varying data sets. A large limitation is placed on research aiming to address effects of ecological processes across scale, which often occurs over long periods of time. Model performances are easily quantified using AIC and BIC methods, and a similarly devised metric for comparing model performance across scales would be ideal.
Despite the small differences in human WNV risk across scales, we hope risk maps like these, with the statistical rigor and methods applied, will be of great use to public health and disease control personnel. Most importantly, our ultimate goal was to allow these risk maps to be dynamic and intuitive with easy-to-interact variables that are analysis ready. Future research would greatly benefit by collaborating with environmental engineers and programmers to facilitate in developing software that can allow for this goal to be achieved.
Key Takeaways.
1. Evaluating ecological processes all too often occurs at scales larger than the process of the underlying mechanisms. This study focused on addressing this problem and compared overall performance of best-fit models and covariates from three scales in the Chicago, IL region.
2. Overall, as extent increased, model performance increased (RMSE decreased and AUC increased). In addition, RMSE was significantly higher only when assessing UFS model performances. Our findings suggest that as extent decreases, covariate importance increases.
3. As scales increase and the sampling of locations decrease, the risk of not capturing heterogeneity that is representative of the entire study area is high. This phenomenon may have occurred at the UFS, as indicated by higher performing models fit to smaller scales.
4. Of the 23 covariates assessed in this study, only 6 (dlipct, Jantemp, MIRlag4, templag3, templag4, and totpop) were included across multiple scales. Despite this variation, fitting one scale’s best-fit model to another resulted in marginally weaker but still high-performing models. Although these variances are mostly captured, the small, but subtle, differences in results elude to differences in underlying ecological mechanisms of WNV that behave uniquely at different scales.
5. These small changes are highlighted by translating each of the scales’ best-fit models into human WNV risk maps. Overall, these maps display similar distributions of disease risk (in overlapping regions) but vary in frequency and size, increasing in patchiness at finer-scales.
6. Despite these subtle differences, these models and risk maps provide useful visual and statistical inferences into the ecological processes of WNV across scales. These tools may be particularly helpful for public health, mosquito, and disease control personnel in predicting and preventing disease before zoonotic spillover occurs.
Supplemental table and figures
Acknowledgments:
We would like to thank Roger Nasci for providing expert insights into vector biology and modeling efforts and the Megan Fritz laboratory for providing confirmatory Culex identification.
Note: Supplemental table and figures at www.ajtmh.org.
REFERENCES
- 1.Skaff NK, Cheruvelil KS, 2016. Fine-scale wetland features mediate vector and climate-dependent macroscale patterns in human West Nile virus incidence. Landsc Ecol 31: 1615–1628. [Google Scholar]
- 2.Patz JA, Campbell-Lendrum D, Holloway T, Foley JA, 2005. Impact of regional climate change on human health. Nature 438: 310–317. [DOI] [PubMed] [Google Scholar]
- 3.Patz JA, Reisen WK, 2001. Immunology, climate change and vector-borne diseases. Trends Immunol 22: 171–172. [DOI] [PubMed] [Google Scholar]
- 4.Patz JA, Githeko AK, McCarty JP, Hussein S, Confalonieri U, 2003. Chapter 6: climate change and infectious diseases. Climate Change and Human Health. Geneva, Switzerland: World Health Organization. [Google Scholar]
- 5.Semenza JC, Menne B, 2009. Climate change and infectious diseases in Europe. Lancet Infect Dis 9: 365–375. [DOI] [PubMed] [Google Scholar]
- 6.Lafferty KD, 2010. Concepts and synthesis: the ecology of climate change and infectious diseases. Ecology 90: 888–900. [DOI] [PubMed] [Google Scholar]
- 7.Ezenwa VO, Milheim LE, Coffey MF, Godsey MS, King RJ, Guptill SC, 2007. Land cover variation and West Nile virus prevalence: patterns, processes, and implications for disease control. Vector Borne Zoonotic Dis 7: 173–180. [DOI] [PubMed] [Google Scholar]
- 8.Larson SR, DeGroote JP, Bartholomay LC, Sugumaran R, 2010. Ecological niche modeling of potential West Nile virus vector mosquito species in Iowa. J Insect Sci 10: 1–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Rochlin I, Faraji A, Healy K, Andreadis TG, 2019. West Nile virus mosquito vectors in North America. J Med Entomol 56: 1475–1490. [DOI] [PubMed] [Google Scholar]
- 10.Petersen LR, Brault AC, Nasci RS, 2013. West Nile virus: review of the literature. JAMA 310: 308–315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Reither P, 2001. Climate change and mosquito-borne disease. Environ Int 109: 141–161. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Cohen JM, Civitello DJ, Brace AJ, Feichtinger EM, Ortega CN, Richardson JC, Sauer EL, Liu X, Rohr JE, 2016. Spatial scale modulates the strength of ecological processes driving disease distributions. Proc Natl Acad Sci U S A 113: E3359–E3364. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Meentemeyer RK, Haas SE, Václavík T, 2012. Landscape epidemiology of emerging infectious diseases in natural and human-altered ecosystems. Annu Rev Phytopathol 50: 379–402. [DOI] [PubMed] [Google Scholar]
- 14.Hurlbert AH, Jetz W, 2007. Species richness, hotspots, and the scale dependence of range maps in ecology and conservation. Proc Natl Acad Sci U S A 104: 13384–13389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Kramer LD, Styer LM, Ebel GD, 2008. A global perspective on the epidemiology of West Nile virus. Annu Rev Entomol 53: 61–81. [DOI] [PubMed] [Google Scholar]
- 16.Goddard LB, Roth AE, Reisen WK, Scott TW, 2002. Vector competence of California mosquitoes for West Nile virus. Emerg Infect Dis 8: 1385–1391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Kilpatrick AM, LaDeau SL, Marra PP, 2007. Ecology of West Nile virus transmission and its impact on birds in the western hemisphere. Auk 124: 1121–1136. [Google Scholar]
- 18.Hamer GL, Kitron UD, Goldberg TL, Brawn JD, Loss SR, Ruiz O, Hayes DB, Walker ED, 2009. Host selection by Culex pipiens mosquitoes and West Nile virus amplification. Am J Trop Med Hyg 80: 268–278. [PubMed] [Google Scholar]
- 19.Loss SR, Hamer GL, Walker ED, Ruiz MO, Goldberg TL, Kitron UD, Brawn JD, 2009. Avian host community structure and prevalence of West Nile virus in Chicago, Illinois. Oecologia 159: 415–424. [DOI] [PubMed] [Google Scholar]
- 20.Andreadis TG, Anderson JF, Vossbrinck CR, 2001. Mosquito surveillance for West Nile virus in Connecticut, 2000: isolation from Culex pipiens, Cx. restuans, Cx. salinarius, and Culiseta melanura. Emerg Infect Dis 7: 670–674. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Petersen LR, 2001. West Nile virus West Nile virus: a reemerging global pathogen. Emerg Infect Dis 7: 611–614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Molaei G, Andreadis TG, Armstrong PM, Anderson JF, Vossbrinck CR, 2006. Host feeding patterns of Culex mosquitoes and West Nile virus transmission, northeastern United States. Emerg Infect Dis 12: 468–474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Bowen RA, Nemeth NM, 2007. Experimental infections with West Nile virus. Curr Opin Infect Dis 20: 293–297. [DOI] [PubMed] [Google Scholar]
- 24.Granwehr BP, Lillibridge KM, Higgs S, Mason PW, Aronson JF, Campbell GA, Barrett ADT, 2004. West Nile virus: where are we now? Lancet Infect Dis 4: 547–556. [DOI] [PubMed] [Google Scholar]
- 25.Colpitts TM, Conway MJ, Montgomery RR, Fikrig E, 2012. West Nile virus: biology, transmission, and human infection. Clin Microbiol Rev 25: 635–648. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.CDC , 2020. West Nile Virus Fact Sheet. Fort Collins, CO: NCEZID. Available at: https://www.cdc.gov/westnile/resources/pdfs/wnvFactsheet_508.pdf. [Google Scholar]
- 27.CDC , 2020. National Arboviral Surveillance system (ArboNET). Fort Collins, CO: NCEZID. [Google Scholar]
- 28.Karki S, Brown WM, Uelmen J, O’Hara Ruiz M, Smith RL, 2020. The drivers of West Nile virus human illness in the Chicago, Illinois, USA area: fine scale dynamic effects of weather, mosquito infection, social, and biological conditions. PLoS One 15: e0227160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Allan BF, et al. 2009. Ecological correlates of risk and incidence of West Nile virus in the United States. Oecologia 158: 699–708. [DOI] [PubMed] [Google Scholar]
- 30.Manore CA, Davis JK, Christofferson RC, Wesson DM, Hyman JM, Mores CN, 2014. Towards an early warning system for forecasting human West Nile virus incidence. PLos Curr Edition 2. 10.1371/currents.outbreaks.f0b3978230599a56830ce30cb9ce0500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Keyel AC, et al. 2019. Seasonal temperatures and hydrological conditions improve the prediction of West Nile virus infection rates in Culex mosquitoes and human case counts in New York and Connecticut. PLoS One 14: e0217854. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Ruiz MO, Tedesco C, McTighe TJ, Austin C, Uriel K, 2004. Environmental and social determinants of human risk during a West Nile virus outbreak in the greater Chicago area, 2002 Int J Health Geogr 3: 8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Kilpatrick AM, Pape WJ, 2013. Predicting human West Nile virus infections with mosquito surveillance data. Am J Epidemiol 178: 829–835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Rosà R, et al. 2014. Early warning of West Nile virus mosquito vector: climate and land use models successfully explain phenology and abundance of Culex pipiens mosquitoes in north-western Italy. Parasit Vectors 7: 269. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Roiz D, Ruiz S, Soriguer R, Figuerola J, 2014. Climatic effects on mosquito abundance in Mediterranean wetlands. Parasit Vectors 7: 1–13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Hahn MB, Monaghan AJ, Hayden MH, Eisen RJ, Delorey MJ, Lindsey NP, Nasci RS, Fischer M, 2015. Meteorological conditions associated with increased incidence of West Nile virus disease in the United States, 2004–2012. Am J Trop Med Hyg 92: 1013–1022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Giordano BV, Kaur S, Hunter FF, 2017. West Nile virus in Ontario, Canada: a twelve-year analysis of human case prevalence, mosquito surveillance, and climate data. PLoS One 12: 1–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Wimberly MC, Lamsal A, Giacomo P, Chuang TW, 2014. Regional variation of climatic influences on West Nile virus outbreaks in the United States. Am J Trop Med Hyg 91: 677–684. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Uelmen JA, Irwin P, Brown W, Karki S, Ruiz MO, Li B, Smith R, 2020. Assessing ultra-fine-scale factors to improve human West Nile virus disease models in the Chicago area. Parasitology, 10.21203/rs.3.rs-19812/v1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Gibbs SEJ, Wimberly MC, Madden M, Masour J, Yabsley MJ, Stallknecht DE, 2006. Factors affecting the geographic distribution of West Nile virus in Georgia, USA: 2002–2004. Vector Borne Zoonotic Dis 6: 73–82. [DOI] [PubMed] [Google Scholar]
- 41.Wiens JA, 1989. Spatial scaling in ecology. Funct Ecol 3: 385–397. [Google Scholar]
- 42.Levin SA, 1992. The problem of pattern and scale in ecology. Ecology 73: 1943–1967. [Google Scholar]
- 43.Stephens PR, et al. 2016. The macroecology of infectious diseases: a new perspective on global-scale drivers of pathogen distributions and impacts. Ecol Lett 19: 1159–1171. [DOI] [PubMed] [Google Scholar]
- 44.Barker CM, 2019. Models and surveillance systems to detect and predict West Nile virus outbreaks. J Med Entomol 56: 1508–1515. [DOI] [PubMed] [Google Scholar]
- 45.Lawton JH, 2016. Nordic society oikos are there general laws in Ecology? Oikos 84: 177–192. [Google Scholar]
- 46.Lord CC, Alto BW, Anderson SL, Connelly CR, Day JF, Richards ST, Smartt CT, Tabachnick WJ, 2014. Can horton hear the whos? the importance of scale in mosquito-borne disease. J Med Entomol 51: 297–313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Bansal S, Chowell G, Simonsen L, Vespignani A, Viboud C, 2016. Big data for infectious disease surveillance and modeling. J Infect Dis 214: S375–S379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Mayer AL, Cameron GN, 2003. Consideration of grain and extent in landscape studies of terrestrial vertebrate ecology. Landsc Urban Plan 65: 201–217. [Google Scholar]
- 49.Birch CPD, Oom SP, Beecham JA, 2007. Rectangular and hexagonal grids used for observation, experiment and simulation in ecology. Ecol Modell 206: 347–359. [Google Scholar]
- 50.MRLC , 2016. National Geospatial Data Asset (NGDA) Land Use Land Cover. Sioux Falls, SD: U.S. Geological Survey, Earth Resources Observation and Sciences (EROS) Center. [Google Scholar]
- 51.Oregon State University , PRISM Climate Group , 2020. Available at: http://prism.oregonstate.edu. Accessed November 12, 2019.
- 52.Falchi F, Cinzano P, Duriscoe D, Kyba CCM, Elvidge CD, Baugh K, Portnov B, Rybnikova NA, Furgoni R, 2016. Supplement to the new world atlas of artificial night sky brightness. GFZ Data Serv, 10.5880/GFZ.1.4.2016.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Falchi F, Cinzano P, Duriscoe D, Kyba CCM, Elvidge CD, Baugh K, Portnov B, Rybnikova NA, Furgoni R, 2016. The new world atlas of artificial night sky brightness. Sci Adv, 10.1126/sciadv.1600377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Centers for Disease Control and Prevention (CDC) NCEZID, Division of Vector-Borne Diseases, Fort Collins Colorado , 2013. West Nile Virus in the United States: Guidelines for Surveillance, Prevention, and Control, 4 Fort Collins, CO: U.S: Department of Health and Human Services Public Health Service. [Google Scholar]
- 55.USGS , 2019. EarthExplorer. Available at: https://earthexplorer.usgs.gov/. Accessed December 17, 2019. [Google Scholar]
- 56.Tibshirani R, Lei J, Sell MG, Rinaldo A, Taylor J, Tibshirani R, 2018. LOCO: the Good, the Bad, and the Ugly [Presentation slides]. Available at: http://www.stat.cmu.edu/∼ryantibs/talks/loco-2018.pdf. [Google Scholar]
- 57.Danforth ME, Reisen WK, Barker CM, 2015. Extrinsic incubation rate is not accelerated in recent California strains of West Nile virus in Culex tarsalis (Diptera: Culicidae). J Med Entomol 52: 1083–1089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Anderson JF, Main AJ, Delroux K, Fikrig E, 2008. Extrinsic incubation periods for horizontal and vertical transmission of West Nile virus by Culex pipiens pipiens (Diptera: Culicidae). J Med Entomol 45: 445–451. [DOI] [PubMed] [Google Scholar]
- 59.Ruiz MO, Chaves LF, Hamer GL, Sun T, Brown WM, Walker ED, Haramis L, Goldberg TL, Kitron UD, 2010. Local impact of temperature and precipitation on West Nile virus infection in Culex species mosquitoes in northeast Illinois, USA. Parasit Vectors 3: 19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Reisen WK, Thiemann T, Barker CM, Lu H, Carroll B, Fang Y, Lothrop HD, 2010. Effects of warm winter temperature on the abundance and gonotrophic activity of culex (Diptera: Culicidae) in California. J Med Entomol 47: 230–237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Ewing DA, Cobbold CA, Purse BV, Nunn MA, White SM, 2016. Modelling the effect of temperature on the seasonal population dynamics of temperate mosquitoes. J Theor Biol 400: 65–79. [DOI] [PubMed] [Google Scholar]
- 62.Uelmen JA, Lindroth RL, Tobin PC, Reich PB, Schwartzberg EG, Raffa KF, 2016. Effects of winter temperatures, spring degree-day accumulation, and insect population source on phenological synchrony between forest tent caterpillar and host trees. For Ecol Manage 362: 241–250. [Google Scholar]
- 63.Ruiz MO, Walker ED, Foster ES, Haramis LD, Kitron UD, 2007. Association of West Nile virus illness and urban landscapes in Chicago and Detroit. Int J Health Geogr 12: 10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Fraterrigo JM, Langille AB, Rusak JA, 2020. Stochastic disturbance regimes alter patterns of ecosystem variability and recovery. PLoS One 15: 1–20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Condeso TE, Meentemeyer R, 2007. Effects of landscape heterogeneity on the emerging forest disease sudden oak death. J Ecol 95: 364–375. [Google Scholar]
- 66.Kitron U, Clennon JA, Cecere MC, Gürtler RE, King CH, Vazquez-Prokopec G, 2006. Upscale or downscale: applications of fine scale remotely sensed data to Chagas disease in Argentina and schistosomiasis in Kenya. Geospat Health 1: 49–58. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Ostfeld RS, Keesing F, 2000. Biodiversity and disease risk: the case of Lyme disease. Conserv Biol 14: 722–728. [Google Scholar]
- 68.Keesing F, Holt RD, Ostfeld RS, 2006. Effects of species diversity on disease risk. Ecol Lett 9: 485–498. [DOI] [PubMed] [Google Scholar]
- 69.Johnson PTJ, Ostfeld RS, Keesing F, 2015. Frontiers in research on biodiversity and disease. Ecol Lett 18: 1119–1133. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.