COVID-19 epidemic prediction and the impact of public health interventions: A review of COVID-19 epidemic models

Abstract

The coronavirus disease outbreak of 2019 (COVID-19) has been spreading rapidly to all corners of the word, in a very complex manner. A key research focus is in predicting the development trend of COVID-19 scientifically through mathematical modelling. We conducted a systematic review of epidemic prediction models of COVID-19 and the public health intervention strategies by searching the Web of Science database. 55 studies of the COVID-19 epidemic model were reviewed systematically. It was found that the COVID-19 epidemic models were different in the model type, acquisition method, hypothesis and distribution of key input parameters. Most studies used the gamma distribution to describe the key time period of COVID-19 infection, and some studies used the lognormal distribution, the Erlang distribution, and the Weibull distribution. The setting ranges of the incubation period, serial interval, infectious period and generation time were 4.9–7 days, 4.41–8.4 days, 2.3–10 days and 4.4–7.5 days, respectively, and more than half of the incubation periods were set to 5.1 or 5.2 days. Most models assumed that the latent period was consistent with the incubation period. Some models assumed that asymptomatic infections were infectious or pre-symptomatic transmission was possible, which overestimated the value of R0. For the prediction differences under different public health strategies, the most significant effect was in travel restrictions. There were different studies on the impact of contact tracking and social isolation, but it was considered that improving the quarantine rate and reporting rate, and the use of protective face mask were essential for epidemic prevention and control. The input epidemiological parameters of the prediction models had significant differences in the prediction of the severity of the epidemic spread. Therefore, prevention and control institutions should be cautious when formulating public health strategies by based on the prediction results of mathematical models.

1. Introduction

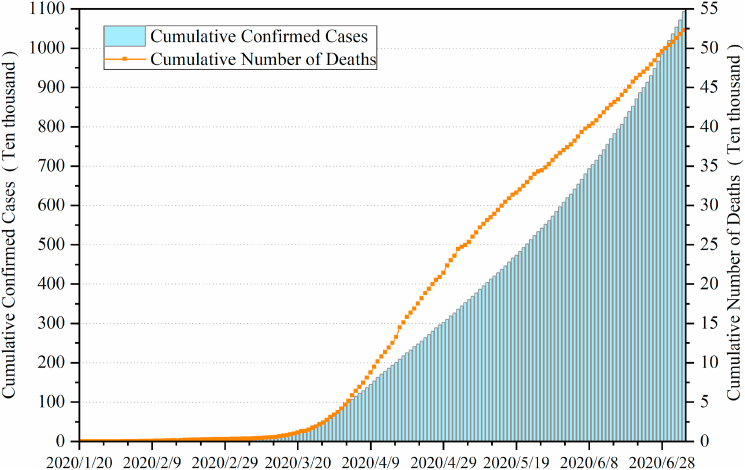
The outbreak of coronavirus disease (COVID-19) caused by the novel coronavirus, SARS-CoV-2, has spread rapidly around the world since the end of 2019, affecting more than 200 countries and regions by early May. The World Health Organization (WHO) declared the COVID-19 outbreak as a public health emergency of international concern (PHEIC) on 31 January(WHO, 2020d) and classified it as a pandemic on 11 March (WHO, 2020b). Globally, as of 4 July 2020, there have been 10,922,324 confirmed cases of COVID-19, including 523,011 deaths, with an average of more than 100,000 new confirmed cases per day (Fig. 1), reported to WHO(WHO, 2020e). More than 2.72 million cases have been confirmed in the United States, with more than 128000 deaths. Furthermore, Brazil, Russia, India, Britain, Spain, Peru and Chile have diagnosed more than 250,000 people in total, and more than 15 countries have diagnosed more than 100000 people in total.

Fig. 1.

Global trend chart of confirmed cases and deaths of COVID-19.

The COVID-19 has raised intense concern internationally about the spread of the epidemic and its development trend. Many mathematical studies focused on the modelling of the development of the COVID-19 and the effect of interventions on the containment of the spread. As recognized by WHO, timely mathematical models play a key role in evidence-based making decision by health policy-makers. In fact, dealing with infectious diseases from a mathematical perspective can reveal the internal pattern and potential structure of epidemic control, and the mathematical models of disease transmission are helpful in gaining insights into the transmission dynamics of infectious diseases and the potential role of different public health intervention strategies(Foppa, 2017; Heesterbeek et al., 2015). Most phenomena observed at the population level are often very complex and are difficult to decipher simply by observing the characteristics of isolated individuals(R.M. Anderson, 1992). The statistical analysis of epidemiological data is helpful to describe, quantify and summarize the mode of transmission of disease in susceptible populations. At present, it is worth noting that mathematical modelling is also an effective method to explore and test various epidemiological hypotheses, which is mainly due to ethical and practical limitations for live human or animal experiments.

It is important to understand the spread of new infectious in time to assess the hazards and the scale of the epidemic. An epidemic model can also provide important information for generating epidemic prevention and control strategies, such as recommendations for the needs of the healthcare infrastructure, isolation of infectious individuals, and tracking of contact activities. With the spread of the epidemic among the general population, public health authorities are interested in obtaining reliable estimates of the epidemic transmission potential, the associated uncertainties, and the impact of public health interventions. How are the existing COVID-19 epidemic models constructed? What are the assumptions based on? What are the effects of different public health interventions? In this paper, we have systematically reviewed and reported the mathematical models of COVID-19 transmission and the impact of public health interventions in answering these questions.

2. Methods

To identify articles for the current study, an initial search using the Web of Science database was conducted on 3 June 2020, using the following search terms or combinations of terms: a) “SARS-CoV-2” OR “COVID-19”, b) “model” OR “modelling”, c) “Interventions” OR “contact tracing” OR “social distancing” OR “quarantine” OR “mask”, d) “Reproduction number” OR “incubation period” OR “latent period” OR “serial interval” OR “Infectious period”. Since the literature on the COVID-19 epidemic model is generally new, it cannot be retrieved in some databases. We also searched on other websites such as Science and Nature. We sorted and analyzed the literature according to the modeling methods and research content, further summarized the setting and evaluation of key input parameters, and studied the impact of different public health interventions on the transmission of COVID-19.

We used the following selection criteria to include eligible articles: a) Transmission dynamics modelling studies of COVID-19 in human populations; b) Models of early epidemic prediction (including the possible short-term track of the developing epidemic), contact tracing, quarantine, isolation, social distancing, protective masks and other public health interventions; c) Models of transmission in a confined space and those not explicitly discussing epidemiological trends or public health interventions were excluded; d) Reports, letters and comments were excluded; e) Articles not in English were excluded.

Forty-eight articles were identified on the Web of Science database, and seventy-eight articles were expanded. Twenty-three articles were further excluded after reading the full text, and leaving fifty-five articles to be included in the current study. Through statistical analysis, we extracted information from each article, including basic ideas, the characteristics of the study, the parameters contained in the model and the impact of interventions.

3. Results

3.1. Research models

As the compartment model can quantitatively evaluate the impact of interventions, 33 of 55 studies were modeled from the population perspective and presented as different compartment models, 18 of which were based on the classic SEIR compartment model and expanded to different degrees (Table 1). In addition, 23 studies were based on the Bayesian method, agent-based model, generalized growth model, and other methods for modelling (Table 2), and one of them(Kai & Guy-PhilippeGoldstein, 2020) also used the compartment model. In general, the COVID-19 epidemic models focused on the following issues: a) the infectivity of SARS-CoV-2, i.e. estimation of the basic reproduction number; b) the estimation of key time periods of COVID-19 infection; c) the prediction of the COVID-19 spread (include short-term prediction and long-term prediction); d) the assessment of the impact of public health interventions.

Table 1.

The 33 selected papers on COVID-19 compartmental models.

Models abbreviation	Model type	Compartments	Study area	Outcomes	References
SEIR/SLIR	Stochastic (Chinazzi & Davis, 2020; Kai & Guy-PhilippeGoldstein, 2020; Kucharski et al., 2020; Sanche et al., 2020; Tian, Liu, & Li, 2020; Wang & Liu, 2020; Wu, Leung, & Leung, 2020; Yang et al., 2020; Zhao, Stone, & Gao, 2020), deterministic (Acuna-Zegarra, Santana-Cibrian, & Velasco-Hernandez, 2020; Boldog et al., 2020; Hauser et al., 2020; Hou et al., 2020; Kuniya, 2020; Mandal, Bhatnagar, & Arinaminpathy, 2020; Ngonghala et al., 2020; Tang, Bragazzi, et al., 2020; Tang, Wang, et al., 2020)	Susceptible(S), exposed/latent(E/L), infectious(I), removed(R)	China(Tang, Bragazzi, et al., 2020; Tian et al., 2020; Wu et al., 2020), Wuhan (Chinazzi & Davis, 2020; Hou et al., 2020; Kucharski et al., 2020; Sanche et al., 2020; Tang, Wang, et al., 2020; Wang & Liu, 2020; Zhao et al., 2020), Hubei, China and northern Italy(Hauser et al., 2020), 38 countries or provinces in Asia, Europe and North America (Kai & Guy-PhilippeGoldstein, 2020), New York(Ngonghala et al., 2020), Mexico(Acuna-Zegarra et al., 2020), Zhejiang, Guangdong, Hubei, China(Yang et al., 2020), Japan(Kuniya, 2020), India (S. Mandal, Bhatnagar, & Arinaminpathy, 2020), outside China(Boldog et al., 2020)	R0(Chinazzi & Davis, 2020; Kucharski et al., 2020; Sanche et al., 2020; Tang, Bragazzi, et al., 2020; Tang, Wang, et al., 2020; Tian et al., 2020; Wang & Liu, 2020; Wu et al., 2020; Zhao et al., 2020, Zhao et al., 2020, Zhao et al., 2020) (Acuna-Zegarra et al., 2020; Boldog et al., 2020; Kuniya, 2020; S.; Mandal, Bhatnagar, & Arinaminpathy, 2020), mortality (Hauser et al., 2020), infectious period(Acuna-Zegarra et al., 2020), doubling time (Chinazzi & Davis, 2020), prediction of epidemic (Ngonghala et al., 2020; Yang et al., 2020), the impact of transmission control measures (Tian et al., 2020), the impact of travel restrictions(Chinazzi & Davis, 2020), the impact of universal masking (Kai & Guy-PhilippeGoldstein, 2020), the impact of behavioral changes (Acuna-Zegarra et al., 2020), the impact of interventions (Ngonghala et al., 2020), the epidemic risk of imported cases from outside China (Boldog et al., 2020), the impact of quarantine of Wuhan city (Hou et al., 2020)	(Acuna-Zegarra et al., 2020; Boldog et al., 2020; Chinazzi & Davis, 2020; Hauser et al., 2020; Hou et al., 2020; Kai & Guy-PhilippeGoldstein, 2020; Kucharski et al., 2020; Kuniya, 2020; S. Mandal, Bhatnagar, & Arinaminpathy, 2020; Ngonghala et al., 2020; Sanche et al., 2020; Tang, Bragazzi, et al., 2020; Tang, Wang, et al., 2020; Tian et al., 2020; Wang & Liu, 2020; Wu et al., 2020; Yang et al., 2020; Zhao et al., 2020, Zhao et al., 2020, Zhao et al., 2020)
SIRD	Deterministic	Susceptible (S), infected (I), recovered (R), dead (D)	China, Italy and France(Fanelli, Piazza, & 2020), Hubei(Anastassopoulou, Russo, Tsakris, & Siettos, 2020)	R0 (Anastassopoulou et al., 2020), the prediction of the COVID-19 outbreak (Fanelli & Piazza, 2020), mortality(Anastassopoulou et al., 2020; Fanelli & Piazza, 2020)	(Anastassopoulou et al., 2020; Fanelli & Piazza, 2020)
SEIRS	Stochastic	Susceptible(S), exposed (E), infectious(I), recovered(R), susceptible(S)	Temperate regions	R0, the transmission dynamics of SARS-CoV-2 through the post-pandemic period	Kissler, Tedijanto, Goldstein, Grad, and Lipsitch (2020)
SIR-X	Deterministic	Infected(I), susceptible(S), removed(R), quarantined(X)	China	R0, the impact of containment policies	Maier and Brockmann (2020)
SEIHARD	Deterministic	Susceptible(S), exposed(E), symptomatic infectious(I), hospitalized(H), asymptomatic infectious(A), recovered(R), deaths(D)	Washington, New York	The impact of universal masking	Eikenberry et al. (2020)
SEIRU	Deterministic	Susceptible(S), asymptomatic noninfectious (E), asymptomatic infectious(I), reported symptomatic infectious (R), unreported symptomatic infectious (U)	China	R0, transmission rate, the role of the exposed or latency period	Liu, Magal, Seydi, and Webb (2020a)
SIRU	Deterministic	Susceptible(S),asymptomatic infectious (I), reported symptomatic infectious(R), unreported symptomatic infectious (U)	Korea, Italy, France and Germany (Magal & Webb, 2020), China, Hubei, Wuhan (Liu, Magal, Seydi, & Webb, 2020c), China(Liu, Magal, Seydi, & Webb, 2020b)	The prediction of cumulative confirmed cases (Liu et al., 2020b, 2020c), the understanding of unreported cases(Liu et al., 2020c)	(Liu et al, 2020b, 2020c; Magal & Webb, 2020)
SEIIN	Stochastic	Susceptible(S), exposed(E), documented infected(I), undocumented infected(I),total population(N)	China	R0, latent period, infectious period, the fraction of undocumented infections and their contagiousness	(R. Li, Pei, et al., 2020)
SEIQR	Deterministic	Susceptible(S), exposed(E), hospitalized infected(I), quarantine(Q), recovered or removed(R)	India	Short-term prediction of COVID-19	(M. Mandal, Bhatnagar, & Arinaminpathy, 2020)
SEIRQ	Stochastic	Susceptible(S), exposed (E), infectious (I), removed (R), quarantine(Q)	Guangdong	Short-term prediction of COVID-19	Hu et al. (2020)
SCIRA	Stochastic	Susceptible (S), closely observed (C), infected patients (I), recovered (R, cured/dead), asymptomatic (A).	Jiangsu, Anhui	Asymptomatic infection ratio, the effects of asymptomatic and imported patients	Sun and Weng (2020)
SEIHR	Deterministic	Susceptible (S), exposed (E), symptomatic infectious (I), hospitalized (H), recovered or death (R)	South Korea	R0, the impact of interventions	Choi and Ki (2020)
SEIPAHRF	Deterministic	Susceptible (S), exposed (E), symptomatic (I), super-spreaders class (P), asymptomatic infectious (A), hospitalized (H), recovery (R), fatality(F).	Wuhan	R0(focus on the transmissibility of super-spreaders individuals)	Ndaïrou, Area, Nieto, and Torres (2020)

Table 2.

The 23 selected papers on other (not compartmental) COVID-19 models.

Models	Model type	Study area	Outcomes	References
Agent based model	Stochastic	38 countries or provinces in Asia, Europe and North America (Kai & Guy-PhilippeGoldstein, 2020), Singapore (Koo, Cook, Park, & Sun, 2020)	The impact of universal Masking (Kai & Guy-PhilippeGoldstein, 2020), the likelihood of human-to-human transmission of SARS-CoV-2 (Koo et al., 2020)	(Kai & Guy-PhilippeGoldstein, 2020; Koo et al., 2020)
Branching process model	Stochastic	Wuhan	The impact of contact tracing and isolation	Hellewell et al. (2020)
Bayesian method	Stochastic	Outside Hubei in Chinese mainland(J. Zhang et al., 2020, Zhang et al., 2020), China(Verity, Okell, Dorigatti, & Winskill, 2020), Singapore, Tianjin(Ganyani et al., 2020)	R0, Incubation period, serial interval (J. Zhang et al., 2020, Zhang et al., 2020), age-stratified estimates of CFR and IFR (Verity et al., 2020), generation interval (Ganyani et al., 2020)	(Ganyani et al., 2020; Verity et al., 2020; J.; Zhang et al., 2020, Zhang et al., 2020)
Generalized Linear Models	Stochastic	China	Incubation period, the effect of human mobility and control measures	Kraemer et al. (2020)
Generalized growth model	Stochastic	Lima (Munayco et al., 2020), Iran (Muniz-Rodriguez et al., 2020), South Korea (Shim, Tariq, Choi, Lee, & Chowell, 2020)	R0(Munayco et al., 2020; Muniz-Rodriguez et al., 2020; Shim et al., 2020), the impact of social distancing (Munayco et al., 2020; Muniz-Rodriguez et al., 2020),doubling time (Shim et al., 2020)	(Munayco et al., 2020; Muniz-Rodriguez et al., 2020; Shim et al., 2020)
Linear growth & exponential growth model	Stochastic	Italy, Japan	The effect of the changes in testing rates on epidemic growth rate	Omori, Mizumoto, and Chowell (2020)
Exponential growth	Stochastic	China	R0 (Thompson, 2020; S. Zhao, Q. Li, Pei, et al., 2020; S. Zhao et al., 2020, Zhao et al., 2020, Zhao et al., 2020), the estimates of the unreported number of COVID-19 (Zhao et al., 2020, Zhao et al., 2020, Zhao et al., 2020), the risk of sustained transmission (Thompson, 2020), the impact of reporting rate (S. Zhao, Q. Li, Pei, et al., 2020)	(Thompson, 2020; S. Zhao, Q. Li, Pei, et al., 2020; Zhao et al., 2020, Zhao et al., 2020, Zhao et al., 2020)
Second derivative model	Stochastic	China	The assessment the detection rate	Chen and Yu (2020)
Poisson Transmission Model	Stochastic	China	R0	Zhu and Chen (2020)
Segmented Poisson model	Stochastic	Canada, France, Germany, Italy, UK and USA	Turning point, duration and attack rate	Zhang et al., 2020, Zhang et al., 2020
Analytically solvable model	Stochastic	China	The estimates of the contribution of different transmission routes, generation time	Ferretti et al. (2020)
Gaussian distribution theory	Stochastic	China, South Korea, Italy, Iran	R0, incubation period	(L. Li, Pei, et al., 2020)
Phenomenological models	Stochastic	China, Hubei(Roosa et al., 2020a), Guangdong, Zhejiang(Roosa et al., 2020b)	Short-term prediction of cumulative confirmed cases	(Roosa et al., 2020a, 2020b)
Transmission model with zoonotic infections	Stochastic	Wuhan	R0, doubling time, incubation period, serial interval	(Q. Li, Pei, et al., 2020)
Data-driven and model-free estimations	–	Canada	The prediction of epidemic trends with different public health interventions, mortality	Scarabel, Pellis, Bragazzi, and Wu (2020)

3.2. Key epidemiological parameters

3.2.1. Basic reproductive number (R0)

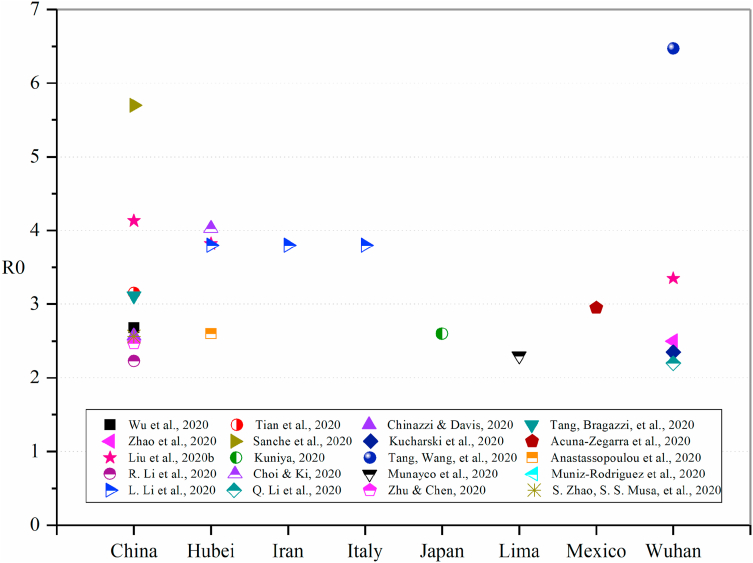
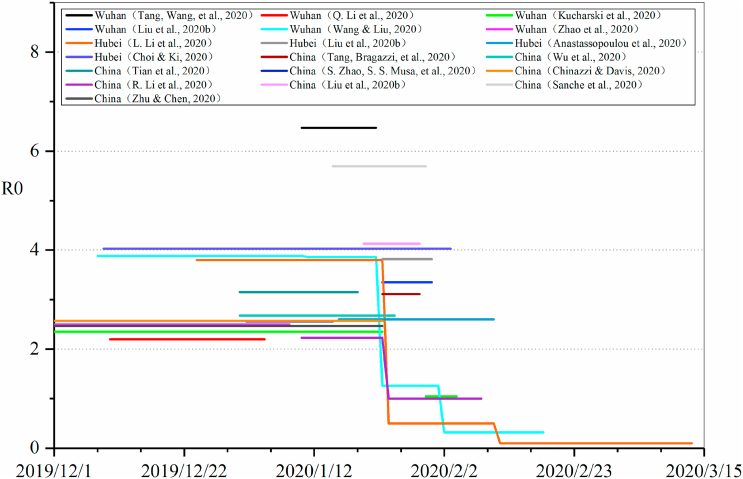
The basic reproductive number (R0) refers to the average number of secondary infected persons infected by one primary infected patient during the infectious period. The calculation of R0 is mainly the product of three factors, namely R0 = cdp, where c is the average contact times of the infectious source in unit time (i.e. contact rate), d is the infectious period, and the product of c and d is the average contact times of each infectious source in the infectious period, p is the probability of transmission through contact (Halloran, 2001). The R0 in the COVID-19 epidemic model is usually estimated based on epidemiological characteristics, confirmed case reports, population movement data and other data, and it also changes with the study areas and time periods. Thirty studies evaluated R0, and the estimated values of R0 were mainly between 2 and 4 (Fig. 2), but some studies(Tang, Wang, et al., 2020; Zhu & Chen, 2020) estimated the value above 5. As the initial outbreak of COVID-19 was in Wuhan, China, many researchers conducted modeling analysis based on the daily confirmed case data published by the China CDC. Fig. 3 shows the comparison of R0 in models based on the data of China (including Hubei and Wuhan), directly showing the change of R0 during the epidemic process, before and after public health interventions. Wang et al.(Wang & Liu, 2020) analyzed the number of confirmed cases in Wuhan, and divided the epidemic into four periods: before January 11, from January 11 to 22, from January 23 to February 1 and from February 2 to 18, and the corresponding values of R0 gradually decreased from 3.88, 3.86, 1.26 to 0.32. Li et al. (Kucharski et al., 2020; L.; Li et al., 2020, Li et al., 2020, Li et al., 2020; R.; Li et al., 2020, Li et al., 2020, Li et al., 2020) also carried out phased evaluation based on key events and interventions, and the value of R0 decreased significantly with the strengthening of interventions.

Fig. 2.

Comparison of R0 in models based on data of different areas.

Fig. 3.

Comparison of R0 in models based on data of China (including Hubei and Wuhan).

3.2.2. Key time periods of COVID-19 infection

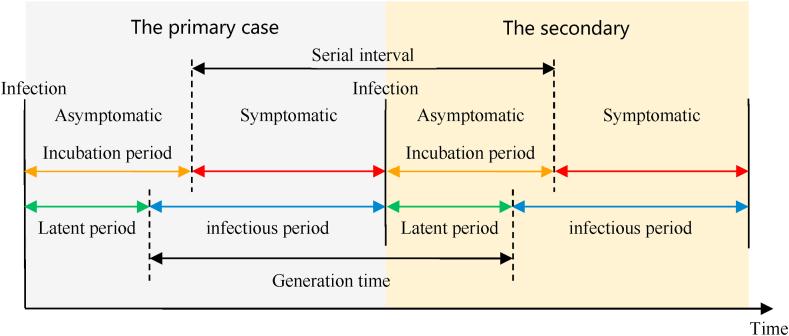
The natural history of disease refers to the development from beginning to end without any treatment or intervention. In fact, given the harmfulness of an epidemic, treatment or intervention measures are inevitable. Therefore, it is difficult for the natural history of COVID-19 to be unaffected by the various coupling factors. Nevertheless, the development of infectious diseases has a regularity from one stage to another. The development of each infectious disease roughly goes through four stages: incubation period, precursor period, obvious symptom period and recovery period. Fig. 4 shows the definitions of the key time periods in different COVID-19 epidemic models. The incubation period is the time between infection and the onset of symptoms. The latent period is the time between infection and the start of infectiousness. The infectious period is the time interval during which the infected individuals can transmit the disease to any susceptible contact. The serial interval is the time from the onset of the symptoms in the primary case to the onset of the symptoms in the secondary case. The generation time (generation interval) is the time from the onset of infectiousness in the primary case to the onset of infectiousness in the secondary case.

Fig. 4.

Definition of key time periods in different COVID-19 epidemic models.

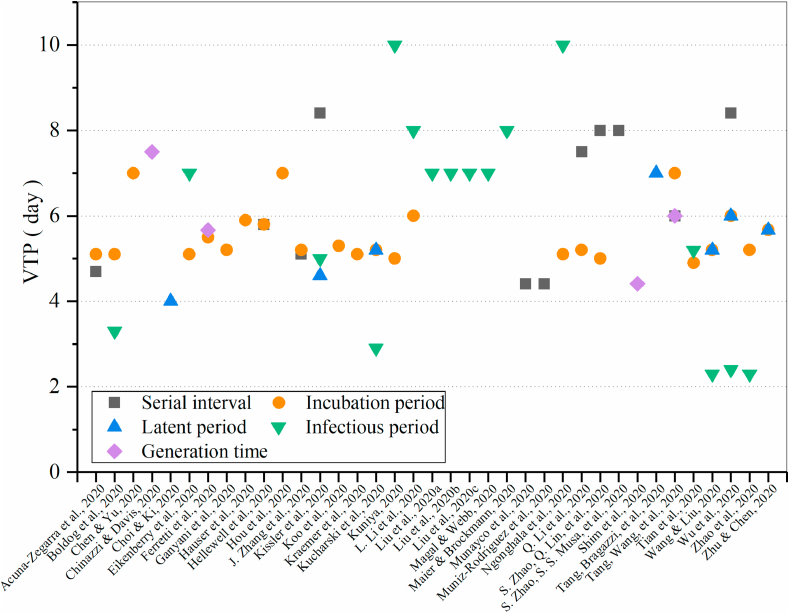
In the COVID-19 epidemic models, there are highly abstracted phenomenological models, compartmental models allowing for behavior changes or clustered transmission, and more complex and highly detailed agent-based models. No matter which model is chosen, their purpose is to describe epidemic parameters (such as basic reproduction number, serial interval, infectious period, etc.) based on limited/early disease monitoring data, and to further understand how the epidemic spread in the early stage of the outbreak. The setting of the key time periods in different models has a direct impact on the prediction of the epidemic and the risk assessment. Therefore, it is very important to understand the value and distribution of the key time periods of COVID-19 infection. Fig. 5 shows a comparison of the value of the time periods in different models. The value of the incubation period was found to vary from 4.9 to 7 days, of which more than half were 5.1 or 5.2 days. Eleven studies (Chinazzi & Davis, 2020; Choi & Ki, 2020; Kissler et al., 2020; Kucharski et al., 2020; R.; Li, Pei, et al., 2020; Sanche et al., 2020; Tang, Bragazzi, et al., 2020; Wang & Liu, 2020; Wu et al., 2020; Zhu & Chen, 2020) made assumptions that the latent period was from 2.2 to 6 days, most of which were consistent with the incubation period. The setting range of the infectious period was large, ranging from 2.3 days (Wang & Liu, 2020; Zhao et al., 2020, Zhao et al., 2020, Zhao et al., 2020) to 10 days(Kuniya, 2020; Ngonghala et al., 2020). The setting of the serial interval fluctuated between 4.41 and 8.4 days, and only four studies (Chinazzi & Davis, 2020; Ferretti et al., 2020; Shim et al., 2020; Tang, Wang, et al., 2020) evaluated or set the generation time, ranging from 4.4 to 7.5 days. In all the reviewed studies, only one study (Ganyani et al., 2020) reported a negative serial interval (i.e., pre-symptomatic transmission existed, and the time of the symptom onset of the secondary case was earlier than the primary case) in evaluation, and the proportion of pre-symptomatic transmission increased from 48% (95% CrI: 32–67) in the baseline scenario to 66% (95% CrI: 45–84) when allowing for negative serial intervals for the Singapore data, and from 62% (95% CrI: 50–76) to 77% (95% CrI: 65–87) for the Tianjin data.

Fig. 5.

Comparison of the value of time period (VTP) in different models.

The differences in the setting and evaluation of several key time periods of COVID-19 infection in different models are not only reflected in the numerical values, but also in the acquisition method and hypothetical distribution (Table 3). For the acquisition method of the key time periods in the models, most studies directly assumed that it was based on other research results and reports or on previous knowledge of coronavirus outbreaks such as SARS and MERS. Some studies also made quantitative evaluations based on current epidemic data. There is a considerable variation in the choice of distributions used for the key time periods. The nature of memory-less free characteristics of the gamma distribution ensures the biology in the transmission process to be more realistic (Kwok et al., 2019). Most studies used the gamma distribution to describe the key time periods. Some studies also assumed a log-normal distribution, Weibull distribution and other distributions. Hellewell et al. (Hellewell et al., 2020) assumed a Weibull-distributed incubation period, and skewed normal-distributed serial interval. Kucharski et al.(Kucharski et al., 2020) used the Erlang distribution when evaluating the incubation period and the infectious period. Ferretti et al.(Ferretti et al., 2020) considered the Weibull distribution as the best fit when evaluating the generation time.

Table 3.

Key time periods setting of COVID-19 infection in the models.

Key parameters	Definition	Acquisition method	Distribution hypothesis
Incubation period	the time between infection and the onset of symptoms	Based on other research’s result and reports (Acuna-Zegarra et al., 2020; Boldog et al., 2020; Eikenberry et al., 2020; Ferretti et al., 2020; Ganyani et al., 2020; Hauser et al., 2020; Hellewell et al., 2020; Hou et al., 2020; Kuniya, 2020; Ngonghala et al., 2020; Tang, Wang, et al., 2020; Tian et al., 2020; Yang et al., 2020; Shi; Zhao, Musa, et al., 2020; Zhu & Chen, 2020) Based on the knowledge of SARS and MERS (Chinazzi & Davis, 2020; Wu et al., 2020; S. Zhao, Q. Li, Pei, et al., 2020) Based on the knowledge of SARS (Koo et al., 2020) Based on current epidemic data (Kraemer et al., 2020; Kucharski et al., 2020; L.; Li, Pei, et al., 2020; Q.; Li, Pei, et al., 2020; J.; Zhang, Litvinova, et al., 2020)	log-normal distribution(Ferretti et al., 2020; Q.; Li, Pei, et al., 2020; J.; Zhang, Litvinova, et al., 2020) gamma distribution(Acuna-Zegarra et al., 2020; Boldog et al., 2020; Ganyani et al., 2020) Erlang distribution(Kucharski et al., 2020) truncated gamma distribution (Kraemer et al., 2020) Weibull distribution(Hellewell et al., 2020) beta-distribution(Zhu & Chen, 2020)
latent period	the time between infection and start of infectiousness	Based on other research’s result and reports (Sanche et al., 2020) Equal to incubation period (Chinazzi & Davis, 2020; Kucharski et al., 2020; Wang & Liu, 2020; Zhu & Chen, 2020) Based on current epidemic data (R. Li, Pei, et al., 2020)	gamma distributions(Sanche et al., 2020)
infectious period	the time interval during which the infected individuals could transmit the disease to any susceptible contacts	Based on other research’s result and reports (Boldog et al., 2020; Kuniya, 2020; L. Li, Pei, et al., 2020; Maier & Brockmann, 2020; Ngonghala et al., 2020; Sanche et al., 2020; Tian et al., 2020; Wang & Liu, 2020; Wu et al., 2020; Zhao et al., 2020, Zhao et al., 2020, Zhao et al., 2020) Based on the knowledge of another beta-coronavirus (Kissler et al., 2020) Based on current epidemic data (Acuna-Zegarra et al., 2020; Kucharski et al., 2020; R.; Li, Pei, et al., 2020)	Erlang distribution(Kucharski et al., 2020) gamma distribution(Boldog et al., 2020; Sanche et al., 2020)
serial interval	the time from the onset of symptoms in the primary case to the onset of symptoms in the secondary case	Based on other research’s result and reports (Acuna-Zegarra et al., 2020; Hellewell et al., 2020; Munayco et al., 2020; Muniz-Rodriguez et al., 2020; Sanche et al., 2020; Tang, Wang, et al., 2020) Based on the knowledge of SARS and MERS (S. Zhao, Q. Li, Pei, et al., 2020; Zhao et al., 2020, Zhao et al., 2020, Zhao et al., 2020) Based on the knowledge of SARS (Kissler et al., 2020; Wu et al., 2020) Based on current epidemic data (Q. Li, Pei, et al., 2020; J. Zhang, Litvinova, et al., 2020)	gamma distribution(Tang, Wang, et al., 2020) (Acuna-Zegarra et al., 2020; Q. Li, Pei, et al., 2020; Muniz-Rodriguez et al., 2020; J. Zhang, Litvinova, et al., 2020; S. Zhao, Q. Li, Pei, et al., 2020; Zhao et al., 2020, Zhao et al., 2020, Zhao et al., 2020) Weibull distribution(Kissler et al., 2020) skewed normal distribution(Hellewell et al., 2020)
generation time	the time the onset of infectiousness in the primary case to the onset of infectiousness in the secondary case	Based on other research’s result and reports (Shim et al., 2020) Based on the knowledge of SARS and MERS (Chinazzi & Davis, 2020) Based on current epidemic data (Ferretti et al., 2020; Ganyani et al., 2020; Tang, Wang, et al., 2020)	Weibull distribution(Ferretti et al., 2020)

At present, the disease natural history of COVID-19 is not clear. Infection may occur before or after symptoms appear. Whether to consider the difference of pre-symptomatic transmission in the model mainly depends on whether to consider the difference between the incubation period and latent period. In this review, ten studies (Ferretti et al., 2020; Ganyani et al., 2020; Kucharski et al., 2020; Liu et al., 2020a; Tang, Wang, et al., 2020; Thompson, 2020; Wang & Liu, 2020; J.; Zhang, Litvinova, et al., 2020) considered pre-symptomatic transmission in their models. Wu (Wu et al., 2020), Kucharski(Kucharski et al., 2020) and other researchers (Chinazzi & Davis, 2020; Thompson, 2020; Wang & Liu, 2020; Zhu & Chen, 2020) assumed that the latent period was as same as the incubation period, and such cases could only infect other people after the onset of the symptoms. Analyzing the key parameters of epidemic transmission by the Bayesian method, Ferretti et al.(Ferretti et al., 2020) estimated the contribution of different transmission routes, indicating that the contribution of pre-symptomatic transmission to R0 was 0.9 (0.2–1.1), accounting for 47% of the total R0, which was almost sufficient to sustain an epidemic on its own, and the fraction of pre-symptomatic transmission events out of the pre-symptomatic plus symptomatic transmission events was 37% (95% CI: 27.5%–45%). However, the contribution of asymptomatic transmission to R0 was only 0.1 (0.0–1.2), which suggests that the transmission from asymptomatic, rather than pre-symptomatic, individuals is not a major driver of disease spreading. Ganyani et al. (Ganyani et al., 2020) estimated the generation interval of COVID-19 using the Bayesian method, where the prevalence of pre-symptomatic infection was relatively high, about 48%–77%, but the transmission of asymptomatic infections was not considered. Zhang et al. (Wang & Liu, 2020) estimated the diagnosis rate in Wuhan was 14%–41%, which also suggested the possibility of pre-symptomatic and asymptomatic transmission. Choi et al. (Choi & Ki, 2020) considered asymptomatic and pre-symptomatic infections in a model, but the infectivity of the asymptomatic and pre-symptomatic infections was not considered.

3.2.3. Asymptomatic infection ratio and mortality

Asymptomatic infections include two groups: the first group is recessive infection with no or mild symptoms throughout the infection, and the other group refers to the incubation period after infection that may show symptoms in the future. The number and proportion of asymptomatic patients may be directly related to the strategies of disease control and prevention. In this review, more than 30 studies considered asymptomatic infection, which were consistent with the related epidemic reports of COVID-19, but there were differences in the hypothesis of the infectivity for asymptomatic infection. Hauser et al.(Hauser et al., 2020) assumed that, after an average incubation period of 5.9 days, 82.1% (95%CrI:79.8–84.5) of infected people developed symptoms of any severity and became infectious, while the remainder were asymptomatic and did not transmit the infection. Some mild cases did not show obvious symptoms that would affect medical treatment or isolation measures. In view of this, Kissler et al.(Kissler et al., 2020; Ngonghala et al., 2020; Verity et al., 2020) included mild or asymptomatic infection in their model. Sanche (Sanche et al., 2020), Ngonghala(Ngonghala et al., 2020) and other researchers (Acuna-Zegarra et al., 2020; S.; Mandal, Bhatnagar, & Arinaminpathy, 2020; Ndaïrou et al., 2020; Shim et al., 2020; Yang et al., 2020) considered asymptomatic infection in their models, and assumed that asymptomatic infection was infectious. Yang et al.(Yang et al., 2020) assumed that the latent [E] populations could remain asymptomatic or become symptomatic in the later stage. Mandal et al. (S. Mandal, Bhatnagar, & Arinaminpathy, 2020) assumed that the infectivity of asymptomatic infections constituted half of the symptomatic infections, and Hou et al. (Hou et al., 2020) assumed that 50% of asymptomatic infections were infectious.

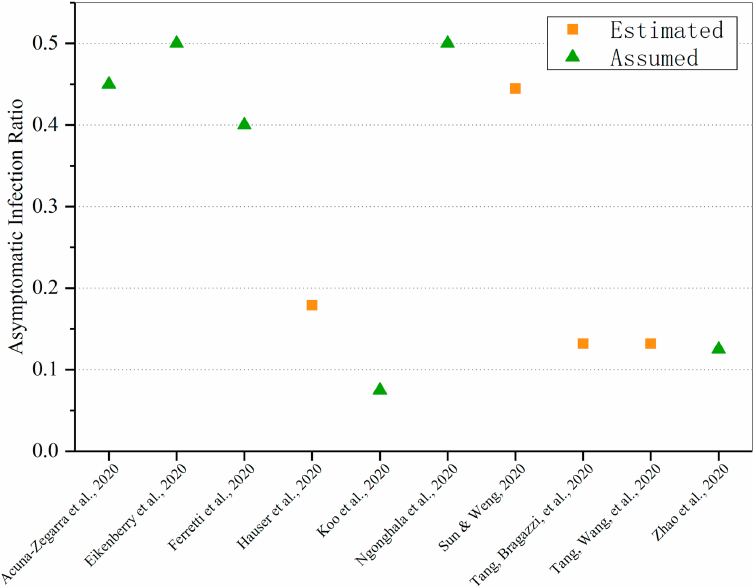
The asymptomatic infection ratio is defined as the proportion of asymptomatic infections among all the infections of the disease. It is an important parameter in measuring the real burden of disease and evaluating the transmission potential, as these directly affect the evaluation of the infection mode, transmission ability, isolation strength, strategies for public interventions and monitoring strength of epidemic. There were also differences in the assessment and hypothesis of the asymptomatic proportion among different models, but none of them was higher than 50% (Fig. 6). Six studies(Acuna-Zegarra et al., 2020; Eikenberry et al., 2020; Ferretti et al., 2020; Koo et al., 2020; Ngonghala et al., 2020; Zhao et al., 2020, Zhao et al., 2020, Zhao et al., 2020) hypothesized the proportion of asymptomatic or symptomatic infections. Koo et al. (Koo et al., 2020) assumed that the asymptomatic infection ratio was 7.5%, and considered value of 22.7%, 30.0%, 40.0%, 50.0% in sensitivity analysis. They also indicated that the impact of public health intervention might be greatly reduced under a higher asymptomatic rate. In this case, effective case management and treatment, vaccine and other preventive measures are needed. Four studies (Hauser et al., 2020; Sun & Weng, 2020; Tang, Bragazzi, et al., 2020; Tang, Wang, et al., 2020) evaluated the proportion of asymptomatic infections. Tang et al. (Hauser et al., 2020; Tang et al., 2020, Tang et al., 2020; Tang et al., 2020, Tang et al., 2020) estimated that the asymptomatic infection ratio was less than 20%, while Sun et al.(Sun & Weng, 2020) estimated a median proportion was approximately 44.46% (interquartile range: [37.31%–53.72%]).

Fig. 6.

Assumed and estimated values of asymptomatic infection ratio in different models.

In order to evaluate the severity of COVID-19, it is crucial to judge the prevalence, hospitalization rate and mortality rate. It is a great challenge to evaluate the mortality rate of an infectious disease during a pandemic. There are two main ways to express the mortality rate: a) the case fatality rate (CFR), which is the number of deaths divided by the number of known confirmed infections; b) the infection fatality rate (IFS), which is the number of deaths divided by all infections (known cases plus unknown cases). In addition, some scholars also used a crude case fatality rate, that was, the number of reported deaths divided by the number of reported cases at a specific time point. However, the crude case fatality rate is not a reliable indicator of the overall mortality rate, which might be misleading. Tang et al.(Tang, Bragazzi, et al., 2020; Tang, Wang, et al., 2020) used the SEIR model to evaluate the disease-induced death rate as 1.7825 × 10^-5, while Verity et al.(Verity et al., 2020) obtained a best estimate of the crude case fatality rate in China of 1.38% (95% CrI: 1.23%–1.53%) with substantially higher values for the elderly, and an overall estimate of the infection fatality ratio of 0.66% (95% CrI: 0.39%–1.33%), again with an increasing profile with age. Anastassopoulou et al.(Anastassopoulou et al., 2020) estimated the case fatality ratio was about 0.15% in the total population. Chen et al.(Chen & Yu, 2020) estimated the population-based mortality rate of COVID-19 was 0.6/1000, or 1/9th of the mortality rate of Wuhan residents. Acuña-Zegarra et al.(Acuna-Zegarra et al., 2020) calculated two case fatality rates using confirmed data from Mexico, one was 0.018 before the Sanitary Emergency Measures (before March 23rd, 2020), and the other was 0.12 after this date. Fanelli et al.(Fanelli & Piazza, 2020) estimated that the apparent mortality rate of COVID-19 seemed to be between 4% and 8% in Italy, higher than that for seasonal flu. Hauser et al.(Hauser et al., 2020) estimated an adjusted mortality rate of 3.3% (95%CrI: 2.0–4.7) among all people infected with SARS-CoV-2 in northern Italy and of 3.0% (95%CrI: 2.6–3.4) in China. The model estimates showed a strong age trend in the mortality rate, with a sharp increase from 50 years old, reaching very high values in people aged 80 and older: 39.0% (95%CrI: 31.1–48.9) in Hubei province and 89.5% (95%CrI: 62.0–99.6) in northern Italy. Scarabel et al.(Scarabel et al., 2020) estimated the case fatality rate in China and Italy to be 2.3% and 7.8% respectively, and pointed out that 80% of deaths occurred among individuals aged 65 years and older. Since the proportion of individuals aged 65 years and older was almost double in proportion in Italy compared to China, an almost doubled case fatality rate could be expected. Shim et al.(Shim et al., 2020) estimated that the crude case fatality rate was higher among males (1.1%) compared to females (0.4%), and increased in older age groups.

3.3. The impact of public health interventions

3.3.1. Overview of public health interventions

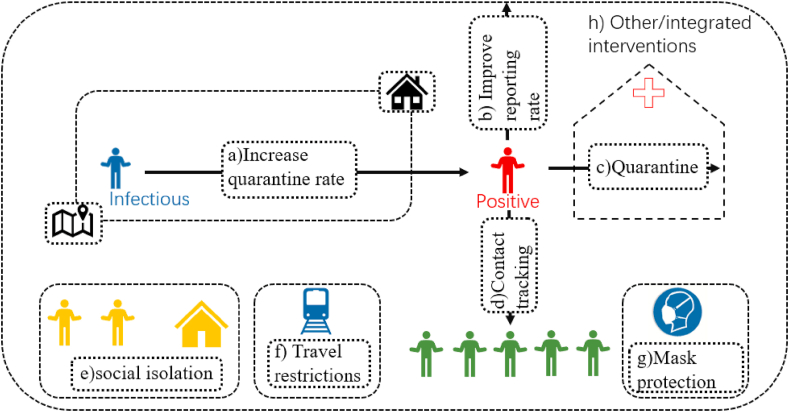
Public health interventions are the control measures for public health emergencies (problems), and the ultimate goal is to prevent the spread of the epidemic and reduce the scale of the outbreak. In the absence of safe and effective vaccines or antivirals, strategies to control and reduce the pandemic pressure focus on public health interventions, such as temperature screening, social isolation, contact tracking, increased quarantine and reporting rates, protective masks, and travel restrictions (Fig. 7). At the same time, people’s awareness of the virus and personal protective measures (such as respirator protection and self-isolation) has been improved. Based on these measures, it leads to the changes in medical seeking behavior and epidemiological characteristics. In order to quantify these differences, many scholars have re-simulated the epidemiological characteristics after taking intervention measures by establishing models and using timely updated data. Fig. 7 shows the distribution of different studies on the impact of public health interventions.

Fig. 7.

Distribution of different studies on the impact of public health interventions a) Increase quarantine rate (Chen and Yu, 2020, Ferretti et al., 2020, Hauser et al., 2020, Hellewell et al., 2020, Hu et al., 2020, Kissler et al., 2020, Omori et al., 2020, Tang et al., 2020, Verity et al., 2020, Wang and Liu, 2020); b) Improve reporting rate (Anastassopoulou et al., 2020, Kucharski et al., 2020, Li et al., 2020, Liu et al., 2020b, Liu et al., 2020c, Zhao et al., 2020); c)e) Quarantine (Chinazzi & Davis, 2020, Ferretti et al., 2020, Hauser et al., 2020, Hellewell et al., 2020, Hou et al., 2020, Hu et al., 2020, Kissler et al., 2020, Koo et al., 2020, Kuniya, 2020, Liu et al., 2020c, Maier and Brockmann, 2020, Mandal et al., 2020, Munayco et al., 2020, Muniz-Rodriguez et al., 2020, Ngonghala et al., 2020, Sanche et al., 2020, Tian et al., 2020); d) Contact tracing (Choi and Ki, 2020, Ferretti et al., 2020, Hellewell et al., 2020, Maier and Brockmann, 2020, Munayco et al., 2020, Ngonghala et al., 2020, Tang et al., 2020); f) Travel restrictions (Boldog et al., 2020, Chinazzi & Davis, 2020, Kraemer et al., 2020, Kucharski et al., 2020, Tang et al., 2020, Tang et al., 2020, Tian et al., 2020, Yang et al., 2020, Zhu and Chen, 2020); g) Mask protection (Eikenberry et al., 2020, Kai and Guy-PhilippeGoldstein, 2020, Ngonghala et al., 2020); h) Other/integrated interventions (Acuna-Zegarra et al., 2020, Choi and Ki, 2020, Eikenberry et al., 2020, Fanelli and Piazza, 2020, Hauser et al., 2020, Hellewell et al., 2020, Hou et al., 2020, Hu et al., 2020, Koo et al., 2020, Kuniya, 2020, Liu et al., 2020a, Maier and Brockmann, 2020, Mandal et al., 2020, Ngonghala et al., 2020, Sanche et al., 2020, Wang and Liu, 2020, Yang et al., 2020, Zhang et al., 2020, Zhao et al., 2020).

3.3.2. Differences in the impact of different public health interventions

There are some differences in the impacts of different public health interventions based on the existing studies.

As for contact tracking, Ferretti et al. (Ferretti et al., 2020) showed that when the success rate of contact tracking was increasing, the exponential growth rate of the disease tended to be negative, indicating that the situation was under control. Tang et al. (Tang et al., 2020, Tang et al., 2020) and Munayco et al. (Munayco et al., 2020) believed that strengthening isolation and reducing the contact rates after contact tracking could significantly reduce the peak value, thus reducing the cumulative number of predicted cases. More specifically, Hellewell (Hellewell et al., 2020) showed that when R0 was 1.5, even if the number of contacts successfully tracked was less than 50%, the epidemic development could be controlled, but when R0 was 2.5, more than 70% of contacts needed to be tracked, and when the severity of the epidemic rose to R0 to 3.5, more than 90% of contacts needed to be tracked to effectively control the epidemic. Maier et al. (Maier & Brockmann, 2020) believed that contact tracking had an inhibitory effect on both susceptible and asymptomatic infections. It could not only protect susceptible persons from infection, but also removed a large part of the entire susceptible population from the transmission process. However, a few scholars pointed out that the preventive measure of contact tracking only had little effect on epidemic prevention, and was not enough to suppress the spread of the epidemic (Choi & Ki, 2020) (Ngonghala et al., 2020).

In the early stage of COVID-19, due to the lack of an authoritative specific diagnostic program, the diagnostic ability was limited, resulting in a low quarantine rate, which could only reach 14%–41% (Wang & Liu, 2020). There was a deviation in the estimation of mortality rate in early research investigations because of the different degrees of quarantine delay (Hauser et al., 2020; Omori et al., 2020; Verity et al., 2020). The research showed that the lower the quarantine rate, the more the imported cases infected people, and the higher the cumulative number of confirmed cases (Chen & Yu, 2020; Hu et al., 2020). Tang et al.(Tang et al., 2020, Tang et al., 2020) used the early data of the Beijing epidemic to evaluate the impact of the quarantine rate on the local epidemic. When the detection rate increased 10 times or 20 times, the peak of the infection would be 6.5 days or 9 days earlier, and the peak of infection would be reduced by 87% or 93%. This showed that increasing the quarantine rate could significantly reduce the peak value and the number of cumulative reported cases. In addition, the longer the quarantine time delay, the longer it would take to control the epidemic (Hellewell et al., 2020). Ferretti et al. (Ferretti et al., 2020) quantified the impact of the interventions by simulating the success rate of the interventions at different levels of epidemic development. The study pointed out that when R0 was 2, the quarantine delay was within 72 h, the daily growth rate was still negative, and the epidemic situation could be controlled. When R0 was 2.5, the quarantine delay was within 48 h. When R0 was 3, the quarantine delay was less than 24 h. When R0 was 3.5, there was almost no delay. In plain language, increasing the quarantine rate is essential for epidemic prevention and control.

The reporting rate is another important factor influencing epidemic trends and simulation results. The reporting rate is very low when there is a lack of early supervision and general attention to the epidemic. Li et al.(R. Li et al., 2020, Li et al., 2020, Li et al., 2020) found that during the period January 10–23, only 14% (95% CI: 9–26%) of the total infections in China were reported, revealing a very high rate of undocumented infections: 86%. The study (R. Li, Pei, et al., 2020) also found that without transmission from undocumented cases, reported infections during January 10–23 were reduced 66.4% across all of China and 64.0% in Wuhan. In view of the impact of different reporting rates on the model estimates, some researchers used China’s epidemic related data to simulate the basic reproduction number R₀ and transmission rate under different reporting rates. The results showed that both the transmission rate and the basic reproduction number decreased significantly with the increase of the reporting rate (Liu et al., 2020b, 2020c). Specifically, a study (Anastassopoulou et al., 2020) showed that when the reporting rate increased by 20 times, the basic reproduction number of each stage decreased, and the average value decreased from 2.6 to 2.0. Magal et al.(Magal & Webb, 2020) obtained similar results using the epidemic data of South Korea, Italy, France and Germany.

With the spread of COVID-19 worldwide, many countries have taken measures of social isolation (Liu et al., 2020c), known as “social distancing” or “physical distancing” (Kissler et al., 2020), such as closing schools and workplaces, and limiting the size of assembly groups. The goals of these strategies are to reduce the peak intensity of the epidemic (flattening the epidemic growth curve) (Roy M. Anderson, Heesterbeek, Klinkenberg, & Hollingsworth, 2020), curb the risks to the overwhelmed health system, and buy time to develop treatments and vaccines. Most models (Chinazzi & Davis, 2020; Ferretti et al., 2020; Maier & Brockmann, 2020; Tian et al., 2020) predicted that early detection and isolation could help effectively control the epidemic. Using data from Lima, Peru, Munayco et al.(Munayco et al., 2020) predicted that the impact of school closures and state emergency announcements slowed the spread of SARS-CoV-2, and the case growth rate dropped from 0.8 to 0.53. Kissleret et al.(Kissler et al., 2020) pointed out that one-time social distancing measures reduced the epidemic peak when the transmission was not subject to seasonal forcing. One-time social distancing might push the epidemic peak of the SARS-CoV-2 epidemic into the autumn. Further, if the transmissibility increased in wintertime, it could potentially exacerbate the load on critical care resources. Intermittent social distancing might maintain critical care needs within current thresholds, but widespread surveillance would be required to time the distancing measures correctly and avoid overshooting critical care capacity. However, Koo et al. (Koo et al., 2020) found that isolation measures would be very effective only in a relatively mild outbreak scenario (R₀ = 1.5), while the extent of the reduction of the outbreak size in severe scenario (R0 = 2.5) would be far lower. Hauser et al. (Hauser et al., 2020) indicated that even if the strict social isolation measures were taken locally, in Italy, the number of deaths would continue to increase for a few weeks.

In order to fight against the outbreak of COVID-19, almost all countries in the world introduced interventions, such as social isolation, in March 2020. Governments are seeking a sustainable path back to relaxed social restrictions and functioning economies. In this situation, more and more voices are supporting that the widespread use of masks. Mask protection has been effectively implemented in most of East Asia. It is an additional and essential component of the mitigation toolkit and helps the local population to escape from the harsh blockade in a sustainable way (Kai & Guy-PhilippeGoldstein, 2020; Ngonghala et al., 2020; WHO, 2020a). Some studies showed that when the coverage rate of 50% effective masks reached 50%, the effective disease transmission rate would be reduced by half. When masks were widely used, for example, when the coverage rate reached 80%, the effective disease transmission rate was reduced by about one third, even if 20% effective masks were used (Eikenberry et al., 2020; Ngonghala et al., 2020). However, some studies also showed that if only 50% of the population wore masks or the popularity of masks was questioned, the daily growth rate of infection would not be significantly reduced (Kai & Guy-PhilippeGoldstein, 2020). Overall, the research showed that mask protection is one of the most effective measures to help control the spread of the epidemic, and it is the most likely measure to be implemented continuously, among all the many epidemic prevention measures.

In addition to the above interventions, the most significant impact was the implementation of travel restrictions in Wuhan and other regions on January 23, 2020, which effectively reduced the number of cases of COVID-19 spatial transmission, locally and overseas(Boldog et al., 2020; Hauser et al., 2020; Zhu & Chen, 2020). Zhong Nanshan’s team pointed out that if the implementation time of travel restrictions were delayed for five days, the scale of the epidemic in mainland China would increase by three times (Yang et al., 2020). For Wuhan, the local average daily reproductive number decreased from 2.35 (95%CI 1.15–4.77) before the travel restriction to 1.05 (95%CI 0.41–2.39) one week later (Kucharski et al., 2020). For Beijing, with travel restriction, the number of infected individuals after seven days would decrease by 91.14%, compared with the scenario of no travel restriction (Tang, Wang, et al., 2020). The travel restriction of Wuhan had a more marked effect at the international scale, where imported cases were reduced by nearly 80% by mid-February (Chinazzi & Davis, 2020). However, some studies believed that there was no strong evidence that travel restrictions had made an outstanding contribution to epidemic prevention and control (Tian et al., 2020). These results indicated that the travel restrictions of Wuhan delayed the overall epidemic progression by only 3–5 days in mainland China, and that the sustained 90% travel restrictions to and from mainland China only modestly affected the epidemic trajectory. No evidence has been provided that the intercity travel ban, which was suspended and implemented after January 23 in Wuhan, had reduced the number of confirmed cases in other cities in China. It was claimed that transmission rate of disease would be significantly reduced only when combined with other public health interventions and behavior changes, (Chinazzi & Davis, 2020; Tian et al., 2020).

3.3.3. Impact of interventions on R0

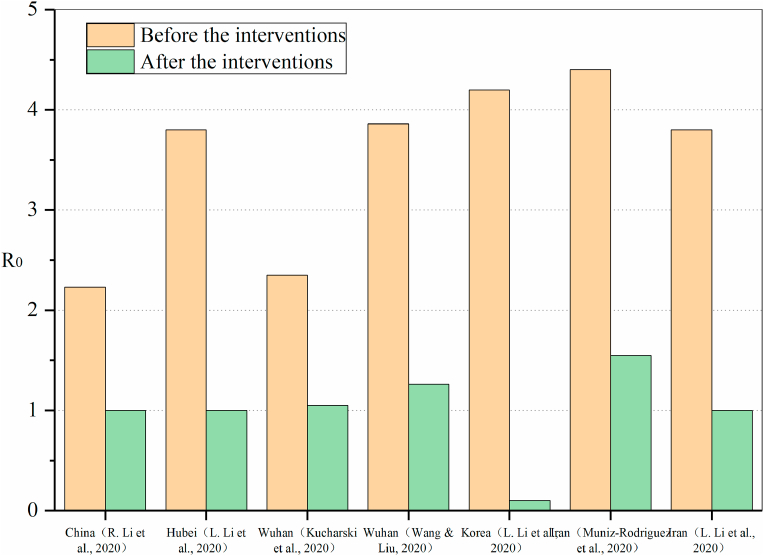
The qualitative conclusions of the impact of different interventions on the transmission of COVID-19 are reviewed above. Fig. 8 shows the comparison of R0 before and after implementation of public health interventions in different studies. It can be seen that although different studies have concluded that R0 will decrease after the implementation of intervention policies, the difference in the predicted results are very significant due to different study areas and intervention measures. Kucharski et al. (Kucharski et al., 2020) predicted that R0 decreased from 2.35 to 1.05 after the intervention, while Wang et al. (Wang & Liu, 2020) believed that the impact of the interventions on R0 was more significant, and R0 decreased from 3.86 to 1.26 after the lockdown of Wuhan. In the other two studies (L. Li, Pei, et al., 2020; R. Li, Pei, et al., 2020), there were also significant differences in the results of the same intervention, the R0 decreased by 1.23 in China and 2.8 in Hubei. There were also two studies on the impact of social distancing and other intervention measures on R0 in Iran (L. Li, Pei, et al., 2020; Muniz-Rodriguez et al., 2020), and the results were very similar. R0 decreased from about 4 to near the critical value, indicating that local intervention policies were very effective in controlling the epidemic. Among the predicted results, the biggest impact of intervention measures on R0 was a study in South Korea(L. Li, Pei, et al., 2020). The results showed that after the implementation of large-scale epidemic prevention and control measures, R0 decreased from 4.1 to 0.1, and R0 was far below the critical value (R0 = 1), indicating that the epidemic had been completely controlled and would eventually disappear.

Fig. 8.

Comparison of R0 before and after implementation of public health interventions in different studies.

4. Discussion

4.1. Uncertainty of model assumptions

During the initial phase of the COVID-19 epidemic, the application of transmission models for epidemiological prediction was hampered not only by the lack of reliable epidemiological information and case incidence data, but also by the gaps in understanding of the mechanisms involved in transmission dynamics in different social backgrounds. To understand the value of the COVID-19 epidemic models, it is crucial to understand how they are modeled and what assumptions they are based on.

The understanding of the first outbreak of COVID-19 is limited, and the process of COVID-19 infection is unclear. Some studies relied on accurate quantification of current epidemic exposure history to make reasonable assumptions, while others relied on the previous knowledge of coronavirus outbreaks such as SARS and MERS. The assessment of epidemic models is very sensitive to hypothesis (numerical values and distributions) of the natural history of the disease, and some models carried sensitivity analysis of parameters during the assessment process. In this review, the median value of the incubation period in more than half of the models was 5.1 or 5.2 days, but there were different assumptions about its average distribution, such as log-normal distribution, gamma distribution, and Erlang distribution. However, the assumption of the infectious period had a large span, fluctuating between 4.41 and 8.4 days, and most studies assumed that the infectious period followed a gamma distribution. This might be due to the impact of quarantine measures on the process of COVID-19 infection in different time periods and different regions, or due to the delay in quarantine or reporting caused by the capacity of medical services in different regions. In the future, if there is more information about the key characteristics of the disease, it will enable a more accurate understanding of the natural history of COVID-19, which will greatly reduce the uncertainty of the model.

It is worth noting that the centralized nucleic acid detection results in Wuhan, China showed that no asymptomatic infections were infectious. However, in the early COVID-19 epidemic models, some studies assumed that asymptomatic infection was infectious, which would overestimate the predicted results. However, it is still unclear whether there is pre-symptomatic transmission of COVID-19, while ignoring the latent period tends to underestimate the value of R0. From the comparison between the model assuming no pre-symptomatic transmission and the model assuming pre-symptomatic transmission, the value of R0 was estimated relatively to be high, and in the model in (Zhu & Chen, 2020) was 0.5 higher.

In addition, the estimation of the asymptomatic infection ratio of COVID-19 varies greatly. As the results of centralized nucleic acid detection in Wuhan, China on June 2, show the detection rate of asymptomatic infections was only 0.303 per 10,000 (China, 2020), while the data published by the Center for Disease Control and Prevention of the United States shows that about one-third of COVID-19 infections in the United States are asymptomatic (CDC, 2020). Firstly, the main reason is the lack of understanding of the SARS-CoV-2. Secondly, the area and time period of the model evaluation are different, and the process of COVID-19 is in different stages. Finally, different regions have different medical resources, and the popularization of disease quarantine and other measures is limited. In fact, the outbreak of the epidemic has gone through the initial period, the rapid growth period, and the recession period. Due to the continuous improvement of medical conditions, the mortality rate lags behind in the early process, is higher in the middle process, and may decline in the later process. Therefore, the model hypothesis also has uncertainty.

In general, it is difficult to accurately estimate the impact of time-related variability factors and to incorporate them into models without high-resolution and reliable epidemiological data. Public health authorities should work closely with other government departments to determine accurate epidemiological data, including the geographical location of cases, information on the contact track and the date of symptoms onset. The availability of persistent case data is helpful to identify the transmission patterns of COVID-19 and its evolution with different epidemic periods.

4.2. The impact of asymptomatic infections on the spread of COVID-19

The population with asymptomatic infections is a special group of people in the epidemic that deserves attention. We found that many studies have mentioned this population group, especially recently, and more and more studies have been modeling asymptomatic infections (Koo et al., 2020; Maier & Brockmann, 2020; S.; Mandal, Bhatnagar, & Arinaminpathy, 2020; Munayco et al., 2020; Sun & Weng, 2020). All these studies believed that asymptomatic infections were infectious, and it was necessary to strengthen the supervision of this population. Even in the study of Mandal et al.(S. Mandal, Bhatnagar, & Arinaminpathy, 2020), it was assumed that asymptomatic infections were half as infectious as symptomatic. Another model (Sun & Weng, 2020), focusing on the study of the asymptomatic population, believed that this population was unpredictable and well hidden. The asymptomatic or covert patients could trigger outbreaks more rapidly and terminate with larger outbreak sizes if the strong control measures became mild. It was suggested that the currently strict interventions should be continuously implemented, and unraveling the asymptomatic pool was critically important before preventive strategy such as vaccines become available.

However, the recent results of centralized nucleic acid detection in Wuhan, China, further deepened the understanding of asymptomatic infections. 9,899,828 people in Wuhan undertook centralized nucleic acid detection (China, 2020), which took half a month (from 0:00 on May 14 to 24:00 on June 1) and cost 900 million yuan. Among the nearly 10 million tested people, no confirmed cases were found, and 300 asymptomatic infections were detected, with a detection rate of only 0.303 per 10,000. Is asymptomatic infection infectious or not? This is based on the following evidence: first, since April 26, the Wuhan CDC had collected sputum and throat swab samples from 106 asymptomatic infectious patients and sent them to the Wuhan Institute of Viruses of the Chinese Academy of Sciences and The Hubei CDC for virus isolation, culture and sequencing analysis. The results showed that no “active virus” had been cultivated. Second, the Wuhan CDC sampled the homes and living environments of 300 asymptomatic infectious patients, including wipe samples such as masks, water cups, toothbrushes and mobile phones, as well as some elevator keys and corridor items. All of 3343 samples were negative. In addition, since May 14, the Wuhan CDC has also tested 300 asymptomatic infectious patients with serum antibody. No single positive IgM was found in recent infection. The above strong evidence suggested that the recessive infections (i.e., asymptomatic infectious patients with no or mild symptoms throughout the infection) were not infectious or the likelihood of being infectious was very low, and the contribution to the transmission of COVID-19 was negligible. This is consistent with the studies of Ferretti et al. (Ferretti et al., 2020) on this asymptomatic population. However, Ferretti et al. believed that the pre-symptomatic infection was infectious and its transmission capacity was almost sufficient to sustain an epidemic on its own; which remains to be studied. Therefore, it is necessary to combine the monitoring results of serological research, recognize the potential transmission characteristics of emerging diseases, and screen infectious pre-symptomatic cases early. This will also contribute to modelers being able to accurately calibrate the epidemic model according to the actual epidemic situation, and then provide feedback and decision support during the outbreak. Specifically, if we can effectively detect and distinguish invisible infections among the asymptomatic population, we can significantly reduce the isolation measures and strict medical observation measures for such people, which will greatly reduce the burden of medical management.

4.3. Suggestions for public health intervention

Transmission dynamics models are the core in designing and evaluating interventions for infectious diseases, especially for public health interventions. What public health interventions do we need to take? When should they be carried out? What is the scope and extent of the adoption? How should we adjust when the epidemic situation changes? If these questions are to be answered rationally, a method is needed to predict the impact on health outcomes, such as reducing the number of confirmed cases or deaths. Policy issues determine the necessary components and complexity of models. However, models need to be simple enough to analyze, but accurate enough to solve problems.

For a single intervention, severe travel restrictions have the most significant effect on suppressing the spread of COVID-19 in the early stage of an outbreak. As COVID-19 continues to spread around the world, improving quarantine and reporting rates is critical for the expert teams to understand the situation more comprehensively. On this basis, the national governments can formulate the most effective prevention and control plan in time, so as to prevent the further spread of the epidemic and curb the large-scale outbreak as much as possible. At the same time, once the epidemic is confirmed, a series of medical prevention and control measures, such as patient isolation and contact tracking should be taken immediately. It is helpful to identify and control the source of infection in a timely and effective manner, block the route of transmission, and protect the susceptible population (Nelson & Wiliams., 2014). Considering that digital tools offer opportunities to strengthen contact tracking, the WHO has published interim guidance on the considerations, opportunities and challenges of integrating digital tools into contact tracking methods (WHO, 2020c). All the above-mentioned interventions need to pay attention to the significant economic and social costs. On the premise of stable control of the epidemic situation through the above-mentioned interventions in the early stage, other long-term sustainable control schemes should be considered to gradually return the social order to the right track. Therefore, mask protection is still essential.

Clearly, more studies (Choi & Ki, 2020; Eikenberry et al., 2020; Kissler et al., 2020) showed that a single measure was not enough to delay the outbreak by several weeks or longer. Targeted stratified containment, that is, a combination of several interventions, can effectively prevent the continued spread of COVID-19, and ultimately reduce the overall scale of the outbreak until the danger alert is removed.

At present, the epidemic has spread to all parts of the world, but the epidemic situation varies from place to place. Therefore, through a summary study of COVID-19 epidemic models, this paper suggests that different countries should take appropriate intervention measures to prevent and control the epidemic on the premise of considering their own national conditions, economic development levels and public cooperation. Those countries that have not been effectively controlling the epidemic can refer to the effective prevention and control experience of Eastern countries, including China, and take strict control measures to effectively control an epidemic in the shortest time. Those countries such as China, where the epidemic has been preliminarily controlled, have begun to return to work gradually and trying to restore normal living standards and social order. Travel restrictions mainly prevent the influx of imported cases from abroad, and the lockdown can be gradually lifted in low-risk cities in China. Social distancing policy can also be relaxed but not completely ended, as some studies (Ngonghala et al., 2020) showed that early termination of social distancing might lead to a devastating second wave of the COVID-19 epidemic. However, in terms of the three basic measures of contact tracing, quarantine and timely reporting, vigilance should not be relaxed until the confirmed end of the epidemic. Of course, the economic and social costs of combating the epidemic at this stage are greatly reduced compared with the period of concentrated outbreak. In addition, protective masks have a significant effect on reducing the effective transmission rate, especially for pre-symptomatic infections. As a sustainable prevention and control measure, it needs to be implemented for a long time. It can be more effective to reduce the mortality rate of infectious diseases and to release the burden of health care system when it is combined with the above-mentioned interventions (especially social distancing and health measures). Following WHO updated guidance on the use of masks on 5 June, the public is encouraged to wear masks where the physical distancing cannot be achieved, such as the public transport, shops or other environments with high population density (WHO, 2020a).

Caution is also required when implementing COVID-19 prevention and control measures. On the one hand, strict disease control measures can reduce the risk of morbidity and mortality associated with COVID-19 outbreaks. However, on the other hand, in the process of infection prevention, in the daily life and behavior of ordinary people are often difficult to achieve a comprehensive unified constraint and standard, and may cause some discontent to a certain extent. These measures may include significant movement restrictions, social distancing and reducing recreational life, continued wearing of uncomfortable masks, frequent cleaning and disinfection, and the financial and spiritual “cost” of implementing these measures. The duration and timing of relaxing or terminating strict social isolation measures are critical to determine the future trajectory of the COVID-19 pandemic. If the strict social alienation measures are terminated early, it may lead to a devastating second wave, with a burden similar to that predicted before the implementation of strict social isolation measures. Therefore, we can conclude that the short-term economic and spiritual “cost” is a necessary condition for the recovery of long-term normal life and better economic development. In the absence of effective drug intervention at present, strict comprehensive intervention measures are essential for epidemic prevention and control.

5. Conclusions and suggestions

With the global pandemic of COVID-19, governments all over the world rely on mathematical prediction to help guide decision-making during the epidemic. Extrapolation of the epidemic impacts from the early growth phases is influenced by model, data, and behavioral uncertainties (Schuster, 2015). Although the complexity and methods are different, simple models in the early growth epidemic phases can still be used as reference information and provide a basis for more complex transmission models in order to understand the progress of disease outbreaks. As George E. P. box, a British statistician, said, “all models are wrong, but some are useful.” Facing the challenge of COVID-19, on the one hand, public health authorities should work closely with other government departments to determine accurate epidemiological data, which is helpful to accurately estimate the impact of time-related change factors and incorporate them into the various models. At the same time, combined with the monitoring results of serology research, it is helpful for modelling researchers to calibrate the epidemiological model accurately based on the actual situation. On the other hand, for the prediction differences under different public health strategies, the most significant effect has been travel restrictions. There were different studies on the impact of contact tracking and social isolation, but it was considered that improving the quarantine rate and reporting rate, and the wearing of protective face masks were essential for epidemic prevention and control. Different countries should take appropriate public health interventions to control the development of the epidemic.

Notably, there is evidence that the recessive infections are not infectious or the likelihood of being infectious is very low, which suggests that the existing COVID-19 epidemiological models might overestimate the epidemic risk. The input epidemiological parameters of the prediction models have significant differences in the prediction of the severity of the epidemic spread. Therefore, prevention and control institutions should be cautious when formulating public health strategies by drawing on the prediction results of mathematical models.

CRediT authorship contribution statement

Yue Xiang: Conceptualization, Methodology, Validation, Formal analysis, Investigation, Resources, Writing - original draft, Writing - review & editing. Yonghong Jia: Conceptualization, Methodology, Validation, Formal analysis, Investigation, Resources, Writing - original draft, Writing - review & editing. Linlin Chen: Investigation, Resources, Writing - original draft. Lei Guo: Writing - review & editing. Bizhen Shu: Writing - review & editing, All authors have read and agreed to the published version of the manuscript. Enshen Long: Conceptualization, Methodology, Validation, Formal analysis, Supervision, Project administration, Funding acquisition.

Declaration of competing interest

The authors declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.

Handling editor: Dr. J Wu