The Application and Implications of Novel Deterministic Sensitivity Analysis Methods

Abstract

Deterministic sensitivity analyses (DSA) remain important to interpret the effect of uncertainties in individual parameters on results of cost-effectiveness analyses. Classic DSA methodologies may lead to wrong conclusions due to a lack of or misleading information regarding marginal effects, non-linearity, likelihood and correlations. In addition, tornado diagrams are misleading in some situations. Recent advances in DSA methods have the potential to provide decision makers with more reliable information regarding the effects of uncertainties in individual parameters. This practical application discusses advances to classic DSA methods and their implications. Three methods are discussed: stepwise DSA, distributional DSA and probabilistic DSA. For each method, the technical specifications, options for presenting results, and its implications for decision making are discussed. Options for visualizing DSA results in incremental cost-effectiveness ratios and in incremental net benefits are presented. The use of stepwise DSA increases interpretability of marginal effects and non-linearities in the model, which is especially relevant when arbitrary ranges are implemented. Using the probability distribution of each parameter in distributional DSA provides insight on the likelihood of model outcomes while probabilistic DSA also includes the effects of correlations between parameters.

Probabilistic DSA, preferably expressed in incremental net benefit, is the most appropriate method for providing insight on the effect of uncertainty in individual parameters on the estimate of cost effectiveness. However, the opportunities provided by probabilistic DSA may not always be needed for decision making. Other DSA methods, in particular distributional DSA, can sometimes be sufficient depending on model features. Decision makers must determine to which extent they will accept and implement these new and improved DSA methodologies and adjust guidelines accordingly.

Key Points for Decision Makers

Limitations to classic deterministic sensitivity analysis (DSA) methodologies may result in wrong conclusions regarding the effect of uncertainties in individual parameters on cost-effectiveness model outcomes.

Developments in DSA methodologies include stepwise DSA, distributional DSA based on parameter probability density functions and probabilistic DSA.

Probabilistic DSA provides the most accurate insight into marginal and non-linear effects, likelihood of outcomes and correlation between parameters. In some cases distributional DSA can be sufficient for decision making.

Decision makers must determine to which extent they will accept and implement these improved DSA methodologies and adjust guidelines accordingly.

Introduction

In health economics, deterministic sensitivity analyses (DSA) are used to inform decision makers about the sensitivity of the outcomes of a cost-effectiveness model to individual parameters (one-way sensitivity analysis) or sets of parameters (two-way or multi-way sensitivity analysis). The sixth report of the ISPOR-SMDM (International Society for Pharmacoeconomics and Outcomes Research and Society for Medical Decision Making) series on good modelling practices discusses model parameter estimation and uncertainty and advocates deterministic and probabilistic sensitivity analyses for all evaluations [1, 2]. Probabilistic sensitivity analyses are recommended for the interpretation of joint parameter uncertainty on cost-effectiveness estimates. In addition, insight into the isolated effects of variations in individual parameters is provided by deterministic methods. Deterministic analyses remain of relevance to decision makers [3–9].

Current DSA methods do not provide reliable insight into the changes to the outcome of the model due to individual parameter uncertainty. Limitations to the classic DSA approach have been well known for years [10–12], and include that (i) the parameter ranges included in DSAs are often chosen arbitrarily and no insight in effects at the margin is provided, (ii) non-linearities in models are not visible, (iii) results of DSAs do not provide insight into the likelihood of the reported parameter values, (iv) correlations between parameters are not taken into account and (v) DSAs are usually reported in the incremental cost-effectiveness ratio (ICER), the mathematical properties of which bring several limitations [1, 12–16].

These limitations imply that the classic approach to DSA can produce biased estimates of the expected costs and outcomes under individual parameter values that differ from the base case [10]. For example, in many oncological models, survival estimates include parametric survival curves that are defined by two correlated parameters (e.g. Weibull or lognormal curves [17, 18]). Evaluating the model outcome for a value of one of the survival curve parameters at the maximum of its predefined range while keeping the other at its base case value will nullify the correlation and thereby provide an incorrect estimate.

Recently, a new method for performing DSAs was published, which the authors called the Probabilistic One-way Sensitivity Analysis (POSA) [12]. This method is explained in more detail later in this paper but in summary entails the use of individual parameter distributions to generate parameter values according to pre-set percentile steps of their probability density function. Subsequently, the sampled value of the parameter of interest is held fixed while all other model parameters are repeatedly randomly sampled from their respective probability distributions, as in a probabilistic sensitivity analysis [12]. This procedure is repeated for each pre-set percentile step for all individual model parameters. Although POSA may be the best approach to provide detailed insight in individual parameter uncertainties, simpler approaches may be sufficient in most situations, the method is computationally burdensome and it does not use the ICER as an outcome even though the ICER represents the preference of many decision makers. Thus, the uptake of POSA may be limited even though it provides methodological advances. Since the impact of any methodological advance on decision-making practices depends on its uptake, more guidance on the application of different DSA methods is necessary.

POSA can be broken down into three methodological advances to classic DSA, each with its own implications for decision makers. These stages of advancement include the use of steps of parameter values (stepwise DSA), the use of distributions for generating parameter values according to these steps (distributional DSA), and the introduction of probabilistic sampling of all other parameters when assessing the parameter of interest (probabilistic DSA). The POSA method is a form of probabilistic DSA but with the model outcome expressed in incremental net benefits instead of the ICER [12].

This practical application systematically discusses the three methodological advances to classic DSA, their interpretation and their implications for decision makers based on a hypothetical case study. Each advance is described in light of what it adds to the previous approach.

Three Stages of Methodological Advances to Deterministic Sensitivity Analysis (DSA)

In this section, three methodological advances will address each of the five limitations to the classic DSA approach as outlined in the introduction. A lack of insight in effects at the margin (i) and in non-linearities (ii) can be addressed by stepwise DSA. Insight into the likelihood of outcomes (iii) can be provided by performing DSA according to individual parameter distributions (distributional DSA). Insight in correlation (iv) can be provided by probabilistic DSA. The use of incremental net benefit instead of the ICER (v) can be applied within all methods. Table 1 summarizes the limitations that each method addresses.

Table 1.

Limitations to the classic deterministic sensitivity analysis (DSA) approach that are addressed by each of the methodological advances

The use of incremental net benefit instead of the incremental cost-effectiveness ratio

The mathematical characteristics of ratios introduce some difficulties with the ICER as a means to report model outcomes [1, 6, 10, 13, 19, 20]. Normally distributed incremental costs and benefits may result in non-normally distributed ICERs due to the denominator approaching zero, and ICERs are not uniquely defined. Good practice guidelines thus advise not to report negative ICERs (and instead report domination) and to clearly distinguish positive ICERs that are located in the southwest quadrant of the cost-effectiveness plane (negative incremental costs and QALYs) [1, 16, 21].

The problems with the ICER as an outcome can be mitigated in two ways. Either one can include in the presentation of DSA results the quadrant of the cost-effectiveness plane that the reported ICER populates, or one can report incremental net benefits instead. Incremental net benefits can be presented in monetary or in health benefits (INMB and INHB). The relation between INMB and INHB is linear and straightforward [19]. In this paper, we use INMB as it represents the more common approach.

We provide results for both approaches to mitigate the problems with the ICER. Each of the three new DSA methods reported in the following sections are presented while giving insight in dominated scenarios but also with the ICER as well as with INMB as the model outcome of interest. We used a willingness-to-pay threshold of €20,000 per QALY to calculate INMB throughout this paper as it is one of the willingness-to-pay reference values used in the Netherlands, while it simultaneously approximates the threshold of £20,000 per QALY used by the National Institute for Health and Care Excellence (NICE) [3, 4].

Model description for the hypothetical case study

For the case study, a simple Markov model was constructed, closely related to recent models seen in oncology [22–29]. The model parameter values were chosen in such a way to be able to show all implications of the DSA methodologies based on a single case study. The model includes three disease states: progression-free survival (PFS), post-progression survival (PPS) and death.

Incremental costs and QALYs were calculated for a new treatment compared with a comparator. Twelve parameters defined the model. Exponential survival curves defined PFS for the new treatment and PFS and overall survival (OS) for the comparator, while a hazard ratio defined OS for the new treatment. Utility between both treatments was set as equal. Thus, only two utility inputs were needed: one for PFS and one for PPS. Three cost parameters applicable to the comparator as well as the new intervention defined costs during PFS, costs during PPS and one-off costs for death. The costs for both disease states were assumed to be correlated (R² = 0.8). A single parameter defined the costs for the new treatment while the comparator did not incur costs. The last two included parameters were the discount rates for costs and benefits (both 3.5%). The model included cycles of 1 month and a time horizon of 5 years (60 months). No half-cycle corrections were applied. The model can be requested from the authors but we note that it serves only illustrative purposes.

The values, ranges and distributions of all 12 parameters are listed in Table 2. On purpose, different types and extents of ranges were included. During probabilistic sampling, the costs were restrained to be at least zero and exponential survival curve parameters were restrained to the interval between zero and one.

Table 2.

Parameter values and their ranges and distributions for the hypothetical case study

Parameter	Base case	Type of range	Range	Distribution	Distribution parameters
Survival parameters					Mean	SD
PFS λ comparator	0.25	95% CI	0.100–0.400	Normal	0.25	0.077
PFS λ intervention	0.05	95% CI	0.017–0.083	Normal	0.05	0.017
OS λ comparator	0.03	95% CI	0.021–0.039	Normal	0.03	0.005
OS HR intervention	1.00	95% CI	0.800–1.250	Lognormal	1.00	0.114
Utility parameters					Alpha	Beta
Utility PFS	0.80	95% CI	0.610–0.930	Beta	17.80	4.70
Utility PPS	0.50	95% CI	0.200–0.800	Beta	4.54	4.54
Cost parameters					Mean	SD
Costs PFS (€)	1200	± 50%	600–1800	Normal	1200	306
Costs PPS (€)	2000	± 25%	1500–2500	Normal	2000	255
Costs death (€)	1500	± 25%	1125–1875	Normal	1500	191
Costs intervention (€)	750	± 25%	563–938	Uniform	N/A	N/A
Discount rates
Discount rate costs	3.5%	Fixed range	0.015–0.055	Uniform	N/A	N/A
Discount rate benefits	3.5%	Fixed range	0.015–0.055	Uniform	N/A	N/A

CI confidence interval, HR hazard ratio, OS overall survival, PFS progression-free survival, PPS post-progression survival, N/A not applicable, SD standard deviation

Stepwise DSA

Stepwise DSA: Addressed Limitations and Methods

Non-linearity and marginal effects

Uncertainty in individual parameters may not have a linear effect on incremental costs, incremental benefits and/or the ICER. Information regarding non-linear effects may nevertheless be relevant for decision making as it conveys whether a small change in a parameter value may have a small or large effect on the model outcome. Additionally, through the provision of insight in non-linearity in the outcomes of the model due to the uncertainty ranges in individual parameters, we also gain insight in the marginal effects at the outer ends of the range of each parameter, which is particularly helpful in the case of arbitrary ranges.

The ISPOR-SMDM good practices report explicitly states that deterministic sensitivity analyses should be based on evidence-informed ranges; the use of arbitrary ranges is actively discouraged. Nevertheless, the use of arbitrary ranges in reimbursement dossiers submitted by manufacturers and in published articles is commonplace [22–26, 30–32]. Thirty-six technology appraisals were published by NICE between January and June 2019. For 20 appraisals, the committee papers including the manufacturer submission of the model was available. Of those, 70% (N = 14) showed the use of arbitrary ranges for multiple parameters within the deterministic sensitivity analysis, ranging between ±10 and 50%, or using unknown percentages [22–26, 30, 32–43]. Furthermore, all of the models used the same percentage for all parameters in case of arbitrary ranges. The ISPOR-SMDM report states that in the case of a lack of pre-specified information on parameter ranges, an appropriately broad range should be implemented for each parameter [1]. Though applying the same fixed percentage for all parameters is convenient and easy to interpret, it is highly unlikely that it is appropriate for each parameter. If the used ranges for the parameters included in the DSA are questionable, so are the results of the DSA.

Stepwise DSA method

Marginal effects and non-linear relations between input parameter values and the model outcome can be demonstrated by replacing the classic approach to DSA, which assesses the outcome at the base case value and at a minimum and a maximum value, with a stepwise approach. Stepwise DSA entails that model outcomes are recorded for the base case, minimum and maximum values and for a number of uniform intermediate steps between the base case and the minimum and the base case and the maximum. In our case study, we used 10 steps above the base case (including the maximum) and 10 steps below (21 steps in total). We took the range of each parameter and inferred that these represented 95% confidence ranges. The interval between the 2.5th and 97.5th percentile of the range can be split into steps of five percentiles, with the mean value (50th percentile) representing a half step between the 10th and 11th step. Sometimes the size of the lower range differs from the size of the upper range. In those cases, the steps between the minimum and the base case may be smaller or larger than those between the base case and the maximum.

Stepwise DSA: Figures and Their Interpretation

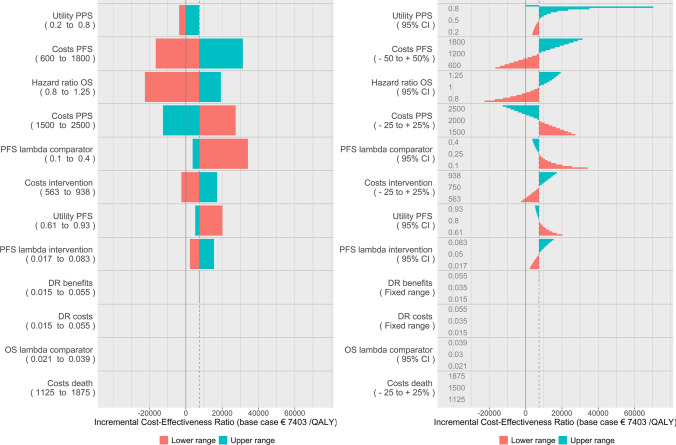
Figure 1 shows the tornado diagrams for both the classic DSA approach (left figure) as well as stepwise DSA (right figure). The model provided a base-case ICER of €7403 per QALY, based on incremental costs of €2665 and incremental QALYs of 0.36.

Fig. 1.

Classic deterministic sensitivity analysis (left) and stepwise deterministic sensitivity analysis (right). DR discount rate, OS overall survival, PFS progression-free survival, PPS post-progression survival

The stepwise DSA figure reads as a classic DSA tornado diagram but instead of looking solely at the outer ends of the range (minimum and maximum), we gain insight in the range between the base case and the minimum and maximum, respectively. The steps are shown as bars, clustered per parameter. For clarity, the applied ranges are reported within the diagram. Note that the costs during PFS were varied by 50% and costs during PPS by 25% (see Table 2). Their relative impact on the ICER (which is not twice as large for PFS costs) illustrates that it is crucial to know the extent of each range when interpreting the tornado diagram. The order of the parameters in the tornado diagram would be different had the same range been used for both parameters, as can be easily inferred by looking at the intermediate steps of the range for PFS costs.

Figure 2 shows the stepwise DSA results in the same plot as in Fig. 1 but with transparent bars to indicate the situations where the new therapy dominates the old (left figure), and the DSA results expressed in INMB (right figure). The order of the parameters has been kept fixed throughout the manuscript to facilitate comparisons between the figures.

Fig. 2.

Stepwise deterministic sensitivity analysis (DSA) with information on situations where the new therapy dominates the old through transparent bars (left) and stepwise DSA expressed in incremental net monetary benefits (right) for the theoretical case study. DR discount rate, OS overall survival, PFS progression-free survival, PPS post-progression survival

Stepwise DSA: Benefits

Incalculable ICERs

From Fig. 1, one benefit of the stepwise DSA approach becomes clear immediately. The maximum value for utility in PPS is equal to the base-case utility in PFS. Since there is no treatment effect on OS in the base case, the resulting QALYs are zero and an ICER cannot be calculated, which means it cannot appropriately be reported in the classic tornado diagram with the ICER. In the classic DSA, this either defaults to zero (as in Fig. 1) or it means modellers leave such cases out of the visualization of the DSA entirely and report it only in text. The stepwise DSA shows clearly that the effect of uncertainty in this parameter on the ICER is actually very substantial. The parameter is at the very top of the stepwise tornado diagram, while it would have been somewhere in the bottom part of the diagram in the classic DSA.

Non-linearity and marginal effects

In Fig. 1, the non-linear relation between several parameters and the ICER are evident. An increase in the hazard rate (lambda) for PFS of the comparator results in a lower ICER due to a simultaneous decrease in costs and increase in incremental QALYs. Due to the exponential curve, the marginal effect on the ICER is small at the outer end of the upper range. In contrast, the marginal effects increase for the lower range. These effects are not visible in the traditional DSA.

For a decision maker who would be willing to accept the intervention if the ICER remains below €20,000 per QALY, the intervention would not be cost effective at the minimum value of this range (the ICER is €34,178 per QALY). A slightly smaller outer end of the range would yield a disproportionally smaller ICER. For example, three steps closer to the base case (hazard rate = 0.15) the ICER is €16,640 per QALY, making the intervention cost effective. The effect of decreasing the range by 32% yields an effect on the ICER of − €17,538 per QALY (− 51%), or a change of 237% relative to the base case ICER. At the other end, uncertainty regarding the boundary of the upper range will be less relevant, as marginal effects are small.

Domination and incremental net monetary benefits

In our hypothetical model, in some situations the new therapy dominated the old (representing the southeast quadrant of the cost-effectiveness plane). In Fig. 2 (right figure) we included in the tornado diagram of the stepwise DSA information regarding what negative ICERs mean. In this case, we only had situations where the new therapy dominated the old (we made these transparent), but we can easily extend this presentation by using more types of transparency, colours or patterns in the bar plots. This way we retain the information included in the stepwise DSA, including the parameter value at which the new therapy starts dominating the old, while also providing information on the meaning of the otherwise uninterpretable ICER values. If we had only reported the minimum and maximum value as resulting in domination or not, we could have omitted useful information about the moment the new therapy started to dominate the old [44]. It would suggest that the whole range means domination while it is perfectly possible that the majority of the range leads to non-dominating situations. In Fig. 2, this is the case for the costs of the new therapy.

The reporting of INMB as opposed to the ICER solves many difficulties associated with the ICER in our case study. In Fig. 2 we can see that there is no problem with incalculability of the upper range of utility during PPS. Additionally, the non-linear relationships in the model become clearer because non-linearity as a consequence of the ICER being a ratio is eliminated, which can be seen in the range for utility during PPS and for the hazard ratio. We can still show situations where the new therapy dominates the old by including transparent bars.

DSA with Percentiles of the Parameter Probability Distribution (Distributional DSA)

Distributional DSA: Addressed Limitations and Methods

Likelihood of the parameter values

A limitation to classic and stepwise DSA is that they assume that each value of a parameter’s range is equally likely to occur. However, in reality most parameter ranges are defined by a probability distribution, which means that the values at the outer ends of the range are not as likely to occur as the values around the mean. By including the probability distribution in the DSA we gain insight in the likelihood of the parameter value and the resulting model outcome. Distributional DSA takes a similar approach as stepwise DSA, but instead of the uniform steps between the base case and the minimum and maximum, the steps represent percentiles of the probability density function of the parameter.

Distributional DSA method

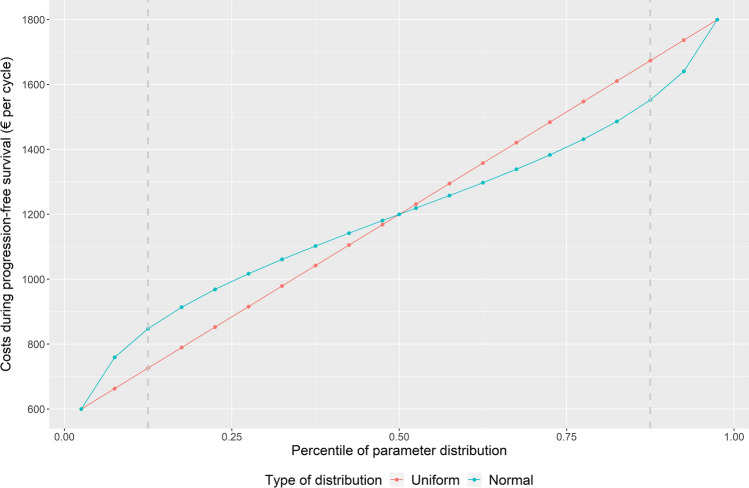
The method is best explained by looking at a normal distribution. For example, take the costs during PFS. These costs are arbitrarily varied by ± 50% in the DSA. To perform distributional DSA (but also in general to perform a PSA), we will need to assume a distribution. In our case study, we assumed a normal distribution with the outer ends of the range representing the 95% confidence interval running from the 2.5th percentile to the 97.5th percentile. As with stepwise DSA, the interval between the 2.5th and 97.5th percentile of the range can be split into steps of five percentiles, with the mean value (50th percentile) representing a half step between the 10th and 11th step. The value of the parameter in the distributional DSA approach was subsequently calculated based on this percentile of the probability density function rather than being based on uniform steps. Because the probability density function is denser around the mean, 1/10th of the distribution does not equal 1/10th of the uniform range. Figure 3 shows this visually.

Fig. 3.

Parameter values of costs during progression-free survival for different percentile steps of uniform and normal distributions

As an example, look at the values that represent 75% of the range around the mean, in Fig. 3 represented between the grey dotted lines. The values for the cost parameter for the uniform steps equal €726–€1674 (range €947) while they equal €848 to €1552 (range €704) for the normal distribution. The difference in the applicable range of €243 (€947–€704) represents 20% of the full range (€600–€1800).

Distributional DSA: Figures and Their Interpretation

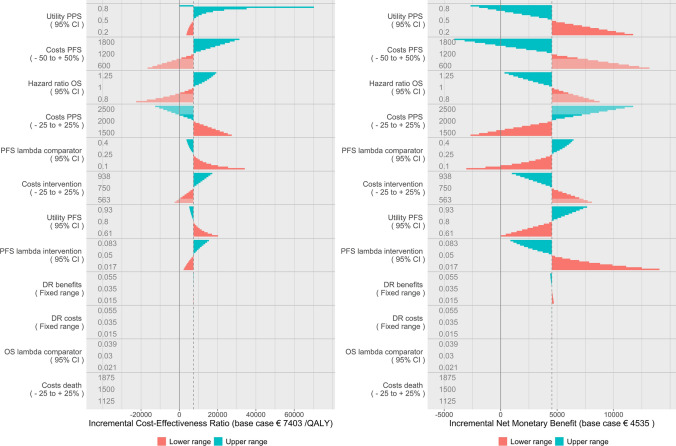
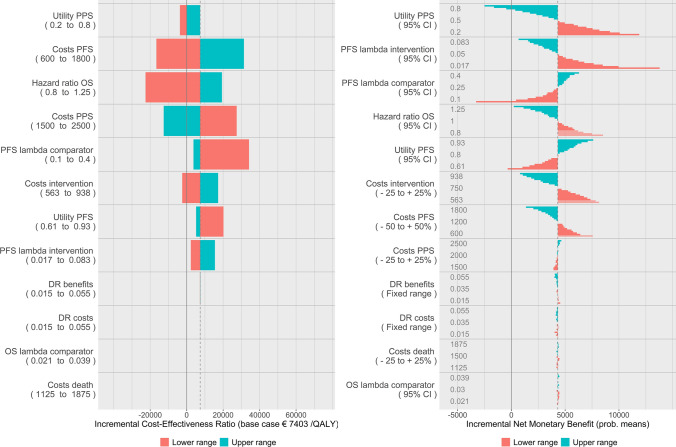
Figure 4 shows the stepwise DSA (left figure) and the distributional DSA (right figure). The interpretation of the distributional DSA is the same as the stepwise DSA. The changes to the shape of the ranges for each parameter are clearly visible, reflecting the normal and beta distributions. Note that the shape of the range does not change for the costs of the intervention, as the distribution of this parameter is defined as uniform. In general, when a probability distribution cannot be assumed, it is advocated to apply the uniform distribution which means the distributional DSA defaults to stepwise DSA for these parameters.

Fig. 4.

Stepwise deterministic sensitivity analysis for reference (left) and distributional deterministic sensitivity analysis (right). DR discount rate, OS overall survival, PFS progression-free survival, PPS post-progression survival

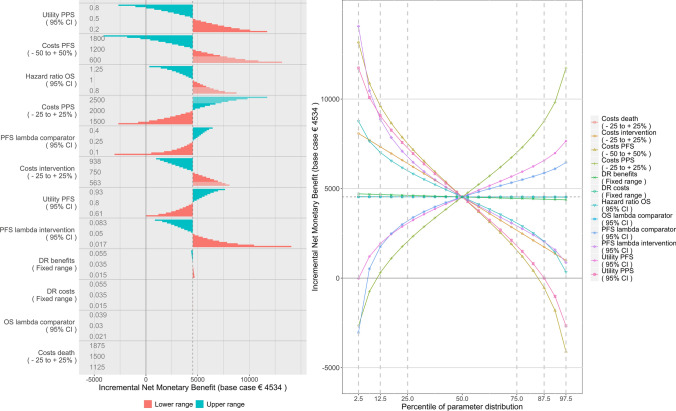
Figure 5 shows the distributional DSA with INMB as the outcome in two ways. The left figure is interpreted in the same way as the INMB figure for the stepwise DSA. The right figure (called a spider plot) is interpreted differently. Because the steps for each parameter are executed according to standardized percentiles of their probability density functions, we can present each parameter on the same axis. The x-axis therefore now represents the percentile of each parameter’s distribution while the y-axis represents the INMB. Each parameter is represented by a different colour and different line markers. Grey dashed lines represent specific percentile ranges around the mean (in this case 50%, 75% and 95%).

Fig. 5.

Distributional deterministic sensitivity analysis with incremental net monetary benefits as the model outcome in a tornado diagram, with information on situations where the new therapy dominates the old through transparent bars (left) and distributional DSA expressed in incremental net monetary benefits in a spider plot (right). DR discount rate, OS overall survival, PFS progression-free survival, PPS post-progression survival

Distributional DSA: Implications of the Results

Likelihood of parameter values

The inclusion of the probability distributions clearly leads to different results. Most notably, the utility in the PPS state appears considerably less relevant. This is explained by the fact that the value of the utility at the next to last step is lower when calculated from the distribution than when it is uniformly calculated. Though we can still infer from Fig. 4 that the ICER will approach infinity when it comes closer to the maximum of the range, we now also can infer that the likelihood of these extreme ICERs is actually quite low. They are outside the next to last step representing the 92.5th percentile of the distribution with an ICER of €32,367. Similarly, only the outer five steps (up until the 22.5th percentile) of the lower range of the costs during PFS represent situations where the new therapy dominates the old, whereas this was the case for the outer seven steps in the stepwise DSA (up until the 32.5th percentile).

Figure 5, which presents model results in INMB, shows the same implications. The right figure makes it easier to interpret the likelihood that parameters cross certain INMB thresholds. For example, there is only one parameter that has a negative INMB within a range representing 75% of its distribution (the range between the 12.5th and 87.5th percentile), namely costs during PFS. Apparently, throughout the ranges of all individual parameters, the likelihood of a negative INMB is relatively small. Additionally, the graph readily shows whether the relation between the parameter and INMB is negative or positive (through the slope).

Probabilistic Non-Fixed Parameters in Deterministic Sensitivity Analysis (Probabilistic DSA)

Probabilistic DSA: Addressed Limitations and Methods

Correlation between parameters

All previously mentioned methods disregard an important element in cost-effectiveness models—correlation between parameters [1]. When a cost-effectiveness model includes correlated parameters, the classic DSA approach as well as stepwise DSA and distributional DSA yield biased results.

In the simple case study we have been using, correlation between the parameters for costs during PFS and during PPS has been present from the beginning (see the description of the case study in section 2). However, it has not shown up in any of the presented DSA results so far.

Probabilistic DSA method

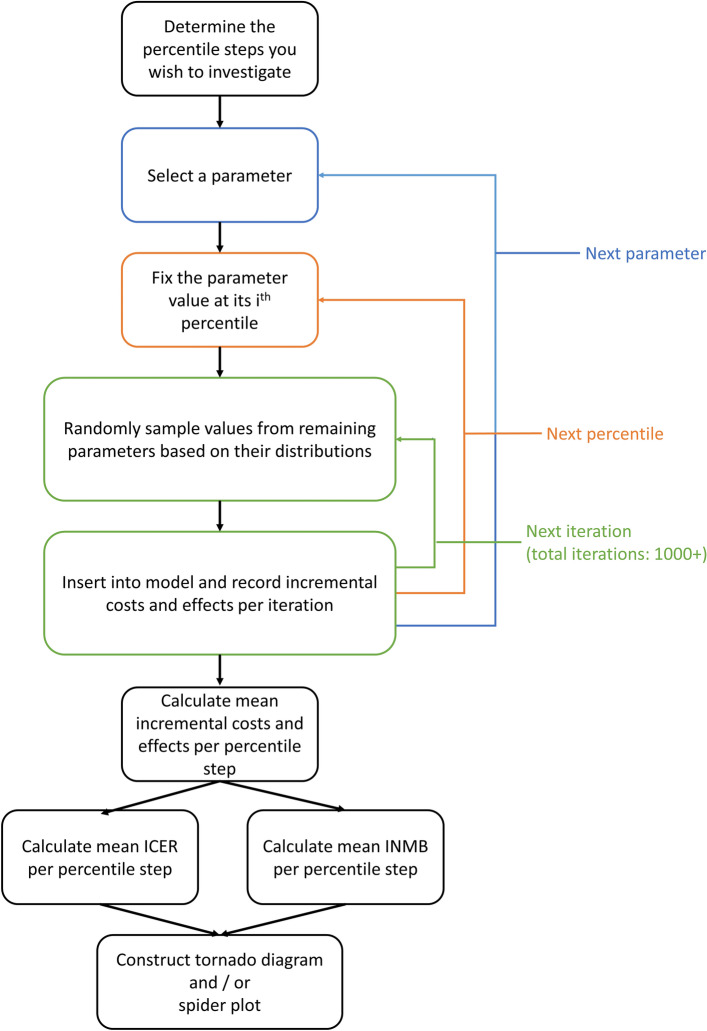
To include correlation in a DSA, we can perform probabilistic DSA where all parameters except the parameter of interest are sampled probabilistically—taking into account any correlation—for each fixed value of the parameter of interest (each quantile step). Probabilistic DSA is slightly more complex than the two methods described previously. The precise methods are described elsewhere by the inventors of the method [12], but here we provide a summary. The process is visualized in Fig. 6.

Fig. 6.

Process for performing probabilistic deterministic sensitivity analysis. ICER incremental cost-effectiveness ratio, INMB incremental net monetary benefit

In probabilistic DSA, each individual parameter is still varied according to fixed percentiles of their probability density function, as in distributional DSA. However, for each parameter, we now include for each of the steps a probabilistic analysis for all the other parameters with as many iterations as would be appropriate for the normal PSA (we used 10,000) [45]. The results for these iterations are recorded and the next percentile step of the parameter of interest is introduced. This is repeated until an inner loop is completed for all predefined percentile steps of all parameters. In our case, 12 parameters defined the model, each with 21 steps. The 10,000 iterations for each of these 252 options results in 2.5 million iterations.

Subsequently, for each step of each parameter, mean incremental costs and mean incremental QALYs are calculated. The ratio of these means provides us with the probabilistic ICER of each deterministic percentile step of the parameter [46]. INMB can also be calculated, based on the mean incremental costs and QALYs and the predefined willingness-to-pay threshold (€20,000 per QALY in our case). Calculated ICERs and INMB are conditional upon the parameter of interest that has been held fixed [12]. The conditionality includes that the possible correlation with the parameter of interest is taken into account. Note that the probabilistic approach with INMB as an outcome has previously been referred to as probabilistic one-way sensitivity analysis (POSA) [12], while probabilistic DSA includes all probabilistic approaches irrespective of the outcome used.

The probabilistic DSA method shares some similarities with expected value of parameter perfect information analysis (EVPPI). Both methods require one parameter to be fixed while all others are varied probabilistically [6, 12, 48]. However, the fixed value of the parameter of interest is sampled randomly from its probability distribution in EVPPI while it is deterministically defined according to a pre-set percentile of the probability distribution in probabilistic DSA. The methods answer different questions. EVPPI could be helpful in answering questions about the value of the reduction of uncertainty within the parameter of interest relative to other parameters, while probabilistic DSA treats the uncertainty associated with a parameter as a given, and subsequently investigates its effects on the outcome of the model.

Probabilistic DSA: Figures and Their Interpretation

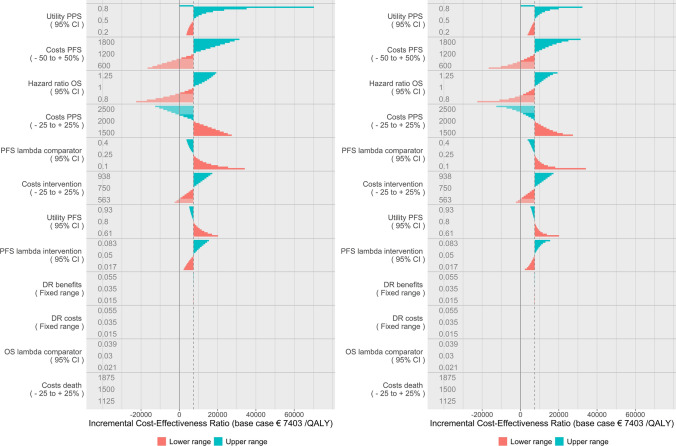
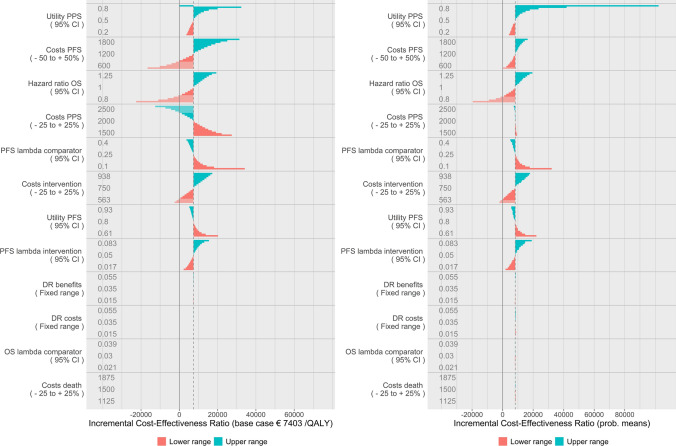
Figure 7 shows the results of the probabilistic DSA (left figure) in comparison with the distributional DSA (right figure). Their interpretation is the same with the exception that the mean ICER in the probabilistic DSA represents the probabilistic mean per parameter of the iterations performed for the base-case scenario of that parameter, rather than the deterministic base case. Note that the incalculable ICER does not apply anymore as the incremental QALYs are not exactly zero due to the probabilistic element. Instead, a very large ICER was found as it approaches infinity when incremental QALYs approach zero. Due to chance, this ICER may just as well have been negative to the same extent.

Fig. 7.

Distributional deterministic sensitivity analysis for reference (left) and probabilistic deterministic sensitivity analysis (right). DR discount rate, OS overall survival, PFS progression-free survival, PPS post-progression survival

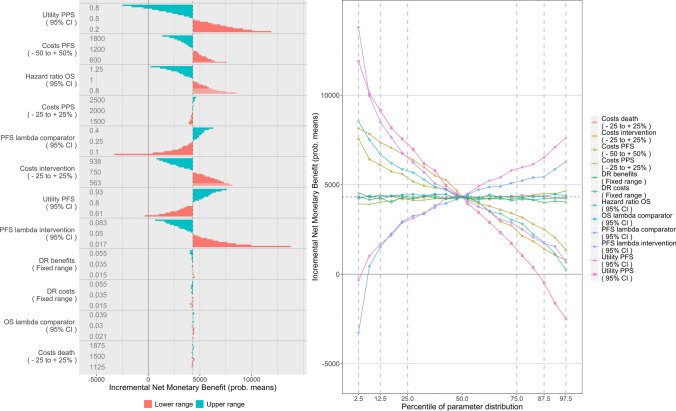
Figure 8 shows probabilistic DSA with conditional INMB as the model outcome. The interpretation of these figures is equal to the interpretation of the figures with INMB for the distributional DSA. Note that the probabilistic nature of the analysis results in slightly variable estimates of the mean ICER and INMB.

Fig. 8.

Probabilistic deterministic sensitivity analysis (DSA) with incremental net monetary benefits as the model outcome in a tornado diagram (left) and probabilistic DSA expressed in incremental net monetary benefits in a spider plot (right). DR discount rate, OS overall survival, PFS progression-free survival, PPS post-progression survival

Probabilistic DSA: Implications of the Results

Correlation

The probabilistic DSA figure shows the relevance of correlation. The parameter that resulted in the largest ICER range in the distributional DSA, namely costs during PFS, is considerably less variable. The range in the ICER resulting from the uncertainty in the costs during PFS is almost completely nullified. The correlation between the two cost parameters readily explains this phenomenon, as the parameters have opposite effects. Where previously costs during PFS was the only parameter that had negative INMB within the 75% confidence interval of its distribution, now the ranges in none of the parameters are very likely to result in negative INMB. The classic, stepwise and distributional DSA approaches thus yielded misleading results.

Note that for interpretability, we did not update the order of the parameters throughout the manuscript, but it is evident that decision makers would draw completely different conclusions from the classic DSA in Fig. 1 than from the probabilistic DSA in Fig. 8. To illustrate this point, Fig. 9 contains the classic DSA tornado diagram and the probabilistic DSA tornado diagram in INMB, both with the most influential parameter at the top of the diagram. Though based on the same model and parameter ranges, the order of the parameters is entirely different. The cost parameters that were the second and fourth most important in the classic DSA are now at the bottom of the diagram. The parameter that seemed the least influential in the classic DSA (PFS lambda intervention, except for those not having an effect at all), is actually the second most influential.

Fig. 9.

Comparison of the classic deterministic sensitivity analysis (DSA) approach (left) and the probabilistic DSA approach (right), based on the same data. DR discount rate, OS overall survival, PFS progression-free survival, PPS post-progression survival

General Discussion

Implications for Decision Makers

Deterministic sensitivity analyses are never the sole method used to draw conclusions on cost effectiveness of interventions. Nevertheless, the insights deterministic analyses provide remain of relevance to decision makers. As we have shown, current DSA methods may yield misleading if not utterly incorrect results (see Fig. 9).

In recent technology appraisals from NICE, the DSA results were used by the Evidence Review Group in the published committee papers for informing decisions in two ways; first, to find the parameters that are drivers of the cost-effectiveness estimates and the extent of sensitivity of the ICER to those parameters, and second, to find out what the most likely upper ICER is under individual parameter uncertainty and whether that ICER falls below a threshold usually considered cost effective [3, 4, 8, 17, 18, 47]. The precise differences in the interpretation of DSA results as a consequence of using different methods will of course vary based on the characteristics of each therapy and cost-effectiveness model. Nevertheless, we have shown in this study that the new methods can substantially alter the interpretation of the extent to which parameters are drivers of the cost-effectiveness estimates (see Fig. 9) as well as the interpretation of whether it is likely that certain thresholds will be crossed (see Figs 4, 5, 7 and 8). Thus, the new methods crucially improve the two main insights the DSA is meant to deliver to decision makers.

Furthermore, information on the marginal effects of a change in one of the input parameters can be very useful for modellers and decision makers when they must decide which alternative scenarios to explore. Even though some parameters may have large overall ranges, sensitivity of the model outcome to one end of the range may not be worth exploring further. Probabilistic DSA can help decision makers decide what scenarios should be explored, what additional information would be helpful, for what parameters an EVPPI or a headroom analysis would be useful and what other aspects of the cost-effectiveness model deserve more or less attention. The probabilistic DSA is effectively a systematic method to explore many scenarios. Depending on the objectives of the modeller or decision maker, the percentiles that determine the distributional or probabilistic DSA percentile steps can be modified to reflect the most relevant scenarios.

Insight in non-linear marginal effects can be especially useful for early health technology assessment (HTA) in which input parameter values and ranges are relatively more uncertain, and usually scenarios are performed to determine threshold values [28, 49–52]. Early HTA can, for example, be used to determine the maximum price at which an intervention remains cost effective, that is, has positive INMB [53]. Additionally, since evidence about medicines is becoming increasingly more limited at the time a reimbursement decision must be made [54–58], the new DSA methods can aid decision makers in weighing the impact of different scenarios. Time is of relevance here, because the estimation of the mean value as well as the corresponding uncertainty may develop over the course of the lifecycle of a new therapy [51]. By performing a comprehensive DSA early in the drug development process, evidence generation can be tailored towards resolving the uncertainties that have the most important impact on the model results and subsequent pricing and reimbursement decisions. Additionally, after an initial reimbursement decision has been made, the scenarios incorporated within the DSA can inform which deviations in clinical practice from the mean value for any individual parameter as used in the model would warrant a reassessment.

Which Method to Use in Which Situation

HTA organizations need to decide which method they find helpful and consequently want to request in company submission procedures. The same goes for international societies that provide guidelines on the execution of cost-effectiveness analyses.

It may be clear from the previous sections that in principle, probabilistic DSA is the preferred method as it addresses all limitations associated with the classic DSA. However, the necessity of probabilistic DSA depends on some of the features of the model. If all model parameters are completely independent, probabilistic DSA may not provide much additional information over distributional DSA. Probabilistic DSA requires the modeller to perform many iterations. In our hypothetical case study this included 2.5 million iterations; when more percentile values of each parameter’s probability distribution are included, this number will grow vastly. Alternatively, in EVPPI analyses it is common to use fewer iterations for the inner loop (e.g. 1000 instead of 10,000), which would drastically reduce the number of iterations. The running time is therefore a combination of how complex the model is (number of parameters and technical complexity), the number of percentile steps assessed, the number of iterations in the probabilistic loop, and of course, computational power. In any case, the number of iterations will probably exceed those of a regular PSA (e.g. 10,000) by at least a factor of ten because a probabilistic loop with 1000 iterations for ten percentile steps for a simple model with ten parameters would already entail 100,000 iterations. For stepwise and distributional DSA, the number of iterations will likely never approximate the running time of a regular PSA because a complicated model with 50 parameters, each tested for 21 percentile steps, would still only require 1050 iterations in total. Therefore, if independence between parameters is guaranteed and computational efficiency is considered important, the less cumbersome distributional DSA may be sufficient. However, it should be noted that complete independence is often unlikely [1]. For any model that contains survival curves that are defined by two or more parameters, correlation is relevant, and the classic, stepwise and distributional DSA approaches will yield misleading results, the extent of which will vary per model. We advocate to at least implement distributional DSA in all cases, as it is as easy to understand as the classic DSA and already provides decision makers with information about marginal effects, nonlinearities and likelihood.

The impact of the methodological advances to DSA presented within this study will depend on the willingness of decision makers to adopt them. Decision makers generally prefer methods that are not overly complicated and that can be readily explained to the public. While some of the new DSA methods add complexity to the DSA process, the results—certainly when presented in a tornado diagram—remain as intuitive as within classic DSA.

Incremental Cost-Effectiveness Ratio Versus Incremental Net Benefit

Previous literature has extensively discussed the advantages of using net benefit over ICERs when reporting cost-effectiveness model results [1, 10, 13, 19]. In general, from a methodological perspective, the net benefit approach is preferred. However, in many HTA guidelines, the ICER remains the most prominent outcome [3, 4, 47]. The ease of its interpretation and the fact that it is well established among people not directly involved in health economic modelling makes it likely that the ICER will remain the preferred outcome over incremental net benefit for the near future. From tornado diagrams expressed in ICERs, the conversion to tornado diagrams or line charts expressed in incremental net benefits is not intuitive (see Fig. 2). To ease the transition and avoid confusion, HTA organizations may require the DSA tornado diagram to be expressed in the ICER in addition to a spider plot expressed in incremental net benefits (INMB or INHB). Since they are based on the same data, it would infer little additional work while it accommodates both the methodological arguments for using incremental net benefit and the societal and cultural arguments for using the ICER.

Limitations and Warnings

Findings from a DSA are rarely, if ever, the sole reason for changing a conclusion on the cost effectiveness of interventions. The discussed methodological advances to DSA methods can help decision makers to decide on those aspects of the model that need more explicit consideration, but should not be interpreted as being able to replace any of the other relevant methodologies to address uncertainty. Probabilistic sensitivity analyses, value of information analyses, cost-effectiveness acceptability curves, scenario analyses and other methods answer different questions than those that are answered within a DSA [1, 6]. The DSA is intended to answer the question of what would happen to the ICER or INMB if the estimation of a mean parameter value were wrong, or would change over time. The PSA provides decision makers with an uncertainty interval regarding the ICER, taking into account uncertainty in all parameters simultaneously, but it does not provide information on individual parameters. Good practice guidelines recommend modellers to perform a DSA as well as a PSA in order to get insight in the effects of uncertainties in individual parameters as well as insight in the combined uncertainty of all parameters [1].

The discussed methods also do not represent a replacement for the application of evidence-informed ranges in input parameters, and should not be interpreted as advocating arbitrary ranges. The recommendations of the ISPOR-SMDM good modelling practice reports apply irrespective of the methods applied to generate and visualize DSA results. However, since the reality is that arbitrary ranges are still often used in cost-effectiveness models, having methods to more adequately interpret the effects associated with the arbitrary range is important. Nevertheless, the new DSA methods in no way justify the use of arbitrary ranges.

We have chosen to model 21 percentile steps (ten smaller and ten bigger than the base case) as that is sufficient to grasp the function of marginal effects. This number is intuitive but remains essentially arbitrary; one could also decide to have less or more steps. Theoretically, it is even possible to make the steps almost continuous but there does not seem to be much added value, and this is computationally intensive.

Our hypothetical case study can be criticized in many ways as it is an extremely simplified model. Some of our simplifying assumptions such as a lack of discounting and zero comparator are not very representative of the real world. The model’s main components such as the structure, the exponential survival curves and utilities are, however, very common within oncology. We chose to keep the model simple as the methodological advances are best explained with a model that is easy to understand and that has a limited set of parameters. We hope that we have provided enough examples of real situations to convince readers of the relevance of the discussed DSA methods and we recommend future studies to investigate the benefits of the new methods in real-world case studies.

Conclusions

Classic DSA approaches may provide biased information because they do not provide insight in marginal effects, nonlinearities, or the likelihood of the outcomes, and because they do not consider correlation. Recent advances in DSA methodologies in the form of stepwise, distributional and probabilistic DSA can address these limitations. This paper poses the argument to modellers and decision makers that methodological advances are worthwhile to implement in their models and decision-making processes. Sometimes distributional DSA may be sufficient, but in most cases probabilistic one-way sensitivity analysis is the recommended method.

Author contributions

RAV, JWG, AKMT, HGML and WGG devised and planned the study. RAV, JWG and SK performed the analyses. RAV, JWG, SK, AKMT, HGML and WGG contributed to the interpretation of the results. RAV drafted the first version of the manuscript. All authors reviewed and revised the manuscript in subsequent iterations. All authors approved the final version of the manuscript.

Declarations

Funding

No funding was received for this research.

Conflicts of interest

During the conduct of the study, JWG was funded by an unrestricted grant from GlaxoSmithKline. HGML is a member of the Lygature leadership team. RAV, SK, AKMT and WGG report no conflicts of interest.

Ethics approval

No animal or human subjects were involved in this study.

Consent to participate

Not applicable.

Consent for publication

Not applicable.

Availability of data and material

All used models and data for this study can be requested from the authors.

Code availability

The R scripts to make the published figures are made publicly available at https://github.com/Vreman/DSA.

Disclaimer

The views expressed in this article are the personal views of the authors and may not be understood or quoted as being made on behalf of or reflecting the position of the agencies or organizations with which the authors are affiliated.