Rapid golden-angle diffusion-weighted propeller MRI for simultaneous assessment of ADC and IVIM

Abstract

Purpose:

Golden-angle single-shot PROPLLER (GA-SS-PROP) is proposed to accelerate the PROPELLER acquisition for distortion-free diffusion-weighted (DW) imaging. Acceleration is achieved by acquiring one-shot per b-value and several b-values can be acquired along a diffusion direction, where the DW signal follows a bi-exponential decay (i.e. IVIM). Sparse reconstruction is used to reconstruct full resolution DW images. Consequently, apparent diffusion coefficient (ADC) map and IVIM maps (i.e., perfusion fraction (f) and the perfusion-free diffusion coefficient (D)) are obtained simultaneously. The performance of GA-SS-PROP was demonstrated with simulation and human experiments.

Methods:

A realistic numerical phantom of high-quality diffusion images of the brain was developed. The error of the reconstructed DW images and quantitative maps were compared to the ground truth. The pulse sequence was developed to acquire human brain data. For comparison, fully sampled PROPELLER and conventional single-shot echo planar imaging (SS-EPI) acquisitions were performed.

Results:

GA-SS-PROP was 5 times faster than conventional PROPELLER acquisition with comparable image quality. The simulation demonstrated that sparse reconstruction is effective in restoring contrast and resolution. The human experiments demonstrated that GA-SS-PROP achieved superior image fidelity compared to SS-EPI for the same acquisition time and same in-plane resolution (1 × 1 mm²).

Conclusion:

GA-SS-PROP offers fast, high-resolution and distortion-free DW images. The generated quantitative maps (f, D and ADC) can provide valuable information on tissue perfusion and diffusion properties simultaneously, which are desirable in many applications, especially in oncology. As a turbo spin-echo based technique, it can be applied in most challenging regions where SS-EPI is problematic.

1. Introduction

Multi-shot techniques have been used to achieve high-resolution diffusion weighted (DW) imaging (Atkinson et al., 2000; Chen et al., 2013; Holdsworth et al., 2008; Pipe et al., 2002; Holdsworth et al., 2019). In this category, turbo spin-echo (TSE) based approaches such as PROPELLER (Periodically Rotated Overlapping ParallEL Lines with Enhanced Reconstruction) can provide high-quality DWI with no distortion (Pipe et al., 2002). Compared with echo-planar imaging (EPI)-based methods, DW PROPELLER has been shown to have superior geometrical fidelity. In addition, the motion artifacts may be corrected by its self-navigation property, as the center of the k-space is repeatedly sampled with a rotating blade trajectory. DW PROPELLER and its variations are now adopted by major vendors. Clinically, due to its robustness to motion and off-resonance artifacts, DW PROPELLER has been used for the diagnosis of lesions in the posterior fossa and brainstem in patients with middle-ear cholesteatomas and acute diffusion abnormalities, as well as in patients with surgical material or with hemorrhage (Attenberger et al., 2009; Jeon et al., 2016; Lehmann et al., 2009; Locketz et al., 2016; Mas-Estelles et al., 2012).

A drawback of DW PROPELLER, which is common to all multi-shot techniques, is the long acquisition time. To improve acquisition efficiency, as well as to reduce specific absorption rate (SAR), gradient echo has been incorporated into the echo train to collect more lines of data per echo train or multiple blades per echo train (Li et al., 2011; Pipe and Zwart, 2006; Srinivasan et al., 2018). For example, X-PROP separates the gradient and spin echoes into individual blades and removes the off-resonance phase, and two to five blades can be acquired within one shot (Li et al., 2011). Despite such improvements, the clinical applications of DW PROPELLER are still limited to DWI trace images within a three-minute time frame (Attenberger et al., 2009; Jeon et al., 2016). Therefore, acceleration of the DW PROPELLER acquisition is greatly de-sired, so that advanced diffusion properties, such as intravoxel incoherent motion (IVIM), can be explored.

An advantageous feature of PROPELLER is that the central k-space is repeatedly sampled. This self-navigated trajectory allows phase and motion correction. It also produces data redundancy. The data redundancy in PROPELLER enables acceleration of data acquisitions by undersampling k-space with fewer shots (Arfanakis et al., 2005), or even one shot. Our previous work has shown that by acquiring one shot per diffusion direction, more diffusion directions can be sampled in a given time and higher angular resolution can be achieved (Wen et al., 2018). The full k-space DWIs may then be recovered by utilizing their similarities in the q-space. By reducing the k-space coverage, we achieve high angular resolution in q-space.

The potential of trading off k-space coverage for q-space resolution with PROPELLER trajectory has been demonstrated, and more can be investigated. For example, in addition to higher angular resolution, which is desirable for diffusion tensor imaging and tractography, acquiring multiple b-values along the same diffusion direction allows for the differentiation of the perfusion compartment, also known as the IVIM, where the signal decay along the b-values follows a biex-ponential decay (Le Bihan, 2019; Le Bihan et al., 1988; Le Bihan and Turner, 1992). IVIM was introduced 30 years ago and is experiencing a remarkable revival for applications throughout the body, especially in oncology, as it can probe the perfusion compartment without contrast agents (Federau et al., 2012; Koh et al., 2011; Li et al., 2017; Sigmund et al., 2011; Kikuchi et al., 2019; Sun et al., 2018). Because the signal evolution along the b-value is smooth, sparsity reconstruction may be incorporated to achieve acceleration, which has not been explored for multiple b-values diffusion acquisition.

Previously, golden-angle rotation has been successfully incorporated with radial trajectory to enable flexible time-resolved acquisitions (Chandarana et al., 2011; Feng et al., 2020; Winkelmann et al., 2007; Feng et al., 2014). Here, we propose to combine PROPELLER with golden-angle rotation, which provides a convenient way for introducing temporal incoherency for the application of sparsity-based reconstruction. The temporal incoherency introduced by golden-angle and the extensive temporal correlations along the time-domain enable the use of sparse reconstruction to recover the high-resolution image. Such a concept can be utilized to accelerate diffusion acquisitions in b-value direction (b-domain) with the rotating blade trajectories as well.

In this work, we proposed a golden-angle single-shot PROPELLER diagram, called GA-SS-PROP, to achieve distortion-free and high-resolution diffusion acquisitions within clinically feasible time. We aimed to demonstrate the use of this scheme to improve the acquisition of diffusion trace images using a fully sampled DW PROPELLER. With this, rather than acquiring each DW image with multiple shots, we achieved comparable image quality by acquiring each DW image with a single shot and sampling at multiple b values. The model of signal evolution in the b-domain was utilized in the sparse reconstruction to recover the full resolution of DW images. As a result, it is possible to reconstruct trace images, apparent diffusion coefficient map (ADC), as well as maps of perfusion fraction (f) and the perfusion-free diffusion coefficient (D). Here, we demonstrated the feasibility of GA-SS-PROP by testing its performance in both simulations and human experiments.

2. Methods

2.1. k-Space trajectory: golden-angle multi-blade acquisition with parallel imaging acceleration

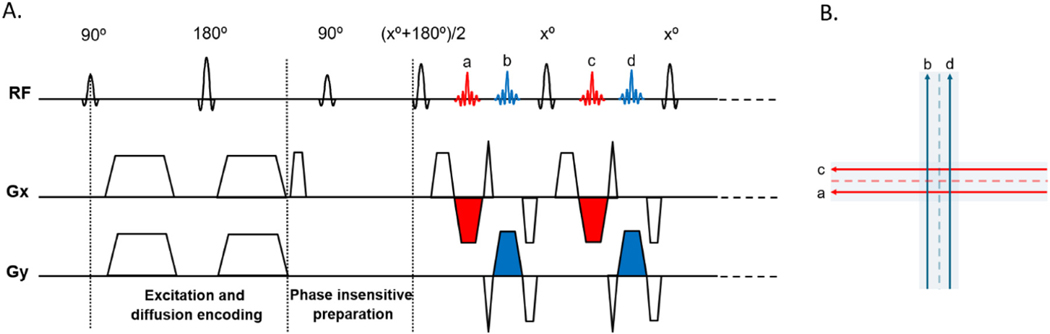
A multi-blade TSE sequence was implemented as shown in Fig. 1. EPI-like readout is used to sample the echoes (e.g. red and blue echoes in Fig. 1A) and generates multiple blades (e.g. two blades in Fig. 1B) for a single k-space, similar to the X-PROP acquisition strategy (Li et al., 2011). The sequence addresses the non-CPMG issue with phase insensitive preparations (Alsop, 1997; Kun Zhou and Cheng, 2018). Specifically, a dephasing gradient is applied in the readout direction right after the diffusion encoding so that each voxel has equal CPMG and non-CPMG components. Then a 90° pulse with specified phase is applied to rotate the non-CPMG component to the longitudinal axis where it will be invisible in the subsequence acquisition. By doing this, low-flip-angle (e.g. x° =120° in Fig. 1) refocusing pulses can be applied, which mitigates the high Specific Absorption Rate (SAR) issue. Parallel imaging (GRAPPA) is used to fill in the missing lines (Fig. 1B dotted lines) with mutual calibration without the need of calibration scans, whereby each blade (e.g. red) serves as the calibration data for its perpendicular pair (e.g. blue) (Li et al., 2011), resulting in a wider blade that is more robust to motion-induced phase error.

Fig. 1.

Multi-blade sequence diagram and corresponding k-space trajectory. A. A two-blade scheme is illustrated. A phase insensitive preparation is applied to push the spin-echo to reach steady state right after the diffusion encoding. By doing this, small-flip-angle (e.g. x° =120°) refocusing can be applied to mitigate the high SAR issue. EPI-like readout gradients are colored in red and blue, corresponding to two perpendicular blades in B. GRAPPA with mutual calibration is used to fill in the missing (dotted) lines.

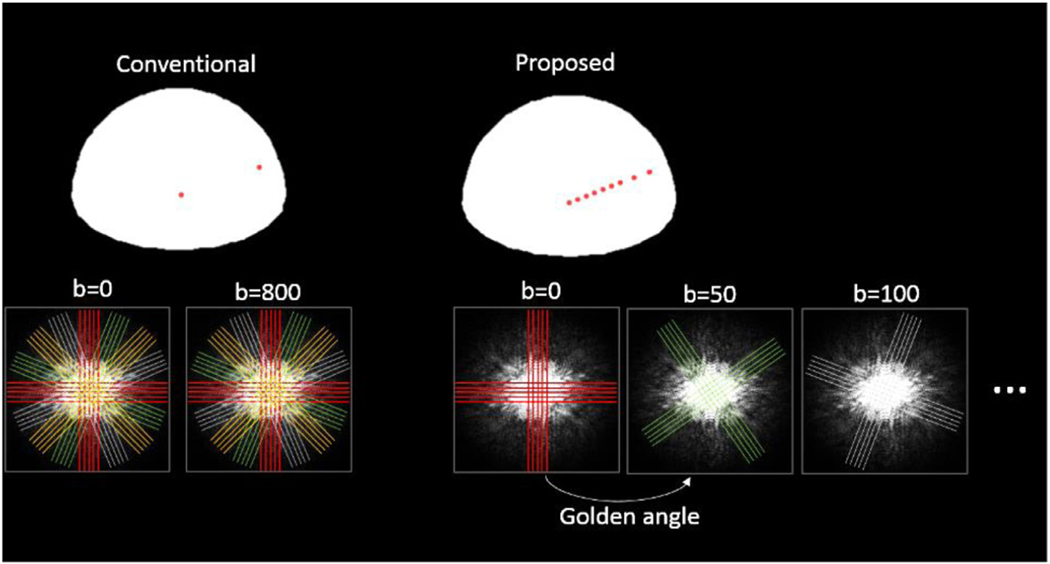
Fig. 2 compares the proposed scheme to the conventional trace image acquisition using the same multi-blade sequence (i.e. two perpendicular blades). Rather than acquiring a full k-space with multiple shots (Fig. 2 left), only one shot is acquired for each b-value in the proposed method. Thus, a number of b-values may be sampled. The two-blade trajectory rotates along the b-values with adjusted golden angle 55.63° (111.25°/2 by considering two perpendicular blades) (Fig. 2 right). The rationale for choosing two blades will be discussed in subsection “Number of blades for each shot” below. The golden angle introduces incoherent artifacts to the acquired images, which can be recovered through sparse reconstruction discussed below.

Fig. 2.

Comparison of conventional fully sampled PROPERLLER scheme with the proposed scheme. In the proposed scheme, only one shot (two-blade) is acquired for each b-value. And multiple shots are placed along multiple b-values and rotate at the golden angle.

2.2. Sparse reconstruction: subspace and locally low-rank constraint (subspace-LLR)

2.2.1. Sparsity in k-b dimensions

Incoherency and sparsity are the two prerequisites for sparsity-based reconstruction. As the blades rotate at the golden-angle, incoherent artifacts are introduced along the b-values direction. Meanwhile, because the signal evolutions along the b-values of each voxel form a smooth curve that follows bi-exponential decay, sparsity can be exploited within this dimension. Similar to the k-t approach used in dynamic MRI and the k-p approach used in parameter mapping, the DWI problem may be considered in the k-b space, where b represents the diffusion weighting dimension along one diffusion direction. Here, we implement sparse re-construction that exploits sparsity in both k-b dimensions by enforcing a combination of an explicit low-rank subspace-constraint and a locally low-rank spatial constraint (subspace-LLR), which is similar to that developed for parameter mapping (Feng et al., 2020; Tamir et al., 2017).

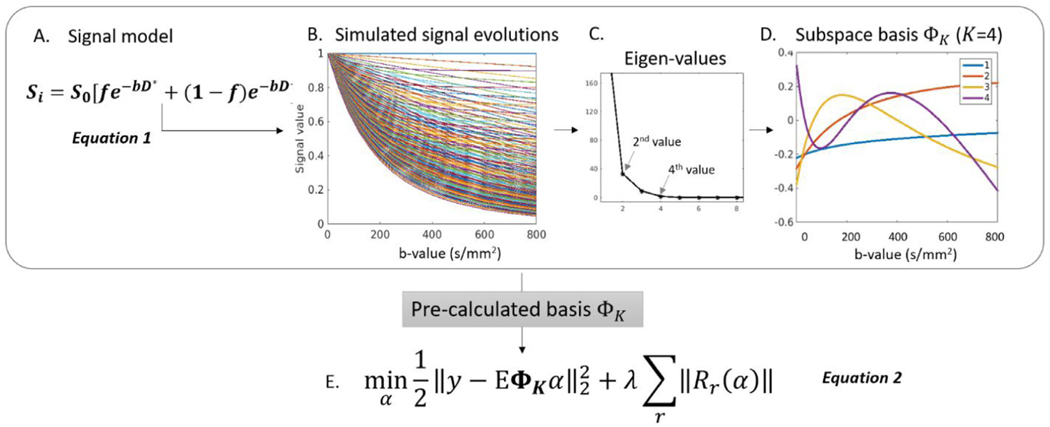
2.2.2. Pre-calculation of subspace basis

The subspace method exploits the sparsity in the temporal space, as dynamic signal curves can be represented in a lower dimensional subspace if the corresponding temporal basis is known in advance. To estimate the temporal basis functions in the k-b dimension, all possible signal evolutions (Fig. 3B) along the b-dimension were first simulated using Equation 1 (Fig. 3A) with physically plausible values for f, D and D^∗ estimated from the histograms of a volunteer data (results not shown). f is the perfusion fraction with a range of [0 0.5] and a step size of 0.05; D is the perfusion-free diffusivity with a range of [400 3000] and a step size of 20 μm²/s, and D^∗ is the pseudo-diffusion coefficient with a range of [8000 20,000] and a step size of 1000 μm²/s. Singular value decomposition was performed to the collection of possible signal evolutions to generate a set of orthogonal bases. The subspace basis Φ_K can be selected as the ones with dominant singular values (Fig. 3B-D). This set of subspace basis Φ_K (Fig. 3D) becomes the sparse representation of all possible signal evolutions and can be used to constrain the reconstructed images using Equation 2 (Fig. 3E). In this case, y is the acquired signal in k-space, α are the K temporal basis coefficients to be solved, and ${\Phi }_{K^{\alpha }}$ forms the temporal signal in the k-b domain. This subspace constraint significantly reduces the dimensionality of the unknown variable (e.g. number of DW images to be solved at different b-values) down to K (e.g., K=4) temporal basis coefficient maps (α) in the optimization problem, where E is the encoding operator incorporating coil sensitivities, Fourier transform, and the undersampling operator. A locally low rank regularization ${\displaystyle \sum _r\Vert R_r(\alpha )\Vert }$ was used to further enforce local sparsity in the image domain, as the set of DW images are rank-deficient when partitioned into local regions. After solving for α, the series of DWIs were computed by projecting through the basis using $x={\Phi }_{K^{\alpha }}$, where trace images, diffusion coefficient (D) and perfusion fraction (f) could be generated.

Fig. 3.

Pre-calculation of basis in the subspace-LLR method. A. The bi-exponential signal model is used to generate a dictionary of signal evolutions using physically plausible values. B. Representative signal evolutions along the b-value generated using equation 1 with different combinations of (f, D, D^∗). C. SVD of the signal evolutions reveal four major eigen values. D. The four corresponding eigen vectors become the pre-calculated basis Φ_K. E. The cost function to be solved in the image reconstruction.

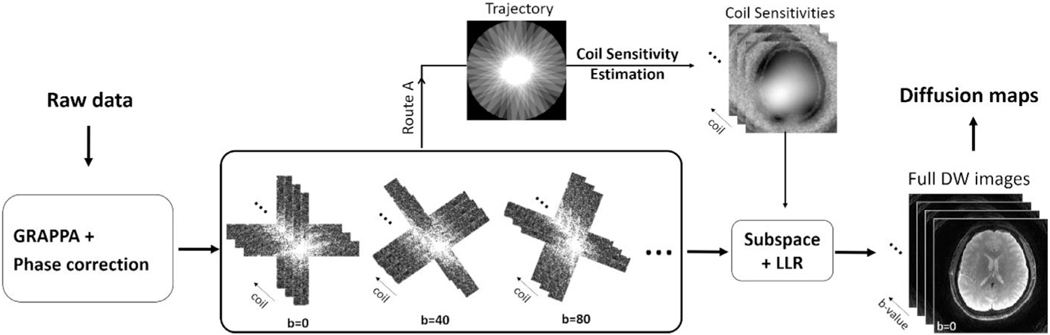
2.2.3. The reconstruction pipeline

The reconstruction pipeline is shown in Fig. 4. Raw k-space data was first reconstructed with GRAPPA and corrected for motion-induced phased errors with a low pass filter, as previously described (Pipe et al., 2002). The blades were first combined to generate coil sensitivity maps (Fig. 4 Route A) and were then fed into the subspace-LLR framework as in Equation 2 (Fig. 3E). A nonuniform fast Fourier transform (NUFFT) operation was used in both the sensitivity estimation and iterative reconstruction. All the reconstructions were implemented in MATLAB (The MathWorks, Natick, MA).

Fig. 4.

The reconstruction pipeline. After GRAPPA and phase correction on each pair of crossing all blades were combined for coil sensitivity estimation (route A). Afterwards, blades at all b-values and coil sensitivity maps were fed into the subspace-LLR to reconstruct the full resolution DW images at all b-values. At the end, quantitative diffusion maps can be produced through model fitting.

2.2.4. Number of blades for each shot

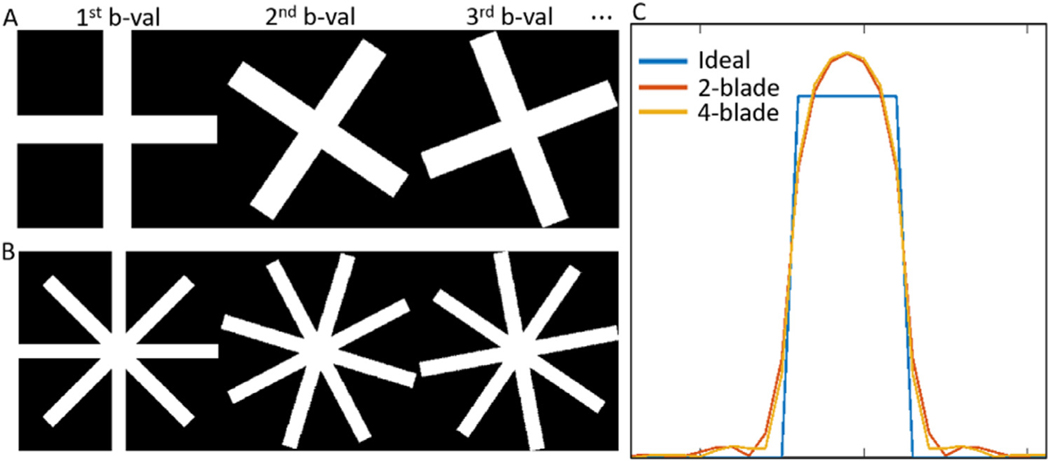
To enable mutual calibration, each blade has to have a perpendicular pair, and the total number of blades has to be even. To choose an optimal number of blades for each shot, we compared the point spread function (PSF) of the system for a two-blade versus a four-blade scheme, while keeping the number of readout lines the same. The input signal containing a uniform patch with a width of 7 in the first temporal coefficient and the resulting PSF is shown in Fig. 5. The two-blade and four-blade scheme yielded similar results, with full-width half max (FWHM) being 6.917 and 6.918, respectively, compared to the ideal FWHM of 7. We chose the two-blade scheme with a wider blade that increases the robustness to both rigid head motion and physiological motion.

Fig. 5.

Comparing point spread function (PSF) for 2-blade (A) and 4-blade (B) trajectories. C. The full width half max values are similar, with 6.917 for the two-blade and 6.918 for the four-blade scheme, compared to an ideal FWHM of 7.

2.2.5. Simulations

To evaluate the performance of the framework, a set of high-quality brain DWI phantom at 1.25 × 1.25 mm² in-plane resolution was developed using a diffusion dataset acquired with a single-shot EPI (SS-EPI) sequence with 50 b-values and 5 averages. Signal model in Equation 1 was used (Fig. 3A) and model coefficients, f, D and D^∗, were derived. The derived coefficients can then be used to generate DWI phantom at an arbitrary b-value. We simulated DW images at 15 b-values ranging from 0 to 800 s/mm² (b = 0, 40, 80, 120, 160, 200, 250, 300, 350, 400, 450, 500, 600, 700, 800) and undersampled the k-space data using the blade trajectories as described above. Realistic coil sensitivity maps were used, and noise was added to each channel at an aggressive noise level of SNR = 5 calculated at b = 0 s/mm². The undersampled DWIs were fed through the subspace-LLR reconstruction pipeline to produce full resolution DWIs. For comparison, the undersampled data were also reconstructed using compressed sensing (CS) with principal component analysis constraint that does not utilize prior knowledge of the bi-exponential signal decay but only enforces sparsity in the k-b dimension (Lustig et al., 2007). To compare the error of the reconstructed maps, the normalized root mean square error (nRMSE) was calculated in the brain region using the following formula: $nRMSE=\frac{1}{\max (DWI)-\min (DWI)}\sqrt{\frac{1}{N}{\displaystyle {\displaystyle \sum _{i=1}^N}(DWI(i)-\widetilde{DWI}(i){)}^2}}$, where DWI is the noise-free fully sampled ground truth; $\widetilde{DWI}$ is the reconstruction, and N is the number of image pixels.

2.2.6. Human experiments

The GA-SS-PROP sequence was performed on a healthy volunteer (23-year-old female) on a 3T system (MAGNETOM Prisma, Siemens Healthcare, Erlangen, Germany) with a 20-channel head/neck coil. Stejskal–Tanner pulsed gradient spin echo was used for diffusion weighting. Fifteen b-values ranging from 0 to 800 s/mm² (the same as in the simulation) along three orthogonal diffusion directions were sampled with one shot per b-value per diffusion direction. Each shot covered an undersampled k-space with two perpendicular blades, with a blade size of 32 × 256 (echo train length=16 and GRAPPA R = 2). Other parameters included 1 × 1 mm² in-plane resolution, TE = 50 ms, TR = 4000 ms, 24 slices with 4 mm thickness, total acquisition time = 3:06. For comparison, a DW PROPELLER with a full k-space coverage was acquired with the match acquisition parameters with an acquisition time of 15:06. SS-EPI with matched resolution was also acquired to compare geometric distortion, with an acquisition of 3:03. The acquisition parameters are listed in Table 1. Written informed consent was obtained from the participant according to procedures approved by the Institutional Committee for the Protection of Human Subjects at Indiana University School of Medicine.

Table 1.

Comparison of acquisition parameters in human experiments.

	GA-SS-PROP	PROPELLER	SS-EPI
Blade size	32 × 256	32 × 256	–
# shot per k-space	1	6	1
TE	49 ms	49 ms	120 ms
TR	4000 ms	4000 ms	1900 ms
Acquisition time	3:06	15:06	3:03

3. Results

3.1. Simulation

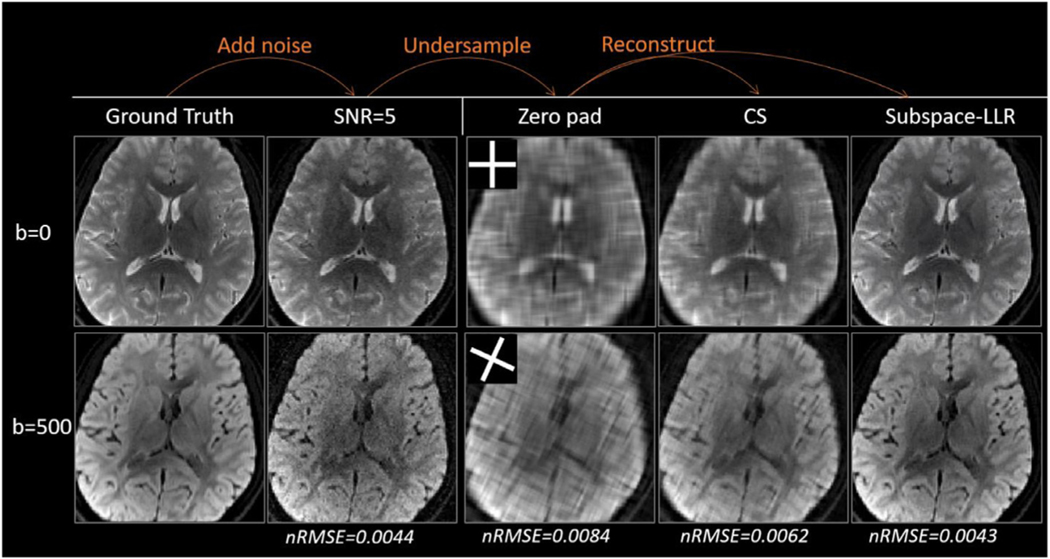
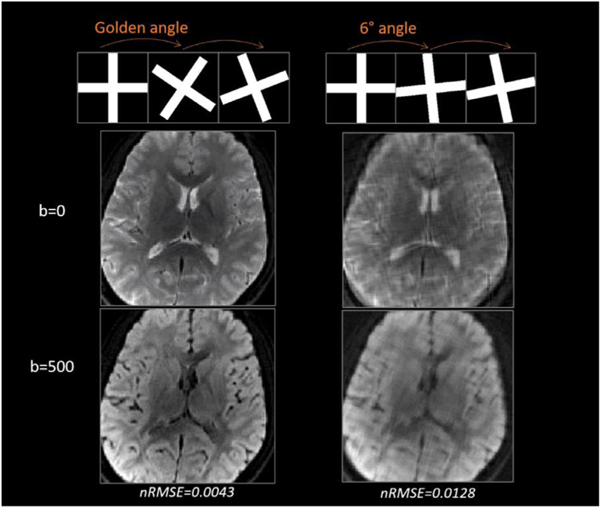
Simulation results are shown in Fig. 6. The GA-SS-PROP trajectory produced incoherent artifacts in zero padded DW images (Fig. 6, 3rd column). CS removed some blurring but not sufficiently (Fig. 6, 4th column). Subspace-LLR restored sharp contrast and similar image quality to the fully sampled images. The “denoise” effect may be appreciated by comparing it to the noise-free DWIs at a higher b-value (i.e. b = 500 s/mm², Fig. 6 lower row). The nRMSE is shown at the bottom, with subspace-LLR having the smallest error compared to the ground truth. As the superior of subspace-LLR has been demonstrated, CS is not compared further in the following context. To demonstrate the advantage of the golden angle over the linear angle with 6° increment, we compared the two trajectories in Fig. 7. The golden-angle rotation (Fig. 7 left panel) results in less blurring in the reconstructed DWIs, with a nRMSE of 0.0043 comparing to 0.0128 in the linear-angle rotation (Fig. 7 right panel). The burring could be due to the fact that when the trajectory rotates at a linear angle, the undersampling artifact becomes less incoherent, and the reconstruction is not able to fully distinguish undersampling artifact from noise and mistakes it for true signals.

Fig. 6.

Comparing CS and subspace-LLR reconstruction on simulated DW images. Noise were first added to produce SNR=5 DW images, which was then undersampled with the blade trajectory to form the blurring images (Zero pad column). The images were reconstructed with CS and subspace-LLR methods (right two columns). nRMSE for each set of DW images were shown at the bottom, where subspace-LLR demonstrated the smallest error.

Fig. 7.

Comparison of golden-angle rotation (left) and linear-angle rotation (i.e. 6°, right). Golden-angle rotation results in less blurring than linear-angle rotation.

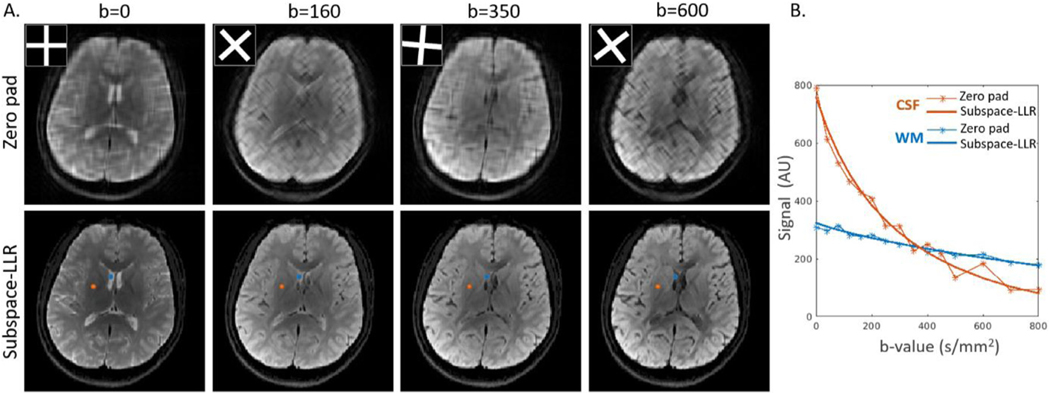
Fig. 8A shows selected DW images before and after subspace-LLR reconstruction. Temporal curves sampled from two voxels (i.e. cerebral spinal fluid (CSF) in orange and white-matter (WM) in blue) are shown in Fig. 8B. Data from the zero-padded images (star-line) deviates from the smooth curve due to noise and undersampling, and the subspace-LLR produces a smooth temporal curve in the reconstructed DWIs by solving the objective function in Equation 2 (Fig. 3E), where each curve is a weighted sum of the subspace basis (Fig. 3D).

Fig. 8.

Simulation results. A. Comparing undersampled (top row, kspace trajectory overlaid on top) and reconstructed (bottom row) DW images at different b-values. B. Temporal curves for two representative voxels in CSF (blue) and WM (orange). AU: arbitrary unit.

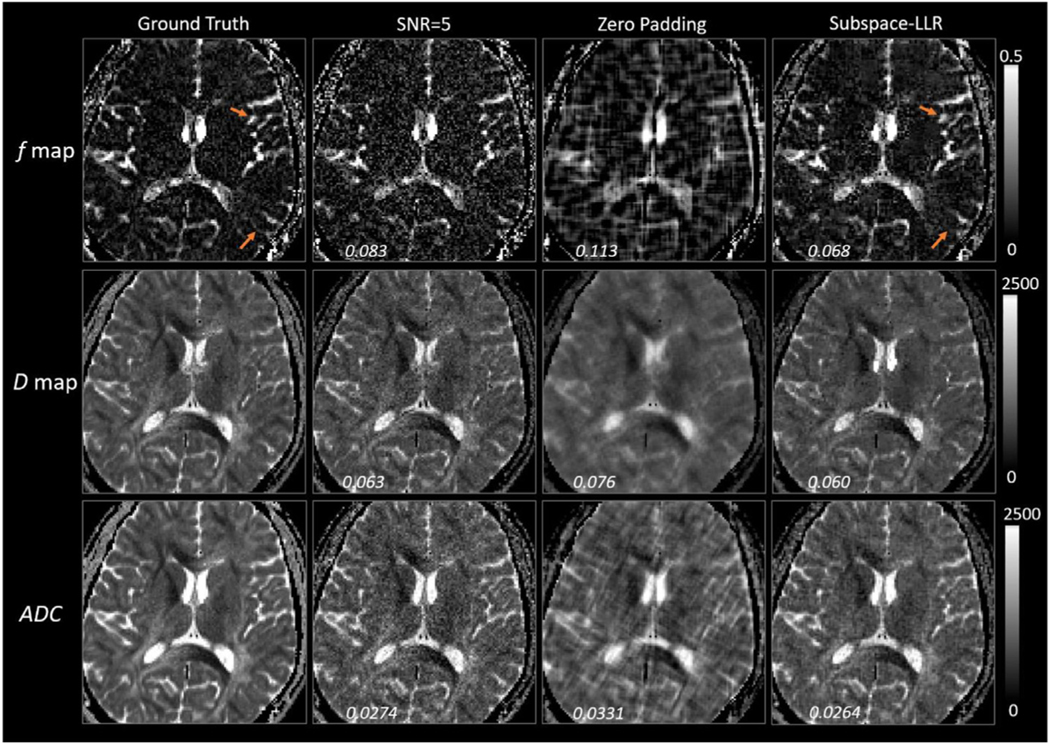
A two-step IVIM fitting (Jalnefjord et al., 2018) was performed on the reconstructed DW images, and f and D maps are compared in Fig. 8, with nRMSE displayed on each map. ADC map is fitted using b = 0 s/mm² and b = 800 s/mm² DW images. In the healthy brain, D^∗ is dependent on cardiac cycle and has limited robustness in non-gated acquisition (Federau et al., 2013; Wu et al., 2015). Thus, it is not discussed in the current context. Subspace-LLR was able to reproduce the diffusion maps (Fig. 8 column 4) with comparable data quality to the ground truth. The nRMSE is comparable to the full resolution maps at SNR=5 (Fig. 8 column 2). Some minor blurring can be observed, which is easier to see in the f map (orange arrows). This could be related to the blurring of the PSF. Comparing D and ADC maps, as expected, the perfusion-free D map has lower signal intensity than ADC in regions rich in blood vessels (e.g. high signal in the f map).

3.2. Human experiments

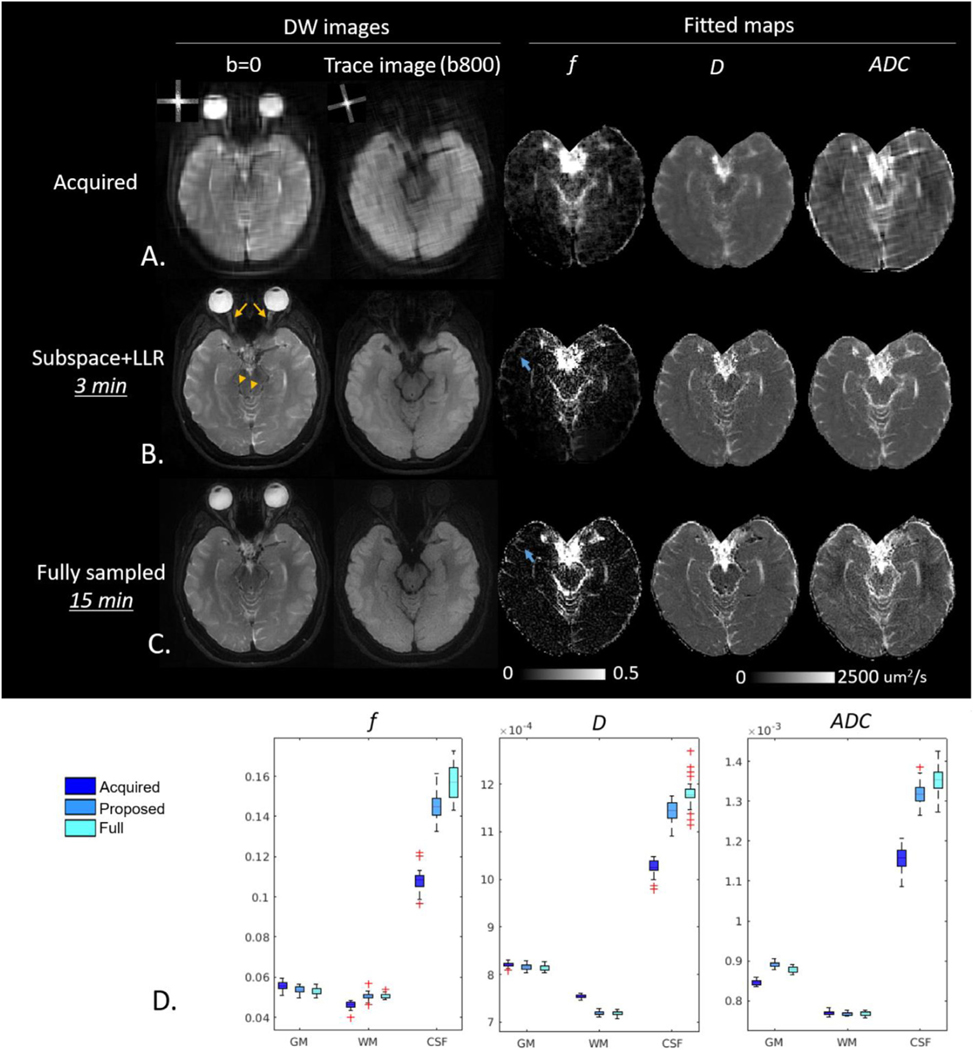
DW images acquired with GA-SS-PROP are shown in Fig. 10A for b = 0 s/mm² and the trace image at b = 800 s/mm², with the corresponding k-space trajectory overlaid on the upper-left corner. The DW images via zero padding (Fig. 10A) showed expected low resolution. The subspace-LLR reconstructed DW images (Fig. 10B) recovered high resolution and fine structural details, such as the wiggly/curved optic nerves (yellow arrows) and blood vessels (yellow arrowheads), whose fidelity can be compared to the fully sampled DW PROPELLER images (Fig. 10C) obtained with the matched diffusion encoding scheme. The f and D maps from bi-exponential fittings and ADC are shown to the right. Similarly, the subspace-LLR method restored high-resolution quantitative maps with sharper contrast. Compared to the fully sampled scheme, some minor blurring may be noticed in the f map (blue arrows), similar to that observed in the simulation. In the ADC maps, the fully sampled data exhibited inhomogeneous appearance and subspace+LLR shows more uniform appearance, likely due to a combination of the denoise effect of the sparse reconstruction and the blurring artifact of the point spread function. Nevertheless, the fitted maps revealed a great mount of structural details that are close to fully sampled images. Comparing the acquisition time, the proposed scheme is five times faster than the fully sampled scheme (Table 1). A quantitative comparison was conducted in gray-matter (GM), WM and CSF between the three methods (Acquired vs. Proposed vs. Full). Mean values of f, D and ADC was extracted for each slice (24 slices in total) and were summarized in the boxplots (Fig. 10D). Comparing to the Acquired, the proposed reconstruction was able to show improvement in all diffusion metrics of all tissue types. The proposed method produced comparable values to the fully sampled scheme in both GM and WM. In CSF, the proposed method demonstrated lower f, D and ADC values (p<0.05). This could be due to the partial volume and blurring effect in the CSF associated with the widening of PSF.

Fig. 10.

Reconstructed DW images and fitted maps. A. Acquired low resolution images with corresponding k-space overlaid on the upper-left corner. B. Reconstructed images restored fine structural details such as the wiggly optical nerve (yellow arrow) and blood vessels (yellow arrowhead). Some minor blurring can be observed in the f map (blue arrows). C. Fully sampled (5-shots, 15 min acquisition time) DW images and fitted maps. D. Boxplot of slice-wise mean values (24 slices = 24 mean values) in GM, WM and CSF. Acquired: acquired undersampled images; Proposed: images reconstructed with proposed subspace+LLR method; Full: fully sampled acquisition.

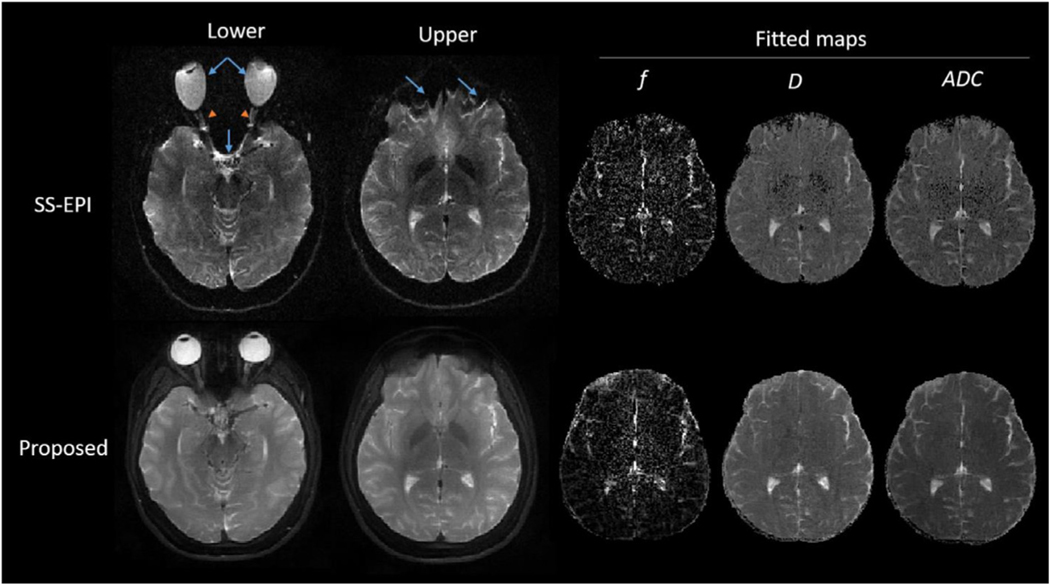
Fig. 11 compares the proposed GA-SS-PROP sequence and SS-EPI. Due to the off-resonance artifact, the stretching (e.g. eyeball) and squeezing (e.g. sinus and lower frontal lobe) of the brain structures is evident in the SS-EPI images (blue arrows), where the structural information was lost (e.g. the curvature of the optic nerves, orange arrow-heads). With a similar acquisition time, the proposed method is immune to the field inhomogeneity and produces distortion-free DW images.

Fig. 11.

Comparison between the proposed GA-SS-PROP sequence and SS-EPI with b-value = 0 s/mm² images at two anatomical locations. Fitted maps of the upper slice are shown to the right. With SS-EPI, the distortion is evident in the lower frontal lobe (blue arrow) and the structures of the optical nerves were lost with minimal diagnostic value (orange arrowheads). With a similar acquisition time, the proposed method produced distortion-free DW images and diffusion maps.

4. Discussion

In this study, we took advantage of the rotating trajectory of PRO-PELLER and modified it to a single-shot acquisition that rotates at the golden angle along different b-values. By utilizing the subspace sparsity of the DW signals in the b-domain, it was possible to reconstruct the full-resolution DW image, as well as the perfusion fraction (i.e. f) and perfusion-free diffusion coefficient (i.e. D). The two maps from the IVIM model have gained increasing attention in recent years and provide valuable information on tissue perfusion and diffusion properties. The full protocol can be performed within a clinically feasible time frame (~3 min) and may be useful for studies throughout the body, especially for oncology. As a TSE based technique, it may be applied in the most challenging regions with high susceptibility, such as spine, breast or liver, etc.

Inheriting from its predecessor, PROPELLER, the proposed multi-blade trajectory has the advantages of self-navigation and robust motion correction. Parallel imaging (i.e. GRAPPA) is incorporated to widen the blade, making the proposed method more robust to the pulsation-related phase variations, and a mutual-calibration technique is implemented that does not require a calibration scan, which further shortens the scan time (Li et al., 2011). Rotating at golden angle, the blade trajectory introduces randomness and incoherency that is essential for sparse reconstruction to be successful. These unique features of the blade trajectory are especially suitable for combining with advanced reconstructions to achieve accelerations for diffusion imaging.

While the present trajectory introduces randomness and has demonstrated promising results in recovering full resolution DW images, minor blurring can be observed. This is related to the blurring of the PSF and can be improved by modifying the trajectory. For example, the crossing blades of a single shot can be placed at golden angle rather than perpendicular. While this eliminates the capability of mutual calibration, it may increase incoherency and therefore less blurring of the PSF. Alternatively, spiral or radial trajectories can also be explored (Knoll et al., 2015; Liu et al., 2004; Trouard et al., 1999; Sarlls et al., 2005; Shi et al., 2015). Nonetheless, results of the current study encourage future studies to explore more sampling trajectories and to combine with different sparse reconstruction schemes to improve the efficacy of diffusion imaging. Future work to evaluate the proposed framework in clinical populations is warranted.

The sparsity being explored in this work is in the b-value dimension, where the signal evolution is smooth following a bi-exponential model. This has a close analogy to MR parameter mapping (Tamir et al., 2017; Zhang et al., 2015; Zhao et al., 2015; Tamir et al., 2019), where signal evolutions follow certain variation models (e.g., exponential decay) and sparsity is exploited in the parameter dimension. Compared to standard compressed sensing reconstruction methods, the subspace-LLR explores sparsity in both the b-domain and spatial domain. It also incorporates prior knowledge of the signal decay model and enforces the smoothness of the reconstructed signal curve. Thus, it is more effective for removing noise and incoherent artifacts compared to model-free sparse reconstruction as demonstrated by our simulation.

In the current work, the subspace basis was estimated from parameters that reflect both normal (GM, WM and CSF) and abnormal brain tissue. For example, the wide range of D [400, 3000] covers tissues with highly restricted water diffusion (e.g. ischemia, tumor) and with less restricted water diffusion (e.g. edema, cysts). Nevertheless, in clinical applications, a good practice is to carefully evaluate and confirm that the subspace estimation matches the targeted tissue/lesion properties to avoid mischaracterization. For example, the subspace basis trained on brain tissue cannot be directly applied to liver. Alternatively, subject-specific subspace basis can be achieved through the low-resolution central k-space region, also known as the data-driven approach (Feng et al., 2020; Zhao et al., 2012). This method may be especially suitable for the proposed blade trajectory, as the central k-space is fully sampled and does not require additional auxiliary data. This data-driven subspace estimation approach will be explored in our future work with clinical populations.

Even though the IVIM is presented here, the proposed framework can be applied to other diffusion imaging models that quantify signal attenuations along b-values, such as diffusion kurtosis imaging (DKI). Herein, we focus on the more clinical-relevant IVIM model that samples fewer diffusion directions (i.e. 3) to explore the performance of the proposed framework. Theoretically, it can be applied to diffusion MRI with higher b-values (e.g. b = 2000 μm²/s) as well, as long as the temporal signal (i.e. along b-values) is smooth and can be described with a proper model (e.g. myelin model).

In conclusion, the proposed framework offers distortion-free, high-resolution DW imaging that provides simultaneous diffusion and perfusion quantification within a clinically feasible time frame. This acceleration is achieved by modifying the multi-shot PROPELLER trajectory to a single-shot golden-angle rotated trajectory that is placed along a number of b-values. The full resolution DW images can then be reconstructed by exploring the sparsity in signal decay along the b-dimension. As a TSE based technique, it can even be used in the most challenging regions with high susceptibility where SS-EPI fails. In addition, as a 2D acquisition technique, it has the flexibility of being combined with simultaneous multi-slice acceleration approaches to further reduce the scan time (Kun Zhou et al., 2017). To the best of our knowledge, it is the first study to combine DW PROPELLER trajectory with sparse reconstruction to accelerate diffusion acquisition along the b-value dimension. The proposed approach could pave the way for future innovative approaches for accelerating diffusion imaging with the blade trajectory (Fig. 9).

Fig. 9.

Evaluation of f and D maps with simulation. Comparing to the ground truth, the proposed method achieved higher resolution and restored fine structural details in both maps, with a nRMSE that is close to the fully sampled images (SNR=5 column).