An assessment of genomic connectedness measures in Nellore cattle

Abstract

An important criterion to consider in genetic evaluations is the extent of genetic connectedness across management units (MU), especially if they differ in their genetic mean. Reliable comparisons of genetic values across MU depend on the degree of connectedness: the higher the connectedness, the more reliable the comparison. Traditionally, genetic connectedness was calculated through pedigree-based methods; however, in the era of genomic selection, this can be better estimated utilizing new approaches based on genomics. Most procedures consider only additive genetic effects, which may not accurately reflect the underlying gene action of the evaluated trait, and little is known about the impact of non-additive gene action on connectedness measures. The objective of this study was to investigate the extent of genomic connectedness measures, for the first time, in Brazilian field data by applying additive and non-additive relationship matrices using a fatty acid profile data set from seven farms located in the three regions of Brazil, which are part of the three breeding programs. Myristic acid (C14:0) was used due to its importance for human health and reported presence of non-additive gene action. The pedigree included 427,740 animals and 925 of them were genotyped using the Bovine high-density genotyping chip. Six relationship matrices were constructed, parametrically and non-parametrically capturing additive and non-additive genetic effects from both pedigree and genomic data. We assessed genome-based connectedness across MU using the prediction error variance of difference (PEVD) and the coefficient of determination (CD). PEVD values ranged from 0.540 to 1.707, and CD from 0.146 to 0.456. Genomic information consistently enhanced the measures of connectedness compared to the numerator relationship matrix by at least 63%. Combining additive and non-additive genomic kernel relationship matrices or a non-parametric relationship matrix increased the capture of connectedness. Overall, the Gaussian kernel yielded the largest measure of connectedness. Our findings showed that connectedness metrics can be extended to incorporate genomic information and non-additive genetic variation using field data. We propose that different genomic relationship matrices can be designed to capture additive and non-additive genetic effects, increase the measures of connectedness, and to more accurately estimate the true state of connectedness in herds.

Introduction

Genetic connectedness is a statistical measurement that allows reliable comparisons of the genetic values across management units (MU) by capturing the linkage among herds. The genetic values of animals from different MU (e.g., contemporary groups, farms, and herds) can be ranked using best linear unbiased prediction (BLUP). However, the accuracy of these comparisons depends on the degree of connectedness among MU: the higher the connectedness, the more reliable the comparison. Genetic connectedness has traditionally been calculated through pedigree-based methods (Lewis et al., 1999b; Kuehn et al., 2007a); however, these methods may underestimate connectedness in production systems such as the beef cattle industry, where commercial herds are poorly registered and multi-sire mating is practiced (Caires et al., 2012; Barbosa et al., 2013; Tonussi et al., 2017; Cavani et al., 2018). A lack of connectedness occurs: when the MU are genetically isolated (or semi-isolated) or there is limited sharing of genetic material; with the use of an incomplete numerator relationship matrix based on poor pedigree data (Carneiro et al., 2001); and with poor use of artificial insemination (AI). Genomic data are expected to more accurately estimate the relationship between individuals using information from genetic markers, such as single nucleotide polymorphisms (SNP), by measuring covariance among relatives and distant relatives previously ignored by a pedigree-based method (Habier et al., 2007).

Yu et al. (2017) evaluated the utility of genome-based connectedness in mice and cattle and noted that genomic relatedness could improve the extent of genetic connectedness measures compared with the pedigree when additive inheritance was assumed. The gain in connectedness measures was later shown to be associated with increased prediction accuracy based on cross-validation (Yu et al., 2018). Genetic connectedness studies were subsequently extended to account for non-additive genetic effects (Momen and Morota, 2018). Those authors performed a computer simulation and found the increased measures of connectedness using additive and non-additive genomic relationship matrices under non-additive gene action. Collectively, those studies demonstrated that genomics can be used to enhance measures of connectedness. However, evaluations of genetic connectedness from field data remain limited.

In Brazil, cattle herds are often separated by large distances, and the rates of AI are low. A recent study by the Brazilian Association of Artificial Insemination (ASBIA, 2019) showed that only 16% of Brazilian dams are inseminated, with just a few farms available to measure expensive traits that require specific techniques or tests, such as postmortem beef quality traits.

The fatty acid (FA) profile of beef is a trait of interest due to its association with cardiovascular disease in humans (Mensink and Katan, 1992). According to Lawrie (2006), C14:0 is one of the most predominant saturated FA in cattle meat, which interferes with hepatic low-density lipoprotein receptors and consequently increases the amount of circulating low-density lipoprotein cholesterol (Grundy and Denke, 1990; Katan et al., 1994; Katan et al., 1995; Sacks and Katan, 2002). Considering the growing consumer demand for protein sources with a healthy lipid profile, several strategies have been applied to identify and manage the FA profile of beef (Faucitano et al., 2008; Liu et al., 2010; Aboujaoude et al., 2016; Berton et al., 2016; Chiaia et al., 2017).

Non-additive genetic variation for FA has been previously reported in cattle. For example, Malau-Aduli et al. (1998, 2000) reported significant dominance effects in Jersey, Limousin, and Jersey × Limousin crossbred cattle. Li et al. (2012) detected significant additive and dominant effects for 19 individual FA in commercial beef steers. Kramer et al. (2016) identified epistatic interactions associated with FA concentrations in Angus cattle. Thus, the use of connectedness metrics including additive and non-additive gene effects may help to improve the quality of genetic value comparisons in breeding programs.

To date, few connectedness studies have been performed in Brazil (Carneiro et al., 2001; Pegolo et al., 2012), and the impact of genomic relatedness on connectedness measures in Nellore cattle has not been reported. Assessing connectedness statistics through genomic information may be useful for designing breeding programs and effectively linking units to improve the quality of across unit genetic evaluations, which in turn enhance the genetic improvement of Brazilian beef cattle. Therefore, the aim of this study was to investigate the extent of genomic connectedness measures in Nellore cattle by applying additive and non-additive relationship matrices, and to estimate variance components considering additive, dominance, and epistatic effects for myristic acid (C14:0).

Material and Methods

Data

Ethics statement

This study was approved by the ethics committee in the Faculdade de Ciências Agrárias e Veterinárias, Universidade Estadual Paulista, Jaboticabal, São Paulo, Brazil.

Fatty acid profile data set

The data set included animals from seven farms located in the southeast, northeast, and mid-west of Brazil, which are part of three beef cattle breeding programs: DeltaGen (F1 [n = 200], F2 [n = 22], F3 [n = 80]); Paint (F4 [n = 190], F6 [n = 292], F7 [n = 51]); and Nelore Qualitas (F5 [n = 90]). These seven farms only collect samples postmortem for analysis of beef quality traits due to the costs of collecting these phenotypes.

The GPS location of each farm was provided by the respective breeding program. The FA profile phenotypes were obtained for Nellore bulls with an average age of 24 mo. The methodology used to determinate FA profiles was consistent with that used in a previous study by Lemos et al. (2016). We analyzed myristic acid (C14:0) because of its importance to human health and high content in animals from feedlots (Zock et al., 1994). The pedigree included 427,740 animals born between 1977 and 2011. A total of $n$ = 925 animals having C14:0 phenotype were genotyped using 777,962 SNP (Illumina, San Diego, CA). Following the removal of markers with a minor allele frequency less than 0.05, 505,367 SNP remained for further analysis. Missing genotypes were imputed using allele frequency estimates from a binomial distribution from the data. The seven farms were treated as MU.

Connectedness statistics

Genetic connectedness statistics are mostly defined as a function of the inverse of the coefficient matrix, which can be obtained from Henderson’s mixed model equations (MME) (Henderson, 1984). In this study, we assessed genome-based connectedness across management units by applying the prediction error variance of difference (PEVD) (Kennedy and Trus, 1993) and coefficient of determination (CD) (Laloë, 1993).

Prediction error variance of difference

Prediction error variance (PEV) was obtained by fitting the following standard linear mixed model:

$${\displaystyle \begin{array}{l}{\displaystyle \mathit{y}=\mathit{X}\mathit{b}+\mathit{Z}\mathit{u}+\epsilon ,}\end{array}}$$

where $\mathit{y}$ is a vector of phenotypes, $\mathit{X}$ is an incidence matrix of systematic effects including management units, $\mathit{b}$ is a vector of systematic effects (contemporary group including animals born in the same farm, year, and from the same management group at yearling, and age at slaughter as linear covariate), Z is an incidence matrix relating individuals to phenotypic records, u is a vector of random additive genetic effects, and $\epsilon$ is a vector of residuals. The joint distribution of random effects for this model is

$${\displaystyle \begin{array}{l}{\displaystyle \left(\begin{array}{l}y\\ u\\ ϵ\end{array}\right)\sim N[\left(\begin{array}{c}Xb\\ 0\\ 0\end{array}\right),\left(\begin{array}{ccc}\mathit{Z}\mathit{K}{\sigma }_u^2{\mathit{Z}}^{\prime }+\mathit{I}{\sigma }_{ϵ}^2& {\displaystyle \mathit{Z}\mathit{K}{\sigma }_u^2}& {\displaystyle \mathit{I}{\sigma }_{ϵ}^2}\\ \mathit{K}{\sigma }_u^2{\mathit{Z}}^{\prime }& {\displaystyle \mathit{K}{\sigma }_u^2}& {\displaystyle 0}\\ \mathit{I}{\sigma }_{ϵ}^2& {\displaystyle 0}& {\displaystyle \mathit{I}{\sigma }_{ϵ}^2}\end{array}\right)],}\end{array}}$$

where ${\sigma }_u^2$ is the additive genetic variance, ${\sigma }_e^2$ is the residual variance, and K is one of the positive (semi) definite relationship matrices defined later.

The inverse of MME coefficient matrix of Henderson (1984) is represented as

$${\displaystyle \begin{array}{l}{\displaystyle \begin{array}{ll}{\mathit{C}}^{-1}& ={\left[\begin{array}{ll}{\mathit{X}}^{\prime }\mathit{X}& {\displaystyle {\mathit{X}}^{\prime }\mathit{Z}}\\ {\mathit{Z}}^{\prime }\mathit{X}& {\displaystyle {\mathit{Z}}^{\prime }\mathit{Z}+{\mathit{K}}^{-1}\lambda }\end{array}\right]}^{-1}\\ & =\left[\begin{array}{ll}{\mathit{C}}^{11}& {\displaystyle {\mathit{C}}^{12}}\\ {\mathit{C}}^{21}& {\displaystyle {\mathit{C}}^{22}}\end{array}\right],\end{array}}\end{array}}$$

where $\lambda$ is the ratio of ${\sigma }_e^2/{\sigma }_u^2$. The PEV for $i$ th individual (${\widehat{u}}_i$) is written as

$${\displaystyle \begin{array}{l}{\displaystyle \begin{array}{ll}PE{V}_i& =Var({{\displaystyle \widehat{u}}}_i-u_i)\\ & =Var(u_i|{{\displaystyle \widehat{u}}}_i)\\ & =Var({{\displaystyle \widehat{u}}}_i|u_i)\\ & ={\mathit{C}}_{ii}^{22}{\sigma }_{ϵ}^2,\end{array}}\end{array}}$$

where ${\mathit{C}}_{ii}^{22}$ represents the $i$th diagonal element of the ${\mathit{C}}^{22}$ coefficient matrix. Then, the PEVD of genetic values between individuals from different MU (Kennedy and Trus, 1993) is given by

$${\displaystyle \begin{array}{l}{\displaystyle \begin{array}{ll}PEVD({{\displaystyle \widehat{u}}}_i-{{\displaystyle \widehat{u}}}_j)& =[PEV({{\displaystyle \widehat{u}}}_i)+PEV({{\displaystyle \widehat{u}}}_j)-2PEC({{\displaystyle \widehat{u}}}_i,{{\displaystyle \widehat{u}}}_j)]\\ & =({\mathit{C}}_{ii}^{22}-{\mathit{C}}_{ij}^{22}-{\mathit{C}}_{ji}^{22}+{\mathit{C}}_{jj}^{22}){\sigma }_{ϵ}^2\\ & =({\mathit{C}}_{ii}^{22}+{\mathit{C}}_{jj}^{22}-2{\mathit{C}}_{ij}^{22}){\sigma }_{ϵ}^2,\end{array}}\end{array}}$$

where $ii$ and $jj$ refer to the diagonal elements of ${\mathit{C}}^{22}$ matrix, corresponding to the $i$th and $j$th individuals, respectively, and the off-diagonal elements of ${\mathit{C}}^{22}$ are denoted by $ij$. $PE{C}_{ij}$ is the prediction error covariance between the errors of genetic values, which is the off-diagonal element of the PEV matrix. Smaller PEVD indicates that the individuals are more connected.

The average PEVD between individuals across two MU was defined as follows:

$${\displaystyle \begin{array}{l}{\displaystyle PEV{D}_{i^{\prime }{j}^{\prime }}=\frac{1}{n_{i^{\prime }}.n_{j^{\prime }}}{\displaystyle \sum _{i\in i^{\prime }}}{\displaystyle \sum _{j\in j^{\prime }}}PEV{D}_{ij},}\end{array}}$$

where $i$ is an animal in MU $i^{\prime }$, $j$ is an animal in MU $j^{\prime },$  $n_{i^{\prime }}$and $n_{j^{\prime }}$ represent the total number of records in $i^{\prime }$ and $j^{\prime }$ units, and the sum of all pairwise differences between two units is $\sum _{i\in i^{\prime }}\sum _{j\in j^{\prime }}PEV{D}_{ij}$.

Coefficient of determination

CD is defined by scaling the inverse of the coefficient matrix by corresponding coefficients from the relationship matrix, in other words, CD accounts for the reduction of connectedness due to relationship variability between individuals under comparison. The extent of CD ranges between 0 and 1, with larger values indicating increased connectedness.

A pairwise CD between individuals $i$ and $j$ is given by (Laloë et al., 1996)

$${\displaystyle \begin{array}{l}{\displaystyle C{D}_{ij}=1-\lambda \frac{{\mathit{C}}_{ii}^{22}+{\mathit{C}}_{jj}^{22}-2{\mathit{C}}_{ij}^{22}}{{\mathit{K}}_{ii}+{\mathit{K}}_{jj}-2{\mathit{K}}_{ij}},}\end{array}}$$

where $K_{ii}$ and $K_{jj}$ are the $i$th and $j$th diagonal elements of K.

The CD between two units can be scaled using the individual average PEVD with the average pairwise relationship differences across individuals to compute the individual average CD as described by Yu and Morota (2020)

$${\displaystyle \begin{array}{l}{\displaystyle C{D}_{i^{\prime }{j}^{\prime }}=1-\lambda \frac{\frac{1}{n_{i^{\prime }}.n_{j^{\prime }}}{\displaystyle \sum _{i\in i^{\prime }}}{\displaystyle \sum _{j\in j^{\prime }}}({\mathit{C}}_{ii}^{22}+{\mathit{C}}_{jj}^{22}-2({\mathit{C}}_{ij}^{22}))}{\frac{1}{n_{i^{\prime }}.n_{j^{\prime }}}{\displaystyle \sum _{i\in i^{\prime }}}{\displaystyle \sum _{j\in j^{\prime }}}({\mathit{K}}_{ii}+{\mathit{K}}_{jj}-2{\mathit{K}}_{ij})}}\end{array}}$$

$${\displaystyle \begin{array}{l}{\displaystyle =1-\frac{\frac{1}{n_{i^{\prime }}.n_{j^{\prime }}}{\sigma }_e^2{\displaystyle \sum _{i\in i^{\prime }}}{\displaystyle \sum _{j\in j^{\prime }}}({\mathit{C}}_{ii}^{22}+{\mathit{C}}_{jj}^{22}-2({\mathit{C}}_{ij}^{22}))}{\frac{1}{n_{i^{\prime }}.n_{j^{\prime }}}{\sigma }_u^2{\displaystyle \sum _{i\in i^{\prime }}}{\displaystyle \sum _{j\in j^{\prime }}}({\mathit{K}}_{\mathit{i}\mathit{i}}+{\mathit{K}}_{\mathit{j}\mathit{j}}-2{\mathit{K}}_{\mathit{i}\mathit{j}})}}\end{array}}$$

$${\displaystyle \begin{array}{l}{\displaystyle 1-\frac{\frac{1}{n_{i^{\prime }}.n_{j^{\prime }}}{\displaystyle \sum _{i\in i^{\prime }}}{\displaystyle \sum _{j\in j^{\prime }}}PEV{D}_{ij}}{\frac{1}{n_{i^{\prime }}.n_{j^{\prime }}}{\sigma }_u^2{\displaystyle \sum _{i\in i^{\prime }}}{\displaystyle \sum _{j\in j^{\prime }}}({\mathit{K}}_{\mathit{i}\mathit{i}}+{\mathit{K}}_{\mathit{j}\mathit{j}}-2{\mathit{K}}_{\mathit{i}\mathit{j}})}}\end{array}}$$

$${\displaystyle \begin{array}{l}{\displaystyle =1-\frac{{\displaystyle \sum _{i\in i^{\prime }}}{\displaystyle \sum _{j\in j^{\prime }}}PEV{D}_{ij}}{{\sigma }_u^2{\displaystyle \sum _{i\in i^{\prime }}}{\displaystyle \sum _{j\in j^{\prime }}}({\mathit{K}}_{ii}+{\mathit{K}}_{jj}-2{\mathit{K}}_{ij})}.}\end{array}}$$

Genomic kernel relationship matrices

Parametric relationship matrices

The extent of connectedness measures depends on the choice of relationship matrix K. In this study, we evaluated six K matrices. The pedigree-based relationship matrix ($\mathit{K}=\mathit{A}$) was calculated to obtain the additive numerator relationship, reflecting the probability that alleles are identical by descendent inherited from a common ancestor (Wright, 1922). The diagonal element $a_{ij}$, which is the numerator relationship coefficient between two animals $i$ and $j$ for a population of $n$ individuals is equal to $1+F_j$, where $F_j$ is the inbreeding coefficient of animal $i$.The off-diagonals of this matrix are twice the kinship coefficients and are equivalent to the numerators of Wright’s correlation coefficients (Wright, 1922; Malécot, 1948). The A matrix among 925 animals was constructed using the pedigree records of 427,740 animals.

The genomic relationship matrix ($\mathit{K}=\mathit{G}$) was used to capture the genomic similarity among individuals, estimating the proportion of the genome between individuals that is identical by state. The G matrix was obtained as a function of the allele content including elements of 0, 1, and 2 representing the copies of reference alleles according to VanRaden (2008) as follows:

$${\displaystyle \begin{array}{l}{\displaystyle \mathbf{G}={\mathbf{W}}_{\mathbf{a}}{\mathbf{W}}_{\mathbf{a}}^{{}^{\prime }}/\left(2{\displaystyle \underset{k=1}{{\displaystyle \sum ^m}}}{p}_k(1-p_k)\right),}\end{array}}$$

where ${\mathbf{W}}_{\mathbf{a}}$ is a centered incidence matrix taking values $0-2p_k$ for zero copies of the reference allele; $1-2p_k$ for one copy of the reference allele; and $2-2p_k$ for two copies of the reference allele. Here $p_k$ is the allele frequency at SNP $\mathrm{k}=1,\dots ,\mathrm{m}$.

To capture dominance genetic effects, we constructed a dominance relationship matrix ($\mathit{K}=\mathit{D}$) according to Vitezica et al. (2013):

$${\displaystyle \begin{array}{l}{\displaystyle \mathbf{D}={\mathbf{W}}_{\mathbf{d}}{\mathbf{W}}_{\mathbf{d}}^{{}^{\prime }}/{\displaystyle \underset{k=1}{{\displaystyle \sum ^m}}}{(2p_k(1-p_k))}^2,}\end{array}}$$

where ${\mathbf{W}}_{\mathbf{d}}$ is the dominance marker incidence matrix, taking values of $-2{p_k}^2$ for zero copies of the reference allele; $2p_k{(1-p_k)}^2$for one copy of the reference allele; and $-2{(1-p_k)}^2$ for two copies of the reference allele.

By combining the aforementioned G and D, we considered the following scenarios: pedigree (A), additive (G), additive and dominance ($\mathit{G}+\mathit{D}$), additive and additive by additive epistasis ($\mathit{G}+\mathit{G}\mathrm{\#}\mathit{G}$), and additive, dominance, and additive by additive epistasis ($\mathit{G}+\mathit{D}+\mathit{G}\mathrm{\#}\mathit{G}$), where $\mathrm{\#}$ denotes the Hadamard product (Henderson, 1985). For a multi-kernel approach, a single kernel matrix was derived by weighting each of these kernels by its relative contribution to the total genetic variation according to Momen and Morota, (2018).

Gaussian kernel

In a Gaussian kernel ($K$  =  $GK)$, the relationship between individuals is defined as distances on the Euclidean space, creating genetic relatedness in terms of spatial distance (de los Campos et al., 2010). The relationship between a pair of individuals $i$ and $j$ with their genotype vectors ${\mathbf{w}}_i\in (0,1,2)$ and ${\mathbf{w}}_j\in (0,1,2)$ is given by

$${\displaystyle \begin{array}{l}{\displaystyle \mathbf{G}\mathbf{K}({\mathbf{w}}_i,{\mathbf{w}}_j)=\exp (-\mathrm{\theta }{d}_{ij}^2)}\end{array}}$$

$${\displaystyle \begin{array}{l}{\displaystyle ={\displaystyle \underset{k=1}{{\displaystyle \prod ^m}}}\mathrm{e}\mathrm{x}\mathrm{p}(-\mathrm{\theta }{(w_{ik}-w_{jk})}^2),}\end{array}}$$

where $d_{ij}=\sqrt{{(w_{i1}-w_{j1})}^2+\cdots +{(w_{ik}-w_{jk})}^2+\cdots +{(w_{im}-w_{jm})}^2}$ is the Euclidean distance between two individuals, and $\mathrm{\theta }$ is a positive bandwidth parameter that controls the overall smoothness of the kernel function. A small Euclidean distance between two individuals means that their genotypes are similar in state, or in other words, that they have a strong relationship. The parameter $\mathrm{\theta }$ is what controls the extent of genomic similarity between individuals. As $\mathrm{\theta }$ increases, the kernel approaches zero (i.e., local kernel), and smaller $\mathrm{\theta }$ produces entries closer to 1, in other words, two individuals match perfectly (i.e., global kernel) (Morota et al., 2013). We employed a kernel averaging approach (de los Campos et al., 2010) by integrating two kernel matrices ($GK1$ and $GK2$) using two extreme values of θ, so the mean of the off-diagonals elements in each kernel were 0.2 and 0.8, respectively. The averaged GK was obtained by

$${\displaystyle \begin{array}{l}{\displaystyle GK=\frac{{\sigma }_{GK1}^2}{{\sigma }_{GK1+}^2{\sigma }_{GK2}^2}GK1+\frac{{\sigma }_{GK2}^2}{{\sigma }_{GK2+}^2{\sigma }_{GK1}^2}GK2,}\end{array}}$$

where ${\sigma }_{GK1}^2$ and ${\sigma }_{GK2}^2$ are variance components attached to kernels $\mathit{G}\mathit{K}\mathbf{1}$ and $\mathit{G}\mathit{K}\mathbf{2}$, respectively. A BLUP model coupled with a Gaussian kernel matrix is known as reproducing Hilbert spaces regression (Morota and Gianola, 2014).

Throughout this study, we used R statistical computing environment (R Development Core Team, 2019) to estimate variance components and connectedness metrics with the following packages: the BGLR package (Pérez and de Los Campos, 2014) to estimate variance components and the GCA package (Yu and Morota, 2020) to compute connectedness measures.

Results

Heritability estimates

Descriptive statistics and genetic parameter estimates for C14:0 are presented in Table 1 for parametric kernel matrices. In this study, we estimated narrow-sense heritability ($h^2$) accounting for additive effects only ($\mathit{K}\mathbf{=}\mathit{A}$ or $\mathit{G}$) and broad-sense heritability ($H^2$) accounting for additive, dominance, and epistasis ($\mathit{K}$=$\mathit{G}\mathbf{+}\mathit{D}\mathbf{,}\mathit{G}\mathbf{+}\mathit{G}\mathbf{\#}\mathit{G}\mathbf{,}$ or $\mathit{G}\mathbf{+}\mathit{D}\mathbf{+}\mathit{G}\mathbf{\#}\mathit{G}$).

Table 1.

Descriptive statistics and heritability estimates for each gene action scenario

			h2		H2
Trait	N	Mean± SD	A	G	G+D	G+G#G	G+D+G#G
C14:0	925	10.26± 0.16	0.142 (0.095)	0.268 (0.081)	0.390 (0.089)	0.420 (0.076)	0.462 (0.092)
Genetic Variance			${\sigma }_u^2=0.120(0.083)$	${\sigma }_g^2=0.225(0.073)$	${\sigma }_g^2=0.201(0.067)$    ${\sigma }_d^2=0.150($0.056)	${\sigma }_g^2=0.183(0.064)$    ${\sigma }_{g\mathrm{\#}g}^2=0.175($0.069)	${\sigma }_g^2=0.155(0.059)$    ${\sigma }_d^2=0.123($0.049)  ${\sigma }_{g\mathrm{\#}g}^2=0.135($0.053)
Residual Variance			${\sigma }_e^2=0.725(0.086)$	${\sigma }_e^2=0.615(0.071)$	${\sigma }_e^2=0.550(0.078)$	${\sigma }_e^2=0.494($0.085)	${\sigma }_e^2=0.481(0.080)$

¹The concentration of fatty acids is expressed as a percentage of total fatty acid methyl esters (FAME). A: pedigree. G: additive genomic kernel relationship matrix. G + D: additive × dominance genomic kernel relationship matrix. G + G#G: additive × epistasis genomic kernel relationship matrix. G + D + G#G: additive × dominance × epistasis genomic kernel relationship matrix. ${\sigma }_u^2:$ additive genetic variance; ${\sigma }_g^2:$ additive genomic variance; ${\sigma }_d^2$: dominance genomic variance; ${\sigma }_{g\mathrm{\#}g}^2$: additive by additive epistasis genomic variance; ${\sigma }_e^2:$ residual variance. Posterior standard errors are shown in the parentheses.

Narrow- and broad-sense heritability estimates for C14:0 ranged from 0.142 (±0.095) to 0.462 (±0.092). Heritability estimates were lower when using the pedigree relationship matrix compared with the other relationship matrices, likely because of incomplete pedigree data. The $h^2$ estimate from $G$ was approximately two-fold higher than that from $A$. Moreover, the inclusion of dominance ($\mathit{G}\mathbf{+}\mathit{D}$) and epistatic effects ($\mathit{G}\mathbf{+}\mathit{G}\mathbf{\#}\mathit{G}$ and $\mathit{G}\mathbf{+}\mathit{D}\mathbf{+}\mathit{G}\mathbf{\#}\mathit{G}$) increased the heritability estimates. These findings suggest that C14:0 may be controlled by additive as well as non-additive gene action.

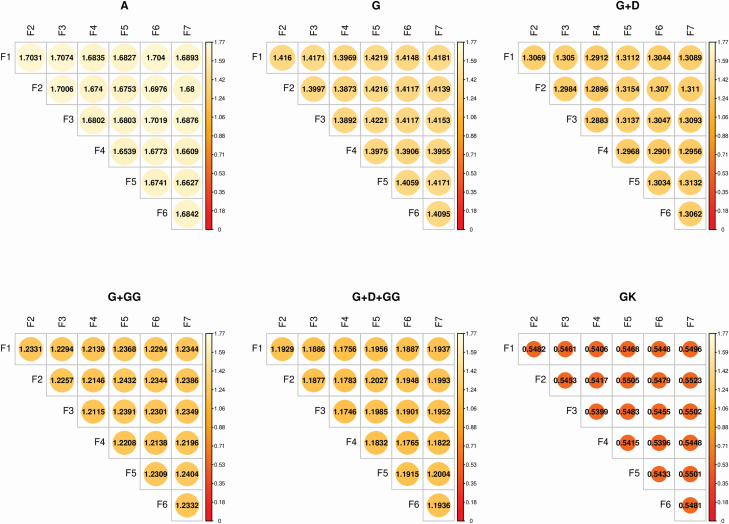
Prediction error variance of difference

Figure 1 shows the PEVD estimates across MU derived from $\mathit{A}$, $\mathit{G}$,$\mathit{G}\mathbf{+}\mathit{D}$,$\mathit{G}\mathbf{+}\mathit{G}\mathbf{\#}\mathit{G}$, and $\mathit{G}\mathbf{+}\mathit{D}\mathbf{+}\mathit{G}\mathbf{\#}\mathit{G}$ for C14:0. The smaller the PEVD, the higher the connectedness. The smallest PEVD connectedness measures were found in $A$, ranging from 1.654 to 1.707. When comparing A with G, enhanced connectedness measures were observed by reduced PEVD (1.387–1.422). The MU were more connected when genomic information was used. The inclusion of dominance ($\mathit{G}\mathbf{+}\mathit{D}$) moderately enhanced the PEVD across MU, with estimates ranging from 1.288 to 1.315. Accounting for additive and additive epistasis ($\mathit{G}\mathbf{+}\mathit{G}\mathbf{\#}\mathit{G}$) in the model marginally increased the measures of connectedness. Including additive, dominance, and additive by additive epistasis ($\mathit{G}\mathbf{+}\mathit{D}\mathbf{+}\mathit{G}\mathbf{\#}\mathit{G}$) resulted in the highest connectedness estimates among the parametric kernel relationship matrices. The use of GK significantly increased estimates of genetic connectedness across all MU. Overall, A yielded the least connected measures, while GK produced most connectedness estimates that were considered to be less connected.

Figure 1.

Individual average PEVD for C14:0. A: pedigree kernel relationship matrix. G: additive genomic kernel relationship matrix. G + D: additive and dominance genomic kernel relationship matrices. G + G#G: additive and epistasis genomic kernel relationship matrices. G + D + G#G: additive and dominance and epistasis genomic kernel relationship matrices. GK: Gaussian kernel relationship matrix.

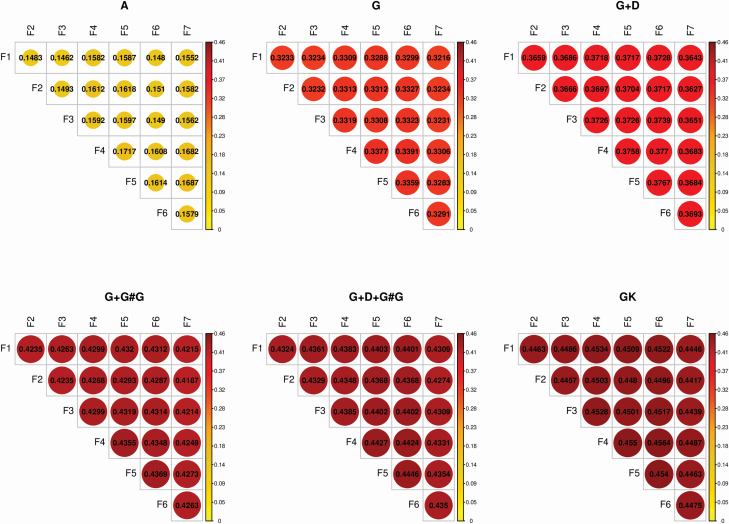
Coefficient of determination

Individual average CD for each of the six scenarios is presented in Figure 2. The higher the CD, the higher the connectedness, and a similar pattern was found as reported for PEVD. The largest measured CD (0.456) was obtained with GK, and the smallest CD (0.146) was obtained with A. The MU presented low levels of connectedness in A, in which the highest estimate was 0.171. Compared to the pedigree-based method, genetic relatedness inferred from G increased the estimates of genetic connectedness across MU, and this trend was enhanced when dominance ($\mathit{G}+\mathit{D}$) and epistasis ($\mathit{G}+\mathit{G}\mathrm{\#}\mathit{G}$) were included. Combining additive, dominance, and epistasis in $\mathit{G}+\mathit{D}+\mathit{G}\mathrm{\#}\mathit{G}$ resulted in greater measures of connectedness than any of the parametric relationship kernel matrices. The estimates of CD for $\mathit{G}+\mathit{D}+\mathit{G}\mathrm{\#}\mathit{G}$ ranged from 0.427 to 0.445. GK presented the highest CD estimates, ranging from 0.442 to 0.456. These results demonstrated the importance of accounting for additive, dominance, and epistasis when the trait is also controlled by non-additive gene action.

Figure 2.

Individual average CD for C14:0. A: pedigree kernel relationship matrix. G: additive genomic kernel relationship matrix. G + D: additive and dominance genomic kernel relationship matrices. G + G#G: additive and epistasis genomic kernel relationship matrices. G + D + G#G: additive and dominance and epistasis genomic kernel relationship matrices. GK: Gaussian kernel relationship matrix.

Connectedness within and across breeding programs

Farms F1–F3 belonged to the DeltaGen breeding program. F1 and F3 farms were found to be the most connected across all scenarios. Farms F4, F6, and F7 belonged to the Paint breeding program. Although all MU presented similar connectedness values for CD, F4 and F6 were found to be the most connected, whereas F7 was well connected with the other two MU. Finally, we investigated the connectedness of the MU between the three different breeding programs and found that only one MU from Nelore Qualitas (F5) was adequately connected with the other MU. This pattern also appeared when we analyzed MU from DeltaGen and Paint, suggesting that these three breeding programs are connected, probably because of the use of AI in recent years.

Discussion

This study presents genome-based connectedness estimates in Nellore cattle using phenotype and genotype samples of commercial herds from the three breeding programs. The phenotype studied in this analysis is not routinely measured in breeding programs. Phenotypic information relating to the C14:0 trait was only available for a small number of contemporary groups in the MU, which could limit the data connection.

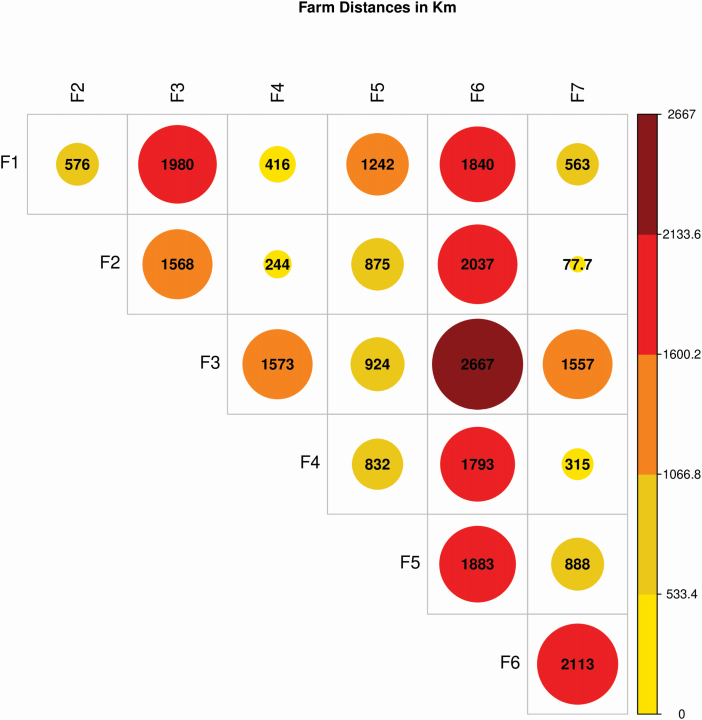
In Brazil, the beef cattle industry is concentrated in two main regions: the southeast and the mid-west. The recent expansion of agriculture has introduced animal husbandry to new regions. Figure 3 shows the distance (in kilometers) between the farms evaluated in our study. Farms F1–F3 are part of the DeltaGen Program and are spread across three regions (mid-west, southeast, and northeast). F1 and F3 are the most distant units in this program. Within the Nellore Paint program, farms F4, F6, and F7 are located in the mid-west and southeast regions in Brazil. The distance between F4 and F6 is the longest, despite being located in the same region.

Figure 3.

Farm distances in Km. F1—Dourados (MS); F2—Valparaíso (SP); F3—Cotegipe (BA); F4—Água Clara (MS); F5—Goianésia (GO); F6—Juruena (MT); F7—Piacatu (SP).

Overall, considering each farm apart from its breeding program, F4 was the closest to any other farm, while F6 was the most distant. The average distance between two farms was 1,188 km. The extent of connectedness may be partially explained by the geographic position of each farm, since Brazilian herds consist of many subpopulations isolated by geographical distance, limiting the sharing of genetic material across MU. Overall, we did not find a clear relationship between connectedness and distance. Thus, geographical location alone does not explain the extent of connectedness.

The degree of connectedness reflects the reliability of comparisons between animals of different MU (Kennedy and Trus, 1993; Tosh and Wilton, 1994; Hanocq et al., 1999; Carneiro et al., 2001; Mathur et al., 2002; Roso et al., 2004). Low connectedness implies that the reliability of genetic value comparisons and animal rankings across MU are not sufficiently reliable (Lewis et al., 1999a; Lewis and Simm, 2000; Kuehn et al., 2008). Theoretically, the extent of connectedness may be of less concern (Fernando et al., 1983; Kennedy and Trus, 1993; Fries and Roso, 1997). Kennedy and Trus (1993), and Tosh and Wilton (1994) reported that disconnected MU may not lead to biased predictions if the genetic values of the base animals are randomly and identically distributed throughout the population. However, this is less true for field populations such as beef cattle in Brazil, because of genetic selection, drift, limited use of AI, and low phenotyping rates in hard-to-measure traits, which have an impact on the genetic means and variance component estimates of the MU (Clément et al., 2001; Tosh and Wilton, 1994; Kuehn et al., 2007b; Tarrés et al., 2010).

Estimates of genetic parameters

Connectedness is often used to design or evaluate the effectiveness of breeding programs prior to phenotyping. However, phenotypic information enters the derivation of connectedness through heritability or the ratio of variance components ($\lambda$). In the present study, we evaluated the FA C14:0 (myristic acid). In general, the narrow-sense heritability estimates for individual FA profiles in the Longissimus thoracis muscle of beef cattle are low to moderate (Tait et al., 2007; Cesar et al., 2014; Lemos et al., 2016; Feitosa et al., 2017), ranging from 0.17 to 0.64. Our estimates for myristic acid using A (0.141) were lower than those reported by Tait et al. (2007), of 0.23, in Angus cattle, but were closer when G (0.274) was used in our study. Using a population of Nellore Cattle, Aboujaoude et al. (2016) reported a genomic $h2$ estimate of 0.25. Cesar et al. (2014) and Feitosa et al. (2017) reported genomic $h2$ estimates of C14:0 in Nellore Cattle of 0.17 and 0.25, respectively.

In the current study, we evaluated six relationship matrices using pedigree and genomic data accounting for additive and non-additive genetic variation into the kernel relationship matrices. We found that the heritability estimates from A were the lowest. In the beef cattle industry, the poor records for herds are problematic, especially for beef quality traits evaluated after slaughter. This affects both the measurement relationships and the genetic parameter estimates (Fouilloux et al., 2008a). Here, approximately 55% of records contained no sire information. The percentage of animals with known sires in each farm was F1 = 13%, F2 = 72%, F3 = 81.25%, F4 = 57.36%, F5 = 63.15%, F6 = 27.39%, F7 = 100%, and for a total 413/925 animals in the data set. This data set is composed by commercial herds, and in Brazil, most farms are under a multiple service sires (MS) mating system, which consists of groups of cows clustered with several bulls in the same paddock during a riding season (Cardoso and Tempelman, 2003). MS improves the conception rate (Lunstra and Laster, 1982), but results in an uncertain paternity scenario. Therefore, incomplete pedigree data due to MS negatively affect the accuracy of genetic evaluations (Cardoso and Tempelman, 2003).

In the breeding programs in our study, the mating season begins with AI in all dams. However, if the dam is not pregnant, the MS mating system is applied. The bulls used in this system are usually from the same farm, and they only produce one generation of progeny. The calf born from the MS mating system is slaughtered because of uncertain paternity. These calves are considered to have unreliable genetic merit, which means that they are not candidates for breeding, while allowing phenotypes to be obtained from the slaughtered animals. The use of genomic information can enhance the feasibility of genetic evaluation and increase the prediction accuracy of these novel traits in the beef cattle industry.

The use of SNP, which capture molecular similarity and Mendelian sampling, determines relationships between individuals at the genomic level, recovering information missing in the pedigree. Cesar et al. (2014) first reported genomic heritability estimates for FA in Nellore cattle and showed that SNP panels are a promising tool for the genetic improvement of Nellore cattle in Brazil, mainly because of the effective cost strategy for their application in breeding programs. We found that the heritability estimates from G were larger compared to those from A, recovering a greater proportion of additive genetic variance. Our observations are consistent with those of Ishii et al. (2013) in Japanese Black cattle and Saatchi et al. (2013) in US Angus cattle.

It is also critical to account for dominance and/or epistatic variation to optimize breeding designs, such as mate allocation. Several animal studies (Serenius et al., 2006; Sun et al., 2014; Moghaddar and van der Werf, 2017; Joshi et al., 2018; Ebrahimi et al., 2019) have reported that dominance heritability is often significantly greater than zero, and its inclusion in prediction models could improve performance in those studies. We observed dominance and epistatic variance for C14:0, suggesting that C14:0 may be controlled by both additive and non-additive genetic variation.

Connectedness statistics

Because of missing pedigree data in the present study, connectedness statistics using the numerator relationship matrix resulted in the lowest connectedness estimates, indicating that A may provide an incorrect picture of connectedness for C14:0 in the population studied. In contrast, G consistently enhanced the measures of connectedness. The results from G highlight how genomic data can help us to better observe the true state of connectedness, particularly when pedigree data are less reliable. This supports the findings of Yu et al. (2017), who reported that genomic relatedness inferred from SNP increases the estimates of genetic connectedness across MU compared to estimates of pedigree information. As noted by Yu et al. (2017, 2018), the availability of genomic information provides an opportunity to improve the quality of genetic value comparisons and revisit a number of critical questions related to connectedness.

The increased interest in non-additive variation (Wolak and Keller, 2014; Varona et al., 2018) suggests that it may be possible to account for such variation in connectedness studies. Momen and Morota (2018) demonstrated that connectedness metrics can be extended to incorporate non-additive genetic variation of complex traits. They showed an increase up to 25% in the capture of connectedness using additive and non-additive genomic kernel relationship matrices when the trait of interest is controlled by non-additive gene action. Our study investigated how the inclusion of such variation could impact connectedness metrics. Increased estimates of connectedness were observed when dominance and epistatic parametric kernels were included. The non-parametric relationship matrix (GK) models higher-order epistatic gene action by taking the Hadamard product between the G matrices when SNP were coded in an additive manner (Jiang and Reif, 2015). In our study, GK was better than all parametric approaches, highlighting the usefulness of GK for incorporating non-additive gene action. Nii et al. (2006) first reported the presence of epistatic quantitative trait loci for perirenal C14:0 in wild boars, and was later reported by Uemoto et al. (2009) on chromosome 16 in swine.

In livestock, the inclusion of dominance effects can be justified by the use of semen from a few genetically superior bulls and reproductive biotechnologies (such as multiple ovulation, embryo transfer, and in vitro fertilization). Consequently, the number of full sibling progenies increases, which increases the relationships within and between generations, as well as dominance genetic relationships (VanRaden, 1992). The inclusion of such effects was reported by Varona and Misztal (1999), who noted that the inclusion of dominance effects into genetic evaluations enables the determination of specific combinations for mating schemes, and the separation of additive variation from the rest, especially in populations containing many full-sibs in their pedigree. Hayes and Miller (2000) and Ishida and Mukai (2004) stated that ignoring non-additive genetic variance in breeds could result in biased predictions of genetic values, which would affect the animal’s classification as well as national and international comparisons.

Fouilloux and Laloë (2001) developed the criterion of admission to the group of connected herds (CACO) method to compare the average CD values of all herds and to cluster them. This method was applied by Pegolo et al. (2012) in Brazilian Nellore cattle using registered animal data from elite herds (National Association of Breeders and Researchers, ANCP, Ribeirão Preto, Brazil). They recorded weight after 210 d ($h2$ = 0.25) to investigate the trajectory of connectedness from 1999 to 2003 and from 2004 to 2008. They found moderate estimates of pedigree-based connectedness and attributed the increase in connectedness to the use of AI, which increased 47% with the semen sales in that period. According to ASBIA (2011), only 10% of dams were inseminated at reproductive age. AI affects the measurement of genetic connectedness among herds (Fouilloux et al., 2008) and strongly influences the quality of pedigree information.

AI can accelerate genetic improvement in a population as it allows semen from animals with a higher genetic value to be utilized, which are not normally available for use in natural matings. It also increases the number of offspring per sire. Despite the growing use of AI, most commercial beef cattle programs in Brazil still use unproven sires for natural mating. In addition, programs that use AI still need a bull to mate with their dams in the case of AI failure, which is common on commercial farms where animals are destined for slaughter. As the MU evaluated in this study were not part of consolidated breeding programs, the use of AI was more than 50% of that in all farms, because of known paternity scenarios needed for the genetic evaluations. Thus, the use of the MS mating system in these programs incurs the costs of maintaining a non-pregnant cow in the herd.

Changes in connectedness levels reported by Pegolo et al. (2012) showed that herd descriptors, such as the number of animals in the herd, the number of sires used in the herd, the percentage of connecting sires, the percentage of progeny from connecting sires, and the percentage of calves with unknown sires, cannot fully explain how the herds are connected. The use of different types or combinations of relationship matrices to those used in our study may be a viable approach to understand the complexity of genetic connectedness in livestock species.

Here, we describe the first application of genomic connectedness in Brazilian Nellore cattle. This study shows how genomic information can increase connectedness measures when pedigree information is not complete due to multiple sire systems. Collectively, through the use of genomics and by accounting for non-additive gene action, we can better reflect signals of connectedness not captured by pedigree-based counterparts.

Conclusions

Genetic connectedness plays a key role in the quality of genetic value comparisons across MU. We used PEVD and CD to assess genomic connectedness measures in Nellore cattle field data, accounting for the presence of non-additive gene action. Our findings show that genomic information can capture connectedness signals that may be missed from the pedigree, providing a more precise picture of connectedness. Working with novel traits can be challenging when they are hard to measure, because only a few breeding programs possess the infrastructure and logistics to collect phenotypes such as the FA profile of meat. We show that it is possible to capture connectedness signals from samples of different farms within and between different breeding programs using a specific phenotype (C14:0) with low heritability. We also confirm that the use of AI, even though still used at low levels in the country (16%), has an important role in connecting herds. Furthermore, we observed that the use of additive and non-additive genomic kernel relationship matrices can enhance the capture of connectedness measures compared to purely additive counterparts.

Glossary

Abbreviations

$H^2$

broad-sense heritability

$h^2$

narrow-sense heritability

${\sigma }_d^2$

dominance genomic variance

${\sigma }_e^2$

residual variance

${\sigma }_g^2$

additive genomic variance

${\sigma }_{g\mathrm{\#}g}^2$

additive by additive epistasis genomic variance

${\sigma }_u^2$

additive genetic variance

A

numerator relationship matrix

BLUP

best linear unbiased prediction

C14:0

myristic acid

CD

coefficient of determination

FA

fatty acid

G

genomic relationship matrix

G+D

additive and dominance relationship matrix

G+D+G#G

additive, dominance, and additive by additive relationship matrix

GK

Gaussian kernel relationship matrix

MME

mixed model equations

MU

management units

PEV

prediction error variance

PEVD

prediction error variance of difference

SNP

single nucleotide polymorphisms

Conflict of interest statement

The authors declare no real or perceived conflicts of interest.