A methodology to investigate the impact of image distortions on the radiation dose when using magnetic resonance images for planning

Abstract

We developed a novel technique to study the impact of geometric distortion of magnetic resonance imaging (MRI) on intensity-modulated radiation therapy treatment planning.

The measured 3D datasets of residual geometric distortion (a 1.5 T MRI component of an MRI linear accelerator system) was fitted with a second-order polynomial model to map the spatial dependence of geometric distortions. Then the geometric distortion model was applied to computed tomography (CT) image and structure data to simulate the distortion of MRI data and structures. Fourteen CT-based treatment plans were selected from patients treated for gastrointestinal, genitourinary, thoracic, head and neck, or spinal tumors. Plans based on the distorted CT and structure data were generated (as the distorted plans). Dose deviations of the distorted plans were calculated and compared with the original plans to study the dosimetric impact of MRI distortion.

The MRI geometric distortion led to notable dose deviations in five of the 14 patients, causing loss of target coverage of up to 3.68% and dose deviations to organs at risk in three patients, increasing the mean dose to the chest wall by up to 6.19 Gy in a gastrointestinal patient, and increases the maximum dose to the lung by 5.17 Gy in a thoracic patient.

1. Introduction

In recent years, there has been increasing utilization of magnetic resonance imaging (MRI) for treatment guidance in the radiation oncology community (Lambert et al 2011, Pötter et al 2011, Lindegaard et al 2013). Compared with computed tomography (CT) images, MRI provides excellent soft tissue contrast without exposing the patient to ionizing radiation (Weygand et al 2016). Additionally, the ability of MRI to visualize other aspects of cellular and organ functions can provide additional information about the levels of hypoxia (Ling et al 2002), diffusion (Dirix et al 2008), chemical exchange (Rivlin et al 2013), cellularity (Dörr et al 2002), and chemical composition of tissues (Wang et al 2013) which can be used for treatment response assessment and adaptive treatment. Adaptive radiation therapy based on frequent MR functional imaging could potentially change many aspects of current clinical practice in radiation oncology. Furthermore, systems that combine MRI with a linear accelerator (linac) are already or soon to become available commercially (e.g. ViewRay, Cleveland, OH, USA; Elekta, Stockholm, Sweden). These integrated MRI-guided radiation therapy systems promise the future of increased precision in radiation delivery to the tumor while reducing toxicity to normal tissue.

However, using MRI for treatment guidance has certain caveats. For instance, one such limitation is that MR images can suffer from geometric distortion. Several previous investigations have studied the geometric distortion (Mizowaki et al 1996, Wang et al 2004, Baldwin et al 2007, 2009, Stanescu et al 2010, Crijns et al 2011, Sun et al 2015).The geometric distortion of MRI has two main causes. The first is the system-related distortion (Walker et al 2016). It is mainly caused by the nonlinearities of the gradient field and the inhomogeneity of the B₀ field due to hardware limitation and imperfection. This kind of distortion typically increases with increasing distance from the MRI isocenter. The second is related to patient susceptibility. This type of distortion arises from variations in the magnetic properties of different tissues in the patient (e.g. tissue and air boundary), which cause local field non-uniformity and the consequential local image distortion. This results in local distortion, which is often called patient-related or susceptibility-related distortion. Some vendor-supplied distortion correction algorithms can reduce—but not completely eliminate—system-related distortion. There are also techniques to minimize susceptibility-related distortion by adjusting MRI acquisition sequences and parameters, but this source of distortion cannot be completely eliminated either. Consequently, there are always some residual geometric distortions in MR images and the impact of these limitations on dosimetry must be carefully evaluated. In this manuscript, the imaging distortion refers to the residual distortion exhibited in the clinical MRI, which is the remaining geometric distortion after applying the vendor-provided geometric distortion correction algorithm.

There are numerous previous studies that have evaluated MRI-based treatment planning (Fransson et al 2001, Chen et al 2004, Wang et al 2008, Jonsson et al 2010, Rank et al 2013). Most of these studies have focused on the accuracy of tissue density corrections for MRI-based treatment planning. However, the dosimetric impact of geometric distortion in MRI on treatment planning has not been well studied. This is partially attributable to the difficulties of performing such studies in patients because the precise magnitude of MRI geometric distortion is difficult to assess, given that distortion is dependent upon many factors, including the specific scanner system, pulse sequences, and acquisition parameters. More importantly, there is no ‘non-distorted’ MRI ‘gold standard’ for comparison.

In this study, we presented a technique to quantitatively study the dosimetric impact of MRI geometric distortion in patients. A model was developed to simulate the geometric distortion of the MRI system based on the 3D geometric measurement data provided by the vendor. The distortion was applied to the clinical CT data and structure set of each patient. Based on the calculated isocenter position using the distorted CT data, the plan was optimized using the distorted structure set. The final dose was calculated using the original undistorted CT data for each patient.

2. Methods

2.1. Model of the 3D geometric distortion

Residual geometric distortion datasets were obtained for a 1.5 T Philips MRI, which is the MRI component of the Elekta’s MRI-linac system. A 3D T1-weighted incoherent gradient echo sequence (T1 FFE) was used to obtain the image distortion of a rigid phantom. The 3D Geometric QA Phantom consists of 1932 oil capsules (markers) in well-defined locations. The markers cover a cylindrical volume (diameter 500 mm, length 330 mm) around the isocenter; the marker spacing is 25 mm × 25 mm × 55 mm.

Sequence parameters were as follows: field of view = 560 × 560 × 200 mm³, volume = 2 × 2 × 2 mm³, matrix = 280 × 280 × 100, echo time/repetition time = 4.6/11 ms, flip angle = 30°, bandwidth = 433 Hz/pixel, and scan time = 3.22 min. Methods for correction of gradient nonlinearity are well established (Glover et al 1986, Janke et al 2004), and typically utilize spherical harmonics to describe the field of each logical gradient axis for conventional cylindrical-bore scanners.

Vendor-provided geometric distortion correction was applied on the system during the geometric distortion data acquisition, which corrects the in-plane and through-plane distortions originating from the gradient field non-linearity.

In order to model the residual distortion after vendor-provided geometric distortion correction, a second-order polynomial model was used to fit the geometric distortion data, as expressed in equation (1), in which X, Y, and Z were defined as the transverse, longitudinal, and vertical directions, respectively.

$$ϵ\left(x,y\right)=a{x}^2+bxy+c{y}^2+dx+ey+f.$$ (1)

For the second-order polynomial model in equation (1), parameters (a, b, c, d, e, f) were estimated by minimizing the mean square error between the model and the measured results for all slices in Z direction. Distortion between two slices was estimated by interpolation.

The polynomial model was constructed in 2D slices for all measured planes in the Z direction. After the models were created, distortions at the measured points were generated and compared with the measured data for evaluation of each dataset.

2.2. Patient selection and dose delivery techniques

Next, we evaluated treatment plans from 14 randomly selected patients who had been treated for tumors at one of five anatomic sites: gastrointestinal tract, genitourinary area, thoracic area, head and neck, or spine. All patients had been treated with intensity-modulated radiation therapy (IMRT), delivered as step-and-shoot IMRT or volumetric modulated arc therapy (VMAT). Patients received hypofractionated, standard fractionated, or hyperfractionated IMRT, stereotactic body radiation therapy (SBRT), or spine stereotactic radiosurgery (SSRS). Dose prescriptions, treatment sites, delivery techniques, and other details are summarized in table 1. Beam energy was 6 MV for all treatments. The treatment system was either a Clinac 2100 or a TrueBeam system (both from Varian Medical Systems, Palo Alto, CA, USA). The slice thicknesses for the simulation CT scans are shown in table 1.

Table 1.

Patient and treatment characteristics.

Patient no.	Tumor site	Prescription, Gy/fraction	Total dose, Gy	Technique	CT slice thickness, mm
1	Gastrointestinal tract (stomach)	1.8/25	45	Step and shoot	3
2	Gastrointestinal tract (liver)	4.5/15	67.5	Step and shoot	3
3	Gastrointestinal tract (liver)	12.5/4	50	Step and shoot	3
4	Genitourinary tract (prostate and seminal vesicle)	2.0/39	78	VMAT	3
5	Genitourinary tract (prostate)	2.0/39	78	VMAT	3
6	Thoracic area (lung)	12.5/4	50	Step and shoot	2.5
7	Thoracic area (lung)	2.4/30	72	Step and shoot	2.5
8	Head and neck (nasopharynx)	2.12/33	70	VMAT	3
9	Head and neck (right neck)	9.0/5, QOD	45	VMAT	1
10	Head and neck (left occiput)	8.5/5, QOD	42.5	VMAT	1
11	Spine (T9-T10)	4.0/10	40	Step and shoot	1
12	Spine (T12)	24/1	24	Step and shoot	1
13	Spine (L3)	24/1	24	Step and shoot	1
14	Spine (T11)	24/1	24	Step and shoot	1

Abbreviations: CT, computed tomography; VMAT, volumetric modulated arc therapy; QOD, every other day.

2.3. Target delineation and margins

Target and organ-at-risk (OAR) contours for each patient were generated based on clinical CT image. All contours were reviewed and approved by the treating radiation oncologists. The typical margin from the clinical treatment volume to the planning target volume (PTV) (Landberg et al 1999) was 3 mm. For head and neck SBRT (patients 9 and 10), the margin could be reduced to 0–1 mm to avoid important OARs such as the optic nerve and the carotid artery. For patients who underwent SSRS (patients 12–14), the gross tumor volume and clinical treatment volume were typically used instead of the PTV owing to the localization of the disease.

2.4. Imaging distortion and treatment planning

The distortion model was applied to the clinical CT images and contours using the same imaging isocenter to simulate the residual geometric distortion created by the MRI system after vendor-provided geometric distortion correction. To simulate treatment, we used the same beam angles (for step and shoot IMRT), arc numbers (for VMAT), collimator angles, dose prescriptions, and optimization constraints as were used for the original treatment plan for each patient. The distorted treatment isocenter was calculated in the clinical CT image based on the distorted CT image. Using the geometric distortion error at the treatment isocenter, we shifted the treatment isocenter to the distorted position in the clinical CT dataset. Using the distorted isocenter and structures, we optimized the treatment plan. Then, using the original treatment isocenter and structures (no distortion), the dose was recalculated using the collapsed cone convolution algorithm (Ahnesjö 1989) for each patient. We refer to this treatment plan optimized on the distorted structures as the distorted plan. For all patients, the distorted plan was re-optimized at least six times to reach the converged results. The dose grid was 3 mm × 3 mm × 3 mm. For comparison, the original clinical plans were considered the ‘control’ plans to evaluate the deviations caused by the MRI geometric distortion.

Dose-volume histograms for the control plans and the distorted plans were calculated by the Pinnacle treatment planning system and used to evaluate differences between the two sets of plans. Dose uniformity and dose coverage of the treatment targets were evaluated in terms of conformity index (CI) and target coverage (TC), as defined in equations (2) and (3) (Landberg et al 1999):

$$\text{CI}=\frac{\text{TV}}{\text{PTV}},$$ (2)

$$\text{TC}=\frac{{\text{PTV}}_{100}}{\text{PTV}},$$ (3)

in which TV is the treatment volume enclosed by a reference isodose line (in this case, 95% of the prescribed dose for each target) (Landberg et al 1999) and PTV₁₀₀ is the fraction of the PTV that is covered by 100% of the prescribed dose for each specific target. We also evaluated differences between the distorted plans and control plans in terms of mean dose and maximum dose to the target and the OARs in each case. We considered the following distortion-induced differences to be clinically meaningful: ΔTC > 3%, ΔCI > 3; ΔD_mean > 2 Gy, and ΔD_max > 3 Gy.

3. Results

3.1. Model of MRI geometric distortion

For the 1.5 T Philips MRI system, the measured maximum residual geometric distortions in the volume of interest were 6.9 mm, 6.1 mm, and 3.6 mm in the X, Y, and Z directions, respectively. The quiver plot of the residual 3D geometric distortion is shown in figure 1. The geometric distortion is more pronounced at the peripheral region. The histogram analysis of polynomial fitting errors is shown in figure 2, with the mean errors in the X, Y, and Z being 0.4 ± 0.4 mm, 0.2 ± 0.2 mm, 0.1 ± 0.2 mm, respectively. A 2D comparison between the measured geometric distortion and fitting results in the Z direction is shown in figure 3.

Figure 1.

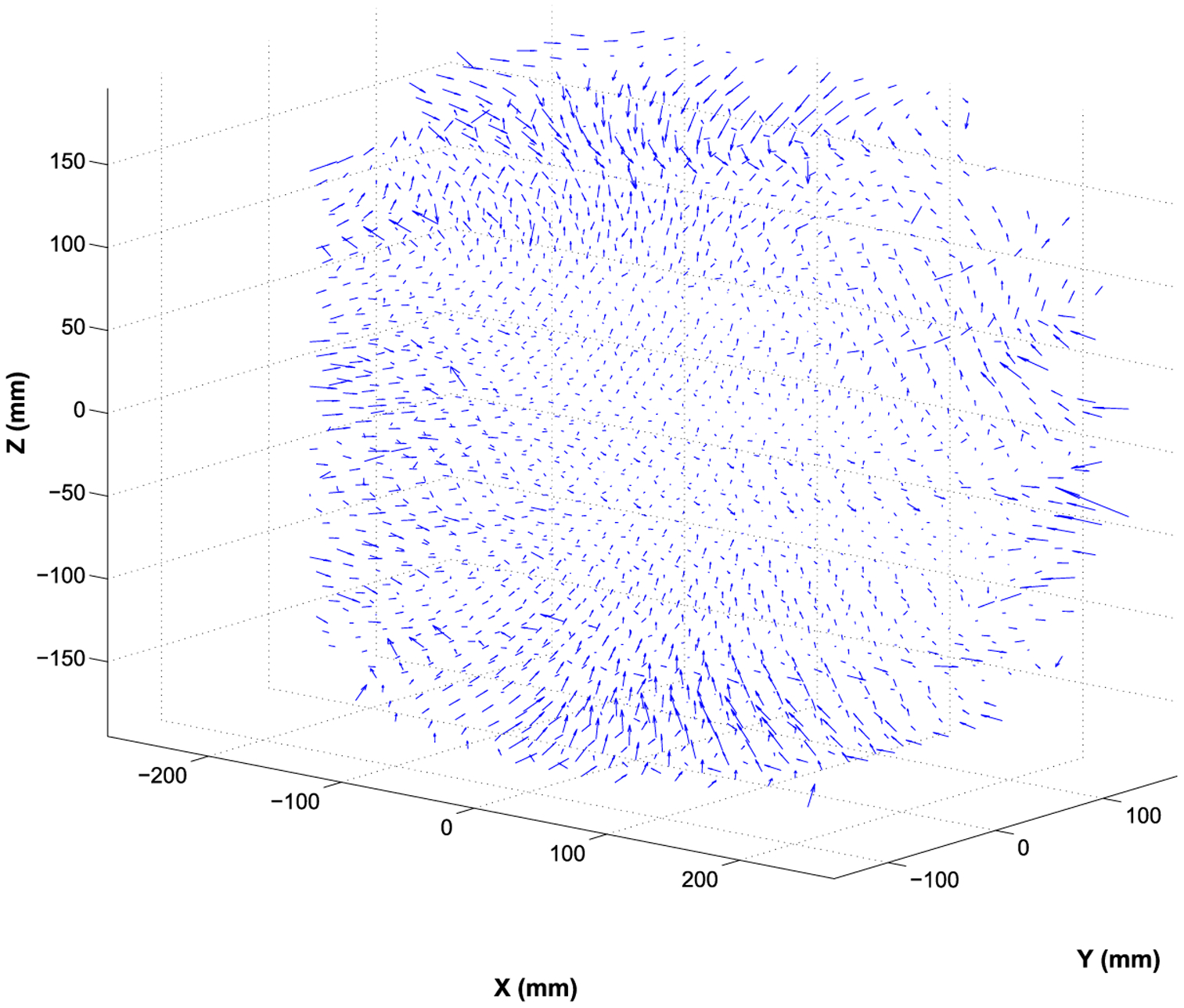
Quiver plot of the measured residual geometric distortions in the 3D space of the 1.5 T Philips MRI system.

Figure 2.

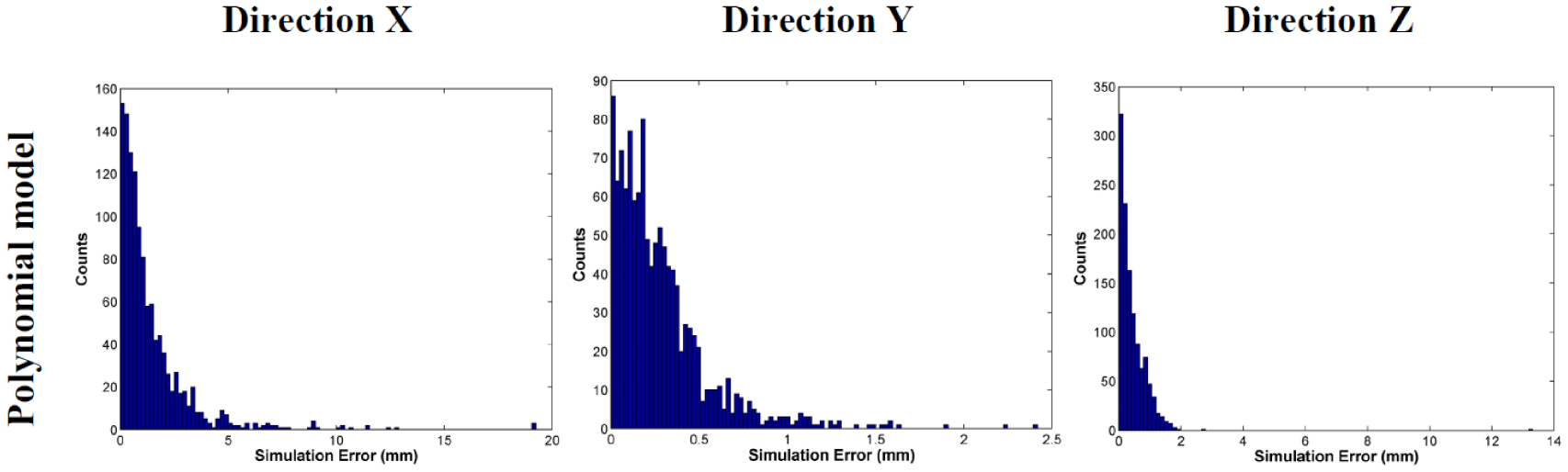
Histogram analysis of fitting errors using the polynomial model.

Figure 3.

Comparison of the measured geometric distortion data and fitting results. (a) Measured distortion in one slice in the Z direction. (b) Fitted distortion in the same slice using the polynomial model.

3.2. Patient study

3.2.1. Target coverage (TC)

Findings from the analysis of TC in terms of CI and TC for the control plans and the distorted plans and distance from the centroid of the target to the imaging isocenter are provided in table 2. In most cases, Distortions in the MRI did not reach clinically meaningful levels (i.e. ΔTC > 3%). However, for patient 8 (with a nasopharyngeal tumor), the distorted plan reduced the CI by 3.56 for PTV 57, which translated to a better sparing of normal tissue in the brain. In terms of TC, the ΔTC for 11 of the 14 patients was quite small. However, in two patients, distortions in the MRI led to some loss in TC: 3.4% for the PTV in patient 5 (genitourinary tumor) and 3.68% for PTV 59.4 in patient 8 (head and neck tumor). For patient 3 (gastrointestinal tumor), the MRI distortion actually improved the TC by 3.4%. Overall, however, as shown in table 2, distortions in the MRI tended to reduce the TC compared with the original control plans.

Table 2.

TC analysis and distance from the centroid of the target to the imaging isocenter of the control (clinical) treatment plans and the distorted treatment plans for all patients.

		Control plan		Distorted plan		Difference		Distance
Patient no.	Target	CI	TC, %	CI	TC, %	ΔCI	ΔTC, %	cm
1	PTV	1.15	0.97	1.13	0.96	−0.02	−1.24	6.09
2	PTV 67.5	1.05	0.77	1.01	0.75	−0.05	−2.54	6.05
	PTV 37.5	2.87	0.91	2.83	0.92	−0.04	1.08	4.25
3	PTV	1.36	0.96	1.64	1	0.28	3.4	1.94
4	PTV	1.41	0.99	1.35	0.99	−0.06	−0.23	5.12
5	PTV	1.26	0.98	1.27	0.94	0.01	−3.34	6.07
6	PTV	1.24	0.96	1.18	0.95	−0.06	−1.36	6.57
7	PTV	1.74	0.96	1.92	0.94	0.18	−1.44	5.06
8	PTV 70	3.28	0.99	3.38	0.98	0.1	−0.62	10.91
	PTV 66	5.37	0.99	5.27	1	−0.1	0.22	9.80
	PTV 59.4	2.58	0.98	2.42	0.94	−0.16	−3.68	9.19
	PTV 57	67.58	1	64.03	0.98	−3.56	−1.21	11.11
9	PTV 45	2.09	0.97	2.12	0.96	0.03	−0.94	6.33
	PTV 40	5.2	0.98	5.33	0.98	0.13	−0.18	6.72
10	PTV 42.5	2.96	1	2.71	0.96	−0.26	−3.4	8.52
	PTV 37.5	1.69	0.98	1.57	0.96	−0.12	−2.16	8.60
11	PTV boost 40	1.43	0.95	1.51	0.92	0.08	−2.48	7.67
	PTV 30	1.99	0.98	1.96	0.97	−0.03	−1.01	8.61
12	GTV 24	1.34	0.96	1.33	0.94	−0.01	−1.66	1.74
	CTV 16	2.28	0.99	2.25	0.98	−0.03	−0.99	1.57
13	GTV 24	0.87	0.96	1.3	0.95	0.43	−1.08	3.65
	CTV 16	1.06	0.95	1.67	0.92	0.61	−2.36	2.76
14	GTV 24	1.81	0.98	1.78	0.98	−0.02	−0.61	7.19
	CTV 16	1.48	0.93	1.52	0.92	0.04	−0.37	7.49

Abbreviations: CI, conformity index; TC, target coverage; PTV, planning target volume; GTV, gross tumor volume.

3.2.2. Dose to OARs

The dose-volume histograms for patients with tumors of the liver (a), prostate (b), lung (c), head and neck (d), and spine (e) are shown in figure 4. Comparisons of mean dose (D_mean) and maximum dose (D_max) for targets and OARs for each patient are shown in supplementary table S1 (stacks.iop.org/PMB/63/085005/mmedia). To summarize, the OARs that were at the greatest distance from the imaging isocenter had the greatest distortion. For example, for patient 3 (liver tumor), the chest wall was the farthest from the isocenter at 197 mm, which led to a distortion-induced difference in D_mean of 6.19 Gy. For patient 8 (nasopharyngeal tumor), the distorted plan increased the D_mean to the right optic nerve by 7.11 Gy. In terms of maximum dose, the change in D_max for the distorted plans ranged from a minimum of 0 Gy to a maximum of 5.17 Gy (dose to the left lung for a lung tumor in patient 7).

Figure 4.

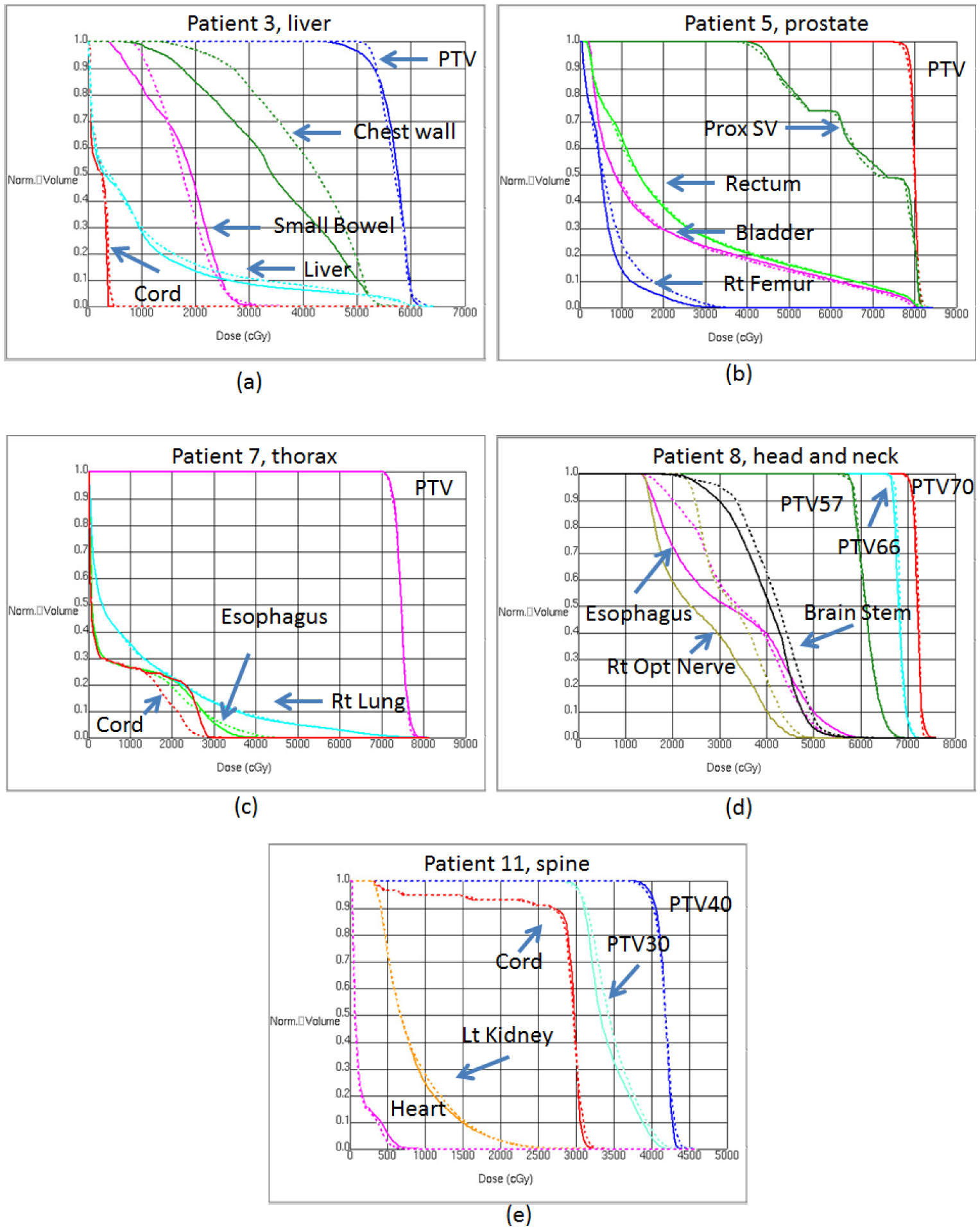
Dose-volume histogram data for patients with a liver tumor (patient 3; (a)), a prostate tumor (patient 5; (b)), a lung tumor (patient 7; (c)), a nasopharyngeal tumor (patient 8; (d)), and a T9–T10 spinal tumor (patient 11; (e)). Solid lines are values from the control plans; dashed lines are values from the distorted plans. Abbreviations: PTV, planning target volume; Prox SV, proximal seminal vesicle; Rt, right; Lt, left.

The greatest deviations in dose-volume histograms were observed for patients 3 (liver tumor) and 8 (nasopharyngeal tumor), as shown in the figure 4. For patient 3 (figures 5(a) and (b)), the 20 Gy and 30 Gy isodose lines clearly covered larger areas of the chest wall in the distorted plan than in the control plan. For patient 8 (figures 5(d) and (e)), the 45 Gy isodose line spared part of the brainstem in the control plan but passed through the whole brainstem in the distorted plan.

Figure 5.

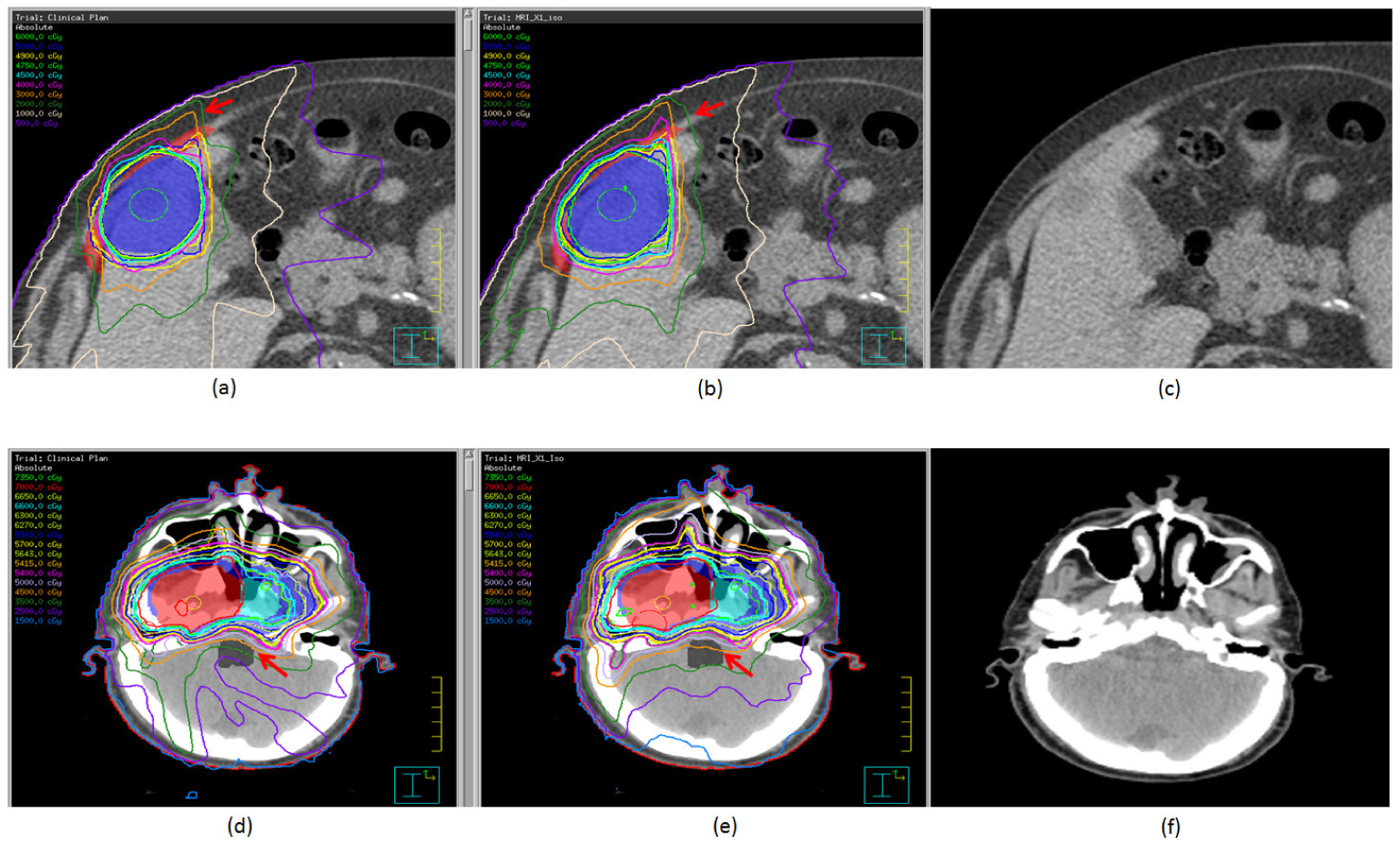
Treatment plans, with isodose distributions, for a patient with a liver tumor (patient 3; (a)–(c)) and a patient with a nasopharyngeal tumor (patient 8; (d)–(f)). Panels (a) and (d) are the control plans, panels (b) and (e) are the distorted plans, and panels (c) and (f) are the distorted CT images. For patient 3, the target (blue) and the chest wall (red) are shown in color wash. For patient 8, targets are shown in color wash. The red arrows point to differences between the control plans and the distorted plans.

Absolute differences in mean dose (|D_mean|) and maximum dose (|D_max|) between the control plans and the distorted plans for all 120 OARs in all 14 patients are plotted in figures 6(a) and (b). Standard deviations of the mean dose (δD_mean) and the maximum dose (δD_max) when d, the distance between the image isocenter and the centroid of each OAR in the distorted image dataset, is smaller than the given value are shown in figures 6(c) and (d). The standard deviation of the mean dose clearly increased with increasing distance from the image isocenter. For the maximum dose, however, the standard deviation was not sensitive to the distance after 40 mm.

Figure 6.

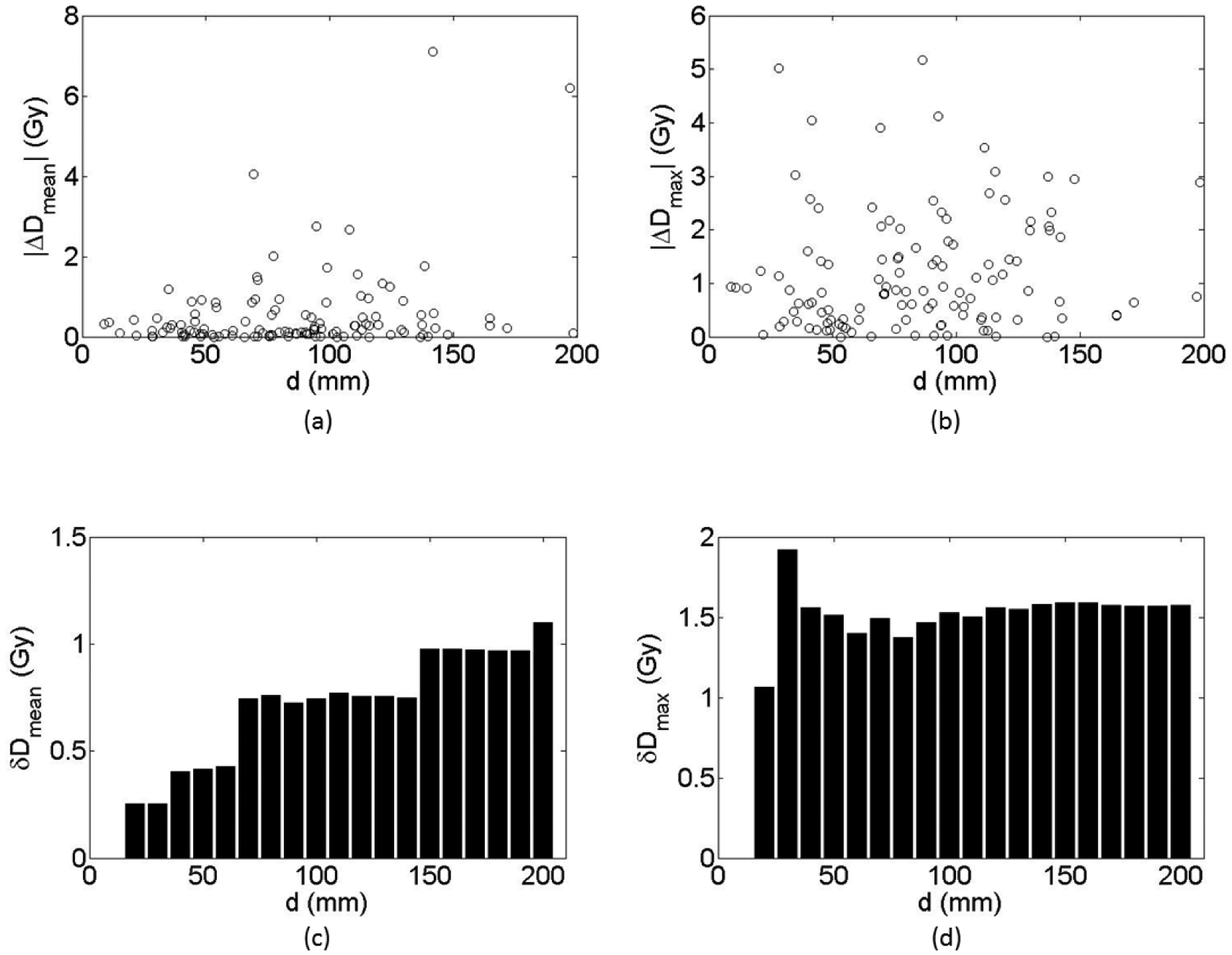
Differences in absolute mean dose (a) and maximum dose (b) between the control plans and the distorted plans for the 120 evaluated organs at risk. (c) and (d) Standard deviations of the absolute mean dose (c) and maximum dose (d) for each maximum distance (d) between the distortion imaging center and the centroid of each organ at risk.

4. Discussion

In the current study, we developed a generalized technique to quantitatively study the dosimetric impact of MRI geometric distortion. By developing a generalized distortion model based on realistic geometric distortion measurements of MRI scanner systems and then applying this model to patient CT datasets and structures, we were able to quantitatively investigate the dosimetric impact of geometric distortion in MRI caused by the imperfection of the hardware system. In 14 patients with tumors at five different anatomic sites, we tested this methodology and studied the dose deviation caused by the MRI system for the general clinical application. Because this was a proof-of-concept study, rather than focusing on one tumor site with a large number of patients, we deliberately used a small number of patients in each group for multiple cancer sites to cover a broad scope of clinical treatments.

In the current study, the distorted plans were optimized in the same way as the control plans. Small differences in the optimized beams certainly contributed to uncertainty in the overall dose calculations of the distorted plans. We have compared the dose in the clinical plan to the dose in the plan with distorted isocenter and structures. Minor differences were observed. Thus, the minor differences in the optimization did not influence the validity of our results.

One important factor to be considered in evaluating dose differences is the volume of the OAR. For OARs with very small volumes (e.g. <1 cm³), the mean dose to these OARs tends to be decided by the maximum point dose, which may not necessarily correlate with large differences in dose distribution. For patient 8 (nasopharyngeal tumor), for example, Distortions in the MRI increased the mean dose to the right cochlea by 2.75 Gy and that to the right optic nerve by 7.11 Gy. For patient 9 (right neck tumor), Distortions in the MRI increased the mean dose to the right parotid critical region by 4.05 Gy. However, the volume of all of these OARs was smaller than 1 cm³. Thus, the large deviations in mean dose in these cases did not necessarily result in important differences in dose distribution.

Unlike mean dose, which is averaged across the volume of the region of interest, the maximum dose is a point dose and does not depend on the volume. Indeed, figures 6(b) and (d) clearly show that the maximum dose was not sensitive to the change in location of the OARs. After the distance exceeded 40 mm, the δD_max values were similar for all OARs. The maximum dose to the OARs was more sensitive to changes in the local dose gradient. In thoracic tumors, density inhomogeneity could lead to rapid changes in local dose gradients, especially at the interface of tissue and air. Changes in the density can lead to large differences in the maximum dose to OARs. Indeed, for patient 7 (lung tumor), substantial differences in D_max were noted for the spinal cord (3.03 Gy), esophagus (4.05 Gy), heart (4.12 Gy), and chest wall (5.02 Gy). For all of these OARs, the distorted plan delivered higher maximum doses than did the control plan.

For conventional radiation therapy, MRI is typically used as a reference image to fuse with CT to delineate the region of interest. The geometric error of the MRI could lead to important distortions of the target and OARs. Extra margins may be used to improve the robustness of the treatment plan. With the scientific community of radiation oncology is moving forward to MRI based treatment planning, the errors in the geometry of targets and OARs will affect the accuracy in dose calculation. Based on our calculation, the deviation of dose caused by geometric distortion is more apparent for the targets and OARs which are far away from the imaging isocenter. Since the geometric distortion of MRI depends on different factors such as hardware design of the system, imaging sequence parameters, and patient specific magnetic susceptibility, a systematic study to explore the dosimetric impact in treatment plan for different cancer sites is needed. Besides, new imaging quality assurance (QA) standard needs to be established to ensure that the distortion of MRI in the region of interest is within the tolerance for MRI guided radiation therapy system.

The current study has some obvious limitations. First, the complexity of the intrinsic geometric distortion of the MRI system made it impossible for us to get universal parameters in equation (1) to represent all geometric distortions for all sequences on all different MRI systems. Thus, the dose deviations presented in the current study are specifically based on the T1 FFE sequence on the imaging component of the Elekta 1.5 T MRI-linac system. Our aim was to provide a proof-of-concept, preliminary study to estimate the baseline of the dose deviation caused by the system imperfection of the 1.5 T Philips MRI system. The dose deviation caused by patient-specific magnetic susceptibility will add to the results presented here. Thus, for clinical application of the MRI-linac system, we may have underestimated the dose deviation caused by the geometric distortion of MRI. The second limitation of our study was the small patient sample size. Further investigation in a large number of site-specific patients is needed to provide more general clinical guidelines for the application of MRI-guided radiation therapy.

Besides, in the clinical scenario, it is possible that the differences between the treatment isocenter and the imaging isocenter of the MRI be even more dramatic compared to the CT scan, which will exacerbate the effect of geometric distortion. Thus, our results could under estimate the dosimetric impact of the geometric distortion in treatment planning.

In addition to the magnitude of geometric distortion, the local dose gradient influenced the dose deviation of the distorted plan. In future work, we will investigate the dependence of the dose deviation on the geometric distortion of the MRI and the local dose gradient for general IMRT treatment plans.

5. Conclusions

In conclusion, we developed a methodology to simulate the hardware-related residual 3D geometric distortion of the MRI system and used it to evaluate the dosimetric deviation caused by such distortion. We found that MRI distortion caused by the hardware imperfection did not result in meaningful dose deviations relative to the control plans for 9 of 14 patients. However, the distortions in the MRI tends to decrease TC compared with clinical plans. For OARs far from the image isocenter, the distortions in the MRI tends to increase the extent of dose deviations compared with clinical plans, which could compromise the quality of the treatment plan. For critical OARs, the corresponding planning organs at risk volume (PRVs) with additional margin expansion comparable to geometry distortion should be considered. Special attention is needed in treating patients with head and neck cancer because of the complex shapes of the OARs surrounding the target. Among the five tumor sites evaluated in the current study, we found that spinal tumors were the least sensitive to geometric distortions caused by using a 1.5 T MRI system for treatment planning.