Deep-learning-based direct inversion for material decomposition

Abstract

Purpose

To develop a convolutional neural network (CNN) that can directly estimate material density distribution from multi-energy CT images without performing conventional material decomposition.

Methods

The proposed CNN (denoted as Incept-net) followed the general framework of encoder-decoder network, with an assumption that local image information was sufficient for modeling the non-linear physical process of multi-energy CT. Incept-net was implemented with a customized loss function, including an in-house-designed image-gradient-correlation (IGC) regularizer to improve edge preservation. The network consisted of two types of customized multi-branch modules exploiting multi-scale feature representation to improve the robustness over local image noise and artifacts. Inserts with various densities of different materials (hydroxyapatite (HA), iodine, a blood-iodine mixture, and fat) were scanned using a research photon-counting-detector (PCD) CT with two energy thresholds and multiple radiation dose levels. The network was trained using phantom image patches only, and tested with different-configurations of full field-of-view phantom and in vivo porcine images. Further, the nominal mass densities of insert materials were used as the labels in CNN training, which potentially provided an implicit mass conservation constraint. The Incept-net performance was evaluated in terms of image noise, detail preservation, and quantitative accuracy. Its performance was also compared to common material decomposition algorithms including least-square-based material decomposition (LS-MD), total-variation regularized material decomposition (TV-MD), and a U-net based method.

Results

Incept-net improved accuracy of the predicted mass density of basis materials compared with the U-net, TV-MD, and LS-MD: the mean absolute error (MAE) of iodine was 0.66, 1.0, 1.33, and 1.57 mgI/cc for Incept-net, U-net, TV-MD and LS-MD, respectively, across all iodine-present inserts (2.0 to 24.0 mgI/cc). With the LS-MD as the baseline, Incept-net and U-net achieved comparable noise reduction (both around 95%), both higher than TV-MD (85%). The proposed IGC regularizer effectively helped both Incept-net and U-net to reduce image artifact. Incept-net closely conserved the total mass densities (i.e. mass conservation constraint) in porcine images, which heuristically validated the quantitative accuracy of its outputs in anatomical background. In general, Incept-net performance was less dependent on radiation dose levels than the two conventional methods; with approximately 40% less parameters, the Incept-net achieved relatively improved performance than the comparator U-net, indicating that performance gain by Incept-net was not achieved by simply increasing network learning capacity.

Conclusion

Incept-net demonstrated superior qualitative image appearance, quantitative accuracy, and lower noise than the conventional methods and less sensitive to dose change. Incept-net generalized and performed well with unseen image structures and different material mass densities. This study provided preliminary evidence that the proposed CNN may be used to improve the material decomposition quality in multi-energy CT.

1. Introduction

A number of material decomposition (MD) algorithms have been developed for use in dual-energy and multi-energy CT^1–6. A major limitation of these methods is the magnified noise in the material-specific images, which is due to the typically ill-conditioned material decomposition problem. A variety of iterative-type methods have been developed in an attempt to suppress noise while preserving image details by exploiting statistical properties of the data^7,8, different regularization strategies^9–12, or structural information between spectral images and material maps^13,14. Nevertheless, existing MD methods are challenged by the non-linear nature of the measurement system, and further technical advancement is required to decrease image noise and improve quantitative accuracy of MD.

Recently, machine-learning-based MD methods have been reported. Lee et al.¹⁵ used a conventional artificial neural work (ANN) with single hidden layer to decompose simulated multi-energy projection data into basis material thicknesses. This method was experimentally evaluated with phantom studies by Zimmerman and Schmidt¹⁶. Touch et al. used a similar ANN with two hidden layers to correct spectral distortion in the projection data before conducting MD¹⁷. However, these ANN methods are generally limited by image noise and artifacts and research efforts are now focused on more complex and robust machine-learning algorithms, e.g., CNN. Clark et al. adapted a well-known CNN (U-net¹⁸) to decompose micro-CT images into material maps¹⁹. Lu et al.²⁰ used classical machine learning algorithms (e.g., ANN and random forest) to decompose multi-energy projection data into material-specific projections (iodine / bone, or biopsy needle / bone); they also adapted two well-known CNNs (DnCNN²¹ and ResNet²²). Zhang et al.²³ developed a butterfly-net that imitated a linear system model based on two basis materials (bone and soft-tissue). These CNN-based methods are, however, limited in several aspects. For instance, the U-net used in¹⁹ still yielded strong image noise in simulation data, e.g., the pixel-wise iodine concentration deviated up to 3 mgI/cc (see the scatter plots of Fig. 4 in¹⁹); the DnCNN and the ResNet used in²⁰ yielded a mean structural similarity index ≤ 0.77 for the decomposed iodine images (see Table 3 in²⁰). Second, the networks in^20,23 were trained using images with anatomical background; the material labeling procedure performed during training is challenging; it is susceptible to registration / quantification errors that propagate to the material-specific images. For example, to generate training labels for butterfly-net²³, a commercial bone-removal software (Syngo.Via, Siemens Healthcare, Inc., Forchheim, Germany) was used to provide initial binary material separation, and then radiologists were recruited to empirically correct pixel-wise artifact, e.g., the bone residual in soft-tissue images and the blurred boundaries. In addition, by its nature, the butterfly-net cannot be readily extended to decompose more than 2 basis materials.

Figure 4.

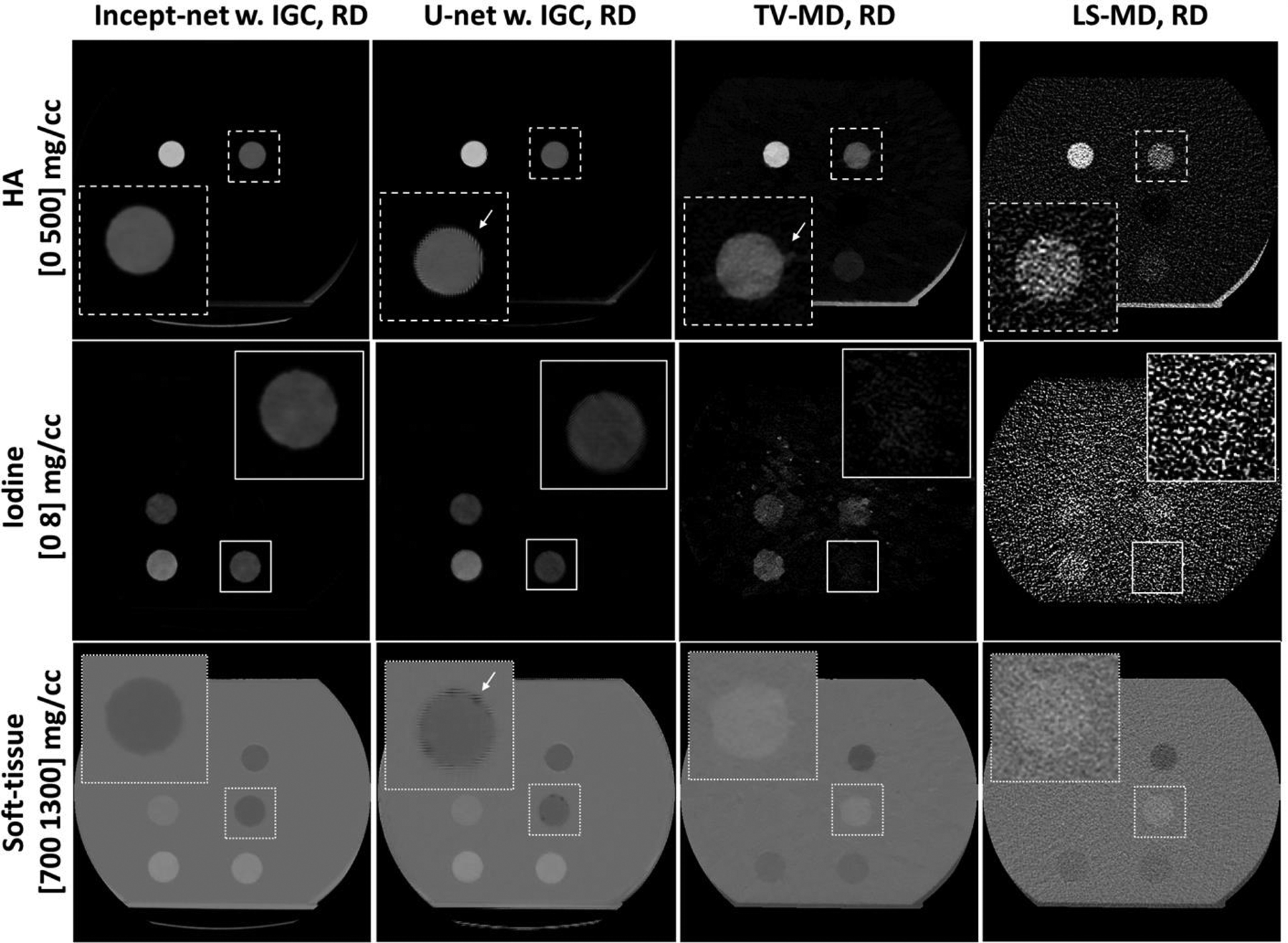
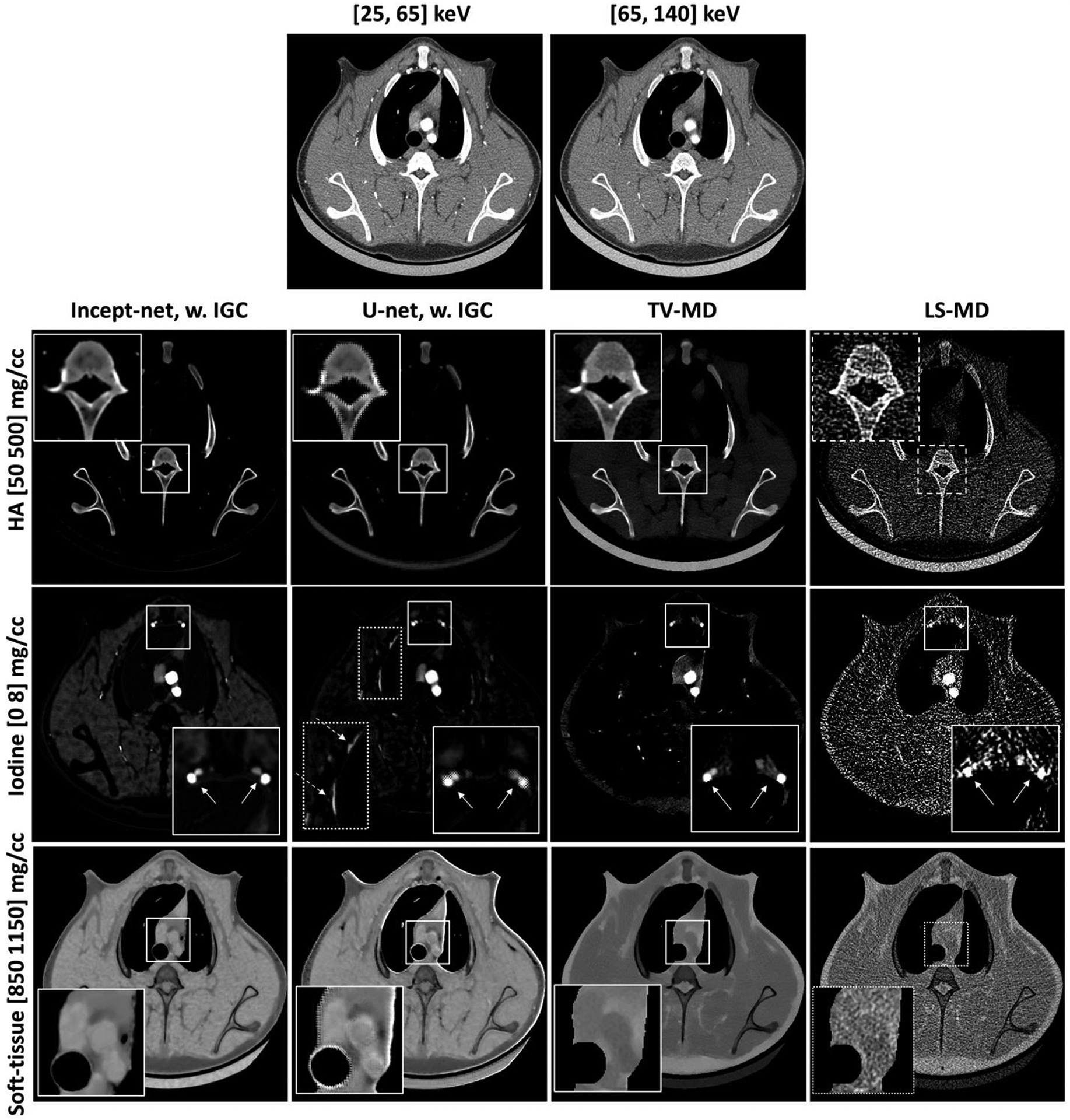
Example material-specific images from the testing hydroxyapatite (HA), iodine / blood mixture, and fat inserts (see Figure 2 and Table 2), using Incept-net, U-net, total-variation (TV-MD), and least-square (LS-MD) based methods. The spatial distributions of HA, iodine and soft-tissue from each method are shown in the top, middle and bottom rows, respectively. Both Incept-net and U-net were trained with mean-square-error and the proposed image-gradient-correlation based regularizer (IGC). The CTDI_vol of regular dose (RD) was 13 mGy. The zoomed inserts are 2.5 times the size of the square region-of-interest. The arrows indicate the examples of edge artifact.

Table 3.

The major parameters of the scanning and image reconstruction protocols

	Thoracic / Abdominal CT
Tube voltage (kV)	140
Energy bins (keV)	#1: [25, 65] #2: [65, 140]
CTDIvol (mGy)	Phantom scans: HD – 23 RD – 13 LD – 7 Animal scans: 16
Number of scans per dose level	5
Field-of-view (mm)	275
Reconstruction algorithm	SAFIRE, D30 kernel Strength 2
Image matrix	512×512
Image thickness (mm)	Phantom: 3 Animal: 1.5

HD = high dose, RD = routine dose, LD = low dose

We previously presented an preliminary investigation of an independently-customized CNN architecture (denoted as Incept-net for convenience) for MD in 2018 annual meeting of American Association of Physicists in Medicine²⁴. The complete Incept-net architecture is presented here and comprehensively evaluated to determine its capability to alleviate the problems noted with previous work. Briefly, Incept-net is used to directly decompose multi-energy CT images into multiple material-specific images, without using any explicit imaging system model. The network architecture was developed based on a hypothesis that local image structure can provide sufficient information for modeling the functional mapping between spectral measurements and material compositions. Compared with the prior CNN-based methods, this network architecture uses customized multi-branch modules to exploit multi-resolution features of local image structure, and excludes the pooling / un-pooling operations, to improve the robustness against local noise and artifacts while preserving the structural details. Additional structural customization was also made to improve the network efficiency and stability. Consistent with the above hypothesis, Incept-net can be trained using phantom images with uniform background alone, while still yielding reasonable generalizability on unseen material density and complex anatomical structure. Further, a gradient-correlation based regularizer was incorporated into the loss function for CNN training, to further improve the edge delineation. In this work, we evaluated Incept-net on a set of phantom and animal datasets that were acquired using a research whole-body photon-counting-detector (PCD) CT^25–28. The major technical contribution of this work includes the proposed network architecture and gradient-correlation based regularizer. We aim to demonstrate that the proposed method can improve multi-material decomposition compared to conventional methods.

2. Method

2.1. CNN architecture

Based on the universal approximation theorem²⁹, the functional mapping between multi-energy CT images and material-specific images may be approximated by a CNN with arbitrary accuracy. The CNN-based reconstruction of material-specific images can be formulated as a deep convolutional framelets expansion³⁰, and the perfect reconstruction of true material-specific images f_GT could be approximated by a stack of optimized local and non-local bases. In this work, a customized encoder-decoder CNN was developed to predict material-specific images, using multi-energy CT images as the inputs (Figure 1a). We hypothesized that the local image information would be sufficient to enable an implicit modeling of the non-linear physical process of spectral CT and thus achieve a high-quality approximation of f_GT. That said, the non-local bases can be fixed as Identity matrix, and thus the pooling / un-pooling operation (i.e. a type of non-local bases) was excluded from the proposed CNN architecture. The details of the CNN architecture are introduced below.

Figure 1.

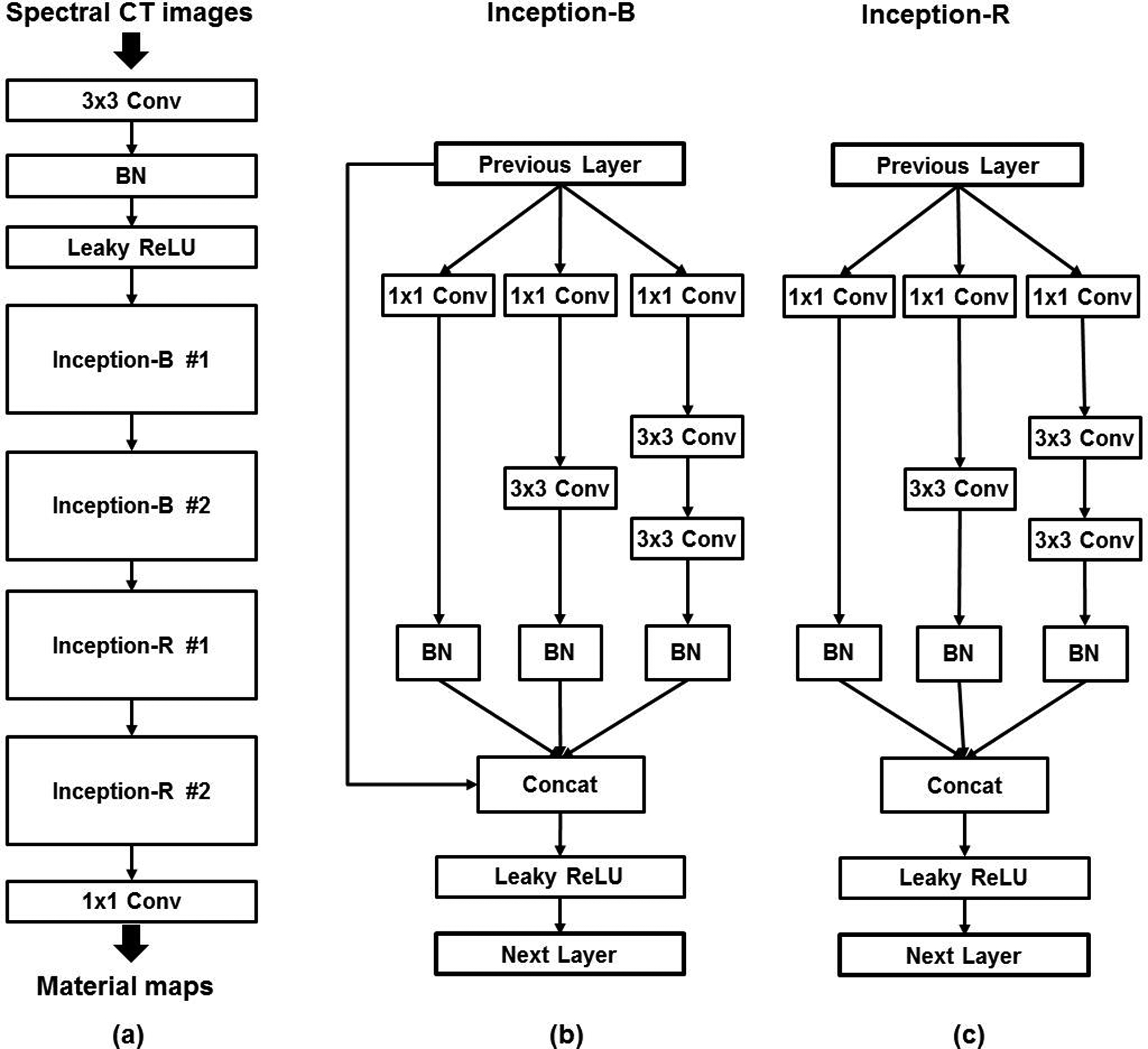
Schematic illustration of the proposed convolutional neural network (CNN) which follows the general Encoder-decoder framework. (a) The overall architecture of the proposed CNN. (b) The architecture of the Inception-B block. (c) The architecture of the Inception-R block. The Inception-B and Inception-R blocks were modified from the naïve Inception blocks. “BN” denotes batch-normalization layer. “Conv” denotes convolution layer. “Concat” denotes concatenation. “Leaky ReLU” denotes leaky rectified linear unit layer.

The batch-normalization (BN) layers were used to address the internal covariate shift issue, i.e. the change in the statistical distribution of the inputs to each layer during the training, which notoriously results in a degraded CNN model with saturating nonlinearity³¹. The leaky rectified linear units (i.e. leaky ReLU)³² were used as the activation layers instead of standard ReLU, to suppress the “dying ReLU” problem which can irreversibly deactivate a substantial amount of neurons and ultimately degrade CNN performance. Further, the multi-branch modules (i.e. Inception-B / -R modules in Figure 1b–c) were modified from the previously-published Inception modules^33,34 that were originally designed for object classification / detection tasks in computer vision. Inception-B modules were used to boost image feature representation, while Inception-R modules were symmetrically placed in the deeper layers to gradually reduce the feature dimensionality and convert the image feature to material-specific images. Both Inception-B and Inception-R used the factorized convolution as was implemented in the prior ones^33,34. For instance, one convolution layer with 5×5 filters can be decomposed into two linearly-stacked convolution layers with 3×3 filters. The factorized convolution was used to reduce the parameter count and accelerate the training. The major modifications used in our Inception-B and Inception-R modules are briefly summarized as follows. In Inception-B, a bypass connection was added to concatenate the module inputs to the outputs of the other branches, to drastically boost the image feature representation. In the meantime, the bypass connection provided an additional path for gradient back-propagation toward the previous layers, and thus the vanishing gradient issue could be further suppressed. Then, in both modules, the BN layer was added to each branch that was coupled with convolutional layers, to further suppress the internal covariate shift in these branches. Further, both modules excluded the branch with the max pooling layers which was used in the previously-published Inception modules. In addition, both modules avoided the use of the factorized convolution with 7×7 or larger filters. The specific configuration of the proposed CNN is listed in Table 1. The total number of CNN parameters was approximately 160, 000. Finally, a customized loss function was formulated for training the CNN:

$$\text{L}\text{=}\frac{1}{N}\sum _{i,j,k}{‖f_{CNN}-f_{GT}‖}_2^2+\frac{1}{\rho \left(\nabla f_{\text{CNN}},\nabla f_{GT}\right)+ϵ}$$ (1)

$$\nabla f_{i,j,k}=\left|f_{i+1,j,k}-f_{i,j,k}\right|+\left|f_{i,j+1,k}-f_{i,j,k}\right|$$ (2)

where the fidelity term is the mean square error between the CNN output f_CNN and the ground truth f_GT, and the regularization term is the reciprocal of the correlation ρ(∙) between the corresponding image gradient. Of note, the regularization term was used to improve the edge preservation. ∇f_i,j,k denotes the anisotropic form of the image gradient of the voxel at the i^th row and j^th column in the k^th material-specific image. ∈ is a small constant number to prevent the denominator from being zero, and it was empirically fixed at 1.0e⁻⁴. A further discussion on the network architecture is presented in Sec. 4.

Table 1.

The configuration of the proposed convolutional neural network

Components	Configuration
Input	2-channel images: #1 channel – CT image from lower energy bin #2 channel – CT image from higher energy bin
1st Convolution (Conv)	3×3 filters w. 60 channels 60 output channels
Inception-B #1	1×1 filters w. 20 channels 3×3 filters w. 20 channels 120 output channels
Inception-B #2	1×1 filters w. 40 channels 3×3 filters w. 40 channels 240 output channels
Inception-R #1	1×1 filters w. 40 channels 3×3 filters w. 40 channels 120 output channels
Inception-R #2	1×1 filters w. 20 channels 3×3 filters w. 20 channels 60 output channels
Last convolution	1×1 filters w. 3 channels 3 output channels
Output	3-channel images: #1 channel – hydroxyapatite image #2 channel – iodine image #3 channel – soft-tissue image

Zero padding was applied to all convolution layers

2.2. Data preparation

2.2.1. CT exam data collection

All data used in this study were acquired from a research whole-body PCD-CT system installed at our institution. The PCD-CT was constructed based on a 2^nd-generation clinical dual-source CT system (SOMATOM Definition FLASH, Siemens Healthineers, Forchheim, Germany). Specifically, the PCD was coupled with one source (referred to as the PCD subsystem), while a conventional energy-integrating detector (EID) was coupled with the other source (referred to as the EID subsystem). The field of view (FOV) of the EID and PCD subsystems is 500 mm and 275 mm in diameter, respectively. To image objects larger than the PCD FOV, a low-dose data completion scan using the EID subsystem is performed. A detailed description of this PCD-CT system can be found in the reference²⁵.

An abdomen-sized water phantom (anterior-posterior dimension of 27 cm; lateral dimension of 35 cm) was used to hold inserts containing common materials (e.g., iodine, calcium, blood, and fat) (Figure 2): the concentration and size of each insert is listed in Table 2. We prepared iodine inserts with concentrations from 3 mg/cc to 24 mg/cc to evaluate quantitative generalizability (see Sec. 2.5). Of note, the typical range of iodine concentration in adult’s aorta is roughly 3 to 18 mgI/cc, with a general > 15 seconds scan delay³⁵. The phantom was scanned at three dose levels (CTDI_vol of 23, 13 and 7 mGy), from which energy-bin images were reconstructed using a commercial iterative reconstruction algorithm (SAFIRE, Siemens Healthcare). Of note, the routine dose (RD) for adult abdomen CT exams at our institute is approximately of 13 mGy CTDI_vol. The high dose (HD, 23 mGy CTDI_vol) and low dose (LD, 7 mGy CTDI_vol) provided additional noise levels in the training data to improve the robustness of the CNN against varying noise levels. To take into account statistical variations from scan to scan, the phantom scans were repeated five times at each dose level. Then, phantom images were processed to prepare a part of training and testing datasets (see Sec. 2.2.2. for details). In addition to the phantom data, we retrospectively selected a porcine abdominal CT scan from our data registry to test the CNN performance in an anatomical background. Briefly, the iodine-based contrast agent was administered intravenously and the scan was performed with a 17 sec delay. The scanning protocol was the same as was used in the phantom studies. Major scanning and reconstruction parameters are listed in Table 3.

Figure 2.

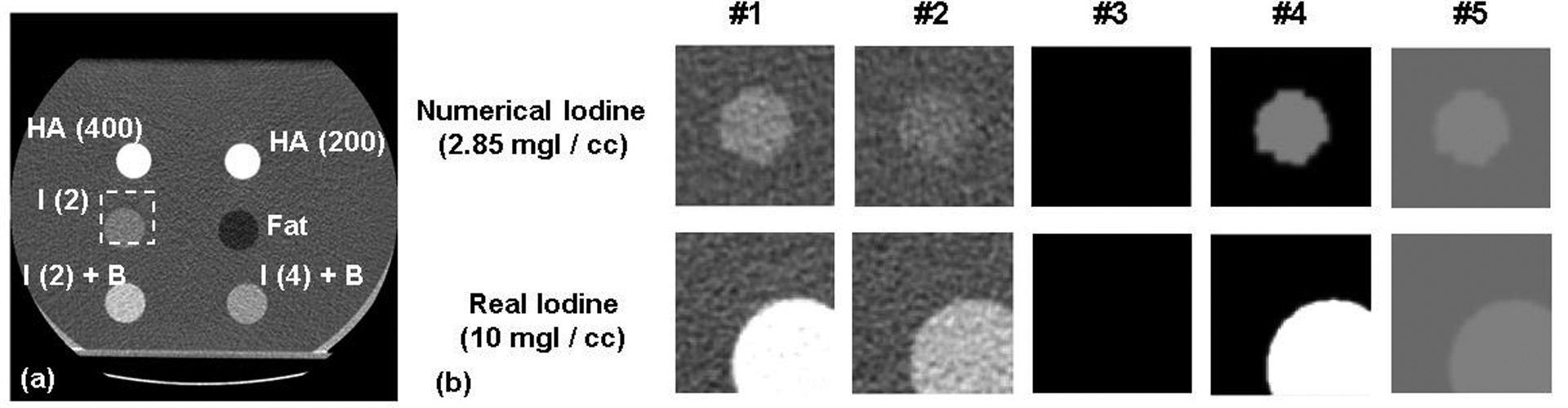
(a) – Example inserts used in the phantom scans. The dashed square region-of-interest (64×64 pixels) indicates the location where CT image patches of a pre-selected iodine insert (i.e. 2 mg/cc, with 30mm diameter; see Table 2 for details) were extracted for training convolutional neural network. The other region of the image was spared from image patch extraction. The range of display window for CT images were [-160, 240] HU. “HA” – hydroxyapatite inserts. “I” – iodine inserts. “I + B” – iodine and blood mixture inserts. The digits within parentheses indicate the nominal density (mg/cc) of inserts. (b) – Example image patches and the corresponding material maps (i.e. ground truth for training neural network) for a numerical random-shaped iodine insert and a real insert. The columns #1 to #5: Energy bin CT image at [25, 65] keV, Energy bin CT image at [65, 140] keV, HA map, iodine map, and soft-tissue map. Display window: [0 500], [0 5], and [850 1100] mg/cc for HA, iodine, and soft-tissue maps, respectively. Please refer to Sec. 2.2.2 for the details of data preparation method.

Table 2.

The concentration and size of real phantom inserts used in CT scans

Inserts	Concentration
Hydroxyapatite	200 mgHA/cc (25 mm in DIA) † 400 mgHA/cc (25 mm in DIA) †
Iodine	2 mgI/cc (30 mm DIA) †† 5 mgI/cc (2, 5, 10, 30 mm DIA) † 10 mgI/cc (30 mm DIA) †† 15 mgI/cc (30 mm DIA) †† 3 mgI/cc (7.5 mm DIA) * 6 mgI/cc (7.5 mm DIA) * 12 mgI/cc (7.5 mm DIA) * 18 mgI/cc (7.5 mm DIA) * 24 mgI/cc (7.5 mm DIA) *
Iodine + blood	2 mgI/cc (30 mm DIA) † 4 mgI/cc (30 mm DIA) †
Fat	956 mgFat/cc (30 mm DIA) †

DIA – diameter

^†these inserts were not included in training dataset

^††these iodine inserts were used to generate a part of training dataset

^*the in-house-made iodine insert that were used as a part of testing dataset

Except for the in-house iodine inserts, the other phantom inserts are standard CT phantom inserts fabricated by the vendor (Sun Nuclear, Inc.); the concentration of the other materials (e.g., the blood mimicking material in the blood-iodine mixture) are available in the technical specifications from the vendor.

2.2.2. Image preprocessing

Due to limited configurations of insert materials and mass densities, we used both real insert materials and numerically-generated inserts to prepare training, validation and testing sets. The insert materials are clinically-validated standard contrast-agent and tissue-mimicking materials. Such insert materials have been used for routine clinical dual-energy CT quality assurance / performance evaluation and the validation of dual-energy CT techniques in many previous studies^14,36–38. As for real inserts, we only used the images of standard iodine inserts with 2, 10, and 15 mgI/cc (with 30 mm diameter) as a part of training set, while the remaining real insert materials (including iodine inserts with other concentrations) were reserved for testing (Table 2). This is because there were relatively more concentrations available for iodine inserts than other insert materials, and we aimed to reserve as many real insert materials for testing as possible. Patch-based training strategy was used: small image patches (64×64 pixels, i.e. 34.4×34.4 mm²) were extracted from the original CT images to boost the number of training samples (Figure 2). The patches were extracted from pre-selected position to avoid including the holder of inserts, since the specific composition of holder material was unknown and the holder material was not the material of interest. Noise-free material-specific images of phantom patches were numerically synthesized as the “ground truth” for CNN (Figure 2), i.e. the nominal mass densities of insert materials (HA, iodine, blood-iodine mixture, water / solid water, and fat). The materials were grouped into three categories, with material-specific images created for each, including a HA image, iodine image, and soft-tissue image (comprising water, solid water, blood, and fat). To ensure image registration, different materials per patch were labeled via thresholding-based segmentation wherein the mean CT number between inserts and water background was used as the threshold. Mirroring and artificial Gaussian noise were also applied to image patches of real inserts to generate additional training samples. The Gaussian noise was added to efficiently increase the diversity of noise levels, so that the network robustness against noise permutation could be improved. Then, numerical inserts were generated as random-shaped polygon (64×64 pixels) with different concentrations. The corresponding CT numbers were estimated by applying linear fitting to the experimentally measured CT numbers of real inserts, as PCD-CT maintained a strong linear relationship between CT numbers and the concentrations of the same material²⁶. For instance, iodine concentration was numerically increased from 2 mg/cc to 30 mg/cc (with 0.05 mg/cc per step), and the corresponding CT numbers were estimated from a linear fitting across the CT numbers measured from real iodine inserts (w. 2, 5, 10, and 15 mg/cc, 30 mm diameter). Additional numerical inserts of HA, iodine-blood mixture, and fat were synthesized in the very similar way. Briefly, the mass density range of the simulated HA, iodine-blood mixture, and fat inserts was [190, 1000] mgHA/cc, [1.9, 30] mgI/cc, and [950, 960] mg/cc, respectively. For each insert material, random splitting was used to split the set of concentrations to generate training (95%) and validation subsets (5%). Of note, the numerical concentration that coincided with that of real testing inserts (shown in Table 2) were excluded from training and validation subsets. For each concentration per insert material, random polygon was repeatedly generated to augment the diversity of insert structure. To mimic real CT noise texture and augment the noise texture diversity, random noise patches extracted from water phantom background were added to the random-shaped numerical inserts (Figure 2). Of note, these random patches involved local image artifacts (e.g. partial beam-hardening and noise streak) and radiation-dose- / location-dependent CT number bias (e.g. this was well-analyzed in references^39–41), which had already induced true non-linear physical process-related CT number perturbation to the simulated inserts. Meanwhile, the formation of the above-mentioned water patches and iodine patches had already involved the complete non-linear physical process of PCD-CT system and vendor’s proprietary non-linear pre-/post-processing procedure. Thus, the non-linear process was already involved in the proposed training dataset, and thereafter was implicitly approximated by the proposed CNN. In total, the image preprocessing procedure generated approximately 110,000 paired training samples: for real inserts, the number of original paired samples was 3 (training iodine inserts per scan) × 102 (images per scan) × 3 (radiation dose levels) × 4 (training scans per dose level), and then further boosted by one realization of random mirroring and Gaussian noise; for numerical inserts, the set of paired samples involved approximately 1, 600 insert material / concentration configurations and 60 realizations of random polygon / noise texture per insert / concentration configuration.

2.3. CNN training

The parameters of Incept-net were initialized by using Xavier normal initializer with default setting. The number of training epochs was fixed at 50, with 100 image patches per mini-batch. The mini-batches were randomly shuffled across consecutive training epochs. The stochastic gradient descent method was used to optimize the parameters of Incept-net. The learning rate was initially set to 0.1, subject to a decay rate of 0.001 across all training epochs. The norm of the gradient was empirically limited to be no greater than 1.0 during the back-propagation (i.e. gradient clipping) to suppress the potential overshooting of gradient which could result in unstable CNN models. Incept-net was implemented using Keras 2.2.4 and Tensorflow 1.13. In addition, we did not apply additional hyper-parameter optimization, and the validation set was used to monitor the occurrence of overfitting in CNN training.

2.4. Evaluation and Comparison

Incept-net performance was compared to two conventional methods, using full-FOV images from the phantom testing cases and porcine scan. The standard least-square based material decomposition (LS-MD) was implemented with volume conservation constraint^6,42, and served as the baseline for comparison. In addition, total-variation regularized material decomposition (TV-MD) was also included. TV-MD was implemented as was shown in our prior study¹⁴. Briefly, the corresponding objective function included the data fidelity term and the TV regularization term dedicated for the material maps (see eq. (7) & (8) in reference¹⁴), and then it was minimized using the alternating direction method of multipliers⁴³. The relaxation parameter λ, i.e. the parameter that controls the preference between data fidelity term and TV term, was empirically fixed at 5×10³ as was used in the reference¹⁴. The original outputs of the TV-MD and LS-MD were linearly blended to alleviate patchy look of the original TV-MD results. Thus the final results of TV-MD $X_{TV}^{\text{'}}$ can be simply formulated as follows:

$$X_{TV}^{\mathrm{\text{'}}}=\alpha \cdot X_{TV}+\left(1-\alpha \right)\cdot X_{\mathit{\text{LS}}}$$ (3)

where X_TV and X_LS denotes the original outputs of the TV-MD and LS-MD, respectively, and α is a weighting factor which was empirically fixed at 0.9. Both LS-MD and TV-MD were performed with volume conservation constraint, assuming HA, iodine, and water as the three basis materials. To determine the coefficients of decomposition matrix used in LS-MD and TV-MD, a separate calibration scan was performed to measure the CT numbers of the basis material (HA and iodine) of known concentrations. These measurements were then used to generate the coefficients of decomposition matrix based on a least-square parameter estimation approach⁴⁴. Besides the comparison with conventional methods, a pilot comparison with additional deep learning based method was also presented. We implemented the same U-net architecture as used in reference¹⁹, except that the output layer was modified to generate three material maps. U-net training used the same loss function as the proposed Incept-net. To achieve a fair comparison, U-net was trained using the same dataset, and the setting of optimizer was consistent to that used in our method. Of note, the selected U-net had roughly 40% more parameters than the proposed Incept-net.

In the evaluation, visual inspection was performed to assess perceived noise levels and structural details, especially on the smaller iodine inserts that were unseen during the training of the CNN, i.e., the 5 mgI/cc iodine inserts with 2, 5, and 10 mm diameter. Material density accuracy across routine and low dose levels was evaluated using nominal material concentration as the reference. The specific composition and the corresponding concentration of the standard CT inserts were provided by the Vendor (Sun Nuclear, Inc.). Bias was assessed using mean absolute error (MAE) of material concentration measured in material maps, i.e. the absolute difference between the averaged material concentration per insert and the corresponding reference. Noise was assessed using the standard deviation of material concentration measured in material maps. Especially, quantitative generalizability of the CNN was evaluated on real insert materials that were not included in training dataset (Table 2).

Further, a pilot evaluation of the effects of the image-gradient-correlation based regularizer (eq. (2) and (3)) on edge preservation was carried out in porcine anatomical background, by comparing the proposed method with two modified implementations. First, the same Incept-net architecture and the comparator U-net was re-trained without the IGC regularizer. Second, an additional branch of the factorized 7×7 convolutional filters was added to each Inception-B / -R module of Incept-net, and the modified Incept-net was also re-trained without the regularizer. The delineation of blood vessels and soft-tissues was qualitatively compared across the corresponding material images. Finally, due to the absence of ground truth, quantitative accuracy of CNN outputs in porcine images was heuristically validated using mass conservation constraint:

$$f_{\mathit{\text{CNN}}}^w=\frac{{\rho }_{\mathit{\text{CNN}}}^{\mathit{\text{HA}}}}{{\rho }_{\mathit{\text{pure}}}^{\mathit{\text{HA}}}}+\frac{{\rho }_{\mathit{\text{CNN}}}^{\mathit{\text{Iodine}}}}{{\rho }_{\mathit{\text{pure}}}^{\mathit{\text{Iodine}}}}+\frac{{\rho }_{\mathit{\text{CNN}}}^{\mathit{\text{Soft}}-\mathit{\text{tissue}}}}{{\rho }_{\mathit{\text{pure}}}^{\mathit{\text{Soft}}-\mathit{\text{tissue}}}}$$ (4)

Where $f_{\mathit{\text{CNN}}}^w$ denote the summed mass fraction, ${\rho }_{\mathit{\text{CNN}}}^{\mathit{\text{HA}}}$, ${\rho }_{\mathit{\text{CNN}}}^{\mathit{\text{Iodine}}}$, and ${\rho }_{\mathit{\text{CNN}}}^{\mathit{\text{Soft}}-\mathit{\text{tissue}}}$ denote material maps from Incept-net, ${\rho }_{\mathit{\text{pure}}}^{\mathit{\text{HA}}}$, ${\rho }_{\mathit{\text{pure}}}^{\mathit{\text{Iodine}}}$ and ${\rho }_{\mathit{\text{pure}}}^{\mathit{\text{Soft}}-\mathit{\text{tissue}}}$ denote the corresponding mass densities of the same basis materials in the pure form, i.e. HA 3,160 mg/cc, iodine 4,933 mg/cc, and soft-tissue 1,000 mg/cc (approximated by water). CNN outputs would perfectly satisfy mass conservation constraint if $f_{\mathit{\text{CNN}}}^w=1.0$.

3. Results

3.1. Loss curves of Incept-net and U-net with IGC

For both CNNs, the loss curves entered plateau region before 50^th epoch, and no obvious overfitting was observed (Figure 3).

Figure 3.

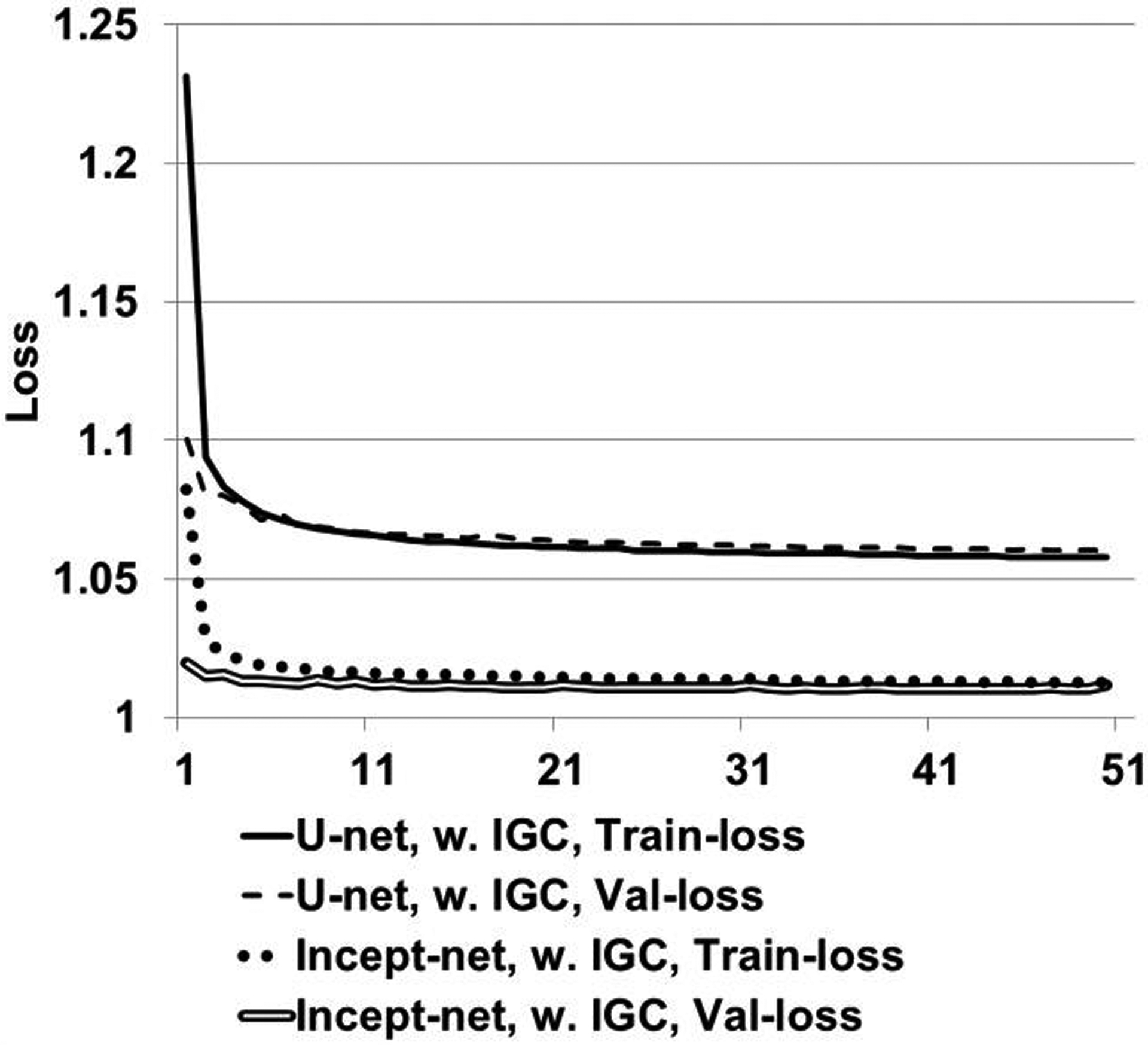
Loss curves of Incept-net and U-net trained with mean-square-error and the proposed image-gradient-correlation (IGC) regularizer. “Train-loss” – training loss curves. “Val-loss” – validation loss curves.

3.2. Phantom studies

Incept-net presented superior performance than the LS-MD and TV-MD, in terms of noise, artifact suppression, and detail preservation. For instance, the iodine image from the LS-MD was heavily corrupted by image noise, while the TV-MD failed to properly delineate the edge of iodine and blood-iodine inserts with lower concentrations (Figure 4). Both CNNs appeared to reduce image noise level. However, Incept-net provided relatively better image quality than the selected U-net, as the latter network yielded observable artifact at insert edge. The mass density of adipose was accurately estimated using both CNNs, while it was overestimated by the other methods (Figure 4). This phenomenon was caused by the fact that fat was not used as a basis material for the conventional methods. The negative CT numbers of fat yielded negative mass densities in HA and iodine images and falsely raised the mass density in soft-tissue images since the conventional methods enforced a linear system model with a volume conservation constraint. In contrast, CNN was capable of correctly assessing fat by directly learning the mapping between CT numbers and mass density. At the lowest radiation dose level (7 mGy), Incept-net still reasonably recovered the smallest iodine insert (5 mgI/cc and 2 mm diameter), which was not used during the training of Incept-net (Figure 5). The comparison of line profiles confirmed that Incept-net provided a better edge preservation at different radiation dose levels (Figure 6). The quantitative evaluation is presented in Sec. 3.3.

Figure 5.

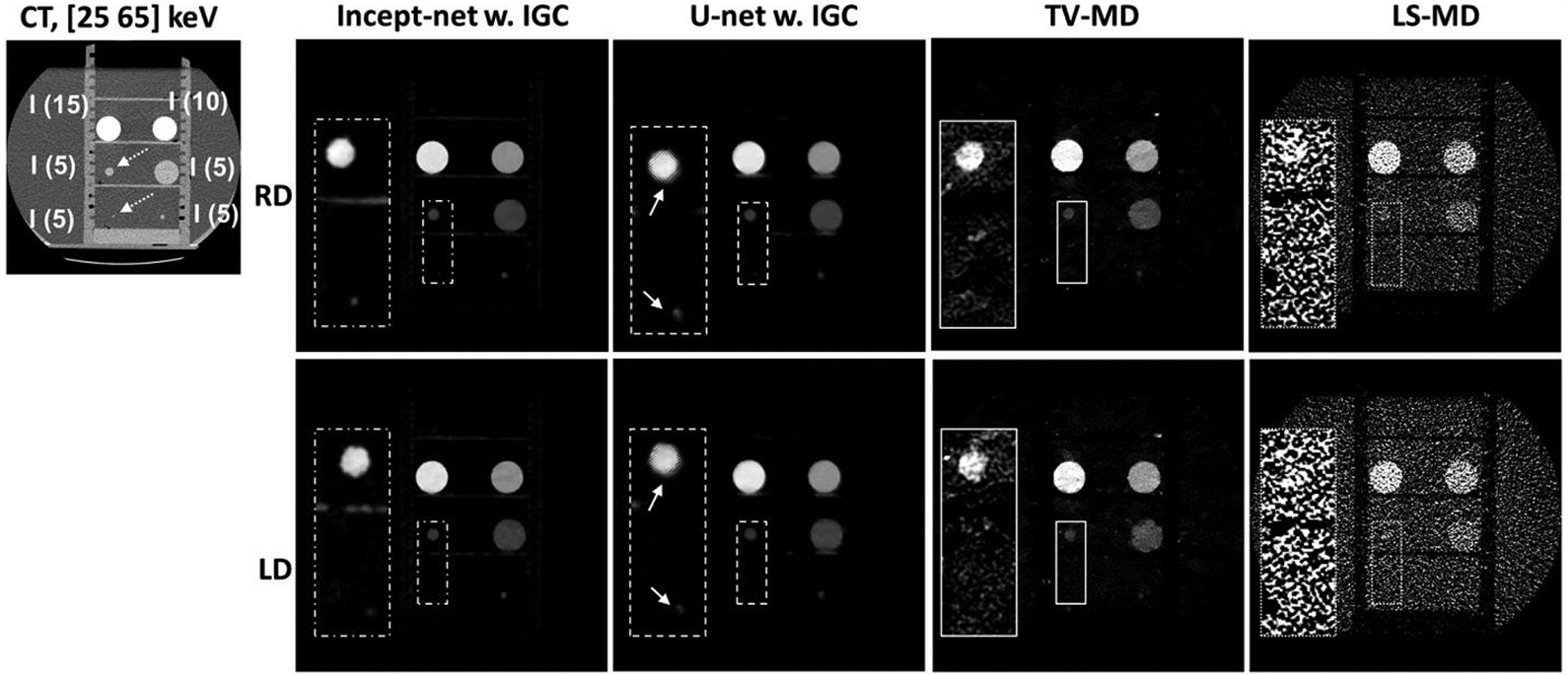
Iodine images from iodine inserts at regular radiation dose (RD) and lower radiation dose (LD) levels, using Incept-net, U-net, total-variation (TV-MD) and least-square (LS-MD) based material decomposition. The inset CT image illustrates the insert configuration (the range of display window [-160 240] HU). “I” – iodine. The digits within parentheses indicate iodine mass densities (mg/cc). Of note, the top two inserts (i.e. 10 and 15 mg/cc) were involved in CNN training, but the remaining inserts (5 mg/cc) were reserved for testing. The dashed arrows indicate the location of the 5 mgI/cc iodine inserts with 2 mm and 10 mm diameter, respectively. The display window for the full field-of-view iodine images is [0, 16] mgI/cc. The zoomed inserts are 2.5 times of the size of the rectangular region-of-interest, and the corresponding display window is narrowed down to [0, 5] mgI/cc for the convenience of illustration. The solid arrows indicate the edge artifact in U-net outputs. The CTDI_vol values for the regular dose (RD) and low dose (LD) scans were 13 mGy and 7 mGy, respectively.

Figure 6.

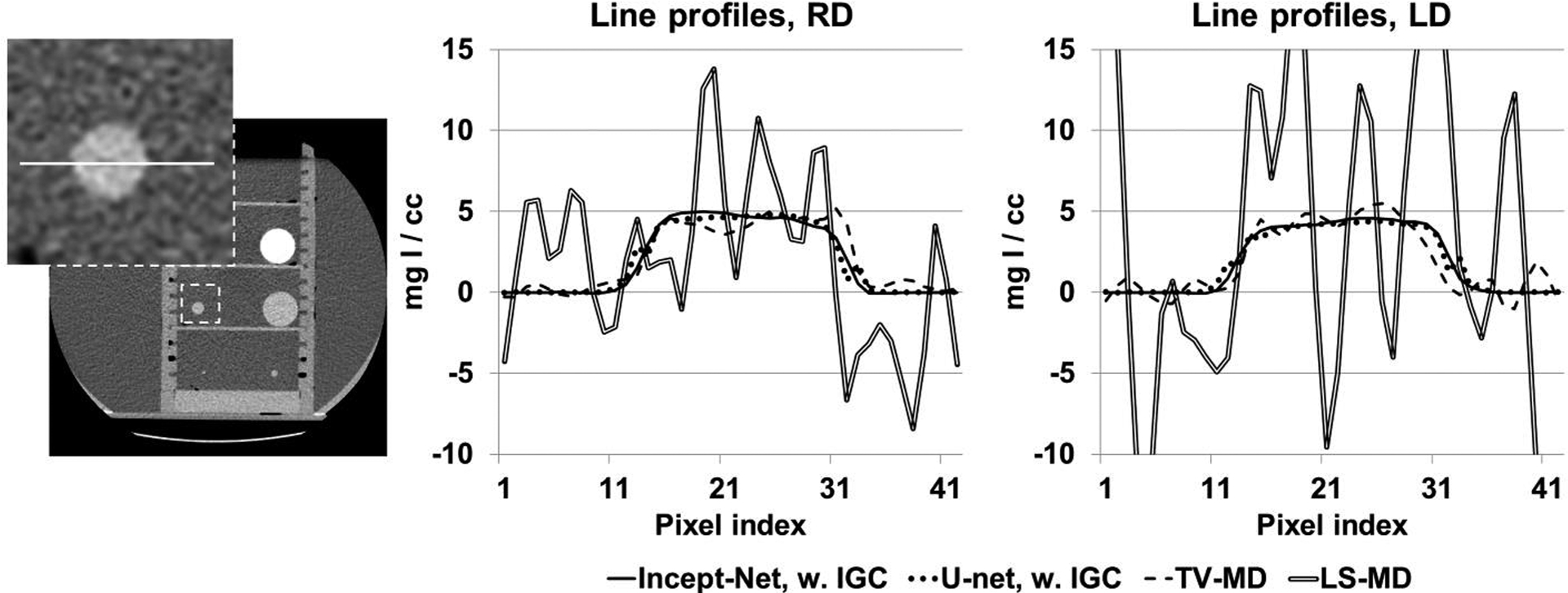
Line profiles from the iodine images (see Figure 5) at routine radiation dose (RD) and low radiation dose (LD) levels, using Incept-net, U-net, total-variation-minimization (TV) and least-square (LS) based material decomposition. The inset image shows the location of line profiles in CT image, i.e. the 5 mgI/cc iodine insert (with 10 mm diameter) that was not used in CNN training. The range of display window for CT image was [-160, 240] HU.

3.3. Quantitative generalizability

Compared to TV-MD and LS-MD, both Incept-net and U-net robustly suppressed image noise across different radiation dose levels (Figure 7), while improving quantitative accuracy (MAE for iodine concentration: Incept-net 0.66 mgI/cc, U-net 1.0 mgI/cc, TV-MD 1.33 mgI/cc, LS-MD 1.57 mg/cc). Of note, the improvement on iodine quantification accuracy is very meaningful for the clinical dual-energy CT tasks that request the differentiation of pathology with low iodine-enhancement (e.g. metastatic lesions)^45–48. The mean percent noise reduction of Incept-net, U-net and TV-MD was 96%, 96% and 82% on HA inserts, respectively, compared to LS-MD. Similarly, the mean percent noise reduction of Incept-net, U-net, and TV-MD was 94%, 93% and 86% on iodine inserts. The noise level remained relatively constant for CNN-processed images acquired at different dose levels (e.g. iodine noise up to approximately 0.7 mgI/cc for both routine and low dose, respectively), which is quite different than the results from the standard LS-MD, where noise substantially increased at lower dose levels (e.g. iodine noise up to approximately 4.0 mgI/cc and 11.0 mgI/cc for routine and low dose, respectively).

Figure 7.

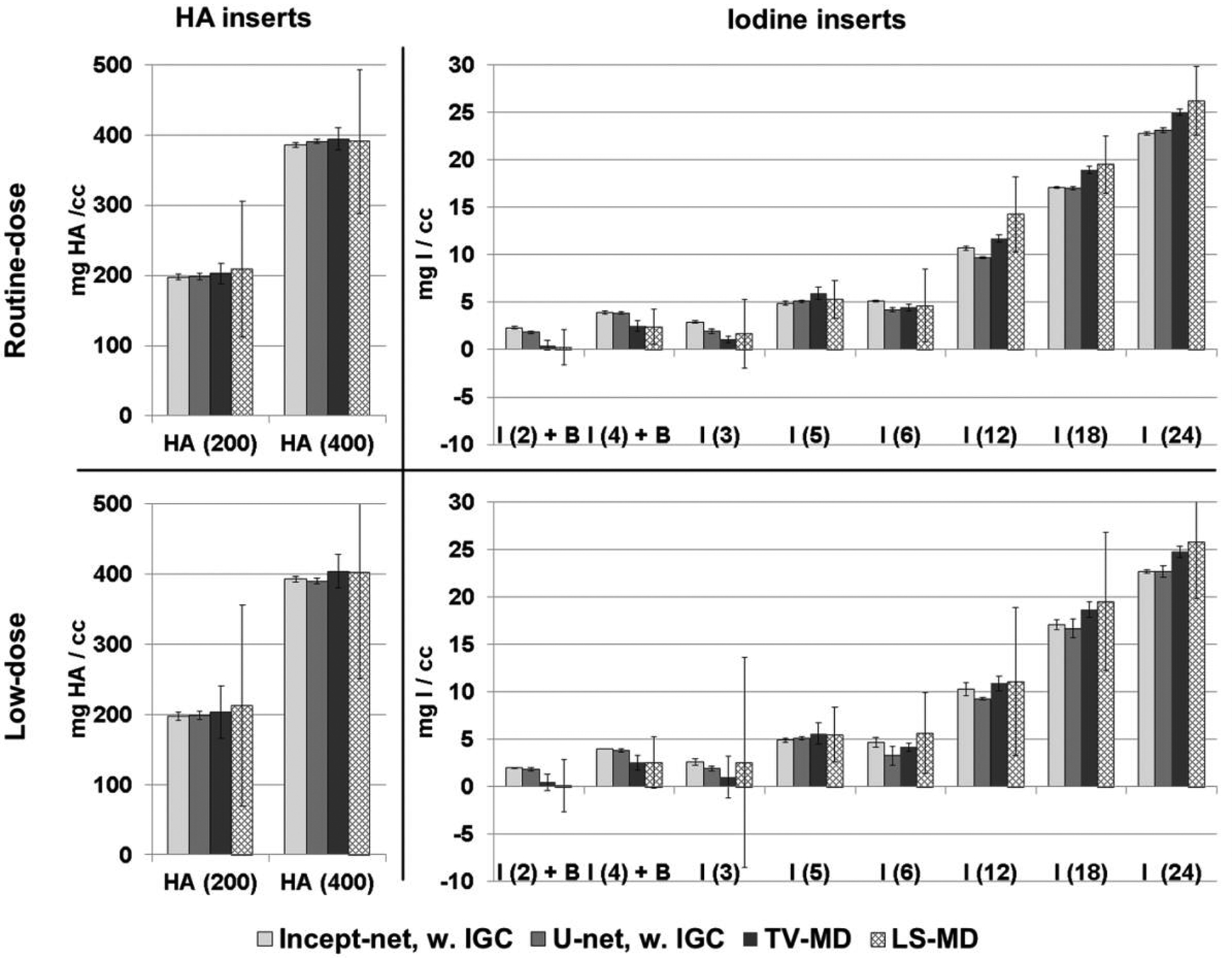
Material mass densities of testing inserts estimated at routine and low dose levels, using Incept-net, U-net, total-variation (TV), and least-square (LS) based methods. The top two charts: routine dose (RD: CTDI_vol 13 mGy) level. The bottom two charts: low dose (LD: CTDI_vol 7 mGy) level. The error bars indicate the standard deviation of the estimated concentration.

3.4. Animal studies

Compared with LS-MD and TV-MD, both Incept-net and U-net improved performance on the animal datasets. Both CNNs were capable of suppressing the soft-tissue residual in the HA image (Figure 8). Both CNNs also provided better visualization of small blood vessels while suppressing the false enhancement of adipose tissue in the iodine image. However, edge artifact was prominent in U-net outputs (mainly for the high-contrast structure). The CNN-synthesized iodine image presented noticeable signal in the tissue / muscle region around the contrast-enhanced blood vessels and kidney, which was partially attributed to the iodine uptake that occurred in the tissue / muscle. The comparison with true non-contrast abdominal CT had at least qualitatively validated the iodine decomposition results (Figure 9). A further discussion is presented in Sec. 4. More interestingly, the Incept-net improved the delineation of anatomical structures in the soft-tissue images compared to TV-MD and LS-MD (Figure 8). Similar to the results of the phantom study (Sec. 3.1), TV-MD and LS-MD reversed the density of the muscle and adipose. TV-MD and LS-MD presented strong signal of table pad in the HA image. The possible reason is described as follows. Table pad was not used as a basis material, and its dual-energy CT number ratio was lower than that of HA and iodine. Since conventional methods used linear system with volume constraint, table pad decomposed strong negative value in iodine map and raised strong positive value in HA map and water map. An additional comparison over the animal thorax region is illustrated in Figure 10. In the iodine map, the comparator “U-net” yielded strong bone residual at the chest wall. This is an apparent decomposition error, as HA was already used as a basis material in CNN training.

Figure 8.

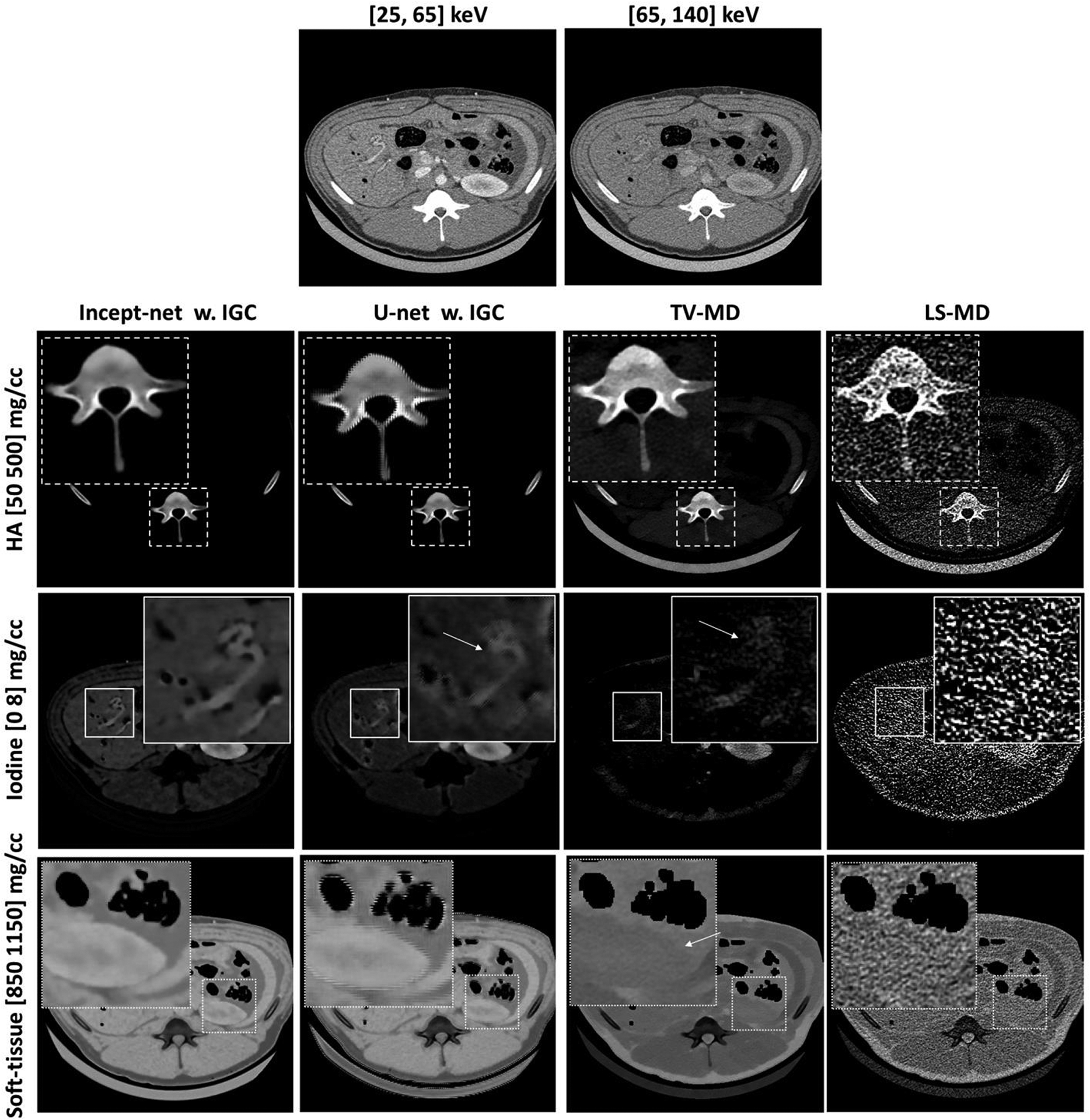
Material-specific images from the porcine abdominal CT scan, using Incept-net, U-net, total-variation (TV-MD), and least-square (LS-MD) based material decomposition methods. The spatial distribution of hydroxyapatite (HA), iodine and soft-tissue are shown in the top, middle and bottom rows, respectively. The CTDI_vol was 16 mGy. The zoomed insets are 3 times the size of the square region-of-interests. The arrows in the zoomed iodine insets indicate the location of blood vessels. The arrows in the zoom-in soft-tissue insets indicate the boundary of kidney. The range of display window for CT images were [-160, 240] HU.

Figure 9.

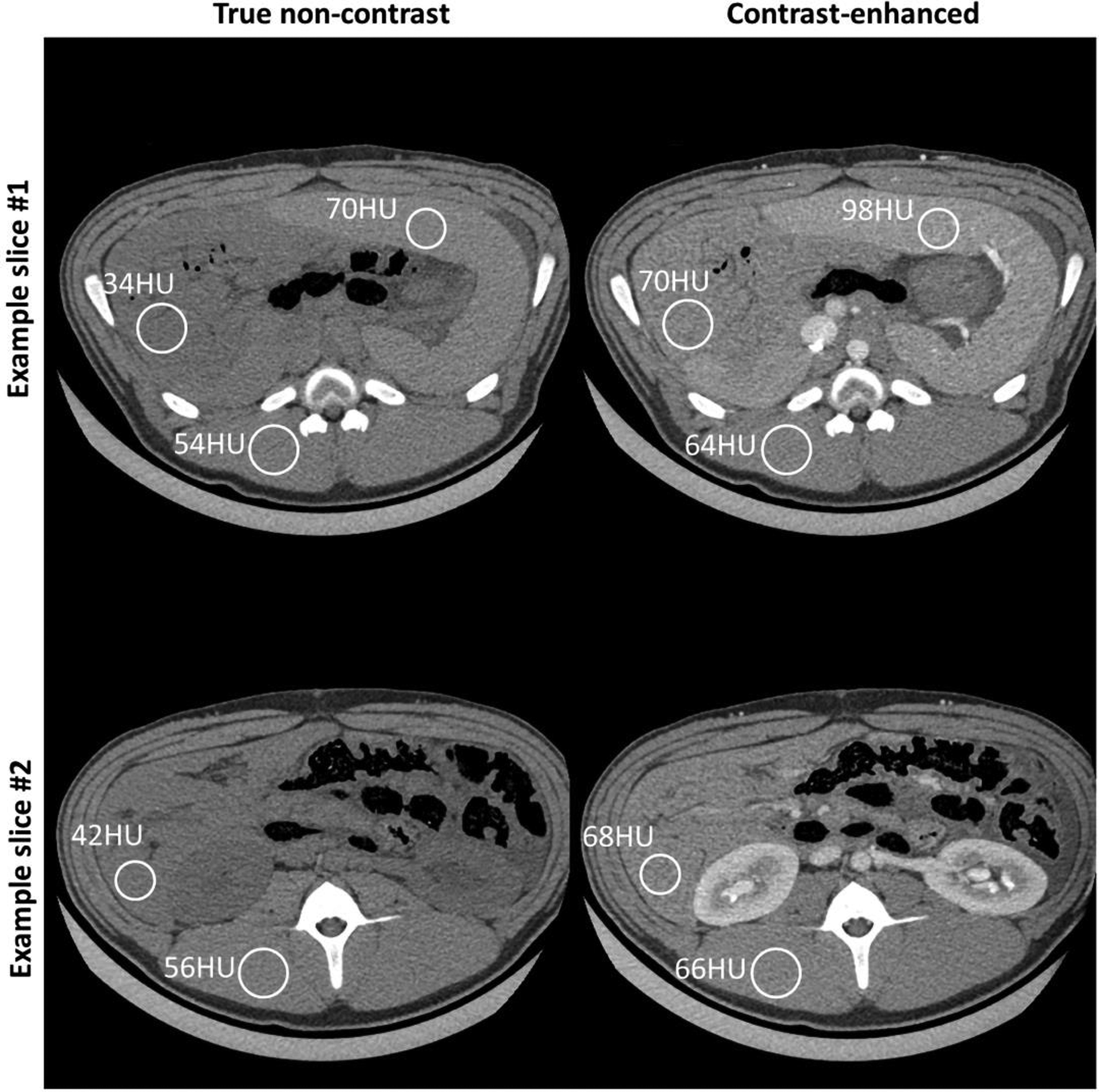
The comparison between true non-contrast (left column) and contrast-enhanced CT (right column) shows apparent CT number enhancement in soft-tissue, i.e. iodine uptake. The digits next to each circular region-of-interest (ROI) represent the measured mean CT numbers from the same ROI. Due to continuous bowel motion, we can only perform rigid alignment of relatively static major structure (e.g. ribs, spinal cord, and major abdominal muscle). However, those ROIs (range of diameter: ~24mm to ~30mm) were still placed in close proximity to the same tissues or organs. Display range: [-160, 240] HU.

Figure 10.

Material-specific images from a porcine chest CT scan (at a randomly-selected slice), using Incept-net, U-net, total-variation (TV-MD), and least-square (LS-MD) based material decomposition methods. The spatial distribution of hydroxyapatite (HA), iodine and soft-tissue are shown in the top, middle and bottom rows, respectively. The CTDI_vol was 16 mGy. The zoomed insets are 2.2 times the size of the square region-of-interests. In the zoomed iodine insets, the solid arrows indicate the location of blood vessels. In the iodine map of U-net outputs, the dashed arrow indicates strong bone residual at chest wall. The range of display window for CT images were [-160, 240] HU.

For both CNNs, the removal of the IGC regularizer caused observable aliasing at some soft-tissue and air boundary in material maps (e.g. the arrows in Figure 11). As for Incept-net, the use of additional 7×7 convolutional filters had no effects of ameliorating the aliasing artifact. As for U-net, subtle checkerboard artifact was observed when IGC was removed, while the use of IGC appeared to reduce checkerboard artifact at the relatively uniform region yet slightly amplify the edge artifact at high contrast blood vessels. Of note, the checkerboard artifact can be typically attributed to the well-known challenges in the up-convolutional operation, max-pooling and gradient artifacts in back-propagation^49–51. A further discussion about these findings is presented in Sec. 4. Finally, the material maps from Incept-net closely conserved the total mass densities (Figure 12), although no explicit mass conservation constraint was implemented. For example, the mean weighted sum of mass densities $f_{CNN}^w$ was 1.04 (±0.01), 1.03 (±0.01), and 1.02 (±0.01), in liver, kidney, and bonny structure, respectively. The slight discrepancy between the measured and ideal value of $f_{CNN}^w$ could be attributed to the fact that water mass density was used to approximate the mass density of pure soft-tissue in eq. (5). This heuristic validation indicated that the use of nominal basis material densities as the ground truth have possibly provided an implicit mass conservation constraint during CNN training.

Figure 11.

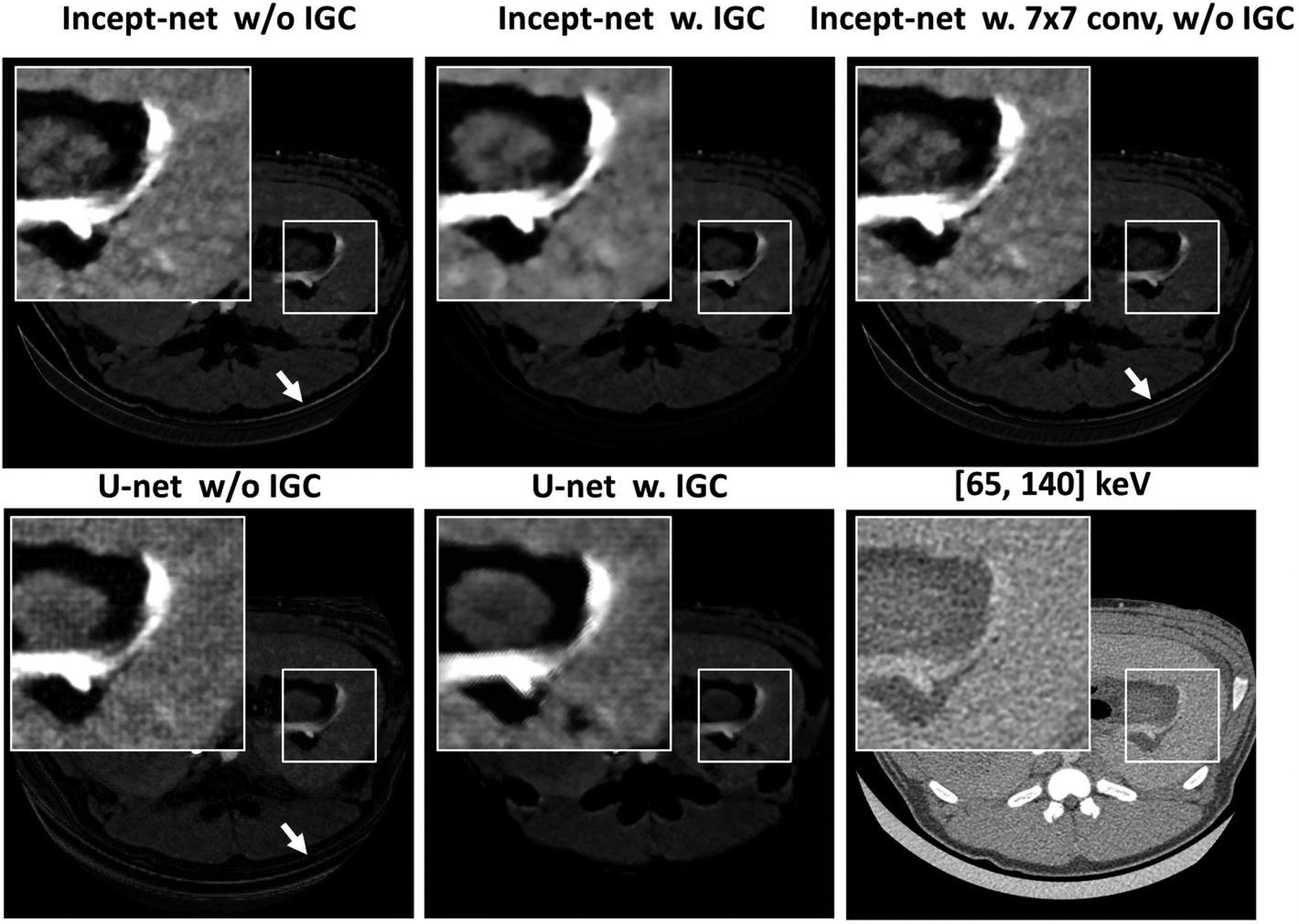
Iodine images showing the effects of the proposed image-gradient-correlation (IGC) based regularizer in both Incept-net and U-net, and the effects of additional factorized convolution with 7×7 filters in Incept-net. The arrows indicate the aliasing at the bottom boundary of the animal. The zoom-in insets are 2.5 times the size of the square region-of-interests. The ranges of display window for full field-of-view iodine images, the zoom-in iodine images, CT images were [0, 10] mg/cc, [0 4] mg/cc, and [-160, 240] HU.

Figure 12.

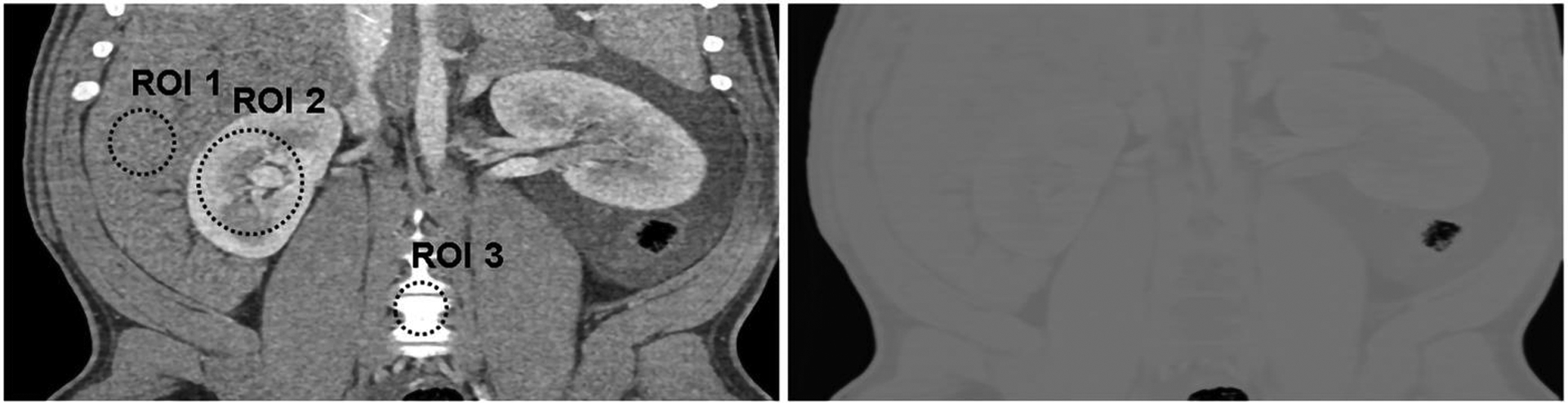
Example of heuristic validation of mass conservation for Incept-net outputs in porcine scan. Left subfigure: low-threshold (i.e. [25, 140] keV) CT image from coronal plane. Right subfigure: pixel-wise weighted sum of mass densities (eq. (5)) across all material maps acquired from the same coronal plane (display window: [0, 2]). The method for calculating the weighted sum is described in Sec. 2.4. The mean value of the weighted sum of mass densities at the three region-of-interests (ROIs #1 – 3, radius 11, 16, and 8 mm) was 1.04 (±0.01), 1.03 (±0.01), and 1.02 (±0.01), respectively. The range of display window for CT images was [-160, 240] HU.

4. Discussion

In this study, a custom Incept-net was developed to perform image-domain-based material decomposition with two energy-bin data sets acquired using a research whole-body PCD-CT. Incept-net was trained with augmented small image patches acquired from phantom scans, and then evaluated using the full-FOV CT images from independent phantom and animal scans. Incept-net demonstrated improved performance and detail-preserving capabilities, robustness against noise amplification and the quantitative accuracy for the materials of interest, even at the lower radiation dose levels. Especially, Incept-net maintained relatively consistent noise level compared to LS-MD at different dose levels. Although the Incept-net was only tested with two energy-bin data, it can be easily adopted to multiple (>2) energy bin data.

Based on universal approximation theory²⁹, a CNN could be used to approximate the functional mapping between multi-energy CT data and material densities. The accuracy of the approximation depends on the learning capacity of the CNN. The learning capacity is determined by the network architecture. To date, there is still a lack of theoretical guideline or consensus on the optimal design of CNN architecture for the purpose of solving general inverse problems. Nonetheless, recent studies have attempted to explore the theoretical link between the CNN and inverse problems in imaging. For example, Mousavi et al.⁵² provided a probabilistic interpretation that the training of the stacked denoising autoencoders minimized the energy of the compressed signal representation, i.e. the reconstruction error would also be minimized when the signal was de-compressed. Then, Jin et al.⁵³ demonstrated that the unrolled regularized iterative algorithms exerted the repeated operations of convolution and pointwise non-linearity, i.e., a form similar to the standard CNN architecture, when the forward model involved a normal-convolutional operator. Especially, Ye et al.³⁰ showed that the deep encoder-decoder neural network can be interpreted as the multi-layer deep convolutional framelets expansion in which the input signal would be represented by the stacked convolution of local and non-local bases. Based on this work, the local bases can be optimally learned from the training dataset, for a given design of non-local bases. The improvement on the design of non-local bases is beyond the scope of this study, but a follow-up study is warranted.

The proposed Incept-net was designed following the general form of encoder-decoder networks, instead of using the standard U-net or ResNet. With the fix-sized convolutional filters and max pooling, standard U-net can rapidly enlarge the receptive field to explore the feature representation of multi-scale non-local image context, which effectively improves the accuracy of object classification and detection. Standard U-net with average pooling still does not guarantee the perfect reconstruction of true signal, and it overly-emphasizes low-frequency components despite the use of skip connection, i.e. the high-frequency detail like edges and tissue interfaces is likely to be smoothed out³⁰. Thus, such networks are likely to demonstrate a strong denoising capability at the cost of smoothing out the fine low-contrast details, when they are used for modeling the point-wise image transformation, e.g., material decomposition in image domain. Furthermore, the standard up-convolutional layer and max pooling could yield the checkerboard artifact^49,50, which would require additional architectural changes for artifact suppression. Of note, despite the “average un-pooling”, the comparator “U-net” still involves un-convolution operation, which occurs in the back-propagation of the gradient of CNN parameters. The contracting path of the comparator “U-net” consists of standard convolutional and max pooling operations. Such contracting path becomes equivalent to the standard up-convolution, when the gradient of CNN parameter was propagated backward to the input layer (this was systematically explained in Odena et al’s work⁴⁹). As a result, any noise in the gradient of CNN parameters would raise checkerboard-like artifact⁴⁹. Additionally, there is no consistent evidence showing that average un-pooling could robustly maintain image quality, e.g. the reference⁵⁴ demonstrated the counter example showing that the paired max-pooling and average un-pooling does not prevent the occurrence of blurring and checkerboard-like image artifacts. It is also important to note the following fact. The study on checkerboard artifact is an active research area. Compared to average un-pooling, a number of advanced methods have been continuously proposed, and none of these methods has been validated to be the ultimate solution^49,50,55,56. Meanwhile, the proposed Incept-net can still learn the multi-scale signal representation without the standard pooling layers (i.e. max, average, and global max / average pooling), by using the different-sized convolutional filters (i.e., multi-scale filtering) in the customized multi-branch modules, i.e., Inception-B / -R modules. Intuitively, these modules enabled Incept-net to learn the image features at different scales and further enhance the network robustness against local noise and artifact perturbation. Of note, the exclusion of standard pooling and up-convolutional layers from Incept-net was mainly based on the aforementioned hypothesis that the local image context shall be sufficient for modeling the inverse mapping from multi-energy CT images to material-specific images. This hypothesis also motivated the strategy of training the CNN using simplistic phantom images and applying the CNN for anatomical images thereafter. Despite the simple insert structure used in training, the CNN output has largely maintained the anatomical structure in animal CT images. The CNN was mainly tasked to perform pixel-to-pixel regression in material-decomposition, and it could readily explore image structure redundancy between the labels and CT images. In this sense, the training for material decomposition task could involve simpler objects compared to several common applications that require CNNs to learn high-level features for perceptual tasks, e.g. image classification and segmentation, in which complex objects are necessary.

The comparison between true non-contrast and contrast-enhance CT exams (Figure 9) had at least qualitatively validated the iodine quantification of our method in anatomical background. Meanwhile, it is also possible that some un-enhanced dense muscle could be partially decomposed into iodine map, as the CT number of the animal’s un-enhanced dense muscle may be close to that of iodine-blood mixture inserts which were involved in CNN training. However, this is not necessarily a limitation or decomposition error of the proposed method. As was already pointed out in previous studies^36,38, the objects containing materials other than the pre-selected basis materials will still be decomposed into the same set of basis materials. Of course, any reliable material decomposition methods should yield accurate results when the objects are only made up with basis materials. Furthermore, the two conventional methods largely decomposed iodine-enhanced soft-tissue to the bone map (Figure 8), and also obviously underestimated iodine concentration in iodine-blood mixture inserts (Figure 7). These findings suggested that conventional methods yielded worse iodine quantification accuracy in the mixture of contrast-media and tissues used in this study. In addition, we did not use the commercial material-decomposition software or the simulation of patient anatomy in evaluation, mainly because such tools were not yet available for the research PCD-CT system. These tools are typically very useful for qualitative evaluation. However, we consider that extra caution should be taken, if one would like to use them in quantitative evaluation. It is impractical to use the commercial software to establish the ground truth of real anatomy, as commercial software has been reported to yield systematic iodine quantification error which varied across different configurations of CT systems and clinical scanning protocols^37,38. The simulation of human anatomy and CT systems can provide a self-consistent CNN training and testing scenario, as the training and testing dataset is in the same domain. Yet, it is still very challenging to realistically simulate all physics effects during data acquisition, processes involved in image reconstruction and tissue complexity. In contrary, with standard CT phantom materials, we can ensure that the same CT systems, clinical scanning protocols, reconstruction settings, and especially the vendors’ proprietary pre-/post-processing procedure were used in both phantom and patient data. Meanwhile, those phantom materials have been well-validated and widely-accepted as good surrogate of real human tissues. It is important to note that: the phantom-based validation has been used in numerous clinical and technical studies, as the major method, to validate the quantification accuracy of the commercial software^{36–38,57,58} or in-house algorithms^{5,7,14,16,59,60}. Although validation using patient images would be preferred in an ideal situation, it is extremely challenging to obtain ground truth in patient images in most scenarios. One potential feasible clinical scenario is multiple-phase CT scans involving both non-contrast and contrast CT scans, where virtual non-contrast images from dual energy material decomposition may be compared with true non-contrast images, although most comparisons are qualitative rather than quantitative^58,61.

One may expect to expand the network width and depth to further enhance performance by adding additional branches with larger convolutional filters in the multi-branch modules or stacking more layers in the network. In doing so, additional care must be taken to properly manage the network width and depth. From the perspective of deep convolutional framelets theory³⁰, the number of filter channels needs to be multiplicatively increased along the layer direction to guarantee the perfect reconstruction, and meanwhile the filter size and the intrinsic rank structure of the signal determine the minimal number of filter channels at each layer and the minimal number of CNN layers. In other words, for a given complicated signal, the use of a larger filter size could result in the exponentially-increased number of CNN parameters. In fact, it is typically not practical to fulfill this “sufficient condition” of perfect reconstruction. This is partially due to the extremely challenging requirement for computer memory. Moreover, it is also difficult to acquire sufficient statistics to determine the rank structure of the patient anatomy from a general population. When the configuration of the CNN does not satisfy the perfect reconstruction condition, the shrinkage behavior of the CNN starts to emerge, and may result in the loss of signal information and / or the rise of new artifacts. The use of proper regularization strategy could suppress the potentially-adversarial effects of shrinkage behavior (Figure 11). However, the shrinkage behavior could still be exploited to achieve an appropriate CNN performance for the material decomposition problem, by adjusting the configuration of filter channels and network layers with a given design of the non-local bases. For example, the shrinkage behavior could be controlled to reach a proper trade-off between the detail preservation and the noise suppression.

In the evaluation of quantitative generalizability, Incept-net consistently yielded smaller MAE than that of the other two methods across varying radiation dose levels. As the corresponding iodine concentration was within the concentration range used in CNN training, this finding indicated that Incept-net had good interpolation generalizability. Due to the highly non-linear nature of the CNN, it could be challenging to configure the network architecture to achieve good extrapolation generalizability especially on the unseen concentration that is far away from the training data manifold⁶². To bypass this challenge, a straightforward solution is to further increase the width and density of the training dataset, i.e., using more iodine concentration from a wider range.

We acknowledge several limitations in this preliminary study. First, the proposed method was only evaluated with CT data acquired from a specific type of research CT system. For other types of clinical CT scanners, the proposed CNN may need to be re-trained to achieve optimal performance for different CT tasks (e.g. head / chest CT exams), using phantom data acquired with the corresponding scanning / reconstruction protocols. Second, the generalizability of CNN in anatomical background was only evaluated using single porcine exam, without human subject studies. Further validation of CNN generalizability over different human body parts and clinical applications would be needed in follow-up studies. One potential direction is to compare CNN generated virtual non-contrast images from contrast enhanced scans to the true non-contrast images in multi-phase CT exams. Despite these limitations, a systematic evaluation of the proposed method for varying CT tasks in a larger patient cohort is warranted in further studies.

5. Conclusion

A CNN with the customized architecture (Incept-net) was developed to directly model the functional mapping from multi-energy CT images to material-specific images. Incept-net was trained using only the small patches of phantom images having a uniform background, but it demonstrated robust quantitative accuracy and detail-preserving capability on phantom materials with unseen concentrations and complex animal anatomical structures. Compared with the conventional LS-MD and TV-MD, the proposed Incept-net demonstrated superior capabilities in preserving fine details and suppressing image noise. Data from multiple dose levels demonstrated that Incept-net is less sensitive on radiation dose and image noise change compared to standard methods. The experimental results provided preliminary evidence that Incept-net could be a promising tool to further improve the quality of material decomposition in multi-energy CT.