Thermal modulation of epicardial Ca²⁺ dynamics uncovers molecular mechanisms of Ca²⁺ alternans

Ca²⁺ alternans can lead to T-wave alternans, a highly arrhythmogenic phenomenon. Through a thermodynamic analysis of the molecular mechanisms involved in generating Ca²⁺ alternans, Millet et al. concluded that Ca²⁺ alternans are produced by an incomplete replenishment of SR Ca²⁺ during tachycardia.

Abstract

Ca²⁺ alternans (Ca-Alts) are alternating beat-to-beat changes in the amplitude of Ca²⁺ transients that frequently occur during tachycardia, ischemia, or hypothermia that can lead to sudden cardiac death. Ca-Alts appear to result from a variation in the amount of Ca²⁺ released from the sarcoplasmic reticulum (SR) between two consecutive heartbeats. This variable Ca²⁺ release has been attributed to the alternation of the action potential duration, delay in the recovery from inactivation of RYR Ca²⁺ release channel (RYR2), or an incomplete Ca²⁺ refilling of the SR. In all three cases, the RYR2 mobilizes less Ca²⁺ from the SR in an alternating manner, thereby generating an alternating profile of the Ca²⁺ transients. We used a new experimental approach, fluorescence local field optical mapping (FLOM), to record at the epicardial layer of an intact heart with subcellular resolution. In conjunction with a local cold finger, a series of images were recorded within an area where the local cooling induced a temperature gradient. Ca-Alts were larger in colder regions and occurred without changes in action potential duration. Analysis of the change in the enthalpy and Q₁₀ of several kinetic processes defining intracellular Ca²⁺ dynamics indicated that the effects of temperature change on the relaxation of intracellular Ca²⁺ transients involved both passive and active mechanisms. The steep temperature dependency of Ca-Alts during tachycardia suggests Ca-Alts are generated by insufficient SERCA-mediated Ca²⁺ uptake into the SR. We found that Ca-Alts are heavily dependent on intra-SR Ca²⁺ and can be promoted through partial pharmacologic inhibition of SERCA2a. Finally, the FLOM experimental approach has the potential to help us understand how arrhythmogenesis correlates with the spatial distribution of metabolically impaired myocytes along the myocardium.

Introduction

T-wave alternans (TW-Alts) are alternating beat-to-beat changes in the T-wave of the electrocardiogram. TW-Alts are an important arrhythmogenic mechanism that can ultimately lead to sudden cardiac death (Cutler and Rosenbaum, 2009; Abdelghani et al., 2016; Stein et al., 2010; Ikeda et al., 2002, 2006; Gold et al., 2000; Rosenbaum et al., 1994; Narayan, 2006; Shimizu and Antzelevitch, 1999). TW-Alts are produced by the alternation in the action potential duration (APD-Alt) across the ventricular wall and are much more likely to develop during tachycardia (Rosenbaum et al., 1994; Pham et al., 2003; Nearing et al., 1991; Verrier and Malik, 2013). In the mouse heart, APD-Alts appear to be induced by alternations in the amplitude of Ca²⁺ transients (Wang et al., 2014; Kornyeyev et al., 2012; Escobar and Valdivia, 2014; Díaz et al., 2004). Ca²⁺ alternans (Ca-Alts), in contrast, seem to be induced by an alternating amount of Ca²⁺ released from the SR in response to L-type Ca²⁺ channel–mediated Ca²⁺ entry during every other beat.

APD-Alts are associated with impaired cardiac metabolism, similar to those generated during ischemia (Ortega Carnicer, 2007; Bounhoure, 1986; Murphy and Lab, 1994) or hypothermia (Floyd and Dillon, 1967; Hsieh et al., 2009; Egorov et al., 2012; Siddiqi et al., 2016). TW-Alts and APD-Alts both show a steep temperature dependency (Hirayama et al., 1993), which could be derived from a highly demanding metabolic process—for example, Ca²⁺ transport during the cardiac cycle. Specifically, Ca²⁺ transport between the cytosol, SR, and the extracellular milieu (via primary and secondary active transporters) could be affected by temperature variations (Bersohn et al., 1991; Obata et al., 2018). Here, the reuptake of the Ca²⁺ released from Ca²⁺ storage sites (SR) is the preponderant path (Escobar and Valdivia, 2014). Additionally, alternans in mechanical activity (pulsus alternans) can also be observed in hypothermic scenarios (Floyd and Dillon, 1967).

Alternans—mechanical, electrical, and Ca²⁺—seem to be an interdependent phenomenon (Kornyeyev et al., 2010, 2012; Escobar and Valdivia, 2014; Yapari et al., 2014; Hazim et al., 2015). However, the mechanistic crosstalk between intracellular Ca²⁺ handling, action potential (AP), and metabolism/temperature is still uncertain (Egorov et al., 2012; Gizzi et al., 2017). Fluorescence local field optical mapping (FLOM) was developed to elucidate the relationship between different types of alternans. FLOM allows for localized (3–13 µm), high-resolution measurements (time and space) of the membrane potential and the intracellular Ca²⁺ handling at the epicardial surface of a Langendorff-perfused heart. FLOM is an alternative to the traditional fast-imaging optical mapping techniques, and tracks changes in physiologic variables, such as propagation of APs, Ca²⁺ transients, and alternans in space and time. Although traditional optical mapping has been useful historically, it lacks the optical spatial resolution seen in FLOM to measure single-cell and subcellular signals. FLOM allowed us to correlate how Ca²⁺ transients and APs change within a specific local area of the ventricular epicardium with a continuous temperature gradient. The effects of temperature and heart rate (HR) on Ca²⁺ transients’ properties and the magnitude of Ca-Alts were then simultaneously evaluated. From FLOM results, it is evident that Ca-Alts depend on both HR and temperature and can occur in the absence of changes in the AP.

Materials and methods

Chemicals

Di-8-ANEPPS, Rhod-2AM, and pluronic acid were purchased from Biotium. Mag-Fluo 4 was purchased from Invitrogen. Thapsigargin (Tg) was bought from Millipore Sigma. Imidazole was from Thermo Fisher Scientific. All other drugs were from Sigma-Aldrich.

Ethical approval

Our animal facilities are Association for Assessment and Accreditation of Laboratory Animal Care accredited and Office of Laboratory Animal Welfare certified and fully comply with all regulations, policies, and standards that protect animal welfare. Animal use in our studies fully complied with the National Institutes of Health Guide for the Care and Use of Laboratory Animals (Committee for the Update of the Guide for the Care and Use of Laboratory Animals, 1996). All animal experiments were performed on adult BALB/c 8-wk-old male mice (Charles River Labs) following a protocol (#2008–201) approved by the Institutional Animal Care and Use Committee of the University of California, Merced.

Whole-heart preparation

Mice were injected intraperitoneally with sodium heparin 15 min before euthanasia via cervical dislocation. Hearts were then dissected and cannulated onto a Langendorff perfusion apparatus for retroperfusion with Tyrode solution containing (in mM) 140 NaCl, 5.3 KCl, 2 CaCl₂, 1 MgCl₂, 0.33 NaPO₄H₂, 10 HEPES, and 10 glucose, pH 7.4. Perfused hearts were allowed to stabilize for 10 min at room temperature. Subsequently, 10 µM blebbistatin was added to the perfusion solution to prevent mechanical activity. A Peltier unit was used to globally change the temperature of the Tyrode solution in a horizontal chamber.

Fluorophore loading of Di-8-ANEPPS, Rhod-2AM, and Mag-Fluo4

The potentiometric dye Di-8-ANEPPS or Ca²⁺ indicator Rhod-2AM were perfused for 30 min after the hearts were stabilized in the Langendorff setup. Di-8-ANEPPS (10 µg) was prepared with 20 µl of 20% pluronic in 5 ml Tyrode solution. Rhod-2AM (50 µg) was prepared with 20 µl of 20% pluronic in 1 ml Tyrode solution. The dye-containing solutions were separately perfused into individual hearts for 30 min at room temperature using two peristaltic pumps. Step-wise details of the preparation of these dyes have previously been published by our group (Aguilar-Sanchez et al., 2017).

Mag-Fluo-4 AM was used to measure changes in the intra-SR Ca²⁺ concentration. The dye was dissolved in 45–60 ml DMSO with 2.5% pluronic and added to a 1 ml normal Tyrode solution. Perfusion with Mag-Fluo-4 AM started after the spontaneous HR became regular (within 10 min after cannulation). After 1 h of perfusion at room temperature (21–23°C), the solution was switched to normal Tyrode and the temperature was steadily increased to 37°C within 10 min. The temperature increase induced washing out of Mag-Fluo-4 from the cytosol, allowing us to measure intra-SR Ca²⁺ signals. Additional information on this technique has been already published by our laboratory (Kornyeyev et al., 2010, 2012; Valverde et al., 2010). In most cases, a downward fluorescence signal reflecting the depletion of the SR was apparent before heating the heart; however, some minor upward (cytosolic) component was still noticeable shortly after electrical stimulation. Interestingly, the observed upward component completely disappeared within 10–20 min after the temperature reached 37°C. After Mag-Fluo-4 was removed from the cytosol, enough dye remained inside the SR to generate detectable signals for at least 2 h.

Steady-state and kinetic measurements of Rhod-2 at different temperatures

To determine the K_d, experiments were done using a Rhod-2 tetra potassium salt (at a final concentration of 0.25 µM). The Rhod-2 fluorescence dye was excited at 532 nm and monitored at different temperatures within the range of 580–630 nm using a spectrofluorometer (QuantaMaster 40; Photon Technology). The dependence of the maximum amplitude of fluorescence, recorded at 600 nm, was measured at the different free Ca²⁺ concentrations.

Kinetic parameters of Rhod-2 were obtained by inducing a Ca²⁺ spike using 10 mM DM-Nitrophen at a resting Ca²⁺ concentration of 10 nM (Escobar et al., 1997). Photolysis was performed using a UV illumination generated by a DPSS UV laser (355 nm; DPSS Lasers) delivered through a quartz multimode fiber optic (NA 0.48). The emitted light of the fluorophore was detected with pulsed local field fluorescence microscopy (PLFFM; Ramos-Franco et al., 2016; López Alarcón et al., 2019; Aguilar-Sanchez et al., 2019) using multimode optical fiber (NA 0.67) and excitation of 532 nm. Finally, the temperature dependency of the association rate constant, k_on, was calculated as

$$k_{on}=\frac{k_{off}}{K_d}.$$

Electrical measurements using sharp microelectrodes

Epicardial APs were recorded with 10–20 MΩ resistance sharp glass microelectrodes pulled from 1/0.58-mm borosilicate glass capillaries (World Precision Instruments) using a Flaming/Brown puller (Sutter Instrument), filled with 3 M KCl and connected to a high-input impedance differential amplifier (Duo 773 Electrometer; World Precision Instruments). An AgCl pellet (World Precision Instruments) was placed in the bath and used as a reference electrode. The microelectrode was positioned at the surface of the heart using a manual mechanical micromanipulator, and their readouts were zeroed before tissue impalement.

FLOM

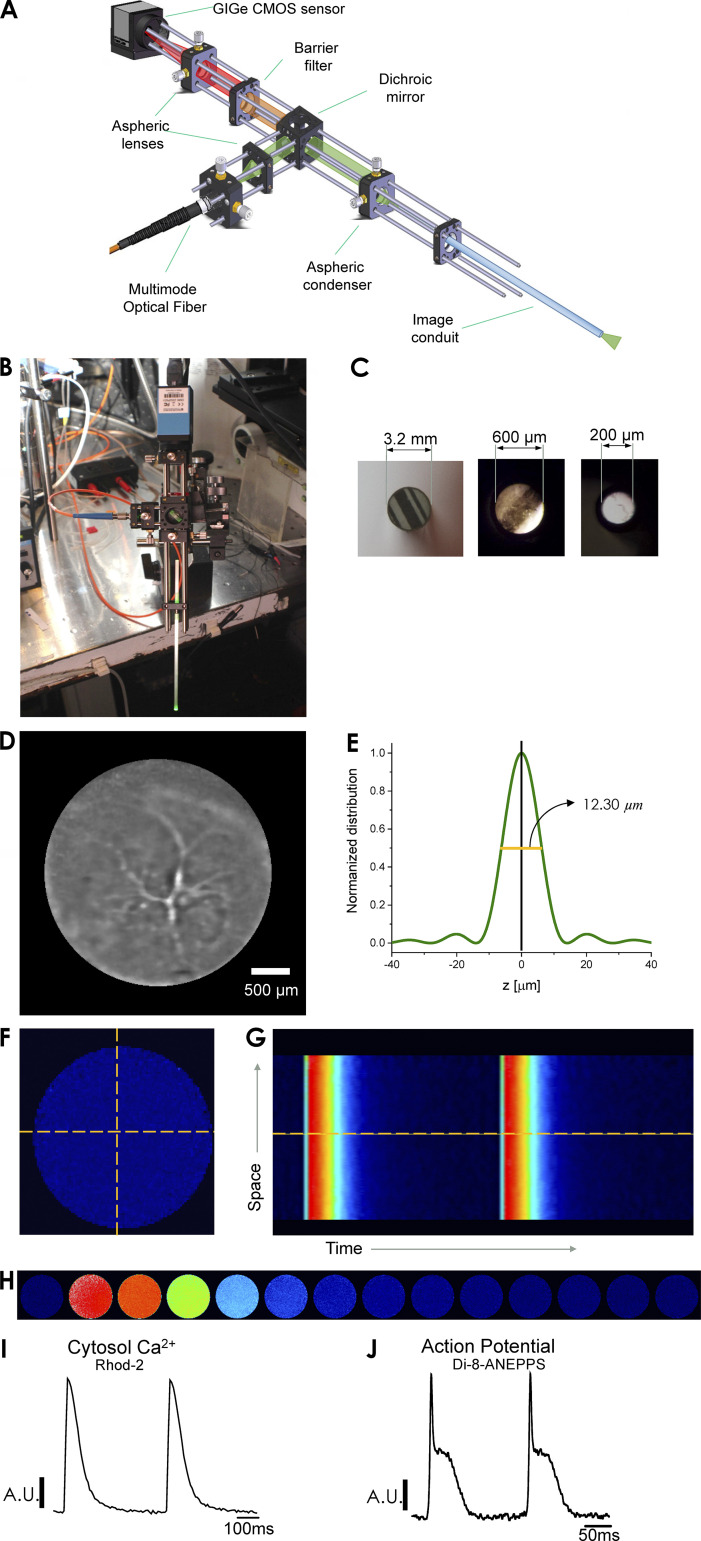
The FLOM setup consists of three main elements: a laser-driven epifluorescence arrangement, an image optical conduit in contact with the tissue, and a fast detection camera (up to 1-kHz frame rate) used for imaging the tissue surface in contact with the tip of the conduit (Fig. 1 A). The FLOM apparatus can be mounted onto a micromanipulator to record different areas of the epicardial layer (Fig. 1 B). The light path in these experiments was manipulated (through filters, expanders, dichroic mirrors, and/or microscope objectives) in the same way as previously described for PLFFM (Mejía-Alvarez et al., 2003; Aguilar-Sanchez et al., 2017). One main difference in FLOM is that instead of using a 200-µm optical fiber for an average signal in the heart epicardium, the light is focused onto an image optical conduit (Edmund Optics or Myriad Fiber Imaging), fused into one solid cylindrical bundle containing thousands of optical fibers. The lasers used for excitation were a blue light (473 nm) obtained from an MBL-10-3 CW Ng-YAG laser (Enlight Technologies) and a Verdi 8 W laser (532 nm; Coherent). The diameter of the optical conduit, which determines the area of a global measurement, varied from 0.2 to 3.2 mm (Fig. 1 C). Each fiber’s diameter, ranging from 3 to 11 µm, determined the x-y resolution of the measurements. FLOM uses a fast charge-coupled device or CMOS camera to record the emitted dye fluorescence, which differs from PLFFM where an avalanche photodiode is used. Furthermore, the FLOM arrangement can measure individual fluorescence signals from multiple contiguous sites within a layer of epicardial cardiomyocytes. These recordings result in 2-D images that can be depicted as line scan surface plots. IC Capture (Imaging Source) and ImageJ (National Institutes of Health) were used for data acquisition and processing, respectively. Fig. 1 D illustrates a typical epicardial FLOM light image obtained with a 3.2-mm optical image conduit, where a high degree of vascularization can be observed.

Figure 1.

The optical arrangement of FLOM. (A) FLOM consists of a laser-driven epifluorescence arrangement that uses an optical image conduit in contact with the tissue. Fluorescence is detected with a fast-recording charge-coupled device or CMOS camera. (B) FLOM apparatus mounted onto a mechanical micromanipulator. (C) Optical image conduits of different sizes. (D) FLOM light image, equivalent to a microendoscope, showing blood vessels in the epicardial ventricular tissue. (E) Normalized detected light distribution of the FLOM microscope in the z axis. (F) Whole FLOM fluorescence Ca²⁺ image during a Ca²⁺ transient is measured with the Ca²⁺ fluorophore Rhod-2. (G) Extracted line scanned epicardial Ca²⁺ transient from FLOM image frames (one image per ms). (H) Frame-by-frame image sequence (one image per 50 ms) of the changes in fluorescence during a Ca²⁺ transient induced by electrical stimulation. The color scale ranges from the blue, which indicates low fluorescence (low cytosolic Ca²⁺), to red (designates high Ca²⁺). (I) Ca²⁺ transients obtained from a line scan of the FLOM image, providing proof that FLOM-recorded images can be analyzed in time and space. (J) Extracted epicardial APs measured with Di-8-ANEPPS from FLOM images indicate that FLOM is amenable to experimentation with a variety of fluorophores.

For visualization purposes, the emitted fluorescence images were color mapped using a lookup table and a color scale. The blue and red colors indicate low- and high-dye fluorescence signals, respectively.

FLOM is an optical instrument and, as such, has a defined depth of field, which was estimated by using a model having cylindrical symmetry and a z energy normalized distribution described by

$$F\left(z\right)={\left\{\frac{sin\left(\frac{\pi \cdot N{A}^2\cdot z}{2\cdot M^2\cdot \lambda }\right)}{\left(\frac{\pi \cdot N{A}^2\cdot z}{2\cdot M^2\cdot \lambda }\right)}\right\}}^{ 2}\mathrm{,}$$

where NA is the numerical aperture of the optical conduit (0.55), z is the axial variable, M is the magnification of the focusing lens, and λ is the wavelength of the excitation beam (0.532 µm). A graph of the normalized distribution of intensities as a function of the z-axis is shown in Fig. 1 E. The estimated depth of field for these parameters was 12.30 µm.

Fig. 1 F depicts a diastolic image of an intact heart loaded with Rhod-2. The time course of intracellular Ca²⁺ transients can be imaged when the heart is externally paced (Fig. 1 H). Images can be individually analyzed to obtain x-t scans (Fig. 1 G) or summed to obtain averaged epicardial Ca²⁺ transients and APs (Fig. 1, I and J, respectively).

Microsome measurements

Cardiac SR microsomes containing a SERCA2a pump with minor RYR2-mediated leak were prepared by combining ventricular tissue from four male Yorkshire-Landrace crossed-breed pigs (3 mo of age and weighing 30–40 kg) following standard protocols (Chamberlain et al., 1983). Tissue preparations were then stored in liquid nitrogen and used within 30 d. For experiments, SR microsomes were split into 100-µl aliquots at a concentration of ∼10 mg protein/ml in 5 mM imidazole-Cl 290 mM sucrose, pH ∼7. They were snap-frozen with liquid N₂ and stored at −80°C. For spectroscopic measurements, aliquots were quickly thawed in water, incubated on ice, and used within 3 h. Ca²⁺ uptake by cardiac SR microsomes was measured as previously described (Neumann and Copello, 2011; Darcy et al., 2016). Ca²⁺ uptake was initiated by adding 40 nM CaCl₂ to a cuvette containing 100 µg SR membranes suspended in 1 ml buffer (in mM: 100 KH₂PO₄, 5 MgCl₂ (∼0.3 mM free Mg²⁺), 5 ATP, and 0.2 absorbance Ca²⁺ indicator antipyrylazo III, pH 7.0). Ca²⁺ uptake at temperatures ranging from 6°C to 38°C was monitored following changes in antipyrylazo III absorbance (710–790 nm) with a spectrophotometer (Cory 50; Varian Medical Systems). The temperature inside the cuvette was measured with a digital thermocouple thermometer (Thomas Scientific). The initial rate of Ca²⁺ uptake (J_Ca), in micromoles of Ca²⁺ per milligram of protein per minute, was estimated from fitting the following equation:

$$J_{Ca}=40 nmol\frac{\Delta O{D}_t}{\Delta O{D}_0}\frac{e^{-kt}}{S}\mathrm{.}$$

The variables are as follows: ΔOD₀, initial OD change produced by adding 40 μM Ca²⁺ to the cuvette; ΔOD_t, decrease in OD as a function of time; S, milligrams of microsomal protein added to the cuvette; k, the rate of uptake (in seconds⁻¹), assuming a first-order process; and t, uptake time (in seconds).

Statistical analysis

The physiologic recordings of the APs, Ca²⁺ transients, Ca²⁺ images, and AP images were evaluated based on well-established parameters in the field of cardiac electrophysiology.

The APs’ traces for each set of experiments were evaluated, and the time for the AP to reach 70% repolarization was assessed. Repolarization times at each temperature and each HR were then evaluated and normalized to the control values for each heart. After normalization, values from five experiments (n = 5 hearts, or as otherwise noted) were compiled, and statistical analysis was performed with Origin 19 using a one-way ANOVA test.

Ca²⁺ transients were also recorded at different temperatures and HRs. Several parameters of the Ca²⁺ transient kinetics were estimated, including the relaxation time of the Ca²⁺ transients, as well as the first derivative of the fluorescent recordings. Data from five experiments (n = 5 hearts or stated otherwise) were compiled and analyzed with Origin 19. Finally, all data are presented as means ± SD.

Online supplemental material

Included at the bottom of the PDF is a mathematical demonstration of how the first derivative of the relaxation of the Ca²⁺ transient can give us information about the relaxation time constant.

Results

Ca²⁺ transient alternans depends on HR and global temperature

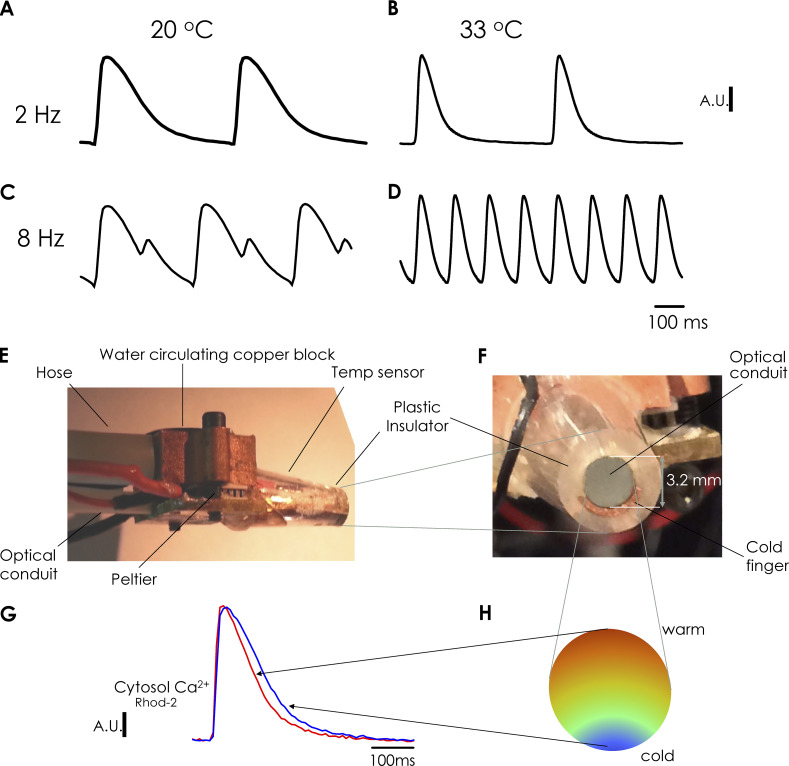
In this study, we assessed how temperature changes the HR dependency of Ca-Alts. In a set of experiments, Ca²⁺ transients were assessed by using FLOM in hearts loaded with the Ca²⁺ indicator Rhod-2, via coronary retroperfusion (Fig. 2). Fluorescent traces represent the average of photons collected from more than 50,000 fiberoptics in an optical image conduit. The temperature of the bath solution was set with an electronically controlled Peltier unit. Fig. 2, A and B, shows marked changes in the kinetics of epicardial Ca²⁺ transients recorded at 20°C and 33°C, respectively. At 33°C, both the rise time and the decay time of Ca²⁺ transients decreased. After increasing the HR from 2 Hz to 8 Hz at 20°C, a dramatic alternating behavior in the amplitude of Ca²⁺ transients was observed (Fig. 2 C). Moreover, at 33°C and an HR of 8 Hz, Ca-Alts were not observed (Fig. 2 D). Altogether, these results suggest the genesis of Ca-Alts involves a process that is highly dependent on cellular metabolism.

Figure 2.

Global temperature dependency of Ca²⁺ alternans and cold finger device. (A–D) Ca²⁺ transients measured with the FLOM apparatus at 20°C (global temperature of heart and bath) and an HR of 2 Hz (A); 33°C and 2 Hz (B); 20°C and 8 Hz (C); and 33°C and 8 Hz (D). Large Ca-Alts can be observed at 20°C and 8 Hz, which are removed by increasing the temperature to 33°C. (E) Lateral view of the tip of the FLOM microscope. The cold finger is positioned inside a plastic device; thus, in this lateral figure, it is not possible to observe the metallic cold finger. It is also possible to observe the Peltier unit and the water circulating copper block that allow for setting the temperature in one of the sides of the Peltier unit. (F) Front figure of the tip of the FLOM microscope. It is possible to observe the optical conduit, the cold finger, and the plastic device covering the cold finger and the optical conduit. Moreover, the cold finger is a copper metallic tube filled down to a semilunar that encloses nearly half of the tip of the optical image conduit in contact with the surface of the heart to generate a temperature gradient. (G) Rhod-2 fluorescence Ca²⁺ transients obtained from FLOM images of the ventricular epicardium. (H) Scheme of the temperature distribution from where the Ca²⁺ transients presented in G were recorded.

Ca-Alts are also sensitive to epicardial local temperature control

Here, we used the FLOM microscope to address how a local change in the metabolic status of the tissue can affect its Ca²⁺ handling dynamics. To address this issue, we developed a novel apparatus to change the local temperature at the epicardial layer with the aid of a cold finger coupled to the FLOM microscope (Fig. 2, E and F).

Cooling was mediated by a Peltier-controlled metallic cold finger, which consisted of a metallic tube soldered to a brass plate with one side contacting a micro-Peltier unit. The other side of the Peltier was kept at a constant temperature via a copper block that allows water circulation to fix the temperature. This process was driven by a pump that dissipated the heat produced by the micro-Peltier unit. The temperature of the cold finger was monitored with a linear temperature sensor (AD590; Analogue Devices) encapsulated within a plastic insulator coating the cool finger (Fig. 2, E and F).

The optical conduit and the semilunar-shaped cold finger (Fig. 2 F) were placed in contact with the epicardial layer of the heart to carry out FLOM imaging experiments. This contiguity allowed us to locally change the epicardial temperature in the area where the conduit directly contacted the tissue. The system generated a temperature gradient where the tissue closest to the cold semilunar finger became cooler, while the temperature of the tissue contacting the opposite side of the conduit remained similar to the temperature of the bath (Fig. 2 H). Example traces of Ca²⁺ transients recordings in cold and warm regions of epicardial tissue are illustrated in Fig. 2 G. Again, we observed faster Ca²⁺ transients in the warmer region, as previously observed in Fig. 2, A and B, for global changes in temperature.

A spatial map of the distribution and magnitude of Ca-Alts in the cold and warm epicardial imaged areas was generated by using a ratiometric procedure (Fig. 3). We used images at the larger Ca²⁺ transient having a larger peak (A_H) and images of the alternating Ca²⁺ transients with a smaller peak (A_L; Fig. 3 A). A normalized map for Ca-Alts was generated from the difference of A_H minus A_L divided by A_H, as in the example in Fig. 3 B. An alternans map for all regions is shown in Fig. 3, C and D, where reddish and yellower areas correspond to epicardial regions with higher and lower alternans, respectively.

Figure 3.

Local temperature dependency of Ca²⁺ alternans. (A) Subtraction and radiometric normalization of images recorded using the FLOM apparatus at the peak of the higher Ca²⁺ and lower Ca²⁺ transients. (B) The resulting image is a map of the distribution of Ca-Alts. (C) Color-coded Ca-Alts distribution. The reddish region indicates large Ca-Alts (top), and the yellower regions (bottom) indicate small Ca-Alts, reflecting the magnitude of the alternans recorded by each individual fiber. (D) A decrease in the local temperature increases the magnitude of Ca²⁺ alterans. (E) Cold and warm region spatial distribution of alternans versus heart pacing frequency (alternans maps computed as described in Results). Hearts were kept in a bath at 32°C and the cold finger was set to 18°C. (F) Effect of HR on the amplitude of Ca-Alts recorded in the warm and cold regions of the ventricular epicardium. Ca-Alts in the cold region are visible at 5 Hz and, at faster pacing (6–8 Hz), develop significantly larger than in the warm region. *, P < 0.01; n = 5 hearts.

Fig. 3 E shows an example of Ca²⁺ transients in cold and warm areas of the epicardial layer when the heart was paced at different frequencies. At a bradycardic HR (4 Hz), alternans in the Ca²⁺ transients were not observed in either warm (top) or cold (bottom) regions. Increasing the rate to 5 Hz created small alternans, specifically noticeable in the cold region. These alternans in the cold regions increased in size with increasing HR, ultimately reaching a large magnitude at 8 Hz. In warm regions, only relatively small Ca-Alts were visible at 7 and 8 Hz. The combined data from five mouse hearts (Fig. 3 F) show the differential increase in the magnitude of Ca-Alts in the cold versus warm regions of the heart when pacing increased from 4 to 8 Hz.

Ca-Alts can be uncoupled from APD-Alts

APD-Alt is thought to play a key role in Ca-Alts by changing the magnitude and time course of Ca²⁺ influx via L-type Ca²⁺ channels and the magnitude of Ca²⁺-induced Ca²⁺ release (CICR; Song et al., 2015; Hayashi et al., 2007). Here, we performed a series of experiments designed to determine if Ca-Alts can be originated in the absence of APD alternation.

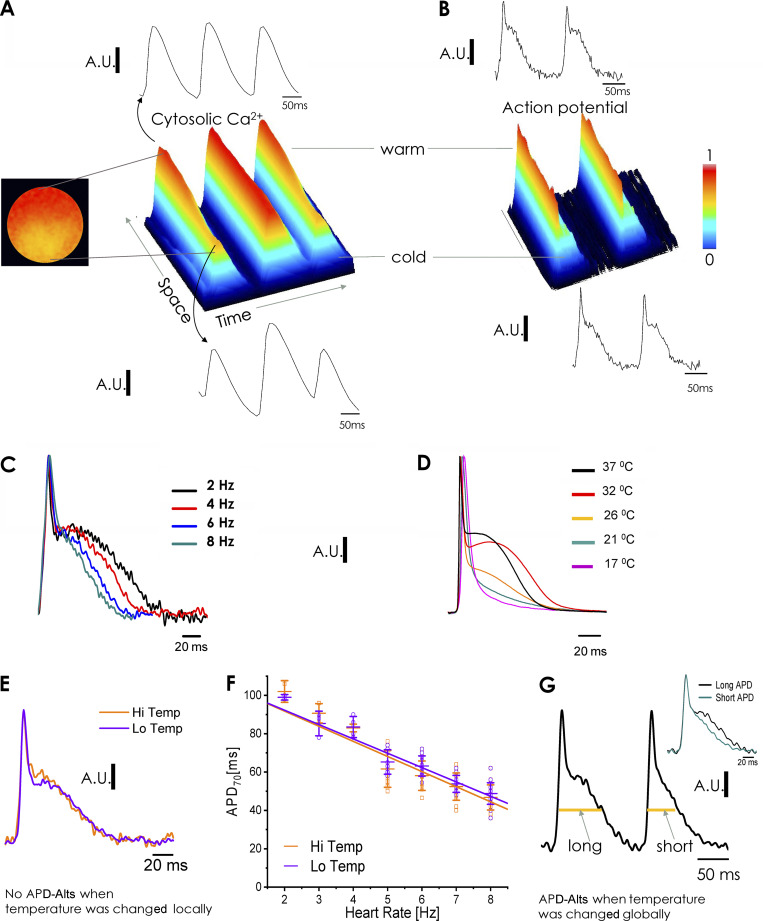
Fig. 4 A shows FLOM images of three consecutive Ca²⁺ transients in a line of the ventricular epicardium where a local temperature gradient was generated by using a local cold finger. When the heart was paced at 7 Hz, the x-t plot shows large Ca-Alts in the first and third Ca²⁺ transient recorded at the coldest region of the epicardium. Analogous to the findings in our Ca-Alts map (Fig. 3 E), the magnitude of the Ca-Alts continuously decreased—until vanishing completely—upon moving toward the direction of warmer temperatures. When the heart was loaded with the potentiometric dye Di-8-ANEPPS, the time course of two consecutive APs was nearly identical in cold and warm regions (Fig. 4, B and E, where the temperature was changed locally). Thus, local gradients of epicardial temperature can generate gradients of Ca-Alts (larger in the cold regions) in the absence of APD-Alts.

Figure 4.

Global and local temperature dependency of action potentials and action potential alternans. (A) Effects of changes in local temperature on epicardial Ca²⁺ transients. The plot is a 3-D (time-space-magnitude) surface representation from a line scan on a FLOM image in a heart loaded with Rhod-2. Ca-Alts are large in the cold region but dissipate when moving away from the cold finger. (B) Local temperature effects on epicardial APs, measured after loading the heart with the potentiometric dye Di-8-ANEPPS. Changes in local temperature did not affect the shape of APs and did not differentially induce APD-Alts in cold regions. (C) Effect of the HR on the repolarization of epicardial APs. Studies at constant 32°C using FLOM in a heart loaded with Di-8-ANEPPS found that the increase in the HR reduces the duration of phase 2 (APD₇₀). (D) Global temperature effects on electrically recorded (microelectrodes) epicardial APs in a heart paced at 5 Hz. Changes in the global temperature have a profound effect on the kinetics of APs. (E) Time course of optically recorded APs in cold and warm regions of the heart after the temperature was locally changed. No significant differences in AP shapes were found between the cold or warm regions. (F) Frequency dependency of APD₇₀ of APs recorded with FLOM in two regions that were locally set at high and low temperatures (n = 5 hearts; P < 0.01). (G) Global cooling induced an alternating behavior in two consecutive APs. In the inset, we show a long and short AP superimposed when the hearts were paced a 7 Hz. The long APD has a half–phase 2 duration for the first set of APs of 75.3 ± 3.63 ms and the short APD has a half–phase 2 duration for the second set of APs of 54.4 ± 3.29 ms (n = 5 hearts; P < 0.01).

We also evaluated the effect of the HR and the global temperature on the shape of the APs. As shown in Fig. 4 C, in hearts bathed at the constant temperature of 32°C, increasing the HR from 4 to 8 Hz caused the phase 2 of the AP to significantly shorten. Based on our previous studies, this observation may reflect the coupling between the negative staircase behavior of SR Ca²⁺ release and the plasma membrane excitability (Ferreiro et al., 2012; Kornyeyev et al., 2012). Fig. 4, E and F, shows that when the epicardial temperature was locally changed with the cold finger, optically recorded APs displayed the same magnitude and frequency-dependent shortening of their 70% repolarization time in cold versus warm regions (n = 5 hearts). On the contrary, when the temperature of the heart and bath were globally decreased (Fig. 4 D), the duration of the AP, as measured with sharp microelectrodes, significantly decreased. Similar results were observed with APs optically recorded with FLOM. At low global temperatures, differences were observed between the kinetics of two consecutive APs (Fig. 4 G), indicating APD-Alts. The inset shows two superimposed consecutive APs. In summary, our data show both local and global changes in temperature can induce Ca-Alts, but only global changes in temperature induce APD-Alts. These observations indicate that the process of Ca²⁺ signaling is controlled at the local cellular level, while the APs cannot be modulated when the temperature changes in a regional/local way as each cardiomyocyte is a part of a network electrically connected via gap junctions (Ramos-Franco et al., 2016).

Estimation of local temperature from the kinetic of relaxation of Ca²⁺ transients

Changes in global bathing temperature from 20°C to 32°C affect the kinetics of Ca²⁺ transients measured from averaged FLOM images from the ventricular epicardium (Fig. 5, A and B). As the temperature increased, the time to peak of the Ca²⁺ transients shortened and the relaxation process became faster. As previously stated, changes in local versus global temperatures seem to affect Ca²⁺ signaling similarly. Unfortunately, we cannot directly measure epicardial temperature while imaging the heart tissue with a conduit. Nevertheless, we can use the rate of relaxation of Ca²⁺ transients, which has a much stronger temperature dependency than the rise time (Fig. 5 B), as a parameter to estimate local temperatures.

Figure 5.

Global temperature dependency of Ca²⁺ transients relaxation. (A) FLOM fluorescent images versus time from a heart loaded with Rhod-2 at various bath temperatures upon electrical stimulation (pacing at 2 Hz). In the scale, blue and red indicate low and high Ca²⁺ bound to dye (CaD), respectively. (B) Ca²⁺ transients averaged from FLOM fluorescent images of a heart loaded with Rhod-2 at decreasing bath temperatures. The temperature was dropped in steps of 2°C and the heart was stabilized for 5 min before every recording. (C) The derivative of the decay phase of the Ca²⁺ transients seen in B, representative of n = 5 experiments performed in different hearts. (D) Arrhenius plot of the rate of decay of the Ca²⁺ transients as a function of the bath temperature. The enthalpy was ΔH = 9.17 ± 0.13 Kcal/mol and the entropy was ΔS = 34.7 ± 0.45 cal/(mol.K). n = 5 hearts. (E) Relationship between the estimated maximum rate of decay and temperature. In the range of 22°C to 32°C, the formal exponential fitting function (green line) can be approximated by linear regression. The Q₁₀ between 22°C to 32°C was 1.68 ± 0.17 (n = 5 hearts).

The decay of the Ca²⁺ transient resembles an exponential process, where the amplitude of the Ca²⁺ transient derivative is inversely proportional to the time constant of the decay. Fig. 5 C shows how the computed derivatives of the normalized Ca²⁺ transients are indicative of the maximum negative derivative, which was larger and occurred sooner at 32°C. The mathematical validation of the method is presented in the Supplemental text (see bottom of PDF). Data collected from five hearts were used to generate an Arrhenius plot in which we correlated the logarithm of the maximum derivative versus the reciprocal of the temperature (Fig. 5 D). The plot was fitted with Eyring's equation:

$$ln\left[\frac{d\left[CaD\left(t\right)\right]}{dt}max\right]=-\frac{\Delta H}{RT}+\frac{\Delta S}{R},$$

where ΔH is the change in enthalpy, ΔS is the change in entropy, R is the gas constant, and T is the temperature in Kelvin. The monotonic linear behavior of the Arrhenius relationship suggests a single thermodynamic process may be dominant for defining the relaxation of the Ca²⁺ transients. This linear relationship allowed us to calculate both the change in enthalpy (ΔH = 9.17 ± 0.13 Kcal/mol) and the entropy (ΔS = 34.7 ± 0.45 cal/[mol.K]) of the relaxation process. We also analyzed changes in the maximum derivative as a function of the temperature in Celsius (Fig. 5 E). Here, exponential behavior best fits the data (Fig. 5 E, green line); however, within this temperature range, the curvature is small enough for us to allow the approximation of a linear relationship between the maximum relaxation rate of the Ca²⁺ transient and the temperature.

The linear relationship was fitted to the data, where a (2.36 s⁻¹) is the intercept, b (0.39 s⁻¹ · °C⁻¹) is the slope, and T is the temperature in Celcius.

Temperature dependency of the Ca²⁺ indicator Rhod-2

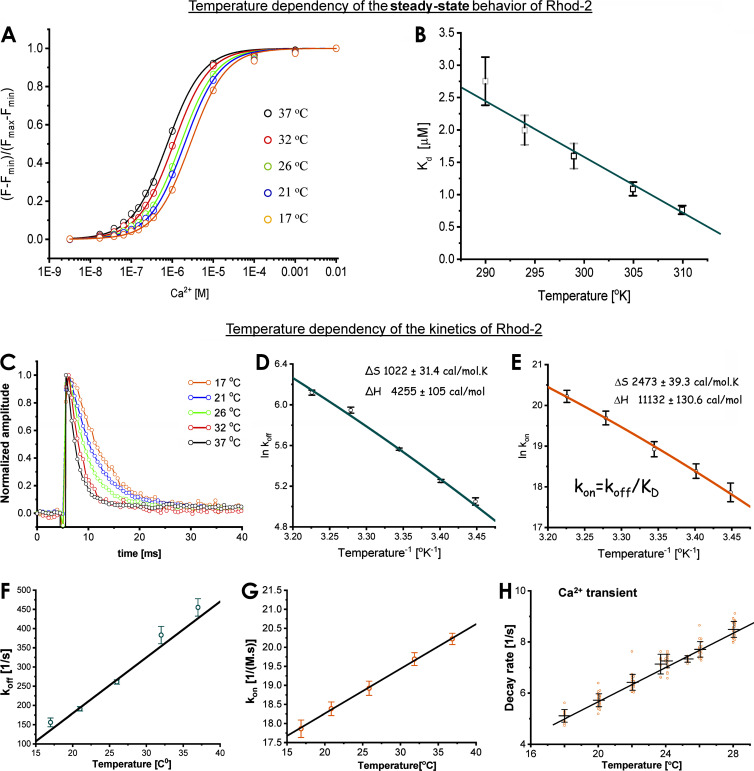
The temperature dependency of the Ca²⁺ dye is a critical factor that needs to be addressed to distinguish whether the temperature effects observed in the Ca²⁺ transients are due to the transport properties of the myocytes or simply defined by the temperature-dependent behavior of the indicator. Fig. 6 A illustrates how the temperature shifts the saturation curve of Rhod-2. A plot of the K_d is shown in Fig. 6 B. Interestingly, the higher the temperature, the higher the affinity of Rhod-2.

Figure 6.

Global temperature dependency of the Ca²⁺ indicator Rhod-2. (A) Steady-state dependency of the Ca²⁺ indicator Rhod-2 at different levels of free Ca²⁺ concentration at five different temperatures. The date was fitted with a saturation function to obtain the K_d value at different temperatures. (B) Plot of the dissociation constant K_d as a function of the temperature in degrees Kelvin. There was an increase in the affinity of the dye as the temperature was increased. (C) Temperature dependency of the unbinding of Ca²⁺ from Rhod-2, the Ca²⁺ indicator. A Ca²⁺ spike induced by photolysis of DM-nitrophen triggered the reaction. (D) Arrhenius plot of the rate of Ca²⁺ unbinding (k_off) from Rhod-2. The entropic change was ΔS = 1,022 ± 31.4 cal/(mol.K) and the change in enthalpy was ΔH = 4,255 ± 105 cal/mol. (E) Arrhenius plot of the association rate constant (k_on) from Rhod-2. The entropic change was ΔS = 2,473 ± 39.3 cal/(mol.K) and the change in enthalpy was ΔH = 11,132 ± 130 cal/mol. (F) Temperature dependency of the dissociation rate constant (k_off) as a function of temperature. (G) Temperature dependency of the association rate constant (k_on) as a function of temperature. (H) Rate of relaxation of epicardial Ca²⁺ transients as a function of temperature. Both the dissociation rate constant and the association rate constants are faster than the relaxation of the epicardial Ca²⁺ transients (n = 4 experiments).

We also defined the temperature dependency of the dissociation rate constant of Ca²⁺ from the fluorescence Ca²⁺ indicators (Fig. 6 C) by using a previously reported method (Escobar et al., 1995, 1997). Briefly, Ca²⁺-DM-nithrophen (nitrophenyl EDTA) was photolyzed in the presence of a large excess of free DM-nitrophen. The photolytic reaction was performed inside a chamber where the temperature was controlled with a Peltier unit. A transient spike of Ca²⁺ was observed as the excess DM-nithrophen captures the Ca²⁺ that is uncaged after the photolysis. The time course of [Ca²⁺] unbinding from the indicator was measured by using the Ca²⁺-sensitive dye Rhod-2. The traces present a monoexponential decay where the time constant of relaxation is the reciprocal of the unbinding rate, k_off [1/s]. Ca²⁺ unbinding from the dye became faster as the temperature increased from 17°C to 37°C (Fig. 6 C). An Arrhenius plot constructed from the data (Fig. 6 D) estimated a change in enthalpy of the dissociation rate constant (k_off), ΔH, of 4.25 ± 0.10 Kcal/mol, was smaller than that observed for the relaxation of the Ca²⁺ transients in the perfused heart epicardium. By using the K_d obtained in Fig. 6, A and B, we calculated the k_on of the reaction. The change in enthalpy for the association rate constant, ΔH, was calculated to be 11.13 ± 0.13 Kcal/mol. This larger change in enthalpy for the association rate constant may be responsible for the temperature dependency of the K_d.

Fig. 6, F and G, shows how the dissociation rate constant (k_off) and the association rate constant (k_on) increased as the temperature increased. Moreover, the rate of Rhod-2 binding and unbinding was faster than the relaxation of the Ca²⁺ transients (Fig. 6 H). As the time constant for the relaxation of the fluorescent decay of the epicardial Ca²⁺ transient of the dye bound to Ca²⁺ will be

$$\tau =\frac{1}{k_{on }\cdot \left[C{a}^{2+}\right]+k_{off }}$$

at 27°C, the off-rate of the dye is ∼281 s⁻¹. This number is at least 35 times larger than the relaxation of the AP-driven Ca²⁺ transient (Ca²⁺ transient relaxation rate ∼8 s⁻¹; Fig. 6 H) at 27°C. This indicates that the thermodynamics of the reaction between Ca²⁺ and Rhod-2 is not the limiting factor in defining the temperature dependency of the rate of relaxation of Ca²⁺ transients in the mouse heart.

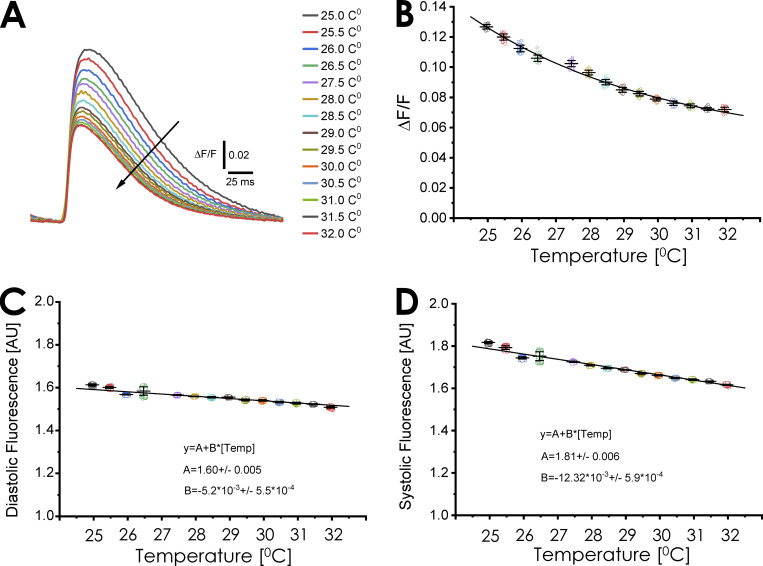
How much is the fluorescence of the dye change related to the resting fluorescence (ΔF/F)?

Performing fluorescent measurements in the intact heart is a challenging feat. In addition to the diastolic fluorescence defined by the resting Ca²⁺ concentration in the myocytes, there is a significant amount of resting fluorescence arising from the endothelial cells in the surrounding capillary system (Escobar et al., 2012); however, assessing of changes in fluorescence in relation to the resting fluorescence level at different temperatures is a typical way to evaluate Ca²⁺ transients. Fig. 7 A illustrates the ΔF/F at different temperatures. Two salient features are presented. The first is the very low values of ΔF/F. This is because the resting diastolic fluorescence is not defined by the diastolic Ca²⁺ level of the myocytes, but is highly defined by endothelial cells, smooth muscle cells, and resident macrophages. This factor dramatically attenuates ΔF/F. The second feature is the decrease in amplitude of the Ca²⁺ transient. One explanation for this phenomenon is, at increasing temperatures, phase 1 of the AP becomes faster (Fig. 4 D). We previously showed that, in mice, Ca²⁺ entry occurs during phase 1 (Ramos-Franco et al., 2016; López Alarcón et al., 2019), and a faster phase 1 will reduce the Ca²⁺ influx through L-type Ca²⁺ channels (López Alarcón et al., 2019). Interestingly, an increase in the temperature promoted a decrease in ΔF/F (Fig. 7 B) and the diastolic fluorescence (Fig. 7 C). In principle, an increase in the temperature could increase the activity of all Ca²⁺ transport systems; however, the decrease in diastolic fluorescence is very mild. This mild decrease in the diastolic fluorescence can be influenced by the fact that there is an increase in the affinity of the Ca²⁺ indicator. Finally, we observed a larger change in the systolic Ca²⁺ (Fig. 7 D) compared with the diastolic fluorescence. As previously discussed, this larger temperature dependency can be influenced by a faster repolarization rate during phase 1.

Figure 7.

Global temperature dependency of Ca²⁺ transients ΔF/F. (A) Temperature dependency of Ca²⁺ transients expressed as ΔF/F. An epicardial Ca²⁺ transient recorded at different temperatures in hearts paced at 4 Hz. It is possible to observe that as we increase the temperature, the ΔF/F decreases. (B) Amplitude of the peak ΔF/F values as a function of temperature. Interestingly, the values of the ΔF/F are smaller than in isolated myocytes due to the fluorescent contribution of endothelial and smooth muscle cells. (C) Temperature dependency of the diastolic fluorescence as a function of temperature. (D) Temperature dependency of the systolic fluorescence as a function of the temperature (n = 4 hearts).

Evaluation of the temperature gradients by computing the rate of relaxation of the Ca²⁺ transients

The correlation between the maximum derivative of the Ca²⁺ transient as a function of temperature in Celsius (Fig. 5 E) was used to analyze the FLOM images. We estimated the local temperature from the local rate of decay of the Ca²⁺ transient, which was obtained under conditions where a temperature gradient was established on the epicardial layer. First, the rate maps were generated by subtracting two consecutive FLOM images and dividing this difference by the time interval between the two images (Fig. 8). The individual images starting at the peak of the Ca²⁺ transient were named I_t, I_t+1…, I_t+n (Fig. 8 A). In Fig. 8 B, we obtained the derivative image sequence by computing

Figure 8.

Relationship between local temperature and Ca²⁺ alternans. (A) Series of FLOM images from I_t to I_t+n with its corresponding average Ca²⁺ transients in a heart externally paced at 5 Hz. (B) A derivative map is constructed from the rate of relaxation of the Ca²⁺ transients (for details, see Evaluation of the temperature gradients...). (C) Left: Map of maximum derivates (obtained from B). They represent the point in time at which the derivative is maximum. Right: Temperature map estimated from maximum derivatives (using the parameters from Fig. 5 E). (D) Distribution of Ca-Alts as a function of temperature, computed by plotting the Ca-Alts value versus the temperature value at the same pixel on FLOM image. (E) Temperature dependency of Ca-Alts at different HRs.

$$\frac{I_{t+n}-I_{t+n-1}}{\Delta t}\mathrm{.}$$

Using this algorithm, we selected the calculated rate map in which the negative derivative was the maximum value. As done in Fig. 5 E, the temperature dependence of the maximum negative derivative was fitted with the equation −(d[CaD(t)]) / dt_max = a + bT, where a is the intercept, b is the slope, and T the temperature in Celsius. Fig. 8 C shows the algebraic transformation used to obtain a temperature map from the rate map. Using the metallic cold finger, we generated a 5°C gradient between 22°C (cold region) and 27°C (warm region) on the epicardial layer of the Langendorff-perfused mice hearts.

Mapping Ca-Alts as a function of temperature

The estimation of the temperature from the rate map (Fig. 8 C) allowed for the assessment of the dependence of Ca-Alts maps on the local temperature. Fig. 8 D shows the correlation between Ca-Alts and temperature in a heart externally paced at 7 Hz. We plotted every spatial point on the Ca-Alts map/image versus the temperature map estimated at the same spatial point. At 7 Hz, there was a steep relationship between Ca-Alts and the local temperature. When the pacing rate was decreased from 7 Hz to 5 Hz (a more bradycardic HR), the relationship of Ca-Alts versus temperature flattened, which was indicative of a decreased magnitude in the Ca-Alts generated by decreasing temperature from 27°C to 22°C (Fig. 8 E).

The rate of change in the magnitude of Ca-Alts versus temperature was calculated from the Q₁₀ temperature coefficient of the process—that is, we estimated how much the magnitude of Ca-Alts changed when the temperature changed by 10°C (Q₁₀) from the following equation:

$$Q_{10}={\left(\frac{R_2}{R_1}\right)}^{\frac{{10}^{o}C}{T_2-T_1}}\mathrm{,}$$

where R₂ and R₁ are the ratios of the smaller alternant to the larger Ca²⁺ transient peak, A_L/A_H, at temperature T₂ and T₁, respectively. In Fig. 9 A, at higher HRs where Ca-Alts were more prominent, the Q₁₀ of A_L/A_H was significantly higher than the Q₁₀ for Ca²⁺ transients decay kinetics. For example, the Q₁₀ of the Ca²⁺ transients relaxation, shown in Fig. 5 E, was 1.68 ± 0.17 (n = 5 hearts). In contrast, the Q₁₀ for Ca-Alts at 6 Hz (1.93 ± 0.09) and 7 Hz (3.34 ± 0.28; n = 4 hearts) were significantly larger than the Q₁₀ values of Ca²⁺ transients relaxation. This indicates the presence of an additional process involved in the generation of Ca-Alts with a much higher temperature dependency than the Ca²⁺ transient relaxation rate. One likely candidate is the rate of Ca²⁺ transport to the SR driven by the SERCA2a pump. To assess the validity of this hypothesis, we performed in vitro experiments to measure the SERCA2a rate of transport as a function of temperature. These experiments were done using microsomes obtained from pig hearts (see Materials and methods), and the rate of transport was evaluated at different temperatures. The experiments were performed with a spectroscopic technique under conditions where RYR2 was pharmacologically blocked with 5 µM Ruthenium red at different temperatures. Fig. 9 B demonstrates how an increase in temperature accelerates the dissipation of a Ca²⁺ gradient. Our results show that, at temperatures below 9°C, the Ca²⁺ uptake by SERCA2a was completely impaired. Fig. 9 C shows the rate of Ca²⁺ uptake by SERCA2a at different temperatures (n = 50 measurements). The rates of Ca²⁺ uptake of the microsomes were significantly slower than those of Ca²⁺ transients relaxation rates. This is due, in part, to the ratio of the density of pumps in the SR to intact heart cell volume is much higher than the ratio of the volume of microsomes to cuvette volume in vitro experiment. Remarkably, the Q₁₀ for the microsome Ca²⁺ uptake obtained from the data presented in Fig. 9 C was 3.13, a value more compatible with the Q₁₀ for Ca-Alts. We also constructed an Arrhenius plot to evaluate the changes in enthalpy and entropy produced during the microsome uptake process. Fig. 9 D shows a plot obtained with the data from the microsome experiments. The temperature effects on Ca²⁺ uptake by SR microsomes was fit as a simple thermodynamic process with a change in enthalpy ΔH = 20.4 ± 0.7 Kcal/mol and a change in entropy ΔS = 57.2 ± 2.4 cal/(mol.K). ΔH measured on the microsomes was much larger than the enthalpy for the relaxation of the Ca²⁺ transient (ΔH = 9.17 ± 0.13 Kcal/mol). Moreover, the large Q₁₀ presented by Ca-Alts at 7 Hz looks like the Q₁₀ of SR Ca²⁺ uptake.

Figure 9.

Maximum local temperature dependency of Ca²⁺ alternans and global temperature dependency of SERCA2a pump. (A) Q₁₀ temperature coefficient of the ratio of the amplitude of the low (A_L) and high (A_H) Ca²⁺ transient for different pacing rates. The Q₁₀ of the ratio A_L:A_H was calculated by using the Q₁₀ equation (see Mapping Ca-Alt as function of the temperature) and data obtained at two temperatures (26.5°C and 21.5°C) in hearts paced from 5 to 7 Hz (n = 5 hearts; *, P < 0.01). (B) Temperature increases the rate of SR Ca²⁺ uptake in heart microsomes. SR Ca²⁺ loading was started by increasing Ca²⁺ in the cuvette to 40 μM. The panel also illustrates examples of Ca²⁺ uptake by cardiac SR microsomes at various temperatures. (C) Uptake rates of cardiac SR microsomes as a function of temperature and at temperatures ranging from 5°C to 39°C (n = 50 measurements). The data in B was fitted by a single exponential function from which the initial rate of Ca²⁺ uptake was derived. The Q₁₀ calculated between 21.8 and 31.8 was 2.78 ± 0.91, and between 26 and 36 was 3.14 ± 0.92. (D) Arrhenius plot of the rate of decay of the Ca²⁺ uptake by SERCA versus temperature. The estimated changes in enthalpy were ΔH = 20.4 ± 0.7 Kcal/mol and the change in entropy was ΔS = 57.2 ± 2.4 cal/(mol.K). n = 5 experiments.

Ca-Alts heavily depend on the intra-SR Ca²⁺ content

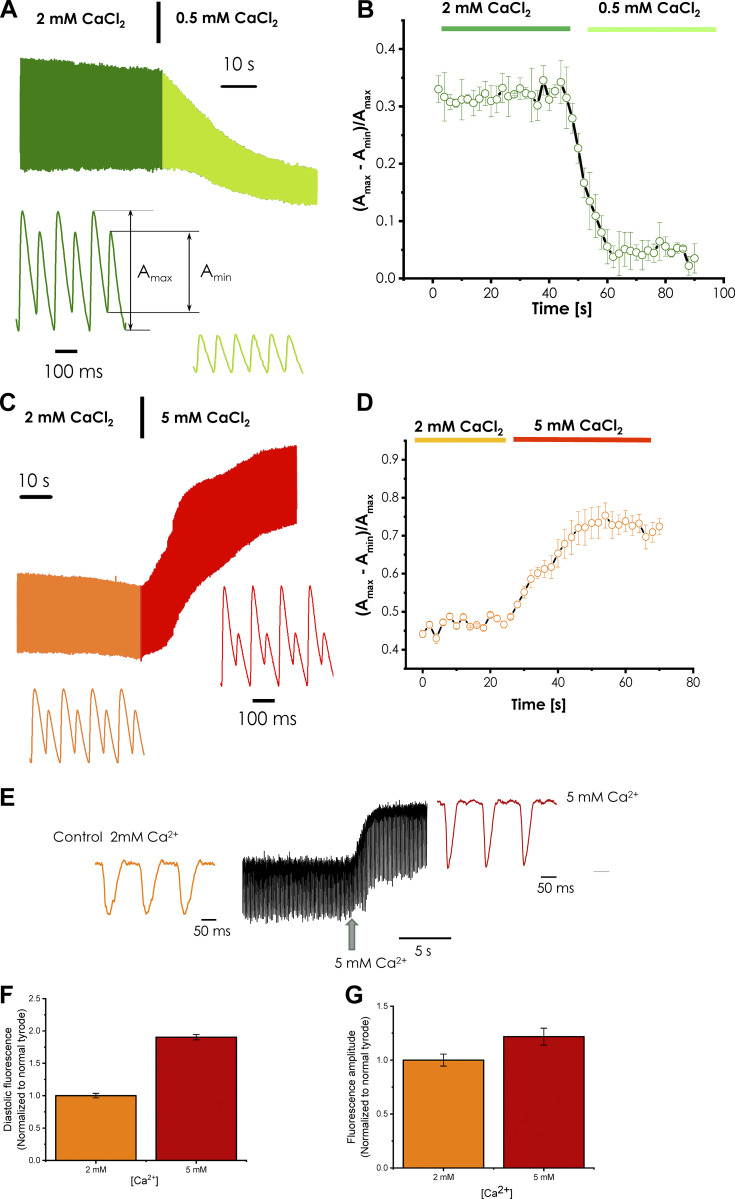
As shown in Fig. 10, Ca-Alts depend heavily on the extracellular and intra-SR Ca²⁺ content. Fig. 10 A shows that the epicardium of the heart paced at 12 Hz at 32°C displays significant Ca-Alts; however, when the extracellular Ca²⁺ was reduced to 0.5 mM, the alternans were highly attenuated. Fig. 10 B presents the statistical analysis of three independent hearts, where a significant reduction of the amplitude of Ca-Alts is observed (n = 3 hearts; P < 0.01).

Figure 10.

Effect of extracellular Ca²⁺ concentration on cytoplasmic Ca-Alts and the intra-SR Ca²⁺ content and depletion measured using fluorescent dyes Rhod 2 and Mag-Fluo-4, respectively. (A) A significant reduction in the amplitude of cytoplasmic Ca-Alts is observed upon reduction of the extracellular Ca²⁺ from 2 mM to 0.5 mM. (B) Statistics of the effect on Ca-Alts produced when the extracellular Ca²⁺ was reduced from 2 mM to 0.5 mM Ca²⁺ (n = 3 hearts). (C) Changing the extracellular Ca²⁺ from 2 mM to 5 mM caused a significant increase in the amplitude of Ca-Alts. (D) Statistics of the effect of increasing extracellular Ca²⁺ from 2 mM to 5 mM (n = 3 hearts). (E) Time course of the intra-SR Ca²⁺ content when the extracellular Ca²⁺ concentration was increased from 2 mM to 5 mM. The diastolic Ca²⁺ level was increased inside the lumen of the SR when the extracellular Ca²⁺ concentration was increased. (F) The diastolic Mag-Fluo-4 fluorescence level before and after the increase in the extracellular Ca²⁺. (G) The degree of intra-SR Ca²⁺ depletion before and after the extracellular Ca²⁺ was increased (n = 4 hearts).

Fig. 10, C and D, shows a different side of this phenomenon, with each panel describing the amplitude of Ca-Alts. Fig. 10 C illustrates changes in the Ca²⁺ transients. Ca-Alts were significantly increased in response to increasing the Ca²⁺ concentration in the perfusion solution from 2 mM to 5 mM. The statistical analysis of these experiments, presented in Fig. 10 D, suggests that the alternans were significantly increased upon elevation of extracellular Ca²⁺ concentration (n = 3 hearts; P < 0.01).

Finally, we performed experiments by using the low-affinity dye Mag-Fluo-4 (Kornyeyev et al., 2010, 2012; Valverde et al., 2010) to determine if the intra-SR Ca²⁺ levels increased. An increase in the extracellular Ca²⁺ induced an increase not only in the diastolic Ca²⁺ level inside the SR, but also induced an augmentation in the amplitude of the intra-SR Ca²⁺ depletion for every electrical stimulus (Fig. 10 E). Fig. 10, F and G shows the average values and SD obtained in several independent experiments (n = 4 hearts; P < 0.01). Interestingly, not only was there a significant increase in the diastolic intra-SR Ca²⁺ level (Fig. 10 F), but also in the amplitude of the intra-SR Ca²⁺ depletion (Fig. 10 G). Under conditions where the heart was paced at 8 Hz at 32°C, it is not possible to observe Ca-Alts inside the SR. These results indicate that higher intra-SR Ca²⁺ content will increase the likelihood of developing Ca-Alts.

Pump rate dependency of Ca-Alts

To further investigate the similarities of the temperature dependency observed in Ca-Alts and SERCA2a described in Figs. 8 and 9, experiments were done to independently assess the role of SERCA2a transport properties as a key factor defining Ca-Alts. Fig. 11 shows independent experiments where the maximum rate of the pump was decreased by perfusing the heart with 200 nM Tg. Fig. 11 A illustrates a control condition at 29°C and a pacing frequency of 9 Hz. Under these conditions, the control presents a very mild level of Ca-Alt (Fig. 11 A). After perfusing the heart for 2 min with 200 nM Tg, the level of Ca-Alts significantly increased (Fig. 11 B). After 8 min of perfusion, the amplitude of Ca-Alts significantly decreased (Fig. 11 C). This correlates with the significantly reduced amplitude of the Ca²⁺ transients (see inset). As previously shown in Fig. 10, a lower intra-SR Ca²⁺ content reduced the amplitude of Ca-Alts. This reduction in the amplitude of Ca-Alts was likely driven by a much lower activity of the SERCA2a pump and the Ca²⁺ leak through the RYR2. As shown in Fig. 11 D, a significant increase in Ca-Alt was observed after perfusing the heart with Tg for 2 min, while a decrease in Ca-Alts was observed at 8 min (n = 4 hearts; P < 0.01). This experiment definitively shows the role of SR Ca²⁺ uptake through SERCA2a in the development of Ca-Alts.

Figure 11.

Effect on Ca-Alts produced by partially blocking the SERCA2a pump with Tg. (A) Control experiment was performed at 29°C and a pacing frequency of 9 Hz. It is possible to observe a small degree of Ca-Alts. (B) Effect of 200 nM Tg after 2 min of coronary perfusion with the drug. We can appreciate a significant increase in the amplitude of Ca-Alts. (C) Effect of 200 nM Tg after 8 min of perfusion with the drug. We can observe that at 8 min of perfusion with 200 nM Tg, the amplitude of Ca-Alts was decreased because of a Ca²⁺ depletion of the luminal SR Ca²⁺ content. (D) Statistics of the effect of Tg on the genesis of Ca-Alts (n = 4 hearts; *, P < 0.01).

Discussion

FLOM measured local Ca²⁺ transients with subcellular spatial resolution and large bandwidth in selected areas of the whole-heart epicardium. An accessory apparatus allowed the local cooling of an area of the imaged tissue, creating a temperature gradient. We observed larger Ca-Alts in the colder regions and at higher frequencies. Furthermore, Ca-Alts occurred in the absence of changes in the AP duration (i.e., AP alternans). The frequency and temperature dependency of Ca-Alts and the pharmacologic inhibition of SERCA2a by Tg suggest they are generated by insufficient SERCA2a-mediated Ca²⁺ uptake into the SR during tachycardia.

Various mechanisms have been proposed for the generation of Ca-Alts, including alternating behavior of APs and Ca²⁺ influx via L-type Ca²⁺ channels (Sicouri et al., 2007; Qu et al., 2000). Most reports, however, point to the SR as the subcellular location where Ca-Alts originate (Escobar and Valdivia, 2014; Díaz et al., 2004; Kornyeyev et al., 2012), although the molecular mechanism remains unclear. It was previously proposed that Ca-Alts are produced by incomplete recovery from inactivation of the RYR (Wang et al., 2014). Moreover, genetic ablation of calsequestrin (Kornyeyev et al., 2012), the major intra-SR Ca²⁺ buffering protein thought to regulate RYRs, dramatically reduces the likelihood of Ca-Alts. Nevertheless, RYR2 activity depends heavily on SR Ca²⁺ content (Fill and Copello, 2002), and alternans are affected by changes in the rate of Ca²⁺ transport by the SERCA2a pump (Laurita et al., 2003; Wan et al., 2005). Escobar and Valdivia (2014) proposed an increasing HR compromise on the activity of SERCA2a to resequester Ca²⁺ into the SR. Our current studies strongly suggest that SERCA’s inability to replenish Ca²⁺ into the SR does not allow enough Ca²⁺ to be inside the SR for the next release. A large release event is then followed by a smaller one under conditions where the local AP remains unchanged.

Effect of temperature on Ca²⁺ dynamics

Hypothermia has been previously observed to cause cardiac arrest (Smith et al., 1988; Furukawa et al., 1980; Badeer, 1958; Mouritzen and Andersen, 1966; Adam et al., 1984). The relationship between hypothermia and cardiac arrest seems to be related to temperature affecting many physiologic processes in the heart, including excitation-contraction coupling and CICR. Temperature is known to significantly modulate the kinetics of L-type Ca²⁺ channels (Kohlhardt, 1975; Klöckner et al., 1990; Puglisi et al., 1999), the Na⁺-Ca²⁺ exchanger (NCX; Ferreiro et al., 2012; Bersohn et al., 1991; Blaustein and Lederer, 1999), and SERCA (Shigekawa et al., 1976); however, less is known about how temperature affects RYRs. Previous single-channel studies in bilayers (with temperatures ranging from 5°C to 23°C) show RYR activity increases at lower temperatures (Sitsapesan et al., 1991), while Ca²⁺ sparks studies suggest little change between 23°C and 32°C (Fu et al., 2005).

In this paper, we simultaneously assessed the effects of changes in the HR and temperature on the genesis of Ca-Alts. Global changes in heart temperature had a much larger effect on the relaxation kinetics of Ca²⁺ transients when compared with the changes in rising times (Fig. 2, A, B, and G). These results were similar to those obtained in intact ventricular epicardium of mouse hearts while recording Ca²⁺ transients at two different temperatures as well as in experiments performed in isolated cardiomyocytes (Puglisi et al., 1996). We determined that changes induced by temperature on the kinetics of the Ca²⁺ transient relaxation are not defined by the unbinding of Ca²⁺ from the dye, which is altogether a much faster process. For example, the time constants (τ) for the decay of the Ca²⁺ transient decreased from 142 ms at 22°C to 98 ms at 32°C (Fig. 5 E), and the rate of Ca²⁺ unbinding from Rhod-2 is 4.8 ms at 22°C to 2.82 ms at 32°C (Fig. 6 F). A complete mathematical description of the validity of this approach using the first derivative of the Ca²⁺ transient relaxation as a way to evaluate the time constant of the relaxation and the rate of relaxation of the Ca²⁺ transient is presented in the Supplemental text (see bottom of PDF).

Temperature dependency of the Ca²⁺ indicator Rhod-2

As discussed in Results, the affinity of the Ca²⁺ indicator increased in response to increasing temperatures (Fig. 6, A and B). The increase in the affinity of the dye as a function of temperature is highly related to the change in enthalpy (ΔH) of the association rate constant k_on being significantly larger (Fig. 6 E; 11.13 ± 0.13 Kcal/mol) than the dissociation rate constant k_off (Fig. 6 D; 4.25 ± 0.10 Kcal/mol). We also found both k_on (Fig. 6 G) and k_off (Fig. 6 F) to be significantly faster than the relaxation rate of the Ca²⁺ transient. This indicates that the kinetics of the dye was not the rate-limiting factor that defined the relaxation of the Ca²⁺ transient. Moreover, k_off, the critical parameter that defines the relaxation rate, was 35 times faster than the relaxation of the epicardial Ca²⁺ transients (Fig. 6 H).

Evaluation of the ΔF/F of the Ca²⁺ transients at different temperatures

Loading of the dye at the whole-heart level is performed by perfusing the heart through the coronary network with either Ca²⁺ indicators or potentiometric dyes. In any case, the first cells to be loaded are the endothelial and smooth muscle cells—this is the main reason these cells of the circulatory network are typically heavily loaded with dyes. Furthermore, the perinuclear region of the endothelial cells displays a very intense fluorescence (Escobar et al., 2012), making it difficult to calculate the ΔF/F at the whole-heart level, but not in isolated myocytes. This very high resting fluorescence makes the ΔF/F values calculated in the intact heart much smaller compared with those obtained in isolated cells (Fig. 7, A and B). We also found a decrease in the diastolic fluorescence as we increased the temperature. This decrease was smaller than the one we expected, but could be explained by the fact that increasing the temperature increased the affinity of the Ca²⁺ dye (Fig. 7 C). Finally, we observed both the ΔF/F and the systolic fluorescence decreased as the temperature of the tissue was increased. Our laboratory has previously shown that the bulk of Ca²⁺ entering the cell occurs during phase 1 of the AP (Ramos-Franco et al., 2016; López Alarcón et al., 2019). Consequently, a faster phase 1 will decrease the L-type Ca²⁺ current. Moreover, Fig. 4 D shows that an increased temperature accelerated phase 1, thereby reducing the amount of Ca²⁺ getting into myocytes.

Effect of the temperature on the myocyte Ca²⁺ transport mechanisms

We estimated kinetic and thermodynamic parameters of the Ca²⁺ transients at several temperatures by imposing a temperature gradient on an area of the epicardium by using a semilunar cold finger (Fig. 2, E and F). While APs remain unchanged, cytosolic Ca²⁺ remained elevated for a longer time in areas at colder temperatures. This may induce a strong temperature dependency in the two major mechanisms for cytosolic Ca²⁺ removal in cardiomyocytes. The mammalian NCX has a Q₁₀ ranging from 3 to 4 (Blaustein and Lederer, 1999; Niggli and Lederer, 1991; Bersohn et al., 1991; Rojas et al., 2004). SERCA was also found to have large temperature dependency (Shigekawa et al., 1976), comparable to Q₁₀ = 3.13, estimated here for SERCA maximal activity in porcine ventricular microsomes (Fig. 9 C). The measured Q₁₀ for NCX and SERCA are much larger than the Q₁₀ for the relaxation of the mouse ventricular Ca²⁺ transients presented in this paper. Although the affinity of SERCA2a is an important parameter, the most precise way to evaluate the effect of temperature is by looking at the kinetic rates. Interestingly, a previous study found that, in the absence of Na⁺ to inhibit NCX, the change in the relaxation rates in rats changed from 0.04 (s⁻¹) at 24°C to 0.38 (s⁻¹) at 37°C when a caffeine pulse was applied (Mackiewicz and Lewartowski, 2006). Moreover, in another paper where the association rate constant was evaluated by using NMR, the authors found the association rate constant to have a mild temperature dependency (Traaseth and Veglia, 2010). As the temperature dependency of K_d depends more on the association rate constant than on the dissociation rate constant, we assume the temperature dependency of K_d is not a critical factor defining the temperature dependency of the Ca²⁺ transient relaxation. This may indicate that the relaxation of ventricular Ca²⁺ transients is shaped by both passive and active pathways. The passive path includes binding/unbinding to intracellular Ca²⁺ buffers (i.e., ATP, calmodulin, etc.), processes with reaction rates with Q₁₀ of ∼2 (Hou et al., 1992; Churcott et al., 1994). In this regard, we estimated the rate of Ca²⁺ unbinding from the dye has a Q₁₀ of ∼1.5. The Ca²⁺ buffering effect is directly proportional to the association rate constants of the cytosolic buffers, which have a lower temperature dependency, and to the free buffer concentration. The active path includes the Ca²⁺ transporters NCX and SERCA, which, as detailed above, have higher temperature dependency. Active Ca²⁺ transport could also play a critical role in maintaining the diastolic cytosolic Ca²⁺ at a low enough level to maximize the fraction of intracellular buffers that are in a free form.

The amplitude and temperature dependence of Ca-Alts increased at increasing frequencies. For large alternans—6 Hz and 7 Hz—the Q₁₀ is much larger than the temperature dependency of RYR (Sitsapesan et al., 1991; Fu et al., 2005). This again suggests that the genesis of Ca-Alts is not directly governed by the kinetics of the RYR, but rather by another factor that regulates Ca²⁺ release from the SR and has a high temperature dependence.

Local cooling and the genesis of Ca-Alts

We also studied the interplay between HR and global temperature on the genesis of Ca-Alts (Fig. 2, C and D). When the heart was paced at 8 Hz, large Ca-Alts were observed at 20°C but not at 33°C. The increase in Ca-Alts as a function of HR agrees with previous findings (Clusin, 2008). Other researchers have also shown that colder temperatures increase the genesis of APD-Alts and Ca-Alts (Egorov et al., 2012).

Whether Ca-Alts are a consequence of electrical alternans or the cause of them is not yet definitively understood, since it has been very difficult to uncouple these two processes (Weiss et al., 2011; Prudat et al., 2016; Hazim et al., 2015; Yapari et al., 2014). Therefore, when we induced a global change in the temperature of the heart and the bath, epicardial APs presented both a strong temperature (Fig. 4 D) and frequency dependency (Fig. 4 C). On the contrary, local cooling induced Ca-Alts and not APD-Alts (Fig. 3, E and F; and Fig. 4, A and B). These results are consistent with a recent report from our group indicating that local changes in both the amplitude of Ca²⁺ transients and Ca²⁺-driven currents do not always result in changes in the time course of APs (Ramos-Franco et al., 2016). The epicardial area cooled with the cold finger is smaller than the space constant of the tissue (Ramos-Franco et al., 2016), and thus the neighboring tissue—subepicardium and midmyocardium—imposes an electrotone. This electrotone acts as an electric sink, preventing changes in the amplitude of Ca²⁺ transients locally induced by cooling to affect the repolarization of the AP. During cooling, the electrotone prevented local changes in the Ca²⁺ transient–induced NCX currents to alter the membrane potential. In summary, global changes in the heart temperature can induce APD-Alts (Fig. 4 G), but local changes are nullified by the electrotone from generating those alternans (Fig. 4 E). The synthicium organization of the cardiomyocytes allowed us to demonstrate that Ca-Alts can be generated independently of changes in AP.

Previous studies have suggested that SR Ca²⁺ load plays an important role in the genesis of Ca-Alts (Díaz et al., 2004). Our studies indicate the Ca²⁺ reloading into the SR, rather than the intrinsic kinetic properties of RYRs, plays a fundamental role in setting the temperature and frequency dependency of Ca-Alts. Under situations in which the Ca²⁺ cycling kinetics is decreased, such as hypothermia, the heart tissue is more prone to develop alternans. The NCX activity is inhibited at lower temperatures, increasing cytosolic Ca²⁺. At lower temperatures, the activity of the SERCA2 pump is also decreased, resulting in slower SR uptake kinetics. Still, an increase in cytosolic Ca²⁺ would eventually result in an SR with a larger Ca²⁺ load. The SR overload makes RYRs more active and then a larger release of Ca²⁺ will occur upon pacing. The fraction of SR depletion will be greater and, due to the compromised SERCA2a activity at colder temperatures, the next release will be smaller at high HRs due to SR depletion.

Intra SR Ca²⁺ load increases the magnitude of Ca-Alts

Fig. 10 shows that the modification of the extracellular Ca²⁺ concentration has a large impact on the amplitude of Ca-Alts. Decreasing the extracellular Ca²⁺ concentration dramatically reduced the magnitude of Ca-Alts (Fig. 10, A and B), while increasing the extracellular Ca²⁺ increased the amplitude of Ca-Alts (Fig. 10, C and D). Furthermore, modifying the extracellular Ca²⁺ concentration had a significant effect on the intra-SR Ca²⁺ concentration (Fig. 10, E–G). An increase in the intra-SR Ca²⁺ will have a big effect on Ca²⁺ release. Indeed, an increase in the luminal SR Ca²⁺ concentration will promote the binding of Ca²⁺ to calsequestrin, a protein that not only serves as an intra-SR Ca²⁺ buffer, but also regulates the open probability of RYR2 by interacting with Triandin and Juntin (Györke et al., 2004; Terentyev et al., 2005), the two proteins that interact with RYR2. When the intra-SR Ca²⁺ decreases, calsequestrin Ca²⁺ reduces the open probability of RYR2. When Ca²⁺ increases, calsequestrin detaches from Triadin and Juntin, increasing the open probability of RYR2. Indeed, a calsequestrin knockout significantly reduces Ca-Alts (Kornyeyev et al., 2012). Thus, at high intra-SR Ca²⁺ levels, the gain of CICR will be high, and when Ca²⁺ inside the SR is reduced (due to Ca²⁺ depletion), the gain of CICR will be lower. These factors can all induce Ca-Alts. Furthermore, if the intra-SR Ca²⁺ is always low, the gain of CICR will be small, preventing intra-SR Ca²⁺ depletion and avoiding Ca-Alts.

Pharmacologic inhibition of SERCA2a induces Ca-Alt

The thermodynamic experiments presented in this paper suggest that the thermodynamic behavior of alternans is similar to the temperature dependency of SERCA2a; however, it is crucial to examine whether partial pharmacologic inhibition of SERCA2a can induce Ca-Alts. Experiments presented in Fig. 11 were designed to directly test the hypothesis that a reduction in the rate of Ca²⁺ transport by SERCA2a induced Ca-Alts. The amplitude of Ca-Alts significantly increased following perfusion of the heart with 200 nM Tg for 2 min (Fig. 11 B), while the amplitude of Ca-Alts significantly decreased after 8 min of perfusion with the drug. As discussed previously, this likely occurs because Tg will induce depletion of the intra-SR Ca²⁺ content, leading to a decreased gain of the CICR process. This decrease in the gain of CICR will, in turn, reduce the intra-SR Ca²⁺ depletion, which finally reduces the amplitude of Ca-Alts.

Conclusion

The new FLOM-based experimental approach presented here has the potential to aid our understanding of how arrhythmogenesis correlates with the spatial distribution of metabolically impaired myocytes along the myocardium. Furthermore, the results presented in this paper are consistent with the idea that electrical alternans are produced during hypothermia (Floyd and Dillon, 1967; Hsieh et al., 2009; Egorov et al., 2012; Siddiqi et al., 2016), as TW-Alts and APD-Alts both show important temperature-dependent behavior (Hirayama et al., 1993). Finally, alternans in mechanical activity (pulsus alternans) directly related to Ca-Alts can also develop in hypothermic conditions (Floyd and Dillon, 1967).