On collaborative reinforcement learning to optimize the redistribution of critical medical supplies throughout the COVID-19 pandemic

Abstract

Objective

This work investigates how reinforcement learning and deep learning models can facilitate the near-optimal redistribution of medical equipment in order to bolster public health responses to future crises similar to the COVID-19 pandemic.

Materials and Methods

The system presented is simulated with disease impact statistics from the Institute of Health Metrics, Centers for Disease Control and Prevention, and Census Bureau. We present a robust pipeline for data preprocessing, future demand inference, and a redistribution algorithm that can be adopted across broad scales and applications.

Results

The reinforcement learning redistribution algorithm demonstrates performance optimality ranging from 93% to 95%. Performance improves consistently with the number of random states participating in exchange, demonstrating average shortage reductions of 78.74 ± 30.8% in simulations with 5 states to 93.50 ± 0.003% with 50 states.

Conclusions

These findings bolster confidence that reinforcement learning techniques can reliably guide resource allocation for future public health emergencies.

INTRODUCTION

The coronavirus disease 2019 (COVID-19) pandemic has challenged nations with shortages of medical supplies to combat the disease. In Northern Italy, doctors rationed equipment and decided which patients to save.¹ In the United States, a few public health officials worked together to share their resources. However, as U.S. entities lack a unified system for equipment redistribution, they resorted to rudimentary techniques such as phone calls and press releases to request help. This reactionary response strongly indicates a nonoptimal redistribution of equipment.^2,3

Here, we investigate how officials can share resources more optimally when facing future public health crises. To evaluate our redistribution system, we created a simulation environment with data from the Institute of Health Metrics, Centers for Disease Control and Prevention, and Census Bureau.^4–6 Preprocessed data is fed into a custom neural network inference model to predict the future demand of ventilators in each state. These predictions are fed into one of five redistribution algorithms to control daily actions.

We evaluate our custom demand prediction model and use its output to test redistribution algorithms. For each algorithm, we determine the average performance in a series of simulations in which 5, 20, 35, or 50 participating states are selected at random. We find that the q-learning redistribution algorithm outperforms all other methods while maintaining a high degree of optimality. Additionally, as the number of participating states increases, the algorithm’s performance improves consistently in terms of both shortage reduction and reliability.

MATERIALS AND METHODS

System overview

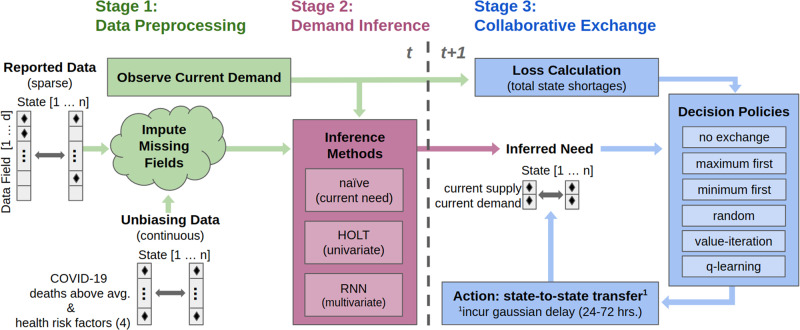
The three-stage pipeline shown in Figure 1 is proposed. First, observed input data are preprocessed. Second, a deep learning inference model predicts future demands. Finally, a preselected redistribution algorithm interprets demand predictions to determine daily actions. The second and third stages of the pipeline are optimized separately each day of the simulation.

Figure 1.

The proposed solution consists of three stages to facilitate the redistribution of ventilators throughout the coronavirus disease 2019 (COVID-19) pandemic.

We frame this redistribution system as an optimization problem to minimize the total ventilator shortages accumulated over the simulation period. Shortages are incurred each day by states that have fewer ventilators in supply than demand. Input parameters dictate the dates for which to run the simulation and the number of random states selected. No new ventilators enter the simulation after initialization, though our system maintains the ability to distribute new supplies from any state or central agent as needed (Supplementary Appendix A).

Data preprocessing and imputation

In the preprocessing stage, critical disease metrics are primarily drawn from the University of Washington Institute for Health Metrics and Evaluation’s widely cited COVID-19 tracking program.^7–9 We include biweekly Centers for Disease Control and Prevention metrics for state-wise deaths above average to assist our inference model in overcoming statistical biases that result from regional differences in the number of COVID-19 tests performed.¹⁰ Furthermore, we include fixed values for state-wise rates of heart disease, asthma, chronic obstructive pulmonary disease, and diabetes from the 2017 Census Bureau to account for varying comorbidities.^6,11 We preprocess data between February 4 and August 4, 2020. Linear interpolation estimates missing fields and guarantees continuity (Supplementary Appendix B).¹²

Statistical assumptions

We make two statistical assumptions for a robust simulation environment. First, that the number of available ventilators in a state is equivalent to the number of COVID-19 intensive care unit (ICU) beds. The use of a proxy variable is made necessary by the lack of a system for tracking and reporting ventilators in hospitals by state. However, previous studies showed that approximately half of COVID-19 ICU patients required mechanical ventilation in the early stages of the pandemic.^13,14 The low scale of this ratio allows us to assume ICU bed data as a proxy for ventilators and expect simulation performance to be an accurate indicator of the model’s extensibility to the real world.

A second statistical assumption defines the model for the logistics downtime of redistributed ventilators. Incurred delays are randomly sampled from a Gaussian i.i.d (mean 3 ± 0.5 days) and rounded to the nearest 2 (∼16% of total), 3 (∼68%), or 4 (∼16%) days. The distribution’s lower bound is based on Department of Health and Human Services’ report that ventilators from emergency stockpiles can be available nationwide in between 24 and 36 hours.¹³ The upper bound includes a considerable time buffer for cleaning and logistics.

Inferring demand

The pipeline’s second stage infers daily future state-wise ventilator demands at the mean redistribution delay interval. The repeating, time-series nature of regional COVID-19 peaks makes recurrent neural networks a good fit for predicting equipment demands. Long short-term memory (LSTM) recurrent neural networks have been demonstrated to perform exceedingly well in similar nonseasonal, multivariate, time-series prediction applications.^15,16 However, it is generally difficult to train a deep learning model to accurately predict future demands without training data from a previous pandemic. In response, we pretrain the LSTM before simulation with a small amount of available data and retrain daily using observations to achieve good online performance.

Primary simulations run for 154 days from March 1 to August 1, 2020. Data are available from February 4, allowing 26 days of processed observations to be used for pretraining the LSTM, which takes series of 14-day observations from states to make predictions. From the available 26 days we compile a set of all unique 14-day series from each state and pretrain the LSTM for 150 epochs. Each day of operation allows a unique series from each state to be aggregated into the set for retraining (100 epochs). Observations from all 50 states are considered even if fewer participate in exchange.

In simulation the LSTM demonstrates a predictive root-mean-square error (RMSE) of 104.74 ventilators per day across all states with a prediction interval of 3 days in the future. The prediction interval is set to the mean logistics delay to provide our redistribution algorithm with the most accurate demand estimates for when its actions are expected to take effect. For comparison, we implemented a univariate Holt exponential smoothing model with the same prediction interval and observed an RMSE of 545.82.¹⁷ As a baseline, we present the naïve case for which the current demand in each state is used as the 3-day prediction and observe a RMSE of 1186.13 (Supplementary Appendix C).

Redistribution algorithms

The final stage is the redistribution algorithm to determine daily actions (state-to-state transfer). Three intuition-based algorithms and two reinforcement learning (RL) algorithms are implemented. We compare algorithmic performance to a baseline case where no ventilators are exchanged (begin and end with initial supplies). Intuition-based approaches allocate surplus ventilators to states by the magnitude of their predicted needs with the following policies: maximum needs first, minimum needs first, or random order. These models demonstrate gains over the status quo that would be achieved if the system consistently applies nonlearning algorithms.

The two RL algorithms are value iteration and q-learning. Both follow similar dynamic programming principles by iterating over possible actions and future supply distributions to optimize daily actions.^18,19 The primary difference between these approaches is that the q-learning algorithm follows a lookup table (predefined and continually updated) to evaluate actions, while value iteration recursively explores all possible actions until convergence to provide a map for the most valuable action in every scenario. Figure 2 visualizes ventilator redistribution under q-learning and demonstrates its ability to avoid shortages when faced with unexpected demand surges by buffering state supplies when possible (Supplementary Appendix D).

Figure 2.

The q-learning algorithm’s redistribution of ventilators throughout the pandemic in a simulation, with four states experiencing surges of coronavirus disease 2019 (COVID-19) cases.

RESULTS

We compare the performance of each redistribution algorithm in a series of simulations selecting 5, 20, 35, and 50 states in random order (1000 simulations for each), using our best-case daily demand predictions from the LSTM inference model. The same series of simulations is run for each redistribution algorithm. Shortage reduction compares the observed shortage (algorithm applied) to the shortage that would have been observed with no actions taken (states maintain initial supplies throughout simulation). Optimality compares the observed shortage to the shortage that would be observed with a theoretically ideal use of ventilators (no excess anywhere when shortage exists elsewhere and no delays). Summary results are determined from viable simulations, and three-sigma outliers are excluded to present the most representative metrics of algorithmic performance. Simulations are determined unviable if neither any shortage is expected following inaction nor any shortage is observed while applying the redistribution algorithm.

The q-learning algorithm demonstrates top performance in both shortage reduction and optimality with 20, 35, and 50 states participating. The q-learning algorithm is only outperformed by the intuition-based Allocate Maximum First algorithm in 5-state simulations. Figure 3 compares the average shortage reduction of q-learning to that of the intuition-based algorithms. The q-learning algorithm improves consistently in average performance (increasing) and standard deviation (SD) (decreasing) as the number of random states participating in exchange increases, from 78.74 ± 30.84% with 5 states to 93.46 ± 0.31% with 50 states. Table 1 shows that q-learning consistently demonstrates an average optimality of 93.33% to 95.56%, with low and decreasing SDs as the number of random participating states increases (Supplementary Appendix E).

Figure 3.

The q-learning outperforms baseline intuition-based redistribution algorithms in simulations with 20, 35, and 50 states, improving in both overall performance (mean increases) and consistency (SD decreases) as number of participating states increases.

Table 1.

The q-learning algorithm performance summary

Number of States	Shortage Reduction	Optimality
5	78.74 ± 30.84	95.03 ± 8.62
20	86.89 ± 16.21	95.56 ± 4.60
35	90.15 ± 8.54	93.33 ± 4.86
50	93.46 ± 0.31	93.46 ± 0.31

DISCUSSION

LIMITATIONS

Performance of value iteration was poor compared with all other methods (shortage reduction degrades from 73.42 ± 31.59% to 23.40 ± 7.72% with 5 to 50 states). Value iteration fails without a priori knowledge of the supply and demand bounds per state. To run value iteration in real-time within the bounds of the observed state space, we increased the convergence threshold and significantly eroded accuracy. The q-learning algorithm avoids this issue with daily adjustments of q-table values, facilitating fast and effective learning. We affirm that RL algorithms should not be applied naïvely to this system and urge future users to consider this limitation.

CONCLUSION

This study bolsters confidence that deep learning and reinforcement learning models can be used to facilitate the efficient redistribution of medical supplies during public health crises. System performance improves with the number of participating states and is significant with only a few states participating. The q-learning algorithm is outperformed by the Allocate Maximum First algorithm with 5 participating states because intuition-based algorithms are well—suited for the logical simplicity of these simulations. In fact, the baselines demonstrate peak optimality in 5-state simulations and degrade with task complexity, while q-learning improves.

High SDs in q-learning’s shortage reduction with fewer states is attributable to simulations where excessive demand from larger states cannot be satisfied by the supplies from smaller participating states. As the number of states increases, these adverse cases become less likely and performance deviations reduce dramatically. This conclusion is supported by q-learning’s consistently high degree of optimality, showing that the algorithm takes near-optimal actions even when the overall reduction is not exceedingly high.

This system could assist officials in managing future public health crises if safety controls are agreed upon and implemented prior to operation. Additionally, algorithm performance for future applications would improve as data collected from this pandemic are used to train that system’s models.

Future work

Future users of this system should consider the following extensions. First, users should verify a unified system to track supplies and enable communication between healthcare entities. Second, users should consider an extension to account for possible noncompliance of entities. Third, users should select a method (eg, a sliding window for training data) to cap inference model retraining time in order to guarantee the accuracy and runtime requirements are met (Supplementary Appendix F).

FUNDING

This research project was not funded by any agency in the public, commercial or not-for-profit sectors.

AUTHOR CONTRIBUTIONS

BPB and ADS conceived project idea and developed system. ADS designed redistribution algorithms. BPB designed simulation environment, prediction models, and optimizations, and was lead author on paper drafts. WMJ provided medical background to the article’s statistical assumptions, citations, and article drafts.

SUPPLEMENTARY MATERIAL

Supplementary material is available at Journal of the American Medical Informatics Association online.

CONFLICT OF INTEREST STATEMENT

The authors have no conflict of interest to declare.

DATA AVAILABILITY

Underlying data available at: https://doi.org/10.5068/D1K39S.