High Systolic Blood Pressure at Hospital Admission Is an Important Risk Factor in Models Predicting Outcome of COVID-19 Patients

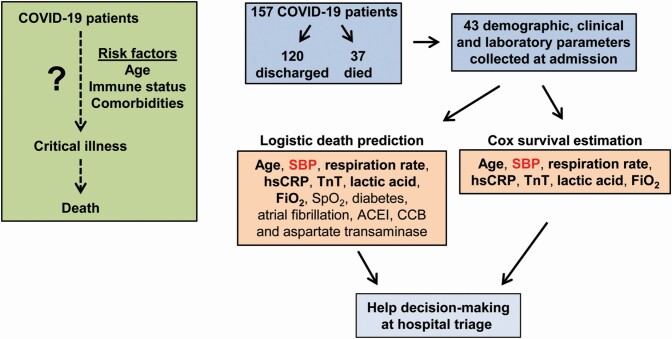
Abstract

BACKGROUND

The risk that coronavirus disease 2019 (COVID-19) patients develop critical illness that can be fatal depends on their age and immune status and may also be affected by comorbidities like hypertension. The goal of this study was to develop models that predict outcome using parameters collected at admission to the hospital.

METHODS AND RESULTS

This is a retrospective single-center cohort study of COVID-19 patients at the Seventh Hospital of Wuhan City, China. Forty-three demographic, clinical, and laboratory parameters collected at admission plus discharge/death status, days from COVID-19 symptoms onset, and days of hospitalization were analyzed. From 157 patients, 120 were discharged and 37 died. Pearson correlations showed that hypertension and systolic blood pressure (SBP) were associated with death and respiratory distress parameters. A penalized logistic regression model efficiently predicts the probability of death with 13 of 43 variables. A regularized Cox regression model predicts the probability of survival with 7 of above 13 variables. SBP but not hypertension was a covariate in both mortality and survival prediction models. SBP was elevated in deceased compared with discharged COVID-19 patients.

CONCLUSIONS

Using an unbiased approach, we developed models predicting outcome of COVID-19 patients based on data available at hospital admission. This can contribute to evidence-based risk prediction and appropriate decision-making at hospital triage to provide the most appropriate care and ensure the best patient outcome. High SBP, a cause of end-organ damage and an important comorbid factor, was identified as a covariate in both mortality and survival prediction models.

Graphical Abstract

Graphical Abstract.

The coronavirus disease 2019 (COVID-19) caused by severe acute respiratory syndrome (SARS) coronavirus-2 (SARS-CoV-2) first observed in December 2019, in Wuhan hospitals, Hubei, China, has spread since to become a worldwide pandemic. The World Health Organization (WHO) reported on 19 November 2020, 55,928,327 confirmed cases with 1,344,003 deaths in 235 countries (https://covid19.who.int/). The majority of the infected subjects have shown mild or even no symptoms, whereas some have presented much worse prognosis. The severe cases of COVID-19 patients developed a severe pneumonia, acute respiratory distress syndrome, a severe coagulopathy, myocardial disease, acute renal failure, encephalopathy, or multiple organ failure and death.^1–4

The most frequent symptoms of COVID-19 are fever, cough, and myalgia or fatigue, and less common symptoms include sputum production, headache, loss of sense of smell and taste, hemoptysis, and diarrhea.^3,5,6 Clinical features have included pneumonia with abnormal or severe clinical features such as acute respiratory syndrome with ground-glass opacities in subpleural regions, acute cardiac ischemia or heart failure, acute renal failure, or neurological manifestations including stroke, associated with microvascular thrombosis, all of which could lead to death. The symptoms of COVID-19 appear approximately 5–6 days after transmission has occurred, and the onset period to death has ranged from 6 to 40 days with a median of 14 days.⁷ The risk of death and period to death are dependent on the age and status of the immune system of the patient and may also be affected by comorbidities like hypertension, cardiovascular disease, diabetes, obesity, cancer, and immune suppression from diseases or treatments. Hypertension or high blood pressure (BP) may have an important impact on the severity of COVID-19 as it is a leading risk factor for cardiovascular disease.⁸

Establishing early the prognosis of COVID-19 patients using prediction models at the time of hospital admission could help relieve pressure on the healthcare system by allowing evidence-based risk prediction and decision-making when triaging patients, and thus contribute to the ability of healthcare workers to provide the most appropriate care to the patients, which could improve outcomes. Shi et al. showed that in addition to age and sex, hypertension was identified as an important risk factor associated with severe cases of COVID-19.⁹ Another study, identified markers of systemic inflammation (elevated neutrophil-to-lymphocyte ratio [NLR], derived NLR ratio [neutrophil count divided by white cell count minus neutrophil count], and platelet-to-lymphocyte ratio) and age as predictors of poor clinical outcome in COVID-19 patients.⁷ Although a high prevalence of comorbidities (88%) including hypertension, diabetes, and heart disease were observed, they were not included as covariates. Yuan et al. determined an optimal cutoff value of computerized tomography scan for the prediction of COVID-19 patients with pneumonia.¹⁰ COVID-19 patients with pneumonia who died presented a high prevalence of comorbidities (80%) including hypertension, diabetes, and cardiac disease that could have contributed to death. Guo et al. demonstrated that elevated troponin T (TnT) plasma levels, a marker of cardiac injury, were associated with greater mortality rate in COVID-19 patients, which was enhanced when TnT was combined with preexisting cardiovascular disease.¹¹ The above studies underscore the importance of factors such as age, respiratory disease, systemic inflammation, and cardiovascular comorbidities at the time of hospital admission in determining the survival or death of COVID-19 patients.

We suggest that the combination of demographic, clinical, and laboratory parameters including age, respiratory disease, systemic inflammation, and comorbidities such as cardiovascular disease could be used to generate models that efficiently allow prediction of risk and development of severe disease leading to worse outcomes in COVID-19 patients at the time of admission to the hospital. To test this hypothesis, we have used the COVID-19 patient dataset from the already published study of Guo et al. from the Seventh Hospital of Wuhan, China¹¹ to determine the probability of death using both logistic regression and proportional hazards survival models. In both cases, an unbiased approach was used to select the covariates among parameters collected at the day of admission to the hospital, and cross-validation was used to estimate model performance.

METHODS

Study design and participants

This is a single-center, retrospective, cohort study performed using electronic medical records of COVID-19 patients admitted from 23 January to 23 February 2020 to the Seventh Hospital of Wuhan City, China, which was a designated hospital to treat patients with COVID-19 and was supervised by the Zhongnan Hospital of Wuhan University in Wuhan, China. The dataset was used originally in the study of Guo et al.¹¹ that complied with the ethical principles for medical research involving human subjects of the 1975 Declaration of Helsinki¹² and was approved by the Institutional Ethics Board of Zhongnan Hospital of Wuhan University and the Seventh Hospital of Wuhan City (No. 2020026). Data were collected in consecutive patients hospitalized with COVID-19, including 211 patients who were successfully treated and discharged, and 45 patients who died. Sixty-seven discharged patients and 2 patients who died were excluded from analysis because of incomplete data, leaving 144 discharged individuals and 43 individuals who died included for final analysis. Consent was obtained from patients or patients’ next of kin. The end point of the study of Guo et al. was the incidence of COVID-19-associated death. Since the data were anonymized and data linkage or recording or dissemination of the results will not generate identifiable information, the Research Review Office of the Jewish General Hospital and the Centre-West Integrated University Network indicated in writing that under Article 2.4 of the TriCouncil (Canada) Policy Statement (2018), no further Research Ethics Review was required, the patient dataset coming from a study with a university hospital Ethics Board approval in China.

Statistical analysis

Data are shown as % for categorical variables and as means ± SD for continuous variables. The primary dependent variable in our analyses was patient discharge or death. We examined this outcome both as a binary variable, and looked at time to these events. All measures in Tables 1 and 2 were considered for their associations with patient outcome. Comparisons between the discharged and death patient groups were done using chi-square tests for categorical data and Wilcoxon rank-sum tests for continuous data. P < 0.05 was considered statistically significant.

Table 1.

Demographics and clinical characteristics of discharged and deceased COVID-19 patients

	COVID-19 patients
Parameters	Discharged	Deceased	P values
Number of patients	120	37
Age (years)	56 (46–65)	72 (66–76)	<0.001
Male sex (%)	43.3	62.8	0.059
Body temperature (°C)	36.8 (36.4–37.2)	36.8 (36.4–37.2)	0.704
Systolic blood pressure (mm Hg)	125 (118–132)	137 (124–150)	<0.001
Diastolic blood pressure (mm Hg)	76 (70–80)	78 (74–86)	0.061
Heart rate (beats/minute)	80 (76–89)	90 (78–110)	0.004
Respiration rate (breaths/minute)	20 (20–20)	20 (20–25)	0.001
Onset of COVID-19 symptom (days)	10 (7–13)	8 (6–11)	0.229
Days of hospitalization	17 (13–24)	11 (5–18)	<0.001
Comorbidities
Diabetes (%)	11.7	27.0	0.035
Hypertension (%)	28.3	59.5	0.001
Cerebrovascular disease (%)	1.7	13.5	0.008
COPD (%)	0.8	5.4	0.139
Liver disease (%)	5.0	0.0	0.337
Renal disease (%)	2.5	5.4	0.337
Cancer (%)	5.0	10.8	0.247
Smoking (%)	7.5	16.2	0.122
Atrial fibrillation (%)	1.7	18.9	0.001
Medications
ACEIs (%)	2.5	10.8	0.054
ARBs (%)	6.7	5.4	1.000
CCBs (%)	15.0	43.2	0.001
β-Blockers (%)	12.5	24.3	0.114

Demographics and clinical characteristics collected on admission and days from onset of COVID-19 symptoms and days of hospitalization of discharged and deceased COVID-19 patients are presented. Data are shown as % for categorical and as median (interquartile range) for continuous variables. Categorical data were compared using chi-square test and continuous data using Mann–Whitney U test. Abbreviations: ACEIs, angiotensin-converting enzyme inhibitors; ARBs, angiotensin receptor blockers; CCBs, calcium channel blockers; COPD, chronic obstructive pulmonary disease.

Table 2.

Laboratory parameters of discharged and deceased COVID-19 patients

	COVID-19 patients
Parameters	Discharged	Deceased	P values
Number of patients	120	37
Blood gas analysis
SpO2 (%)	98 (95–99)	90 (85–93)	<0.001
PaO2 (mm Hg)	93 (77–12)	56 (49–67)	<0.001
FiO2 (volumetric fraction of O2)	0.21 (0.21–0.29)	0.45 (0.35–0.61)	<0.001
PaO2/FiO2 (mm Hg)	402 (298–493)	120 (98–203)	<0.001
Blood electrolytes and proteins
Sodium (mEq/l)	139 (137–143)	139 (137–144)	0.946
Potassium (mEq/l)	3.68 (3.39–3.97)	3.56 (3.20–4.21)	0.631
Calcium (mmol/l)	2.17 (2.08–2.25)	2.07 (1.99–2.12)	<0.001
Albumin (g/l)	37.0 (33.4–39.1)	32.3 (29.5–34.9)	<0.001
Globulin (g/l)	27.5 (25.6–29.8)	29.2 (27.4–33.4)	0.002
Albumin/globulin ratio	1.35 (1.15–1.51)	1.09 (0.94–1.24)	<0.001
Blood cell counts and fractions
White blood cell number (109/ml)	4.7 (3.8–6.1)	8.1 (5.6–12.2)	<0.001
Neutrophil number (109/ml)	3.3 (2.4–4.9)	7.4 (4.7–11.5)	<0.001
Neutrophil fraction (%)	73.5 (64.2–80.3)	88.5 (81.8–92.9)	<0.001
Lymphocyte number (109/ml)	0.86 (0.64–1.14)	0.61 (0.30–0.93)	0.001
Lymphocyte fraction (%)	17.6 (12.1–25.4)	6.5 (3.8–9.8)	<0.001
Neutrophil-to-lymphocyte ratio	4.1 (2.5–6.5)	13.5 (8.4–25.0)	<0.001
Liver and kidney functions
Alanine aminotransferase (U/l)	21.0 (14.0–31.5)	31.0 (19.0–39.0)	0.007
Aspartate aminotransferase (U/l)	28.0 (20.8–47.0)	47.0 (31.0–65.0)	<0.001
Creatinine (mg/dl)	0.67 (0.58–0.81)	0.78 (0.67–1.07)	0.003
Cardiac, inflammatory, and metabolic makers
Troponin T (ng/ml)	0.009 (0.006–0.012)	0.30 (0.014–0.077)	<0.001
hsCRP (mg/l)	31.3 (12.5–61.3)	93.3 (63.6–179.1)	<0.001
Lactic acid (mmol/l)	1.70 (1.30–2.00)	2.40 (1.70–3.10)	<0.001

Laboratory parameters collected on admission to the hospital of discharged and deceased COVID-19 patients are presented. Data are shown as % for categorical and as median (interquartile range) for continuous variables. Continuous data were compared using Mann–Whitney U test. Abbreviations: FiO₂, fraction of inspired oxygen; hsCRP, high-sensitivity C-reactive protein; PaO₂, partial pressure of oxygen; SpO₂, peripheral oxygen saturation.

Pearson correlation coefficients between variables were calculated, and visualized with a correlogram generated by the R package “corrplot.” Correlations with P < 0.01 were considered statistically significant.

The probability of death was estimated using L1 penalized logistic regression. Fivefold cross-validation was performed with the R package “caret,” ¹³ a wrapper to the “glmnet” package, to optimize the area under the receiver operator characteristic (ROC) curve in a penalized model.¹⁴ The penalization parameter α was fixed to 1.0 to force L1 penalization, and the second penalization parameter λ was estimated with cross-validation. After estimating the optimal number of predictors, post-selection inference was performed by fitting a standard logistic regression model, retaining only the predictors estimated to have nonzero coefficients after the first penalized regression. The variables in this post-selection inference table may not meet traditional significance thresholds since they have been selected through the cross-validation process in the penalized regression, not by their P values. Furthermore, with these variables, we used 5-fold cross-validation to estimate an ROC curve, and to estimate model performance with the area under the curve.

An L1 penalized survival time model was estimated using Cox proportional hazards in the R package glmnet.¹⁵ First, a regularized Cox regression model, with outcome defined as time to death since onset of symptoms (right-censored model), was fit. Fivefold cross-validation was used to select the optimal subset of predictors by minimizing the deviance of the Cox model. Thereafter, post-selection inference was performed with the selected predictors with an interval-censored proportional hazards model for time to death since symptom onset, matching time of hospitalization to the period when the individual was observed. This approach accounts appropriately for the fact that all variables were measured at the day of hospitalization rather than at the time of onset of symptoms. The proportional hazards assumption was checked using the diagnostic test proposed by Grambsch and Therneau.¹⁶ The coefficients in the formula calculating the probability of survival up to a certain time were generated with the R function “survfit.coxph.” ¹⁷ Performance was assessed with Harrell’s concordance statistic.¹⁸

RESULTS

Demographic and clinical characteristics of COVID-19 patients

The dataset contained 58 parameters from data collected on day of admission to the hospital (including demographics, clinical characteristics, and laboratory parameters), discharge/death status, days from onset of COVID-19 symptoms, and days from hospitalization to discharge from the hospital or death during hospitalization for 187 patients with COVID-19. Of the 58 data parameters collected, 12 variables were removed where more than 15 individuals had missing values, leaving 43 parameters collected on admission plus discharge/death status, days from onset of COVID-19 symptoms, and days of hospitalization. The cutoff for missing values in 15 individuals was based on the distribution shown in Supplementary Figure S1 online. As standard prediction models do not tolerate missing values, our analysis was done using 157 patients with no missing data, a subset of the original 187 patients reported in the study of Guo et al.¹¹ The demographics, clinical characteristics, and laboratory parameters of COVID-19 patients without and with missing data are presented in Supplementary Tables S1 and S2 online. Only 1 parameter was significantly different, neutrophil number, which was lower in patients with missing data.

COVID-19 patients were separated in 2 groups, discharged from the hospital (120 patients) or death during hospitalization (37 patients) (Tables 1 and 2). Deceased patients were older and presented higher systolic BP (SBP), heart rate, and respiration rate (RR), and more comorbidities including diabetes, hypertension, cerebrovascular disease, and atrial fibrillation compared with discharged patients (Table 1). As well, proportionally more deceased patients took angiotensin-converting enzyme inhibitors (ACEIs) or calcium channel blockers (CCBs). Laboratory results correlated with the respiratory distress and the presence of more comorbidities in deceased compared with discharged patients (Table 2). In addition, higher levels of markers of liver dysfunction (alanine aminotransferase and aspartate aminotransferase [AST]) and kidney function (creatinine) were observed in deceased patients. TnT, a marker of cardiac injury, was higher in deceased compared with discharged patients (Table 2). Systemic inflammation assessed by blood cell counts and fractions and high-sensitivity C-reactive protein (hsCRP) levels was elevated in deceased vs. discharged patients. All patients presented elevated lactic acid (>1 mmol/l), to a greater degree in deceased vs. discharged patients.

A penalized logistic regression model efficiently predicts the probability of worse outcomes of COVID-19 patients with 13 parameters collected at admission

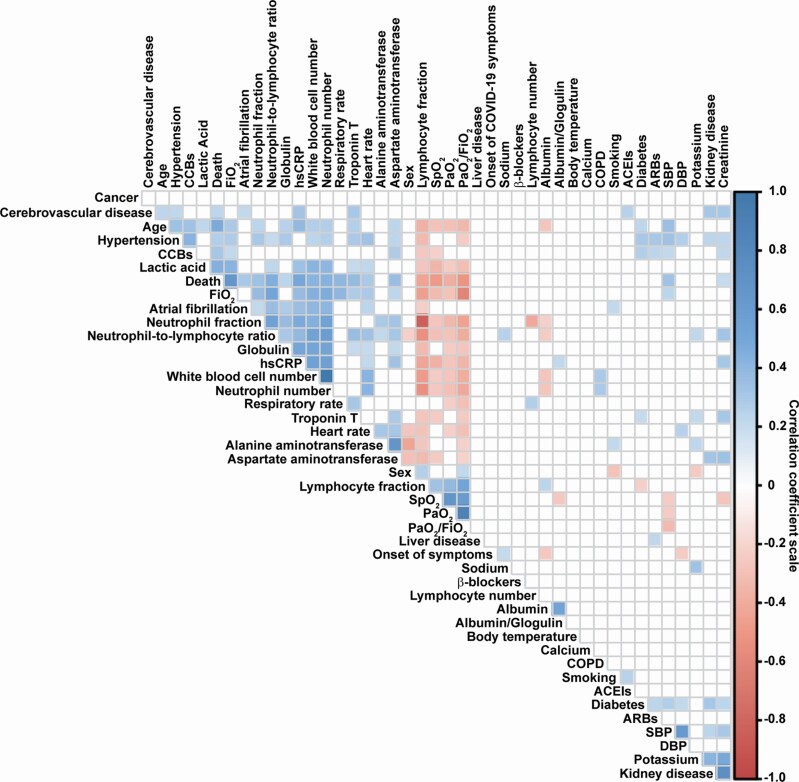
Pearson correlations determined between 43 covariates collected on admission and death status revealed associations between mortality and 22 covariates (Figure 1). Interestingly, hypertension and SBP were associated with parameters of severe cases of COVID-19 including death and respiratory distress parameters, as already suggested in early studies (reviewed in ref. ¹⁹). A penalized logistic regression with a 5-fold cross-validation identified a model predicting death in COVID-19 patients using 13 parameters collected at admission; the optimum value of the penalization parameter λ was 0.034, the area under the ROC curve was 0.943, sensitivity was 0.966, and specificity was 0.764. The 13 parameters included age, SBP, RR, peripheral oxygen saturation (SpO₂), DM, atrial fibrillation, ACEIs, CCBs, hsCRP, AST, TnT, lactic acid, and the fraction of inspired oxygen (FiO₂). When fitting a standard logistic regression using only these 13 variables to perform post-selection inference, the probability of death can be calculated as:

Figure 1.

Correlogram of the correlation coefficients of the 43 parameters collected at admission and death status. Correlations were determined using a Pearson Product Moment correlation. Correlations with P value <0.01 were considered significant. The insignificant correlation coefficient values are left blank. Correlation coefficient scale is represented on the right of the figure with the blue square showing positive correlation and red square negative correlation. Abbreviations: ACEIs, angiotensin-converting enzyme inhibitors; ARBs, angiotensin receptor blockers; CCBs, calcium channel blockers; COPD, chronic obstructive pulmonary disease; DBP, diastolic blood pressure; FiO₂, fraction of inspired oxygen; hsCRP, high-sensitivity C-reactive protein; PaO₂, partial pressure of oxygen; SBP, systolic blood pressure; SpO₂, peripheral oxygen saturation.

$${\displaystyle \begin{array}{l}{\displaystyle \mathrm{P}\mathrm{r}\mathrm{o}\mathrm{b}\mathrm{a}\mathrm{b}\mathrm{i}\mathrm{l}\mathrm{i}\mathrm{t}\mathrm{y}\mathrm{o}\mathrm{f}\mathrm{d}\mathrm{e}\mathrm{a}\mathrm{t}\mathrm{h}=\frac{\mathrm{e}\mathrm{x}\mathrm{p}(\eta )}{1+\mathrm{e}\mathrm{x}\mathrm{p}(\eta )}}\end{array}}$$

where η depends on the values of predictors and it takes the form

$${\displaystyle \begin{array}{l}{\displaystyle \begin{array}{ll}\eta =& -15.191+0.158\times \mathrm{a}\mathrm{g}\mathrm{e}+0.013\times \mathrm{S}\mathrm{B}\mathrm{P}+0.676\times \mathrm{R}\mathrm{R}\\ & -0.258\times \mathrm{S}\mathrm{p}{\mathrm{O}}_2+1.433\times \mathrm{d}\mathrm{i}\mathrm{a}\mathrm{b}\mathrm{e}\mathrm{t}\mathrm{e}\mathrm{s}\\ & +3.515\times \mathrm{a}\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{a}\mathrm{l}\mathrm{f}\mathrm{i}\mathrm{b}\mathrm{r}\mathrm{i}\mathrm{l}\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}+4.629\times \mathrm{A}\mathrm{C}\mathrm{E}\mathrm{I}\mathrm{s}\\ & +0.678\times \mathrm{C}\mathrm{C}\mathrm{B}\mathrm{s}+0.003\times \mathrm{h}\mathrm{s}\mathrm{C}\mathrm{R}\mathrm{P}1+0.018\times \mathrm{A}\mathrm{S}\mathrm{T}\\ & +12.464\times \mathrm{T}\mathrm{n}\mathrm{T}+1.920\times \mathrm{l}\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{a}\mathrm{c}\mathrm{i}\mathrm{d}+16.499\times \mathrm{F}\mathrm{i}{\mathrm{O}}_2\end{array}}\end{array}}$$

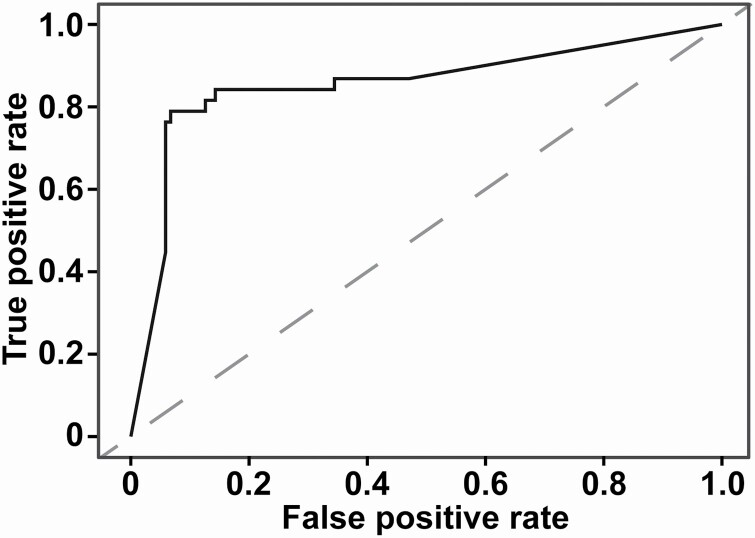
This information is also shown in Table 3, with standard errors and P values; as stated in Methods, traditional significance is not observed for all variables since they were selected through the penalized L1 regression. The performance of these 13 variables to predict death was estimated by using logistic regressions embedded in 5-fold cross-validation; the overall area under the curve was 0.886 (Figure 2).

Table 3.

Post-selection inference from logistic regression l predicting death in COVID-19 patients

Variables	Regression coefficient	Std. error	Z values	P values
Intercept	−15.191	8.926	−1.702	0.089
Age	0.158	0.067	2.348	0.019
SBP	0.013	0.028	0.462	0.644
Respiration rate	0.676	0.366	1.846	0.065
SpO2	−0.258	0.090	−2.857	0.004
Diabetes	1.433	1.222	1.277	0.202
Atrial fibrillation	3.515	1.649	2.131	0.033
ACEIs	4.629	2.128	2.205	0.028
CCBs	0.678	1.181	0.574	0.566
hsCRP	0.003	0.010	0.262	0.794
Aspartate aminotransferase	0.018	0.021	0.848	0.397
Troponin T	12.464	16.924	0.736	0.462
Lactic acid	1.920	0.937	2.049	0.041
FiO2	16.499	6.115	2.698	0.007

The post-selection generalized linear model of death prediction was determined using 13 variables identified by penalized logistic regression. Abbreviations: ACEIs, angiotensin-converting enzyme inhibitors; CCBs, calcium channel blockers; FiO₂, fraction of inspired oxygen; hsCRP, high-sensitivity C-reactive protein; SBP, systolic blood pressure; SpO₂, peripheral oxygen saturation.

Figure 2.

ROC curve of the model predicting death in patients with COVID-19 using 13 selected parameters collected on admission to the hospital. The dashed line represents the reference line. The area under the ROC curve is 0.886. Abbreviation: ROC, receiver operator characteristic.

A regularized Cox regression model predicts the probability of survival of COVID-19 patients with 7 parameters collected at admission

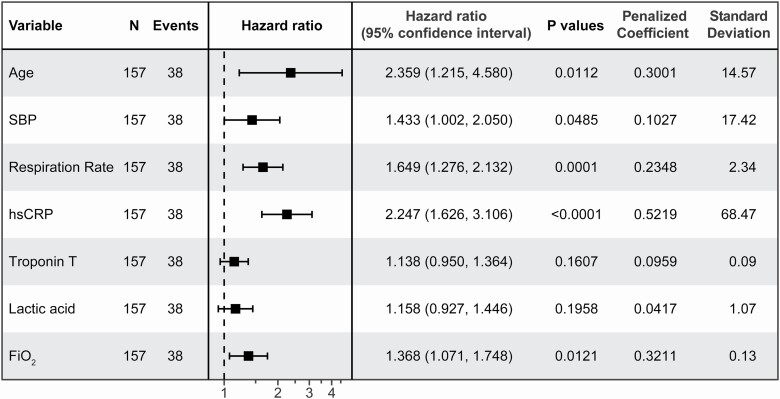
Using time to death since onset of COVID-19 symptoms as the outcome, a regularized Cox regression model with 5-fold cross-validation identified 7 parameters collected at admission as the most relevant variables to generate a model predicting survival of COVID-19 patients (partial likelihood deviance of 0.2805). The 7 parameters are age, SBP, RR, hsCRP, TnT, lactic acid, and FiO₂. Using time to death since symptoms as an interval-censored (or counting process) observation, a post-selection inference Cox proportional hazards model generated a model predicting survival of COVID-19 patients using 7 parameters identified above (Figure 3). The probability of survival of COVID-19 patients up to time t, indicated by our Cox model, was calculated as described below.

Figure 3.

The estimated hazard ratios for each predictor of the counting process Cox proportional hazard regression model predicting survival of COVID-19 patients. Hazard ratios in the figure are for a 1-SD change in the covariate. Abbreviations: FiO₂, fraction of inspired oxygen; hsCRP, high-sensitivity C-reactive protein; PaO₂, partial pressure of oxygen; SBP, systolic blood pressure.

$${\displaystyle \begin{array}{ll}& P(T>t|\mathrm{a}\mathrm{g}\mathrm{e},\mathrm{S}\mathrm{B}\mathrm{P},\mathrm{R}\mathrm{R},\mathrm{h}\mathrm{s}\mathrm{C}\mathrm{R}\mathrm{P},\mathrm{T}\mathrm{n}\mathrm{T},\mathrm{l}\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{a}\mathrm{c}\mathrm{i}\mathrm{d},\mathrm{F}\mathrm{i}{\mathrm{O}}_2)\\ & {\displaystyle \begin{array}{c}=S_0{(t)}^{\mathrm{e}\mathrm{x}\mathrm{p}(\mathrm{a}\mathrm{g}\mathrm{e}\times 0.0589+\mathrm{S}\mathrm{B}\mathrm{P}\times (0.0207)+\mathrm{R}\mathrm{R}\times 0.2141+\mathrm{h}\mathrm{s}\mathrm{C}\mathrm{R}\mathrm{P}\times 0.0118}\\ {}^{+\mathrm{T}\mathrm{n}\mathrm{T}1\times 1.3890+\mathrm{l}\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{a}\mathrm{c}\mathrm{i}\mathrm{d}\times 0.1374+\mathrm{F}\mathrm{i}{\mathrm{O}}_2\times 2.3598)}\end{array}}\end{array}}$$

where (t) is the baseline survival function, which can be estimated from data using a nonparametric approach.²⁰ Harrell’s concordance statistic for this model was 0.91. Figure 3 shows the hazard ratios per SD of each covariate, in contrast to this equation which shows the log hazard ratios for a single unit change on the original scale.

DISCUSSION

In this study, we have generated models predicting risk of developing severe disease leading to worse outcomes. Our study includes consecutive patients recruited at the Seventh Hospital of Wuhan, and followed until death or discharge, and therefore any selection bias should be minimal, and related only to the catchment pool for the hospital. First, we developed a logistic regression model that allows prediction of worse outcomes of COVID-19 patients with 13 covariates identified using by allowing cross-validation to determine the optimal number of covariates to retain from among a combination of 43 demographic, clinical, and laboratory parameters collected at the time of admission to hospital. Similarly, we created a Cox proportional hazards model predicting the probability of survival of COVID-19 patients with 7 covariates identified using a similar unbiased approach among the same set of 43 parameters, taking into account the time to death since appearance of symptoms as counting process. It is noteworthy that these 7 covariates containing SBP on arrival to the hospital were included in the 13 covariates of the model predicting a worse outcome.

Candidate approaches have been used to identify important risk factors associated with severe cases of COVID-19.^7,9–11 In this study, we used an unbiased approach to identify the covariates in order to generate an optimal worse outcome predicting model. This approach was successful as the area under the ROC curve was 0.886. The identified covariates are a combination of parameters already shown to be important risk factors associated with severe cases of COVID-19. Interestingly, the unbiased approach identified covariates that were shown previously to demonstrate synergistic effect when combined. The high mortality rate observed in COVID-19 patients with high TnT levels was double in presence of cardiovascular disease.¹¹ The 7 covariates used to generate the model predicting survival of COVID-19 patients were contained within the 13 covariates of the mortality predicting model. This may underscore the importance of these parameters in the outcome of COVID-19 patients. The common identified covariates are age, SBP, RR, hsCRP, TnT, lactic acid, and FiO₂. A similar unbiased approach was used by Liang et al. to develop a model predicting the risk of developing critical illness of COVID-19 patients at the time of admission with an area under the ROC curve of 0.88.²¹ Critical illness was defined as a composite of admission to the intensive care unit, invasive ventilation, or death. These authors identified similar covariates among 72 parameters of COVID-19 patients collected at admission: age, pulmonary compromise markers (chest radiographic abnormality, dyspnea, hemoptysis), coma, number of comorbidities, cancer history, a marker of systemic inflammation (NLR), a marker of tissue damage (lactate dehydrogenase), and a marker of liver function (direct bilirubin). Differences in identified covariates may be due to a different predicted outcome and parameters determined at admission.

SBP but not hypertension was identified as a covariate in both mortality and survival prediction models. SBP was elevated in deceased compared with discharged COVID-19 patients. It is unclear whether SBP was already elevated before or rose after infection with the SARS-CoV-2 in the deceased COVID-19 patient group. High SBP in the deceased COVID-19 patient group may be due to untreated or uncontrolled hypertension. It is also possible that SBP elevation is the consequence of reduced enzymatic activity of angiotensin-converting enzyme 2 (ACE2) induced by binding of a higher SARS-CoV-2 load, with decreased generation of the vasodilator peptide angiotensin 1–7 from angiotensin II, or results from effects of systemic inflammation. However, the deceased group of patients were older, and hypertension is more prevalent in the elderly. Accordingly, significantly higher SBP in the deceased group could be the result of confounding due to the older age of the patients that died.¹⁹ Elevated SBP could be a marker of preexisting end-organ damage and is an important comorbid factor. It is also unknown whether TnT was elevated in deceased compared with discharged COVID-19 patients before infection with SARS-CoV-2 or rose later. Two drugs used to control BP, ACEIs and CCBs, were identified as covariates for the prediction of death of COVID-19 patients. There is no evidence that these drugs contribute to the pathophysiology of COVID-19.¹⁹ The greater frequency of use of these drugs in deceased COVID-19 patients may be related to the higher SBP or rate of prevalence of cardiovascular disease (Table 1).

Limitations

The relatively small number of patients from 1 center in 1 country is a limitation. A larger cohort of patients from multiple centers and countries would allow validating our prediction models. As well, confirmation that these models are applicable in other healthcare systems is important. Secondly, the number of parameters collected on admission could be considered limited. A larger number of parameters could ensure identification of the best covariates. For example, it would have been nice to know time of infection, and to have detailed immune characterizations of the patients at admission, but these data are either unknowable or not available. Thirdly, it is unknown whether high SBP and high TnT levels in deceased patients were preexisting conditions or developed after onset of COVID-19 symptoms. Although the interval-censored survival models are more appropriate in this context, the implementation of penalized survival analysis does not allow the counting process specification. Therefore, we fit right-censored penalized models and only used interval censoring for post-selection inference. This is unlikely to materially change our results since right-censored models starting at time of hospitalization gave similar results.

This study generated an efficient model to predict critical disease leading to worse outcome in COVID-19 patients at admission to the hospital using 13 covariates selected among 43 demographic, clinical, and laboratory parameters using an unbiased approach. A model predicting survival which included 7 of these 13 covariates was generated using a similar approach. Age, RR, and hsCRP1 were the 3 main covariates that predict the outcome of COVID-19 patients; both in the prediction of survival and mortality. High SBP on arrival at the hospital, which is an important comorbid factor, was identified as a covariate in both models. The prediction of critical illness and survival of COVID-19 patients at admission to the hospital could contribute to risk stratification and evidence-based decision-making at triage, which would help to provide appropriate care to COVID-19 patients, potentially contributing to improve their outcomes. These parameters predicting outcome on admission would help in both ethical crisis triage following evidence-based patient survival probability, as well as contribute to dedicating in anticipation of deterioration available resource-intensive approaches to those patients for who critical disease can be predicted. A caveat to this conclusion is that the model described here is specific to the management available at the time that these data were collected. Progress in treatment since then is reducing case-fatality rates and may eventually supersede this particular model of risk prediction and necessitate development of new models adapted to a new reality.

FUNDING

This research was supported by Canadian Institutes of Health Research (CIHR) First Pilot Foundation Grant 143348 to E.L.S., by the Special Project for Significant New Drug Research and Development in the Major National Science and Technology Projects of China (project 2020ZX09201007) to Z.L., by a grant from Genome Canada (2017 B/CB) to K.O.K., by a Canadian Vascular Network fellowship to A.C., and by a scholarship from the Fonds de recherche Québec santé to K.Z.

DISCLOSURE

This manuscript was sent to Guest Editor, Hillel W. Cohen, MPH, DrPH for editorial handling and final disposition. The authors declared no conflict of interest.

DATA AVAILABILITY

The data and analytic methods will be/have been made available to other researchers for the purpose of reproducing the results or replicating the procedure.