Beyond the average view of dopamine

Abstract

Dopamine responses are synonymous with the ‘reward prediction error’ of reinforcement learning, and are thought to update neural estimates of expected value. A recent study by Dabney et al. enriches this picture, demonstrating that dopamine neurons track variability in rewards, providing a readout of risk in the brain.

Imagine you wanted to track the average temperature in July. Each day you might take a measurement, and average it with previous days’ readings. You can maintain this running average, and update it each day according to the “prediction error,” or difference between your current estimate and the measured temperature that day. This approach, however, gives you no measure of the variability of the temperature—your estimate will be the same for a month with the same temperature every day and one in which the temperature fluctuates wildly around the same mean. Instead, imagine that your group of friends perform the same learning procedure, but some are particularly influenced by days hotter than expected, others by surprisingly cold days. These idiosyncrasies in relative learning from positive versus negative prediction errors would produce either optimistic (warm) or pessimistic (cold) biases in their estimate of the mean, depending on how much temperatures vary from day to day. Collectively, the ensemble of biased temperature expectations across this group of friends would characterize the full temperature distribution for July.

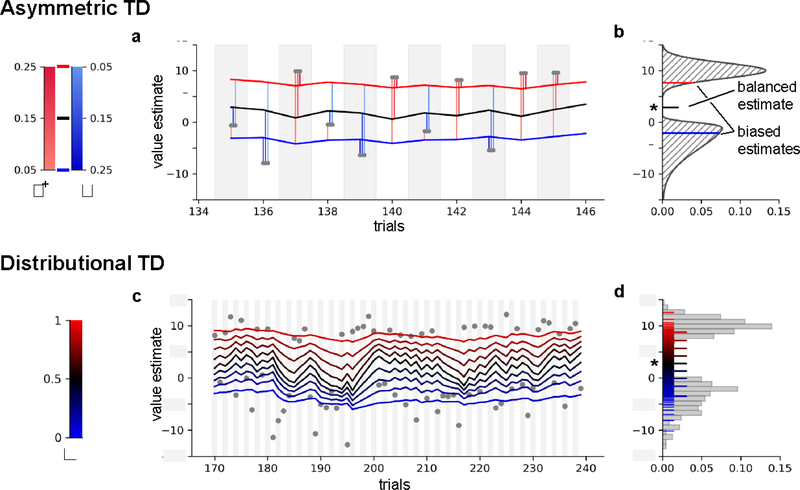
Midbrain dopamine (DA) neurons have long been hypothesized to support a similar averaging process, called temporal difference (TD) learning: by conveying a prediction error for reward (RPE), rather than temperature. This RPE is thought to allow the brain to learn to predict ‘value’—the expected (i.e., mean) aggregate future reward—from trial-by-trial experience, and thereby guide choice. However, this classic model, according to which many neurons broadcast a common signal for learning a single quantity, has struggled increasingly with mounting evidence of all sorts of puzzling variation in DA responses. In a recent study, Dabney et al. [1] detail one such dimension of systematic variation: like your group of friends, different DA neurons reliably differ in their relative sensitivity to negative vs. positive prediction errors. Dabney et al. reasoned that such unbalanced sensitivity should make the neurons’ value estimates, like your friends’, span a range of variability-dependent biases from optimistic to pessimistic [2]. If so, the population’s response would implicitly represent not just the mean reward but a set of ‘expectiles’ (an asymmetric generalization of the mean in the same way a quantile is an asymmetric generalization of the median; [3]), thus reflecting the entire distribution of outcomes used in the experiment (see Figure 1). Indeed, after showing the neurons complied with many specific predictions of this account, the researchers were ultimately able to reconstruct that distribution from the population responses. The success of this decoding shows that the spread of learning asymmetry across neurons is relatively broad, allowing biased estimates far from the mean to be represented.

Figure 1: Distributional TD learning is an ensemble of biased TD learning agents.

Typically, TD learning assumes a single learning rate (here, η), thus the influence of positive and negative prediction errors is balanced, ensuring convergence of the value estimate to the mean return. a) Asymmetric TD learning produces biased value estimates through different learning rates for positive and negative prediction errors. Divergence between optimistic (red) and pessimistic (blue) learners may be sufficient to produce prediction errors in opposite directions to the same outcome (for e.g., trial 138; outcomes in gray). Opposite phasic responses to identical reward amounts was one of the striking features of DA responses predicted by Dabney et al. according to distributional RL. b) Classic TD learning (black) balances the influence of positive and negative prediction errors, and the value estimate will converge to the true mean of the distribution of outcomes (marked by a star). Asymmetric TD learning will converge to an expectile, the value at which positive and negative RPEs are biased in proportion to the asymmetry of η⁺ and η⁻. c) Distributional TD learning uses an ensemble of asymmetric TD learners that cover a range of learning rate biases ($\tau =\frac{{\eta }^{+}}{{\eta }^{+}+{\eta }^{-}}$), tracking many expectiles of the outcome distribution. d) Distributed value estimates learned via distributional TD learning (here, 101 expectiles uniformly covering the range τ = (0,1]), compared to the observed distribution of outcomes (grey). A subset of biased value estimates corresponding to c) are highlighted.

Would this information also be useful to the brain? And for what purpose? Classically, approaches to reinforcement learning (RL) in artificial intelligence focus on predicting only the mean reward, since this is all you need to choose the action expected to be best on average. Dabney et al relate the dopamine responses to a newer class of distributional RL algorithms [4], which work like your ensemble of friends to predict a large range of possible value estimates. Even if you still use only the mean for choice, the mere presence of such variation, in practice, seems to help deep neural networks learn challenging tasks faster. But it also raises the intriguing possibility of actually using pessimistic or optimistic estimates to guide choice – and even dynamically switching among them. The strategy of down- or up-weighting better or worse outcomes closely mirrors the classic formalism of risk sensitivity in economics, in which a chooser is more willing to gamble for a larger outcome if they overweight its value. Accordingly, distributional RL allows an engineer training a network to fly a drone to take risks in simulation, then pilot more carefully when actually flying expensive equipment. There is also some intriguing evidence that biological organisms can modulate their risk sensitivity to circumstance: for instance, animals forage more desperately when in danger of starvation [5]. In human neuroimaging, links have also been demonstrated between asymmetric scaling of prediction errors and risk-sensitive choices, though so far using a single prediction error rather than an ensemble [6]. Risk adjustment may also go wrong in mental illness: many diverse symptoms of anxiety disorders can be understood as reflecting pathologically pessimistic evaluation [7]. An exciting future direction for this work, then, is to examine whether the distributional response of dopamine neurons, shown here in the context of classical conditioning, might also relate to risk-sensitive choice behavior in the context of decision-making tasks.

Neurobiologically, the results also bring new data and a new formal perspective to bear on longstanding questions about the nature and degree of heterogeneity in DA neuron responses, and the corresponding patterns of precision vs diffusion in their inputs and outputs [8]. In addition to recent reports of heterogeneity in the environmental and behavioral dimensions to which DA neurons respond [9], the current results establish variability in DA responses related to the single dimension of value. Perhaps surprisingly, the current data also indicate a notable degree of separation in the ensemble of feedback loops between these distinct value estimates and the prediction errors that train them. That is, there cannot be substantial cross-talk between value estimates learned from each pool of RPE-signaling DA neurons with a particular learning asymmetry, or the entire ensemble would collapse to the mean estimate predicted by classic TD learning. This implied separation actually raises a further computational puzzle, though, because the full goal of TD learning is predicting not just a single number – like the temperature, or the single water bolus given the animals in each trial of these experiments – but instead chaining these together in sequential steps to predict the long-run sum of future rewards.

Chaining together sequential predictions is what allows these algorithms (and, it is believed, the brain) to solve difficult real-world tasks like mazes that involve multiple steps of choice. But extending distributional RL from estimating a single outcome, as in this study, to the full problem of tracking variation over a sequence of outcomes, actually does require bringing together information across all the channels of the learning ensemble at each step of value update. It’s as yet unclear how (or indeed whether) the dopamine system is wired up to square this circle. Perhaps one additional piece of the puzzle is that dopamine efflux in striatal target regions (thought to mediate learning-related plasticity) bears a complicated relationship to spiking in dopamine neurons and features volumetric diffusion of released DA through the intracellular fluid [10]. All this provides another locus in the learning circuit in which functional asymmetry in prediction error-driven value updates, and anatomical crosstalk across channels, might arise. Whether it is through cellular or circuit mechanisms local to the VTA, or mediated through striatal, and perhaps even cortical, loops, the detailed results of Dabney et al. make clear that DA responses are indeed able to maintain rich information about the experienced distribution of outcomes. Ultimately, whether and how this distributional information in DA might be used to guide decisions involving risk is the next test of the algorithm: to go beyond the average course of action and into the complex calculus of choice.