Beyond simple dichotomies in reinforcement learning.

Abstract

Reinforcement learning (RL) is a framework of particular importance to psychology, neuroscience, and machine learning. Interactions between these fields, as promoted through the common hub of RL, has facilitated paradigm shifts relating multiple levels of analysis within a singular framework (e.g dopamine function). Recently, more sophisticated RL algorithms have been incorporated to better account for human learning, and in particular its oft documented reliance on two separable systems. However, along with many benefits, this dichotomous lens can distort questions, and may contribute to an unnecessarily narrow perspective on learning and decision making. Here we outline some of the consequences that come from over-confidently mapping algorithms, such as model-based vs. model-free RL, with putative cognitive processes. We argue that the field is well positioned to move beyond simplistic dichotomies, and we propose a means of re-focusing research questions toward the rich and complex components that comprise learning and decision making.

1. Introduction

The empirical study of learning and decision making, in both human and non-human animals, has catalogued a wealth of evidence consistent with the idea that behavior is governed by at least two separable controllers. Behavior has been dichotomized across several dimensions, including emotion (Hot/Cold)¹, action selection (habitual/goal-directed)², judgements (associative vs. rule based)³, and more recently, model-free/model-based (MF/MB)⁴. Although the terms used to characterize these controllers vary, and have largely been absorbed into the terms System1/System2^5,6, many seemingly ‘irrational’ behaviours have been argued to emerge from a system that is fast, reactive, implicit, retrospective and emotionally charged. This has been contrasted with a system described as slow, deliberative, explicit, prospective and calculating^5,6. Our understanding of the processes driving behavior, from the neural implementations to social factors, has advanced considerably through the use of these dichotomies in terms of both experimental and theoretical development.

However, despite a common philosophical core, the various frameworks used to describe these behavioral controllers vary in terms of their formalism and scope, and as such, they are not interchangeable, nor are the phenomena they purport to explain. More importantly, the aforementioned dichotomies do not constrain the neural or cognitive mechanisms that dissociate the two systems, making it deceptively difficult to uniquely and reliably classify behavior as being driven by any one particular controller. To address this, dual-system theories of learning and decision making have been drawn toward the formalization offered by the field of machine learning, readily found in the literature as a mapping to model-based (MB) / model-free (MF) reinforcement learning (RL)⁷.

Computational formalization promises important benefits: it promotes a precise quantitative definition of important concepts, and often enable us to bridge levels of analysis⁸ across cognitive concepts to their underlying neural mechanisms. Parameters of formal computational models are often thought to capture meaningful information about how we learn, in a low-dimensional and easily quantifiable (parameter) space. While the MB/MF RL formalization has realized such benefits⁹, it has also brought some challenges¹⁰. Here we address some of the limitations presented by dual-system theories that have the potential to impede progress in the associated fields of study. We argue that the dimensionality of learning – the axes of variance that describe how individuals learn and make choices – is well beyond two, as proposed by any given dual-system theory. We contend that attempts to better understand learning and decision making by mapping it onto two a-priori defined components may cause the field to lose sight of some essential features of learning. We focus on the example of the MB vs. MF RL dichotomy for one key reason: MB vs. MF is one of the most well-defined dichotomous theories of learning and decision-making, and has often been interpreted as capturing the essence of other dual-system theories computationally. We show that this confidence induced by a strong formalism does not obviate the limitations of the dual-system approach. Although the strengths offered by the MB/MF RL framework are well documented^9,11, it has become increasingly clear that accurately labelling behavior or neurological signals as uniquely associated with one algorithm or the other can be deceptively difficult^12–16. Here, we address some of the MB/MF framework’s limitations, highlighting sources of misattribution, the challenges associated with aligning computational and mechanistic primitives, and what is lost when our theoretical lens is narrowed to a single dimension. We propose that refocusing on the computationally defined primitives of learning and decision making that bridge brain and behavior may offer a more fruitful path forward.

2. What is Reinforcement learning?

Reinforcement learning (RL) is a term widely used in at least three separate, though overlapping, fields of research: computational sciences (machine-learning, artificial intelligence, computer science); behavioral sciences (psychology, cognitive sciences); and neuroscience (systems, cellular) (fig. 1). Although use of a shared language has mutually enriched these three disciplines, slight conceptual distinctions can lead to confusion across the three domains. In computational settings, RL refers to a class of learning environments and algorithms in which learning is driven by a scalar value (the reinforcement) and the algorithm’s goal is to optimize the future cumulative reinforcement (see box 1 for details). Behavioral sciences use RL in reference to learning processes that promote behavior by pairing it with a valued outcome (or the removal of an undesired outcome), and discouraged otherwise. The field of neuroscience typically treats RL as a process through which neuronal pathways are shaped in the brain, and is most often thought of as dopamine-dependent plasticity that shapes learning within and between various brain regions (including cortico-striatal networks).

Figure 1. RL across fields of research.

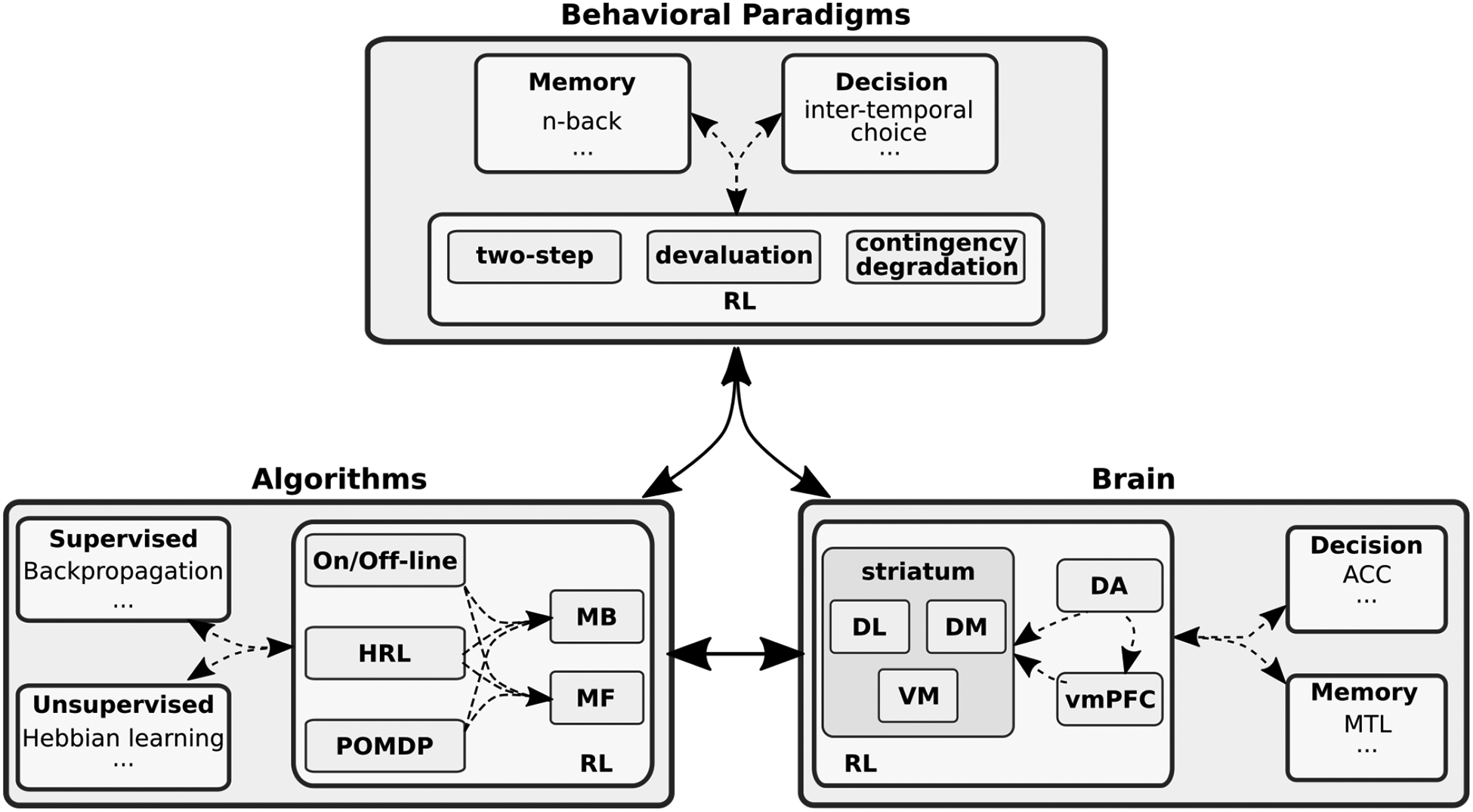
Many fields of research use the term reinforcement learning (RL), notably computational, behavioral, and neurosciences. The meaning of RL in each field is used in contrast to other concepts (e.g. supervised in machine learning). While computational sciences frames dichotomies between algorithmic approaches, behavioral sciences contrast and define cognitive constructs by way of experimental designs (e.g. habits are devaluation insensitive behaviors²), and neuroscience focuses on the brain’s separable neural circuits. It is also well accepted that the segregation, both conceptually and empirically, are practical though imperfect simplifications. For example, both memory and decision making processes make significant contributions to the neural circuits involved in RL, meaning that brain regions not uniquely associated with RL contribute to RL behavior nonetheless (dashed arrows). It is important to remember that while the three RL definitions are related (full arrows), they are not equivalent. dorso-lateral (DL); dorso-medial (DM); ventral-medial (VM); ventral-medial prefrontal cortex (vmPFC); dopamine (DA); anterior cingulate cortex (ACC); mediotemporal lobe (MTL).

Box 1: Formal RL algorithms.

Most commonly, RL problems are formalized as a Markov decision process (MDP), which is defined as; a set of states, S; a set of actions, A; a function R(s,a) that defines the reward delivered after taking action a ∈ A while in state s ∈ S, and a function T(s′|s,a) that defines which state, s′ ∈ S, the agent will transition into if action a ∈ A is performed while in state s ∈ S

MF-RL algorithms

One approach to solving a reinforcement learning problem is to re-distribute reward information in a way that reflects the environment’s structure. MF-RL methods make no attempt to represent the environment’s dynamics; rather, they store a set of state/action values that estimate the value of what’s expected without explicitly representing the identity of what’s to come. This implies that learned values reflect a blend of both the environment’s reward and transition structure as encountered reward values are propagated back to be aggregated in preceding states/actions values. For example, having chosen to visit the cafeteria (action a₁) while hungry in their office (state s₁), the student encounters new cafe’s booth (state s₂) and samples their food (reward r₁). In one variant of MF-RL, the agent learns about the circumstances that lead to reward using a reward prediction error:

$$\delta =\left(r_1+\gamma \cdot Q\left(a_2,s_2\right)\right)-Q\left(a_1,s_1\right)$$ (1)

$$Q\left(a_1,s_1\right)\leftarrow Q\left(a_1,s_1\right)+\alpha \cdot \delta$$ (2)

where the difference between the predicted value of going to the cafeteria for lunch, Q(a₁,s₁), and the actual value (r₁ + γ Q(a₂,s₂)), is quantified as a temporal difference reward prediction error (δ). The mismatch between expected and experienced outcomes is then used to improve the agent’s prediction according to learning rate α (equ 2). Note that both the reward value (r₁) and the discounted expected value of subsequent events (Q(a₂,s₂)) are considered as part of the prediction error calculation, offering a path through which rewards can be propagated back to their antecedents.

MB-RL algorithms

As implied by their name, MB algorithms tackle RL problems using a model of the environment to plan a course of action by predicting how the environment will respond to its interventions. While model can have very different meanings, the model used in MB RL is very specifically defined as the environment’s transition function, T(s′|a,s), and reward function, R(a,s). Commonly referenced MB-RL methods either attempt to learn, or are endowed with the model of the task to work with from the start. With a model of the environment, the agent can estimate cumulative state-action values online by planning forward from the current state, or backward from a terminal state. The optimal policy can can be computed using the Bellman equation:

$$Q_{MB}\left(a_1,s_1\right)=R\left(a_1,s_1\right)+\sum _{s^{\prime }}T\left(s^{\prime }|s_1,a_1\right)\cdot \gamma {\mathit{\text{max}}}_{a^{\prime }}\left[Q_{MB}\left(a^{\prime },s^{\prime }\right)\right]$$ (3)

where the value of each action available in the current state, Q_MB(a₁,s₁), considers the expected reward R(a₁,s₁), and the discounted expected value of taking the best action at the subsequent state, γmax_a′ [Q(a′,s′)] weighted by the probability of actually transitioning into that state T(s′|s₁,a₁). This approach can be recursively rolled out to subsequent states, deepening the plan under consideration. Thus, when faced with a choice of what to do for lunch, a MB strategy can flexibly consider the value of going back to the cafeteria or of visiting the new cafe by dynamically solving the Bellman equation describing the choice problem.

2.1. RL algorithms

Computational RL defines a class of learning problems and algorithms such as model-free (MF) and model-based (MB) RL. In contrast to supervised learning where correct answers are provided, or unsupervised learning where no feedback is available at all, RL problems involve learning how to achieve a goal by using the rewards and punishments induced through interactions with the environment. The family of RL algorithms is defined by their objective function: to find a strategy that maximizes the accumulated future reward. Some tasks are simple enough that an RL approach can solve the learning problem completely by identifying the best actions from start to finish in all possible scenarios (e.g. playing tic-tac-toe). However, most real world problems (like driving to work) are far more complex: the number of possible circumstances in which the agent might find itself (the state space) can be huge, as are the number of available actions, while measures of progress can be murky. In cases such as this, RL algorithms are limited to learning how to make ‘good’ decisions as opposed to completely solving what is often an intractable problem.

A formal description of an RL problem consists of a set of states in which the learning agent might find itself, and a set of actions the agent can take. It also includes a transition function that describes how the environment will respond to the agent’s actions, and a reward function that defines how good (or bad) observed events are. It is important to note that a formal specification is, as with any model, an approximation of the real problem. Most RL algorithms decompose decision making into two steps: first, derive value estimates for the different states or action available, then choose actions that are deemed most valuable.

RL algorithms can be categorized along many dimensions. MB vs. MF algorithms are contrasted based on the extent to which they represent the environment. MB algorithms maintain a representation of the problem beyond the state and action space, usually the transition and reward function. Equipped with a task model, the agent guides its decisions by considering the consequences of its actions to construct a plan that will move it toward its goal. Model-free (MF) algorithms, as their name implies, do not maintain such an explicit model. Instead, they store a set of value estimates, each representing the aggregated reward history of choices selected by the agent in the past, from which the algorithm can gauge the expected benefit of the options on offer (see Box 1).

These two strategies can be contrasted with respect to how they respond to changes in the environment or the agent’s goal. MB algorithms adapt more readily as they can leverage their task model to dynamically plan toward an arbitrary goal, though they suffer the additional hindrance of computing this action plan, which can rapidly become intractable. MF algorithms cannot adapt as easily due to their strategy of integrating reward history into a single value estimate; however, they offer an efficient approach to learning and decision making. Consider, for example, a student arriving at the main cafeteria for lunch, where they unexpectedly find a stand offering samples from a new cafe on campus (fig. 2). In contrast to the bland offerings from the cafeteria, the sample food is fresh and delicious and would clearly be a better lunch option. The next day the student considers their meal options. A MB strategy would consult its map of the campus and the items available to devise a plan of action that would route the student to the new cafe for lunch. In contrast, a MF strategy would consult its value estimates and simply repeat yesterday’s choice to visit the cafeteria since that option has been rewarding in the past, particularly after the last visit. In contrast to the potentially complex, and often intractable planning problem faced by a MB agent, MF choice is considerably less effortful as it relies on a cached value estimate that can be derived using simple computation that rely only on easily accessible information (see box 2) signalling how “off” the current estimate is. However, the computational efficiency of a MF approach causes it to be relatively inflexible as it can only look to the past to inform its choices, whereas the prospective capacity of the MB agent¹⁷ allows it to flexibly adapt to changes in the environment or its own goals.

Figure 2. Contrast between MB and MF algorithms in response to environmental changes.

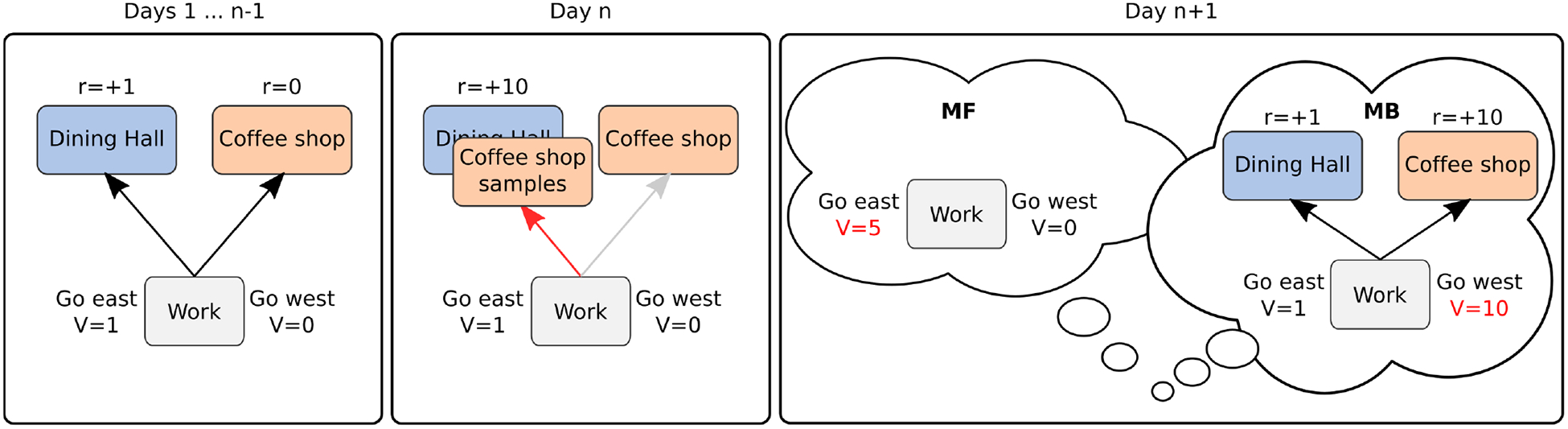
A student has learned that the cafeteria is to the east of their lab, and the coffee shop is to the west. Having visited both several times in the past, they have also learned that the lunch offerings at the cafeteria are passable (reward of +1), while the coffee shop does not offer food (reward of 0). On day n, the student opts to visit the cafeteria (which both MB and MF strategies agree to as the best option). However, the student encounters a stand in front of the cafeteria offering delicious items from a new menu at the coffee shop (reward of +10). The next day, the student must decide which direction to take for lunch. A MB strategy will consult its model of the environment to identify the path toward the best lunch option, which is now at the coffee shop (go west). A MF strategy, in contrast, will consult its value estimates, and owing to the unexpectedly good lunch the previous day, it will repeat the action of heading east (toward the cafeteria).

Box 2: Learning as a mixture of MB and MF-RL.

The original paper reporting the two-step task showed that human behavior exhibited both MB and MF components⁷. Since then, many have used versions of this task to replicate and expand on these findings in what has become rich and productive line of research, highlighting the relevance of MB vs. MF RL in understanding learning across many different domains. We do not provide an exhaustive review here (see¹⁴⁵), but highlight the impact on neural systems, individual differences, and non-human research to show the breadth of the impact of this theoretical framework on the computational cognitive neuroscience of learning community, and beyond.

Separable neural systems in humans

Subsequent research showed that the dual systems identified by the 2-step task and MB-MF mixture model can be largely mapped to separable systems, either by identifying separate neural correlates⁴⁸, or by identifying causal manipulations that taxed the systems independently. Causal manipulations have typically targeted executive functions and as such, the majority (if not all) research using this paradigm have been found to modulate the MB, but not the MF, component of behavior. Successful manipulations that reduced the influence of the MB component included taxing attention via multi-task interference⁴⁵ or task-switching⁷², inducing stress⁴⁶, disrupting regions associated with executive function¹⁴⁶, and pharmacology⁴⁷. Manipulations targeting the MF system are largely absent, potentially pointing to that system’s primacy or heterogeneity.

Individual differences

Individuals vary in their decision making process and how they learn from feedback. The MB-MF theoretical framework, along with the 2-step task, was successfully used to capture such individual differences and relate them to predictive factors¹⁴⁷. For example, in a developmental cohort,⁹⁶ showed that the MB component increased from age 8 through 25, while the MF component of learning remained stable. This framework has also been used to identify specific learning deficits in psychiatric populations, such as people with obsessive compulsive disorders¹⁴⁸ or repetitive disorders¹⁴⁹,addiction¹⁵⁰, schizophrenia¹⁵¹ and other psychiatric constructs^49,152.

Non-human studies

Early models of animal behavior described a causal relationship between stimuli and response¹⁵³, which was expanded upon to show that some behavior was better accounted for by models that included a cognitive map of the environment⁴⁴. However, more refined investigations suggested that both strategies, a stimulus-driven response and an outcome motivated action, can emerge from the same animals². Anatomical work in rats has dissociated these strategies, indicating that pre-limbic regions are involved in goal-directed learning^98,154, while infralimbic cortex has been associated with S-R control¹⁵⁵. This dissociation mirrors a functional segregation between dorsolateral and dorsomedial striatum, with the former implicated in S-R behavior, and the later being associated with goal-directed planning^156–158.

The scientific progress resulting from applying a RL computational framework is plainly apparent through the rapid advances in cognitive neuroscience. RL has been pivotal in providing a sound quantitative theory of learning, and a normative framework through which we can understand the brain and behavior. As an explanatory framework, RL advances our understanding beyond phenomenology in ascribing functional structure to observed data. Here we highlight some of the key findings.

2.2. MF-RL and the brain

Early research into the principles that govern learning likened behavior to the output of a stimulus-response association machine that builds links between stimuli and motor responses through reinforcement¹⁸. Various models described the relationship between stimuli, response, and reward, with nearly all sharing a common theme of an associative process driven by a surprise signal^19–21. Computational reinforcement learning theory built on the principles animal behaviorists had distilled through experimentation to develop the method of temporal difference (TD) learning (a model-free algorithm), which offers general purpose learning rules while also formalizing the reinforcement learning problem²².

The TD-RL algorithm sparked a turning point in our understanding of dopamine function in the brain. In a seminal set of studies, the phasic firing patterns of dopamine (DA) neurons in the ventral tegmental area (VTA) were shown to mirror the characteristics of a TD-RL reward prediction error (see equ 1), offering a bridge between behaviorally descriptive models and a functional understanding of a learning algorithms embodied by the brain^23–25. Continued work along this line of research has probed the details of DA activity in greater detail, linking it to various flavors of MF-RL^26,27. Importantly, this work has shifted the conceptualization of S-R instrumental learning away from inflexible reflex-like behaviour toward one of adaptable value based learning.

The role of DA as a MF-RL teaching signal is supported by work in both human and non-human animals showing that DA affects cortico-striatal plasticity as predicted by the theory²⁸. Subsequent research has focused on the causal import of dopaminergic input to show that systematic modulation of DA cell activity is sufficient for the development of cue-induced reward seeking behavior^29,30. Work in humans using fMRI has implicated striatal targets of DA as learning about state values (ventral striatum) and action policies (dorsal striatum)^31,32, suggesting that dopaminergic signals support both instrumental (action-value) and non-instrumental (state-value) learning in striatum. Consistent with MF value learning, additional research has shown shown that dopaminergic targets, such as dorsal striatum, appear to track MF cached value representations^33,34. Drug and genetic studies involving humans have shown that variation in dopaminergic function and manipulation of striatal DA sensitivity foster altered learning from positive and negative reward prediction errors^35–37. Furthermore, DA signals need not be limited to learning outwardly observable ‘actions’, as projections to cortex have also been suggested to be involved in learning cognitive ‘actions’ such as determining which items should be held in working memory^36,38–40, implicating the DA learning signal as a general purpose learning signal. In sum, a broad set of methodologies and experimental protocols have shown a consistent link between brain/behavior and computationally defined MF signals associated with the predictive value of the current state (e.e V(s)) and/or actions (e.g. Q(s,a)) according to motivationally significant events (r_t). Although some work challenges the DA/TD-RL framework^41–43, a broad corpus supports it; the computational RL theory has driven very rich new understanding of learning in the brain.

2.3. Learning as a mixture of MB and MF-RL

More research has built on the successes of using MF RL algorithms to explain brain and behavior by including MB RL as a mechanism through which a broader spectrum of phenomena may be understood. It has long been recognized that animal behavior is not solely determined by reinforcement history, but also exhibits planning characteristics that depend on a cognitive representation of the task at hand⁴⁴. Model-based RL presents a useful computational framework through which this aspect of behavior may be captured.

Attention to MB RL has increased considerably since the creation of the 2-step task in which the behavioral signatures of MF response and MB planning can be dissociated⁷. In this task, a choice between two available options stochastically leads to one of two second stage states, where a second choice can lead to reward. Each first-level option typically moves the participant into a specific second-stage state (e.g. a₁ → s₁, and a₂ → s₂). However, on rare occasions, the participant’s choice will lead to the alternative state (e.g. a₁ → s₂). Choices following rare transitions can dissociate MB from MF RL: MF-RL agents credit reward to the option that was chosen irrespective of the path that led to that reward and will thus be more likely to repeat a rewarded first-stage choice after a rare transition. In contrast, a MB strategy will plan to reach the rewarded second-stage state once more¹⁷, and thus will be less likely to repeat the first-stage choice, favoring the alternative option that most reliably returns it to the reward state (see Figure 2).

Investigations into the relationship between MB/MF-RL and other cognitive/psychological processes have identified links to MB-RL^45–49 more readily than to MF processe⁵⁰. There are several potential explanations for this, one being that the experimental protocols used to probe MB/MF processes, such as the two-step task, are more sensitive to MB control. Additionally, MB-RL could broadly relate to multiple processes that are highly dependent on a singular mechanism such as attention, offering a unique and easily manipulable cognitive resource through which a disparate processes may be disrupted. Alternatively, this may highlights a problem in the strict dichotomization in learning from MB-MF, as we develop in the next section.

3. Risks

Like any conceptual framework, the MB-MF theory of learning and decision making has intrinsic limitations. Ironically, its increasing popularity and scope of application could erode its potential by advancing a misinterpretation that data must be described along this singular dimension¹⁰. Indeed, researchers may be led to force a square peg through a round hole when analyzing separable components of their data through the lens of a coarse grained MB-MF dichotomy. Here, we detail some of the more important limitations this presents and how much richer learning theory should become.

3.1. Challenge of disambiguation

3.1.1. MF behaviour can look MB, and vice versa

Despite the ubiquity of MB control⁵¹, labelling behaviour as uniquely MB has been surprisingly difficult⁵². Notably, there are several channels through which behavior rooted in MF cached valuation may emerge to appear reflective of planning, and thus be labeled MB. For example, a MF strategy can flexibly adapt to outcome revaluation in a MB-like way when compound stimuli are formed using previous observations in conjunction with current stimuli¹⁴, a process that has been suggested as a means of transforming a partially observable markov decision processes (POMDPs) into a more tractable MDP⁵³. The same can occur when contextual information is used to segregate circumstances in which similar stimuli require different actions⁵⁴, or when a model is used retrospectively to identify a previously ambiguous choice¹³. Furthermore, applying a MF learning algorithm to a specific state representation that captures features of trajectories in the environment (e.g. the successor representations⁵⁵), mimics some aspects of MB-behavior (while also making separate predictions). In sum, coupling additional computational machinery such as working memory with standard MF algorithms can mimic a MB planning strategy.

Similarly, there are several paths through which a MB controller may produce behavior that looks MF. For example, one critical measure of MB control is sensitivity to devaluation, where an outcome that had been previously desired is rendered aversive (e.g. by associating that outcome with illness). However, it is not always clear which aspect of MB control has been interfered with should the test subject remain devaluation insensitive (and thus appear MF). In order for MB control to materialize, the agent must first identify its goal, search its model for a path leading to that goal, then act on its plan. Should any of these processes fail (e.g. using the wrong model, neglecting to update the goal, or planning errors), then the agent could appear to be acting more like a MF agent if that is the only alternative under consideration^12,56,57.

Further contributing to the risk of strategy misattribution, non-RL strategies can masquerade as RL when behavior is dichotomized across a singular MB/MF dimension. Simple strategies that rely only on working memory, such as win-stay/lose-shift, can mimic, or at the very least be difficult to segregate from MF control. Although simple strategies such as WS/LS can be readily identified in tasks explicitly designed to do so⁵⁸, more complex non-RL strategies, such as superstitious behavior (e.g. gambler’s fallacy, in which losing in the past is though to predict a better chance of winning in the future), or intricate inter-trial patterns (e.g. switch after 2 wins or 4 losses) can be more difficult to identify⁵⁹. Unfortunately, when behavioral response patterns are analyzed within a limited scope along a continuum of being either MB or MF, non-RL strategies are necessarily pressed into the singular axis of MF/MB.

3.1.2. Model use in MF-RL

More generally, other theories of learning assume that agents employ a model of the environment but do not adopt a MB-planning strategy for decision making. For example, the specific type of model used by classic MB algorithms for planning (the transition function) can be used to apply MF-RL updates on retrospectively inferred latent states¹³. This constitutes an example of a class of model-dependent MF-RL algorithms. Models of the environment in this class can include knowledge other than transition and reward functions. A model of the relationship between the outcome of two choices, for example, facilitates counterfactual MF value updates^60,61, while a model of the environment’s volatility can be used to dynamically adjust and optimize MF-RL learning rates⁶². Other features of learning using MF-RL updates in conjunction with models of the environment’s include work on hidden states, such as non-directly observable rules^54,63–65, demonstrating a rich set of phenomena to which a strict segregation between MB and MF learning and decision making is not well suited.

3.2. MB/MF are not primitive

MB and MF learning are often treated as a singular learning primitives (e.g. “manipulation X increases model-based-ness”). However, the measurable output of either algorithm relies on many computational mechanisms that need not be considered as unique components associated with a singular system. Indeed, MB/MF learning and decision making is arguably better understood as a high-level process that emerges through the coordination of many separable sub-computations, some of which may be shared between the two systems. Thus, the MB/MF dichotomy may not be helpful in identifying unique, separable mechanisms underlying behavior.

3.2.1. Independent underlying computations

It is often forgotten that MB and MF algorithms contain many independent computational sub-components. Although these sub-components are usually thought of from a theoretical perspective as parts uniquely contributing to a particular whole, they may also be recombined in beneficial ways that make the strong separation between MB and MF-RL less meaningful, particularly in light of research investigating their neural implementation and behavioral signatures (fig. 3 B).

Figure 3.

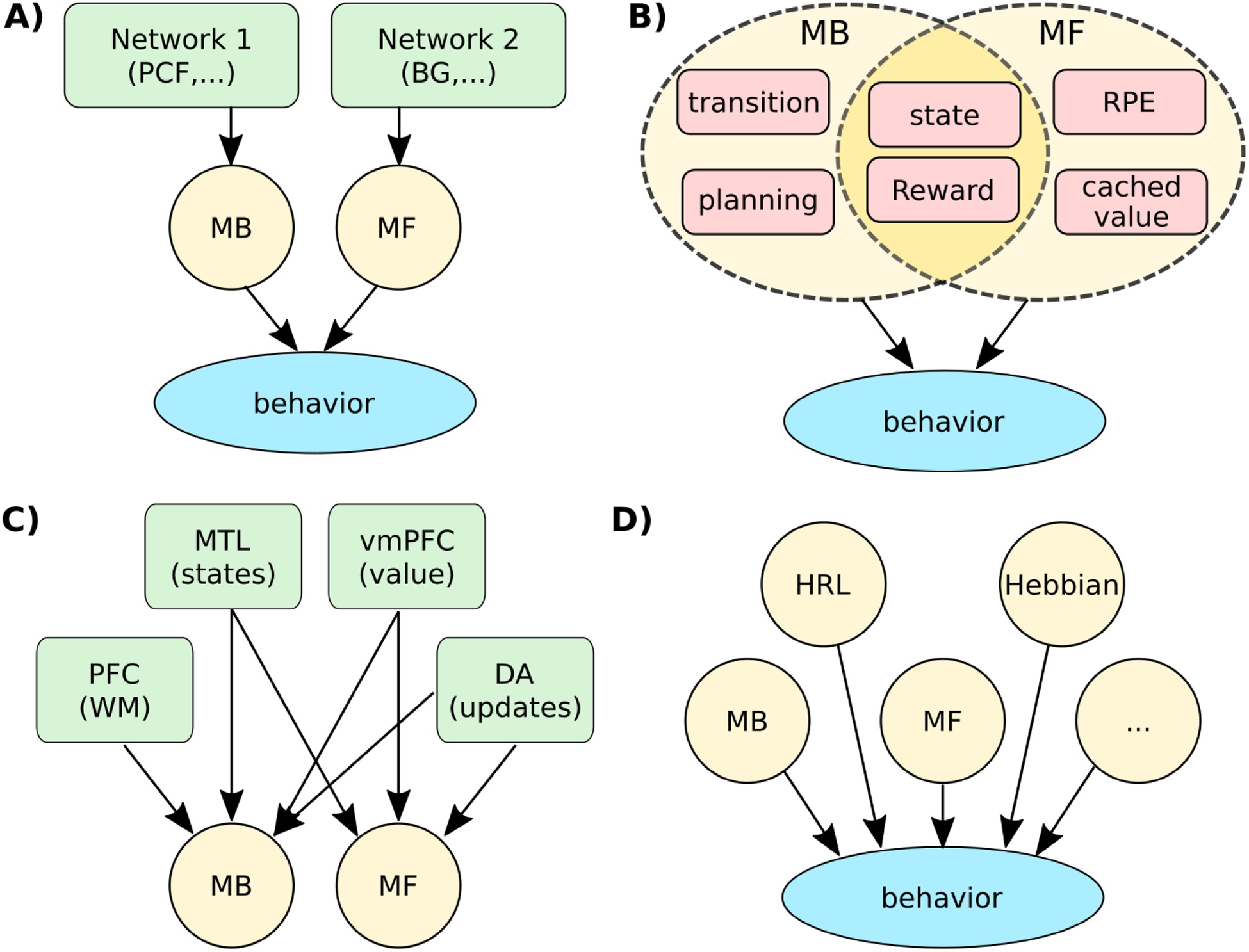
Decompositions of learning. A. Classic interpretations of the MB-MF RL theory cast the space of learning behavior as a mixture of two components, with MB and MF as independent primitives implemented in separable neural networks (green). B) In reality, MB and MF are not independent computational dimensions, and rely on multiple partially shared computational primitives (red). For example, MB planning depends on learned transitions, which in turn, relies on state representations that may be shared across MB/MF strategies. C) MB and MF’s computations do not map on to unique underlying mechanisms. For example, MB learning may rely on prefrontal (PFC) working memory to compute forward plans, medial temporal lobe (MTL) to represent states and transition, and ventro-medial (vm) PFC to represent reward expectations. MF also relies on the latter two, as well as other specific networks, non-exhaustively represented here. D) Additional independent computational dimensions are needed to account for the space of learning algorithm behaviors, such as hierarchical task decomposition (HRL) or hebbian learning.

For example, MB-RL is characterized by its use of both reward and transition functions to dynamically re-compute expected values. This process, commonly called forward planning, is in fact a high level function that incorporates multiple separable processes. Planning relies on a representation of reward and transition functions; however, it is important to bear in mind that those representations may not necessarily be used for planning at all⁶⁶, or they may serve other processes such as credit assignment, indicating they are not uniquey associated with a ”planning” system^13,63. Furthermore, the transition function, which is often assumed to be known and learned using explicit reasoning⁷, may also be shaped using MF-RL-like learning strategy that relies on state prediction errors⁶⁷, opening the potential for very different representational structures over which planning must take place. Lastly, planning is simplified by using a mixture of MF and MB valuation whereby MF cached values can be substituted for more costly MB derivations (e.g. by substituting Q_MF(s′) for γmax_a′ [Q_MB(a′,s′) in equation 3 at some point in the planning process⁶⁸, suggesting a highly adaptable and varied planning capability. Thus, indicating that manipulation X affects model-based-ness is only weakly informative, as any independent computational sub-component contributing to MB-RL could drive the effect.

Some sub-components may even be shared by the two systems. RL agents make choices by considering scalar values, whether those be dynamically derived (MB) or aggregated cached values (MF). However, agents operating in a real-world environment do not encounter scalar value; rather, they encounter sensory phenomena that must be converted into a valued representation. This translation could be a simple mapping (e.g. a slice of apple is worth 5 units), or it could be conditioned on complex biological and cognitive factors such as the organism’s state (hunger, fatigue etc…), the environment (e.g seasonal change, rival competition etc…), or components of the reward itself⁶⁹. Thus, both MF and MB strategies demand some form of reward evaluation process, be it a common resource, or unique to each controller (fig. 3 B).

Similarly, both MB and MF RL algorithms prescribe methods through which option values may be derived, but neither specify how those values should be used to guide decisions (the policy). However, the policy has an often important influence on learning: agents need to balance their drive to exploit (pick the best current estimate) and a drive to explore (pick lesser valued options in order to learn more about them). Exploration can be independent of task knowledge (e.g. ε-greedy, where a random choice is made with some probability²²), or directed toward features of the task model (e.g. uncertainty-guided exploration^70,71). As such, the action policy, which ultimately guides observable behavior, should be considered independent of the strategy through which valuation, be it MB or MF, occurs.

3.2.2. Independent underlying mechanisms

As we have previously noted, studying brain, behavior, and computational theory through the lens of a MB/MF dichotomy has propelled important advancements across many fields. However, we argue that a singularly dichotomous approach risks promoting an artificial segregation where in fact the computational components that constitute each algorithm are not necessarily unique to either strategy, suggesting they are more richly interconnected than they are distinct. But more importantly to our understanding of brain function and its applicable import (e.g. treatment of mental disease), we suggest that these computations themselves may not map cleanly onto singular underlying neural mechanisms (fig. 3 C). For example, learning a model of the environment and using that model to plan a course of action may rely on shared use of working memory resources^67,72, suggesting some functional overlap at the level of implementation in the brain.

An important, but often overlooked detail is that the primitive functions of RL algorithms assume a pre-defined state and action space²². When humans and animals learn, the task space must be discovered, even if MF-RL learning mechanisms then operate over them^{54,64,65,73–76}. State space creation likely involves separate networks, such as medial prefrontal cortex⁷⁷, lateral prefrontal cortex⁷⁴, orbitofrontal cortex^78,79, and hippocampus⁸⁰. Furthermore, a state identification process likely shares functions such as categorization, generalization or causal inference^54,63,64,81. Critically, the process through which a state space comes to be defined can have dramatic effects on behavioral output. For example, animals can rapidly reinstate response rates following extinction^82,83. A learning and decision mechanisms that relies on a singular cached value (as is commonly implement using MF-RL) has difficulty capturing this response pattern as it learns, and relearns value symmetrically. However, some implementations can readily elicit reinstatement by learning new representational values for the devalued option, and as such, return to prior response rates rapidly not as a result of learning per se, but as a result of state identification^81,84,85.

Finally, MF value updates may not, in all cases, be a relevant computational primitive matching a clear underlying mechanism to describe behavior, despite the fact that it seems to account for behavioral variance and be reflected in underlying set of neural mechanisms. The family of MF algorithms is extremely broad, and can describe extremely slow learning (such as used to train deep-Q-nets over millions of trials⁸⁶, with very low learning rates) or very fast learning (as is often observed in human bandit tasks with high learning rates⁸⁷). It is unlikely that the functions embodied by a singular dopamine-dependent brain network implementing a form of MF-RL are solely responsible for such a broad range of phenomena. Instead it is more likely that the DA-dependent neural MF-RL process is fairly slow (as reflected in the comparably slow learning of many non-human animals), and that faster learning, even when it seemingly can be captured by MF-RL algorithms, actually reflects additional underlying memory mechanisms, such as WM^88–90 and episodic memory^91–95.

In summary, it is important to remember that neither MB nor MF-RL are an atomic unified principal component of learning that map on to unique and separable underlying neural mechanism. The MB-MF dichotomy should be remembered as a convenient description of some aspects of learning that includes forward planning, knowledge of transitions, and outcome valuation, but one that depends on multiple independent sub-components.

3.3. The challenge of isomorphism

The computational MB/MF RL framework has drawn attention as a promising formal lens through which some of the many dichotomous psychological frameworks of decision making may be reinterpreted and unified¹¹, offering a potential successor to the commonly used but vaguely defined System1/System2 rubric^5,6. However, hybrid MB/MF RL cannot be the sole basis of a solid theoretical framework for modeling the breadth of learning behavior. In this section, we highlight separable components of learning that do not cleanly align with a MB/MF dichotomization (fig. 3 D), focusing primarily on the habitual vs. goal-directed dichotomy as it is often treated as synonymous with MB and MF RL.⁹⁶.

A substantial body of evidence points to two distinguishable modes of behavior: a goal-directed strategy that guides action according to the outcomes they bring about, and habitual control in which responses are induced by external cues². The principal sources of evidence supporting this dichotomy come from devaluation and contingency degradation protocols aimed at probing outcome directed planning, with the former indexing behavioral adaptations to changes in outcome values, and the latter manipulating the causal relationship between action and outcome (see^97,98 for review). Behavior is considered to be habitual if there’s no detectable change in performance despite devalued outcomes or degraded action/outcome contingencies.

The outcome-seeking and stimulus-driven characteristics of goal-directed and habitual behavior mirror the response patterns associated with MB and MF RL respectively⁹⁹. However, as pertinent experimental variables have been probed in more detail, growing evidence suggests that these constructs are not interchangeable. Studies have investigated individual difference measures across the goal-directed/habitual dimension in attempts to relate those to indices of MB/MF control^49,100. These studies have demonstrated the predicted correspondence between goal-directed response and MB control, but establishing a relationship between habits and MF control has proven more elusive. Indeed, eliciting robust habits is challenging¹⁰¹, more so than would be expected if habits related to in-lab measures of MF-RL.

Additional facets of learning and decision making have fallen along the emotional axis, with a ‘hot’ system driving emotionally motivated behavior, and a ‘cold’ system guiding rational decision making^1,102,103. Likewise, others have contrasted decisions based on an associative system rooted in similarity based judgements, and a rule based system that guides choice in a logical manner^3,5,6. Axes have further segregated strategic planning, where one can describe why and how they acted, and implicit “gut-feeling” choice^104,105. It is tempting to map these contrast to MF/MB RL along a shared thoughtfulness axis, but they are theoretically distinct. The MF/MB distinction makes no accommodation for the emotional state of the agent. Both similarity-based judgements and rule creation are beyond most RL algorithms, highlighting fully independent axes of theory, nor has it been established that MB/MF maps cleanly to a contrast between explicit/implicit decision making.

In summary, many dual system frameworks share common themes, thus motivating the more general reference of System 1/System2^5,6. Although many of the phenomena explained by these dual system frameworks mirror the thrust of the MB/MF dichotomy, none are fully reducible to it. Contrasting some of these dichotomies highlights the fact that MB/MF is not simply a quantitative formalism for those more qualitative theories, but is indeed theoretically distinct from most (e.g. the hot/cold emotional dimension), and offers patchy coverage of others (e.g. habitual/goal-directed).

3.4. What is lost.

Considering other dichotomous frameworks highlights the multi-faceted nature of learning and decision making by showing independent axes along which behavior can be described. Although aligning cognitive/neural/behavioral data across various dualities offers a means by which key variables can be exposed and examined, something is necessarily lost when a system as complex as the brain is scrutinized through a dichotomous lens. Indeed, absorptive terms of description often lack predictive precision (e.g. System1 / System2), while a proliferation of isolated contrastive frameworks tax our progress toward a coherent understanding of brain and behaviour^106–108. The application of RL in this campaign marks notable headway by offering a formal framework through which theorems may be proven¹⁰⁹, axiomatic patterns may be described¹¹⁰, brain function can be probed²⁹, and theories may be falsified. However, distilling learning and decision making to a single MB/MF dimension risks conflating many other sources of variance, but more importantly, threatens to dilute the formal merits of the framework to that of a verbal theory (e.g. the agent ”uses’ a ”model”).

4. Paths forward

Identifying the computational primitives that support learning is an essential question of basic cognitive (neuro)science, but also has the potential to have important implications in all domains that rely on learning - education, public health, human factors, and so on. It is also of great importance if we are to gain deeper insight into learning differences across populations, including developmental trajectories¹¹¹, across environmental factors, or for psychiatric or neurological diseases¹¹². Here, we highlight ways in which past research has successfully identified learning primitives that go beyond the MB/MF RL dichotomy, covering many separable dimensions of learning and decision making. These successful approaches offer explicit paths forward in the endeavor of deconstructing learning into its interpretable, neurally implementable basic primitives. This is essential to bridging brain and behavior, and to better understand individual differences across the lifespan as well as in clinical populations^111,112.

Disparities or inconsistencies between classic psychological theoretical frameworks offer opportunities to refine our understanding of the underlying computational primitives. For example, the apparent gaps between MB/MF RL and goal-directed/habitual behavior could promote both theoretical and experimental advances. Failure to elicit a detectable change in post-devaluation response rate using a devaluation protocol (i.e habits) could be caused by a range of mechanisms worthy of further investigation, some of which we have outlined here (e.g. degradation of the transition model, compromised goal maintenance, or engagement of a MF controller etc…). This points to the importance of considering additional dimensions of learning and decision making such as hebbian learning as a mechanism fostering value-free response maintenance¹¹³, and other facets of behavior such as exploration or state-space composition as sources of behavioral variance that may unwittingly appear more MB or MF^14,56.

Computer science research (see 1)also strongly inspires the identification of additional relevant dimensions of learning. For example, algorithms have used hierarchical organization as a means of embedding task abstraction. In hierarchical reinforcement learning (HRL), information is learned and decisions are made at multiple levels of abstraction in parallel. This offers potentially beneficial task abstractions that can span across time^114–116 or the state/action space, and have been observed in humans^{54,63,74,117,118}. Notably, HRL may be implemented using either MB planning or MF response, which offers a rich set of computational tools but also compounds the risk of misattribution when a singular MB/MF dimension is considered. Benefit can also come from considering the classic AI partition between supervised learning, where explicit teaching signals are used to shape system output, and unsupervised learning in which the system relies on properties of the input to drive response. Research has shown that human behavior is shaped by, and exhibits interactions between instructed and experienced trajectories through an environment³⁹. Proposals have outlined frameworks where supervised, unsupervised, and RL systems interact in order to build and act on representations of the environment^119,120; which further bend the notion that a singular spectrum of MB/MF control can sufficiently explain behavior. A third algorithmic dimension that warrants consideration, as it may compound worries of misattribution, is the the distinction between offline and online learning. Online learning agents integrate observations as they arrive, while offline learners can use information at a later point for “batch” updating, relying heavily on information storage and the ability to draw from it²². Offline learning has been suggested to occur in between learning trials involving working memory or hippocampal replay^121,122 or during consolidation in sleep¹²³, and may contribute to both model and reward learning (e.g. the Dyna learning algorithm²²).

Insights garnered from neuroscience should also continue contributing to enrich our understanding of the dimensions of learning and decision making, as regional specificity has implicated separable aspects of behavior across cortical and subcortical regions. For example, studies in which memory load was systematically manipulated exposed separable roles of MF-RL and working memory in learning^88–90,124, with the two processes mapping on to expected underlying neural systems^88,125,126. Further examples of using insights from neuroscience to illuminate the computations underlying learning behavior follow from a long history of research into hippocampal function. Previous work has fostered a dichotomy between the hippocampus and the basal ganglia, with the former being implicated in declarative learning, and the latter in implicit procedural learning^127–129. More recent workhas begun to probe how these two systems may compete for control⁹¹, or collaborate¹³⁰. This collaboration may emerge through relational associations maintained in hippocampus upon which value may be learned^131,132, or through developing a representation that captures transition structure in the environment¹³³. Further strengthening a functional relationship, research has also offered evidence of a cooperative computation role between systems during reward learning as a means of actively sampling previous events to improve value estimates^93–95,95.

It is important to note that identifying separable components of learning and decision making is complicated by the existence of interactions between different neural systems. Most theoretical frameworks treat separable components as independent strategies in competition for control. However, they often interact in complex ways beyond competition for choice¹³⁴. For example, in the MB/MF framework⁴, striatal signals show that MB information seeps into MF reward prediction error. Similar findings have also been observed in DA recordings^135,136. Even functions known to stem from largely separable neural underpinning exhibit such interactions: for example information in WM appears to influence MF-RL’s RPE computations^89,124–126. Going beyond simple dichotomies will not only necessitate increasing the dimensionality of the space of learning processes we consider, but also consider how different dimensions interact.

In summary, there are numerous axes along which learning and decision making vary, identified through various traditions of research (e.g psychology, AI and neuroscience). Future research should carry on identifying these axes, and recent work has made much progress identifying many additional dimensions of learning capture other important sources of variance in how we learn, such as meta-learning mechanisms^137,138, learning to use attention^73,139,140, strategic learning⁵⁹, and uncertainty-dependent parameter changes^62,141,142. This is evidence that learning and decision making vary along numerous dimensions that cannot be reduced to a simple two-dimensional principal component space, whether that axis is labelled as MB/MF, hot/cold, goal-directed vs. habitual, or otherwise.

5. Conclusions

We attempted to show the importance of identifying the primitive components supporting learning and decision making as well as the risks inherent to compressing complex and multi-faceted processes into a two-dimensional space. While dual-system theories are a means through which unique and dissociable components of learning and decision-making may be highlighted, key aspects could be fundamentally mis-attributed to unrelated computations, and scientific debate could become counterproductive when different sub-fields use the same label, even as well computationally defined as as MB and MF-RL, to mean different things.

We also propose ways forward. One is to renew a commitment to being precise in our vocabulary and conceptual definitions. The success of the MB-MF RL framework had begun to transition clearly defined computational algorithms toward a range of terms synonymous to many with various dichotomous approximations that may or may not touch on shared functional or neural mechanisms. we have argued that this is a dangerous approximation of a much higher dimensional space. The rigor of computationally defined theories should not hide their limitations: the equations of a model are defined in a precise environment and do not necessarily expand seamlessly to capture neighboring concepts.

Most importantly, we should remember David Marr’s advice and consider our goal when attempting to find primitives of learning⁸. The MB and MF family of algorithms, as defined by computer scientists, offers a high-level theory of what information is incorporated and how it is used during decision making, and how learning is shaped. This may be satisfactory for research that cares about the application of learning science to other domains, such as AI or education. However, for all research whose goal is to understand something that is dependent on the mechanisms of learning (the brain’s implementation), such as the study of individual differences in learning, it is indeed particularly important to ensure that the high-level theory of learning primitives proposes computational primitives that do relate carefully to the underlying circuits. This may benefit from a renewed enthusiasm from computational modelers for the basic building blocks of psychology and neuroscience^143,144, and a better appreciation for the functional atoms formalized by a rich computational theory.