Abstract
We study if government response to the novel coronavirus COVID-19 pandemic can mitigate investor herding behaviour in international stock markets. Our empirical analysis is informed by daily stock market data from 72 countries from both developed and emerging economies in the first quarter of 2020. The government response to the COVID-19 outbreak is measured by means of the Oxford COVID-19 Government Response Tracker, where higher scores are associated with greater stringency. Three main findings are in order. First, results show evidence of investor herding in international stock markets. Second, we document that the Oxford Government Response Stringency Index mitigates investor herding behaviour, by way of reducing multidimensional uncertainty. Third, short-selling restrictions, temporarily imposed by the national and supranational regulatory authorities of the European Union, appear to exert a mitigating effect on herding. Finally, our results are robust to a range of model specifications.
Keywords: COVID-19, International stock markets, Investor herding, Short-selling restrictions, Stringency Index
1. Introduction
The outbreak of the novel coronavirus COVID-19 in January 2020 has triggered a public health emergency of international concern and has exacerbated national health systems across the globe. Although the coronavirus crisis has become a major threat to particularly vulnerable members of the society, governments in both developed and emerging market countries have responded with a varying degree of stringency to save lives and alleviate growing pressures on their health sectors. In general, the ‘gold command’, elaborated by government strategists, has envisaged school and workplace closures, social distancing measures, and travel restrictions, along with fiscal stimulus packages and aggressive monetary expansions, to mention just few.
Nevertheless, the flip side of the coin had become an eye-opener for policy makers, politicians and financial regulators. Namely, the coronavirus crisis is predicted to descend into a business cycle recession and a global financial crisis. As a result, stock market investors have succumbed to the growing uncertainty surrounding the economy and the financial system, and have instigated massive sales of risky assets (Baker, Bloom, Davis, Terry, 2020, Ramelli and Wagner, 2020). In periods of financial market jitters and heightened uncertainty (Schmitt & Westerhoff, 2017), particularly of multiple dimensions (Avery & Zemsky, 1998), investors have a tendency to mimic decisions of their peers, i.e., follow the crowd (Kurz & Kurz-Kim, 2013).
Against this background, our study is founded on three main research questions. First, is there evidence of investor herding behaviour in international stock markets during the coronavirus crisis? Second, is the degree of stringency of government response instrumental in mitigating herding behaviour? Third, are the recent short-selling restrictions in the European Union effective in curbing herding behaviour?
To address these questions, our methodology builds on Christie and Huang (1995) and Chang et al. (2000), who proposed the cross-sectional absolute deviation () and the cross-sectional standard deviation () as measures of investor herding behaviour. and measure the average distance between an individual stock return and the market return, and help to ascertain whether an investor’s decisions feature herding. If the investor decides to mimic the group’s behaviour in periods of heightened stock market volatility, individual stock returns become less dispersed around the market return, which leads to a decline in and .
We contribute to the related literature in three ways. First, research that examines the effects of pandemic crises on financial asset valuations has been embryonic (Baker, Bloom, Davis, Kost et al., 2020). Two notable exceptions are (i) Donadelli et al. (2017), who study if investor mood, driven by news on globally dangerous diseases (i.e. SARS, Influenza A(H1N1), Polio and Ebola) is priced in pharmaceutical stocks in the US and (ii) Ichev and Marinč (2018), who report that the Ebola outbreak events were followed by elevated perceived risk in the US financial markets. In relation to COVID-19, only recently, Onali (2020) documents limited effects of COVID-19 cases and deaths on the US stock market returns. Moreover, Corbet et al. (2020) find that the volatility relationship between the Chinese stock market and cryptocurrencies evolved significantly during the pandemic. Further, Uddin et al. (2020) examine the connected dynamics of Asian financial markets and find a strong, positive dependence among the investigated markets due to the outbreak of COVID-19. Our study is conceptually closer to Yarovaya et al. (2020), who show that COVID-19 does not amplify herding in cryptocurrency markets. To the best of found knowledge, there is no research on investor herding behaviour in international stock markets during pandemic crises. Contrary to regular business-cycle recessions and financial crises, which typically begin with a moderate slowdown in economic activity, followed by an accelerating decline, the rapid global spread of the coronavirus poses a rare, sudden shock (Fetzer et al., 2020, Maćkowiak and Wiederholt, 2018). This global shock is estimated to cause disruptions to the global economy and stock market of biblical proportions. Since financial market investors can mitigate or exacerbate the economic and financial effects of the COVID-19 pandemic, this highlights the need to re-assess herding behaviour during the ongoing pandemic crisis, which was coined by Dr. Campbell Harvey on 03/04/2020 as ‘Great Compression’.1 Such rare events provide an unedited opportunity to throw new light on investor herding behaviour (Wagner, 2020). Thus, our research aims to fill this void by considering 72 international stock markets during the COVID-19 pandemic. Specifically, we ask whether the recent widespread stock market collapse is associated with the presence of herding behaviour in international stock markets.
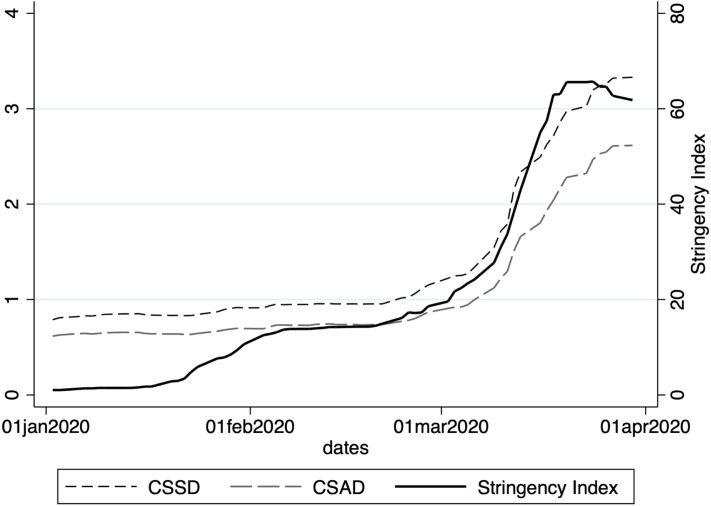
Second, unlike previous studies on herding behaviour in international stock markets (e.g., Chen et al., 2019, Chiang and Zheng, 2010a, Gebka and Wohar, 2013, Lin, 2018, Yarovaya et al., 2020), this study exploits the possibility that government response to the coronavirus pandemic can mitigate herding behaviour. For instance, fiscal stimulus packages that incentivise companies to temporarily furlough employees with a public subsidy (UK), and contribute to information sets of international investors, can potentially trigger no-herding or anti-herding effects. This possibility can be illustrated by means of a time series plot that depicts , and the Oxford Government Response Stringency Index (see Fig. 1). The second contribution underlines the seminal work of Avery and Zemsky (1998), which documents that an increase in the dimensionality of uncertainty is conducive to investor herding behaviour in financial markets. For instance, the coronavirus pandemic can be regarded as a sudden adverse shock, which can cause economic anxiety (Fetzer et al., 2020), and can fuel speculations among traders as to (i) how deadly is the disease, (ii) whether the coronavirus pandemic will spread further infecting an increasingly larger population share, (iii) the extent of such a spread of the pandemic, (iv) the cost of the deteriorating public health outcomes to the economy and the society, and (v) whether and, if so, when a vaccine can be developed.
Fig. 1.
Stringency Index and herding behaviour.
Notes: The left vertical axis of Fig. 1 depicts and , while the right vertical axis shows the Stringency Index. All three variables represent the weighted values from the 72 examined countries.
Fig. 1 shows that all series move in unison, which supports the notion that a more stringent government response to the coronavirus crisis is associated with higher values, hence lower herding.
Our third contribution consists of evaluating the effectiveness of short-selling restrictions, imposed by the authorities of the national and supranational regulatory authorities on herding behaviour. This effectiveness is informed by the so-called overpricing hypothesis, advanced by Miller (1977). This hypothesis posits that, in the presence short-selling restrictions, and under the assumption of heterogeneous beliefs of investors, stock prices will reflect only the valuations of bullish and bearish investors who currently own the stock. Although a comprehensive study on the effectiveness of the short-selling constraints during the Global Financial Crisis of 2008–2009, conducted by Beber and Pagano (2013), does not lend decisive support to the overpricing hypothesis, our study seeks to re-examine this hypothesis in a new light cast by the coronavirus pandemic. Our study is conceptually similar to Bohl et al. (2014), who examine the influence of short selling on herding behaviour in stock markets during the Global Financial Crisis of 2008–2009. Bohl et al. (2014) find that in France, Germany and UK, where short-selling constraints were imposed by the national regulatory bodies, an increase in the absolute value of the market return triggered a disproportionately high increase in the dispersion of returns around the market compared to rational asset pricing. Along similar lines, such an increase in the return dispersion agrees with the Miller’s overpricing hypothesis.
In our study, we find evidence of investor herding behaviour during the coronavirus crisis in the first quarter of 2020. We also find that the Oxford Government Response Stringency Index exerts a positive (i.e., anti-herding) and significant effect on in international stock markets. In line with the hypothesis of Avery and Zemsky (1998), government responses can reduce multidimensional uncertainty surrounding the coronavirus pandemic, which can effectively limit investor herding behaviour. Further, the short-selling restrictions are associated with anti-herding behaviour in international stock markets. This finding agrees with the overpricing hypothesis of Miller (1977).
The paper is structured as follows. In Section 2 we discuss our main hypotheses. In Section 3, we describe data. In Section 4, we lay out the methodology. In Section 5, we analyse our research findings. Finally, Section 6 concludes.
2. Hypotheses development
The aim of this section is to outline the hypotheses of the study. Initially, we underline the implications of herding behaviour especially during a financial turmoil. Next, we discuss the rationale for investor herding behaviour during a pandemic crisis, as well as the impact mechanism of both the government responses and short-selling restrictions on herding.
Herding drives trading in the same direction by a group of investors, which impedes the capability of financial markets to operate efficiently. In periods of financial market jitters, investors have a tendency to mimic decisions of their peers because they are occupied by heightened uncertainty (Kurz & Kurz-Kim, 2013). Waves of herding behaviour pose a threat to financial stability, and make the financial system more vulnerable (Philippas et al., 2013). This is due to the fact that correlated trades increase co-movement across different financial assets and thus a portfolio risk diversification becomes formidable (Chang et al., 2000). Empirical research into investor herding behaviour during financial crises is abundant, albeit inconclusive. For example, Galariotis et al. (2016) find no evidence of herding in the bond market during the EU crisis, and Yarovaya et al. (2020) do not provide evidence of herding in cryptocurrency markets during the COVID-19 pandemic crisis. By contrast, studies on stock markets commonly document that during financial crises herding is amplified (see Balcılar et al., 2017, Clements et al., 2017, Economou et al., 2018). Differently from historical previous business cycle recessions and financial crises, which were essentially driven by structural causes (e.g., the Global Financial Crisis of 2008–2009) (Sharif et al., 2020), the ongoing financial crisis was driven by a sudden, sharp COVID-19 shock. Contrary to regular business-cycle recessions, which typically begin with a moderate slowdown in economic activity, followed by an accelerating decline, the rapid global spread of the coronavirus poses a rare, sudden shock (Fetzer et al., 2020, Maćkowiak and Wiederholt, 2018). This global shock is estimated to cause disruptions to the global economy and stock market of biblical proportions. This shock also manifested in both the alarming levels of spread and the severity of the COVID-19 pandemic, which triggered extreme economic anxiety and uncertainty across the globe and spilled over to the global economy and stock market. In this regard, our first research hypothesis supports that herding behaviour increases during the COVID-19 pandemic crisis.
Hypothesis 1 H1 —
Investors show herding behaviour during the pandemic crisis.
Turning to the effects of government interventions on investor herding behaviour, it is paramount to gain better understanding of the economic and financial conditions surrounding the pandemic crisis. There is a consensus in the emerging body of research that COVID-19 triggered a dramatic increase in global uncertainty. A shock to the COVID-19-induced uncertainty is forecast to exert a negative and prolonged effect on economic output. For instance, at the global scale, the cumulative global output loss one year after the shock is estimated at 14% (Caggiano et al., 2020). In the US, the COVID-19 uncertainty shock is predicted to trigger a cumulative output loss of 12.75% over 10 months, and a decline in service-sector employment by an astounding 17% (Ludvigson et al., 2020). In the Euro Area, in a fairly conservative scenario, the cumulative output loss is estimated at 15.41% (Pellegrino et al., 2020). Bloom (2009) asserts that time-varying uncertainty shocks interact with the labour and capital adjustment costs and generate real-option effects; so firms scale back their plans. In turn, this drives fluctuations in employment and investment. In periods of heightened economic uncertainty, investor herding behaviour intensifies (Hsieh, 2013, Lin, 2018). Higher uncertainty and a delayed feedback about the underlying fundamentals can amplify psychological biases (Hirshleifer, 2001).
Following Avery and Zemsky (1998), multidimensional uncertainty is conducive to investor herding behaviour during a crisis. For instance, the heightened uncertainty about future prospects reduces risk tolerance of investors, who become reluctant to deviate from their peers and tend to herd on the market consensus (Lin & Lin, 2014). In the pandemic crisis, government responses to the propagation of the COVID-19 pandemic, such as containment and closure policies, might signal to the investors that the pandemic crisis is under control. Thus, uncertainty can be diminished with a decisive response by governments (Sharif et al., 2020), which restores investor confidence in international stock markets. In this regard, findings documented in Caggiano et al. (2020) provide support to such unprecedented policy interventions, put in place by governments and monetary authorities, which appear to limit the recessionary effects of the COVID-19-induced uncertainty shock. Timely announcements of government interventions improve the quality of information available for international investors and diminish economic-policy uncertainty. Building on the above mentioned theoretical and empirical evidence, our second hypothesis is formulated as follows:
Hypothesis 2 H2 —
Government responses to COVID-19 alleviate herding behaviour.
Pursuant to the overpricing hypothesis, in the presence of short-selling restrictions, and under the assumption of heterogeneous beliefs of investors, stock prices will reflect only the valuations of bullish and bearish investors (Miller, 1977). Short sellers who do not own the stock are crowded out from the market, so their valuation decisions do not influence the price. As a result, price should rise above its full-information rational-equilibrium level. The overpricing hypothesis receives support from Boulton and Braga-Alves (2010), who study the effects of the Emergency Order, issued on 15/07/2008 by the SEC, which restricted naked short sales of the common stock of 19 US financial firms. Boulton and Braga-Alves (2010) find that abnormal returns at the announcement of the short-sale restrictions are positive for the affected stocks. Lin and Lin (2014) find that trading strategies of short sellers – who tend to trade in high-volatility stock – are notably different from other traders in Taiwan. Although they argue that this finding owes to government short-selling restrictions, they do not formally test this argument. Beber and Pagano (2013) also ask if short-selling restrictions met the regulators’ objective to stabilise the stock price midst economic crisis. Beber and Pagano (2013) find that this objective was attained in the US, albeit not in other countries. Lastly, Bohl et al. (2014) provide empirical evidence that short-sale bans either decreased or had no impact on investor herding behaviour in various markets during the Global Financial Crisis. Therefore, if the overpricing hypothesis holds for stock markets, in which short selling is restrained, we anticipate that short-selling restrictions during the pandemic crisis are more likely to decrease investor herding behaviour in international stock markets.
Hypothesis 3 H3 —
Short-selling restrictions alleviate herding behaviour.
3. Data
The objective of this study is to investigate the effect of COVID-19 government response on investors’ herding in international stock markets. To this end, we focus on 72 stock market indices from both developed and emerging economies (see Table 1), which are obtained from the Thomson Reuters Eikon database, for the period from 01 January 2020, when the COVID-19 pandemic started spreading around the globe, to 31 March 2020. The COVID-19 government response data is retrieved from https://www.bsg.ox.ac.uk/research/research-projects/oxford-covid-19-government-response-tracker (Hale et al., 2020). Information on short-selling restrictions is retrieved from https://www.esma.europa.eu/regulation/trading/short-selling. This creates a strongly balanced dataset of 4536 market-day observations.
Table 1.
Stock markets indices.
| # | Stock market | # | Stock market | # | Stock market |
|---|---|---|---|---|---|
| 1 | FTSE100 UK | 25 | RIGA Latvia | 49 | KOPSI Korea |
| 2 | XETRA DAX Germany | 26 | MSE Malta | 50 | SENSEN India |
| 3 | CAC 40 France | 27 | BIST30 Turkey | 51 | JKSE Indonesia |
| 4 | FTSE MIB Italy | 28 | CROBEX Croatia | 52 | KLSI Malaysia |
| 5 | IBEX 35 Spain | 29 | MOEX Russia | 53 | NZX50 N.Zealand |
| 6 | AEX Netherlands | 30 | OMX Lithuania | 54 | SET Thailand |
| 7 | OMXS30 Sweden | 31 | BRIS Bosnia & Herzegovina | 55 | TWII Taiwan |
| 8 | WIG20 Poland | 32 | MBI10 North Macedonia | 56 | PSI Philippines |
| 9 | BEL20 Belgium | 33 | Belex15 Serbia | 57 | VNI Vietnam |
| 10 | ATX Austria | 34 | SMI Switzerland | 58 | KARACHI Pakistan |
| 11 | OMXC20 Denmark | 35 | OBX Norway | 59 | CSE Sri Lanka |
| 12 | ASE Greece | 36 | OMXI Iceland | 60 | TOP40 South Africa |
| 13 | HEX25 Finland | 37 | S&P/TSX Canada | 61 | EGX30 Egypt |
| 14 | PSI20 Portugal | 38 | Bovespa Brazil | 62 | TDW Saudi Arabia |
| 15 | BUX Hungary | 39 | MERVAL Argentina | 63 | QE Qatar |
| 16 | ISEQ Ireland | 40 | IPC Mexico | 64 | ADX UAE |
| 17 | BETI Romania | 41 | IBC Venezuela | 65 | CASA Morocco |
| 18 | SAX Slovakia | 42 | LIMA Peru | 66 | BB Bahrain |
| 19 | SBITOP Slovenia | 43 | NASDAQ Comp U.S. | 67 | MSM30 Oman |
| 20 | SOFX Bulgaria | 44 | JPXNK400 Japan | 68 | TUN Tunisia |
| 21 | CYMAIN Cyprus | 45 | STRAITS Singapore | 69 | AMM Jordan |
| 22 | PX Czech Republic | 46 | SSEC China | 70 | PLE Palestine |
| 23 | Tallin Estonia | 47 | S&P/ASX200 Australia | 71 | ALSIUG Uganda |
| 24 | LUXX Luxembourg | 48 | HKEX Hong Kong | 72 | NSE Nigeria |
Notes: Table 1 visualises the stock market indices that are included in our study.
3.1. COVID-19 government response stringency index
The Government Response Tracker systematically records government responses to deal with COVID-19. These responses are synthesised into an overall score, which represents the Stringency Index. The Stringency Index varies significantly from one country to another, which allows a cross-country comparison of different government responses. The information content of this index is based on 11 indicators of government response. The index comprises: (1) school closures, (2) workplace closures, (3) public event cancellation, (4) public transport closure, (5) public information campaigns, (6) restriction on internal movement, (7) international travel controls, (8) fiscal measures, (9) monetary measures, (10) emergency investment in healthcare and (11) investment in vaccines. The Government Response Tracker also records the number of confirmed cases and deaths due to COVID-19.
The data are obtained from publicly available information by a cross-disciplinary Oxford University team of over one hundred students and staff. Specifically, the data are collected from Internet sources, including news, articles, government press releases and briefings from every part of the world (Hale et al., 2020). The team records both the data and the original source. Thus, the data can be coded, checked and validated. The same criteria are applied to all countries across the globe; therefore, the data can be deemed reliable.
Amid growing concerns over the coronavirus pandemic, and its rapidly rising costs to the economy and the society, the government response data came under increased scrutiny by academics (Malik et al., 2020, Sabat et al., 2020), as well as media such as Roser et al. (2020), The Financial Times,2 The Guardian,3 and The Wall Street Journal.4 The fact that the COVID-19 Government Response Tracker is closely monitored by both academic journals and media attests its visibility and impact on investors’ decision making.
3.2. Measuring herding behaviour
To measure investor herding, we follow Christie and Huang (1995), who suggest the use of cross-sectional standard deviation () of returns to detect investor herding behaviour in an international market setting. Specifically, for country on day is defined as:
| (1) |
where is the return in country on day and is the global market return, which is calculated as the cross-sectional value-weighted average return from the 72 countries. is a dynamic measure of herding behaviour in country , which is calculated as the 22-day () rolling-window standard deviation of country’s return from the global market return on day . In the presence of herding behaviour, during large swings in stock prices and returns, country’s return should deviate ‘less’ from the global market return than during less volatile periods. In other words, ‘small’ values signal stronger evidence of herding behaviour, whereas ‘large’ values signal weaker evidence. In a similar vein, we use a second measure of herding behaviour, in the spirit of Chang et al. (2000), referred to as the cross-sectional absolute deviation, . This measure is calculated as:
| (2) |
Like , is a dynamic measure of herding behaviour in country , which is calculated as the 22-day ()5 rolling-window absolute deviation of country’s returns from the global market return on day .
Table 2.
Descriptive statistics.
| Variable | Obs | Mean | Std. Dev. | Min | Max |
|---|---|---|---|---|---|
| 4536 | 1.3840 | 1.0951 | 0.2117 | 7.5668 | |
| 4536 | 1.0508 | 0.8368 | 0.1711 | 6.4001 | |
| Stringency Index (INDEX) | 3434 | 21.7364 | 26.7476 | 0 | 100 |
| 4438 | −0.4651 | 2.6499 | −18.5411 | 13.6594 | |
| 4464 | −0.46211 | 1.5515 | −7.1404 | 3.1920 | |
| School Closing | 4171 | 0.3665 | 0.7650 | 0 | 2 |
| Workplace Closing | 4171 | 0.2347 | 0.6185 | 0 | 2 |
| Cancel Events | 4171 | 0.3879 | 0.7539 | 0 | 2 |
| Transportation Closing | 4171 | 0.0913 | 0.3905 | 0 | 2 |
| Information Campaigns | 4171 | 0.4066 | 0.4912 | 0 | 1 |
| Internal Restriction Movements | 4171 | 0.2728 | 0.6368 | 0 | 2 |
| Travel Controls | 4171 | 0.8921 | 1.2325 | 0 | 3 |
| Fiscal Measures | 4170 | 0 | 0.7318 | −0.3218 | 7.8112 |
| Monetary Measures | 4171 | 1.8587 | 5.7970 | −0.75 | 31.8316 |
| Investments in Health | 4169 | 0 | 0.5603 | −0.2620 | 7.8112 |
| Investments in Vaccines | 4171 | 0 | 0.3697 | −0.5247 | 7.8112 |
| Confirmed Cases (CASES) | 4171 | 1364.5871 | 8729.6721 | 0 | 143,025 |
| Confirmed Deaths (DEATHS) | 4170 | 52.1774 | 430.2485 | 0 | 10,781 |
| VIX | 4536 | 30.2882 | 21.8945 | 12.1 | 82.69 |
| REGION | 4536 | 1.9861 | 1.0737 | 1 | 4 |
| ESMA notification (ESMAN) | 4536 | 0.0679 | 0.2516 | 0 | 1 |
| ESMA ban (ESMAB) | 4536 | 0.0121 | 0.1095 | 0 | 1 |
Notes: Table 2 summarises the descriptive statistics of our research data for 72 countries: number of observations (Obs), mean (Mean), standard deviation (Std. Dev.), minimum (Min) and maximum (Max).
3.3. Short-selling restrictions
Our research design also controls for the recent regulatory measures, issued by the European Securities and Markets Authority (ESMA), a financial regulatory agency and supervisory authority of the European Union, which aimed at stabilising EU stock markets. Specifically, ESMA issued two measures. First, it decided to temporarily require the holders of net short positions in equities traded in the EU to notify the relevant regulatory body if the position reached 0.1% of the issued equity capital. Since this measure is applied uniformly across all EU countries, it can be regarded as a restraint on the degree of co-movement of stock market returns and, consequently, on herding behaviour. To this end, we construct a dummy variable (referred to as the ‘short-selling notification’), , which takes on value 1 from 16/03/2020, when ESMA reached this decision, and takes value 0 for the periods on or before 15/03/2020. Second, the national competent authorities of Austria, Belgium, France, Greece, Italy and Spain, decided to temporarily ban short selling of stocks in these countries from 18/03/2020, on which ESMA issued positive opinions.6 Accordingly, we define a dummy variable (referred to as the ‘short-selling ban’), , which takes on value 1 from the day when the short-selling ban became effective in these countries and takes on value zero before the ban was imposed. The two short-selling measures are summarised in Table 2.
3.4. Descriptive statistics
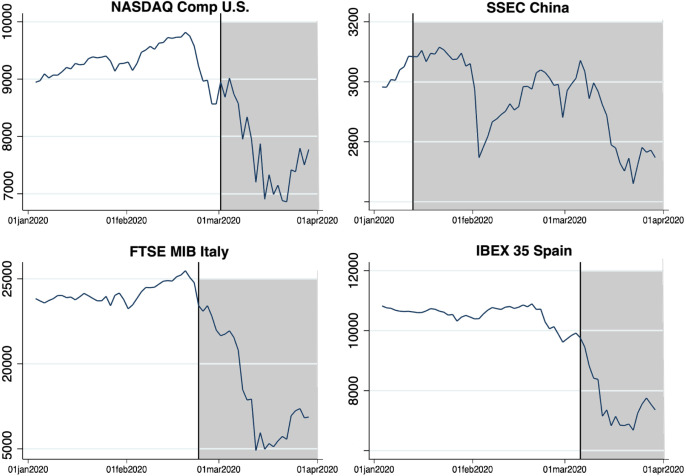
Table 2 reports the descriptive statistics of the variables used. () indicates that a return on the stock market index of country deviates on average from the world market return by 1.3840% (1.0508%). The standard deviation of is () is 1.0951% (0.8368%). The Stringency Index takes on values from 0 to 100, where higher values describe countries with stricter government responses. It averages 21.7364 index points and deviates from the mean on average by 26.7476 index points. We also note that both and feature negative average values, −0.4651% and −0.4621%, respectively, which illustrates the meltdown of equity value of companies across the globe. Values of and deviate from the world market return on average by 2.6499% and 1.5515%, respectively. Considering individual countries, Fig. 2 depicts stock market indices for four countries (US, China, Italy and Spain), where the shaded interval runs from the first recorded death due to the coronavirus pandemic.
Fig. 2.
Stock market indices and first recorded COVID-19 death.
Notes: Fig. 2 shows stock market indices of countries, where many COVID-19 cases have been reported. Shaded area is the period after the first death in the country under examination.
4. Methodology
In this section, we present our research design that we employ to study the existence of investor herding behaviour during the coronavirus pandemic, and the effects of government responses and short-selling restrictions on investor herding. In episodes of large swings in asset prices, investors herd around the average market consensus, which translates into a negative relation between and the squared market return (Chang et al., 2000). Building on this non-linear function, our first empirical methodology utilises a panel data set to test for the effects of our new determinants of herding behaviour, government responses to COVID-19, and short-selling restrictions (see for example Bouri et al., 2019, Philippas et al., 2013). Our second methodology comprises quantile regressions, which (i) aim to ratify the first methodology, and (ii) consider the conditional distribution of herding behaviour. In this instance, we ask whether, in line with Gebka and Wohar (2013), is more responsive to extreme stock market swings for low quantiles of the distribution. This conjecture owes to the fact that is likely to be lower in those countries and periods, in which stock prices and returns are driven by herding. This methodology contrasts with the linear regression model, estimated by means of OLS, which scrutinises the average/expected response of to large market swings. In other words, we now distinguish among the various levels of herding. Our third methodology seeks to address concerns that the Stringency index can be endogenously determined, which biases the coefficient estimates of the model. To this end, we carry out two-stage least-squares regressions.
4.1. Panel data regression
Our empirical methodology builds on the following panel regression:
| (3) |
where is either or . In periods of market stress, and are likely to sustain a non-linear relation (Lux, 1995). In the absence of herding, should be positive and insignificant (Mobarek et al., 2014). Investors herd if is negative (Chang et al., 2000); they anti-herd if is positive (Bouri et al., 2019). Importantly, if the coefficient of interest, , is negative (positive), then government responses amplify (reduce) herding behaviour. In our model, we also control for global uncertainty by means of the implied volatility index () (Aharon, 2020). represents the uncertainty of the sophisticated derivatives’ market participants regarding the short-term expected market volatility, or the investor “fear gauge” (Whaley, 2000). When fear prevails in the market, investors are more likely to herd (Philippas et al., 2013).
Further, we hypothesise that short-selling restrictions, imposed by the EU national and supranational regulatory bodies, should have positive (ant-herding) effects on . The short-selling notification, measured with , is applied uniformly across the EU. It places a constraint on the degree of co-movement of international stock market returns and, consequently, on herding behaviour. Hence, we expect . Along similar lines, the short-selling ban, is expected to exert an anti-herding effect on international stock markets, i.e., This effect is attained by restraining short selling and relieving downward pressures on stock prices and returns. Finally, we examine if in different regions, responds differently to the varying degree of stringency of government measures. To this end, we construct dummy variables for four World regions (Europe, America, Asia-Pacific and Africa). Results are presented under the Pooled OLS estimations. In all model specifications, we use robust standard errors. We also note that the model is free of multicollinearity.
Table 5.
Regressions: Stringency Index components and short-selling restrictions on herding behaviour.
| (1) | (2) | |
|---|---|---|
| 0.63506*** | 0.48231*** | |
| (0.02701) | (0.02054) | |
| −0.06075*** | −0.04914*** | |
| (0.00434) | (0.00330) | |
| School Closing | 0.22740*** | 0.17364*** |
| (0.03208) | (0.02440) | |
| Workplace Closing | 0.15979*** | 0.12342*** |
| (0.03603) | (0.02740) | |
| Cancel Events | 0.20993*** | 0.16676*** |
| (0.03098) | (0.02356) | |
| Transportation Closing | 0.07175* | 0.03611 |
| (0.04052) | (0.03081) | |
| Information Campaigns | 0.00547 | −0.00948 |
| (0.03387) | (0.02575) | |
| Internal Restriction Movements | 0.14156*** | 0.11440*** |
| (0.02743) | (0.02086) | |
| Travel Controls | −0.10749*** | −0.07169*** |
| (0.01530) | (0.01163) | |
| Fiscal Measures | 0.06992 | 0.05416 |
| (0.04964) | (0.03774) | |
| Monetary Measures | 0.00597** | 0.00634*** |
| (0.00234) | (0.00178) | |
| Investments in Health | −0.04600 | −0.02141 |
| (0.04959) | (0.03771) | |
| Investments in Vaccines | 0.03945*** | 0.02667*** |
| (0.01276) | (0.00970) | |
| 0.34225*** | 0.22483*** | |
| (0.05947) | (0.04532) | |
| 1.07843*** | 0.80991*** | |
| (0.11952) | (0.09107) | |
| −2.02083*** | −1.49855*** | |
| (0.11777) | (0.08955) | |
| 0.75859*** | 0.57796*** | |
| (0.02281) | (0.01735) | |
| YES | YES | |
| Obs | 4103 | 4103 |
| Adjusted | 0.50413 | 0.50985 |
Notes: Table 5 reports the coefficient estimates based of Eq. (3), by substituting the Stringency Index variable with its components. is computed by means of Eq. (1), and is computed by means of Eq. (2). is the market return in absolute value, and is the squared market return. denotes the Oxford Government Response Stringency Index, and are the dummy variables corresponding to short-selling notification and short-selling ban, respectively. represents the uncertainty of the sophisticated derivatives’ market participants regarding the short-term expected market volatility. is the regression constant term. is the dummy variable that takes on value one if the country is located in a given region (Europe, America, Asia-Pacific, Africa), and takes on value 0 otherwise. Robust standard errors are reported in parentheses. Asterisks ***,**,* denote the 1%, 5%, 10% significance levels, respectively.
4.2. Quantile regression
It should be noted that panel data regressions (see Section 5.1) assume that the effects of government and regulatory responses do not vary across different parts of the distribution of values. Nevertheless, this assumption may be overly restrictive during the coronavirus pandemic, when abrupt changes in herding behaviour in international stock markets become a commonplace. In order to relax this assumption, we employ a quantile regression model, which was introduced by Koenker and Bassett (1978), and it was used to study herding behaviour in Gebka and Wohar (2013). While the Pooled OLS estimation method estimates the average relation between the dependent and the explanatory variables, a quantile regression allows estimating such a relation at specific quantiles of the distribution of the dependent variable. Hence, a quantile regression is more suitable when the sample features abrupt changes and extreme values, which are reflected in a fat-tailed and/or asymmetric distribution of the dependent variable. Concretely, we investigate coefficients that describe the 5%, 25%, 50%, 75% and 95% of the conditional distribution. A quantile regression model can be linearly represented as:
| (4) |
where is the dependent variable, is the intercept, is the vector of coefficients of the explanatory variables, where the coefficients are sub-indexed as in Eq. (3), signifies the random disturbance term, and refers to the quantile of distribution. We assume that the random disturbance term at the conditional quantile [] is equal to zero, where . Also, the vector of coefficients for any given quantile for a sample of observations can be calculated with linear programming as follows:
where check function is defined as:
We use bootstrap estimates of in order to calculate the covariance matrix. We compute standard errors with 1000 bootstrap replications and thus we obtain asymptotically normally distributed estimates, which are valid under heteroskedasticity.
In order to investigate if exerts heterogeneous effects on herding, we test if the coefficient does not vary across the conditional quantiles by means of an equality test. The null hypothesis is that the partial slope of does not vary across quantiles. The alternative hypothesis implies that unequally influences herding.
Table 6.
Quantile Regressions: Stringency Index and short-selling restrictions on herding behaviour.
| quantile 0.05 |
quantile 0.25 |
quantile 0.50 |
quantile 0.75 |
quantile 0.95 |
||||||
|---|---|---|---|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | |
| 0.1564*** | 0.1195*** | 0.2689*** | 0.1937*** | 0.3053*** | 0.2265*** | 0.3587*** | 0.2884*** | 0.5821*** | 0.4248*** | |
| (0.0251) | (0.0127) | (0.0244) | (0.0132) | (0.0249) | (0.0228) | (0.0340) | (0.0346) | (0.1499) | (0.0839) | |
| −0.0117** | −0.0096*** | −0.0244*** | −0.0181*** | −0.0270*** | −0.0215*** | −0.0329*** | −0.0286*** | −0.0562*** | −0.0423*** | |
| (0.0046) | (0.0026) | (0.0037) | (0.0022) | (0.0036) | (0.0035) | (0.0050) | (0.0039) | (0.0173) | (0.0112) | |
| 0.0101*** | 0.0076*** | 0.0129*** | 0.0099*** | 0.0179*** | 0.0130*** | 0.0229*** | 0.0163*** | 0.0276*** | 0.0231*** | |
| (0.0006) | (0.0005) | (0.0004) | (0.0004) | (0.0007) | (0.0005) | (0.0006) | (0.0009) | (0.0020) | (0.0017) | |
| 0.2212*** | 0.1410*** | 0.4086*** | 0.2620*** | 0.2253*** | 0.2162*** | 0.0978 | 0.1557*** | 0.2774 | 0.2874 | |
| (0.0411) | (0.0288) | (0.0473) | (0.0363) | (0.0581) | (0.0465) | (0.0685) | (0.0557) | (0.2189) | (0.1758) | |
| 0.9838*** | 0.6865*** | 0.7314*** | 0.5059*** | 0.6516*** | 0.4648*** | 0.8879*** | 0.5662*** | 3.5751*** | 3.0717*** | |
| (0.0731) | (0.0511) | (0.0840) | (0.0644) | (0.1032) | (0.0826) | (0.1217) | (0.0989) | (0.3887) | (0.3120) | |
| −0.4386*** | −0.3105*** | −0.6413*** | −0.5039*** | −0.8543*** | −0.6364*** | −1.0687*** | −0.8112*** | −1.9981*** | −1.4790*** | |
| (0.0860) | (0.0480) | (0.0555) | (0.0506) | (0.0896) | (0.0605) | (0.0638) | (0.0969) | (0.4539) | (0.1902) | |
| 0.4455*** | 0.3479*** | 0.5406*** | 0.4233*** | 0.6474*** | 0.5106*** | 0.7850*** | 0.6179*** | 1.1530*** | 0.9017*** | |
| (0.0079) | (0.0075) | (0.0074) | (0.0064) | (0.0079) | (0.0074) | (0.0140) | (0.0091) | (0.0355) | (0.0437) | |
| YES | YES | YES | YES | YES | YES | YES | YES | YES | YES | |
| WT | 112.02*** | 64.51*** | 88.25*** | 43.80*** | 58.18*** | 25.50*** | 35.19*** | 35.76*** | ||
| WT | 1.57 | 0.43 | 16.18*** | 6.57** | 9.47*** | 3.03* | 21.77*** | 34.37*** | ||
| WT | 3.17* | 0.99 | 0.06 | 0.07 | 0.98 | 0.00 | 33.90*** | 71.53*** | ||
| Obs | 3381 | 3381 | 3381 | 3381 | 3381 | 3381 | 3381 | 3381 | 3381 | 3381 |
| Pseudo- | 0.1902 | 0.1888 | 0.2405 | 0.2375 | 0.3542 | 0.3483 | 0.4697 | 0.4650 | 0.4809 | 0.4878 |
Notes: Table 6 reports coefficient estimates of the quantile regression (Eq. (4)). Results for quantile 0.05 (0.25, 0.50, 0.75, 0.95) are summarised in Columns 1 and 2 (3 and 4, 5 and 6, 7 and 8, 9 and 10). is computed by means of Eq. (1), and is computed by means of Eq. (2). is the market return in absolute value, and is the squared market return. denotes the Oxford Government Response Stringency Index, and are the dummy variables corresponding to short-selling notification and short-selling ban, respectively. represents the uncertainty of the sophisticated derivatives’ market participants regarding the short-term expected market volatility. is the regression constant term. Bootstrapped standard errors (1000 replications) are provided in parentheses. Asterisks ***,**,* denote 1%, 5%, and 10% significance levels. The WT (Wald test) compares different slopes with the median slope, where , , and . The same applies for WT and WT.
4.3. Two stage least squares regression
In addition to the above, a panel two stage least squares regression is utilised to further solidify our results against possible endogeneity concerns (Casavecchia, 2016). Endogeneity can arise through simultaneity or omitted variable bias. Specifically, a news that triggers a government response and concurrently drives herding behaviour of investors may induce endogeneity in the panel data model. As a remedial measure, we first need to identify characteristics (instruments) that are both conceptually and methodologically correct and are correlated with the first-stage dependent variable (Stringency Index) but not with the residuals of the second-stage regression. Thus, in the first stage, we estimate a Stringency Index model. We select three instruments that meet the above criteria. The first instrument is the first lag of the Stringency Index. This is because governments build gradually their measures based on previous decisions, which are not randomly distributed over time. This implies that the lagged value of , , should be able to explain variations in the contemporaneous value, . Second, an increase in the number of confirmed cases with COVID-19 can signal the need for more stringent measures. Third, for a similar reason, the number of deaths can be regarded as instrumental in tighter restrictions undertaken by the government, which should be able to explain the Stringency Index. Based on the above, the first stage model is shown below:
| (5) |
In the second-stage equation, we use the fitted values of from the first stage (Eq. (5)) and we include it as an independent variable in the following model:
| (6) |
where comprises the fitted values from Eq. (5). In a similar vein to the panel data model, panel two-stage least squares regression uses robust standard errors. The Sargan test of over-identified restrictions is also reported to validate our selected instruments.
5. Results
5.1. Panel data regression
Table 3 reports estimation results. In Columns 1 and 2 indicate the existence of herding behaviour, since the variable exerts a negative and significant effect on both and . In Columns 3–8, a more stringent government response – which translates into larger values of – is associated with larger values of and . For instance, the value of the coefficient estimate of , 0.0174%, that is recorded in Column 4, implies that a 10 index points increase in the degree of stringency of government response, increases the daily cross-sectional absolute deviation by 0.174 percentage points. This lends support to the notion that more stringent government responses mitigate investor herding behaviour. It is also worth mentioning the Stringency Index increases the Adjusted of the estimated model by more than 20 percentage points. When , and are included in the model (see Columns 5–8), the positive and significant effect of remain unaltered. Moreover, the dummy variable, which indicates that a short-selling ban is place, , exerts a positive effect on . In particular, the value of the coefficient estimate of , recorded in Column 6, indicates that the daily is 0.8185 percentage points higher in countries where the short-selling ban was imposed relative to countries where short selling was not banned. As expected, the short-selling restrictions moderate herding behaviour in international stock markets. Table 3 also displays a positive but insignificant effect of the short-selling notification on herding behaviour. This result is not surprising, insofar as the notification does not directly restrict short selling. Thus, the fact that the effect of is stronger relative to agrees with our prior expectation. Taken together, the effect of short-selling restrictions supports the Miller’s overpricing hypothesis. Turning to the partial relation between and investor fear gauge (), Columns 7 and 8 exhibit that this relation is strongly negative. For instance, the coefficient estimate, displayed in Column 8, implies that a one market index point increase in implied volatility leads to a decrease in the cross-sectional absolute deviation by 1.0915 percentage points. In consonance with (Philippas et al., 2013), investor fear tends to exacerbate herding behaviour in international stock markets.
Table 3.
Regressions: Stringency Index and short-selling restrictions on herding behaviour.
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | |
|---|---|---|---|---|---|---|---|---|
| 0.8440*** | 0.6506*** | 0.2853*** | 0.2269*** | 0.2812*** | 0.2235*** | 0.4002*** | 0.3151*** | |
| (0.0267) | (0.0204) | (0.0301) | (0.0233) | (0.0300) | (0.0232) | (0.0316) | (0.0244) | |
| −0.1006*** | −0.0803*** | −0.0334*** | −0.0292*** | −0.0314*** | −0.0276*** | −0.0379*** | −0.0326*** | |
| (0.0047) | (0.0036) | (0.0049) | (0.0038) | (0.0049) | (0.0038) | (0.0049) | (0.0038) | |
| 0.0228*** | 0.0174*** | 0.0204*** | 0.0156*** | 0.0202*** | 0.0154*** | |||
| (0.0006) | (0.0005) | (0.0007) | (0.0005) | (0.0007) | (0.0005) | |||
| 0.1111 | 0.0879 | 0.0569 | 0.0462 | |||||
| (0.0675) | (0.0704) | (0.0556) | (0.0518) | |||||
| 1.1028*** | 0.8185*** | 1.1303*** | 0.8395*** | |||||
| (0.1202) | (0.0931) | (0.1186) | (0.0919) | |||||
| −1.4205*** | −1.0915*** | |||||||
| (0.1297) | (0.1004) | |||||||
| 0.7591*** | 0.5791*** | 0.6678*** | 0.5153*** | 0.6571*** | 0.5071*** | 0.6574*** | 0.5071*** | |
| (0.0235) | (0.0179) | (0.0233) | (0.0181) | (0.0231) | (0.0179) | (0.0232) | (0.0180) | |
| YES | YES | YES | YES | YES | YES | YES | YES | |
| Obs | 4536 | 4536 | 3434 | 3434 | 3434 | 3434 | 3381 | 3381 |
| Adjusted | 0.3008 | 0.3015 | 0.5166 | 0.5115 | 0.5313 | 0.5254 | 0.5326 | 0.5275 |
Notes: Table 3 reports the coefficient estimates of Eq. (3). is computed by means of Eq. (1), and is computed by means of Eq. (2). is the market return in absolute value, and is the squared market return. denotes the Oxford Government Response Stringency Index, and are the dummy variables corresponding to short-selling notification and short-selling ban, respectively. represents the uncertainty of the sophisticated derivatives’ market participants regarding the short-term expected market volatility. is the regression constant term. is the dummy variable that takes on value one if the country is located in a given region (Europe, America, Asia-Pacific, Africa), and takes on value 0 otherwise. Robust standard errors are reported in parentheses. Asterisks ***,**,* denote the 1%, 5%, 10% significance levels, respectively.
Next, in Table 4 we examine if the Stringency Index can have different effects on investor herding behaviour across different regions. Results indicate that, in general, government responses mitigate investor herding behaviour. The coefficient estimate of is always positive and significant, in line with our baseline model, summarised in Table 3. Americas are an exception (see coefficient in Columns 3 and 4), in line with previous literature (Chiang & Zheng, 2010b). We argue that in this region, governments responded heterogeneously and with a delay relative to their (say) European counterparts, China or South Korea. Noting that Americas comprise both developed and emerging market countries, we also report the estimates for these two country groups (Columns 9–12). The results lend further support to the presence of investor herding. Turning to the short-selling restrictions, we now find that both the short-selling notification and ban exert a positive and significant effect on . It is worth noting that prohibiting short selling has a larger effect than the requirement to notify the national regulatory body of a significant position in the equity capital. Since information on the short-selling restrictions is only available for EU countries, we only use the respective dummies in the European and Developed countries sub-samples. Further, as in the baseline model, the effect of is always negative and significant. The variation of is explained reasonably well for the European sub-sample, as reflected in the Adjusted , which takes on values 67.11% and 65.30% for and , respectively.
Table 4.
Regressions by region: Stringency Index and short-selling restrictions on herding behaviour.
| Europe |
America |
Asia-Pacific |
Africa |
Developed |
Emerging |
|||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) | (12) | |
| 0.2005*** | 0.1651*** | 0.4105** | 0.2750** | 0.5225*** | 0.4245*** | 0.5615*** | 0.3808*** | 0.3976*** | 0.3163*** | 0.5487*** | 0.4297*** | |
| (0.0400) | (0.0314) | (0.1597) | (0.1232) | (0.0702) | (0.0558) | (0.1001) | (0.0674) | (0.0435) | (0.0340) | (0.0670) | (0.0530) | |
| −0.0138** | −0.0142*** | −0.0304 | −0.0235 | −0.0524*** | −0.0448*** | −0.0503*** | −0.0370*** | −0.0358*** | −0.0317*** | −0.0519*** | −0.0432*** | |
| (0.0062) | (0.0046) | (0.0227) | (0.0174) | (0.0098) | (0.0076) | (0.0161) | (0.0107) | (0.0069) | (0.0051) | (0.0099) | (0.0076) | |
| 0.0163*** | 0.0121*** | 0.0339*** | 0.0295*** | 0.0143*** | 0.0101*** | 0.0157*** | 0.0122*** | 0.0140*** | 0.0109*** | 0.0149*** | 0.0110*** | |
| (0.0011) | (0.0009) | (0.0037) | (0.0030) | (0.0015) | (0.0012) | (0.0030) | (0.0020) | (0.0011) | (0.0009) | (0.0015) | (0.0012) | |
| 0.3377*** | 0.2719*** | 0.1650* | 0.1038 | −0.0125 | 0.0416 | |||||||
| (0.0769) | (0.0597) | (0.0880) | (0.0686) | (0.1209) | (0.1042) | |||||||
| 1.1926*** | 0.8961*** | 1.3580*** | 1.0168*** | |||||||||
| (0.2438) | (0.2104) | (0.2425) | (0.2086) | |||||||||
| −0.6904*** | −0.5350*** | −1.8223*** | −1.3070*** | −1.8295*** | −1.4420*** | −2.0449*** | −1.3711*** | −1.2689*** | −0.9583*** | −1.9560*** | −1.5302*** | |
| (0.1366) | (0.1020) | (0.6570) | (0.4950) | (0.2039) | (0.1566) | (0.3370) | (0.2200) | (0.1511) | (0.1122) | (0.2327) | (0.1782) | |
| 0.7409*** | 0.5720*** | 1.7116*** | 1.3120*** | 0.5682*** | 0.4392*** | 0.7413*** | 0.5720*** | 0.6620*** | 0.5093*** | 0.9527*** | 0.7281*** | |
| (0.0141) | (0.0111) | (0.1190) | (0.0908) | (0.0295) | (0.0232) | (0.0388) | (0.0255) | (0.0167) | (0.0133) | (0.0401) | (0.0309) | |
| Obs | 1687 | 1687 | 372 | 372 | 1054 | 1054 | 268 | 268 | 1789 | 1789 | 1583 | 1583 |
| Adjusted | 0.6711 | 0.6530 | 0.3395 | 0.3709 | 0.4590 | 0.4383 | 0.5761 | 0.6015 | 0.5786 | 0.5604 | 0.2921 | 0.2775 |
Notes: Table 4 reports the coefficient estimates based of Eq. (3). Results for the European subsample (American, Asia-Pacific, African, Developed, Emerging) are summarised in Columns 1 and 2 (3 and 4, 5 and 6, 7 and 8, 9 and 10, 11 and 12). is computed by means of Eq. (1), and is computed by means of Eq. (2). is the market return in absolute value, and is the squared market return. denotes the Oxford Government Response Stringency Index, and are the dummy variables corresponding to short-selling notification and short-selling ban, respectively. represents the uncertainty of the sophisticated derivatives’ market participants regarding the short-term expected market volatility. is the regression constant term. Robust standard errors are reported in parentheses. Asterisks ***,**,* denote the 1%, 5%, 10% significance levels, respectively.
Moreover, in Table 5 we decompose into 11 components. When governments close schools, cancel events, restrict transportation and impose restrictions on movements, investor herding decreases. These measures aim to minimise the transmission of COVID-19 within and across countries, which is perceived by investors as positive news for both public health and long-term growth prospects. It is worth noting that only travel controls seem to induce herding behaviour, which manifests as a lower cross-country dispersion of stock returns. This finding is not surprising insofar as media tends to exaggerate low-probability high-consequence events, such as major threats to public health (Donadelli et al., 2017) or aviation disasters (Akyildirim et al., 2020, Kaplanski and Levy, 2010), which can transmit risk spillovers to the whole economy. We argue that the same argument can be extended to travel restrictions.
5.2. Quantile regression
Table 6 summarises the results of the quantile regression. The coefficient estimates from the quantile regression are displayed as described by Eq. (4). We report the results for both and at the 5%, 25%, 50%, 75% and 95% quantiles of the conditional distribution. Lower quantiles denote lower () and thus higher levels of herding behaviour, whereas upper quantiles indicate higher deviations from the market return and thus lower levels of herding behaviour (Gebka & Wohar, 2013). We also report the Wald statistic, which is used to test for the equality of the , , and partial slopes across the above-mentioned quantiles. We find that the effects of , , and on / are always positive and, in most cases, are significant, except for the coefficient of at the 75% and 95% quantiles. This finding corroborates the results from the panel data regression, which lends support to the notion that government and regulatory responses exert mitigating effects on herding behaviour in international stock markets. We also document that this effect varies significantly over the conditional distribution of , as witnessed by the significant Wald tests.
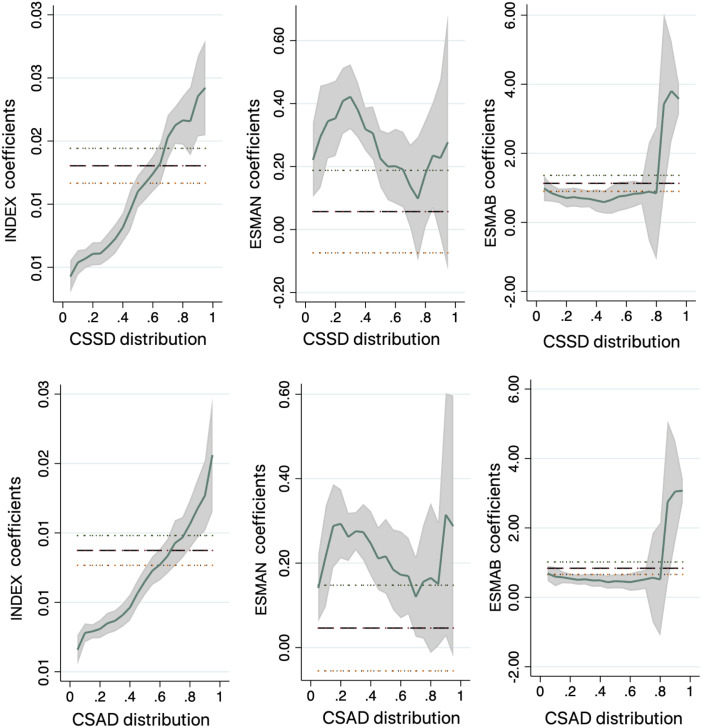
The effects of , and are also summarised graphically in Fig. 3. Fig. 3 shows that more stringent government responses are conducive to lower herding, since the coefficient is always positive and significant. Noteworthy, partial slopes generally exhibit an increasing pattern as quantiles increase. The coefficient takes on smaller values in markets with higher levels of herding behaviour, and it takes on larger values in markets with lower levels of herding behaviour. Thus, we find that government responses are more effective at lower levels of herding behaviour. Fig. 3 also indicates that the short-selling notification () has a positive effect on , while this effect experiences a significant variation across the conditional distribution. Further, the effect of the short-selling ban () is always positive and significant throughout the whole distribution of . This effect is flat for the first three quartiles, but it increases sharply in the fourth quartile. Thus, both government responses to COVID-19 and outright short-selling bans can (i) prevent investors from herding and (ii) effectively mitigate herding behaviour at lower levels of herding (upper quantiles of the conditional distribution).
Fig. 3.
Stringency Index and short-selling restrictions on herding distribution.
Notes: Fig. 3 illustrates the non-linear effects of Stringency Index, and on herding distribution. The grey area measures the confidence intervals calculated with 1000 bootstrap replications. The dashed lines represent the OLS estimates with their confidence intervals (dotted lines). The lower part of the distribution shows evidence of herding behaviour, while the upper part denotes anti-herding behaviour.
We additionally examine whether the level of government response moderates our main findings. For this reason, we use the median value to split the sample into two sub-samples, which contain high and low values of the Stringency Index. Table 7 displays the results. Columns 1 and 2 comprise observations with relatively strict government responses. They show that a further rise in leads to lower levels of herding behaviour, in line with the previous results. However, in the low-stringency sub-sample (Columns 3 and 4), a rise in can be causal of herding behaviour in international stock markets. This is very interesting because it implies that governments should be determined on dealing with COVID-19. By contrast, a lenient government response can only exacerbate market uncertainty, which by turn can provoke a collapse of international stock markets. The effect of the short-selling notification on is insignificant in the high-stringency sub-sample. However, it becomes positive and significant in the low-stringency sub-sample, in line with our prior expectation. The short-selling ban exerts a positive and significant effect on , as expected. In the low-stringency sample, this variable coincidentally takes on value 0, and it drops out of the model. All in all, the short-selling restrictions appear to exert a mitigating effect on herding behaviour in international stock markets.
Table 7.
High vs Low Stringency sample: Stringency Index and short-selling restrictions on herding behaviour.
| High Stringency Index |
Low Stringency Index |
|||
|---|---|---|---|---|
| (1) | (2) | (3) | (4) | |
| 0.3454*** | 0.2811*** | 0.2425*** | 0.1514*** | |
| (0.0387) | (0.0300) | (0.0531) | (0.0378) | |
| −0.0300*** | −0.0278*** | −0.0094 | −0.0047 | |
| (0.0057) | (0.0043) | (0.0079) | (0.0057) | |
| 0.0219*** | 0.0169*** | −0.0402*** | −0.0321*** | |
| (0.0012) | (0.0009) | (0.0074) | (0.0055) | |
| −0.0020 | −0.0051 | 1.5848*** | 1.2659*** | |
| (0.0728) | (0.0563) | (0.0271) | (0.0195) | |
| 1.0345*** | 0.7611*** | |||
| (0.2477) | (0.2135) | |||
| −1.4626*** | −1.1122*** | −0.5225*** | −0.3547*** | |
| (0.1498) | (0.1112) | (0.1740) | (0.1243) | |
| 0.5465*** | 0.4054*** | 0.7408*** | 0.5863*** | |
| (0.0402) | (0.0299) | (0.0172) | (0.0127) | |
| YES | YES | YES | YES | |
| Obs | 1712 | 1712 | 1607 | 1607 |
| Adjusted | 0.5861 | 0.5882 | 0.3769 | 0.3929 |
Notes: Table 7 reports the coefficient estimates based on Eq. (3). Results for the high-stringency (low-stringency) subsample are summarised in Columns 1 and 2 (Columns 3 and 4). is computed by means of Eq. (1), and is computed by means of Eq. (2). is the market return in absolute value, and is the squared market return. denotes the Oxford Government Response Stringency Index, and are the dummy variables corresponding to short-selling notification and short-selling ban, respectively. represents the uncertainty of the sophisticated derivatives’ market participants regarding the short-term expected market volatility. is the regression constant term. is the dummy variable that takes on value one if the country is located in a given region (Europe, America, Asia-Pacific, Africa), and takes on value 0 otherwise. Robust standard errors are reported in parentheses. Asterisks ***,**,* denote the 1%, 5%, 10% significance levels, respectively.
5.3. Two stage least squares regression
Next, in order to account for any endogeneity concerns (Kremer & Nautz, 2013), we instrument with the number of cases and deaths, as well as with the lagged values. Since the Sargan test is insignificant (see Table 8), we conclude that the model is correctly specified. The results from the first-stage regressions are reported in Column 1, where is treated as the dependent variable. The results from the second-stage regressions are displayed in Columns 2 and 3. Table 8 shows that has a positive and significant effect on . Hence, we can confirm the robustness of our results afresh. Also corroborating the results from our benchmark model, summarised in Table 3, the effect of the short-selling notification is not significant, whereas the effect of the short-selling ban is positive and significant on .
Table 8.
Two stage least squares regressions: Stringency Index and short-selling restrictions on herding behaviour.
| First stage | Second Stage |
||
|---|---|---|---|
| (1) | (2) | (3) | |
| 0.8406*** | 0.4241*** | 0.5349*** | |
| (0.21033) | (0.0319) | (0.0411) | |
| 0.01709 | −0.0446*** | −0.0527*** | |
| (0.031531) | (0.0047) | (0.0061) | |
| 0.0127*** | 0.0169*** | ||
| (0.0007) | (0.0008) | ||
| −0.3793 | −0.0435 | −0.0673 | |
| (0.4304) | (0.0565) | (0.0725) | |
| 0.5183 | 0.8679*** | 1.1662*** | |
| (0.8837) | (0.1066) | (0.1368) | |
| 0.9809*** | |||
| (0.00446) | |||
| 0.00000288 | |||
| (0.00002) | |||
| −0.0000775 | |||
| (0 .000417) | |||
| −4.4386*** | −0.9162*** | −1.2466*** | |
| (0.91017) | (0.1373) | (0.1770) | |
| 0.55317*** | 0.5658*** | 0.7421*** | |
| (0.12718) | (0.0191) | (0.0247) | |
| YES | YES | YES | |
| Obs | 2669 | 2669 | 2669 |
| Sargan test () | 0.7191 | 1.3008 | |
| Adjusted | 0.9708 | 0.3729 | 0.3849 |
Notes: Table 8 reports the coefficient estimates of the first-stage (Eq. (5)) in Column 1 and second-stage regressions (Eq. (6)) in Columns 2 and 3. is computed by means of Eq. (1), and is computed by means of Eq. (2). is the market return in absolute value, and is the squared market return. denotes the Oxford Government Response Stringency Index, and is the estimated from Eq. (5). and are the dummy variables corresponding to short-selling notification and short-selling ban, respectively. denotes the lagged value of the Stringency Index variable. denotes the confirmed number of cases, and denotes the confirmed number of deaths. represents the uncertainty of the sophisticated derivatives’ market participants regarding the short-term expected market volatility. is the regression constant term. is the dummy variable that takes on value one if the country is located in a given region (Europe, America, Asia-Pacific, Africa), and takes on value 0 otherwise. Robust standard errors are reported in parentheses. Asterisks ***,**,* denote the 1%, 5%, 10% significance levels, respectively. Insignificant Sargan test indicates that the over-identified restrictions are valid.
5.4. Robustness check
As a final robustness check, we use principal component analysis (PCA) to construct an alternative composite indicator of stringency. The goal of this method is (a) to validate our main findings and (b) to verify the reliability of the Oxford Stringency Index. PCA is a multivariate technique that reduces the dimensionality of a complex data set by transforming it into a smaller number of principal components while retaining most of the variation in the data set. An advantage of this method is that original variables are organised in clusters, which facilitate the interpretation and scrutiny of their average effects (OECD, 2008). Furthermore, it is likely that government response variables correlate with each other. In this regard, PCA can be particularly effective in dealing with overlapping information sets. It assumes that variables of the original information set, , are generally correlated. The variables are normalised by setting and , . Also, the principal components should be uncorrelated, where denotes the number of principal components. The PCA equation is as follows:
| (7) |
where are the factor loadings. They show the contribution of the variable indexed with to the principal component indexed with , and therefore are key for the interpretation of the principal components. For example, Table 9 shows that mainly closure and containment variables significantly load on the first principal component, . Therefore, this component can be thought of as a closure and containment stringency indicator. The PCA also indicates that and represent investment in health/vaccines and economic stimulus. According to the Kaiser criterion, components with eigenvalues lower than 1 should not be included in the analysis. Following the Kaiser criterion, we retain these three components, which account for approximately 67% of the total variance of the eleven variables. We can now proceed to test whether the principal components affect investor herding.
Table 9.
Principal component analysis.
| Variable | |||
|---|---|---|---|
| School Closing | 0.4286 | ||
| Workplace Closing | 0.4053 | ||
| Cancel Events | 0.4173 | ||
| Transportation Closing | 0.3639 | ||
| Information Campaigns | 0.3224 | ||
| Internal Restrictions Movements | 0.3725 | ||
| Travel Controls | 0.3633 | ||
| Fiscal Measures | 0.7009 | ||
| Monetary Measures | 0.7009 | ||
| Investment in Health | 0.7023 | ||
| Investment in Vaccines | −0.5213 | ||
| Eigenvalue | 4.36605 | 1.94973 | 1.05065 |
| Variance Proportion | 0.3969 | 0.1772 | 0.0955 |
Table 10 summarises the panel data regressions, in which the Stringency Index is replaced by the first three principal components. Results show that the coefficient estimates of , and are positive and significant. This further solidifies our main findings that government responses decrease investor herding during the COVID-19 pandemic. It also validates the use of Oxford Government Response Stringency Index as a robust method to approximate the stringency of a country’s response to COVID-19. Lastly, both and appear positive and thus we show that short-selling restrictions decrease herding afresh. To sum up, all three hypotheses have been confirmed.
Table 10.
Regressions: Principal Components of the Stringency Index and short-selling restrictions on herding behaviour.
| (1) | (2) | |
|---|---|---|
| 0.5932*** | 0.4548*** | |
| (0.0330) | (0.0251) | |
| −0.0538*** | −0.0443*** | |
| (0.0049) | (0.0036) | |
| 0.1506*** | 0.1211*** | |
| (0.0108) | (0.0086) | |
| 0.0078* | 0.0157*** | |
| (0.0044) | (0.0035) | |
| 0.0481*** | 0.0425*** | |
| (0.0164) | (0.0131) | |
| 0.3972*** | 0.2739*** | |
| (0.0770) | (0.0569) | |
| 1.0440*** | 0.7866*** | |
| (0.2400) | (0.2068) | |
| −2.0067*** | −1.4996*** | |
| (0.1174) | (0.0856) | |
| 0.8815*** | 0.6819*** | |
| (0.0208) | (0.0159) | |
| YES | YES | |
| Obs | 4103 | 4103 |
| Adjusted | 0.5035 | 0.5086 |
Notes: Table 10 summarises the coefficient estimates based on Eq. (3). The Stringency Index variable is substituted with the first three principal components from Eq. (7). The structure of the principal components is reported in Table 9. is computed by means of Eq. (1), and is computed by means of Eq. (2). is the market return in absolute value, and is the squared market return. and are the dummy variables corresponding to short-selling notification and short-selling ban, respectively. represents the uncertainty of the sophisticated derivatives’ market participants regarding the short-term expected market volatility. is the regression constant term. is the dummy variable that takes on value one if the country is located in a given region (Europe, America, Asia-Pacific, Africa), and takes on value 0 otherwise. Robust standard errors are reported in parentheses. Asterisks ***,**,* denote the 1%, 5%, 10% significance levels, respectively.
6. Conclusion
In this research, we study the effects of the Government Response Stringency Index and short-selling restrictions on herding behaviour in international stock markets during the novel coronavirus COVID-19 outbreak. Our tests support evidence of herding behaviour in the first three months of 2020. We also document that a more stringent government response to the coronavirus crisis mitigates investor herding behaviour, which manifests as a decrease in the and indicators. We argue that differential responses of national governments to the coronavirus crisis can lead to differential rates of arrival of new information about stock market fundamentals in our sample of countries. Such a variation in the rate of information arrival across countries, by turn, alleviates the presence of herding behaviour in international stock markets. Through the lens of Avery and Zemsky (1998), government responses can reduce multidimensional uncertainty surrounding the coronavirus crisis, which can effectively restrain herding behaviour. Moreover, consistently with the overpricing hypothesis of Miller (1977), we find that the short-selling restrictions imposed by the national and supranational regulatory bodies in the EU are associated with lower levels of herding behaviour. Furthermore, the VIX volatility index – which can be thought to capture investor ‘fear gauge’ – is conducive to herding behaviour.
Herding behaviour is regarded to have been a catalyst of the Global Financial Crisis (Galariotis et al., 2016), stock price instabilities (Cai et al., 2019, Kremer and Nautz, 2013), stock price bubbles and other anomalies (Devenow and Welch, 1996, Hott, 2009), but only if herding is driven by non-information based reasons (Choi & Skiba, 2015). Herding behaviour can also lead to an increase in the degree of co-movement among financial asset returns, which reduces the benefits of portfolio diversification (Economou et al., 2011). These undesirable consequences of herding highlight the need to identify herding behaviour in financial markets. Such information can be of paramount importance for (i) companies, who seek to source equity capital during pandemic crises, (ii) investors who evaluate investment opportunities in international stock markets, (iii) national and supranational financial regulators and policy makers, who are tasked with designing optimal policies that aim to avert or mitigate financial crises, and prevent speculative bubbles from gathering steam in international stock markets.
Our study also contributes to the ongoing public debate, which revolves around the trade-off between public health and the economy. Our results show that the government and regulatory restraints imposed to control the transmission of COVID-19 within and across countries can alleviate the presence of investor herding behaviour in international stock markets.
Future research can examine whether rational or irrational herding behaviour in international stock markets is more responsive to government interventions and short-selling restrictions during pandemic crises.
CRediT authorship contribution statement
Renatas Kizys: Term, Conceptualization, Methodology, Formal analysis, Investigation, Validation, Resources, Supervision, Project administration, Writing - original draft, Writing - review & editing, Visualisation. Panagiotis Tzouvanas: Conceptualization, Methodology, Software, Formal analysis, Investigation, Data curation, Resources, Writing - original draft, Writing - review & editing, Visualization. Michael Donadelli: Conceptualization, Investigation, Writing - original draft, Writing - review & editing.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Footnotes
We also considered a 25-day rolling window and the results were very robust.
In Spain, this decision became effective on 17/03/2020.
References
- Aharon D.Y. Uncertainty, fear and herding behavior: evidence from size-ranked portfolios. Journal of Behavioral Finance. 2020;0(0):1–18. [Google Scholar]
- Akyildirim E., Corbet S., Efthymiou M., Guiomard C., O’Connell J.F., Sensoy A. The financial market effects of international aviation disasters. International Review of Financial Analysis. 2020 [Google Scholar]
- Avery C., Zemsky P. Multidimensional uncertainty and herd behavior in financial markets. The American Economic Review. 1998;88(4):724–748. [Google Scholar]
- Baker S.R., Bloom N., Davis S.J., Kost K.J., Sammon M.C., Viratyosin T. National Bureau of Economic Research; 2020. The unprecedented stock market impact of COVID-19: Working paper series 26945. [Google Scholar]
- Baker S.R., Bloom N., Davis S.J., Terry S.J. National Bureau of Economic Research; 2020. COVID-induced economic uncertainty: Working Paper Series 26983. [Google Scholar]
- Balcılar M., Demirer R., Ulussever T. Does speculation in the oil market drive investor herding in emerging stock markets? Energy Economics. 2017;65:50–63. [Google Scholar]
- Beber A., Pagano M. Short-selling bans around the world: Evidence from the 2007–09 crisis. The Journal of Finance. 2013;68(1):343–381. [Google Scholar]
- Bloom N. The impact of uncertainty shocks. Econometrica. 2009;77(3):623–685. [Google Scholar]
- Bohl M.T., Klein A.C., Siklos P.L. Short-selling bans and institutional investors’ herding behaviour: Evidence from the global financial crisis. International Review of Financial Analysis. 2014;33:262–269. [Google Scholar]
- Boulton T.J., Braga-Alves M.V. The skinny on the 2008 naked short-sale restrictions. Journal of Financial Markets. 2010;13(4):397–421. [Google Scholar]
- Bouri E., Gupta R., Roubaud D. Herding behaviour in cryptocurrencies. Finance Research Letters. 2019;29:216–221. [Google Scholar]
- Caggiano G., Castelnuovo E., Kima R. The global effects of Covid-19-induced uncertainty. Economics Letters. 2020;194 doi: 10.1016/j.econlet.2020.109392. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cai F., Han S., Li D., Li Y. Institutional herding and its price impact: Evidence from the corporate bond market. Journal of Financial Economic. 2019;131(1):139–167. [Google Scholar]
- Casavecchia L. Fund managers’ herding and the sensitivity of fund flows to past performance. International Review of Financial Analysis. 2016;47:205–221. [Google Scholar]
- Chang E.C., Cheng J.W., Khorana A. An examination of herd behaviour in equity markets: An international perspective. Journal of Banking & Finance. 2000;24(10):1651–1679. [Google Scholar]
- Chen Z., Matousek R., Stewart C., Webb R. Do rating agencies exhibit herding behaviour? Evidence from sovereign ratings. International Review of Financial Analysis. 2019;64:57–70. [Google Scholar]
- Chiang T.C., Zheng D. An empirical analysis of herd behavior in global stock markets. New Contributions to Retail Payments: Conference at Norges Bank (Central Bank of Norway) 14–15 November 2008Journal of Banking & Finance. 2010;34(8):1911–1921. [Google Scholar]
- Chiang T.C., Zheng D. An empirical analysis of herd behavior in global stock markets. Journal of Banking & Finance. 2010;34(8):1911–1921. [Google Scholar]
- Choi N., Skiba H. Institutional herding in international markets. Global governance and financial stabilityJournal of Banking & Finance. 2015;55:246–259. [Google Scholar]
- Christie W.G., Huang R.D. Following the pied piper: Do individual returns herd around the market? Financial Analysts Journal. 1995;51(4):31–37. [Google Scholar]
- Clements A., Hurn S., Shi S. An empirical investigation of herding in the US stock market. Economic Modelling. 2017;67:184–192. [Google Scholar]
- Corbet S., Larkin C.J., Lucey B.M. 2020. The contagion effects of the COVID-19 pandemic: Evidence from gold and cryptocurrencies. Available at SSRN 3564443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Devenow A., Welch I. Rational herding in financial economics. Papers and proceedings of the tenth annual congress of the European Economic AssociationEuropean Economic Review. 1996;40(3):603–615. [Google Scholar]
- Donadelli M., Kizys R., Riedel M. Dangerous infectious diseases: Bad news for main street, good news for wall street? Journal of Financial Markets. 2017;35:84–103. [Google Scholar]
- Economou F., Hassapis C., Philippas N. Investors’ fear and herding in the stock market. Applied Economics. 2018;50(34–35):3654–3663. [Google Scholar]
- Economou F., Kostakis A., Philippas N. Cross-country effects in herding behaviour: Evidence from four south European markets. Journal of International Financial Markets, Institutions and Money. 2011;21(3):443–460. [Google Scholar]
- Fetzer T., Hensel L., Hermle J., Roth C. Coronavirus perceptions and economic anxiety. The Review of Economics and Statistics. 2020:1–36. [Google Scholar]
- Galariotis E.C., Krokida S.-I., Spyrou S.I. Bond market investor herding: Evidence from the European financial crisis. International Review of Financial Analysis. 2016;48:367–375. [Google Scholar]
- Gebka B., Wohar M.E. International herding: Does it differ across sectors? Journal of International Financial Markets, Institutions and Money. 2013;23:55–84. [Google Scholar]
- Hale T., Webster S., Petherick A., Phillips T., Kira B. Oxford covid-19 government response tracker. Blavatnik School of Government. 2020;25 doi: 10.1038/s41562-021-01079-8. [DOI] [PubMed] [Google Scholar]
- Hirshleifer D. Investor psychology and asset pricing. The Journal of Finance. 2001;56(4):1533–1597. [Google Scholar]
- Hott C. Herding behavior in asset markets. Journal of Financial Stability. 2009;5(1):35–56. [Google Scholar]
- Hsieh S.-F. Individual and institutional herding and the impact on stock returns: Evidence from Taiwan stock market. International Review of Financial Analysis. 2013;29:175–188. [Google Scholar]
- Ichev R., Marinč M. Stock prices and geographic proximity of information: Evidence from the ebola outbreak. International Review of Financial Analysis. 2018;56:153–166. doi: 10.1016/j.irfa.2017.12.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaplanski G., Levy H. Sentiment and stock prices: The case of aviation disasters. Journal of Financial Economic. 2010;95(2):174–201. [Google Scholar]
- Koenker R., Bassett G. Regression quantiles. Econometrica. 1978;46:33–50. [Google Scholar]
- Kremer S., Nautz D. Causes and consequences of short-term institutional herding. Journal of Banking & Finance. 2013;37(5):1676–1686. [Google Scholar]
- Kurz C., Kurz-Kim J.-R. What determines the dynamics of absolute excess returns on stock markets? Economics Letters. 2013;118(2):342–346. [Google Scholar]
- Lin M.-C. The impact of aggregate uncertainty on herding in analysts’ stock recommendations. International Review of Financial Analysis. 2018;57:90–105. [Google Scholar]
- Lin A.Y., Lin Y.-N. Herding of institutional investors and margin traders on extreme market movements. International Review of Economics & Finance. 2014;33:186–198. [Google Scholar]
- Ludvigson S.C., Ma S., Ng S. National Bureau of Economic Research; 2020. Covid19 and the macroeconomic effects of costly disasters: Technical report. [Google Scholar]
- Lux T. Herd behaviour, bubbles and crashes. The Economic Journal. 1995;105(431):881–896. [Google Scholar]
- Maćkowiak B., Wiederholt M. Lack of preparation for rare events. Journal of Monetary Economics. 2018;100:35–47. [Google Scholar]
- Malik K., Meki M., Morduch J., Ogden T., Quinn S., Said F. COVID-19 and the future of microfinance: Evidence and insights from Pakistan. Oxford Review of Economic Policy. 2020;36(1):S138–S168. [Google Scholar]
- Miller E.M. Risk, uncertainty, and divergence of opinion. The Journal of Finance. 1977;32(4):1151–1168. [Google Scholar]
- Mobarek A., Mollah S., Keasey K. A cross-country analysis of herd behavior in Europe. Journal of International Financial Markets, Institutions and Money. 2014;32:107–127. [Google Scholar]
- OECD A. OECD Publishing; Paris: 2008. Handbook on constructing composite indicators: Methodology and user guide. [Google Scholar]
- Onali E. 2020. Covid-19 and stock market volatility. Available at SSRN 3571453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pellegrino G., Ravenna F., Züllig G. 2020. The impact of pessimistic expectations on the effects of COVID-19-induced uncertainty in the euro area. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Philippas N., Economou F., Babalos V., Kostakis A. Herding behavior in REITs: Novel tests and the role of financial crisis. International Review of Financial Analysis. 2013;29:166–174. [Google Scholar]
- Ramelli S., Wagner A.F. Swiss Finance Institute; 2020. Feverish stock price reactions to COVID-19: Swiss finance institute research paper series 20-12. [Google Scholar]
- Roser M., Ritchie H., Ortiz-Ospina E., Hasell J. Coronavirus pandemic (COVID-19) Our World in Data. 2020 [Google Scholar]
- Sabat I., Neuman-Böhme S., Varghese N.E., Barros P.P., Brouwer W., van Exel J., Schreyögg J., Stargardt T. United but divided: policy responses and people’s perceptions in the EU during the COVID-19 outbreak. Health Policy. 2020 doi: 10.1016/j.healthpol.2020.06.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmitt N., Westerhoff F. Herding behaviour and volatility clustering in financial markets. Quantitative Finance. 2017;17(8):1187–1203. [Google Scholar]
- Sharif A., Aloui C., Yarovaya L. COVID-19 pandemic, oil prices, stock market, geopolitical risk and policy uncertainty nexus in the US economy: Fresh evidence from the wavelet-based approach. International Review of Financial Analysis. 2020;70 doi: 10.1016/j.irfa.2020.101496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uddin G.S., Yahya M., Goswami G.G., Ahmed A., Lucey B.M. 2020. Stock market contagion of COVID-19 in emerging economies. Available at SSRN 3573333. [Google Scholar]
- Wagner A.F. What the stock market tells us about the post-COVID-19 world. Nature Human Behaviour. 2020 doi: 10.1038/s41562-020-0869-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whaley R.E. The investor fear gauge. The Journal of Portfolio Management. 2000;26(3):12–17. [Google Scholar]
- Yarovaya L., Matkovskyy R., Jalan A. 2020. The effects of ‘Black Swan’ event (COVID-19) on herding behavior in cryptocurrency markets: Evidence from cryptocurrency USD, EUR, JPY and KRW markets. Available at SSRN 3586511. [Google Scholar]