Numerical simulation of the force of infection and the typical times of SARS-CoV-2 disease for different location countries

Abstract

The new coronavirus disease appeared at the end of 2019 which is now a very big problem by spreading over the world and there are multiple parameters that can be discussed to be tools for the forecasting and the spreading of the pandemic such as the force of infection, the exponential base…etc. In this work, we estimate the force of infection and the specific times of the disease. For estimating the force of infection and the specific times, we use SEIR (susceptible cases of the disease, infectious cases of the disease, and recovered cases of the disease) epidemic model and the numerical analysis methods for simulating the values. We use the collected data of the new coronavirus pandemic reported up to 21 September, 2020 in different geographical location countries, which are, China, USA, Russia, the United Kingdom, Brazil, Spain, Bahrain, Egypt, India, Iran, Cyprus and the Syrian Arab Republic. We found that the force of infection and the specific times of SARS-CoV-2 disease are different for different location in countries. We find that there is no actual relation between the force of infection and the specific times of the pandemic of the new coronavirus disease with the weather and the geographical location of the countries.

Introduction

The new coronavirus disease appeared at the end of 2019 in China in Wuhan and became a very big problem by spreading over the world; there are multiple parameters that can be discussed to be tools for the forecasting and the spreading of the pandemic such as the basic reproductive ratio, the exponential growth base and so on. The force of infection is a specific tool when we talk about a specific pandemic such as Ebola and the new coronavirus disease because it represents the transmission from susceptible cases to the infectious cases. The force of infection can be estimated from one of the models used in the epidemiology where there are multiple models in epidemiology used to simulate the forecasting and the spreading of a specific pandemic, some use fractional derivatives and others use ordinary differential equations, some with vaccination, and some with the deceased cases (Al-Raeei 2018; Tarabichi 2010). The definition and derivation of the first epidemic model, which is SIR (susceptible cases of the disease, infectious cases of the disease, recovered cases of the disease) model, was by Kermack (1927) and the models derived from this model were used for forecasting lots of disease such as Ebola virus spread as Osemwinyen (2015), Kamara (2020) and Zhu (2019) and with vaccination as (Gao 2007). Recently, the model and the modified models were used for forecasting and spreading of the new coronavirus disease where (Malavika et al 2020) used SIR and logistic growth models for the forecasting of COVID-19 epidemic in India and high incidence states, (Al-Raeei 2020a, b) found the basic reproduction number values of the disease for multiple countries, (Lifshits et al. 2020) studied the forecasting of the pandemic in Russia, (Roy et al 2020) discussed the forecasting of the disease in India using ARIMA (autoregressive integrated moving average) model and the same model was applied for Russia by Fang et al. (2020), Rejaur Rahman et al. (2020) studied the forecasting of the disease in Bangladesh with geospatial modelling, Gupta et al (2020) discussed the effect of the geographical locations in India on the disease, Santosh (2020) discussed the prediction models with unexploited data of the disease, Neto et al .(2020) showed the new coronavirus industrial impact with the fourth industrial revolution, Aabed et al. (2020) discussed the analytical study of the forecasting factors on the spread of the disease, Ali et al. (2020) discussed the effects of the PM_2.5 on the spreading of the disease, Khan et al. (2020) discussed the effects of underlying morbidities on the occurrence of deaths in COVID-19 patients, Al-Raeei (2020a, b) discussed the forecasting of the disease for multiple countries with mortality and Bhadra et al (2020) discussed the effects of population density on the infection and the mortality of the disease. In this work, we use the SEIR epidemic-model for simulating force of infection of the new coronavirus disease values for multiple countries. Besides, we use the same model for simulating the values of the specific times namely the typical time between contacts T_C and the typical times up to removal T_R of SARS-CoV-2 pandemic. The SEIR model take the exposed cases into part and this model is composed of four differential equations. The first two equations of this model are non-linear equations and describe the change of the susceptible cases and the change of the exposed cases with respect to the time and the others equations describe the rate of the infections and the recovery in respect to the time. The four equations of the SEIR epidemiological model are given as follows:

$$\frac{\text{d}s(t)}{\text{d}t}=-{\nu }_{2}i(t)s(t)+{\nu }_1[1-s(t)]$$ 1

$$\frac{\text{d}e(t)}{\text{d}t}=-({\nu }_1+{\nu }_3)e(t)+{\nu }_{2}i(t)s(t)$$ 2

$$\frac{\text{d}i(t)}{\text{d}t}=-({\nu }_1+{\nu }_4)i(t)+{\nu }_{3}e(t)$$ 3

$$\frac{\text{d}r(t)}{\text{d}t}=-{\nu }_{1}r(t)+{\nu }_{4}i(t)$$ 4

where ν₁, ν₂, ν₃ and ν₄ are the parameters of the model and s(t), i(t), r(t) and e(t) are the normalized susceptible cases of the disease, the normalized infectious cases of the disease, the normalized recovered cases disease and the normalized exposed cases of the disease, respectively. In this study, we consider the previous SEIR model to estimate the force of infection values and the specific times values of the new coronavirus disease in China, where the first case appeared at the end of 2019, the US, where the first case of the pandemic was observed in January 2020, UK, where the first case of the pandemic was observed in January 2020, Brazil, where the first case of the pandemic was observed in February 2020, Spain, where the first case of the pandemic was observed in January 2020, India, where the first case appeared in February 2020, Russia, where the first case of the pandemic was observed in January 2020, Bahrain, where the first case of the pandemic was observed in February 2020, Egypt, where the first case of the pandemic was observed in February 2020, Iran, where the first case of the pandemic was observed in February 2020, Cyprus, where the first case of the pandemic was observed in March 2020 and Syrian Arab Republic, where the first case of the pandemic was observed in March 2020. which are considered located in different locations in all of the world and the locations as following: China is located in the Far East, USA is located in north America, Russia located between Asia and Europe, the UK is located at north-west Europe, Brazil is located in south America, Spain is located at south-west Europe, Bahrain is located in Arabian Gulf, Egypt is located in Africa, India and Iran located in west Asia, Cyprus located in Mediterranean and the Syrian Arab Republic is located at East of Mediterranean. In the section-2, we include the principle of the method used to find the force of infection and the specific times of SARS-CoV-2 using the applied epidemiological model and in the section-3, we include the resulted values, in the section-4 we illustrate the discussion of the results and in the last section, we include the conclusion of resulted values.

Methods

We collected the observed data of the new-coronavirus disease recorded in USA, Russia, the United Kingdom, Brazil, India, Spain, Bahrain, Egypt, Iran, Cyprus and the Syrian Arab Republic up to date 21 September 2020. After that, we applied Runge–Kutta simulation method for the SIER epidemiological model for determining the force of infection of the new coronavirus pandemic by fitting the collected results of the infectious cases, the recovered cases and the total cases of the new coronavirus pandemic in the previous different countries. From the fitting values of the recorded data, we find the coefficient of exposing, the coefficient of infection, the coefficient of recovery and the coefficient of mortality of the SEIR model in case of the new coronavirus disease in the previous countries. Where we used the conservation of the total population condition:

$$\frac{\text{d}s(t)}{\text{d}t}+\frac{\text{d}e(t)}{\text{d}t}+\frac{\text{d}i(t)}{\text{d}t}+\frac{\text{d}r(t)}{\text{d}t}=0$$ 5

We use the Runge–Kutta method for the purpose of the numerical simulation and in sense of the Runge–Kutta simulation method, the normalized susceptible cases of the pandemic individual, the normalized infectious cases of the pandemic individual, the normalized recovered cases of the pandemic individual and the normalized exposed cases of the pandemic individual are governed by the following four equations:

$$s(t_{n+1})\approx s(t_n)+\tau \sum _{m=1}^{m=z}{l}_m^1{k}_m^1$$ 6

$$i(t_{n+1})\approx i(t_n)+\tau \sum _{m=1}^{m=z}{l}_m^2{k}_m^2$$ 7

$$r(t_{n+1})\approx r(t_n)+\tau \sum _{m=1}^{m=z}{l}_m^3{k}_m^3$$ 8

$$e(t_{n+1})\approx e(t_n)+\tau \sum _{m=1}^{m=z}{l}_m^4{k}_m^4$$ 9

With the following functions:

$$k_1^1=f_1(t_n,s_n)$$ 10

$$k_2^1=f_1(t_n+c_2^1\tau ,s_n+\tau (a_{21}^1{k}_1^1))$$ 11

$$\begin{array}{cc}\hfill k_Z^1& =f_1(t_n+c_Z^1\tau ,s_n+\tau (a_{Z1}^1{k}_1^1\hfill \\ \hfill & +a_{Z2}^1{k}_2^1+a_{Z3}^1{k}_3^1+\cdots +a_{Z,Z-1}^1{k}_{Z,Z-1}^1))\hfill \\ \hfill \end{array}$$ 12

$$k_1^2=f_2(t_n,i_n)$$ 13

$$k_2^2=f_2(t_n+c_2^2\tau ,i_n+\tau (a_{21}^2{k}_1^2))$$ 14

$$\begin{array}{cc}\hfill k_Z^2& =f_2(t_n+c_Z^2\tau ,i_n+\tau (a_{Z1}^2{k}_1^2\hfill \\ \hfill +a_{Z2}^2{k}_2^2+a_{Z3}^2{k}_3^2+\cdots +a_{Z,Z-1}^2{k}_{Z,Z-1}^2))\\ \hfill \end{array}$$ 15

$$k_1^3=f_3(t_n,r_n)$$ 16

$$k_2^3=f_3(t_n+c_2^3\tau ,r_n+\tau (a_{21}^3{k}_1^3))$$ 17

$$\begin{array}{cc}\hfill k_Z^3& =f_3(t_n+c_Z^3\tau ,r_n+\tau (a_{Z1}^3{k}_1^3\hfill \\ \hfill & +a_{Z2}^3{k}_2^3+a_{Z3}^3{k}_3^3+\cdots +a_{Z,Z-1}^3{k}_{Z,Z-1}^3))\hfill \\ \hfill \end{array}$$ 18

$$k_1^4=f_4(t_n,e_n)$$ 19

$$k_2^4=f_4(t_n+c_2^4\tau ,e_n+\tau (a_{21}^4{k}_1^4))$$ 20

$$\begin{array}{cc}\hfill k_Z^4& =f_4(t_n+c_Z^4\tau ,e_n+\tau (a_{Z1}^4{k}_1^4\hfill \\ \hfill & +a_{Z2}^4{k}_2^4+a_{Z3}^4{k}_3^4+\cdots +a_{Z,Z-1}^4{k}_{Z,Z-1}^4))\hfill \\ \hfill \end{array}$$ 21

where τ is the step of the time and s(t_n), i(t_n), r(t_n) and e(t_n) are the normalized susceptible cases of the pandemic individual, the normalized infectious cases of the pandemic individual, the normalized recovered cases of the pandemic individual and the normalized exposed cases of the pandemic individual, respectively at the moment t_n and s(t_n+1), i(t_n+1), r(t_n+1) and e(t_n+1) are the normalized susceptible cases of the pandemic individual, the normalized infectious cases of the pandemic individual, the normalized recovered cases of the pandemic individual and the normalized exposed cases of the pandemic individual, respectively at the moment t_n+1. The coefficients l_m^j and c_u^j are the weights and the nodes of the function expansion and a_qu^j are the Runge–Kutta matrix coefficients, all the previous coefficients can be found using Butcher tableau and the weights are normalized to one under the following condition:

$$\sum _{m=1}^{m=z}{l}_m^j=1$$ 22

After that, we calculate the force of infection and the specific times of the new coronavirus disease-2019 in the considered countries where the force of infection is given from the normalized infection individual by the following equation:

$$F(t)=\beta i(t)$$ 23

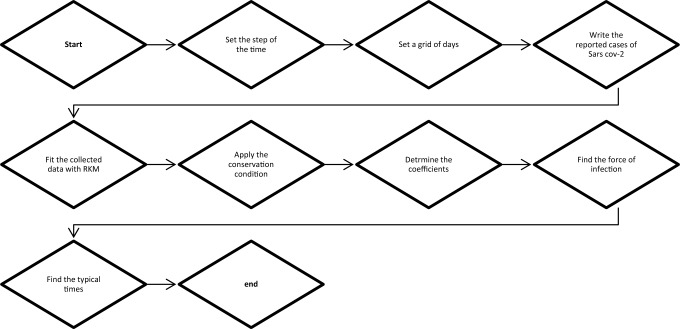
In Fig. 1, we illustrated a schematic chart for clarifying the algorithm we used for the calculations.

Fig. 1.

Schematic plot of the fitting algorithm

Results

We calculated the coefficient of exposed persons, the coefficient of infectious persons, the coefficient of recovered persons and the coefficient of mortality of SARS-CoV-2 for China, USA, Russia, India, the UK, Brazil, Spain, Bahrain, Egypt, Iran, Cyprus and Syrian-Arab-Republic based on the collected data of all diseased persons of the coronavirus disease-2019 in each country. The results of the coefficients of the SEIR model are included in Table 1 which includes the coefficients in d⁻¹ unit and the countries.

Table 1.

The coefficient of exposed persons, the coefficient of infectious persons, the coefficient of recovered person and the coefficient of mortality of the new coronavirus disease in the United States, Russia, the United Kingdom, Brazil, Spain, Bahrain, Egypt, Iran, India, Cyprus and Syrian Arab Republic

	${\nu }_1(d^{-1})$	${\nu }_2(d^{-1})$	${\nu }_3(d^{-1})$	${\nu }_4(d^{-1})$
India	$3.2752\times {10}^{-2}$	$1.2812\times {10}^{-2}$	$1.2812\times {10}^{-3}$	$1.2835\times {10}^{-3}$
USA	$2.2812\times {10}^{-3}$	$624.0641\times {10}^{-3}$	$0.2154\times {10}^{-3}$	$14.3910\times {10}^{-3}$
China	$0.1182\times {10}^{-2}$	$0.2456\times {10}^{-2}$	$0.01\times {10}^{-2}$	$4.90\times {10}^{-2}$
Russia	$0.0901\times {10}^{-3}$	$114.1212\times {10}^{-3}$	$0.0750\times {10}^{-3}$	$23.1612\times {10}^{-3}$
UK	$0.2851\times {10}^{-3}$	$160.153\times {10}^{-3}$	$0.1561\times {10}^{-3}$	$23.2882\times {10}^{-3}$
Brazil	$0.0812\times {10}^{-3}$	$454.476\times {10}^{-3}$	$0.1040\times {10}^{-3}$	$93.4610\times {10}^{-3}$
Spain	$0.1181\times {10}^{-3}$	$60.4712\times {10}^{-3}$	$0.1232\times {10}^{-3}$	$20.4473\times {10}^{-3}$
Bahrain	$0.0600\times {10}^{-2}$	$47.91\times {10}^{-2}$	$0.04\times {10}^{-2}$	$6.06\times {10}^{-2}$
Egypt	$0.0100\times {10}^{-2}$	$22.5\times {10}^{-2}$	$0.01\times {10}^{-2}$	$2.59\times {10}^{-2}$
Iran	$2.63\times {10}^{-2}$	$90.36\times {10}^{-2}$	$0.02\times {10}^{-2}$	$23.83\times {10}^{-2}$
Cyprus	$4.89\times {10}^{-2}$	$68.69\times {10}^{-2}$	$0.01\times {10}^{-2}$	$4.90\times {10}^{-2}$
The Syrian Arab Republic	$0.01\times {10}^{-2}$	$13.67\times {10}^{-2}$	$0.01\times {10}^{-2}$	$0.1000\times {10}^{-2}$

Based on the coefficient of exposed persons, the coefficient of infectious persons, the coefficient of recovered persons and the coefficient of mortality of SARS-CoV-2 pandemic which we determined, we calculated the force of infection values for India, USA, Russia and the Syrian Arab Republic. We included the resulted values of the force of infection values of COVID-19 in Table 2 for the the previous different location countries and this table included the locations of the countries.

Table 2.

The force of infection of the new coronavirus disease in India, the United States, Russia and Syrian Arab Republic for the middle of three months of 2020 year

	FL(d−1) June	FL(d−1) July	FL(d−1) August
India	7.2838e−006	5.0284e−006	5.4519e−005
USA	0.0020	0.0032	0.0013
Russia	4.0872e−005	1.8345e−004	1.9950e−004
The Syrian Arab Republic	1.0007e−005	2.2307e−006	6.3176e−007

In addition to the force of infection, we determined the typical time between contacts and the typical time between removal of SARS-CoV-2 disease for India, China, the United States, Russia, the United Kingdom, Brazil, Spain, Bahrain, Egypt, Iran, Cyprus and the Syrian Arab Republic. The results of the specific times are illustrated in Table 3 which contains the different geographical locations of the countries.

Table 3.

The typical time between contacts and the typical time between removal of the new-coronavirus-2019 pandemic in India, China, the United States, Russia, the United Kingdom, Brazil, Spain, Bahrain, Egypt, Iran, Cyprus and the Syrian Arab Republic

The country	The location of the country	TC (days)	TR (days)
India	South Asia	78.0518	779.1196
USA	North America	1.6024	69.4879
China	Far East-Asia	407.1661	20.4082
Russia	Easter Europe–Northern Asia	8.7626	43.1757
UK	North-West Europe	6.2440	42.9402
Brazil	South America	2.2003	10.6997
Spain	South-Western Europe	16.5368	48.9062
Bahrain	Arabian Gulf	2.0872	16.5017
Egypt	North Africa	4.4444	38.6100
Iran	West Asia	1.1067	4.1964
Cyprus	Mediterranean	1.4558	20.4082
Syrian Arab Republic	East of Mediterranean	7.3153	1000

Discussions

As we see from the second table, the force of infection in India, Russia and the Syrian Arab Republic increases up to middle of August 2020 and in the United States increases up to middle of September 2020 and then decreases. Also, we see from Table 3 that the value of the typical time between contacts of the coronavirus-2019 pandemic for China is the greatest value in the previous different countries and the value of this typical time of the coronavirus-2019 pandemic for Iran is the smallest between the previous different countries and the values of this time are located in the interval [1–500] for the different geographical location countries. Besides, the values of the typical time of removal are located in the interval [1–1000] in the same countries.

Conclusions

We employ one of the epidemic models, namely, the SEIR model with the normalized cases for estimating the values of the force of infection and the values of the typical times between contents and removal of SARS-CoV-2 in twelve different location countries, namely, India, China, USA, Russia, the United Kingdom, Brazil, Spain, Bahrain, Egypt, Iran, Cyprus and Syrian Arab Republic. The choice of the countries was based on the different geographical location of the countries on the earth and the different with the type of the weather in each countries. We used the recorded data, up to date 21 September 2020, of the collected cases of the coronavirus-2019 pandemic in the different countries to find the coefficient of exposing, the coefficient of infection, the coefficient of recovery and the coefficient of mortality of the new coronavirus pandemic for every country. We calculated the force of infection and the values of the specific times of the new coronavirus pandemic in the different countries based on the coefficients of the SEIR model and the Runge–Kutta simulation method.

We found that typical time between contacts values of COVID-19 pandemic (Table 3) are in the interval [1–500] for the different countries. Besides, we found that the values of the typical time between removal are in the interval [1–1000] for the same countries. We can use the same method for determining the same variables for other countries with different numbers of the new coronavirus pandemic, however, we chose the previous countries to clarify the relation between the force of infection and the typical times of SARS-CoV-2 with the geographical location and the weather of the country.

Funding

Not applicable.

Availability of data and materials

The author declared that the materials in the manuscript will be available for non-commercial purposes.

Code availability

MATLAB software was used for purpose of doing the numerical simulation.

Compliance with ethical standards

Conflict of interest

The author confirmed that he does not have a conflict of interest.