Abstract
Measurements of skeletal muscle cross-sectional area (SMA) at the level of the third lumbar (L3) vertebra derived from clinical computed tomography (CT) scans are commonly used in assessments of sarcopenia, the loss of skeletal muscle mass and function associated with aging. As SMA is correlated with height and Body Mass Index (BMI), body size adjustment is necessary to fairly assess sarcopenic low muscle mass in individuals of different height and BMI. The skeletal muscle index, a widely used measure, adjusts for height as but uses no BMI adjustment. There is no agreed upon standard for body size adjustment. We extracted L3 SMA using non-contrast-enhanced CT scans from healthy adults, split into ‘Under-40’ and ‘Over-40’ cohorts. Sex-specific allometric analysis showed that height to the power of one was the optimal integer coefficient for height adjusted SMA in both males and females. We computed two height-adjusted measures and , comparing their Pearson correlations versus age, height, weight, and BMI separately by sex and cohort. Finally, in the ‘Under-40’ cohort, we used linear regression to convert each height-adjusted measure into a z-score (, ) adjusted for BMI. was less correlated with height in both males and females (, and , ) than ( and , ). was uncorrelated with BMI and weight, and minimally correlated with height in males and females (, and , ). The final equation was: , where , , , and sex = 1 if male, 0 if female. We propose for optimal height adjustment and the score for optimal height and BMI adjustment. By minimizing correlations with height and BMI, the score produces unbiased assessments of relative L3 skeletal muscle area across the full range of body sizes.
Subject terms: Ageing, Skeletal muscle, Risk factors, Diagnostic markers
Introduction
The European Working Group on Sarcopenia in Older People (EWGSOP) defines sarcopenia as the loss of both muscle mass and function1. This manuscript directly addresses only the muscle mass half of that definition. Computed tomography (CT) measurements of skeletal muscle cross-sectional area (SMA) performed at the third lumbar vertebra (L3) are prevalent in assessments of sarcopenic low muscle mass2–12, though other vertebrae or muscle groups have been used13–16. Cutoffs for sarcopenic muscle quantity set at two standard deviations below the mean of a healthy, young adult population were recommended by EWGSOP. The 18 (or 20) to 40 age range has been widely used to define ‘young, adult’ reference populations12,15–21, and is further supported by the observation that muscle mass loss increases after age 40. Revised EWGSOP guidelines note that ‘fundamentally, muscle mass is correlated with body size; i.e., individuals with a larger body size normally have larger muscle mass’22, and identify three examples of body size adjustment: dividing muscle mass by height-squared, by weight, or by BMI directly with muscle measurements derived from CT, dual-energy X-ray absorptiometry (DXA), or bioelectrical impedance analysis (BIA)18,23. However, no specific recommendation for body size adjustment was made22.
The purpose of body size adjustment is to remove the association between the original measure and a biologically related body size measure, thus enabling unbiased comparisons to be made across the range of body sizes. For example, human body mass (weight) scales approximately with so a relative weight index, Body Mass Index (BMI), was created and validated as using allometric analysis24–26. By design, BMI is uncorrelated with height and as such, enables unbiased comparisons of body mass between individuals of different heights. Similar to weight, L3 SMA is correlated with height; so a relative (for height) skeletal muscle index () was developed based upon the work of Baumgartner et al. with DXA measurements2,4,9,15,27,28. However, the height adjustment used in L3 SMI may be neither optimal nor sufficient. Our analysis shows that CT-derived L3 SMI remains correlated with height, suggesting that height-squared is not the optimal height adjustment factor. Furthermore, multiple studies have noted that SMI is correlated with BMI29,30, suggesting that height adjustment is insufficient and that BMI adjustment is also warranted. Diagnosis of sarcopenic low muscle mass using fixed cutoff values that have been adjusted for height but not BMI can result in under-diagnosis in high BMI individuals with relatively low muscle (i.e., sarcopenic obese) and over-diagnosis in low BMI individuals with relatively normal muscle quantity (i.e., healthy lean)9. Despite this fact, an appropriately BMI-adjusted CT skeletal muscle index is not widely used.
Attempts to adjust sarcopenia cutoffs to address the association between SMI and BMI include: Newman et al. proposed a method based on the residuals of a linear regression model in an elderly cohort29; Martin et al. proposed different cutoffs for high BMI () males, but not females in an elderly cancer cohort5; Zhuang et al. proposed Asian (Wenzhou, China) cutoffs for males and females with a low mean BMI9; and Van der Werf et al. provided sex-, age-, and BMI-specific predicted percentiles for SMA and SMI in healthy subjects between age 20–60 and 20–8211.
Sarcopenia is a condition that may exist at any body mass, and properly adjusting muscle quantity measures for body mass is widely recognized as necessary22,31,32. Human body mass (weight) is determined by height and absolute skeletal muscle quantity, along with fat, bone, and other tissue. Since height and weight are correlated, height and BMI (which are uncorrelated) should be the primary targets for body size adjustment. Therefore, we suggest that the optimal body size adjusted skeletal muscle index meet two simple criteria: it should be uncorrelated with (1) height and (2) BMI in a young, healthy reference population. By doing so, the index excludes the variation in muscle quantity explained by height and BMI (relative weight). The resulting relative muscle index distinguishes between ‘more muscular’ and ‘less muscular’ body compositions at any BMI. We suggest that this index would optimally quantify sarcopenic low muscle mass across the full range of human body sizes; it would be unbiased in tall, short, thin, or obese individuals.
We previously published fixed sarcopenia cutoffs for SMA and SMI, however, we did not assess whether dividing SMA by resulted in a measure that was uncorrelated with height, nor did we address the underlying association between SMI and BMI12,15. In this manuscript, we focus on CT measurements of skeletal muscle cross-sectional area at the third lumbar vertebra (L3). Our aim is to determine the optimal body size adjusted L3 skeletal muscle index that meets the above criteria, i.e, it is uncorrelated with height and BMI in a young, healthy population.
Results
Population summary
On average, the ‘Under-40’ cohort males and females had greater muscle quantity than those in the ‘Over-40’ cohort (), were slightly taller (), but were not significantly heavier by weight or BMI () (Table 1). Females were 1.64 meters tall with a BMI of 27 on average, while males were 1.79 meters with a BMI of 28 in both cohorts. Mean SMA was 7.7% lower in females, and 4.5% lower in males in the ‘Over-40’ versus ‘Under-40’ cohort. The average z-scores were significantly lower in the ‘Over-40’ cohort compared to the ‘Under-40’ cohort, reflecting increased sarcopenia in the older group.
Table 1.
Sex- and cohort-specific demographics and skeletal muscle measures.
| Sex | Variable | Under-40 | Over-40 | p | ||||
|---|---|---|---|---|---|---|---|---|
| N | Mean | s.d. | N | Mean | s.d. | |||
| F | Age (year) | 610 | 31.06 | 5.90 | 512 | 49.73 | 6.36 | <0.001 |
| Height (m) | 610 | 1.64 | 0.07 | 512 | 1.64 | 0.06 | 0.020 | |
| Weight (kg) | 610 | 73.68 | 15.79 | 512 | 72.66 | 12.97 | 0.237 | |
| BMI (kg/m2) | 610 | 27.22 | 5.41 | 512 | 27.17 | 4.58 | 0.863 | |
| Underweight | 8 | 1.3% | 0 | 0% | ||||
| Normal | 241 | 39.5% | 181 | 35.4% | ||||
| Overweight | 167 | 27.4% | 196 | 38.3% | ||||
| Obese class I | 138 | 22.6% | 104 | 20.3% | ||||
| Obese class II | 45 | 7.4% | 28 | 5.5% | ||||
| Obese class III | 11 | 1.8% | 3 | 0.6% | ||||
| Race | 610 | 512 | 0.005 | |||||
| African American | 65 | 10.7% | 33 | 6.4% | ||||
| Asian | 8 | 1.3% | 4 | 0.8% | ||||
| Caucasian | 339 | 55.6% | 291 | 56.8% | ||||
| Other | 22 | 3.6% | 7 | 1.4% | ||||
| Unknown | 176 | 28.9% | 177 | 34.6% | ||||
| SMA (cm2/) | 610 | 130.09 | 18.78 | 512 | 120.07 | 15.84 | <0.001 | |
| SMA/ht (cm2/m) | 610 | 79.08 | 10.55 | 512 | 73.43 | 9.26 | <0.001 | |
| (cm2/m2) | 610 | 48.15 | 6.52 | 512 | 44.97 | 5.94 | <0.001 | |
| z(SMA/ht) | 610 | 0.00 | 1.00 | 512 | − 0.63 | 0.94 | <0.001 | |
| 610 | 0.00 | 1.00 | 512 | − 0.58 | 0.98 | <0.001 | ||
| M | Age (year) | 448 | 30.29 | 5.81 | 279 | 49.64 | 6.73 | <0.001 |
| Height (m) | 448 | 1.79 | 0.07 | 279 | 1.78 | 0.07 | 0.071 | |
| Weight (kg) | 448 | 88.87 | 16.85 | 279 | 88.00 | 12.72 | 0.427 | |
| BMI (kg/m2) | 448 | 27.70 | 4.67 | 279 | 27.73 | 3.37 | 0.918 | |
| Underweight | 2 | 0.4% | 0 | 0% | ||||
| Normal | 126 | 28.1% | 61 | 21.9% | ||||
| Overweight | 198 | 44.2% | 154 | 55.2% | ||||
| Obese class I | 83 | 18.5% | 57 | 20.4% | ||||
| Obese class II | 36 | 8.0% | 7 | 2.5% | ||||
| Obese class III | 3 | 0.7% | 0 | 0% | ||||
| Race | 448 | 279 | 0.008 | |||||
| African American | 46 | 10.3% | 12 | 4.3% | ||||
| Asian | 7 | 1.6% | 1 | 0.4% | ||||
| Caucasian | 244 | 54.5% | 147 | 52.7% | ||||
| Other | 10 | 2.2% | 9 | 3.2% | ||||
| Unknown | 141 | 31.5% | 110 | 39.4% | ||||
| SMA (cm2/) | 448 | 195.61 | 25.91 | 279 | 186.74 | 24.08 | <0.001 | |
| SMA/ht (cm2/m) | 448 | 109.31 | 13.79 | 279 | 104.89 | 12.72 | <0.001 | |
| (cm2/m2) | 448 | 61.18 | 8.12 | 279 | 59.01 | 7.44 | <0.001 | |
| z(SMA/ht) | 448 | 0.00 | 1.00 | 279 | − 0.39 | 0.95 | <0.001 | |
| 448 | 0.00 | 1.00 | 279 | − 0.32 | 0.93 | <0.001 | ||
p-values less than 0.01 shown in bold.
Body size adjustment
Allometric analysis of weight versus height resulted in optimal coefficients of 2.07 (male) and 1.84 (female), or 2 when rounded to the nearest integer. SMA versus height analysis resulted in optimal coefficients of 1.02 (males) and 1.33 (females), or 1 when rounded to the nearest integer.
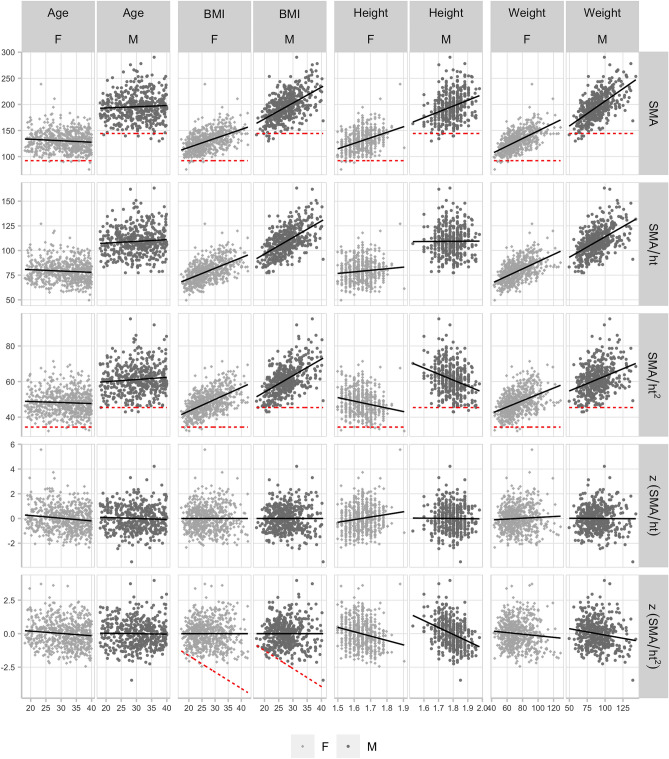
Unadjusted L3 SMA and height-adjusted SMA measures were differently correlated with age, BMI, height, and weight in both cohorts (Figs. 1, 2). In the ‘Under-40’ cohort, SMA, , and were uncorrelated with age (Table 2). SMA, , and were positively correlated with BMI and weight. SMA was positively correlated with height and was negatively correlated with height. correlations with height were closer to zero than . Of the z-scores, was uncorrelated with age and BMI, and negatively correlated with height and weight, though the age (, ) and weight (, ) correlations were borderline in females. was uncorrelated with age, BMI, height, and weight in males, and in females was uncorrelated with BMI and weight, negatively correlated with age, and positively correlated with height. The correlation with height was closer to zero than .
Figure 1.
Under-40 cohort: scatter plots of L3 skeletal muscle area measures versus age, BMI, height, and weight, split by sex. Best-fit linear regression line overlaid (black, solid), and previously reported (Derstine, 2018)15 sarcopenia ‘fixed’ cutoff values (red, dashed) where applicable.
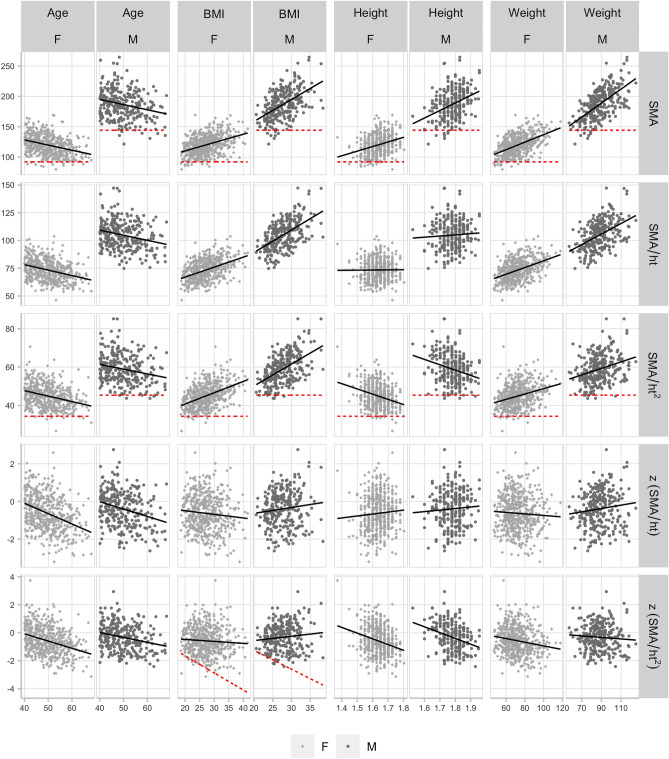
Figure 2.
Over-40 cohort: Scatter plots of L3 skeletal muscle area measures versus age, BMI, height, and weight, split by sex. Best-fit linear regression line overlaid (black, solid), and Derstine, 201815 sarcopenia ‘fixed’ cutoff values (red, dashed) shown for SMA, , and vs. BMI.
Table 2.
Sex-specific Pearson correlation, p-value, and 95% CI shown for each L3 skeletal muscle area measure versus age, BMI, height, and weight for each cohort.
| Cohort | Variable | Sex | N | Age | BMI | Height | Weight |
|---|---|---|---|---|---|---|---|
| Under-40 | SMA | F | 610 | − 0.089 p=0.028 | 0.495 p<0.001 | 0.383 p<.001 | 0.610 p<0.001 |
| (− 0.167, − 0.009) | (0.433, 0.553) | (0.314, 0.449) | (0.558, 0.658) | ||||
| M | 448 | 0.053 p=0.259 | 0.547 p<.001 | 0.308 p<0.001 | 0.619 p<0.001 | ||
| (− 0.039, 0.145) | (0.478, 0.608) | (0.222, 0.390) | (0.558, 0.673) | ||||
| SMA/ht | F | 610 | − 0.075 p=0.065 | 0.548 p<0.001 | 0.102 p=0.012 | 0.546 p<0.001 | |
| (− 0.153, 0.005) | (0.490, 0.601) | (0.023, 0.180) | (0.488, 0.600) | ||||
| M | 448 | 0.073 p=0.121 | 0.567 p<0.001 | 0.005 p=0.912 | 0.506 p<0.001 | ||
| (− 0.019, 0.165) | (0.500, 0.626) | (− 0.087, 0.098) | (0.434, 0.572) | ||||
| F | 610 | − 0.052 p=0.200 | 0.552 p<0.001 | − 0.205 p<0.001 | 0.428 p<0.001 | ||
| (− 0.131, 0.028) | (0.494, 0.605) | (− 0.280, − 0.128) | (0.360, 0.490) | ||||
| M | 448 | 0.087 p=0.064 | 0.532 p<.001 | − 0.301 p<0.001 | 0.344 p<0.001 | ||
| (− 0.005, 0.179) | (0.463, 0.596) | (− 0.383, − 0.214) | (0.260, 0.423) | ||||
| z(SMA/ht) | F | 610 | − 0.128 p=0.002 | 0.000 p=1.000 | 0.145 p<0.001 | 0.053 p=0.189 | |
| (− 0.205, − 0.049) | (− 0.079, 0.079) | (0.066, 0.222) | (− 0.026, 0.132) | ||||
| M | 448 | − 0.045 p=0.347 | 0.000 p=1.000 | − 0.009 p=0.848 | − 0.006 p=0.899 | ||
| (− 0.137, 0.048) | (− 0.093, 0.093) | (− 0.102, 0.084) | (− 0.099, 0.087) | ||||
| F | 610 | − 0.101 p=0.012 | 0.000 p=1.000 | − 0.223 p<0.001 | − 0.094 p=0.021 | ||
| (− 0.179, − 0.022) | (− 0.079, 0.079) | (− 0.297, − 0.146) | (− 0.172, − 0.014) | ||||
| M | 448 | − 0.019 p=0.691 | 0.000 p=1.000 | − 0.369 p<0.001 | − 0.161 p=0.001 | ||
| (− 0.111, 0.074) | (− 0.093, 0.093) | (− 0.447, − 0.287) | (− 0.250, − 0.069) | ||||
| Over-40 | SMA | F | 512 | − 0.341 p<0.001 | 0.397 p<0.001 | 0.300 p<0.001 | 0.508 p<0.001 |
| (− 0.415, − 0.262) | (0.321, 0.467) | (0.219, 0.377) | (0.440, 0.569) | ||||
| M | 279 | − 0.237 p<0.001 | 0.506 p<0.001 | 0.356 p<0.001 | 0.608 p<0.001 | ||
| (− 0.345, − 0.123) | (0.413, 0.588) | (0.249, 0.454) | (0.529, 0.677) | ||||
| SMA/ht | F | 512 | − 0.339 p<0.001 | 0.445 p<0.001 | 0.009 p=0.847 | 0.426 p<0.001 | |
| (− 0.413, − 0.259) | (0.373, 0.512) | (− 0.078, 0.095) | (0.352, 0.494) | ||||
| M | 279 | − 0.242 p<0.001 | 0.538 p<0.001 | 0.057 p=0.339 | 0.475 p<0.001 | ||
| (− 0.349, − 0.128) | (0.449, 0.616) | (− 0.060, 0.174) | (0.379, 0.561) | ||||
| F | 512 | − 0.305 p<0.001 | 0.455 p<0.001 | − 0.286 p<0.001 | 0.305 p<0.001 | ||
| (− 0.382, − 0.225) | (0.383, 0.521) | (− 0.364, − 0.205) | (0.225, 0.382) | ||||
| M | 279 | − 0.224 p<0.001 | 0.516 p<0.001 | − 0.257 p<0.001 | 0.290 p<0.001 | ||
| (− 0.333, − 0.109) | (0.425, 0.597) | (− 0.364, − 0.144) | (0.179, 0.394) | ||||
| z(SMA/ht) | F | 512 | − 0.371 p<0.001 | − 0.093 p=0.035 | 0.069 p=0.119 | − 0.055 p=0.210 | |
| (− 0.443, − 0.294) | (− 0.178, − 0.007) | (− 0.018, 0.155) | (− 0.141, 0.031) | ||||
| M | 279 | − 0.277 p<0.001 | 0.111 p=0.064 | 0.059 p=0.323 | 0.119 p=0.048 | ||
| (− 0.382, − 0.165) | (− 0.006, 0.226) | (− 0.058, 0.176) | (0.001, 0.233) | ||||
| F | 512 | − 0.337 p<0.001 | − 0.065 p=0.139 | − 0.263 p<0.001 | − 0.175 p<0.001 | ||
| (− 0.412, − 0.258) | (− 0.151, 0.021) | (− 0.342, − 0.180) | (− 0.258, − 0.090) | ||||
| M | 279 | − 0.253 p<.001 | 0.112 p=0.061 | − 0.306 p<0.001 | − 0.075 p=0.212 | ||
| (− 0.359, − 0.139) | (− 0.005, 0.227) | (− 0.409, − 0.196) | (− 0.191, 0.043) |
p-value less than 0.01 shown in bold.
In the ‘Over-40’ cohort, all measures were more strongly and negatively correlated with age (Table 2). As in the younger cohort, SMA, , and were positively correlated with BMI and weight. SMA was positively correlated with height and was negatively correlated with height. was uncorrelated with height. was uncorrelated with BMI, and negatively correlated with height and weight, though the correlation did not reach significance in males (, ). in the older cohort was uncorrelated with height, weight, and BMI.
In supplemental analysis, we explored direct adjustment for BMI and weight without the use of regression. For the weight and BMI alternative measurements, SMA/BMI and SMA/wt were significantly lower in the ‘Over-40’ versus ‘Under-40’ cohort (Table S2), and both were negatively correlated with age, BMI, and weight in both cohorts (Table S2, Fig. S1). SMA/wt was negatively correlated with height, and SMA/BMI was positively correlated with height (Table S2). These results suggest that dividing SMA by BMI or weight directly would not be optimal.
Discussion
We analyzed two height-adjusted skeletal muscle area measures ( and ) and converted these into BMI-adjusted z-scores, assessing the correlation between each of these measures and age, height, weight, and BMI.
Allometric analysis confirmed that weight scales with height to the integer power of two, though the height coefficient for females (1.84) was further from the integer than males (2.07). Additionally, we found that L3 SMA scales with height to the integer power of one, and not two as has been commonly used. Once again, the coefficient for females (1.33) was further from the integer than males (1.02). These deviations explain why the height adjustment in does not fully remove the correlation with height in females.
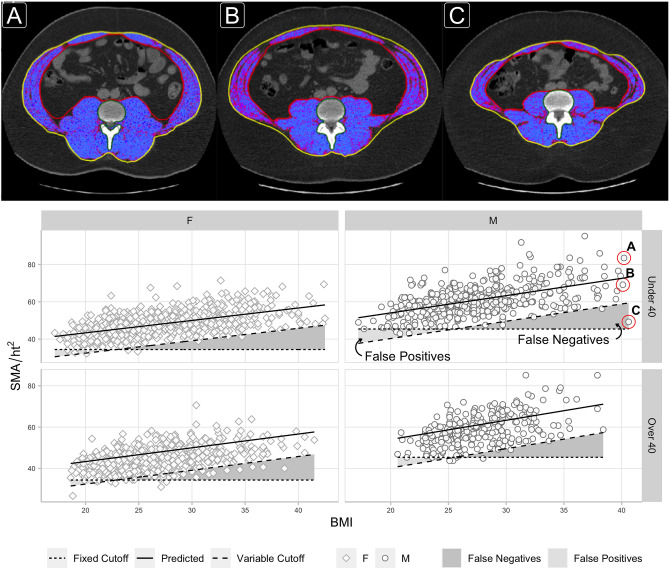
Following current practice, using a power of two to normalize SMA for height produces a measure () that retains a significant negative correlation with height in both males () and females (), resulting in cutoff values that are biased towards identifying sarcopenia in taller individuals (Fig. 1). This measure also retains a significant positive correlation with BMI in both males () and females (), and because cutoff values are constant for all BMI values, the cutoffs are additionally biased to identify sarcopenia in those with low BMI (Fig. 3). Specifically, these ‘fixed’ cutoffs appear prone to falsely identifying sarcopenia in low BMI individuals with muscle mass between − 1 to − 2SD of what would be expected relative to their BMI (false positives), while failing to identify sarcopenia in high BMI individuals with muscle mass more than − 2SD below what would be expected relative to their BMI (false negatives) (Fig. 3). A similar argument could be made against using ‘fixed’ cutoffs computed from (Fig. S2). Conversely, ‘variable’ cutoffs based on the z-score increase linearly with BMI, following the natural distribution of muscle mass with BMI, and better identify low muscle mass at any height and BMI.
Figure 3.
L3 axial CT images highlighting skeletal muscle area for three males of similar age (28–29) and BMI 40.1–40.6, but different scores (A = 1.56, B = − 0.51, C = − 3.47) are compared. The third individual (C) has a muscle area more than 3 s.d. below the mean value expected for a BMI of 40. He would be classified as not sarcopenic using the fixed cutoff, but would be sarcopenic using the variable (z-score) cutoff. Scatter plots show L3 skeletal muscle area divided by height-squared () versus BMI, split by sex and cohort. Lines overlaid for (1) the mean value predicted by our linear regression model (solid line), (2) previously reported (Derstine, 2018)15 sarcopenia ‘fixed cutoff’ values (dotted line), and (3) bmi-adjusted ‘variable cutoff’ values (dashed line) computed as two s.d. below the predicted mean. Regions of ‘False Positives’ and ‘False Negatives’ sarcopenia diagnosis are shown based on the difference between the ‘fixed’ and ‘variable’ cutoffs.
Based on our analysis, we suggest using and its z-score in sarcopenia analyses for several reasons. First, using a power of one to normalize SMA for height () results in a measure that is minimally correlated with height. Second, subtracting the regression model’s predicted mean value and dividing by the standard deviation produces the score that is uncorrelated with BMI (by design). Third, the score is negatively correlated with age in the ‘Over-40’ cohort, which is desirable, as it ensures that sarcopenia prevalence increases with age, as would be expected. Fourth, since z-scores have mean 0 and standard deviation 1, they are quite easy to interpret—values above zero indicate ‘more muscular’ BMI and values below zero indicate ‘less muscular’ BMI. Furthermore, they can be directly compared since they use common units of standard deviations. Finally, the sarcopenia cutoff value is simply − 2.0 according to the EWGSOP definition, although optimal z-score cutoff values should be investigated further. Individual studies using the same z-score equation could report whether the − 2.0 cutoff was optimal for a given cohort and clinical outcome.
The score is quite simple to compute in practice (for simplicity, the coefficients in the following equation have been rounded). For each subject, i (sex = 1 if male, and 0 if female):
compute the (cm2/m): ,
compute the predicted mean from BMI and sex: ,
compute the sex-specific standard deviation:
compute the z-score: .
For those who prefer to use the existing height-squared SMA normalization, computing the score would be similar:
compute the (cm2/m2): ,
compute the predicted mean from BMI and sex: ,
compute the sex-specific standard deviation: ,
compute the z-score: .
Differences between sarcopenia cutoffs derived in different cohorts have been attributed to disease, ethnicity, or nationality while simultaneously reporting large differences in BMI and/or age2,4,5,9,15,33. Comparing sarcopenia cutoff values derived from studies using different age and BMI distributions is a flawed premise when both age and BMI are correlated with the metric used to define sarcopenia. Age and BMI distributions naturally vary between populations and study cohorts, and this is desirable. However, it is undesirable to require different sarcopenia cutoffs for every disease, ethnicity, or nationality, particularly if those differences can be explained by anthropometric factors. Indeed a visual examination of versus BMI, split by self-reported race (Fig. S3), did not suggest that adjustment for race is necessary after adjusting for height and BMI. In other words, observed differences between cohorts should not be attributed to racial or ethnic differences without first controlling for age, sex, height, and BMI. To that end, we suggest that unbiased comparisons between cohorts of different age, sex, race, height, and BMI instead be made using z-scores calculated from our equations.
This study has important limitations. These equations do not apply to SMA measured at other vertebra levels or measured via other imaging modalities, they apply to CT-derived L3 SMA only. They also have not been tested for validity in children under age 18. While we hope that these equations accurately quantify the relationship between SMA, sex, height, and BMI in healthy, young adult (age 18–40) populations around the world, we cannot be sure, and this should be investigated further. The − 2.0 z-score cutoff has not been tested against clinical outcomes. We used non-contrast-enhanced CT scans; previous research has shown that IV contrast has a clinically insignificant effect on SMA12,33,34.
We propose that this z-score method, using these equations, be used as a consistent global framework for measuring and reporting height- and BMI-adjusted sarcopenic low L3 skeletal muscle area cutoffs across different cohorts.
Methods
Study cohort
We retrospectively studied persons who underwent CT scans at the University of Michigan as part of evaluation for kidney donation between 1999 and 2017. We have previously studied subsets of these kidney donor candidates as a healthy reference population12,15.
Patient age, sex, height (m), and weight (kg) were obtained from their medical record proximal to the date of evaluation for kidney donation, and the month and year of the evaluation appointment was recorded35. Candidates were included if they had a non-contrast-enhanced series CT scan performed as part of evaluation for kidney donation, with a complete fascia boundary visible in the display field of view, had age, sex, height, and weight recorded in their electronic medical record, and were medically, surgically, and psycho-socially approved for donation.
Body mass index (BMI) was computed and categorized into groups according the World Health Organization International Classification standard36. Self-reported race, unavailable for 31% of the cohort, was not specifically analyzed, however, it was used in a visual evaluation of the final z-score (Fig. S3).
CT imaging was extracted for 1849 total donor candidates between the ages of 18 and 68 scanned using the GE ‘Standard’ reconstruction algorithm at 120 kVp and 5mm slice thickness in a Discovery or LightSpeed scanner. Tube current was automatically modulated in proportion to body mass.
The study was split into two cohorts; the ‘young adult’ candidates age 18–40 (‘Under-40’) and the candidates over age 40 (‘Over-40’).
CT image processing
After being transferred into a spatial database, CT images were processed using Analytic Morphomics, a semi-automated image analysis method that has been previously described12,37. A combination of automated and user-guided algorithms written in matlab (The Mathworks Inc, Natick, MA) identified vertebral bodies. Next, the outer abdominal fascia and inner muscle wall were identified to create enclosed regions of interest, which were confirmed by multiple trained researchers.
SMA was measured as the area of pixels between − 29 and +150 Hounsfield Units (HU) in the region of interest on the axial slice nearest the inferior aspect of the third lumbar vertebral body (L3) as previously validated12,33,38.
Statistical methods
Male and female demographics, CT parameters, and skeletal muscle measurements were summarized separately as mean and standard deviation (s.d.) for continuous variables and proportion for categorical variables. Means were compared using two-tailed t-tests assuming unequal variance and proportions were compared using the Chi-squared test.
Using the ‘Under-40’ cohort, sex-specific allometric regression models were fit to find the optimal integer coefficient for the relationship between weight versus height, and SMA versus height. The allometric model was transformed into the logarithmic form and linear regression was used to find the coefficient (optimal power of height)39. The resulting coefficient rounded to 1 as the nearest integer in both males and females, ergo two height-adjusted skeletal muscle indices were computed for comparison: the ‘standard’ SMI using a height power of two (), and an alternative using a height power of one (), as suggested by allometric modeling.
For completeness, a BMI-adjusted measure (, mathematically equivalent to ), and a weight-adjusted measure () were computed and analyzed, with results included in supplemental materials (Tables S1, S2, Fig. S1).
To describe the relationship between BMI and height-adjusted SMA in a young, healthy adult cohort, two multiple linear regression models were constructed using the ‘Under-40’ cohort; one for and one for . In each model, the height-adjusted index (I) was the response, while BMI, male sex, and their interaction were predictors, allowing for different intercept and slope by sex, e.g., .
Finally, each index was converted into a z-score with mean zero and standard deviation one by subtracting the expected mean (predicted value from the regression equation) and dividing by the sex-specific ‘Under-40’ standard deviation (residual standard error from the regression equation), e.g., .
The final regression equations were as follows (sex = 1 if male, and 0 if female):
, for
, for
Sex and BMI explained 60% of the variation in and 73% of the variation in (Adjusted ), with residual standard errors of 5.4/6.9 (Female/Male) and 8.8/11.4 (Female/Male) respectively, and all model coefficients statistically significant (p ≤ 0.01).
Bivariate scatter plots and Pearson correlation coefficients were used to assess the linear association between each skeletal muscle measure and age, BMI, height, and weight separately for males and females and each cohort.
An alpha level of 0.01 was used to determine statistical significance. All statistical tests were performed in R version 3.5.340, using the package ‘ggplot2’41 for data visualization.
Ethical approval and informed consent
This study was approved by the Institutional Review Board of the University of Michigan. All methods were performed in accordance with the relevant guidelines and regulations of the United States. Because existing CT scans were used retrospectively, the requirement for informed consent was waived by the Institutional Review Board of the University of Michigan.
Supplementary information
Acknowledgements
The authors would like to thank Rebecca Goulson and Nidhi Shah for their help with extracting CT scan measurements.
Author contributions
B.D., S.H., G.S. and S.W. designed the study. N.W. and S.H. developed the Analytic Morphomics processing code. B.D. and B.R. performed CT processing. B.D. collected and interpreted the data, performed the data analyses, and wrote the manuscript. All authors reviewed the manuscript.
Data availibility
The datasets generated during and/or analyzed during the current study are available from the corresponding author upon reasonable request.
Competing interests
Brian A Derstine, Brian E Ross, Nicholas C Wang, and Grace L Su declare that they have no conflict of interest. Sven A Holcombe and Stewart C Wang are listed as inventors on a US Patent for Analytic Morphomics (#US 20140064583 A1). Stewart C Wang holds equity interest in Applied Morphomics, Inc.
Footnotes
Publisher's note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
is available for this paper at 10.1038/s41598-020-79471-z.
References
- 1.Cruz-Jentoft AJ, et al. Sarcopenia: European consensus on definition and diagnosis: Report of the European working group on sarcopenia in older people. Age Ageing. 2010;39:412–23. doi: 10.1093/ageing/afq034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Prado CM, et al. Prevalence and clinical implications of sarcopenic obesity in patients with solid tumours of the respiratory and gastrointestinal tracts: A population-based study. Lancet Oncol. 2008;9:629–635. doi: 10.1016/s1470-2045(08)70153-0. [DOI] [PubMed] [Google Scholar]
- 3.Prado CM, et al. Sarcopenia as a determinant of chemotherapy toxicity and time to tumor progression in metastatic breast cancer patients receiving capecitabine treatment. Clin. Cancer Res. 2009;15:2920–6. doi: 10.1158/1078-0432.ccr-08-2242. [DOI] [PubMed] [Google Scholar]
- 4.Van Vledder M, et al. Body composition and outcome in patients undergoing resection of colorectal liver metastases. Br. J. Surg. 2012;99:550–557. doi: 10.1002/bjs.7823. [DOI] [PubMed] [Google Scholar]
- 5.Martin L, et al. Cancer cachexia in the age of obesity: Skeletal muscle depletion is a powerful prognostic factor, independent of body mass index. J. Clin. Oncol. 2013;31:1539–47. doi: 10.1200/jco.2012.45.2722. [DOI] [PubMed] [Google Scholar]
- 6.Prado CM, Heymsfield SB. Lean tissue imaging: A new era for nutritional assessment and intervention. J. Parenter. Enteral Nutr. 2014;38:940–53. doi: 10.1177/0148607114550189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Reisinger KW, et al. Loss of skeletal muscle mass during neoadjuvant chemoradiotherapy predicts postoperative mortality in esophageal cancer surgery. Ann. Surg. Oncol. 2015;22:4445–4452. doi: 10.1245/s10434-015-4558-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Vugt J, et al. Systematic review and meta-analysis of the impact of computed tomography-assessed skeletal muscle mass on outcome in patients awaiting or undergoing liver transplantation. Am. J. Transplant. 2016;16:2277–2292. doi: 10.1111/ajt.13732. [DOI] [PubMed] [Google Scholar]
- 9.Zhuang, C.-L. et al. Sarcopenia is an independent predictor of severe postoperative complications and long-term survival after radical gastrectomy for gastric cancer: Analysis from a large-scale cohort. Medicine95 (2016). [DOI] [PMC free article] [PubMed]
- 10.Shachar SS, et al. Skeletal muscle measures as predictors of toxicity, hospitalization, and survival in patients with metastatic breast cancer receiving taxane-based chemotherapy. Clin. Cancer Res. 2017;23:658–665. doi: 10.1158/1078-0432.CCR-16-0940. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Werf A, et al. Percentiles for skeletal muscle index, area and radiation attenuation based on computed tomography imaging in a healthy caucasian population. Eur. J. Clin. Nutr. 2017;72:282. doi: 10.1038/s41430-017-0034-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Derstine BA, et al. Quantifying sarcopenia reference values using lumbar and thoracic muscle areas in a healthy population. J. Nutr. Health Aging. 2017;21:1–6. doi: 10.1007/s12603-017-0983-3. [DOI] [PubMed] [Google Scholar]
- 13.Englesbe MJ, et al. Sarcopenia and mortality after liver transplantation. J. Am. Coll. Surg. 2010;211:271–8. doi: 10.1016/j.jamcollsurg.2010.03.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Hamaguchi Y, et al. Proposal for new diagnostic criteria for low skeletal muscle mass based on computed tomography imaging in asian adults. Nutrition. 2016;32:1200–1205. doi: 10.1016/j.nut.2016.04.003. [DOI] [PubMed] [Google Scholar]
- 15.Derstine BA, et al. Skeletal muscle cutoff values for sarcopenia diagnosis using t10 to l5 measurements in a healthy us population. Sci. Rep. 2018;8:11369. doi: 10.1038/s41598-018-29825-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kang DO, et al. Prognostic impact of low skeletal muscle mass on major adverse cardiovascular events in coronary artery disease: A propensity score-matched analysis of a single center all-comer cohort. J. Clin. Med. 2019;8:712. doi: 10.3390/jcm8050712. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Stamler J, et al. Low risk-factor profile and long-term cardiovascular and noncardiovascular mortality and life expectancy: Findings for 5 large cohorts of young adult and middle-aged men and women. JAMA. 1999;282:2012–2018. doi: 10.1001/jama.282.21.2012. [DOI] [PubMed] [Google Scholar]
- 18.Janssen I, Heymsfield SB, Ross R. Low relative skeletal muscle mass (sarcopenia) in older persons is associated with functional impairment and physical disability. J. Am. Geriatr. Soc. 2002;50:889–896. doi: 10.1046/j.1532-5415.2002.50216.x. [DOI] [PubMed] [Google Scholar]
- 19.Ogden CL, et al. Prevalence of overweight and obesity in the united states, 1999–2004. JAMA. 2006;295:1549–1555. doi: 10.1001/jama.295.13.1549. [DOI] [PubMed] [Google Scholar]
- 20.Geiger AM, Castellino SM. Delineating the age ranges used to define adolescents and young adults. J. Clin. Oncol. 2011;29:e492–e493. doi: 10.1200/JCO.2011.35.5602. [DOI] [PubMed] [Google Scholar]
- 21.Hingson RW, Heeren T, Edwards EM, Saitz R. Young adults at risk for excess alcohol consumption are often not asked or counseled about drinking alcohol. J. Gen. Intern. Med. 2012;27:179–184. doi: 10.1007/s11606-011-1851-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Cruz-Jentoft AJ, et al. Sarcopenia: Revised European consensus on definition and diagnosis. Age Ageing. 2018;48:16–31. doi: 10.1093/ageing/afy169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Cawthon PM, et al. Cutpoints for low appendicular lean mass that identify older adults with clinically significant weakness. J. Gerontol. A Biol. Sci. Med. Sci. 2014;69:567–75. doi: 10.1093/gerona/glu023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Quetelet LAJ. A Treatise on Man and the Development of his Faculties. Edinburgh: W. and R. Chambers; 1842. [DOI] [PubMed] [Google Scholar]
- 25.Keys A, Fidanza F, Karvonen MJ, Kimura N, Taylor HL. Indices of relative weight and obesity. J. Chronic Dis. 1972;25:329–43. doi: 10.1016/0021-9681(72)90027-6. [DOI] [PubMed] [Google Scholar]
- 26.Heymsfield SB, Heo M, Thomas D, Pietrobelli A. Scaling of body composition to height: Relevance to height-normalized indexes. Am. J. Clin. Nutr. 2011;93:736–40. doi: 10.3945/ajcn.110.007161. [DOI] [PubMed] [Google Scholar]
- 27.Baumgartner RN, et al. Epidemiology of sarcopenia among the elderly in New Mexico. Am. J. Epidemiol. 1998;147:755–63. doi: 10.1093/oxfordjournals.aje.a009520. [DOI] [PubMed] [Google Scholar]
- 28.Shen W, et al. Total body skeletal muscle and adipose tissue volumes: Estimation from a single abdominal cross-sectional image. J. Appl. Physiol. 2004;1985(97):2333–8. doi: 10.1152/japplphysiol.00744.2004. [DOI] [PubMed] [Google Scholar]
- 29.Newman AB, et al. Sarcopenia: Alternative definitions and associations with lower extremity function. J. Am. Geriatr. Soc. 2003;51:1602–1609. doi: 10.1046/j.1532-5415.2003.51534.x. [DOI] [PubMed] [Google Scholar]
- 30.Kim KM, Jang HC, Lim S. Differences among skeletal muscle mass indices derived from height-, weight-, and body mass index-adjusted models in assessing sarcopenia. Korean J. Intern. Med. 2016;31:643. doi: 10.3904/kjim.2016.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Studenski SA, et al. The fnih sarcopenia project: Rationale, study description, conference recommendations, and final estimates. J. Gerontol. A Biol. Sci. Med. Sci. 2014;69:547–58. doi: 10.1093/gerona/glu010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Chen LK, et al. Sarcopenia in Asia: Consensus report of the asian working group for sarcopenia. J. Am. Med. Dir. Assoc. 2014;15:95–101. doi: 10.1016/j.jamda.2013.11.025. [DOI] [PubMed] [Google Scholar]
- 33.Werf A, et al. Skeletal muscle analyses: Agreement between non-contrast and contrast ct scan measurements of skeletal muscle area and mean muscle attenuation. Clin. Physiol. Funct. Imaging. 2017;38:366. doi: 10.1111/cpf.12422. [DOI] [PubMed] [Google Scholar]
- 34.Fuchs G, et al. Quantifying the effect of slice thickness, intravenous contrast and tube current on muscle segmentation: Implications for body composition analysis. Eur. Radiol. 2018;28:2455. doi: 10.1007/s00330-017-5191-3. [DOI] [PubMed] [Google Scholar]
- 35.Hanauer DA, Mei Q, Law J, Khanna R, Zheng K. Supporting information retrieval from electronic health records: A report of university of Michigan’s nine-year experience in developing and using the electronic medical record search engine (emerse) J. Biomed. Inf. 2015;55:290–300. doi: 10.1016/j.jbi.2015.05.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Organization WH. Obesity: Preventing and Managing the Global Epidemic. Geneva: World Health Organization; 2000. [PubMed] [Google Scholar]
- 37.Krishnamurthy V, et al. Use of analytic morphomics of liver, spleen, and body composition to identify patients at risk for cirrhosis. Clin. Gastroenterol. Hepatol. 2015;13:360. doi: 10.1016/j.cgh.2014.07.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Aubrey J, et al. Measurement of skeletal muscle radiation attenuation and basis of its biological variation. Acta Physiol. 2014;210:489–497. doi: 10.1111/apha.12224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Kaitaniemi P. Testing the allometric scaling laws. J. Theor. Biol. 2004;228:149–153. doi: 10.1016/j.jtbi.2003.12.007. [DOI] [PubMed] [Google Scholar]
- 40.R Core Team. R: A Language and Environment for Statistical Computing. (R Foundation for Statistical Computing, Vienna, 2016). https://www.R-project.org/.
- 41.Wickham H. ggplot2: Elegant Graphics for Data Analysis. New York: Springer; 2009. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The datasets generated during and/or analyzed during the current study are available from the corresponding author upon reasonable request.