Numerical analysis of mechanical ventilation using high concentration medical gas mixtures in newborns

Abstract

When administered in relatively high concentrations the mechanical properties of inhaled gas can become significantly different from air. This fact has implications in mechanical ventilation where adequate respiration and injury to the lungs or respiratory muscles can worsen morbidity and mortality. Here we use an engineering pressure loss model to analyze the administration of medical gas mixtures in newborns. The model is used to determine the pressure distribution along the gas flow path. Numerical experiments comparing medical gas mixtures with helium, nitrous oxide, argon, xenon, and medical air as a control, with and without an endotracheal tube obstruction were performed. The engineering pressure loss model was incorporated into a model of mechanical ventilation during pressure control mode, a ventilator mode that is often used for neonates. Results are presented in the form of Rohrer equations relating pressure loss to flow rate for each gas mixture with and without obstruction. These equations were incorporated into a model for mechanical ventilation resulting in pressure, flow rate, and volume curves for the inhalation-exhalation cycle. In terms of accuracy, published values of airway resistance range from 50 to 150 cmH₂O/L per second for a normal 3 kg infant. With air, the current results are 55 to 80 cmH₂O/L per second for 0.3 to 5 L/min. It is shown that density through inertial pressure losses has a greater influence on airway resistance than viscosity in spite of relatively low flow rates and small airway dimensions of newborns. The results indicate that the high-density xenon mixture can be problematic during mechanical ventilation. On the other hand, low density heliox (a mixture of helium and oxygen) provides a wider margin of safety for mechanical ventilation than the other gas mixtures. The argon or nitrous oxide mixtures considered are only slightly different from air in terms of mechanical ventilation performance.

INTRODUCTION

Gases with proven or exploratory medical use in adults also have possible beneficial indications for children, including neonates.1,2,3,4 When administered in relatively high concentrations the mechanical properties of the inhaled gas (dynamic viscosity and density) can become significantly different from air.5 This physical fact has implications in mechanical ventilation where adequate respiration and injury to the lungs or respiratory muscles can worsen morbidity and mortality due to purely physical mechanisms.6 The challenges of mechanical ventilation are heightened when treating newborns.7,8,9,10,11,12 Lung injury in the neonatal lung is often provoked due to the immature morphology, inducing defective alveolar septation, impaired angiogenesis and pathologic extracellular matrix remodeling resulting in lung growth impairment. Furthermore, a recent Cochrane analysis noted that there is an urgent need for more information in full-term newborns to optimize oxygenation and ventilation during mechanical ventilation.13 Thus, it is interesting to assess the effects of the medical gas mixture on the mechanical ventilation of newborns.

Numerical analysis using in silico biomechanical models that consider the fluid mechanics and neonate morphology can add insight to mechanical ventilation through the ability to perform perfectly controlled and parameterized experiments. Numerical modeling can especially be helpful to understand the mechanical ventilation of neonates because in vivo data is difficult to obtain in this vulnerable population.14

Building on a previous paper reporting a numerical analysis of mechanical ventilation parameters with air in full-term newborns,15 in this paper we use an engineering pressure loss model16,17,18 to analyze the administration of medical gas mixtures. Only pressure control mode mechanical ventilation will be considered at it is most often used for neonates.9,13

Particular gases of interest in this context are helium, nitrous oxide, argon, and xenon, with medical air as a control case. Helium-oxygen mixtures (often referred to as heliox) are generally used to improve respiration,19 not as pharmaceutical agent. For example, the addition of heliox to the standard practice of permissive hypercapnia in neonates facilitated improvement in gas exchange, which allowed a decrease in ventilator settings and oxygen exposure, both of which are known to contribute to lung injury in this population.2 While one study found that nitrous oxide may be helpful for intubating preterm neonates, it was noted that a thorough evaluation of effectiveness and safety was needed.1 A neonatal rat model study indicated that argon and xenon (but not helium) provide neuroprotection against moderate and severe hypoxia-ischemic brain injuries likely via reduction of apoptosis.3 Indeed, due to its neuroprotective properties,20,21 xenon and argon have been considered as an additional treatment to cooling for neonatal encephalopathy. Broad et al.4 showed the potential of this therapy by administering 45–50% inhaled argon from 2–26 hours using a mechanical ventilator in a neonatal piglet model. Furthermore, cardiovascular safety of this argon therapy was assessed in newborn piglets in a study and found that argon ventilation did not result in a significant change of heart rate, blood pressure, cerebral oxygen saturation, electrocortical brain activity, or blood gas values.22 However, this study did not directly address ventilation safety. The chemically inert anesthetic xenon may provide a safe alternative to meet the growing concern that there are developmental problems associated with anesthetic exposure of the infant brain.23 Xenon-based anesthesia is not indicated for children; however, in a pilot trial, xenon-augmented sevoflurane anesthesia in school-aged children was shown to be feasible, and associated with decreased ephedrine requirements.24 Furthermore, there has been development of a recirculating xenon ventilator for newborn piglets to study neuroprotection25,26 that was employed in xenon clinical studies.27,28

MATERIALS AND METHODS

Design

The numerical analysis is based on the system shown schematically in Figure 1. As the inhalation cycle begins, the ventilator maintains a constant pressure (thus called Pressure Control Mode) at the Y-Piece after a prescribed rise time, thus driving gas flow into the external breathing circuit (here consisting of a filter and endotracheal tube) and into the lung starting at the trachea and terminating at the alveoli. As gas accumulates in the alveoli, the pressure there rises proportional to the lung compliance. The exhalation cycle begins when the ventilator opens the breathing circuit to the ambient through a valve that maintains constant positive pressure at the Y-Piece (positive end expiratory pressure, PEEP). The higher pressure in the lung now drives gas out of the lung, through the external breathing circuit, and the ventilator (including the PEEP valve) to the ambient. The numerical analysis consists of a calculation of the pressure changes occurring along the gas flow path during both inhalation and exhalation that is then used to calculate the flow rate. Representative pressure, flow rate, and volume cycles are shown in Figure 2.

Figure 1.

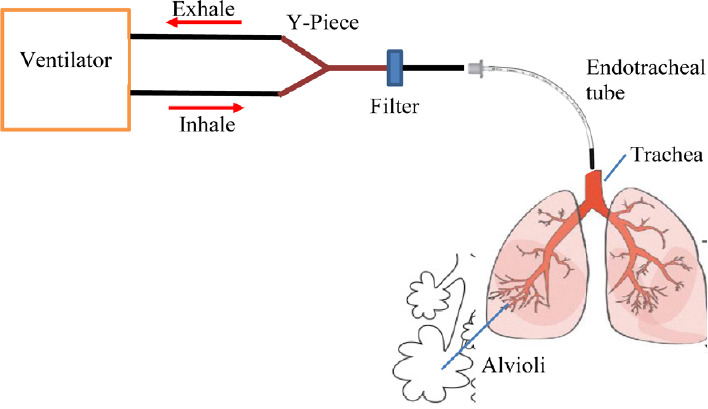
Schematic diagram of the flow path through the external breathing circuit and internal airways.

Figure 2.

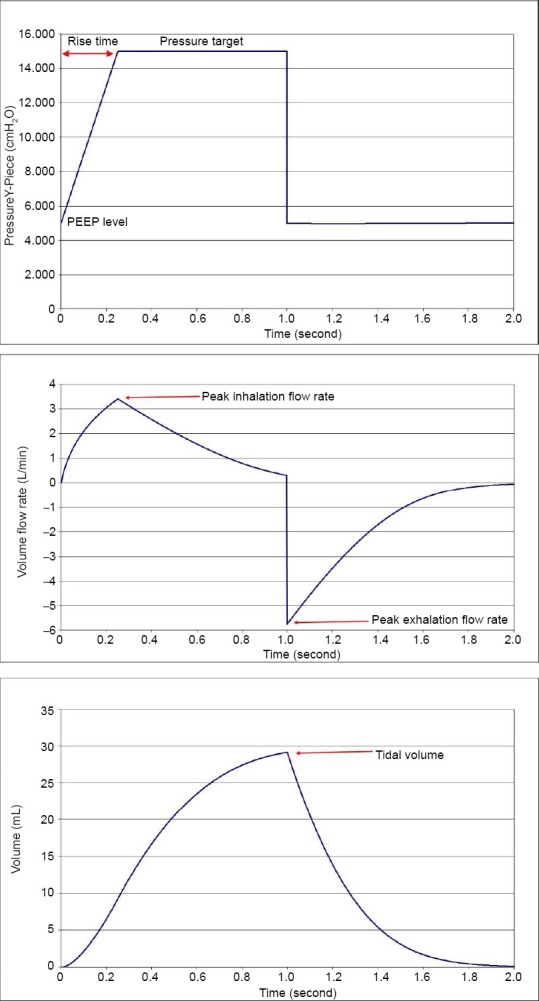
Pressure control mode ventilation patterns for Y-Piece pressure (top), flow rate (middle) and volume (bottom) as would be seen on a ventilator control screen.

Note: Input and output variables used in the simulations also are defined on the graphs. The rise time was fixed at 0.25 second for all of the simulations. 1 cmH₂O = 98 Pa.

Engineering pressure loss model

An engineering pressure loss model is used to determine the pressure distribution along the gas flow path. This model as applied to respiratory mechanics is described in a previous paper.17 This approach is formulated as a steady mechanical energy balance on flow and the pressure at any location, in this case the Y-Piece in the breathing circuit, compared to the alveolar pressure for both inhalation and exhalation. This equation can be calculated for any set of gas mixture property values and breathing circuit assumptions by employing an engineering approach; i.e., a summation of all the pressure losses in all of the straight flow conduits (called “major”) and all the components that change the velocity distribution (local acceleration or deceleration of the gas, are called “minor”). Assuming that the lungs airways are stiff and neglecting the effect of elevation changes, we can relate the pressure difference as shown in Equation (1),

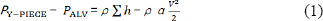
where P_Y-PIECE and V are the pressure and velocity at the Y-Piece, P_ALV the pressure in the alveoli (the velocity in the alveoli is taken to be zero), ρ is the gas density, and α is a coefficient related to kinetic energy that depends on the flow profile (for a blunt (turbulent) velocity profile α = 1, and for a parabolic (laminar) profile α = 2). The summation on the right-hand-side of Equation (1) represents the head loss of pressure, due to the resistance of the external elements and the pulmonary airways that is expanded in Equation (2).

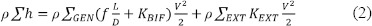
The first sum on the right hand of Equation (2) accounts for pressure losses in each lung generation (GEN). The major losses are due to straight flow in an airway generation of length L and diameter D and the minor losses due to geometrical variation (a bifurcation of the respiratory tract) and characterized by a coefficient K_BIF.

To characterize the flow, we use the non-dimensional Reynolds number that compares the effect of inertial forces over viscous forces.

where ρ is the density of the gas, μ its viscosity, v the velocity and d the diameter. In the lungs, the flow is considered to be turbulent when Re > 2000 and under this value, the flow is considered laminar.

For a laminar fully developed flow:

For a turbulent pipe flow, the Blasius correlation for smooth tubes is:

The minor loss coefficients, K_BIF, representing the effects of airway bifurcations were previously calculated based on computational fluid dynamics simulations for inhalation and exhalation and as a function of the local Re.17 Then the minor loss coefficient data were fit to curves to the formula:

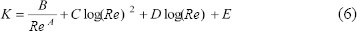
The minor loss coefficients were recalculated on the bases of the flow rate and the gas mixture of the flow entering the bifurcation. Thus, the use of computational fluid dynamics simulations provided an estimate of the complex flow fields within the respiratory tract.

The external breathing circuit consists of two elements each with its own minor loss coefficient (K_EXT): a filter and an endotracheal tube (ETT). For the ETT K_EXT was calculated based on the model given in Jarreau et al.29 The filter was also accounted for in the tubing circuit and modelled with a minor loss coefficient in the form of Equation (6) and listed in Table 1.16

Table 1.

Constants used in Equation (6) for determining bifurcation minor loss coefficients

	Minor loss coefficient equation constants
	A	B	C	D	E
Inhale trachea	0.2585	9.7695	0	0	0
Inhale bifurcating generations 1–9	0.0261	10.0247	0.8963	–3.3898	–0.9207
Exhale trachea	0.2912	6.081	0	0	0
Exhale bifurcating generations 1–9	0.0797	1.0735	0.2517	–0.9683	3.3347
Filter	1.531	1046700	34.0166	–277.0965	572.953

Neonate morphology model

There is very little neonate morphological data (e.g., airway dimensions) in the literature. For the analysis performed herein we adopted the morphology model previously used to study unsteady surfactant-laden liquid plug propagation in neonatal airways.30 Based on the Weibel representation of the lung as a symmetric dichotomous tree,31 the neonate model assumes that the trachea is the same dimensions as the 7^th generation of the adult model and continues the adult sub-tree to its conclusion at generation 23 resulting in a neonate model from generations 0–16. The dimensions of the model are given in Table 2. The constants A, B, C, D, E for Equation (6) are given in Table 1 for generations 0 to 9; after generation 9 the minor losses are considered negligible.

Table 2.

Neonate morphology model dimensions

Generation	Diameter (mm)	Length (mm)
0-Trachea	3.57	23.81
1	2.83	18.9
2	2.25	15
3	1.78	11.91
4	1.42	9.45
5	1.12	7.5
6	0.89	5.95
7	0.71	4.72
8	0.56	3.75
9	0.45	2.98
10	0.35	2.36
11	0.28	1.88
12	0.22	1.49
13	0.18	1.18
14	0.14	0.94
15	0.11	0.74
16	0.09	0.59

Obstruction model

A recognized hazard of prolonged endotracheal intubation is progressive airway occlusion resulting from deposition of secretions on the inner surface of the ETT.32 An obstruction model in the ETT was based on a numerical representation of the Rp50 resistor which is the smallest resistance value provided for use with an infant test lung (Michigan Instruments, Kentwood, MI, USA).33 The Rp resistors are simple orifice plates, a metal disc with a concentric hole in it that creates a purely inertial loss, such that the loss is a parabolic function of the flow rate.

Gas mixture properties and pressure equations

Property values of the gas mixtures given in Table 3 were calculated based on the methods described in the study by Katz et al.5

Table 3.

Gas mixture property values at 1 atm and 37°C

Gas	Viscosity (× 105 kg/(s·m))	Density (kg/m3)
Medical air (N2 78%/O2 22%)	1.876	1.135
Heliox (He 70%/O2 30%)	2.264	0.487
Nitrous oxide (N2O 50%/O2 50%)	1.659	1.404
Argon (Ar 50%/O2 50%)	2.152	1.414
Xenon (Xe 70%/O2 30%)	2.397	3.989

Note: 1 atm = 101.325 kPa.

For each gas mixture with an ETT of 3 mm, both with and without the obstruction model, Equation (1) was evaluated from the Y-Piece to the alveoli over a range of inhalation and exhalation flow rates. These data were fit using Excel (Microsoft, Redmond, WA, USA) to the quadratic form similar to a Rohrer equation,34

ΔP_Y-PIECE = A_GQ² + B_GQ      (7)

where Q is the inhalation or exhalation flow rate, and A_G and B_G are the fit constants specific to each gas on inhalation and exhalation, and with or without obstruction.

Numerical integration

The implementation in Excel of the pressure loss model as a ventilator is achieved by updating the pressure and flow over discrete time steps (2000 steps per ventilation cycle). In pressure control mode this is done by first updating the pressure target at the Y-Piece as would be controlled by the ventilator. Equation (7) is then solved for the updated flow rate based on the comparison of this fixed pressure to alveolar pressure from the previous time step. With a new value for Q the increased (or decreased in the case of exhalation) volume that accumulates in the lung is calculated, ΔVolume=QΔt, where Δt is the time step. Then the alveolar pressure can be updated based on this volume change and the compliance (C), ΔP _ALV=ΔVolume/C.

For exhalation, it is also necessary to calculate the pressure losses from the Y-piece of the breathing circuit through the ventilator, including the valve to produce PEEP.

ΔP_VENT = aρQ² + bμQ      (8)

For pressure in units of N/m², Q in L/min, ρ in kg/m³, μ in kg/(s·m)(×10⁵), α = 0.25 and b = 1.

Numerical experiments

Numerical experiments comparing the five medical gas mixtures with and without the ETT obstruction were performed. First, using the engineering pressure loss model, the fit constants for Equation (7) were determined. These results were then incorporated into the numerical integration of mechanical ventilation during pressure control mode, the ventilator mode often recommended to be used for neonates.9 The ventilation settings are for 30 breaths per minute, a pressure target of 15 cmH₂O, the PEEP level is 5 cmH₂O, and the inhalation:exhalation ratio is 1:1. The ETT diameter is 3 mm and the lung compliance is 3 mL/cmH₂O. The out parameters of interest are illustrated in Figure 2. They are peak inhalation flow rate, peak exhalation flow rate, tidal volume, and tidal volume retained.

RESULTS

Pressure drop

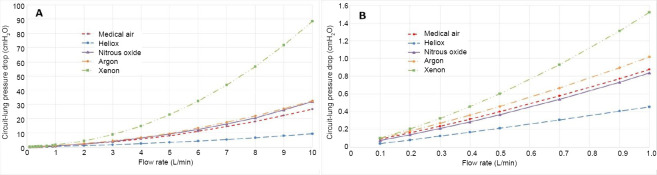
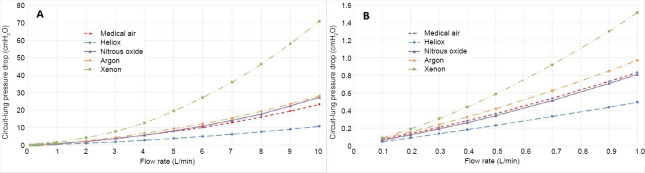
For each of the gas mixtures a Rohrer equation for pressure drop in the form of Equation (7) was calculated. These data for the unobstructed cases are shown in Figures 3 and 4. The fit coefficients in the form of Equation (7) for all of the cases are given in Table 4.

Figure 3.

Pressure drop for each gas mixture over the inhalation flow rate range from 0–10 L/min (A) and zoomed to the 0–1 L/min range (B).

Figure 4.

Pressure drop for each gas mixture over the exhalation flow rate range from 0–10 L/min (A) and zoomed to the 0–1 L/min range (B).

Table 4.

Fit coefficients for Equation (7) for each gas mixture with and without obstruction, for inhalation and exhalation

	Medical air		Heliox		Nitrous oxide		Argon		Xenon
	Without obstruction	With obstruction	Without obstruction	With obstruction	Without obstruction	With obstruction	Without obstruction	With obstruction	Without obstruction	With obstruction
Inhalation
AGi	20.352	439.65	5.2908	185.2	26.835	545.51	25.429	547.8	83.054	1556.7
BGi	59.364	59.364	38.944	38.944	43.727	43.727	66.825	66.825	34.333	34.333
Exhalation
AGe	15.183	434.48	6.3508	186.26	21.027	539.7	18.788	541.16	62.423	1536.1
BGe	75.372	75.372	42.277	42.277	53.949	53.949	87.679	87.679	68.894	68.894

Pressure control mode ventilation

Simulations of pressure control mode ventilation were performed for each gas mixture. Figure 5 shows the flow rate curves for each of the five gas mixtures superimposed for comparison over one inhalation-exhalation cycle. The key features of the curves are 1) a nonlinear increase in flow rate during the rise time of pressure (here 0.25 second as shown in Figure 2), 2) a decrease in flow rate during the constant pressure period during inhalation due to the rising back pressure in the lung, 3) the change in the ventilator to exhalation due to the opening of the exhaust PEEP valve (modeled as an instantaneous change to a negative exhalation flow), and 4) the nonlinear decrease in exhalation flow rate (decreasing due to the lower driving pressure in the lung as volume is decreased).

Figure 5.

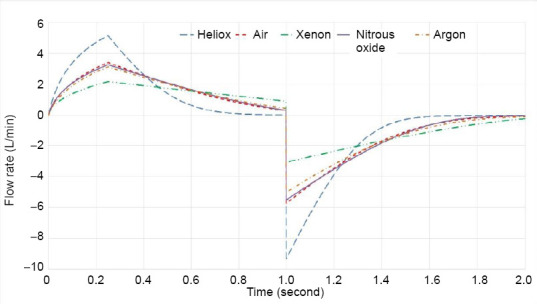
Flow rate curves for each of the five gas mixtures superimposed for one inhalation-exhalation cycle.

Figures 6 and 7 depict the effect of the obstruction on pressure control mode ventilation. First note, that the pressure is controlled by the ventilator in this mode and ideally (and as modelled numerically) is the same as for the non-obstruction case. However, this driving pressure is much less effective in creating gas flow with the added resistance of the obstruction; thus, the inhaled tidal volume decreases and incomplete exhalation results in retained volume. The output variables that are visually compared in Figures 5 and 7 for each test case are given quantitatively in Table 5.

Figure 6.

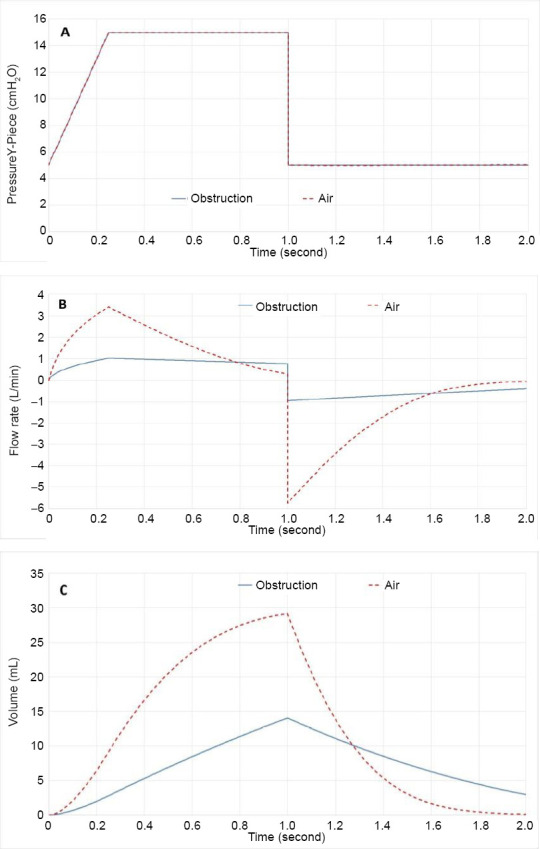
Pressure control mode ventilation patterns for Y-Piece pressure (A), flow rate (B) and volume (C) for air and superimposed the curves in the presence of the obstruction with air.

Figure 7.

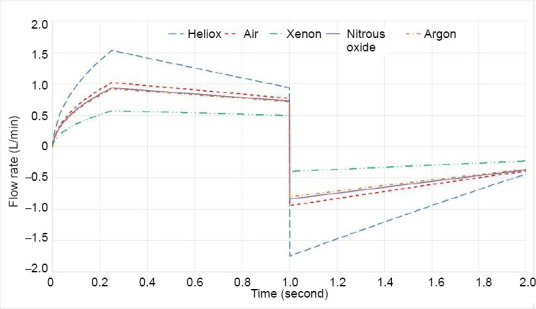
Flow rate curves for each of the five gas mixtures in the presence of the obstruction superimposed for one inhalation-exhalation cycle

Table 5.

Test case results in Figures 5 and 7

Gas mixture	Peak inspiratory flow (L/min)	Peak inspiratory flow with obstruction (L/min)	Peak expiratory flow (L/min)	Peak expiratory flow with obstruction (L/min)	Tidal volume (mL)	Tidal volume with obstruction (mL)	Tidal volume retained (mL)	Tidal volume retained with obstruction (mL)
Medical air	3.4	1	5.7	0.9	29.2	14.1	0.11	2.99
Heliox	5.2	1.5	9.3	1.7	30	19.7	0	1.72
Nitrous oxide	3.3	0.9	5.5	0.8	29.3	13	0.03	2.96
Argon	3.6	0.9	5.5	0.8	27.6	12.4	0.39	3.1
Xenon	2.2	0.6	3.1	0.4	25.1	8.3	0.61	3.07

DISCUSSION

In this paper, a numerical engineering pressure loss model has been used with a neonate lung morphology model to analyze the use of high concentration medical gas mixtures during mechanical ventilation in newborns. A key concept to glean from this work is the relative effects of gas mixture properties viscosity and density on ventilator performance. For laminar flow major losses are linearly proportional to the flow rate and to the viscosity. For turbulent flow the relationships are mathematically more complex and include density. Minor losses are largely inertial in nature, proportional to the density and the square of the flow rate. These facts about gas properties in association with the ventilator parameters and lung and breathing circuit characteristics determine the performance of the mechanical ventilation. Two broad categories of safety concerns related to mechanical ventilation are considered, lung injury related to the flow rate and adequate respiration based on the inhaled tidal volume and retained volume. In a previous paper15 parametric results considering several ventilation variables with air were presented such that only the effect of gas properties for a single control case are considered herein.

The use of pressure control mode normally avoids barotraumas by limiting the alveolar pressure. However, there is usually a higher peak inhalation flow rate compared to volume control mode that could pose problems because the strain rate due to high inspiratory flow has been shown to cause lung injury in an animal model35 while a reduction of inspiratory flow has been shown to provide lung protection.36 However, regarding adequate respiration, a key factor is to obtain adequate tidal volume that is more feasible due to the higher flow rates. The development of an obstruction in the ETT could pose a challenge to providing adequate tidal volume and respiration. Occlusion is a recognized hazard of prolonged endotracheal intubation resulting from deposition of secretions on the inner surface of the ETT. When volume-controlled ventilation is used, progressive ETT occlusion may be detected by monitoring the difference between peak and plateau airway pressures. In pressure control mode, however, inspiratory airway pressures are preset and thus cannot act as a warning indicator. Instead, changes in delivered tidal volumes may aid in the detection of ETT obstruction.37 Furthermore, the high tidal volume retained would eventually result in a less compliant lung. Thus, ventilation safety is considered in terms of the variables peak flowrates, tidal volume, and volume retained.

The pressure loss-flow curves for inhalation and exhalation, shown in Figures 3 and 4, respectively, indicate the important role of density in determining airway resistance. Xenon has the highest and heliox the lowest pressure drop, with air, nitrous oxide, and argon between the two extremes in the order of density. Also, note the nonlinear nature of the curves over the 10 L/min range in the top plots. In the bottom plots at low flow rates with the low density inertial losses are almost negligible making the effect of viscosity more pronounced, especially for heliox that has a relatively large viscosity; thus its curve is virtually linear. Regarding the difference between Figures 3 and 4, that pressure losses are somewhat less for exhalation. This occurs within the model because the minor losses for the bifurcations are incorporated for inhalation, but losses for the converging streams during exhalation are considered negligible. Table 4 that provides the Rohrer equation (7) fit coefficients that the inertial coefficient A is greater for inhalation than for exhalation except for heliox where they are approximately the same for the reason that inertial effects are small.

The flow curves for an inhalation-exhalation cycle in pressure control mode are shown in Figure 5. The obvious effect of the gas mixture is to reduce the peak inhalation and exhalation flow rates as gas viscosity and density increase, though the relative effect of each property is complicated. Heliox has the highest peak flow rate due to the lowest airway resistance that allows for faster filling and emptying of the lung. Thus in practice, there is room to increase the respiratory rate to achieve more overall ventilation if necessary. The tabulated results (Table 5) indicate that care should be taken when administering xenon in pressure control mode because the volume is 14% less than for air in the control case.

In Figure 6 the increased airway resistance caused by an obstruction is clearly visible and the influence of the obstruction increases with increased density as shown in Figure 7. This result follows the purely inertial form of the obstruction model. For example, in Table 4 only the inertial, A, term for the fits increases with the obstruction. From Table 5 it is clear that this level of obstruction would require corrective action, except perhaps when using heliox. Thus, this case illustrates the clear motivation for using heliox, its significant reduction in airway resistance, making mechanical ventilation possible with more margin for error or spontaneous breathing easier.

The use of heliox to reduce turbulent flow and, it follows, airway resistance, is well documented.38,39 At the relatively low flow rates for newborns the presence of turbulence is less likely. The largest flow rates present in pressure control ventilation mode occurred at the start of expiration. As shown in Table 6, for air and the other heavier gas mixtures Re is > 2000 and therefore in the turbulent range. Nevertheless, for heliox, even with the fact that its peak flow rate is the greatest, Re = 1415 is in the laminar range. Thus, from this narrow standpoint, the motivation for using heliox on newborns is confirmed.

Table 6.

Peak expiratory Re

Gas mixture	Peak expiratory flow (L/min)	ReETT at peak expiratory flow
Medical air	5.7	2439
Heliox	9.3	1415
Nitrous oxide	5.5	3292
Argon	5	2556
Xenon	3.1	3649

Note: ETT: Endotracheal tube; Re: Reynolds number.

In terms of overall accuracy, published values of airway resistance range from 50–150 cmH₂O/L per second for a normal 3 kg infant.7 For the control case with air, the current results are 55 to 80 cmH₂O/L per second for 0.3 to 5 L/min, respectively.

Results have been presented for pressure control mode because this ventilator mode is often recommended to be used for neonates.9 Also, the use of pressure control alleviates a critical need for flow measurement, to obtain volume, for volume based ventilation. This could be important when using medical gas mixtures other than air because the flow measurement is often dependent on the gas properties. However, the use of pressure control mode for neonates, especially pre-terms is an active area of study.40,41

There are several limitations to this study. There exists very limited morphological data for neonate lungs in the literature. Thus, the morphology model is somewhat speculative. The lung morphology is considered to be perfectly rigid, an assumption that is shown to cause errors as lung compliance increases, so it is expected that peak inhalation flow rates calculated in this study are higher than would be seen on the ventilator. The exhalation pressure drop, rise time, and general ventilator performance will depend on the make and model. The criterion of Re > 2000 used for turbulent flow is problematic because it is known that turbulence created upstream of the trachea is convected into the lung at lower Reynolds numbers.42,43,44 Indeed, there is no simple analytical expression available to assess the losses due to the convected turbulence. However, in engineering practice for pipe flow calculations with these kinds of assumptions are very common and the results are within well-accepted margins of error for design.

In summary, This paper has presented a numerical study of mechanical ventilation in newborns with the goal of providing insight into the effects of gas properties. It is shown that density through inertial pressure losses has a greater influence on airway resistance than viscosity in spite of relatively low flow rates and small airway dimensions of newborns. The results indicate that the high density xenon mixture could be problematic during mechanical ventilation. On the other hand, low density heliox provides a wider margin of safety for mechanical ventilation than the other gas mixtures. The argon and nitrous oxide mixtures considered are only slightly different from air in terms of mechanical ventilation performance.