Reaction Mechanism, Origins of Enantioselectivity, and Reactivity Trends in Asymmetric Allylic Alkylation: A Comprehensive Quantum Mechanics Investigation of a C(sp³)–C(sp³) Cross-Coupling

Abstract

We utilize quantum mechanics to evaluate a variety of plausible mechanistic pathways for the entirety of the catalytic cycle for asymmetric decarboxylative allylic alkylation of allyl β-ketoesters. We present a mechanistic picture that unites all current experimental observations, including enantioinduction, reaction rate, catalyst resting state, enolate crossover experiments, water tolerance, and the effects of solvation on inner- and outer-sphere mechanisms. Experiments designed to evaluate the fidelity and predictive power of the computational models reveal the methods employed herein to be highly effective in elucidating the reactivity of the catalytic system. On the basis of these findings, we highlight a computational framework from which chemically accurate results are obtained and address the current limitations of the decarboxylative asymmetric allylic alkylation reaction.

Graphical Abstract

INTRODUCTION

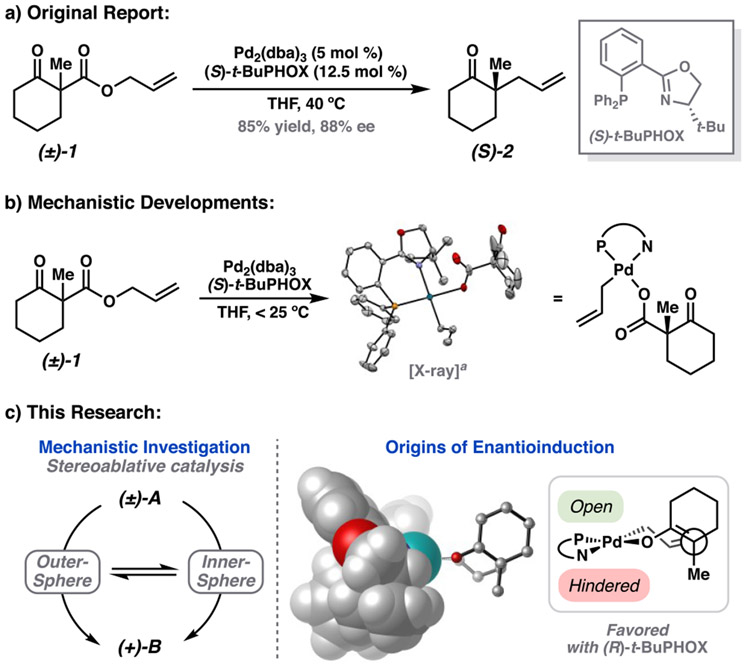
The construction of chiral all-carbon quaternary centers remains a forefront challenge in synthetic chemistry.¹ Over the years, our group has pursued the development of the decarboxylative asymmetric allylic alkylation reaction as a practical entry into these highly sought-after structural motifs. This approach has proved fruitful in asymmetric synthesis,² particularly in the early stage preparation of chiral building blocks. However, our efforts to further extend the scope of these transformations have highlighted limitations of the current catalytic systems.³ We recognize that a comprehensive mechanistic understanding is crucial in our ability to address these shortcomings and to realize general improvements.

Owing to the intricate interplay of several plausible inner- and outer-sphere processes, the unification of a comprehensive, stereochemically complete mechanistic hypothesis has remained elusive for the Pd(PHOX) system. In order to explore the mechanistic subtleties of the Pd(PHOX) system, our group carried out experimental studies geared toward evaluating the prevalence of inner- and outer-sphere pathways. Namely, crossover experiments involving deuterium labeling of both the allyl and enolate fragments ofthe allyl enol carbonate class of masked enolate synthons were explored.³ The distribution of cross products in these experiments was attributed to either an outer-sphere mechanism, in which C─C bond formation occurs through external nucleophilic attack by a free solvated enolate on an electrophilic π-allyl palladium species, or to an inner-sphere mechanism in which a Pd-bound enolate undergoes C─C bond formation via reductive elimination.⁴ Furthermore, the same system demonstrated remarkable tolerance to exogenous water, with reaction yields and enantioselectivity being largely unaffected.⁴ These results suggest that the presence of an unbound enolate with a conjugate acid pK_a significantly higher than that of water is unlikely. Given the tolerance to water, an inner-sphere mechanism for C─C bond formation is generally invoked for the Pd(PHOX) system.

In contrast, mechanistic studies with the bis-phosphine (R,R)-ANDEN-phenyl Trost ligand on similar allyl enol carbonate substrates by Trost and co-workers suggest alkylation occurs via an outer-sphere mechanism.⁶ As anticipated with an ionic outer-sphere mechanism, highly charge-stabilized “soft” enolates perform well in these systems.⁷ However, in contrast to the Trost methods, the PHOX catalytic manifold performs poorly and often provides low levels of enantioselectivity with stabilized enolate nucleophiles,^3,8 yet several PHOX systems excel with more basic “hard” enolates, as well as substrates that contain heteroatoms.⁹

Previous quantum mechanics (QM) investigations geared toward evaluating the possibility of an inner-sphere mechanism suggested this hypothesis to be plausible for a related PHOX system.¹⁰ While these investigations provided evidence for an initial mechanistic hypothesis, significant questions pertaining to the practical development of the catalytic system persist. For example, the mechanism by which decarboxylation (the rate limiting process) occurs in the allyl β-ketoester system remains unexplored. A thorough understanding of this process will support our efforts to develop systems with reduced catalyst loading and decreased reaction temperature—key considerations in the scalability of a catalytic transformation. Further convoluted by the complex interplay of several mechanistic pathways, the origin of enantioinduction has yet to be determined. Elucidation of the mechanism by which stereoselectivity is achieved will be central to a systematic approach to ligand design. Lastly, we aim to evaluate the current experimental findings, including water tolerance and crossover experiments, in the context of a thorough mechanistic picture.

Aided by recent experimental advances, including kinetic studies and characterization of intermediate complexes,⁴ we turn our attention to the synthetically valuable allyl β-ketoester class of substrates and the (R)-t-BuPHOX ligand as the basis for a comprehensive computational study (Figure 1a).³ To provide useful insight into factors underlying enantiomeric selectivity, very high quantum mechanical accuracy is required. Given this, we use this study as an opportunity to compare the efficacy of various modern computational methods (density functional theory and localized coupled-cluster theory) in the context of asymmetric Pd⁰/Pd^II catalysis.

Figure 1.

Previous research by the Stoltz group. (a) Original report of allyl β-ketoester substrate class.⁵ (b) Mechanistic developments.^{4 a}Crystal structure of the (S)-t-BuPHOX carboxylate complex (opposite enantiomer as used in this study). (c) Scope of this research.

A detailed QM investigation into each step of the reaction mechanism, oxidative addition, decarboxylation, and C─C bond formation, reveals a mechanistic picture that unites all current experimental observations, including enantioinduction, reaction rate, catalyst resting state, enolate crossover, water tolerance, and solvent effects on the interplay between inner- and outer-sphere pathways in the PHOX system. Experiments are carried out to explore the mechanistic hypotheses derived from the ab initio calculations. Lastly, we address the shortcomings of the present state-of-the-art catalyst systems and offer theory-based insight into future development.

COMPUTATIONAL METHODS

Density functional theory (DFT) geometry optimizations, energy, vibrational frequency, and coupled-cluster calculations were performed using ORCA version 4.1.2.¹¹ Geometry optimizations were carried out with the BP86 generalized gradient approximation (GGA) functional¹² with Becke-Johnson damped D3 dispersion corrections (herein referred to as D3).¹³ A mixed basis set was implemented, in which palladium is described by the small core LANL2TZ(f) basis set with the Hay–Wadt effective core potential (ECP),¹⁴ while the 6-31G(d) basis set was used on all other atoms. Key structures were optimized at various levels of theory and compared to crystallographic data to ensure that consistent results are obtained across multiple methodologies (see SI for details).

Triple-ζ quality single point calculations were carried out on all stationary points with a variety of density functionals, including BP86-D3,¹² B3LYP-D3,¹⁵ PBE0-D3,¹⁶ M06,¹⁷ and DSD-BLYP-D3¹⁸ (see SI for comprehensive list) with the def2-TZVP basis set¹⁹ on all atoms (including the small core def2-ECP²⁰ on palladium). Corrections for solvation (THF or otherwise as specified) were carried out for single point calculations with the implicit Conductor-like Polarizable Continuum Model (CPCM).²¹ Unless otherwise noted, all energies reported are G₂₉₈ values from single point calculations at the M06/def2-TZVP–CPCM(THF) level of theory on BP86-D3/LANL2TZ(f)–6-31G(d) optimized geometries with thermodynamic corrections applied from frequency calculations obtained at the optimization level of theory. The Quasi-RRHO method is applied to correct for the breakdown of the harmonic oscillator approximation for low frequency vibrations.²² All stationary points are characterized by the appropriate number of imaginary vibrational modes (zero for optimized geometries and one for transition states). Intrinsic reaction coordinate (IRC) analyses were carried out to ensure all transition states connect the appropriate starting materials and products. Molecular illustrations were made from CLYview.²³

Additional single point calculations were performed on all optimized structures with the domain based local pair natural orbital coupled-cluster (DLPNO-CCSD(T), “NormalPNO” settings unless otherwise noted) method as described by Neese and co-workers and as implemented in ORCA (further details included in the SI section).²⁴ The cc-pVTZ basis set is used on all atoms in the DLPNO-CCSD(T) calculations, with the SK-MCDHF-RSC effective core potential²⁵ on palladium. Throughout the text, free energies calculated from electronic energies at the DLPNO-CCSD(T)/cc-pVTZ–CPCM(THF) level of theory are provided in brackets next to the DFT (M06–CPCM(THF)) values for comparison.

RESULTS

Our investigation began with the experimental observation of the [(PHOX)Pd(η¹-allyl)(RCO₂)] complex (3) as the resting state of the catalyst (Figure 2). The structure of this unusual η¹-allyl complex was previously confirmed by X-ray crystallography while the solution phase behavior was studied by NMR spectroscopy.⁴ Importantly, 3 is competent in the reaction, and affords the ketone product 2 from β-ketoester 1 in similar yield and enantioselectivity to that obtained from the catalytic transformation. Also noteworthy is the thermal instability of 3, which readily effervesces gaseous carbon dioxide at ambient temperatures to afford the ketone product. Kinetic studies revealed first order rate dependence of this process in 3,⁵ with an overall rate constant measured to be 1.58 × 10⁻⁴ s⁻¹ (at 24 °C in THF-d₈).⁴ Given that loss of CO₂ is the rate-limiting step, the experimental ΔG^‡ of decarboxylation is calculated to be 22.6 kcal/mol.

Figure 2.

Pathways considered for oxidative addition to either 3 or 4 from 5.

Oxidative Addition.

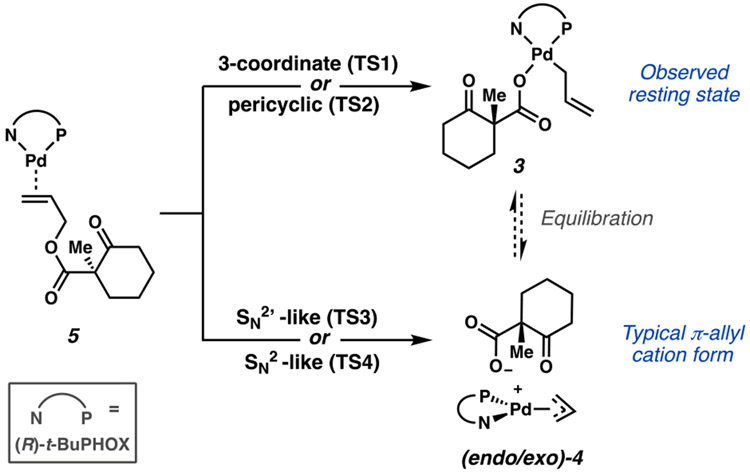
To better understand the role of the catalyst resting state (3) in the overall mechanistic picture, we first sought to examine the mechanism of oxidative addition of allyl β-ketoester 1 to the Pd⁰(PHOX) precatalyst. Oxidative addition of allyl acetate to palladium(0) complexes is generally represented as directly generating the [L_nPd(η³-allyl)](OAc) ion pair in situ in a reversible fashion.²⁶ Interestingly, we observed that the square planar η¹-allyl form of the catalyst is the exclusive resting state (3) (Figure 2). This prompted us to question whether oxidative addition proceeds through a unique mechanism in which 3 is yielded directly or if an analogous [(PHOX)Pd(η³-allyl)]⁺(RCO₂⁻) ion pair (4) is first formed followed by rapid equilibration to 3 (Figure 2). An understanding of the mechanics of oxidative addition is critical in the validation and interpretation of experimental findings because retention/inversion of the stereocenter at the leaving group site is often utilized as a mechanistic probe to infer the presence of inner- or outer-sphere pathways.^6,27

As noted previously, racemic starting material 1 is employed in the reaction. Nevertheless, as the chiral center is not directly involved but rather appended to the site of oxidative addition through freely rotatable bonds, we expect comparable energies of the diastereomeric transition states arising from both enantiomers of the starting material 1. As such, our initial explorations considered the (R) enantiomer of 1. For completeness, the relevant oxidative addition pathways studied for (R)-1 are also evaluated for (S)-1. A similar consideration is employed with regard to the orientation of the allyl fragment in the η³-bound form. Here, the prefix endo describes the η³-(allyl) conformer in which the apical carbon (i.e., C2) of the allyl group is cis to the t-Bu group of the PHOX ligand, and exo the trans isomer. Experimentally, the endo and exo isomers were found to be nearly identical in energy. Thus, both endo and exo geometries will be considered where relevant.

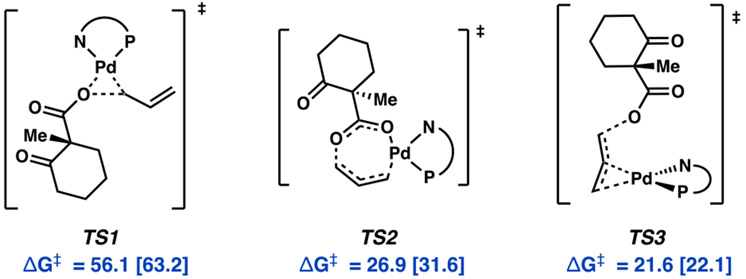
Starting from olefin-bound Pd⁰(PHOX) complex 5, a variety of transition states that achieve C─O bond cleavage were considered (Figure 3). Three- (TS1) and seven-membered (TS2) cyclic transition states^28-30 afford barrier heights greater than that of the experimentally known rate-determining step (ΔG^‡ = 22.6 kcal/mol).⁴ Oxidative addition via a syn conjugate displacement-type mechanism (TS3) offers a lower energy alternative, yet with a ΔG^‡ of 21.6 [22.1] kcal/mol, it remains unlikely.

Figure 3.

Initial transition states considered for oxidative addition. Free energies (M06) given in kcal/mol with free energies calculated at the DLPNO-CCSD(T) level in brackets.

Analogous to TS3, an anti displacement-type mechanism (TS4) via electrophilic addition to Pd⁰ was investigated and found to possess substantially lower barrier heights to that of the other pathways considered (Figure 4). Unlike TS3, in which C─O bond breaking occurs through the filling of σ*(C–O) by the olefin-based π*(C–C) orbital, TS4 achieves the same overall result with direct overlap between σ*(C–O) and the palladium d_x²_−y² -based HOMO.

Figure 4.

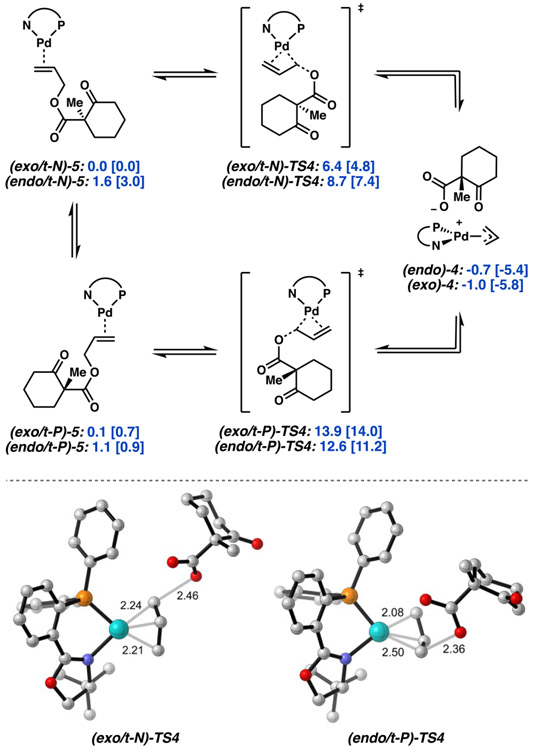
Free energy network encompassing all four isomeric forms of TS4. Free energies (M06) given in kcal/mol with free energies calculated at the DLPNO-CCSD(T) level in brackets.

Isomeric transition states are possible in which the displacement event occurs trans to either the nitrogen or phosphorus of the PHOX ligand to afford either the endo or exo isomer of 4. The abbreviations t-N and t-P refer to C─O bond breaking occurring trans to N and trans to P, respectively. Likewise, the prefix endo/exo describes the predisposition of the transition state to yield the endo/exo π-allyl 4. This nomenclature is extended to describe the orientation of the precursor olefin-bound complexes, 5. Here, we assume free equilibration between the isomers of 5. Therefore, we consider the apparent barrier height to be that of the lowest energy transition state from the lowest energy isomer of 5, (exo/t-N)-5.

From the corresponding olefin-bound palladium precursors 5, we found barrier heights of 13.8 [13.3] and 11.5 [10.3] for (exo/t-P)-TS4 and (endo/t-P)-TS4, respectively. Interestingly, considerably lower energy pathways were obtained for displacements trans to nitrogen, with barriers to (exo/t-N)-TS4 and (endo/t-N)-TS4 of 6.4 [4.8] and 7.1 [4.4] kcal/mol. In total, the lowest energy pathway of oxidation addition via direct displacement starts with (exo/t-N)-5 to form the ion pair product (exo)-4 via (exo/t-N)-TS4 with an apparent ΔG^‡ of 6.4 [4.8] kcal/mol and ΔG of −1.0 [−5.8] kcal/mol. A similar energetic preference for displacement trans to nitrogen is observed across several DFT methods. Additionally, as anticipated by experiment, the energy of (exo)-4 and (endo)-4 were found to be nearly identical, with the exo-isomer favored by 0.3 [0.4] kcal/mol. Henceforth, reference to TS4 will specifically refer to the lowest energy isomer, (exo/t-N)-TS4.

In summary, of all the oxidative addition pathways considered, olefin binding, followed by anti displacement (TS4) affords the lowest barrier height by a considerable margin. The displacement is stereospecific to inversion of chirality with respect to that of the leaving group, whereas the pathways involving a three-centered transition state (TS1), a 7-membered pericyclic transition state (TS2), or a syn conjugate displacement (TS3) would be expected to retain the configuration of the carboxylate leaving group (when substitution is present on the allyl terminus). We emphasize that the consideration of each mechanistic pathway is crucial in order to reliably interpret net inversion/retention of stereochemistry as a general mechanistic probe in the Tsuji–Trost reaction.

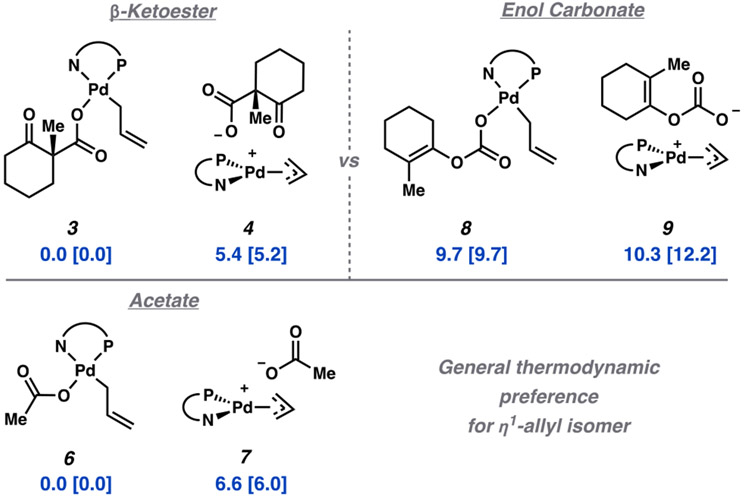
Furthermore, the two lowest energy pathways (direct/anti and conjugate/syn displacement) directly afford the ion pair 4 rather than 3 as the product of oxidative addition. These results suggest that the observed η¹-(allyl) catalyst resting state (3) is not the direct product of oxidative addition but is rather generated through a subsequent equilibration from ion pair 4. To realize the magnitude of the difference in energy between η¹-allyl 3 and ion pair 4, and whether a similar preference for 3 would be found computationally, we compare the calculated free energies of the two complexes. We arrive at the same result, in which [(PHOX)Pd(η¹-allyl)(RCO₂)] (3) is favored over the [(PHOX)Pd(η³-allyl)]⁺(RCO₂⁻) ion pair 4 by 5.4 kcal/mol (Figure 5). Single point calculations with several other density functionals give rise to similar results (ΔG = 4.6 to 9.3 kcal/mol), showing that this outcome is not an artifact of the DFT functional. A difference in free energy of 5.2 kcal/mol favoring 3 is obtained at the DLPNO-CCSD(T) level of theory, in agreement with the DFT values.

Figure 5.

Relative free energies (M06) in kcal/mol of constitutional isomers of η¹ and η³-bound allyl palladium complexes with masked enolate synthons (top). Analogous case for complexes derived from allyl acetate (bottom). Free energies calculated at the DLPNO-CCSD(T) level in brackets.

Interestingly, this trend appears not to be an extraneous effect of the β-ketocarboxylate leaving group but rather a potential feature of the PHOX ligand framework. Control experiments have been previously reported by our group in which the allyl β-ketoester was replaced with allyl acetate to similar effect.⁴ The corresponding [(PHOX)Pd(η¹-allyl)(OAc)] complex (6) was isolated and characterized by X-ray crystallography and solution phase NMR spectroscopy.⁴ Accordingly, the difference in free energies between 6 and ion pair 7 was calculated to be 6.6 [6.0] kcal/mol, favoring the η¹-allyl form.

Since computational results were in excellent agreement with experiment, we sought to explore these trends for the allyl enol carbonate substrate class,³¹ for which a crystal structure of the catalyst resting state has yet to be obtained. As with the β-ketocarboxylates, the analogous [(PHOX)Pd(η¹-allyl)-(ROCO₂)] (8) was similarly predicted to be favored over the [(PHOX)Pd(η³-allyl)]⁺(ROCO₂⁻) ion pair (9) (Figure 5). Calculations with the M06 density functional predict a 0.6 kcal/ mol preference for the η¹-allyl form, while DLPNO-CCSD(T) theory refines the energy difference to 2.5 kcal/mol, still favoring the η¹-allyl form. Accordingly, ³¹P NMR studies suggest the catalyst resting state may be an analogous η¹-allyl complex.⁴ Taking experimental and theoretical results into account, we anticipate that the η¹-allyl form similarly dominates the solution phase character of the catalyst resting state.

It is important to note that complexes 3, 4, 8, and 9, are constitutional isomers. Since the subsequent reaction yields identical palladium enolate intermediates, we note that the enol carbonate substrate is predicted to undergo a more exergonic reaction than the β-ketocarboxylate isomer by ca. 10 kcal/mol. While investigation into the mechanism of decarboxylation of the enol carbonates 8/9 lies outside the scope of this investigation, we postulate the following: If the resting state of the catalyst in the enol carbonate system is described by 8/9 (analogous to the carboxylates), and if the absolute energy of the barrier to decarboxylation is similar to that of 3, then a significantly higher reaction rate is anticipated. We therefore wish to highlight the design of the enolate synthon as one avenue by which future improvements may be achieved.

Decarboxylation.

We then sought to explore the mechanism through which decarboxylation occurs. Loss of CO₂ was experimentally determined to be the rate-limiting step of catalyst turnover.⁴ Thus, theory-guided optimization of the decarboxylation step may offer the practical benefit of increased reaction rate. In turn, this brings secondary advantages of potentially lower catalyst loading and reduced reaction temperature. Furthermore, certain classes of allyl β-carbonyl ester substrates, such as lactones and other particularly electron rich enolates, fail to decarboxylate or require higher reaction temperatures.³² In order to address these limitations and capitalize on opportunities for future development, a detailed mechanistic understanding of the decarboxylative pathways is required.

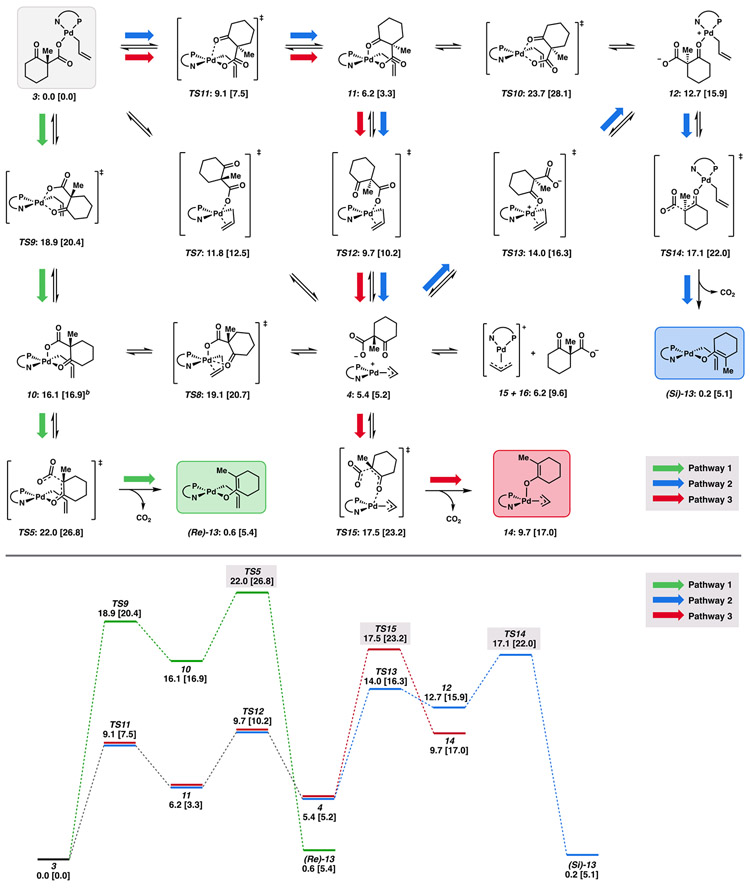
As noted previously, the minimum energy pathways in the first step of the mechanism through oxidative addition directly afford ion pair 4, rather than the catalyst resting state 3. To explore the interconnectivity between these intermediates, as well as potential decarboxylative pathways, we constructed the free energy network depicted in Scheme 1.

Scheme 1.

Free Energy Network of Intermediates from Oxidative Addition Products and Catalyst Resting State through Decarboxylation to Palladium Enolates^a

^aFree energy network from derived the (R) enantiomer of starting material 1. Relative free energies (in kcal/mol) obtained with M06/def2-TZVP–CPCM(THF), with energies at the DLPNO-CCSD(T)/cc-pVTZ–CPCM(THF) level of theory in brackets. Lowest energy conformers depicted. ^bFree energy of lowest energy conformer obtained with DLPNO-CCSD(T) corresponds to chair flip of the lowest energy conformer obtained with M06.

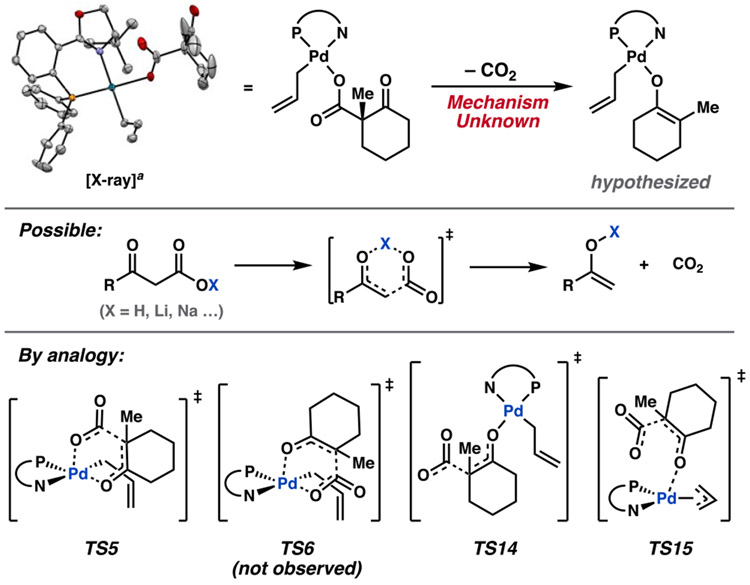
Deriving inspiration from the canonical 6-membered ring transition states in the decarboxylation of β-ketocarboxylic acids, we considered analogous cases for palladium (Figure 6). Two isomeric square pyramidal transition states may be envisioned: one in which the carboxylate group is apically bound to palladium (TS5), and another with an equatorially bound carboxylate (TS6). Both transition states require the square pyramidal precursors 10 and 11, respectively (Scheme 1). Sufficiently low energy pathways connecting resting state 3 to the necessary decarboxylation precursor 10 are found (Scheme 1).

Figure 6.

Decarboxylative transition states considered herein. ^aX-ray structure of one diastereomer of 3 with 50% probability ellipsoids (opposite enantiomer of PHOX ligand used in this study).⁴

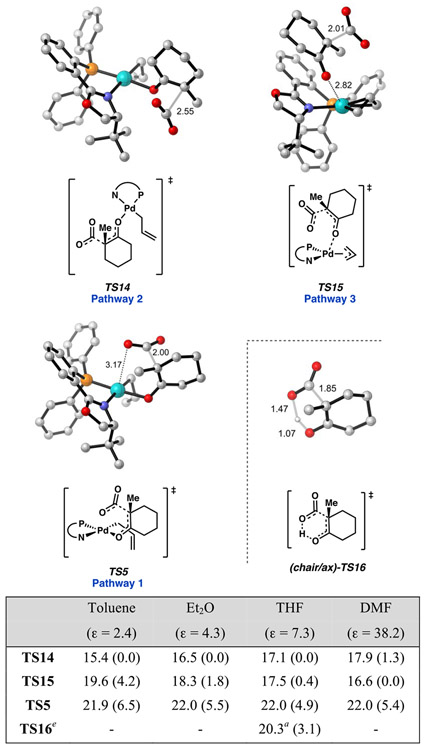
Decarboxylation is observed only through transition states in which the carboxylate group is poised axially on the 6-membered ring, whether it be in a boat ((boat)-TS5) or chair ((chair)-TS5). This may result from orbital overlap requirements, since the C–CO₂⁻ σ orbital experiences enhanced overlap with the π* of the ketone when occupying an axial position. While the chair conformers dominate the equilibrium geometries of 10, both M06 and DLPNO-CCSD(T) methods predict decarboxylation through (boat)-TS5 to be lower in energy than (chair)-TS5 by 1.8 and 2.8 kcal/mol, respectively, with corresponding apparent ΔG^‡ values of 22.0 and 26.8 kcal/mol (from resting state 3). We will henceforth refer to this sequence as decarboxylative pathway 1.

While the barrier to decarboxylation via (boat)-TS5 is quite low with respect to 10 (5.9–9.9 kcal/mol), decarboxylation directly from 11 is not observed. This result is not unexpected, since weak axial binding is generally observed in square planar d⁸ complexes (in the absence of π back bonding) by virtue of the filled, axially oriented metal-based d_z² orbital, here of slight Pd─O σ* character. With consideration of the role of the Pd^II center as a Lewis acid in promoting the decarboxylation, the weak axial binding of the ketone carbonyl in 11 to the metal center results in a complex that is poorly predisposed to decarboxylation. Furthermore, the LUMO of the square-planar/square-pyramidal d⁸ complexes are largely of metal-based d_x²_−y² character. As such, compared to 11, the equatorially bound carbonyl of 10 exhibits greater overlap with the Pd-based LUMO, allowing for more effective charge transfer to the electropositive metal center. This, combined with the greater positive partial charge of the palladium center in 10, due to the weakly bound axial carboxylate counterion, results in facile decarboxylation.

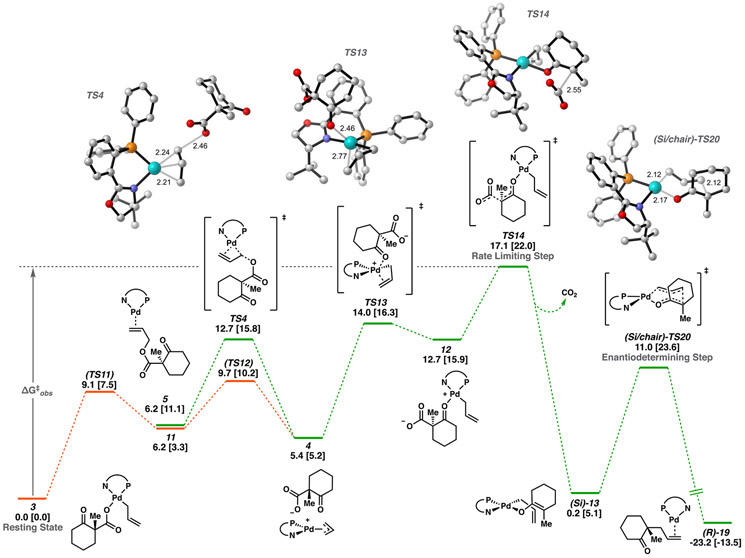
Analogous to the highly charge-separated cyclic form of 10, we were intrigued to find an acyclic variant, 12, as a stable intermediate on the potential energy surface. Given the complete potential energy surface (PES), we presume 12 equilibrates with resting state 3 through the lower energy TS11-11-TS12-4-TS13 pathway (Scheme 1). Here, the highest barrier is that of TS13 at 14.0 [16.3] kcal/mol, with 12 at 12.7 [15.9] kcal/mol higher in energy than 3.

As with 10, decarboxylation from 12 may then occur with the carboxylate oriented axially in either a chair or boat conformer, with the chair being lowest in energy (TS14). From 12, a barrier height of 4.4 [6.1] kcal/mol through TS14 is found. With respect to resting state 3, the overall barrier to decarboxylation through this pathway is 17.1 [22.0] kcal/mol. As with TS5, decarboxylation through this route directly affords the η¹-(allyl) O-bound palladium enolate (Si)-13 (a stable rotamer of (Re)-13). We will henceforth denote this sequence as decarboxylative pathway 2.

We next envisioned the possibility for decarboxylation to occur directly from the [(η³-allyl)Pd(PHOX)]⁺(RCO₂⁻) ion pair, 4. We will term this sequence decarboxylative pathway 3. In pathway 3, the overall barrier height through decarboxylation was found to be 17.5 [23.2] kcal/mol via the lowest energy conformer of TS15. Dissimilar to pathways 1 and 2, pathway 3 does not lead directly to (Re/Si)-13 but rather the η³-allyl isomer 14. The relevance of this detail becomes apparent below in the free energy networks through which C─C bond forming occurs (Scheme 2).

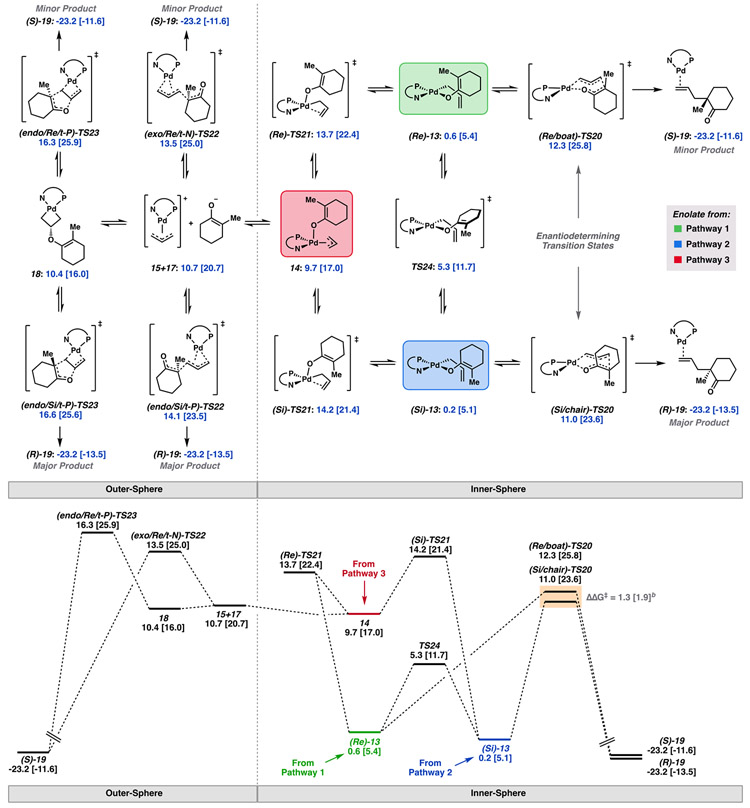
Scheme 2.

Free Energy Network Connecting Various C─C Bond Forming Pathways^a

^aFree energy network of postdecarboxylation intermediates and key C─C bond forming transition states. Free energies relative to 3 (in kcal/mol) obtained with M06/def2-TZVP–CPCM(THF), with energies at the DLPNO-CCSD(T)/cc-pVTZ–CPCM(THF) level of theory in brackets. Lowest energy conformers depicted. ^bΔΔG^‡ refined to 1.9 kcal/mol with TightPNO settings.

Loss of CO₂ is the overall rate-determining step for pathways 1, 2, and 3.

Of the three, we found pathway 2 to have the lowest barrier at 17.1 [22.0] kcal/mol; however, pathway 3 is comparable in energy, with a barrier height of 17.5 [23.2] kcal/mol, and the difference between these pathways is likely within the accuracy of DFT. Single point calculations with B3LYP-D3, PBE0-D3, and DSD-BLYP-D3 favor TS14 by 5.0, 2.0, and 0.4 kcal/mol, respectively; thus, we suggest an energetic preference for pathway 2. However, both pathways 2 and 3 remain mechanistically relevant under the reaction conditions.

Since the dipole moment of TS15 (19.7 D) is large compared to those of TS5 (12.2 D) and TS14 (13.6 D) (with M06/CPCM(THF)) we investigated the effect of solvation on the relative free energy barriers of the three pathways. Experimentally, high yields and enantioselectivities are observed across a variety of nonpolar aprotic solvents, while yields and enantioselectivities diminish in polar, aprotic solvents.³

Our initial efforts to assess solvent dependence were focused on solvent effects from single point calculations using the implicit Conductor-like Polarizable Continuum Model (CPCM) for geometries optimized in the gas phase. As stated above, we found net barrier heights of 17.1, 17.5, and 22.0 kcal/mol in THF (ε = 7.3) for decarboxylation pathways 2, 3, and 1, respectively. Control computation experiments were carried out in which optimizations of select intermediates were additionally carried out in THF (see SI), yielding similar results.

In addition to THF (ε = 7.3), we compared the barrier heights of the three decarboxylative pathways in the less polar solvents toluene (ε = 2.4) and diethyl ether (ε = 4.3), along with the more polar DMF (ε = 38.3). A clear trend arises in which a continuum with a reduced charge permittivity (ε < 8) favors pathway 2 (TS14), while pathway 3 (TS15) is preferred in solvents with higher dielectric constants (ε > 8) (Figure 7).

Figure 7.

Structures of rate-limiting transition states for decarboxylation pathways 1, 2, and 3 (top). Apparent barriers to decarboxylation (ΔG^‡ from 3) with ΔG^‡_rel in parentheses (bottom). Free energies reported in kcal/mol, calculated with M06/def2-TZVP–CPCM-(solvent) on gas phase geometries. ^aWith respect to the corresponding β-ketoacid (16-H).

Specifically, TS14 is 4.2 kcal/mol lower in energy than TS15 in toluene, compared to ΔΔG^‡ values of 1.8 and 0.4 kcal/mol (favoring TS14) in Et₂O and THF, respectively. In DMF, pathway 3 is predicted to be most favorable, with TS15 being 1.3 kcal/mol lower in energy than TS14. Furthermore, we found these trends to be a result of the simultaneous lowering of the barrier of TS14 and raising that of TS15 with decreasing solvent polarity. For example, ΔG^‡ of decarboxylation through TS14 with M06/def2-TZVP–CPCM(toluene) was found to be 15.4 kcal/mol, compared to 17.1 kcal/mol in THF. Meanwhile, the barrier height to TS15 is 19.6 kcal/mol in toluene, compared to 17.5 kcal/mol in THF. In conclusion, less polar solvents afford greater selectivity for pathway 2 while lowering the overall barrier height to decarboxylation through this pathway.

Since the polarizable continuum implicit solvation model considers electrostatics as the sole component of solute–solvent interaction, it may be inadequate to quantitatively capture all effects in the experimental solvent variations. We expect the general trends to remain qualitatively consistent with these findings and, thus, valuable for considerations in future reaction development.

As previously mentioned, decarboxylation was found experimentally to be the rate-determining step of catalytic turnover. NMR experiments determined the rate constant of decarboxylation of isolated 3 in THF-d₈ to be 1.58 × 10⁻⁴ s⁻¹ at 24 °C, corresponding to ΔG^‡ = 22.6 kcal/mol, which is consistent with the observed reaction time of 8–12 h. Indeed, this experimental observation affords an opportunity to compare the computational methods utilized in this study. Interestingly, all density functionals employed predict lower barriers than that of experiment. The most accurate values are obtained with the global hybrid PBE0-D3 and the spin-component-scaled double-hybrid DSD-BLYP-D3, with calculated barriers of 20.2 and 18.6 kcal/mol, respectively. The popular B3LYP-D3 density functional affords the least accurate ΔG^‡ of 16.5 kcal/mol. With a barrier of 17.1 kcal/mol, M06 also overestimates the rate of decarboxylation. Calculations with DLPNO-CCSD(T) provide a barrier height of 22.0 kcal/mol (k_calc = 4.65 × 10⁻⁴ s⁻¹) in good agreement with experiment and are the most accurate of the methods tested.

As racemic allyl β-ketoester 1 is employed in the stereoablative transformation, we carried out an analogous investigation for the (S) enantiomer of 1. A qualitatively similar situation is encountered. Details are included in the Supporting Information section.

Previous mechanistic studies found both the reaction yield and product enantioenrichment to be tolerant of super-stoichiometric equivalencies of water.⁴ This result formed the basis of evidence for an inner-sphere mechanism. Additionally, crossover experiments with deuterium labeling of both the allyl fragment and enolate were performed. Since nearly equal quantities of the crossed products were observed, the involvement of an outer-sphere mechanism in which a solvated free enolate is indifferent to attacking either the labeled or unlabeled η³-allyl complexes may be considered but is inconsistent with the water-stability of the system. As previously noted,⁴ these results may also be accommodated within the inner-sphere mechanistic hypothesis as well. This may be the case when the carboxylate/carbonate intermediates are sufficiently stable to undergo exchange prior to decarboxylation.

For the β-ketocarboxylate intermediate, this mechanism appears to take place. With a comparison of the difference in free energy between ion pair 4 and solvent separated ions 15 and 16, it is reasonable that free exchange between the carboxylate anion and palladium cation may occur at a rate superseding that of decarboxylation (Scheme 1). Both inner- and outer-sphere mechanisms may thus accommodate the results of the crossover experiments. Therefore, under these conditions, the observation of the enolate/allyl electrophile crossover is irrelevant to differentiation between the two mechanistic pathways.

With regard to water tolerance, we compared the barrier heights to decarboxylation for the conjugate acid of β-ketocarboxylate 16 (16-H) via the canonical 6-membered cyclic transition state to those of the palladium catalyzed pathways mentioned above. With ΔG^‡ = 20.3 [26.1] kcal/mol for TS16, the lowest apparent barriers to decarboxylation remain those involving the palladium catalyst (pathways 2 and 3). Furthermore, the lower pK_a of 16-H compared to water (ca. 10 units) affords a low effective concentration 16-H and, thus, a substantially slower reaction than that indicated from the relative ΔG^‡ from 16-H is expected. This offers an explanation as to why, in the Pd(PHOX) catalyzed systems, the decarboxylated but nonalkylated starting material is not observed. Hence, the experimentally observed water tolerance is well explained for this system.

C─C Bond Formation.

Given the postdecarboxylation palladium enolate intermediates 14, (Re)-13, and (Si)-13, we then sought to explore possible mechanisms for C(sp³)–C(sp³) bond formation. We further exploit this opportunity to revise and expand upon previous investigations in this area.¹⁰

First, inner-sphere mechanisms are considered. We envisioned four unique classes of transition states through which reductive elimination may occur: (i) a 3-membered ring transition state from a C-bound Pd enolate (TS17), (ii) a 5-membered cyclic transition state from a C-bound Pd enolate in which the carbon atom of the palladium enolate migrates to the γ-carbon of the allyl fragment (TS18), (iii) a different 5-membered ring transition state from an O-bound Pd enolate in which the carbon atom of the enolate bonds with the α-carbon of the allyl fragment (TS19), and (iv) a 7-membered cyclic transition state (TS20)³³ (Figure 8). Previous investigation suggests that the isomerization between oxygen and carbon-bound palladium enolates is facile.¹⁰ Thus, we initially focused on evaluating the C(sp³)–C(sp³) bond forming event.

Figure 8.

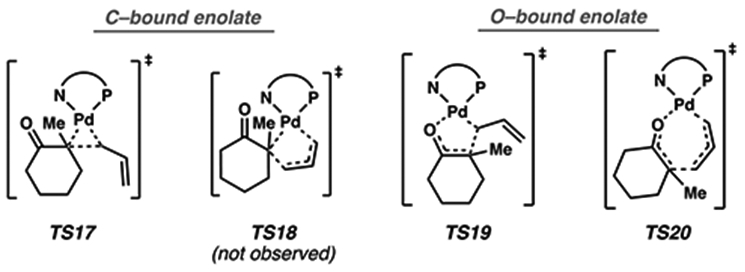
Inner-sphere C(sp³)–C(sp³) bond forming transition states considered.

Consistent with previous observations,¹⁰ three-centered transition state TS17 was calculated to be intractably high in energy, with an apparent barrier of 33.7 [46.4] kcal/mol. To determine whether a lower energy transition state could be found by expanding the ring size, we considered the vinylogous case of the 5-centered transition state (TS18). However, the planarity of the allyl fragment in the transition state mandates a still highly strained 5-membered ring. Despite our best efforts, a transition state fitting this connectivity was never found on the PES, and any transformation similar would likely be intractably high in energy. Next, we turn our attention to an alternative 5-membered cyclic transition state, TS19. Beginning from the O-bound palladium enolate 13, the barrier to TS19 is found to be 32.6 [46.3] kcal/mol and, thus, is likely not responsible for C─C bond formation.

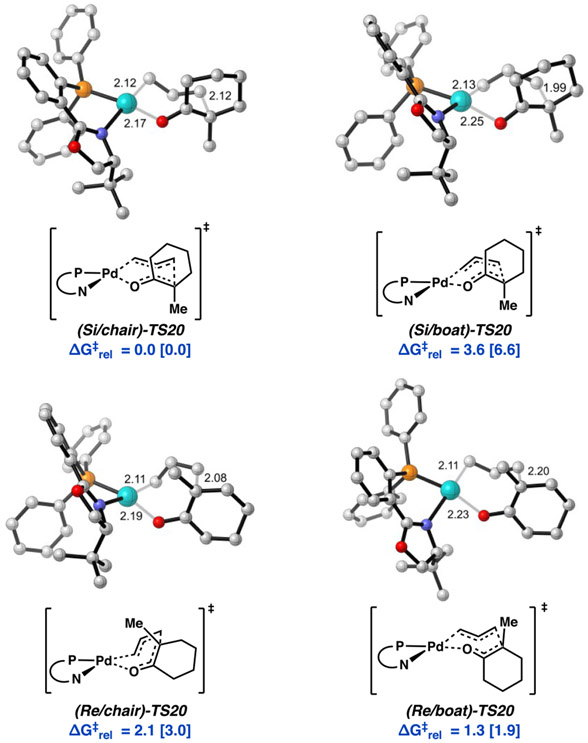
Lastly, we considered the fully expanded 7-membered cyclic transition state, TS20. Here, the 7-membered ring may adopt either a boat or chair conformer for both Re and Si faces of the enolate. Additionally, the 6-membered ring of the cyclohexanone enolate fragment may adopt two unique half chair conformers, giving rise to eight total transition states to be considered (Figure 9). Here, bond formations from the Re and Si faces afford the S and R enantiomers of product, respectively. The prefixes chair/boat refer to the conformation of the 7-membered ring, and axial/equatorial denote the half chair geometry of the cyclic enolate.

Figure 9.

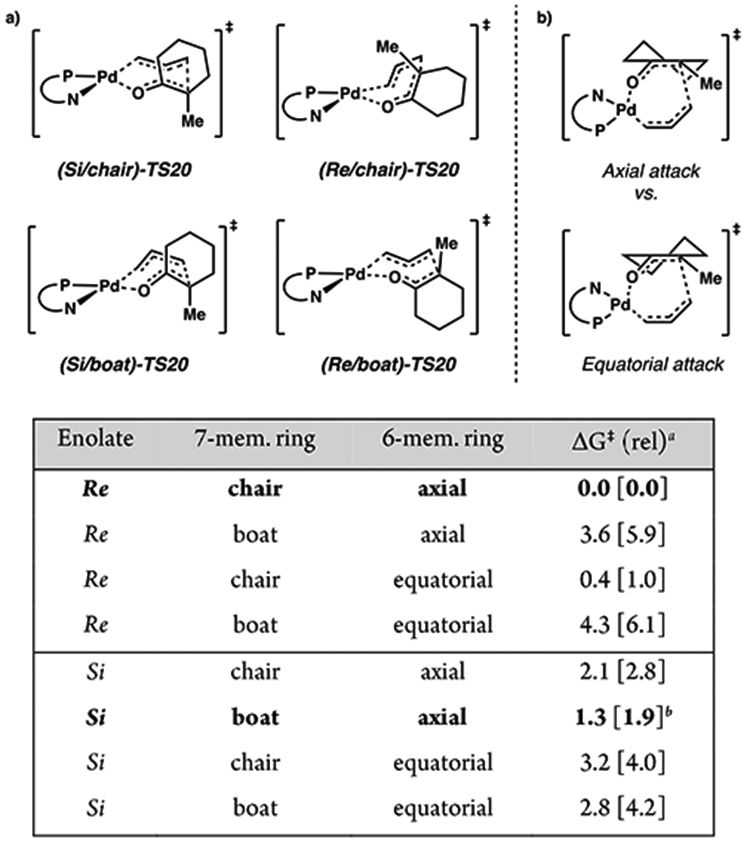
(a) Four conformational geometries of the seven-membered ring (top). (b) Two cyclic enolate half-chair conformers possible for each of the four conformers depicted in part a. Comparison of relative free energy barrier heights among eight 7-membered ring reductive elimination transition states ( bottom; TS20). ^aRelative free energies given in kcal/mol at the M06/def2-TZVP–CPCM(THF) level of theory with DLPNO-CCSD(T)/cc-pVTZ–CPCM(THF) values in brackets. ^bWith TightPNO settings.

Transition states that feature equatorial attack of the allyl fragment by the enolate half chair are all higher in energy than their axial counterparts by 0.4 to 1.5 kcal/mol. Henceforth, in our discussion, the axial/equatorial suffix will be omitted with all references being to the favorable axial transition states. In comparison with the previously mentioned inner-sphere transition states, all eight of the 7-membered cyclic transition states (TS20) offer substantially lower barriers to C─C bond formation, with ΔG^‡ ranging from 10.8 [18.5] to 15.1 [24.6] kcal/mol.

Experimentally, the (R)- enantiomer of the t-BuPHOX ligand yields (R)-2-allyl-2-methylcyclohexan-1-one ((R)-2) as the major product with 88% ee. At a reaction temperature of 25 °C, this corresponds to an effective energetic difference of 1.6 kcal/mol between the enantiodetermining transition states. Albeit, this assumes a single predominant pathway to the enantioenriched product.

From O-bound Pd enolate (Si/Re)-13, we found the lowest energy difference between Re/Si diastereomeric transition states to be (Si/chair)-TS20 and (Re/boat)-TS20, with barrier heights of 10.8 and 12.1 kcal/mol, respectively (ΔΔG^‡ = 1.3 [1.9] kcal/mol) (Figure 9). This initial result is in good agreement with the experimentally observed enantioselectivities.

Because the reliable obtaining of relative energies within a subkcal/mol error from QM is challenging, we performed a variety of control calculational experiments. Single point calculations on the BP86-D3/LANL2TZ(f)-6-31G(d) optimized geometries were carried out with a suite of 15 density functionals, encompassing several classes of functionals. Electronic energies obtained at the DLPNO-CCSD(T) level of theory (with both “NormalPNO” and “TightPNO” settings) were employed for benchmarking. The four lower energy axial conformations of TS20 (Figure 10) were also optimized with a subset of density functionals (with and without empirical dispersion corrections (D3)), followed by single point calculations as previously described (see SI for details). All results from the control experiments correctly predict (Si/chair)-TS20 to be the overall lowest energy transition sate, with (Re/boat)-TS20 as the lowest energy pathway for the formation of the minor product (S)-2 (see SI for details). Thus, we propose C─C bond formation via TS20 to be the enantiodetermining step in the decarboxylative asymmetric allylic alkylation reaction with the Pd(PHOX) catalyst (Figure 9).

Figure 10.

Relative free energies of boat and chair conformers of (Re)- and (Si)-TS20 obtained with M06/def2-TZVP–CPCM(THF), with energies at the DLPNO-CCSD(T)/cc-pVTZ–CPCM(THF) level of theory in brackets.

An investigation of a related system by our groups highlighted internal rearrangements of a palladium enolate as a potential mechanism by which product enantioselectivity is determined.^10b Although outside the scope of that investigation, the authors noted that a subsequent equilibration between (Si/Re) enolates may be facile. Thus, a definite conclusion as to the origin of the enantioinduction was not drawn. Accordingly, we found a facile interconversion between (Si)-13 and (Re)-13, with a rotational barrier several kcal/mol lower in energy than that of C─C bond formation (TS24) (Scheme 2). Therefore, the rate of kinetic quenching of intermediates (Si)-13 and (Re)-13 will not be sufficient to preserve any stereochemical induction of previous mechanistic steps.

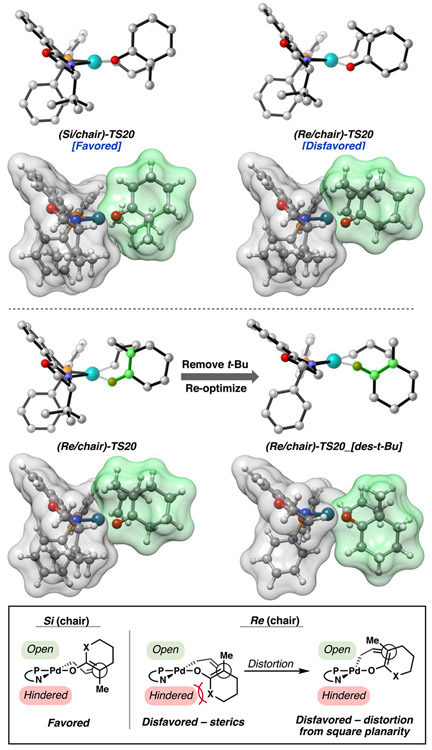
Upon further examination, it becomes clear that in the case of the favored (Si)-TS20 geometries, adverse interaction between the α-methyl substituent of the enolate fragment and the t-Bu group of the PHOX ligand is minimal compared to the analogous clash between the t-Bu group and the carbocyclic backbone of the enolate found in (Re)-TS20. The four atoms ligating palladium, along with the two carbon termini of the newly forming σ(C─C) bond, are nearly coplanar (Figure 11). In the Re transition states, the resulting steric clash between the ligand and substrate leads to a distorted chair/boat transition state as well as deviation from square planarity at the palladium center. We performed a control calculation in which the t-Bu group of the PHOX ligand was replaced with a hydrogen atom, followed by subsequent transition state optimization. The [des-t-Bu] suffix is used to describe these geometries. The (Re/chair)-TS20-[des-t-Bu] structures regain similar planarity and relative energies to that of the (Si/chair)-TS20-[des-t-Bu], with (Re/chair)-TS20-[des-t-Bu] being 1.4 [0.5] kcal/mol lower in energy than the (Si/chair) counterpart. With the t-BuPHOX ligand, the relative barrier heights of the diastereomeric chair transition states are 2.1 [2.8] kcal/mol apart in energy, favoring the (Si) enolate. These results suggest that the steric interaction from the carbocyclic scaffold and the t-Bu group of the PHOX ligand, along with the accompanying distortion from square planarity, is the primary origin of enantioinduction.

Figure 11.

Hypothesized mechanism of stereoinduction. Side on view of relevant transition states.

Although previous work suggests an inner-sphere mechanism to be prevalent, we do not discount the possibility that a competing outer-sphere mechanism is also present. In fact, with the Pd(PHOX) system, stabilized “soft” enolates generally remain competent in the reaction, albeit with substantially reduced enantioselectivities.³ In the canonical Tsuji–Trost allylic alkylation, differentiation between inner- and outer-sphere pathways is highly reliant on the nature of the nucleophile,³⁴ with hard nucleophiles proceeding through inner-sphere attack and soft nucleophiles via outer-sphere mechanisms. As such, we hypothesize that the poor enantioselectivities observed with stabilized enolates are likely the result of a less selective outer-sphere mechanism dominating the C─C bond formation step. In an effort to continue the development of this methodology to include previously inaccessible substrate classes, we sought to explore the intricacies of the interplay between outer-sphere and inner-sphere mechanisms.

From O-bound enolates (Si)-13 and (Re)-13, an associative displacement of the enolate by the olefin of the allyl fragment ((Si/Re)-TS21) directly affords 14 (as two inconsequential rotamers) (Scheme 2). Its noteworthy that 14 is also the product of decarboxylation through TS15 (decarboxylative pathway 3) (Scheme 1). As expected, in 14, bonding between the axial enolate oxygen and Pd is dominated by electrostatic attraction. Intermediate 14 presents a Pd─O bond length of 2.72 Å and Löwden bond order of 0.23, compared to the 2.08 Å Pd–O bond length and bond order of 0.60 as observed in (Si)-13. As such, disassociated ions 15 and 17 are comparable in free energy to 14. This was found to be the lowest energy entry into the outer-sphere mechanistic space (Scheme 2).

In considering C─C bond formation through an outer-sphere attack of enolate 17 on the [(η³-allyl)Pd(PHOX)]⁺ complex (15), we note that attack may occur either trans to N (t-N) or trans to P (t-P), from the Si or Re face of the enolate, in both enolate half chairs, and to either exo or endoallyl 15. On the basis of our previous findings, we considered only the enolate half chair which gives rise to the favored axial attack. Here, we found six of the eight hypothesized transition states for this outer-sphere process (TS22).

Unlike the inner-sphere transition states TS20, which give rise to ΔΔG^‡ of 1.3 [1.9] kcal/mol between the lowest energy diastereomeric transition states, the outer-sphere transition states afford reduced selectivity. From transition states (exo/Si/t-P)-TS22 and (endo/Re/t-N)-TS22, a ΔΔG^‡ of 0.6 [1.4] kcal/mol was calculated.

In addition to reactivity at the π-allyl carbon termini, nucleophilic attack at the central carbon of the allyl fragment to afford palladacyclobutane species is known.³⁵ Previous experimental and computational studies find the mode of reactivity to be highly dependent on the σ-donating/π-accepting nature of the ancillary ligand and the basicity of the nucleophile.³⁵ Palladacyclobutane complexes have been proposed as mechanistic intermediates in palladium-mediated cyclopropanation reactions,³⁶ as well as isolated and characterized by X-ray crystallography.³⁷

With relevance to this work, we considered that 15 and 17 may combine in such a way that the oxygen atom of 17 forms a covalent bond with the β carbon of the allyl fragment to afford metallacyclobutane 18. Here, the prefix endo/exo describes the relative stereochemistry at the central carbon atom of the allyl fragment of the η³-allyl precursor 15.

In this conformation, the C─C π orbitals of the enolate fragment are in potentially good overlap with the Pd─C σ* of the allyl terminus. Thus, we envisioned intermediate 18 may be a competent precursor to the desired C─C bond formation via (Si/Re)-TS23. IRC analysis reveals that (Si/Re)-TS23 directly connects metallacyclobutane 18 and the complexed ketone product (R/S)-19 on the potential energy surface without the intermittency of ion pair 15+17. Therefore, TS23 represents a C─C bond forming pathway unique to that of TS22. Complex 18 is well poised for reductive elimination to form 19. The apparent barrier to this process (relative to enolate (Si)-13) is 16.4 [20.5] and 16.1 [20.8] kcal/mol for (endo/Si/t-P)-TS23 and (endo/Re/t-P)-TS23, respectively.

From analysis of the free energy network encompassing palladium enolates (Si)-13, (Re)-13, and 14, with the accompanying C─C bond forming pathways, the following conclusions are drawn:

1. Given facile rotation about the Pd─O and C─O σ bonds in palladium enolates (Si)-13 and (Re)-13, preservation of stereochemical information through differentiation in energy between prior diastereomeric transition states should largely be erased. We found the rotational barrier from (Si)-13 to (Re)-13 to be 5.1 [6.6] kcal/mol (via TS24), whereas the minimum energy barrier to C─C bond formation is 10.8 [18.5] kcal/mol. Therefore, the rate of kinetic quenching of intermediates (Si)-13 and (Re)-13 will not be sufficient to preserve any stereochemical induction from previous mechanistic steps. However, this feature of the PES may be substrate specific and more extrapolated scaffolds may experience rotational barriers similar to or greater than that of C─C bond formation.

2. The mechanism through which decarboxylation of the β-ketoester occurs plays an important role in determining the predisposition for C─C bond formation to occur through either an inner- or outer-sphere process. As previously mentioned, decarboxylations via TS5, TS14, and TS15 yield palladium enolates (Re)-13, (Si)-13, and 14, respectively. From (Re/Si)-13, direct C─C bond formation through the inner-sphere transition states (Si/chair)-TS20 or (Re/boat)-TS20 represents the lowest energy pathway to the product. From (Re/Si)-13, the apparent barrier height to C─C bond formation via an outer-sphere mechanism corresponds to the isomerization of (Re/Si)-13 to the axially bound enolate 14 via (Re/Si)-TS21, as Re/Si)-TS21 are found to be higher in energy than the outer-sphere C─C bond forming transition states (TS22).

Therefore, decarboxylation through TS5 or TS14 (pathway 1 or 2) to directly afford (Re/Si)-13 carries a predisposition for inner-sphere C─C bond formation.

Alternatively, decarboxylation via TS15 (pathways 3) directly leads to apical enolate 14. When this is the case, C─C bond formation through both inner- and outer-sphere processes becomes highly competitive. From 14, the highest barrier to the outer-sphere mechanism is that of the outer-sphere C─C bond forming event (TS22). While the barrier heights for the inner-sphere C─C bond forming transition states are lower in energy than those of the outer-sphere mechanism, the palladium enolate must first undergo an isomerization from apically bound 14 to square planar complexes (Re/Si)-13. In fact, the barrier heights of these isomerizations (via (Re/Si)-TS21) are comparable to that of the outer-sphere C─C bond formation. Therefore, less preference for the inner- over outer-sphere mechanism is expected for the case in which decarboxylation proceeds through TS15 (pathway 3). Qualitatively similar results are obtained across a variety of density functional methods (see SI).

• We previously discussed the effects of solvation on the differentiation between decarboxylative pathways. We find that nonpolar solvents such as toluene impose a large preference for decarboxylation through the less polar TS14, while polar solvents result in preference for the more charge-separated TS15. Given the similarities in the free energies of the inner- and outer-sphere mechanisms, along with the experimentally observed solvent dependencies described in the literature, an analogous investigation into the solvent effects on differentiation of the inner- and outer-sphere mechanistic pathways was carried out.

First, we note the relative free energies between the low energy palladium enolates (Re/Si)-13 and the transition states for their isomerization to 14 are independent of the continuum dielectric constant (Table 1). However, the barrier for C─C bond formation via inner-sphere TS20 demonstrates a dependence on solvent polarity in which less polar solvents afford reduced barrier heights. As anticipated, the generation of solvent separated ions 15 and enolate 17 from 14 becomes increasingly unfavorable with decreasing dielectric constant of the solvent. As the relative free energy of 15 and 17 increases dramatically in nonpolar solvents, the outer-sphere C─C bond formation from the separate ions via TS22 is anticipated to become less prevalent. In contrast, solvation in a continuum with a high dielectric constant favors the separate ions 15 and 17 over palladium enolate 14. The barriers to outer-sphere C─C bond formation also decrease, now favoring an outer-sphere mechanism from 14.

Table 1.

Comparison of Relative Free Energy Barrier Heights along Reductive Elimination Pathways^a

Intermediate	PhMe	Et2O	THF	DMF
(Re)-13	0.6	0.5	0.5	0.4
(Si)-13	0.0	0.0	0.0	0.0
14	8.8	9.3	9.5	9.8
15 + 17	33.2	17.5	9.2	−0.5
(Re)-TS21	13.5	13.5	13.5	13.6
(Si)-TS21	14.1	14.1	14.1	14.1
(Si/chair)-TS20	9.5	10.3	10.8	11.5
(Re/boat)-TS20	10.9	11.7	12.1	12.7
(endo/Si/t-P)-TS22	14.9b	13.9b	13.3	12.6
(exo/Re/t-N)-TS22	16.0b	14.7b	13.9	12.9
(endo/Si/t-P)-TS23	19.8	17.8	16.6	15.1
(endo/Re/t-P)-TS23	19.1	17.2	16.1	14.8

^aRelative free energies given in kcal/mol at the M06/def2-TZVP–CPCM(solvent) level of theory on geometries obtained in the gas phase.

^bBarrier less than free energy of separated ions (exo)-15 and 17.

Taken together with the results for solvent effects on decarboxylation, we conclude that in polar solvent, decarboxylation via TS15 is favored, affording intermediate 14. From 14, the minimum energy pathway to C─C bond formation is via a less enantioselective outer-sphere mechanism (TS22). Conversely, nonpolar solvents favor loss of CO₂ through TS14, yielding enolate (Si)-13. Reductive elimination via the 7-membered pericyclic transition state TS20 then ensues. Given the sensitivity of relative barrier heights to changes in solvation, we highlight the need to consider both the mechanism of decarboxylation and that of the C─C bond forming pathways in determining the inner-sphere or outer-sphere mechanism to be more favorable.

Complete Catalytic Cycle.

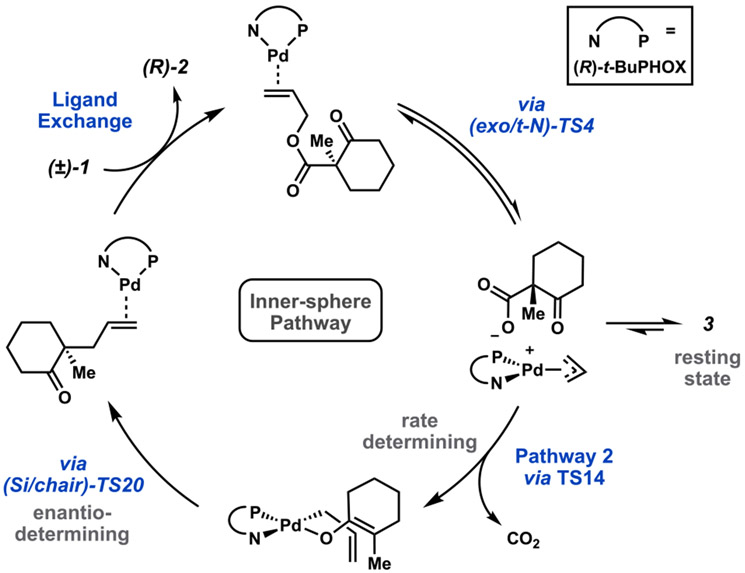
Considering the findings for each step of the decarboxylative allylic alkylation reaction, we now construct a mechanistic picture that unites theoretical and experimental findings (Figure 12). First, the π-basic Pd⁰(PHOX) precatalyst coordinates to the olefin of the allyl β-ketoester starting material (1), followed by net oxidative addition to form the [Pd(PHOx)(η³-allyl)]⁺(RCO₂⁻) ion pair (4). Oxidative addition occurs trans to the nitrogen of the PHOX ligand via direct displacement of the carboxylate leaving group (TS4). Validation of this displacement-type mechanism supports the basis from which previous claims have been made using inversion/retention of stereochemistry as a probe for determination of inner- versus outer-sphere mechanisms (when substitution on the allyl terminus is present).^6,27 The mechanism of Bäckvall was found to be unlikely for these substrates.³⁰ Furthermore, both enantiomers of the starting material have similar barriers to oxidative addition. This is in accordance with experimental evidence that a kinetic resolution of the allyl β-ketoester starting material is generally not observed.

Figure 12.

Complete catalytic cycle for the allylic alkylation reaction.

Ion pair 4 then equilibrates to the more thermodynamically stable [Pd(PHOX)(η¹-allyl)(RCO₂)] complex (3) via a stepwise mechanism (Scheme 1). Experiment and computation agree in identifying 3 as the resting state of the catalyst. We further extend the analogous comparison to that of the enol carbonate substrate class (8/9). Given the equilibration between 3 and 4, along with the similar relative energies of the separated ions, we conclude that observation of crossover products in deuterium labeling experiments does not necessarily indicate an outer-sphere C─C bond forming mechanism but rather is still accommodated within the inner-sphere mechanistic hypothesis.⁵ That is, charge-separated ion pairs may undergo facile anion exchange to afford the observed cross products. Additionally, the pK_b of the carboxylate/carbonate anions is such that quenching with water to render an inactive or decomposed species is not anticipated, in accordance with the observed water tolerance experiments.⁴

Subsequent loss of CO₂ occurs through one (or more) of three unique decarboxylative transition states, each leading to a different palladium enolate intermediate. Our investigation determines that ion pair 4 (the initial product of oxidative addition) is a common intermediate along the two lowest energy pathways through decarboxylation. Therefore, the catalyst resting state (3) is best described as an off-cycle intermediate (Figure 13). In agreement with experiment, decarboxylation is determined here to be rate-limiting. Furthermore, the calculated rate of decarboxylation (4.65 × 10⁻⁴ s⁻¹) is in excellent agreement with that of experiment (1.58 × 10⁻⁴ s⁻¹)⁴.

Figure 13.

Free energy profile of minimum energy pathway through full catalytic cycle (green) as well as pathway for equilibration to off cycle resting state 3 (orange). Note that decarboxylation is considered irreversible as CO₂ is lost to reaction headspace/atmosphere.

From the four-coordinate palladium enolates (Re/Si)-13, the most facile pathway to C─C bond formation is inner-sphere reductive elimination via a 7-membered pericyclic transition state (TS20). We establish that this C─C bond forming event is the enantiodetermining step. Calculated enantioselectivities agree with the experiment and are assessed across a variety of computational methods. We propose a model for the origin of enantioinduction (Figure 11).

We investigated the interplay of inner- and outer-sphere mechanisms. In particular, we assess effects of solvation on the differentiation of these two processes. The highly enantioselective inner-sphere process is favored in nonpolar solvents, whereas the less selective outer-sphere mechanisms become increasingly relevant in polar solvents. The origin of this solvent dependence is 2-fold. In addition to stabilization of charged intermediates encountered in the outer-sphere processes, we find that increasingly polar solvents favor decarboxylation via the formally charge-separated transition state TS15, leading directly to the square pyramidal enolate complex 14. Above, we discuss the implications of this in the context of a more facile entry into the outer-sphere mechanistic space.

EXPERIMENT AND DISCUSSION

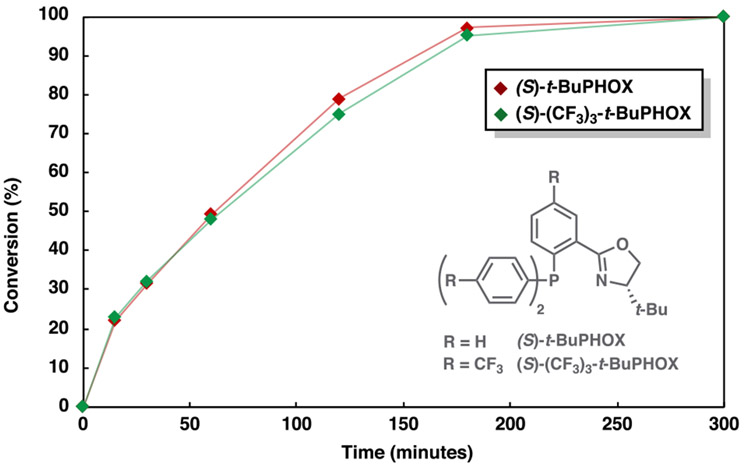
We then sought to experimentally evaluate the mechanistic predictions obtained through our computational investigation. In the case of α-methyl allyl enol carbonate 8, prior research reveals that the reaction rate is dramatically increased with the use of the more electron poor (S)-(CF₃)₃-t-BuPHOX ligand.³⁸ While a similar trend for the analogous β-ketoester (1) may be anticipated, reaction time course studies reveal that the same rate enhancement is not observed (Figure 14). In fact, when the catalyst resting state (3) and both low energy transition states responsible for decarboxylation (TS14 and TS15) are reoptimized with the (S)-(CF₃)₃-t-BuPHOX ligand, the barrier to decarboxylation is calculated to be 22.2 kcal/mol (DLPNO-CCSD(T), TightPNO): nearly identical to the 21.9 kcal/mol (DLPNO-CCSD(T), TightPNO) barrier height of the original system. This experiment further highlights the fidelity of the computational methods employed in this study in describing the reactivity trends in the catalytic system.

Figure 14.

Time course of conversion of 1 to (S)-2 under standard conditions with the (S)-t-BuPHOX and (S)-(CF₃)₃-t-BuPHOX ligands. Conversion as determined by GC-FID with respect to tetradecane internal standard.

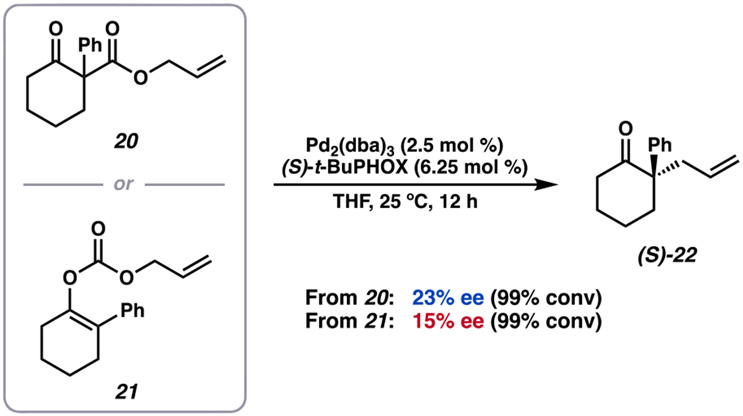
We prepared α-phenyl allyl β-ketoester substrate 20 to probe the interplay of inner- and outer-sphere processes (Figure 15). In comparison to α-methylated β-ketoester 1, the enolate derived from 20 experiences significant electronic stabilization through conjugation. As anticipated from the discussion provided above, as well as prior experimental trends, substrate 20 affords the desired product (S)-22 in 99% yield, however, in a modest 23% ee.

Figure 15.

Standard conditions for the decarboxylative asymmetric allylic alkylation as investigated herein applied to substrates that afford a stabilized α-phenyl palladium enolate.

It is worth noting that the reduction in enantioselectivity is likely not exclusively a consequence of steric interactions. A variety of sterically encumbered substrates, which do not provide significant electronic stabilization, such as the analogous α-t-Bu, α-Bn, α-prenyl, etc., compounds afford the corresponding allylic alkylation products in 82–91% ee.^5,31 Furthermore, we compute a ΔΔG^‡ of 1.3 kcal/mol between the enantiodetermining inner-sphere transition states derived from substrate 20 (corresponding to 80% ee at 25 °C). These results suggest that an enantioselective inner-sphere pathway persists; however, under the standard reaction conditions, the less selective outer-sphere mechanisms dominate.

In addition to α-phenyl β-ketoester 20, the corresponding α-phenyl allyl enol carbonate synthon (21) was also evaluated in the transformation (Figure 15). Interestingly, under identical conditions to those employed with β-ketoester 20, enol carbonate 21 affords (S)-22 in a reduced 15% ee, compared to 23% ee as obtained starting from 20.⁸ After decarboxylation, both 20 and 21 share access to the same network of enolate intermediates (Scheme 2). By virtue of the differing mechanisms of decarboxylation, however, the point at which the intermediates derived from each substrate enter the postdecarboxylation mechanistic space is anticipated to vary. As prefaced by our computational investigation, this may lead to altered levels of product enantioenrichment due to the resulting predisposition for C─C bond formation to occur via inner- or outer-sphere mechanisms to varying extent (vida supra). Naturally, differences in enantioselectivities based on enolate synthon (i.e., β-ketoester versus enol carbonate) are expected to be increasingly pronounced in the case of stabilized enolates (20/21), for which an outer-sphere mechanism is readily accessible. These results highlight the importance in considering the effect of the mechanism of decarboxylation and subsequent behavior of enolate intermediates in the overall enantioselectivity of the transformation.

With compound 20 in hand, we then sought to probe the effects of solvation and ligand electronics on observed enantioselectivity (Table 2). As previously mentioned, the enantioselective inner-sphere pathway to C─C bond formation to (S)-22 is expected to be largely outcompeted by less selective outer-sphere mechanisms. Our computational investigations suggest that for allyl β-ketoesters, inner-sphere mechanisms are favored by (1) disfavoring the charge-separated intermediates required for an outer-sphere approach and (2) favoring decarboxylative mechanisms that lead directly to η¹-allyl square planar palladium enolates (i.e., via decarboxylation pathways 1 and 2). Calculations further predicted that this may be accomplished by utilizing nonpolar solvents, as well as through the installation of electron withdrawing groups on the PHOX ligand framework.

Table 2.

Effects of Solvation and Ligand Electronics on Enantioselectivity

Entry	Ligand	Solvent [ε]	ee (%)a	Yield 22 (%)b	ΔGeqc
1	(S)-t-BuPHOX	THF [7.4]	23	99	1.8
2	(S)-t-BuPHOX	PhMe [2.4]	28	96	24.0
3	(S)-(CF3)3-t-BuPHOX	PhMe [2.4]	32	90	31.0
4	(S)-(CF3)3-t-BuPHOX	2:1 MeCy/PhMe [2.1]	36	69d	35.2

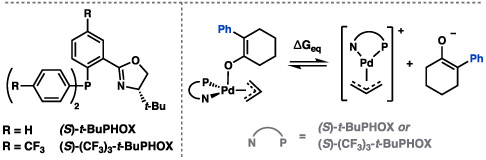^aObtained by chiral SFC.

^bDetermined by ¹H NMR with respect to internal standard.

^cChange in free energy (in kcal/mol, 1 M standard state) from square pyramidal enolate to free ions.

^d34% 20 remaining after 12 h (¹H NMR with respect to internal standard).

Indeed, we observe an increase from 23 to 28% ee simply by implementing toluene (ε = 2.4) in place of THF (ε = 7.3) as the reaction solvent (entries 1–2, Table 2). Utilizing the more electron poor (S)-(CF₃)₃-t-BuPHOX ligand in toluene (entry 3) and a 2:1 methylcyclohexane/toluene solvent mixture (ε = 2.1), enantioselectivity was further enhanced to 32% and 36% ee, respectively (entries 3–4). Given the initial improvements from perturbations of ligand electronics and solvation alone, we suggest in silico high-throughput screening of ligands with different steric environments as a practical next step in future developmental efforts.

CONCLUSIONS

We report a detailed quantum mechanics investigation into the three mechanistic steps (oxidative addition, decarboxylation, and reductive elimination) of the decarboxylative asymmetric allylic alkylation with the Pd(PHOX) catalyst system. Experiments were carried out to explore the mechanistic hypotheses derived from the ab initio calculations.

Beginning with allyl β-ketoester 1, oxidative addition of Pd⁰(PHOX) proceeds through precoordination of the olefin of the allyl fragment of 1 (to give 5), followed by an S_N2-like electrophilic addition to Pd to yield the [(PHOX)Pd(η³-allyl)]⁺(RCO₂⁻) ion pair (4). Ion pair 4 then rapidly equilibrates to the catalyst resting state, [(PHOX)Pd(η¹-allyl)(RCO₂)] (3). Complex 3 is best described as an off-cycle intermediate. Given the equilibration between 3 and 4, along with the similar relative energies of the separated ions, we corroborate that the results from our previously reported crossover experiments are not necessarily indicative of an outer-sphere mechanism but still are accommodated within the inner-sphere mechanistic hypothesis.

From the catalyst resting state (3), we find three dominant pathways (1, 2, and 3) through which decarboxylation may occur. Each pathway leads to a unique palladium enolate with the ability for subsequent interconversion between the three. However, the ensuing analysis of the C─C bond forming potential energy surface reveals that the enolates derived from pathways 1 and 2 are more predisposed to undergo an inner-sphere C─C bond formation via the 7-membered pericyclic transition state, TS20. Decarboxylation via pathway 3 directly affords square pyramidal enolate 14 which may undergo a more facile dissociation and enter the outer-sphere mechanistic space.

We predict relative barrier heights among the decarboxylative and C(sp³)–C(sp³) bond forming pathways to be highly solvent dependent. Decreasing solvent polarity favors inner-sphere processes by destabilizing the ionic intermediates of the outer-sphere mechanism as well as promoting decarboxylation via pathway 2. Decarboxylation is determined to be rate-limiting in accordance with experiment. Furthermore, the calculated decarboxylation rate constant in THF obtained with DLPNO-CCSD(T) (4.65 × 10⁻⁴ s⁻¹, ΔG^‡ = 22.0 kcal/mol) is in excellent agreement with that of experiment (1.58 × 10⁻⁴ s⁻¹, ΔG^‡ = 22.6 kcal/mol).⁴ In comparison, the DFT methods applied in this study all predict a rate constant 10³–10⁷ times larger in magnitude (ΔG^‡ = 12.5–18.9 kcal/mol) than that experimentally observed.

We considered several inner-sphere reductive elimination transition states. In accordance with previous research in our group, the 7-membered, doubly vinylogous transition state (TS20)³⁹ provides the lowest energy pathway to C─C bond formation in nonpolar solvents. We establish that the C(sp³)–C(sp³) bond forming event is the enantiodetermining step. Calculated ΔΔG^‡ are in excellent agreement with experimentally observed enantioselectivities and are assessed across a variety of computational methods.⁴⁰ A model is proposed for the origin of the enantioinduction.

We also investigated outer-sphere processes, which we found to be competitive in barrier height with the inner-sphere reactions, albeit slightly less favorable. Unlike the inner-sphere transition states, however, severely degraded enantiocontrol is anticipated for outer sphere mechanisms.

Additionally, enolate synthon design is highlighted as an area for future development. Herein, we compare the relative thermodynamics of catalyst resting states derived from different enolate precursors. From this, we suggest that in conjunction with catalyst design, the development of more activated masked enolates may achieve a desirable increase in reaction rate. With a complete mechanistic picture in hand, in silico development may now accompany ensuing experimental efforts.

In order to evaluate the fidelity of the mechanistic hypotheses, a stabilized enolate equivalent (20) was employed as a probe for inner- and outer-sphere competition. Experimental results support the computation-based predictions in solvent trends as well as effects of ligand substitution. Furthermore, a comparison between 20 and 21 demonstrates the intricacies in the equilibration of the palladium enolate intermediates as described herein. While α-methyl ketone 1 is employed throughout the majority of this study as a “standard” substrate, many of the experimentally observed trends mentioned throughout the text remain consistent among more highly decorated heterocyclic scaffolds alike. Thus, the conclusions presented herein are expected to serve as robust first-order approximations to a broad variety of substrate classes.

Density functional theory and localized coupled-cluster theory are employed in this study. We find the DLPNO-CCSD(T) method of Neese et al. highly effective in obtaining accurate barrier heights and thermodynamic relations.²⁴ Thus, we recommend DLPNO-CCSD(T) for routine use in future quantum mechanics-based investigations in asymmetric catalysis.

These avenues of thought, coupled with the detailed mechanistic hypothesis presented herein, provide a powerful tool in addressing current limitations and aiding in the future development of the decarboxylative asymmetric allylic alkylation reaction.