Abstract
Traditional bulk RNA-sequencing of human pancreatic islets mainly reflects transcriptional response of major cell types. Single-cell RNA sequencing technology enables transcriptional characterization of individual cells, and thus makes it possible to detect cell types and subtypes. To tackle the heterogeneity of single-cell RNA-seq data, powerful and appropriate clustering is required to facilitate the discovery of cell types. In this paper, we propose a new clustering framework based on a graph-based model with various types of dissimilarity measures. We take the compositional nature of single-cell RNA-seq data into account and employ log-ratio transformations. The practical merit of the proposed method is demonstrated through the application to the centered log-ratio-transformed single-cell RNA-seq data for human pancreatic islets. The practical merit is also demonstrated through comparisons with existing single-cell clustering methods. The R-package for the proposed method can be found at https://github.com/Zhang-Data-Science-Research-Lab/LrSClust.
INTRODUCTION
Background on the biological problem
Human pancreatic islets consist of multiple types of cells, which play important roles in diabetes pathophysiology. Among them, beta (54%) and alpha (35%) cells are dominant. In bulk RNA-seq of human pancreatic islets, gene expression mainly reflects the information of these two cell types. Single-cell RNA-seq technology enables transcriptional characterization of individual cells, and thus facilitate cell-type discoveries. In a single-cell experiment, individual cells are isolated, amplified and sequenced. In this process, the information on the identities of cells is commonly missing. Currently, researchers have to use clustering techniques to partition the data into several clusters and try to infer the represented cell types based on some known marker genes. Therefore, in single-cell data analysis, the quality of clustering is crucial. In this paper, motivated by the problem of detecting cell types in human pancreatic islets, we propose a graph-based model to accomplish this clustering task.
Graph-based clustering methods
Graph-based models have been widely used in biological and biomedical research (1–9) to represent the relationships among objects. Graph can also serve as a tool for a single-cell clustering problem. In this scenario, cell relationships are represented by a similarity graph with its nodes corresponding to cells and weighted edges reflecting similarities among cells. For instance, PhenoGraph (3) takes an N × p single-cell gene expression matrix for N cells and p genes as its input, and utilizes Euclidean distance to find the k nearest neighbors (KNN) of each cell. The weight for an edge connecting two cells is calculated as the proportion of their shared neighbors over the union of all neighbors. Then, PhenoGraph employs the Louvain method to identify the graph communities presenting the clusters of cells. SNN-cliq (2) is also a graph-based clustering method proposed for single-cell clustering. It first calculates the pairwise Euclidean distances of cells, connects a pair of cells with an edge if they share at least one common neighbor in KNN, and then defines the weight of the edge as the difference between k and the highest averaged ranking of the common KNN. SNN-cliq then employs a greedy algorithm to find a maximal quasi-clique associated with each node, and finally identifies clusters by iteratively combining significantly overlapping subgraphs starting with the quasi-cliques.
In this paper, we treat RNA-seq counts as compositional data. We first make an appropriate centered log-ratio (clr) transformations. Then, we propose a graph-based clustering method for single-cell data with the following major components: (i) choosing an appropriate type of measure to represent the dissimilarity patterns of cells; (ii) transforming pairwise dissimilarities to similarities as the weights of edges connecting the corresponding cells; (iii) cutting the graph into disjoint sub-graphs representing clusters of cells. Each step can be accomplished by various methods depending on the dataset of interest. In this paper, we employ appropriate methods based on our motivating single-cell RNA-seq data for human pancreatic islets.
The rest of this paper is organized as follows. We first introduce the proposed method. We then apply our method to clr-transformed single-cell RNA-seq data for human pancreatic islets and compare with other methods. Furthermore, we conducted a simulation study. Finally, we conclude our paper.
MATERIALS AND METHODS
Single-cell RNA-seq and compositional data analysis
RNA-seq data are compositional in nature. For all next-generation sequencing abundance data, a property cannot be ignored: the abundances for each sample are limited by its arbitrary total sum (the library size). Thus, to analyze RNA-seq data, effective library size normalization is usually employed before conventional data analysis. However, the assumptions of normalization methods are often untestable in reality. Compositional data measure each sample as a composition, a vector of non-zero positive values (i.e. components) carrying relative information (10). Treating RNA-seq as compositional data opens a new perspective on data analysis, which avoids normalization. Please refer to (11) for a comprehensive treatment on this subject.
In this paper, we apply the clr-transformation (11) to raw RNA-seq counts. Before the application of clr-transformation, we add one to each raw count at first. The reason we employ this addition operation is to avoid the occurrence of minus infinity when we do natural logarithm transformation. Next, for each cell vector, 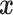 , we calculate its geometric mean denoted by
, we calculate its geometric mean denoted by 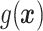 . Then we perform the following clr-transformation for each sample j (10,11):
. Then we perform the following clr-transformation for each sample j (10,11):
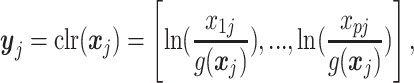 |
(1) |
where p is the total number of features.
We then develop our graph-based clustering method based on the clr-transformed data.
New graph-based clustering framework
The graph-based clustering aims to use graphs to represent the patterns of similarities among cells and to obtain clusters by dropping the weak edges. First, we need to define an appropriate metric to evaluate the dissimilarity between two cells. While Euclidean distance (based on L2 norm) is commonly used to measure the dissimilarity between two objects, for our single-cell RNA-seq data from human pancreatic islets, we found that Euclidean distance is not appropriate. Although single-cell RNA-seq data is high-dimensional, it is possible that only a small set of genes can determine the underlying types of cells. Thus, we will investigate more types of distances in our clustering framework including the Manhattan distance (based on L1 norm) and the L∞ distance. The L∞ distance is defined as the maximum absolute deviation of two vectors across all coordinates. Namely, for two cells 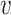 i and
i and 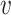 j, suppose their clr-transformed transcriptomic profiling vectors are
j, suppose their clr-transformed transcriptomic profiling vectors are 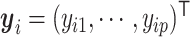 and
and 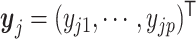 , the L∞ measure is calculated by the maximum of |yi1 − yj1|, ⋅⋅⋅, |yip − yjp|. For the convenience of the following theoretical investigation, we define L∞ dissimilarity as
, the L∞ measure is calculated by the maximum of |yi1 − yj1|, ⋅⋅⋅, |yip − yjp|. For the convenience of the following theoretical investigation, we define L∞ dissimilarity as
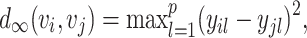 |
(2) |
Euclidean or L2 dissimilarity as
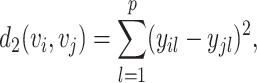 |
(3) |
and Manhattan or L1 dissimilarity as
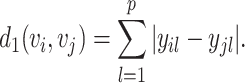 |
(4) |
We want to quantify the performance of these different measures in clustering tasks. Intuitively, a good dissimilarity measure should be able to distinguish the ‘within-cluster’ dissimilarities and the ‘between-cluster’ dissimilarities. For well-separated clusters, we expect the within-cluster pairwise dissimilarity to be small and the between-cluster dissimilarity to be as large as possible. Based on this obvious rationale in clustering problems, we propose to use the ratio of the average between-cluster dissimilarity and the average within-cluster dissimilarity to quantify the goodness of the corresponding distance measure. More formally, for objects 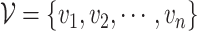 , we denote
, we denote  as the ith cluster,
as the ith cluster, 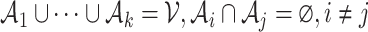 . The dissimilarity score between two cells is denoted by d(
. The dissimilarity score between two cells is denoted by d(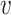 i,
i, 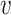 j), where d(
j), where d(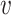 i,
i, 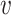 j) can be L∞ dissimilarity, L2 dissimilarity, or L1 dissimilarity. Then, we consider the ratio of the expected between and within dissimilarities, denoted by Rd, in the form of
j) can be L∞ dissimilarity, L2 dissimilarity, or L1 dissimilarity. Then, we consider the ratio of the expected between and within dissimilarities, denoted by Rd, in the form of
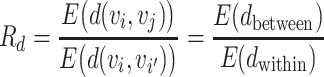 |
(5) |
where 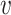 i and
i and 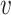 j are from different clusters, and
j are from different clusters, and 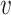 i and
i and 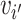 belong to the same cluster.
belong to the same cluster.
We first provide some intuitive comparisons on the clustering effects when we choose d(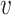 i,
i, 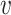 j) to be d2(
j) to be d2(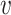 i,
i, 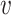 j) or d1(
j) or d1(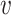 i,
i, 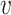 j) or d∞(
j) or d∞(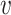 i,
i, 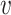 j) through a simple example. Assume there are two clusters with measures
j) through a simple example. Assume there are two clusters with measures 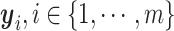 and
and 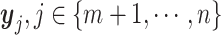 . We first consider
. We first consider 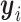 (i ∈ {1, ⋅⋅⋅, m}) and
(i ∈ {1, ⋅⋅⋅, m}) and 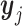 (j ∈ {m + 1, ⋅⋅⋅, n}), which independently follow multivariate normal distributions with means
(j ∈ {m + 1, ⋅⋅⋅, n}), which independently follow multivariate normal distributions with means 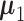 and
and 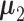 , and a common p × p covariance matrix
, and a common p × p covariance matrix 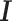 , where p is the number of features. We further assume that a subset of features separates the clusters. Without loss of generality, let
, where p is the number of features. We further assume that a subset of features separates the clusters. Without loss of generality, let 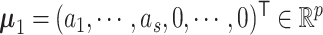 , where ai ≠ 0, and let
, where ai ≠ 0, and let 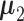 be a p-dimensional zero vector. Naturally, for within-cluster difference,
be a p-dimensional zero vector. Naturally, for within-cluster difference,  (i′ ≠ i, i, i′ ∈ {1, ⋅⋅⋅, m}) or
(i′ ≠ i, i, i′ ∈ {1, ⋅⋅⋅, m}) or 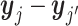 (j′ ≠ j, j, j′ ∈ {m + 1, ⋅⋅⋅, n}) follows the multivariate normal distribution
(j′ ≠ j, j, j′ ∈ {m + 1, ⋅⋅⋅, n}) follows the multivariate normal distribution 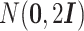 . For the between-cluster difference,
. For the between-cluster difference, 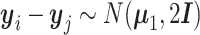 .
.
When d(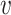 i,
i, 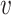 j) = d2(
j) = d2(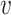 i,
i, 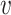 j) and
j) and 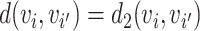 , Rd is denoted by
, Rd is denoted by 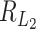 . If the total number of genes p is of the same order as
. If the total number of genes p is of the same order as 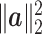 ,
, 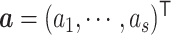 ,
, 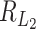 is of order 1. The reason is as follows. For numerator of
is of order 1. The reason is as follows. For numerator of 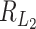 , it can be decomposed into the variations coming from signals and noises. The first s coordinates of
, it can be decomposed into the variations coming from signals and noises. The first s coordinates of  correspond to the signal source, having expectation
correspond to the signal source, having expectation 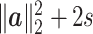 , and the rest of the coordinates are from the noise source with expectation 2(p − s). Therefore, the numerator of
, and the rest of the coordinates are from the noise source with expectation 2(p − s). Therefore, the numerator of 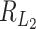 is
is 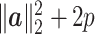 . The denominator of
. The denominator of 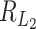 is 2p. The ratio is
is 2p. The ratio is 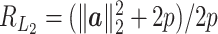 . Thus, if the total number of genes p is of the same order as
. Thus, if the total number of genes p is of the same order as 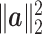 , then
, then 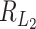 is of order 1, which means it is hard to separate the clusters. Under this setting, the critical size for
is of order 1, which means it is hard to separate the clusters. Under this setting, the critical size for 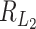 is of the same order as
is of the same order as 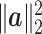 . Similarly, the critical size of
. Similarly, the critical size of 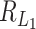 is of the same order as
is of the same order as 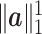 , i.e.
, i.e. 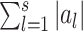 .
.
When d(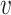 i,
i, 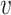 j) = d∞(
j) = d∞(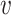 i,
i, 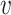 j) and
j) and 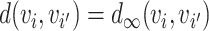 , Rd is denoted by
, Rd is denoted by 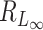 . Let
. Let 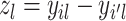 be a random sample of within-in cluster difference determined by feature l, then
be a random sample of within-in cluster difference determined by feature l, then 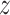 l ∼ N(0, 1) (following the assumption of the simple example) and
l ∼ N(0, 1) (following the assumption of the simple example) and 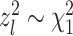 , where l = 1, ⋅⋅⋅, s. We have:
, where l = 1, ⋅⋅⋅, s. We have:
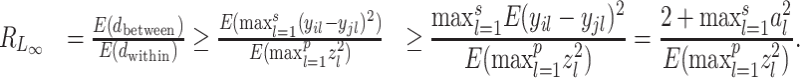 |
Let Tp be the maximum value of p 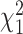 random variables, then (Tp − dp)/2 → G, where G is a Gumbel random variable, and dp = 2(lnp − 1/2ln(lnp) − lnΓ(1/2)) (12). Thus, the denominator of
random variables, then (Tp − dp)/2 → G, where G is a Gumbel random variable, and dp = 2(lnp − 1/2ln(lnp) − lnΓ(1/2)) (12). Thus, the denominator of 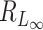 is of the same order as ln p. When p is of the same order as
is of the same order as ln p. When p is of the same order as 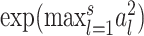 ,
,  is of order 1. In this setting, the critical size of
is of order 1. In this setting, the critical size of  is of the same order as
is of the same order as 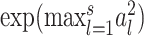 . When the number of noise features increases,
. When the number of noise features increases, 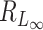 can have lower signal contamination rate than
can have lower signal contamination rate than 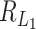 and
and 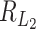 .
.
Furthermore, dropping the aforementioned Gaussian assumption on 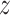 l, let’s consider a scenario where
l, let’s consider a scenario where 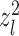 follows a distribution with sub-Gaussian tail. We have the following theorem:
follows a distribution with sub-Gaussian tail. We have the following theorem:
Theorem 1. For i.i.d. random variables W1, ⋅⋅⋅, Wp which have sub-Gaussian tail, i.e. P(|Wi| ≥
) = O(exp ( − β
α)), where α > 0 and β > 0, then as p → ∞,
.
Thus, the critical size for 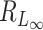 under this setting is of the same order as
under this setting is of the same order as 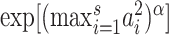 . This can be much larger than the critical sizes of
. This can be much larger than the critical sizes of 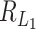 and
and 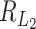 , which are of the same order as
, which are of the same order as 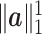 and
and 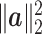 respectively.
respectively.
In summary, the rationale indicates that the L∞ measure can be a better choice compared to the Manhattan measure and the Euclidean measure in certain scenarios.
Given a set of cell vectors 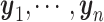 , where
, where 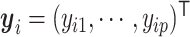 stands for the clr-transformed transcriptomic values for p genes in cell i, and an appropriate metric to evaluate the pairwise dissimilarity of cells, we can build a graph, denoted by
stands for the clr-transformed transcriptomic values for p genes in cell i, and an appropriate metric to evaluate the pairwise dissimilarity of cells, we can build a graph, denoted by 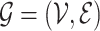 , to represent the similarities among these cells, where
, to represent the similarities among these cells, where 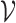 is the set of cells {
is the set of cells {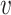 1, ⋅⋅⋅,
1, ⋅⋅⋅, 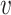 n},
n}, 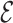 is the set of edges with weight eij for the edge connecting
is the set of edges with weight eij for the edge connecting 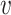 i and
i and 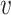 j (i, j ∈ {1, ⋅⋅⋅, n}, i ≠ j). We determine the weights of edges using an entropy equalizer similarity measure (13). Specifically, if there is no edge between
j (i, j ∈ {1, ⋅⋅⋅, n}, i ≠ j). We determine the weights of edges using an entropy equalizer similarity measure (13). Specifically, if there is no edge between 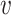 i and
i and 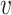 j, we set the weight to be zero. We define the similarity between
j, we set the weight to be zero. We define the similarity between 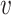 i and
i and 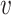 j (i ≠ j) as the normalized conditional probability pj|i,
j (i ≠ j) as the normalized conditional probability pj|i,
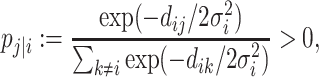 |
(6) |
where dij is the dissimilarity between i and j, and 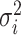 is the variance parameter for the Gaussian kernel. Please refer to Supplementary Algorithm 1 for the calculation of σi. In addition, we define pi|i = 0 for i ∈ {1, ⋅⋅⋅, n}. Then, for any cell
is the variance parameter for the Gaussian kernel. Please refer to Supplementary Algorithm 1 for the calculation of σi. In addition, we define pi|i = 0 for i ∈ {1, ⋅⋅⋅, n}. Then, for any cell 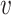 i, the similarity measures between
i, the similarity measures between 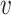 i and any other cells induce a probability distribution, i.e.
i and any other cells induce a probability distribution, i.e.
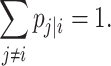 |
(7) |
The corresponding entropy is the form of
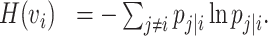 |
(8) |
The perplexity is defined as 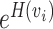 , which is a tuning parameter affecting cluster assignments. Intuitively, the perplexity can be interpreted as a smooth measure of the effective number of neighbors. Smaller perplexity will encourage forming clusters with small sizes. Larger perplexity will yield larger cluster configuration. Furthermore, it is notable that the defined similarity in Equation (6) may be asymmetric: pj|i is not necessarily equal to pi|j. Thus, we set
, which is a tuning parameter affecting cluster assignments. Intuitively, the perplexity can be interpreted as a smooth measure of the effective number of neighbors. Smaller perplexity will encourage forming clusters with small sizes. Larger perplexity will yield larger cluster configuration. Furthermore, it is notable that the defined similarity in Equation (6) may be asymmetric: pj|i is not necessarily equal to pi|j. Thus, we set 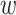 ij = (pi|j + pj|i)/2.
ij = (pi|j + pj|i)/2.
With the weighted graph, we then employ an appropriate graph-cutting procedure to obtain clusters (sub-graphs). Specifically, we cut the graph 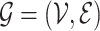 into several sub-graphs, such that cells within the same sub-graph share more similarity than the other cells. We define a cluster as a subset of cells,
into several sub-graphs, such that cells within the same sub-graph share more similarity than the other cells. We define a cluster as a subset of cells, 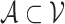 . All clusters form a partition of the whole set,
. All clusters form a partition of the whole set, 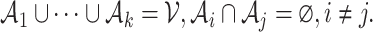 In addition, a ‘cut’ means that for all clusters
In addition, a ‘cut’ means that for all clusters 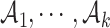 , there is no edge between
, there is no edge between 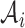 and
and 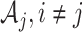 . Due to cutting, the ‘loss of similarity’ between two clusters is the summation of all pairwise original weights of the edges between these two clusters, denoted by
. Due to cutting, the ‘loss of similarity’ between two clusters is the summation of all pairwise original weights of the edges between these two clusters, denoted by
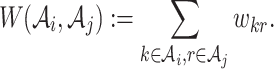 |
(9) |
For our real data, we expect to see some relative large and biologically meaningful clusters for future study. Thus, we adopt the RatioCut approach (14) defined as below
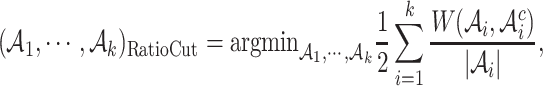 |
(10) |
where 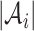 denotes the number of cells in a cluster, and
denotes the number of cells in a cluster, and 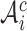 is the complement of
is the complement of 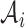 . The RatioCut optimization problem is equivalent to the following (15),
. The RatioCut optimization problem is equivalent to the following (15),
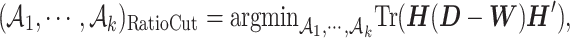 |
(11) |
where 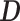 is a diagonal matrix, and its diagonal elements are
is a diagonal matrix, and its diagonal elements are 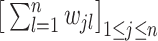 ,
, 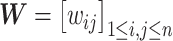 ,
, 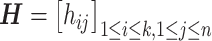 , and
, and
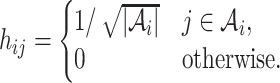 |
(12) |
This optimization problem is NP hard. In practice, we employ a spectral clustering method to solve the relaxed optimization problem through a spectral decomposition. Denote 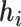 to be the indicator vector for cells belong to
to be the indicator vector for cells belong to 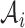 ,
, 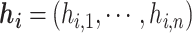 . Based on the construction of hij,
. Based on the construction of hij, 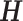 is an orthogonal matrix,
is an orthogonal matrix, 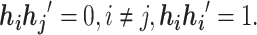 Instead of finding a cut, we can optimize the objective function by searching
Instead of finding a cut, we can optimize the objective function by searching 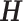 among orthogonal matrices. The relaxed problem becomes
among orthogonal matrices. The relaxed problem becomes
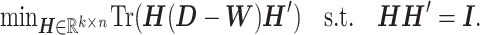 |
(13) |
By Poincaré separation theorem,
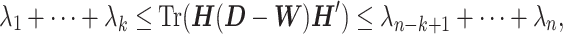 |
(14) |
where λ1 ≤ ⋅⋅⋅ ≤ λn are eigenvalues of a Laplacian matrix 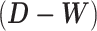 . Thus,
. Thus, 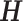 is the matrix which contains the first k eigenvectors as its columns.
is the matrix which contains the first k eigenvectors as its columns.
To select the optimal number of clusters and perplexity, we maximize a Gap-statistic (16) type of objective function. Here, the total within-cluster dissimilarity for all clusters 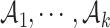 under perplexity p is
under perplexity p is
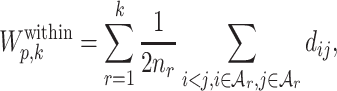 |
(15) |
where nr is the number of cells in the rth cluster. It is clear that as the number of clusters increases, the total within-cluster dissimilarity may always decrease. In the extreme case, all cells form their own clusters, the total within-cluster dissimilarity is zero. We extend the Gap statistic (16) to select the tuning parameters. More formally, the Gap-statistic type of criterion under perplexity p and the number of clusters k is defined as
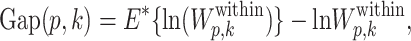 |
(16) |
where 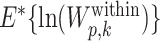 is estimated from bootstrap samples, which are uniformly drawn from the range of the values for that feature (16). Given the number of replicates B in simulation and the standard error of the bootstrap replicates sd(p, k), the standard error of the Gap statistic can be computed as
is estimated from bootstrap samples, which are uniformly drawn from the range of the values for that feature (16). Given the number of replicates B in simulation and the standard error of the bootstrap replicates sd(p, k), the standard error of the Gap statistic can be computed as
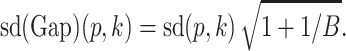 |
(17) |
We then use the 1-standard-error rule to select the smallest number of clusters k, and the largest perplexity p with a large Gap-statistic value no less than the largest Gap-statistic minus its one standard error.
RESULTS
Application to single-cell RNA-seq data from human pancreatic islets
We used existing single-cell RNA-seq data for 638 cells from nondiabetic (ND) and type 2 diabetes (T2D) human islet samples (17). (17) employed a Gaussian mixture model to classify the cells based on some known biomarkers, and only reported cell types for 617 (out of 638 in total) cells from T2D and ND islets. Specifically, these cell types include (the corresponding marker gene is shown in bracket): beta cell (INS), alpha cell (GCG), delta cell (SST), PP/gamma cell (PPY), acinar cell (PRSS1), stellate cell (COL1A1) and ductal cell (KRT19). The remaining 21 (638–617) cells were not clustered to any cell type in (17).
In this paper, we applied the proposed clustering method to single-cell RNA-seq data from the whole 638 cells without knowing the marker genes. We downloaded the raw single-cell RNA-seq data from GEO (www.ncbi.nlm.nih.gov/geo/) under accession number GSE86469. To analyze this single-cell RNA-seq dataset, we first added one count to each entry of the data matrix to avoid zeros, then applied clr-transformation. Then, we applied the proposed graph-based clustering framework (with L∞, L1 and L2 norms as the corresponding dissimilarities, denoted by Linf-SClust, L1-SClust and L2-SClust, respectively), to the clr-transformed single-cell RNA-seq data with the total of 26,616 genes and 638 cells from human pancreatic islets. For comparison, we also applied the existing graph-based clustering methods for single-cell RNA-seq data, i.e. PhenoGraph and SNN-cliq (with default parameter setting) to this dataset. We also applied CIDR and SC3 that can report the final optimized number of clusters and had good performances based on the investigation in (18). Tables 1 and 2 summarize the final clustering results of Linf-SClust, L1-SClust, L2-SClust, SNN-cliq, PhenoGraph, CIDR and SC3. We also visualized their results using uniform manifold approximation and projection (UMAP) in Figure 1 and Supplementary Figure S1. For Linf-SClust results, most cells in cluster 3 are stellate cells. Similarly, cluster 6, 7 and 8 can represent acinar, PP/gamma, ductal and delta cells, respectively. Cluster 1 and 5 primarily consist of ductal and alpha cells, respectively. Both cluster 2 and 4 mainly contain beta cells. We found that 71.22% of the cells in cluster 2 are non-diabetic cells, while 93.54% of the cells in cluster 4 are T2D cells. Therefore, cluster 2 may represent the non-diabetic beta cell group, and cluster 4 may represent the T2D beta cell group. For the L1-SClust, L2-SClust, SNN-cliq, PhenoGraph, CIDR and SC3 results, the clusters are harder to interpret biologically.
Table 1.
Comparison of the inferred cluster assignments for the whole 638 cells in the human pancreatic islets dataset by Linf-SClust, L1-SClust, L2-SClust, SNN-cliq and Pheno-Graph, as well as the cluster configuration for the 617 cells based on the known gene markers reported in (17)
| Cluster | Acinar | Alpha | Beta | Delta | Ductal | PP/Gamma | Stellate | Other |
|---|---|---|---|---|---|---|---|---|
| Linf-SClust | ||||||||
| 1 | 1 | 0 | 0 | 1 | 26 | 0 | 0 | 6 |
| 2 | 0 | 3 | 233 | 1 | 2 | 0 | 2 | 6 |
| 3 | 0 | 0 | 0 | 0 | 0 | 0 | 16 | 0 |
| 4 | 0 | 0 | 31 | 0 | 0 | 0 | 1 | 0 |
| 5 | 0 | 236 | 0 | 0 | 0 | 0 | 0 | 5 |
| 6 | 23 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7 | 0 | 0 | 0 | 0 | 0 | 18 | 0 | 0 |
| 8 | 0 | 0 | 0 | 23 | 0 | 0 | 0 | 0 |
| L1-SClust | ||||||||
| 1 | 6 | 58 | 51 | 6 | 7 | 2 | 2 | 12 |
| 2 | 0 | 0 | 65 | 2 | 1 | 11 | 0 | 0 |
| 3 | 0 | 55 | 32 | 4 | 0 | 2 | 0 | 2 |
| 4 | 4 | 108 | 61 | 13 | 7 | 8 | 7 | 6 |
| 5 | 14 | 0 | 0 | 0 | 10 | 0 | 9 | 1 |
| 6 | 0 | 13 | 17 | 0 | 3 | 1 | 1 | 0 |
| 7 | 0 | 1 | 4 | 2 | 0 | 0 | 0 | 0 |
| L2-SClust | ||||||||
| 1 | 2 | 1 | 2 | 3 | 6 | 0 | 3 | 9 |
| 2 | 0 | 5 | 185 | 15 | 1 | 9 | 0 | 2 |
| 3 | 0 | 0 | 0 | 0 | 0 | 0 | 14 | 0 |
| 4 | 2 | 136 | 15 | 7 | 1 | 8 | 2 | 8 |
| 5 | 8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6 | 0 | 0 | 0 | 0 | 20 | 0 | 0 | 2 |
| 7 | 0 | 95 | 0 | 0 | 0 | 1 | 0 | 0 |
| 8 | 0 | 0 | 62 | 0 | 0 | 0 | 0 | 0 |
| 9 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 0 |
| 10 | 12 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| SNN-cliq | ||||||||
| 1 | 0 | 0 | 0 | 1 | 21 | 0 | 0 | 2 |
| 2 | 21 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 3 | 239 | 264 | 24 | 7 | 18 | 19 | 19 |
| Phneo-Graph | ||||||||
| 1 | 0 | 0 | 147 | 0 | 0 | 3 | 0 | 1 |
| 2 | 0 | 1 | 101 | 1 | 2 | 12 | 1 | 5 |
| 3 | 0 | 83 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0 | 73 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 3 | 2 | 0 | 22 | 3 | 1 | 17 | 8 |
| 6 | 2 | 2 | 16 | 2 | 6 | 2 | 1 | 7 |
| 7 | 0 | 31 | 0 | 0 | 0 | 0 | 0 | 0 |
| 8 | 0 | 27 | 0 | 0 | 0 | 0 | 0 | 0 |
| 9 | 0 | 20 | 0 | 0 | 0 | 0 | 0 | 0 |
| 10 | 18 | 0 | 147 | 0 | 0 | 0 | 0 | 0 |
| 11 | 1 | 0 | 0 | 0 | 17 | 0 | 0 | 0 |
‘Other’ indicates the 21 (638–617) cells that were not assigned to any cell type in (17).
Table 2.
Comparison of the inferred cluster assignments for the whole 638 cells in the human pancreatic islets dataset by CIDR and SC3, as well as the cluster configuration for the 617 cells based on the known gene markers reported in (17)
| Cluster | Acinar | Alpha | Beta | Delta | Ductal | PP/Gamma | Stellate | Other |
|---|---|---|---|---|---|---|---|---|
| CIDR | ||||||||
| 1 | 2 | 2 | 1 | 2 | 5 | 0 | 0 | 9 |
| 2 | 0 | 0 | 99 | 1 | 0 | 1 | 0 | 1 |
| 3 | 0 | 2 | 148 | 3 | 0 | 0 | 0 | 0 |
| 4 | 0 | 0 | 0 | 1 | 0 | 0 | 18 | 5 |
| 5 | 0 | 84 | 13 | 5 | 0 | 6 | 0 | 0 |
| 6 | 1 | 151 | 3 | 12 | 2 | 11 | 0 | 3 |
| 7 | 21 | 0 | 0 | 1 | 21 | 0 | 1 | 3 |
| SC3 | ||||||||
| 1 | 0 | 213 | 0 | 0 | 0 | 0 | 0 | 1 |
| 2 | 0 | 2 | 0 | 0 | 0 | 0 | 0 | 3 |
| 3 | 0 | 10 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0 | 2 | 156 | 0 | 0 | 0 | 0 | 1 |
| 5 | 0 | 0 | 5 | 0 | 1 | 0 | 0 | 0 |
| 6 | 0 | 0 | 16 | 0 | 0 | 0 | 0 | 0 |
| 7 | 0 | 0 | 78 | 0 | 0 | 0 | 0 | 0 |
| 8 | 0 | 0 | 0 | 1 | 25 | 0 | 0 | 5 |
| 9 | 22 | 3 | 3 | 1 | 0 | 0 | 19 | 4 |
| 10 | 0 | 0 | 0 | 22 | 1 | 17 | 0 | 0 |
| 11 | 2 | 9 | 6 | 1 | 1 | 1 | 0 | 7 |
‘Other’ indicates the 21 (638–617) cells that were not assigned to any cell type in (17).
Figure 1.
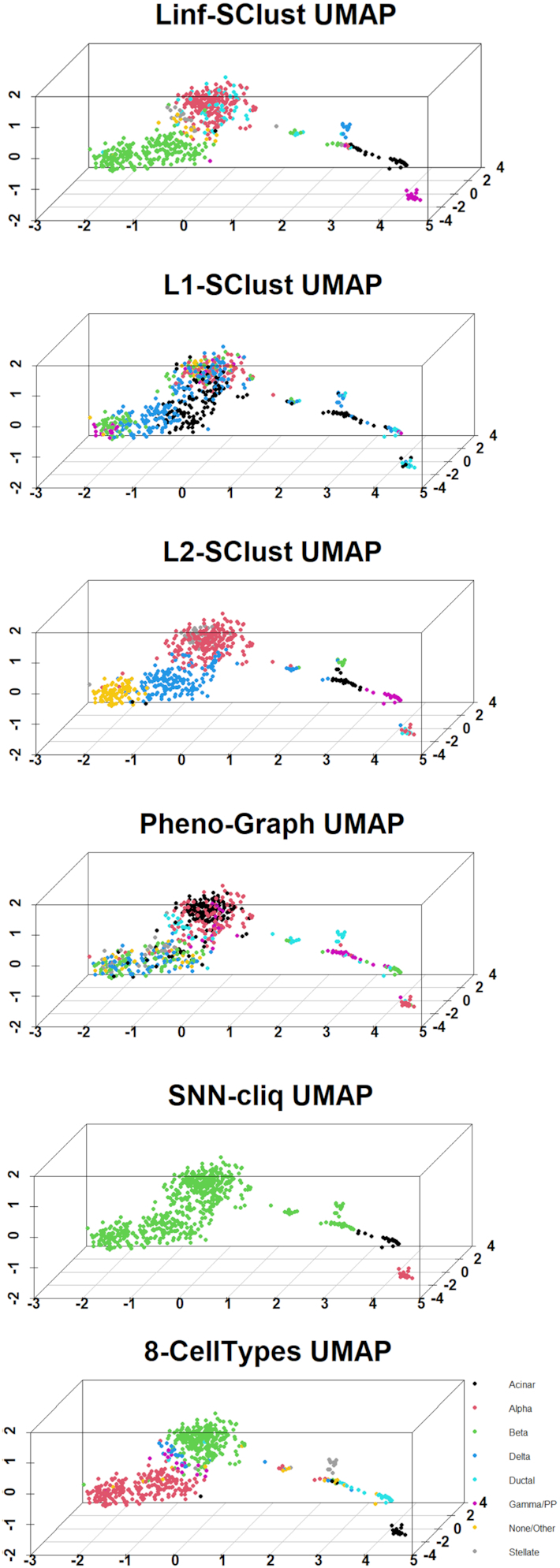
UMAP Plot for Linf-SClust, L1-SClust, L2-SClust, Pheno-Graph, SNN-cliq, and the original clustering results reported in (18) with eight clusters: beta cells (INS), alpha cells (GCG), delta cells (SST), PP/gamma cells (PPY), acinar cells (PRSS1), stellate cells (COL1A1), ductal cells (KRT19) and other cells.
The original clustering result reported in (17) is visualized in the bottom panel in Figure 1. To quantify the difference between the result from each method and the original result in (17), we computed a purity measure. Specifically, we first identified the most frequent class in each cluster reported by each compared method based on the original cell type assignment in (17). Then, we counted the number of consistently assigned cells by each method compared with the original cell type assignment result in (17). Then, we calculated the purity by dividing this count by the total number of cells (638). The purity for each compared method is shown in Table 4. One can see that Linf-SClust is the most consistent with the original cell type assignment result in (17), which was based on one known biomarker for each cell type. This finding is consistent with the methodological nature of Linf-SClust. We further illustrated this point in Table 3 by computing the between/within-cluster dissimilarity ratios calculated based on L∞, L1 and L2 norms for the cells assigned to the seven types by the corresponding seven known biomarkers in (17). The L∞ norm resulted in the largest average ratio (around 1.26) compared to the ratios based on the L1 norm (around 1.06) and the L2 norm (around 1.05). This is consistent with the performance of Linf-SClust, L1-SClust and L2-SClust applied to this real dataset.
Table 4.
Purity of seven methods in human pancreatic islets data containing eight cell types: beta cell (INS), alpha cell (GCG), delta cell (SST), PP/gammacell (PPY), acinar cell (PRSS1), stellate cell (COL1A1), ductal cell (KRT19) and other cell
| Method | Linf-SClust | L1-SClust | L2-SClust | Pheno-Graph |
|---|---|---|---|---|
| Purity | 0.9467 | 0.5627 | 0.8511 | 0.8699 |
| Method | SNN-cliq | CIDR | SC3 | |
| Purity | 0.4796 | 0.8307 | 0.8856 |
Table 3.
Comparison of between/within-cluster dissimilarity ratios for the seven cell types in the human pancreatic islets dataset (17)
| Genes | PRSS1 | GCG | INS | SST | KRT19 | PPY | COL1A1 |
|---|---|---|---|---|---|---|---|
| Cells | acinar | alpha | beta | delta | ductal | gamma | stellate |
| L ∞ | 1.23 | 1.31 | 1.26 | 1.32 | 1.18 | 1.33 | 1.17 |
| L 1 | 1.10 | 1.06 | 1.02 | 1.05 | 1.04 | 1.04 | 1.09 |
| L 2 | 1.08 | 1.06 | 1.02 | 1.04 | 1.06 | 1.03 | 1.06 |
Biologically, we further investigated the genes contributed to the clustering in Linf-SClust. Specifically, we calculated pairwise distances for all the 638 cells based on the L∞ norm. In total, we obtained 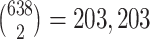 dissimilarities. For each obtained dissimilarity, we investigated which gene made the contribution in L∞. We summarized the frequencies of the ‘gene contributors’, and ranked them in Table 5. One can see that GCG, INS, SST and PPY are the top four ‘gene contributors’, PRSS1 is the eighth and COL1A1 is the 180th. The existing study in (17) only assigned 617 cells to certain known cell types based on these seven marker genes. There were 21 (638–617) cells without cell type information. Our Linf-SClust method and the analyses provide the potential direction to improve the cell-type discovery for human pancreatic islets based on single-cell RNA-seq data. Furthermore, for running time, it took about 1.2 min to run the Linf-SClust method with a specified perplexity value and the number of clusters on the single-cell RNA-seq dataset with 26,616 genes and 638 cells using a computer with one Intel64 processor.
dissimilarities. For each obtained dissimilarity, we investigated which gene made the contribution in L∞. We summarized the frequencies of the ‘gene contributors’, and ranked them in Table 5. One can see that GCG, INS, SST and PPY are the top four ‘gene contributors’, PRSS1 is the eighth and COL1A1 is the 180th. The existing study in (17) only assigned 617 cells to certain known cell types based on these seven marker genes. There were 21 (638–617) cells without cell type information. Our Linf-SClust method and the analyses provide the potential direction to improve the cell-type discovery for human pancreatic islets based on single-cell RNA-seq data. Furthermore, for running time, it took about 1.2 min to run the Linf-SClust method with a specified perplexity value and the number of clusters on the single-cell RNA-seq dataset with 26,616 genes and 638 cells using a computer with one Intel64 processor.
Table 5.
Selected frequencies for known marker genes by Linf-SClust in the clustering of the total 638 cells, which include 617 cells based on the known gene markers reported in (17) and other 21 (638–617) cells that were not assigned to any cell type in (17)
| GeneIndex | GeneName | CellType | Frequency | Percent | Order | |
|---|---|---|---|---|---|---|
| 1 | ENSG00000115263 | GCG | Alpha | 40340 | 19.85% | 1 |
| 2 | ENSG00000254647 | INS | Beta | 34360 | 16.91% | 2 |
| 3 | ENSG00000115263 | SST | Delta | 9469 | 4.66% | 3 |
| 4 | ENSG00000115263 | PPY | PP/Gamma | 9161 | 4.51% | 4 |
| 5 | ENSG00000115263 | PRSS1 | Acinar | 5283 | 2.60% | 8 |
| 6 | ENSG00000115263 | COL1A1 | Stellate | 92 | 0.05% | 180 |
Simulations
We further investigated Linf-SClust, L1-SClust, L2-SClust and 13 other methods including CIDR, FlowSOM, monocle, PCAHC, PCAKmeans, pcaReduce, RaceID2, RtsneKmeans, SAFE, SC3, SC3svm, Seurat and TSCAN using 15 simulated single-cell RNA-seq datasets in (18). Table 6 provides an overview of these simulated datasets. These simulated datasets were generated based on certain real datasets using different methods (named as HVG10, Expr10 and M3Drop10), and provided true cell labels (18). We used four evaluation criteria, i.e. ARI (Adjusted Rand Index) (19), NMI (Normalized Mutual Information) (20), purity and classification error rate, to investigate the performances of the 16 methods applied to the 15 simulated datasets.
Table 6.
A simple introduction to 15 simulation datasets
| Dataset | Cells | Genes | TrueClass |
|---|---|---|---|
| Koh_HVG10 | 531 | 4898 | 9 |
| Koh_Expr10 | 531 | 4898 | 9 |
| Koh_M3Drop10 | 531 | 4898 | 9 |
| Kumar_HVG10 | 246 | 4515 | 3 |
| Kumar_Expr10 | 246 | 4515 | 3 |
| Kumar_M3Drop10 | 246 | 4515 | 3 |
| Zhengmix4eq_HVG10 | 3300 | 1557 | 4 |
| Zhengmix4eq_Expr10 | 3555 | 1556 | 4 |
| Zhengmix4eq_M3Drop10 | 3430 | 1557 | 4 |
| Zhengmix4uneq_HVG10 | 5079 | 1644 | 4 |
| Zhengmix4uneq_Expr10 | 6414 | 1644 | 4 |
| Zhengmix4uneq_M3Drop10 | 3830 | 1644 | 4 |
| Zhengmix8eq_HVG10 | 3798 | 1572 | 8 |
| Zhengmix8eq_Expr10 | 3971 | 1571 | 8 |
| Zhengmix8eq_M3Drop10 | 2662 | 1572 | 8 |
Koh, Kumar, Zhengmix4eq, Zhengmix4uneq and Zhengmix8eq are the name of five real datasets name, as well as HVG10, Expr10 and M3Drop10 are three methods of filtering gene from real datasets (18). ‘TrueClass’ is a synonym for ‘True Cluster’ in simulation datasets.
We first investigated the effects of perplexity on the performances of Linf-SClust, L1-SClust and L2-SClust applied to the simulated datasets. Supplementary Figures S2–4 show the effects of perplexity on the four evaluation criteria applying Linf-SClust, L1-SClust and L2-SClust to the 15 simulated datasets with various perplexity values. One can see that Linf-SClust has the best overall performances on datasets Zhengmix4eq, Zheng4uneq and Zhengmix8eq with various perplexity values. L2-SClust has the best overall performance on dataset Koh. L1-SClust and L2-SClust have good overall performances on dataset Kumar. These findings suggest that it is necessary to have the options for different types of distances for single-cell RNA-seq clustering methods to facilitate the applications to diverse biological contexts.
We then compared Linf-SClust, L1-SClust and L2-SClust with the 13 clustering methods including CIDR, FlowSOM, monocle, PCAHC, PCAKmeans, pcaReduce, RaceID2, RtsneKmeans, SAFE, SC3, SC3svm, Seurat and TSCAN using the simulated datasets. We used the perplexity values that yielded the best performances for Linf-SClust, L1-SClust, L2-SClust in this study. Figures 2, 3, 4 show the comparison results for the 16 clustering methods. To summarize the comparisons, at least one of the proposed methods (i.e. Linf-SClust, L1-SClust and L2-SClust) was among the top five methods with good performances. In particular, L1-SClust ranks the first on the dataset HVG10_Kumar, Linf-SClust ranks the second on dataset Expr10_Zhengmix8eq, and L2-SClust ranks the second on dataset M3Drop10_Kumar. These findings suggest the graph-based spectral clustering techniques can be helpful for single-cell RNA-seq clustering problems.
Figure 2.
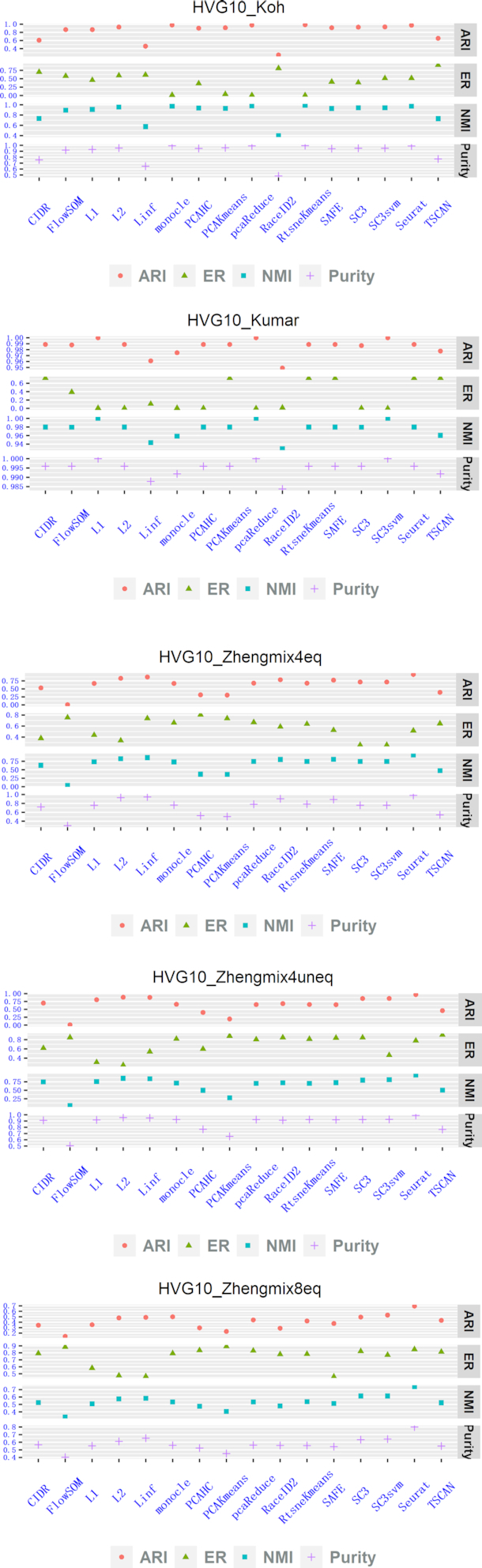
Method comparisons on five simulation datasets obtained via gene-filtering method ‘HVG10’.
Figure 3.
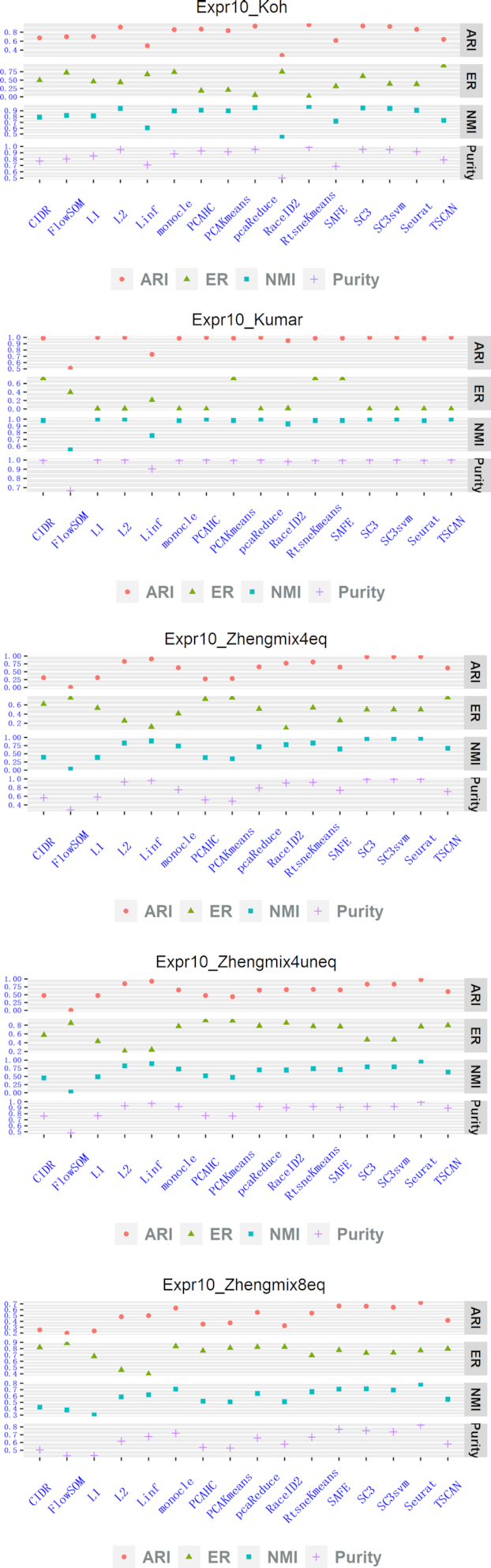
Method comparisons on five simulation datasets obtained via gene-filtering method ‘Expr10’.
Figure 4.
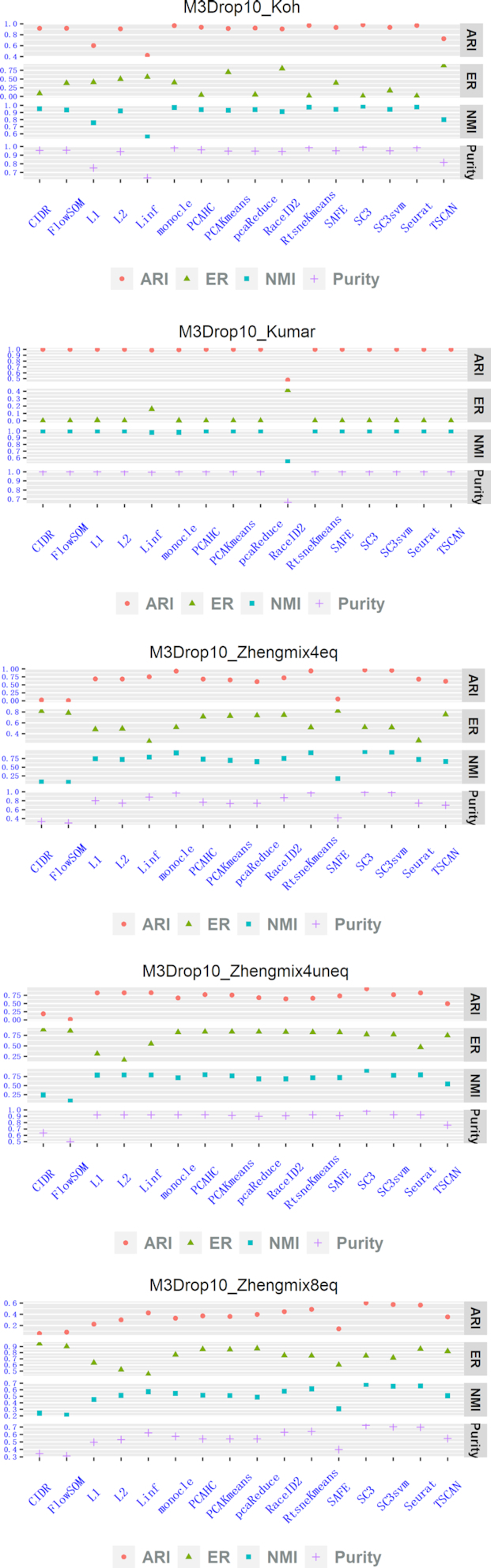
Method comparisons on five simulation datasets obtained via gene-filtering method ‘M3Drop10’.
CONCLUSION
We developed a new graph-based single-cell clustering framework. Under this framework, we investigated the choices on different measures (i.e. L∞, L1 and L2) used for dissimilarity characterization on clr-transformed single-cell RNA-seq data. We theoretically investigated the effects of L∞, L1 and L2 measures used for dissimilarity calculations on clustering. We applied the proposed methods to the clr-transformed single-cell RNA-seq data from human pancreatic islets. We found that the Linf-SClust method is suitable for this dataset, which provides biologically meaningful insights. We also compared the proposed methods with existing single-cell clustering methods through real data application and simulations. These analyses suggest the proposed methods are valuable additions to single-cell clustering methods.
Supplementary Material
ACKNOWLEDGEMENTS
The authors acknowledge the comments and suggestions from anonymous reviewers.
Contributor Information
Hao Wu, Department of Statistics, University of Connecticut, 215 Glenbrook Rd., Storrs, CT 06269, USA.
Disheng Mao, Department of Statistics, University of Connecticut, 215 Glenbrook Rd., Storrs, CT 06269, USA.
Yuping Zhang, Department of Statistics, University of Connecticut, 215 Glenbrook Rd., Storrs, CT 06269, USA.
Zhiyi Chi, Department of Statistics, University of Connecticut, 215 Glenbrook Rd., Storrs, CT 06269, USA.
Michael Stitzel, The Jackson Laboratory for Genomic Medicine, 10 Discovery Drive, Farmington, CT 06032, USA.
Zhengqing Ouyang, Department of Biostatistics and Epidemiology, School of Public Health and Health Sciences, University of Massachusetts, 715 North Pleasant Street, Amherst, MA 01003, USA.
SUPPLEMENTARY DATA
Supplementary Data are available at NARGAB Online.
FUNDING
Faculty Research Excellence Program Award from the University of Connecticut (to Y.Z.).
Conflict of interest statement. None declared.
REFERENCES
- 1. Macosko E.Z., Basu A., Satija R., Nemesh J., Shekhar K., Goldman M., Tirosh I., Bialas A.R., Kamitaki N., Martersteck E.M. et al. Highly parallel genome-wide expression profiling of individual cells using nanoliter droplets. Cell. 2015; 161:1202–1214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Xu C., Su Z. Identification of cell types from single-cell transcriptomes using a novel clustering method. Bioinformatics. 2015; 31:1974–1980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Levine J.H., Simonds E.F., Bendall S.C., Davis K.L., Amir E.A.D., Tadmor M.D., Litvin O., Fienberg H.G., Jager A., Zunder E.R. et al. Data-driven phenotypic dissection of AML reveals progenitor-like cells that correlate with prognosis. Cell. 2015; 162:184–197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Esteva A., Kuprel B., Novoa R.A., Ko J., Swetter S.M., Blau H.M., Thrun S. Dermatologist-level classification of skin cancer with deep neural networks. Nature. 2017; 542:115–118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Zhang Y., Ouyang Z., Zhao H. A statistical framework for data integration through graphical models with application to cancer genomics. Ann. Appl. Stat. 2017; 11:161–184. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Liu Q., Zhang Y. Joint estimation of heterogeneous exponential Markov Random Fields through an approximate likelihood inference. J. Stat. Plan. Infer. 2020; 209:252–266. [Google Scholar]
- 7. Linder H., Zhang Y. Iterative integrated imputation for missing data and pathway models with applications to breast cancer subtypes. Commun. Stat. Appl. Methods. 2019; 26:411–430. [Google Scholar]
- 8. Linder H., Zhang Y. A pan-cancer integrative pathway analysis of multi-omics data. Quant. Biol. 2020; 8:1–13. [Google Scholar]
- 9. Zhang Y., Qian M., Ouyang Q., Deng M., Li F., Tang C. Stochastic model of yeast cell-cycle network. Physica D. 2006; 219:35–39. [Google Scholar]
- 10. Aitchison J. The statistical analysis of compositional data. J. R. Stat. Soc. B. 1982; 44:139–160. [Google Scholar]
- 11. Quinn T.P., Erb I., Richardson M.F., Crowley T.M. Understanding sequencing data as compositions: an outlook and review. Bioinformatics. 2018; 34:2870–2878. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Embrechts P., Klüppelberg C., Mikosch T. Modelling Extremal Events: for Insurance and Finance. 2013; 33:Heidelberg, Germany: Springer-Verlag. [Google Scholar]
- 13. Hinton G.E., Roweis S.T.. Becker S, Thrun S, Obermayer K Stochastic neighbor embedding. Advances in Neural Information Processing Systems. 2003; Cambridge, MA, USA: MIT Press; 857–864. [Google Scholar]
- 14. Hagen L., Kahng A.B. New spectral methods for ratio cut partitioning and clustering. IEEE T. Comput. Aid. D. 1992; 11:1074–1085. [Google Scholar]
- 15. Von Luxburg U. A tutorial on spectral clustering. Stat. Comput. 2007; 17:395–416. [Google Scholar]
- 16. Tibshirani R., Walther G., Hastie T. Estimating the number of clusters in a data set via the gap statistic. J. R. Stat. Soc. B Stat. Methodol. 2001; 63:411–423. [Google Scholar]
- 17. Lawlor N., George J., Bolisetty M., Kursawe R., Sun L., Sivakamasundari V., Kycia I., Robson P., Stitzel M.L. Single-cell transcriptomes identify human islet cell signatures sqand reveal cell-type–specific expression changes in type 2 diabetes. Genome Res. 2017; 27:208–222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Duò A., Robinson M.D., Soneson C. A systematic performance evaluation of clustering methods for single-cell RNA-seq data. F1000Res. 2018; 1141–1163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Yeung K.Y., Ruzzo W.L. Details of the adjusted rand index and clustering algorithms, supplement to the paper an empirical study on principal component analysis for clustering gene expression data. Bioinformatics. 2001; 17:763–774. [DOI] [PubMed] [Google Scholar]
- 20. Knops Z.F., Maintz J.A., Viergever M.A., Pluim J.P. Normalized mutual information based registration using k-means clustering and shading correction. Med. Image. Anal. 2006; 10:432–439. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


