Evaluation of the properties of daughter bubbles generated by inertial cavitation of preformed microbubbles

Highlights

• •DBs properties from theoretical dissolution curves and measured scattering intensity curves.
• •Increasing PNP reduced the mean size and lifetime of DBs, and narrowed size range.
• •Increasing PL caused a decrease in mean size, lifetime and size range of DBs.
• •IC dose negatively correlated with mean size, lifetime and size range of DBs.

Abstract

Inertial cavitation (IC) of the preformed microbubbles is being investigated for ultrasound imaging and therapeutic applications. However, microbubbles rupture during IC, creating smaller daughter bubbles (DBs), which may cause undesired bioeffects in the target region. Thus, it is important to determine the properties of DBs to achieve controllable cavitation activity for applications. In this study, we theoretically calculated the dissolution dynamics of sulfur hexafluoride bubbles. Then, we applied a 1-MHz single tone burst with different peak negative pressures (PNPs) and pulse lengths (PLs), and multiple 5-MHz tone bursts with fixed acoustic conditions to elicit IC of the preformed SonoVue microbubbles and scattering of DBs, respectively. After the IC and scattering signals were received by a 7.5-MHz transducer, time- and frequency-domain analysis was performed to obtain the IC dose and scattering intensity curve. The theoretical dissolution curves and measured scattering intensity curves were combined to determine the effect of the incident pulse parameters on the lifetime, mean radius and distribution range of DBs. Increased PNP reduced the lifetime and mean size of the DBs population and narrowed the size distribution. The proportion of small DBs (less than resonance size) increased from 36.83% to 85.98% with an increase in the PNP from 0.6 to 1.6 MPa. Moreover, increased PL caused a shift of the DB population to the smaller bubbles with shorter lifetime and narrower distribution. The proportion of small bubbles increased from 25.74% to 95.08% as the PL was increased from 5 to 100 µs. Finally, increased IC dose caused a smaller mean size, shorter lifetime and narrower distribution in the DB population. These results provide new insight into the relationship between the incident acoustic parameters and the properties of DBs, and a feasible strategy for achieving controllable cavitation activity in applications.

1. Introduction

The preformed artificial microbubbles are being developed for novel ultrasound imaging and therapeutic applications [1], [2]. Some techniques in ultrasound-mediated diagnosis and therapy are dependent on the rapid collapse and fragmentation of microbubble (inertial cavitation (IC)) after receiving ultrasonic pulses with high peak negative pressure (PNP) [3], [4]. For example, in flash echo imaging [5], destruction-reperfusion imaging [6] and acoustic angiography [7], [8], the acoustic emissions from the rapid destruction of microbubbles are acquired to increase the sensitivity of detection in the target region. Shockwave or directional microjects from collapsing bubbles during IC can violently crack cancerous tissue, improving the efficiency of ablation[9], or perforate plasma membrane [10], [11] and open blood–brain-barrier [12], thus facilitating the delivery of therapeutic agents into the target region.

Early optical observations showed that after rupture of the preformed microbubble shell, unconstrained smaller daughter bubbles (DBs) are generated [13], [14]. Passive cavitation detection revealed that short rebound signals follow the IC signals, which also indicates that the preformed microbubbles rupture to form DBs [15], [16]. Before DBs disappear because of static dissolution, they are able to grow and collapse essentially as new bubbles, thus undergo similar acoustic responses as the preformed microbubbles (i.e. scattering, linear or non-linear oscillation and fragmentation) [17], [18]. This acoustically-driven behavior, which is closely related to the properties of the DBs, including gas diffusion, dissolution velocity and size distribution, may cause undesirable and uncontrolled bioeffects in the targeted region, such as cell necrosis or hemorrhage, thus influencing the biosafety and efficiency of ultrasound-based applications [19], [20], [21]. Therefore, to control the biological responses elicited by IC, it is crucial to determine the properties of the DBs generated by IC.

Various optical and acoustic methods have been used to estimate the lifetime and size distribution of cavitation bubbles and their relationships with the parameters of the used incident pulse. For example, two laser techniques, including laser diffraction and phase Doppler interferometry, are commonly used to measure the size distribution of microbubble clouds (e.g. from distilled water exposed to a 20-kHz horn) for different acoustic pressures [22], [23]. Sonoluminescence (i.e. the light emission from collapsing microbubbles) or sonochemical luminescence (i.e. the light produced through chemical reaction of hydroxyl radicals with luminol) have also been used to determine the cavitation bubbles size for different acoustic frequencies and powers [24], [25]. In another study, the void rate curve of bubbles was measured using an electromagnetic resonator and the theoretical dissolution curve revealed that the size distribution of a cavitation bubble cloud (from air-saturated water exposed to 308-kHz ultrasound) is related to the acoustic pulse shape, acoustic pressure and exposure time [26], [27]. Moreover, a recent study that used a time–intensity curve and bubble dissolution kinetics found that increasing the pulse length (PL) and PNP increases the proportion of large bubbles and small bubbles (from the nanodroplets exposed to a tone bust pulse of 1.2-MHz), respectively [28]. Numerical calculations have also predicted that the active cavitation bubble size decreases and the size distribution narrows with increasing acoustic frequency, and that the radius decreases with increasing acoustic pressure [29], [30]. Although the original of the cavitation bubbles (e.g. distilled water, luminol solution and nano- or micro-droplets that exposed to acoustic waves with high PNP) are essentially different from that of DBs (e.g. preformed microbubbles), these methods can also be used for reference to analyze the properties of DBs. Notably, previous study has discriminated small DBs based on the measured dissolution process and the resonance features of dissolving bubbles [31]. However, there has not been a comprehensive study evaluating the effect of the incident acoustic parameters on the properties of DBs generated by IC of the preformed bubbles.

In this study, we established an experimental platform to evaluate the properties (lifetime, mean size and distribution range) of the DB population produced by IC of preformed SonoVue microbubbles. A single tone burst with different PNPs or PLs was used to elicit the fragmentation of microbubbles in an agarose phantom. Multiple tone bursts with fixed low PNP, PL and pulse repetition frequency (PRF) were used to track the temporal distribution of the scattering intensity of the resulting DBs. The lifetime and size distribution were calculated from the experimentally determined scattering intensity curves and the theoretically calculated dissolution curves of the DBs. Finally, the relationships between the properties of the DBs and the PNP and PL of the incident single tone burst were statistically determined.

2. Materials and methods

2.1. Performed microbubbles preparation and agarose-gel phantom fabrication

Before every experiment, 5 mL physiological saline solution (PSS) was mixed with lysophilisate (Bracco Research, Switzerland), followed by violently shaking to freshly reconstitute the SonoVue microbubble suspension, which had a size distribution of 2–8 µm. The preformed microbubble solution was then diluted with degassed PSS to a concentration of 0.1% v/v with an estimated 2–5 × 10⁵ microbubbles per milliliter, which is lower than that used in clinical ultrasound imaging [32].

A cubic agarose-gel phantom (45 mm × 35 mm × 50 mm) was fabricated according to the details described in our previous reports [33], [34]. A cavity (10 mm × 5 mm × 5 mm) in the bottom of the phantom was deliberately reserved to contain the preformed microbubble suspension. After the suspension was gently added into the cavity, the cavity was carefully sealed with a thin film. Noted that air bubbles must be prevented from entering the cavity to eliminate the influence of cavitation bubbles. In our previous studies, we showed that the acoustic properties of this phantom are similar to those of soft tissue of the human body [33], [34].

2.2. Experimental measurements

2.2.1. External triggering signals

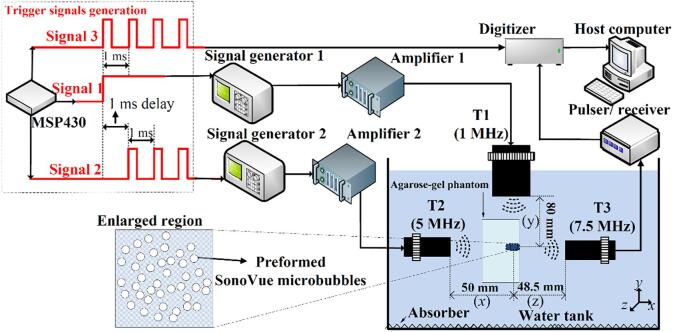
Three different external triggering signals generated by a single-chip microcomputer (MSP430) (Texas Instruments, USA) were used to enable two signal generators and a digitizer, as shown in the dotted box of Fig. 1. Specifically, a 3.3 V signal 1 was generated to trigger signal generator 1 (33120A, Agilent Technologies, USA) to produce a single sinusoid signal with varied PNP and PL. After a 1-ms delay, a square wave signal (signal 2) with the repetition frequency of 1 kHz was output to periodically trigger signal generator 2 (33120A, Agilent Technologies, USA) by its rising edge. This produced multiple tone bursts signals with a PNP of 0.08 MPa, PRF of 1 kHz and PL of 4 µs. A third square wave (signal 3) with a PRF of 1 kHz, which was synchronous with signal 1, was created by MSP430. Its rising edge was used as an external trigger to periodically enable the digitizer (Spectrum, Germany) to acquire the received acoustic signals.

Fig. 1.

A. Schematic representation of the experimental platform for measuring the IC of preformed microbubbles and the temporal distribution of the scattering intensity of the DBs. The data in the dotted box are the single-chip microcomputer output signals for triggering signal generators 1 and 2, and the digitizer. 1- and 5-MHz plane transducers were used to elicit IC of the preformed microbubbles and the scattering of DBs, respectively. The signals from IC scattering were received by a 7.5-MHz plane transducer, and then amplified using a pulser/receiver, acquired by the digitizer, and transferred to the host computer.

2.2.1.1. Emission of acoustic pulses and calibration

As shown in the experiment platform in Fig. 1, two transmitting transducers, T1 and T2, were immersed into degassed water, and perpendicularly installed to excite IC of the preformed SonoVue microbubbles and scattering of the DBs, respectively. A damping material (UA-1, Institute of Acoustics, Chinese Academy of Sciences, China) was placed at the bottom of the water tank to minimize acoustic reflections, thereby forming a travelling wave field during exposure. Specifically, first, a single sinusoid signal with 1 MHz frequency and varied voltage amplitude and cycles (i.e. PL), produced by the signal generators 1 and amplified by a 50-dB radiofrequency amplifier (2100L; Electronics &Innovation Ltd, USA), was used to drive a 1-MHz single element plane transducer T1 with active diameter of 25.4 mm (Advanced Devices, Wakefield, MA). This transducer was placed at a distance of 80 mm from the microbubble suspension in the agarose-gel phantom. This distance was above the theoretical near-field of the transducer on the acoustic axis, reducing the influence of slight variations in position (due to installment) on the acoustic pressure distribution in the target region. Because this transducer was used to elicit the violent collapse and disintegration of the preformed SonoVue microbubbles, the PNP should exceed the PNP threshold for inducing IC of the microbubbles. We varied the PNP and PL to analyze the influence of these parameters on the properties of the DBs.

Next, 1 ms after the emission of the single tone burst, the multiple tone bursts signal with 5 MHz frequency, fixed voltage amplitude, PL and PRF, (output from signal generator 2 and amplified by another 50-dB radiofrequency amplifier), was applied to drive a 5-MHz plane transducer (T2) (Advanced Devices, Wakefield, MA). This transducer had an active diameter of 13 mm and was installed at a distance of 50 mm from the sample region. We note that the pulse parameters need to be rationally selected to obtain a temporal distribution of the scattering intensity of DBs. According to our preliminary measurements, a 1-kHz PRF was selected to achieve high temporal resolution when tracking the static dissolution process of DBs and to avoid acoustically-driven diffusion, which can occur at higher PRFs. A PL of 4 µs was selected to reduce the probability of acoustically-driven diffusion. The PNP of 0.08 MPa is sufficient for exciting the scattering of DBs, while avoiding acoustically-driven diffusion or stable cavitation.

The transmitting pressure waveforms from these two transducers were separately calibrated using a capsule hydrophone (HGL-0200, ONDA, USA) in the sample region for different voltage amplitudes. The calibration details are provided in our previous reports [33], [34]. The-3-dB -6 dB profiles of T1 and T2 have diameters of ~ 15.5 and ~ 7.3 mm, respectively. These values are substantially greater than the length (5 mm) of the planar cross-section of the sample zone. Thus, the spatial distribution of the PNP within the sample zone is relatively homogeneous, which ensures the reliability of the experimental results.

2.2.1.2. Detection of inertial cavitation and scattering signals

As shown in Fig. 1, a plane transducer (T3) (Advanced Devices, Wakefield, MA) was used to receive the IC signals from the microbubbles and the scattering signals from the DBs. This transducer had a frequency of 7.5 MHz and an active diameter of 13 mm. This was perpendicularly installed with the above two transducers T1 and T2 at a distance of 48.5 mm from the sample region. The signals were amplified by a pulser-receiver with variable gain, and recorded using a 16-bit high-speed digitizer (Spectrum, M4i.4410, Germany) at a sampling rate of 6.5 × 10⁷ samples per second (sampling frequency $f_s=65\mathrm{M}$), before being saved in a host computer. The digitizer was activated by trigger signal 3, which was synchronized with signal generator 1. Noted that during inertial cavitation signals sampling, because the maximal PL of the single tone burst was 100 µs, and the real cavitation signals was recorded at 85.67 µs$[\approx (80+48.5mm)/(1500m/s)]$ after the digitizer activation, the minimal sampling point must be greater than 185.67 × 65$=12068.$ Thus,$16384=2^{14}$ was set as the number of sampling points. Finally, the recorded data were processed by fast Fourier transform and power spectrum analysis using MATLAB (Mathworks, USA).

2.2.1.3. Calculation of the inertial cavitation dose

Enhancement of broadband emission in the frequency spectrum (excluding the fundamental, harmonic, sub-harmonic and ultra-harmonic frequencies) represents the occurrence of inertial cavitation. After exposure to the single tone burst, the acquired signal from the preformed SonoVue microbubble suspension can be written as x(i) (i = 0, 1, ···, N − 1) (N: the number of sampling points). Fast Fourier transform was used to obtain the frequency spectrum:

$$X(k)=\sum _{i=0}^{N-1}x(i)e^{-j\frac{2\pi }{N}ik}(k=0,1,\dots ,N-1)$$ (1)

where k is the frequency point in the frequency spectrum. To determine the intensity of the broadband frequency components, the power spectrum of the signal was then calculated by

$$P(k)=X{(k)}^2(k=0,1,\dots ,N-1)$$ (2)

A notch filter with a 0.2-MHz stopband, centered at the harmonics and ultra-harmonics in the range of 1–10 MHz, was used to obtain the intensity of broadband emission:

$$\mathit{IC}{D}_m=252.06\times {10}^{-6}\times \sum _{a=1}^{16}\sum _{b=1}^{76}{P}_a\left(b\right)$$ (3)

where a and b are the number of broadband components and the number of frequency points in every broadband component, respectively. Noted that 16 broadband components ranged from $\left[0.5\times \left(a+3\right)+0.1\right]\mathrm{M}\mathrm{H}\mathrm{z}$ to $\left[0.5\times \left(a+4\right)-0.1\right]\mathrm{M}\mathrm{H}\mathrm{z}$, (a = 1,2, ···,16), and the total number (76) of frequency points in every broadband component can be calculated by $0.3M\times \left(16384/65M\right)\approx 76$. In equation (3), the coefficient $252.06\times {10}^{-6}\left(s\right)=N/f_s=16384/\left(65\times {10}^6\right)$ was the sampling time for inertial cavitation signals. After ICD_c from the control degassed saline solution was obtained, the real ICD from the preformed microbubbles can be calculated by:

$$\mathrm{I}\mathrm{C}\mathrm{D}={\mathrm{I}\mathrm{C}\mathrm{D}}_{\mathrm{m}}-{\mathrm{I}\mathrm{C}\mathrm{D}}_{\mathrm{c}}$$ (4)

2.2.1.4. Temporal distribution of the scattering intensity of daughter bubbles

To determine the change of the scattering intensity of the DBs with the exposure time, the scattering signals were temporally analyzed. The voltage amplitude of the recorded signal in a sampling period is V_n (j) (j = 1, ···, p; n = 1, 2, ···, q), where p and q are the number of sampling points in the sampling period and the number of the sampling period, respectively. Noted that a 16-bit AD conversion module was used in digitizer, and the reference voltages were $\pm 10V.$ After the binary source code (BS) was obtained, the voltage amplitude (V) of the recorded signal can be calculated by $V=BS\times (20/2^{16}).$The scattering intensity of DBs in a sampling period was calculated by

$I_{\mathrm{m}n}={\sum }_{j=1}^p{\left(V_n\left(j\right)\right)}^2·20.51\times {10}^{-6}$ (n = 1, 2, ···, q) (5)

where Thus, the temporal distribution of the scattering intensity from the DBs can be obtained by

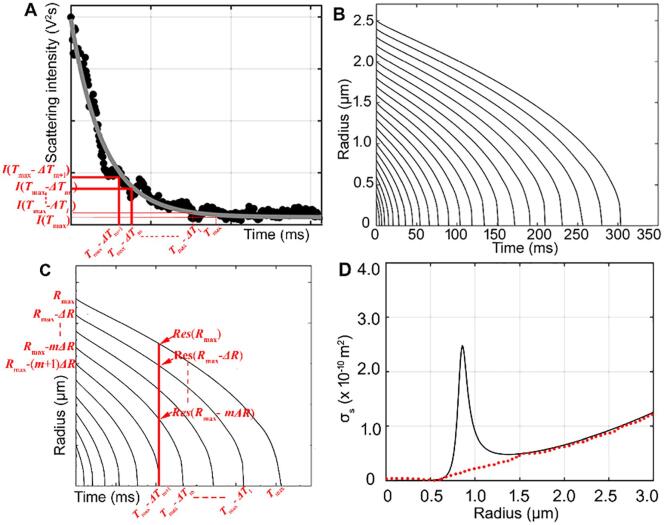
$I_n=I_{\mathrm{m}n}-I_{\mathrm{c}n}$(n = 1,2, ···, q) (6)where I_cn is the scattering intensity of the control saline solution, as shown in Fig. 2A. Finally, an exponential equation with three parameters (Please see section 2.3.2) was used to fit the experimental temporal distribution of the scattering intensity from the DBs, as shown in Fig. 2A.

Fig. 2.

A. Temporal distribution of the scattering intensity of DBs formed by IC of the microbubbles. The black dots are the experimentally-measured scattering intensity in one period of the multiple tone bursts ultrasound. The gray curve is the scattering intensity fitted by an exponential equation with three parameters. B. Theoretical dissolution curves for sulfur hexafluoride bubbles with different initial radii. C. Theoretical dissolution model for determining the residual radius of the dissolving bubble at a certain time point. D. (Black solid curve) the change of the theoretically calculated scattering intensity with the bubble radius. (Red dotted line) the change of the fitted scattering intensity with the bubble radius by exponential function. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

2.3. Theoretical calculations

2.3.1. Dissolution dynamics of bubbles

After the preformed SonoVue microbubbles were ruptured by the ultrasonic pulse with high PNP, unshelled DBs were produced. The dissolution process of a shell-ruptured bubble was theoretically calculated. For an air bubble in water undergoing static dissolution, the dissolution rate, which is mainly dependent on the initial bubble radius and the concentration of air in solution, can be calculated by the following equation [35]:

$\frac{\mathit{dR}}{\mathit{dt}}=-D_a{L}_a\frac{1-\frac{c_{\infty }}{c_0}+\frac{\tau }{R{\rho }_a}}{1+\frac{2\tau }{3R{\rho }_a}}\left(\frac{1}{R}+\frac{1}{\sqrt{\pi D_{a}t}}\right);\tau =\frac{2M_a\gamma }{R_{G}T}$ (7)

Noted that the SonoVue microbubbles used in the experiment contain a less water-soluble sulfur hexafluoride gas and no other gas is present in the degassed PSS. Thus, the gas enclosed in the bubble is the same as that dissolved in the solution, and the DB suspension can be considered as a single-component system. As $c_{\infty }=0$ in this system, the dissolution dynamics of a free bubble can be calculated by [35]

$\frac{\mathit{dR}}{\mathit{dt}}=-D_s{L}_s\frac{1+\frac{\tau }{R{\rho }_s}}{1+\frac{2\tau }{3R{\rho }_s}}\left(\frac{1}{R}+\frac{1}{\sqrt{\pi D_{s}t}}\right);\tau =\frac{2M_s\gamma }{R_{G}T}$ (8)

All parameters are defined in Table 1. The diffusion coefficient of sulfur hexafluoride can be calculated by [36]

$$D_s=A{e}^{-E_a/R_{G}T}$$ (9)

Table 1.

Parameters used in the study.

Symbol	Description	Value
$D_a$	Diffusion coefficient of air at 25℃	2 × 10−9 m2/s
$D_s$	Diffusion coefficient of SF6 at 25℃	1.20 × 10−9 m2/s
$L_a$	Ostwald coefficient of air	1.71 × 10−2
$L_s$	Ostwald coefficient of SF6	6.46 × 10−3
$c_{\infty }$	Concentration of dissolved gas in solution	0 kg/m3
$c_0$	Saturation concentration of dissolved gas
${\rho }_a$	Density of air	1.16 kg/m3
${\rho }_s$	Density of SF6	6.1 kg/m3
$M_a$	Molecular weight of air	29 × 10−3 kg/mol
$M_s$	Molecular weight of SF6	146 × 10−3 kg/mol
$\gamma$	Surface tensile	73 × 10−3N/m
$R_G$	Gas constant	8.314 J/mol°K
$T$	Absolute temperature	298 K
${\eta }_L$	Shear viscosity of water	0.001 kg/ms
$\omega$	Frequency	3.14 × 107 rad/s
${\rho }_w$	Density of water	1000 kg/m3
$c$	Sound speed	1500 m/s
$P_0$	Ambient pressure	105 Pa
A	Preexponential factor	0.029 cm2/s
Ea	Activation energy	19.4 kJ/mol

According to equation (8), the dissolution dynamics of sulfur hexafluoride bubbles with different initial radii is shown in Fig. 2B. Noted that the frequency ($\omega =3.14\times 107\mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s}$) in Table 1 corresponds to the frequency (5 MHz) of T2 transducer, which was used to excite the scattering of DBs. The −6 dB bandwidth of the used 7.5 MHz receiving transducer (T3) ranges from 4.5 MHz to 10.5 MHz, which covers the scattering signal of 5 MHz, thereby being suitable for receiving the scattering signals of DBs.

2.3.2. Calculation and modification scattering intensity of the bubble population

Because the microbubble radius is much shorter than the acoustic wavelength, microbubbles scatter acoustic waves, producing scattering signals in all directions. After determining the size (R) of a dissolving bubble at a given time according to equation (8), the corresponding theoretical scattering cross-section is calculated by [37]

$${\sigma }_s=4\pi R^2\frac{{\mathrm{\Omega }}^4}{{\left({\mathrm{\Omega }}^2-1\right)}^2+{\mathrm{\Omega }}^4{\delta }^2}$$ (10)

where Ω=$\omega /{\omega }_0$, and δ is the total damping constant, which includes viscous damping, δ_η, radiation damping, δ_R and thermal damping, δ_th. The resonance frequency ${\omega }_0$ can be calculated by

$${\omega }_0=\sqrt{\frac{1}{{\rho }_w{R}^2}\left[3R_G{P}_0+\frac{2\gamma \left(3R_G-1\right)}{R}\right]}$$ (11)

Because the thermal damping constant is an order of magnitude smaller than the sum of the viscous and radiation damping constants, the thermal damping is neglected for simplicity. The viscous and radiation damping are defined as

$${\delta }_{\eta }=\frac{4{\eta }_L}{{\omega }_0{\rho }_w{R}^2}$$ (12)

$${\delta }_R=\frac{{\omega }^{2}R}{{\omega }_{0}c}$$ (13)

For the low microbubble concentration, the interaction among microbubbles and the multiple scattering from microbubbles can be ignored. The scattering intensity from the bubble population can be expressed as [38]

$$I=\sum _{l=0}^{u}N\left(R_l\right){\sigma }_s\left(R_l\right)$$ (14)

N and l are the number of the bubbles in population and the size of the bubble. Therefore, the scattering intensity is dependent on the scattering cross-section of the bubbles and the number of bubbles.

For the equation (14), first, an exponential function$(a\times e^{\mathit{bt}}+l,$where t is the related time during the static dissolution of the bubbles) was used to fit the temporal curve of the scattering intensity, and these coefficients were estimated using iterative least squares estimation. Second, in our experimental system, the 5-MHz incident wave can elicit the resonance of bubbles with a radius of ~ 0.86 µm. During the static dissolution process of the bubbles, the change of scattering cross-section with the bubble radius doesn’t follow the exponential decay function, and had a sudden peak when the radius of the dissolving DBs approached to the resonance size, as shown in Fig. 2D. Specifically, for the radius of the dissolving DBs larger than 1.3 µm or smaller than 0.6 µm, the scattering cross-section exponentially increases with the radius approximately. However, for the radius of the dissolving DBs ranging from 0.6 µm to 1.3 µm, the scattering section quickly increases when the radius is below resonance size (0.86 µm), and then rapidly reduces when the radius is above resonance size, therefore forming a resonance peak. To eliminate the difference between the measured scattering intensities and the theoretically calculated values (because of the influence of resonance peak), another exponential function ($(-7.68\times {10}^{-20})\times e^{5.78\times {10}^{-6}\times R}+(1.74\times {10}^{-11})\times e^{0.66\times {10}^{-6}\times R}$, where R is the radius of the dissolving bubbles) was obtained by fitting the scattering cross-section curve when the radius was above 1.3 µm. Finally, when applying equation (14), for the bubbles with radius below 1.3 µm, the scattering cross-section was modified using this exponential function. For the bubbles with radius below 1.65 µm, the scattering cross-section was theoretically calculated by equation (10).

2.4. Determination of the properties of daughter bubbles by the integration of theory and experiment

2.4.1. Lifetime estimation of the daughter bubble population

From the temporal curve of the scattering intensity of DBs in Fig. 2A, the scattering intensity first rapidly decayed and then gradually decreased, eventually reaching a relatively stable level (close to the control level). This trend describes the dissolution process of DBs (i.e. the size of the bubbles gradually decreases until they disappear). If the scattering intensity gradually reduced to a certain value (${I(T}_{\mathit{max}})$) in the temporal curve, the decreasing amount of which didn’t exceed 1% of the maximum intensity in the later time, the time ($T_{\mathrm{m}\mathrm{a}\mathrm{x}}$) corresponding to this value was considered as the lifetime of the daughter bubble population , as shown in Fig. 2A.

2.4.2. Estimation of the size distribution of daughter bubbles

First, after the $T_{\mathrm{m}\mathrm{a}\mathrm{x}}$ was determined by ${I(T}_{\mathit{max}})$, the maximal radius ($R_{\mathrm{m}\mathrm{a}\mathrm{x}}$) in DBs population can be obtained by the theoretical dissolution curve of the bubbles in Fig. 2C. Then, for DBs with an initial radius ($R_{\mathrm{m}\mathrm{a}\mathrm{x}}-1\times \mathrm{\Delta }R$), the complete dissolution time ($T_{\mathrm{m}\mathrm{a}\mathrm{x}}-{\mathrm{\Delta }T}_1$) of the bubbles can be theoretically determined by Fig. 2C (Noted that step size $\mathrm{\Delta }R$ in this study was selected as 0.2 µm. Because the bubbles behavior doesn’t change significantly when the bubble size has such relatively small change, the difference between the scattering from bubbles with smaller difference in radii cannot be detected by our experiment system with 16-bit AD). At this time point ($T_{\mathrm{m}\mathrm{a}\mathrm{x}}-{\mathrm{\Delta }T}_1$), the DBs with an initial radius less than ($R_{\mathrm{m}\mathrm{a}\mathrm{x}}-1\times \mathrm{\Delta }R$) has completely dissolved, and only the DBs with maximal radius ($R_{\mathrm{m}\mathrm{a}\mathrm{x}}$) remained due to incomplete dissolution (the corresponding remained radius $R_{\mathrm{r}\mathrm{e}\mathrm{s}}\left(R_{\mathrm{m}\mathrm{a}\mathrm{x}}\right)$can be obtained by theoretical dissolution curve in Fig. 2C). Moreover, the measured scattering intensity ${I(T}_{\mathit{max}}-{\mathrm{\Delta }T}_1)$ at this time point which were produced from those remained DBs can be obtained by the fitted curve in Fig. 2A. According to the Equation (14), at this time point, the fitted scattering intensity ${I(T}_{\mathit{max}}-{\mathrm{\Delta }T}_1)$ was approximately equal to the theoretically calculated intensity,

$$I\left(T_{\mathrm{m}\mathrm{a}\mathrm{x}}-\mathrm{\Delta }{T}_1\right)=N\left(R_{\mathrm{m}\mathrm{a}\mathrm{x}}\right)\times {\sigma }_s{[R}_{\mathrm{r}\mathrm{e}\mathrm{s}}\left(R_{\mathrm{m}\mathrm{a}\mathrm{x}}\right)]$$ (15)

Thus, the relative number $N\left(R_{\mathrm{m}\mathrm{a}\mathrm{x}}\right)$of the DBs with maximal radius ($R_{\mathrm{m}\mathrm{a}\mathrm{x}}$) can be calculated by equation (15).

Next, based on the obtained $N\left(R_{\mathrm{m}\mathrm{a}\mathrm{x}}\right),$ the relative number $N\left(R_{\mathrm{m}\mathrm{a}\mathrm{x}}-m\mathrm{\Delta }R\right)(m=1,2,···)$of the DBs with radius $R_{\mathrm{m}\mathrm{a}\mathrm{x}}-m\mathrm{\Delta }R,\left(m=1,2,···\right)$can be recursively obtained step by step. Specifically, for the bubbles with an initial radius$R_{\mathrm{m}\mathrm{a}\mathrm{x}}-m\mathrm{\Delta }R$, the corresponding complete dissolution time $T_{\mathrm{m}\mathrm{a}\mathrm{x}}-{\mathrm{\Delta }T}_m$ $(m=1,2,···)$ can be obtained by Fig. 2C. At the time point $T_{\mathrm{m}\mathrm{a}\mathrm{x}}-{\mathrm{\Delta }T}_{m+1}$, although the DBs with an initial radius less than $R_{\mathrm{m}\mathrm{a}\mathrm{x}}-(m+1)\mathrm{\Delta }R$ had completely dissolved, those with an initial radius greater than $R_{\mathrm{m}\mathrm{a}\mathrm{x}}-(m+1)\mathrm{\Delta }R$(i.e. $R_{\mathrm{m}\mathrm{a}\mathrm{x}}$,$R_{\mathit{max}}-\mathrm{\Delta }R,···,R_{\mathrm{m}\mathrm{a}\mathrm{x}}-m\mathrm{\Delta }R$) remained. The radius of these remained bubbles $R_{\mathrm{r}\mathrm{e}\mathrm{s}}$($R_{\mathrm{m}\mathrm{a}\mathrm{x}}-(m+1)\mathrm{\Delta }R$) at the time point of $T_{\mathrm{m}\mathrm{a}\mathrm{x}}-{\mathrm{\Delta }T}_{m+1}$, can be obtained by theoretical dissolution curve, as shown in Fig. 2C. Theoretically, at this time point, the scattering intensity from these remained bubbles can be calculated as

$$N\left(R_{\mathrm{m}\mathrm{a}\mathrm{x}}\right)\times {\sigma }_s{[R}_{\mathrm{r}\mathrm{e}\mathrm{s}}\left(R_{\mathrm{m}\mathrm{a}\mathrm{x}}\right)]+N\left(R_{\mathrm{m}\mathrm{a}\mathrm{x}}-\mathrm{\Delta }R\right)\times {\sigma }_s{[R}_{\mathrm{r}\mathrm{e}\mathrm{s}}\left(R_{\mathrm{m}\mathrm{a}\mathrm{x}}-\mathrm{\Delta }R\right)]+···+N\left(R_{\mathrm{m}\mathrm{a}\mathrm{x}}-\mathrm{m}\mathrm{\Delta }R\right)\times {\sigma }_s{[R}_{\mathrm{r}\mathrm{e}\mathrm{s}}\left(R_{\mathrm{m}\mathrm{a}\mathrm{x}}-m\mathrm{\Delta }R\right)](m=1,2,···)$$ (16)

Moreover, at this time point, the measured scattering intensity$I\left(T_{\mathrm{m}\mathrm{a}\mathrm{x}}-\mathrm{\Delta }{T}_{m+1}\right)$ can be also obtained from the fitted curve in Fig. 2A. Therefore,

$$I\left(T_{\mathrm{m}\mathrm{a}\mathrm{x}}-\mathrm{\Delta }{T}_{m+1}\right)=N\left(R_{\mathrm{m}\mathrm{a}\mathrm{x}}\right)\times {\sigma }_s{[R}_{\mathrm{r}\mathrm{e}\mathrm{s}}\left(R_{\mathrm{m}\mathrm{a}\mathrm{x}}\right)]+N\left(R_{\mathrm{m}\mathrm{a}\mathrm{x}}-\mathrm{\Delta }R\right)\times {\sigma }_s{[R}_{\mathrm{r}\mathrm{e}\mathrm{s}}\left(R_{\mathrm{m}\mathrm{a}\mathrm{x}}-\mathrm{\Delta }R\right)]+···+N\left(R_{\mathrm{m}\mathrm{a}\mathrm{x}}-\mathrm{m}\mathrm{\Delta }R\right)\times {\sigma }_s{[R}_{\mathrm{r}\mathrm{e}\mathrm{s}}\left(R_{\mathrm{m}\mathrm{a}\mathrm{x}}-m\mathrm{\Delta }R\right)](m=1,2,···)$$ (17)

$N\left(R_{\mathrm{m}\mathrm{a}\mathrm{x}}-m\mathrm{\Delta }R\right)(m=1,2,···)$ could be recursively derived step by step by equation (17). Finally, the mean size and the full width at half height (FWHH) were used to evaluate the characteristics of the DB size distribution. The mean size was calculated using the following equation:

$$\mathrm{M}\mathrm{S}=\frac{{\sum }_{n=0}^{m-1}N\left(R_{\mathrm{m}\mathrm{a}\mathrm{x}}-n\mathrm{\Delta }R\right){\times (R}_{\mathrm{m}\mathrm{a}\mathrm{x}}-n\mathrm{\Delta }R)}{{\sum }_{n=0}^{m-1}N\left(R_{\mathrm{m}\mathrm{a}\mathrm{x}}-n\mathrm{\Delta }R\right)}$$ (18)

2.5. Statistics analysis

Under the used single tone burst and multiple tone bursts, a minimum of three replicates experiments were carried out in both the control saline solution and the preformed SonoVue microbubbles solution. The standard deviation and mean were calculated for the related conditions.

3. Results

3.1. Inertial cavitation of preformed microbubbles

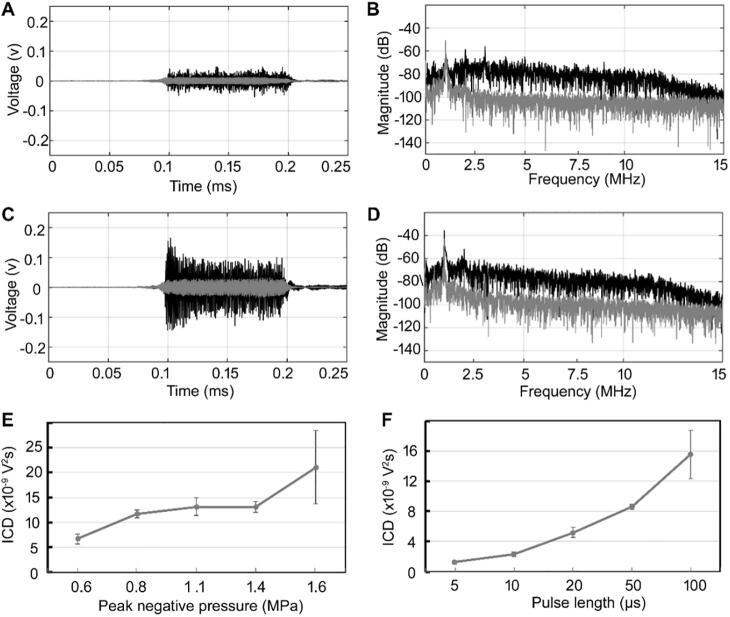
To analyze the characteristics of the DBs, the first step is to determine the occurrence and dose of IC of the preformed microbubbles after exposure to a single tone burst. In our previous reports, we determined that the PNP threshold for inducing IC of SonoVue microbubbles is ~ 0.40 MPa. Therefore, we used 0.60 MPa as the minimum PNP for inducing IC in this study. After the control saline solution and preformed SonoVue microbubbles were exposed to a single tone ultrasound pulse with a PL of 100 µs and PNP of 0.60 MPa, the time- and frequency-domain curves of the acoustic signals were measured and shown in Fig. 3A and 3B. As shown in Fig. 3A, the mean amplitude of the signal from the preformed microbubbles was higher than that from the saline solution. Only the fundamental frequency was observed in the frequency spectrum from control saline solution in Fig. 3B. By contrast, in the frequency spectrum of the microbubbles, the fundamental frequency and the broadband frequency components were enhanced, suggesting that the microbubbles had underwent IC. After exposure to a single tone burst with a higher PNP of 1.1 MPa and 100-µs PL , in the control saline solution, although the amplitude of signals in time-domain markedly increased in Fig. 3C (compared with those in Fig. 3A), only fundamental frequency and almost no obvious broadband signals were observed in Fig. 3D, suggesting the used acoustic parameters don’t induce the occurrence of cavitation in control saline solution (including agarose-gel phantom and water). However, in the microbubbles solution, the amplitudes of both the time-domain signals and broadband components notably increased (Fig. 3C and 3D), suggesting an enhancement of IC of the preformed microbubbles.

Fig. 3.

(A) Time-domain and (B) frequency spectra after the preformed microbubble and control saline solutions were exposed to a single tone burst with 0.60-MPa PNP and 100-µs PL. (C) Time-domain and (D) frequency spectra after the microbubbles and control saline solutions were exposed to a single tone burst with 1.1-MPa PNP and 100-µs PL. (Gray line: control saline solution; black line: microbubbles). (E, F) Relationships between the IC dose and the PNP (corresponding 100-µs PL) and PL (corresponding 1.1-MPa PNP), respectively.

We further determined the relationships between the IC dose and the PNP and PL. As shown in Fig. 3E, the IC dose gradually increased with increasing PNP. For example, the IC dose was 6.65 × 10⁻⁹ V²s at 0.6 MPa and 2.10 × 10⁻⁸ V²s at 1.6 MPa. Similarly, the IC dose was positively correlated with PL, as shown in Fig. 3F. When the PL was increased from 5 to 100 µs, the IC dose increased from 1.26 × 10⁻⁹ to 1.56 × 10⁻⁸ V²s. These results show that the extent of microbubble collapse and fragmentation increases at higher acoustic energy, which can be achieved either by increasing the PNP or PL. These results are consistent with those of previous reports from us and others [33], [34].

3.2. Temporal scattering intensity of daughter bubbles

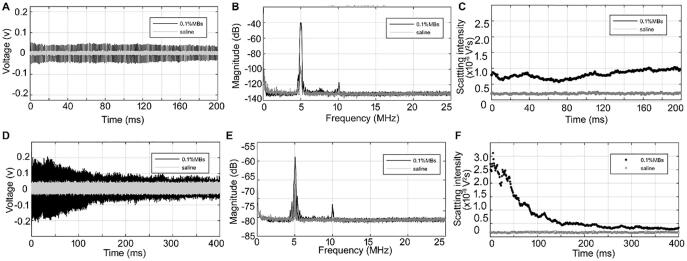
To determine the static dissolution process of DBs, 1000 acoustic pulses with a PNP of 0.08 MPa, PL of 4 µs and PRF of 1 kHz were applied. These conditions were appropriate to excite the scattering from DBs while avoiding acoustically-driven diffusion. Fig. 4A and 4B show the time- and frequency-domain curves of the control saline and preformed microbubble solutions exposed to these pulses. The amplitudes of the time-domain signals (Fig. 4A) from the control and microbubble solutions were relatively stable for a long period (here, we only show a 200-ms period), suggesting that the size of the microbubbles remained unchanged, and the microbubble population did not undergo acoustically-driven diffusion. Only the fundamental frequency of 5 MHz could be observed in the control saline solution, as shown in Fig. 4B. In addition to the fundamental frequency, almost no sub-harmonics, harmonics or ultra-harmonics were observed in the frequency spectrum of the microbubbles solution (only second-order harmonics with very small magnitude were observed), suggesting that the microbubble population only produced scattering signals, and did not nonlinearly oscillate after receiving these acoustic pulses. Fig. 4C shows that the scattering intensities from the control and microbubble solution are stable with the exposure time. These results show that the application of multiple tone bursts has little influence on the stability of the microbubbles, and could therefore be used to investigate the static dissolution process of DBs.

Fig. 4.

(A) Time-domain curve and (B) and frequency spectrum of the signals from the preformed SonoVue microbubble and control saline solutionsexposed to multiple tone bursts with 0.08-MPa PNP, 4-µs PL and 1-KHz PRF. C. Corresponding temporal distribution of the scattering intensity. (D) Time-domain curve and (E) and frequency spectrum after the preformed microbubble and control saline solutions were exposed to a single tone burst with 0.6-MPa PNP, followed by multiple tone bursts with 0.08-MPa PNP and 4-µs PL and 1-kHz PRF. (F) Corresponding temporal distribution of scattering intensity.

After the preformed microbubbles were exposed to a single tone burst with a high PNP, multiple tone bursts were used to excite the scattering from the DB population during their static dissolution. Fig. 4D showed that the amplitude of the scattering signal from DBs graduallyreduced to the control level with increasing exposure time. Only the fundamental frequency was observed in the frequency spectrum (Fig. 4E), suggesting that DBs only scatter the incident acoustic waves. Moreover, the scattering intensity gradually decreased with the exposure time, and finally approached the control level, as shown in Fig. 4F. These results show that the static dissolution process of DBs can be tracked by the used multiple tone bursts.

3.3. Relationship between PNP and the properties of the daughter bubbles

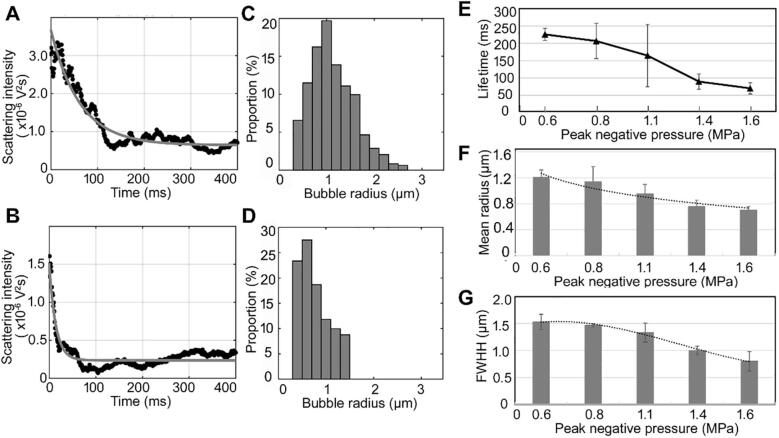
A single tone burst with a PL of 100 µs and different PNPs (0.60–1.6 MPa) was used to induce IC of preformed microbubbles and to determine the effect of PNP on the properties of the DBs. Fig. 5A and 5B show two typical scattering intensity curves from the samples. The samples were first exposed to single tone burst with PNPs of 0.6 and 1.6 MPa, respectively, and then, after a l-ms delay, were exposed to a 4-µs pulse with 0.08-MPa PNP and 1-kHz PRF for 1 s. The fitted scattering intensity curve in Fig. 5A shows that the amplitudes of the scattering signals from the bubble solution (which was excited by a single tone burst with 0.6-MPa PNP) continuously decreased in the first ~ 150 ms, and then gradually approached a stable level (close to that in the control saline solution) after ~ 220 ms. This trend indicates that the scattering cross-section of the DB population gradually decreased owing to the decreasing bubble radius during static dissolution. From Fig. 5A, we can see that the scattering intensity deceased to 0.16 × 10⁻⁶ v²s at ~ 225 ms after exposure to multiple tone bursts, followed by a very small reduction (less than the 1% of the maximum intensity) in the next time, so ~ 225 ms corresponds to the lifetime of the DB population. The calculated size distribution of DBs is shown in Fig. 5C. The distribution was Gaussian, with the proportions of bubbles larger and smaller than the resonance size (≈ 0.86 µm) being 65.70% and 34.30%, respectively. The corresponding mean size and FWHH were 1.21 µm and 1.52 µm, respectively. By contrast, after exposure to a single tone burst with PNP of 1.6 MPa, similar scattering intensity trend but with a faster decay was observed in Fig. 5B, suggesting a faster dissolution rate of the DBs formed. Similar distribution characteristics can be seen in Fig. 5D, although the lifetime (89.37 ms), mean size (0.77 µm) and FWHH (0.82 µm) are smaller in this case.

Fig. 5.

(A, B) Scattering intensity curves after the microbubble solution was exposed to a single tone burst with a PL of 100 µs and PNPs of 0.6 or 1.6 MPa. (The black dots are the experimentally-measured scattering intensity in one period of the multiple tone bursts. The gray curve is the scattering intensity fitted by an exponential equation with three parameters.) The corresponding size distributions are shown in (C) and (D), respectively. (E, F, G) Relationships between the PNP and lifetime, mean radius, and FWHH of the DB population, respectively.

The relationships between the PNP and the lifetime, mean bubble size and FWHH are shown in Fig. 5E–G, respectively. The lifetime decreases from 222.5 to 76.3 ms with an increase of the PNP from 0.6 to 1.6 MPa. In the DB population, the proportion of corresponding smaller bubbles (<resonance size) increased from 36.83% to 85.98% while the proportion of larger bubbles (>resonance size) decreased from 63.17% to 14.02%. With increasing PNP, the mean bubble size decreased from 1.21 to 0.70 µm and the distribution (FWHH) narrowed from 1.52 to 0.79 µm. These results show that the increasing PNP caused a shift of DBs to smaller bubbles with shorter life time.

3.4. Relationship between PL and the properties of the daughter bubbles

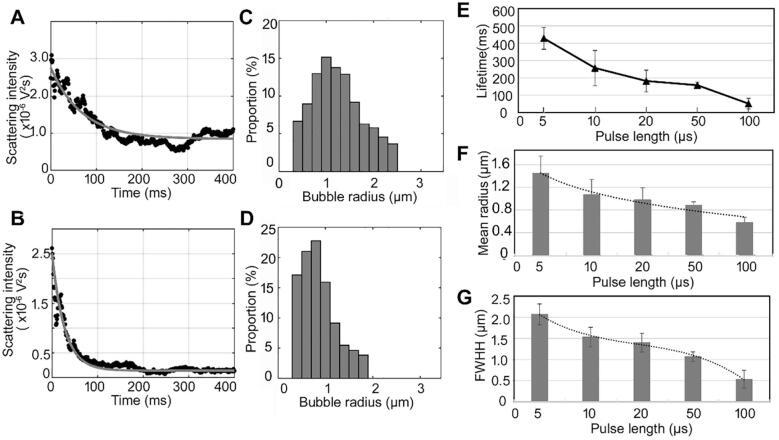
A single tone burst with a 1.1-MPa PNP and different PLs (5–100 µs) was used to investigate the effect of PL on the properties of the DB population. Two typical scattering intensities and size distribution curves from the preformed microbubbles exposed to 10- and 50-µs pulses are shown in Fig. 6A–D. The scattering intensity of the DBs formed after the 50-µs pulse exhibited faster exponential decay than for those formed after the 10-µs pulse (Fig. 6A and 6B), suggesting that longer pulse can cause faster dissolution rate of DBs. Moreover, the size distribution also shifted from big bubbles to small bubbles, as shown in Fig. 6C and 6D.

Fig. 6.

(A, B) Scattering intensity curves after the microbubble solution was exposed to a single tone burst with a PNP of 1.1 MPa and PLs of 10 or 50 µs, respectively. (The black dots are the experimentally-measured scattering intensity in one period of the multiple tone bursts ultrasound. The gray curve is the scattering intensity fitted by an exponential equation with three parameters.) The corresponding size distributions are shown in (C) and (D), respectively. (E, F, G) Relationships between the PNP and lifetime, mean radius, and FWHH of the DB population, respectively.

The relationships between the PL of the incident single tone burst and the lifetime, mean size and FWHH of DBs are shown in Fig. 6E–G. Fig. 6E shows that the lifetime gradually decreased with increasing PL. The rate of decrease was greatest at PL less than 20 µs, suggesting that these PLs have the greater influence on the formation of large DBs. The proportion of large bubbles (>resonance size) decreased with increasing PL, from 74.26% for a 5-µs pulse to 4.92% for a 100-µs pulse. The corresponding proportion of small bubbles (<resonance size) increased from 25.74% to 95.08%. Moreover, it can be seen in Fig. 6F and 6G that with increasing PL from 5 to 100 µs, the mean size of the DBs decreased from 1.45 µm to 0.58 µm, and the FWHH decreased from 2.07 to 0.53 µm. These results show that the increasing PL caused a larger proportion of small bubbles with shorter lifetime in the DB population.

4. Discussion

4.1. Summative recap of findings

Our results can be compared with those of a previous study that investigated the size distribution of DBs produced from biSphere^TM microbubbles (exposed to a single tone burst with 1.1-MHz frequency and 1.5-MPa PNP), as the used acoustic excitation conditions and calculation method in the present study are similar [31]. Based on their observation, we conclude that the preformed microbubbles fragmented into DBs because the scattering intensity rapidly decreased to a relatively lower level than that obtained before the single tone burst emission. Moreover, the size of DBs (0.23–2.7 µm) in their study is in agreement with our results, showing the effectiveness of our approach.

Our results show that an increase of the PNP reduces the lifetime and mean size of the DB population (due to the increase of small bubble), and narrows the size distribution range. A previous study that measured void rate dissipation showed that an increase in acoustic pressure increased the proportion of small bubbles in the cavitation bubble cloud [26]. Other studies using the ultrasound wide-beam method also found that a higher PNP favored the formation of the small bubbles in acoustic droplet vaporization. Therefore, our results are consistent with those of these studies. Further, early optical observations, which provide direct proof of this relationship, determined that a higher PNP can increase the amplitude (in the expansion phase) of microbubble oscillation, and increase the velocity and acceleration of the shell wall (i.e. enhancing instability) [13]. This means that the violent collapse produces more shell fragments, resulting in the larger proportion of small DBs.

Our results also show that a longer PL causes a shift of the DB population to the smaller bubbles with shorter lifetime and narrower distribution. This result is also consistent with an early study, which used the ‘rebound’ signal to detect DBs generated by the rupture of the preformed bubbles [15]. In that study, the amplitude of the rebound signal markedly increased with PL for a given incident PNP, indicative of more small bubbles in DBs population [15]. However, other studies have reported that a longer PL increases the size of cavitation bubbles [28]. This discrepancy may be due to the following reason. The DBs in our study were produced from pre-formed microbubbles exposed to a single tone burst, whereas cavitation bubbles are formed from the solution (e.g. degassed water, luminol solution and nanodroplets solution) exposed to high-intensity ultrasound. Moreover, in previous studies, no obvious increase was observed in the extent of bubble expansion when increasing the PL; however, a longer PL was found to cause preformed microbubbles to produce more shell fragments, therefore resulting in the increase in the proportion of small bubbles [13], [14]. In addition, a longer PL could cause the coalescence of cavitation bubbles or gas diffusion from the surrounding medium, leading to an increase in the mean bubble size [17], [26], [28].

Fig. 3E and 3F show that the IC dose positively correlated with the PNP and PL.

Noted that the same sampling points (16384) (or sampling time $252.06\times {10}^{-6}\mu s$) were used when the PL was changed in the single tone burst. Therefore, ICD proportional to PL is mainly due to the increasing intensities of the broadband components (the increasing IC extent). Moreover, the degree of microbubble rupture increased with increasing PNP and PL [24], [25], [29], [30]. Therefore, we conclude that the increase of the IC dose can cause an increase in the degree of microbubble rupture, resulting in a large proportion of small DBs with a short lifetime and narrow distribution. This trend is consistent with the results of previous studies looking at the effect of acoustic power using laser diffraction and phase Doppler interferometry [22], [23]. However, our results differ from those obtained using the sonoluminescence intensity method, which determined that the radius increases with an increase in acoustic power [24]. This may due to the relativity low acoustic power range used in this research. However, at higher acoustic power, numerical calculations of multi-bubble systems determine that because of the stronger nonlinear pulsations, the radius decreases with the increasing acoustic pressure (from increasing acoustic power) [30].

4.2. Some points to be noticed

The experimentally measured scattering intensity curve and theoretically calculated dissolution dynamics were used to determine the properties of the DB population. It is known that when the excitation frequency approaches the resonance frequency of the bubbles, the bubbles start to resonate [39]. Thus, during the dissolution process of DBs, the change of scattering cross-section with the radius will undergo a resonance peak, and doesn’t follow the exponential decay function. However, in our lots of repeated experiments, the temporal curve of the measured scattering intensity still exhibited exponential attenuation trend, and almost no obviously sudden change (corresponding to the resonance peak) was observed. Previous report explained that the resonance peak for each bubble may be smeared due to the polydispersity of the DBs population, resulting in the exponential decay of the measured scattering intensity [28]. Thus, similar to the previous report [28] , the exponential decay function was used to fit the time variation of scattering cross-section during the static dissolution process. On the other hand, although another exponential decay function was fitted to eliminate the influence of the resonance peak, the modified scattering cross-section will cause some errors in the estimated size distribution. Therefore, to obtain accurate size distribution of DBs, using monodisperse microbubbles or a single microbubble may ensure the curve of measured scattering intensity is consistent with the theoretical calculations.

According to the theoretical calculation, the dissolution time of DBs with 0.2 µm radius is ~ 1.6 ms. The time interval between turning off the 1 MHz ultrasound and turning on the 5 MHz ultrasound is 1 ms in this measurement system. The propagation time of acoustic waves in experimental system is ~ 85.67 µs. So, the minimal radius that can be differentiated by this system was ~ 0.2 µm, and DBs with radius less than 0.2 µm can’t detected. Thus, some smaller DBs may be out of consideration when using this measurement system. More fast and accurate measurement system is needed for the cases of smaller DBs generation.

Previous experimental and numerical studies also determined that a higher acoustic frequency increases the proportion of small cavitation bubbles and narrows the size distribution [17], [24]. The expansion amplitude of the preformed bubbles is also dependent on the ultrasonic frequency, with previous studies showing that a lower frequency increases the expansion amplitude and fragmentation, which increases the number of small bubbles [13]. However, due to the limitation of experimental conditions, we did not investigate the influence of the ultrasound frequency on the properties of the DB population. This will be performed in future work.

4.3. Related to the application

For cavitation-based clinical applications, it is essential to achieve controllable cavitation activity in the target region for improved efficiency and biosafety. Our method to determine the properties of DBs can provide a feedback for optimizing the incident acoustic parameters (i.e. the PNP, PL and center frequency). For example, although some pulse modes (e.g. short pulses with high PRF) achieve uniform spatiotemporal distribution of cavitation dose in the target region [40], [41], the DBs formed by the previous incident pulse may generate secondary cavitation after receiving the next incident pulse, resulting in non-uniform distribution of the cavitation activity. To eliminate these undesired acoustic responses, the PRF in short-pulse mode should be as long as possible to exceed the lifetime of DBs. Moreover, an appropriate period between pulses can stabilize the bubble size distribution within the active radius range, thereby producing a controllable bubble response [25], [27]. Therefore, understanding the properties of DBs generated by IC could provide guidance for achieving controllable and desirable outcomes in cavitation-based applications.

5. Conclusion

We used theoretical dissolution curves and experimentally-measured scattering intensity curves of bubbles to determine the relationship between the properties (lifetime, mean radius and distribution range) of DBs and the acoustic parameters (PNP and PL) applied to elicit IC of SonoVue microbubbles. We determined that increasing the PNP reduces the lifetime and mean size of the DB population, and narrows the size distribution. Moreover, increasing the PL increases the proportion of small bubbles with short lifetime, and narrows the size distribution of the DBs. We conclude that the IC dose is related to the properties of the DB population. With increasing IC dose, the mean bubble size decreases, the lifetime of the DB population shortens and its size distribution narrows. Thus, this study shows that the properties of DBs can be predetermined according to the parameters of the incident acoustic pulse, and that controllable cavitation activity can be achieved by optimizing the acoustic parameters.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.