Abstract
Room-temperature skyrmions in magnetic multilayers are considered to be promising candidates for the next-generation spintronic devices. Several approaches have been developed to control skyrmions, but they either cause significant heat dissipation or require ultrahigh electric fields near the breakdown threshold. Here, we demonstrate electric-field control of skyrmions through strain-mediated magnetoelectric coupling in ferromagnetic/ferroelectric multiferroic heterostructures. We show the process of non-volatile creation of multiple skyrmions, reversible deformation and annihilation of a single skyrmion by performing magnetic force microscopy with in situ electric fields. Strain-induced changes in perpendicular magnetic anisotropy and interfacial Dzyaloshinskii–Moriya interaction strength are characterized experimentally. These experimental results, together with micromagnetic simulations, demonstrate that strain-mediated magnetoelectric coupling (via strain-induced changes in both the perpendicular magnetic anisotropy and interfacial Dzyaloshinskii–Moriya interaction is responsible for the observed electric-field control of skyrmions. Our work provides a platform to investigate electric-field control of skyrmions in multiferroic heterostructures and paves the way towards more energy-efficient skyrmion-based spintronics.
Subject terms: Ferroelectrics and multiferroics, Magnetic properties and materials, Spintronics
The common approaches to control of skymions cause significant heat dissipation or require high electric fields near the breakdown threshold. Here, the authors demonstrate electric-field control of skyrmions through strain-mediated magnetoelectric coupling in multiferroic heterostructures.
Introduction
Skyrmions are topologically protected particle-like spin textures and have potential applications in information storage, such as, skyrmion-based racetrack memory, due to their small size and high mobility1,2. Typically, skyrmions are stabilized by the Dzyaloshinskii–Moriya interaction (DMI) originated from the spin–orbit coupling in a noncentrosymmetric chiral helimagnet2–4. In B20-type compounds5, skyrmions exist in a narrow temperature and magnetic field phase diagram, usually far away from room temperature6,7, which is unfavorable for applications. By contrast, the asymmetric multilayer stacks consisting of heavy metal (HM) and ferromagnetic (FM) can stabilize Néel-type skyrmions at room temperature and enable fast current-driven skyrmion motion8,9, due to the interfacial DMI induced by the broken interfacial inversion symmetry and the large spin–orbit coupling of HM10–12. The multilayer structure is particularly appealing, because of the variety of materials and the enhanced interfacial DMI of HM/FM interfaces13. Furthermore, due to the compatibility with standard semiconductor techniques14, room-temperature skyrmions in multilayers are promising candidates for the next-generation spintronic devices with high-density, low-power consumption and nonvolatility2.
The ability to control (that is, create15, delete,16 and move17) skyrmions by external stimuli are essential for applications. Electrical stimuli, such as spin-polarized current18 and electric-field gating15, are most industrially compatible. However, electric currents dissipate a significant amount of heat, while the ultrahigh electric fields currently used in electric-field gating is near the breakdown threshold value of the dielectric layer19. From a fundamental perspective, due to the short charge-screening length of the metallic ferromagnet, electric-field gating mainly affects the FM/dielectric interface19–22, with little influence on the HM/FM interface including the interfacial DMI.
Strain-mediated electric-field control of magnetism in multiferroic heterostructure consisting of FM and ferroelectric layers has been widely studied23–25. In contrast to electric-field gating, electric-field-induced strains in the ferroelectric can be transferred to the FM layer over hundreds of nanometers26 or more, which should lead to a more effective skyrmion manipulation by modulating both the magnetic anisotropy and the interfacial DMI of the HM/FM interface. Notably, electric-field control of the interfacial DMI of the HM/FM interface has so far only been observed through ionic-liquid-gating-induced carrier density change27, and the ionic-liquid may damage the sample. Instead, a nondestructive HM/FM interfacial DMI modulation could be achieved via the strain-mediated electric-field control in all-solid-state heterostructures/devices. Strain-mediated electric-field-induced creation28, deletion,29 and motion30 of skyrmions have been computationally demonstrated.
In this work, we demonstrate strain-mediated electric-field control of skyrmions through magnetoelectric coupling in multiferroic heterostructure composed of [Pt/Co/Ta] × 5 magnetic multilayer and ferroelectric Pb(Mg1/3Nb2/3)0.7Ti0.3O3 (PMN-PT). Through performing magnetic force microscopy (MFM) measurements with in situ electric fields, we demonstrate creation, deformation, and annihilation of skyrmions. Electric-field control of the interfacial DMI of the HM/FM interface and perpendicular magnetic anisotropy (PMA) are also demonstrated experimentally. Micromagnetic simulations are performed for understanding the mechanisms of skyrmion manipulation. Our findings will stimulate more research for electric-field control of skyrmions in multiferroic heterostructures, with application to skyrmion-based low-power spintronic devices.
Results
Multilayer structure
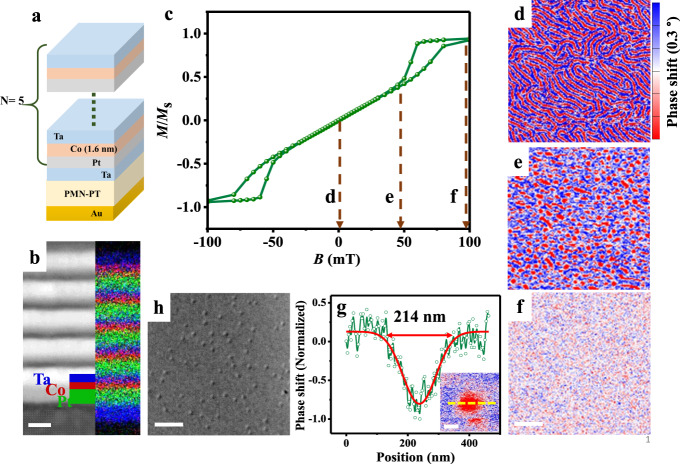
Ta(4.7 nm)/[Pt(4 nm)/Co(1.6 nm)/Ta(1.9 nm)] × 5 (hereafter Pt/Co/Ta) multilayers were deposited by using ultrahigh vacuum magnetron sputtering on PMN-PT(001) single-crystal substrate (as shown in Fig. 1a), and separately on a 30-nm-thick Si3N4 membrane for Lorentz transmission electron microscopy (L-TEM) observation. The stack structure and setup for MFM measurement with in situ electric fields are schematically shown in Supplementary Fig. 1. The bottom Ta layer was used to flat the surface of substrate and promote the interface quality14, which enables a large PMA in the multilayer and a strong interfacial DMI at the Pt/Co interface31. Pt/Co and Ta/Co interfaces generate strong interfacial DMI and very weak interfacial DMI (see ref. 8), respectively, leading to a considerable net interfacial DMI, which is beneficial for stabilizing Néel-type skyrmions. All experiments were performed at room temperature. Figure 1b shows the high angle annular dark-field scanning transmission electron microscopy (HAADF-STEM) image of the sample, revealing flat and distinct interfaces. Energy dispersive X-ray (EDX) mapping further confirms the periodical Pt/Co/Ta tri-layer structure. Figure 1c shows the out-of-plane magnetic hysteresis loop (in-plane one in Supplementary Fig. 2).
Fig. 1. Structure and skyrmion characterizations.
a Schematic of the sample configuration. b Cross-sectional HAADF-STEM image of the multilayer and corresponding EDX mapping for element distributions of Pt (green), Co (red) and Ta (blue) with a scale bar of 5 nm. c Out-of-plane magnetic hysteresis. d–f Magnetic-domain evolutions with increasing magnetic field with the same scale bar of 1 μm. g Line-cut profile along the yellow dot line in the inset with Gaussian fitting (red curve), the inset is magnified individual skyrmion with a scale bar of 100 nm. h Representative L-TEM image of skyrmions with a scale bar of 1 μm.
Microscopic imaging of skyrmions
Due to its high-spatial resolution and the ease of operation, MFM has been widely used for studying skyrmions9,19,32. Figure 1d–f shows the magnetic-domain structures with an out-of-plane bias magnetic fields of B = 0, 48, and 100 mT, respectively, where the blue (red) contrast indicates magnetization along the positive (negative) z direction. At B = 0 mT, the sample shows a labyrinthine domain pattern (Fig. 1d), consistent with the vanishing remnant magnetization of the multilayer (Fig. 1c). Upon applying magnetic fields, the labyrinth domain transforms into skyrmions (e.g., Fig. 1e), which shrink with increasing magnetic field. At the saturation magnetic field (100 mT), the skyrmions transform into an FM single domain state (Fig. 1f). A full set of MFM images are shown in Supplementary Fig. 3. A Gaussian fitting of a typical skyrmion profile (Fig. 1g), extracted from the inset of Fig. 1g along the yellow dot line, gives a skyrmion size/diameter of 214 nm comparable to the previous reports8,14,32,33. Furthermore, the state of multiple isolated skyrmion was also observed (Fig. 1h) using L-TEM for sample grown on Si3N4 membrane (other images in Supplementary Fig. 4). Both the MFM and L-TEM imaging demonstrate the existence of skyrmions with small differences in skyrmion density and size due to different substrates.
Variations of strain, interfacial DMI, and magnetic anisotropy with electric field
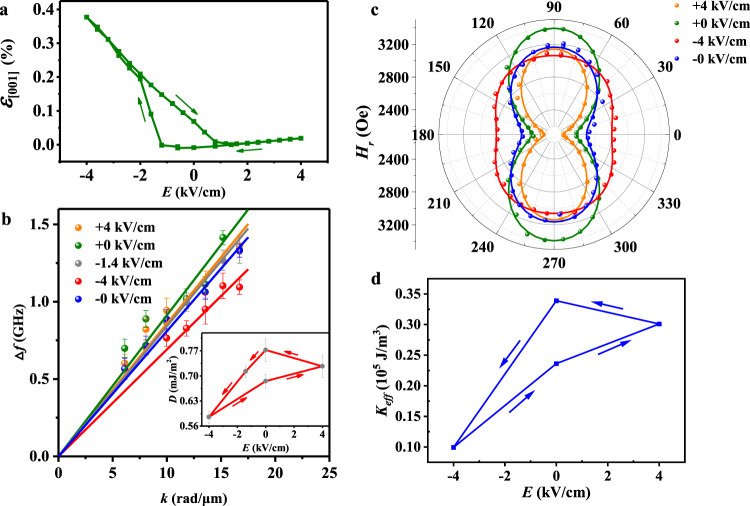
Variations of strain, interfacial DMI, and magnetic anisotropy with electric field are then investigated. To obtain the strains in PMN-PT induced by electric fields, we performed in situ X-ray diffraction (XRD) measurements under different electric fields to get lattice constants c(E), calculated using (002) peak by Bragg’s law (raw data in Supplementary Fig. 5). Electric-field-induced out-of-plane strain (Fig. 2a), defined as [c(E) − c(+0 kV/cm)]/c(+0 kV/cm), can be used to calculate the in-plane compressive strain (Supplementary Fig. 6) based on the crystal symmetry of (001)-poled PMN-PT (see ref. 34). The out-of-plane strain is largely volatile when decreasing electric field and asymmetric for positive and negative electric fields. Moreover, the strain is close to 0.4% at −4 kV/cm, much larger than the typical value of 0.1% (see ref. 34). More discussion is shown in Supplementary Fig. 5. The strain and magnetization under different electric fields were measured for thousands of times in previous studies35,36, which demonstrated the stability and durability of our devices.
Fig. 2. Variations of strain, interfacial DMI, and magnetic anisotropy.
a Out-of-plane strain variations of PMN-PT(001) substrate. b Wave-vector dependence of Δf under different electric fields with the interfacial DMI values in the inset with the error bar obtained from the standard error of Lorentzian fitting. c Angle-dependent FMR resonance field Hr(θ) and corresponding Kittel formula fitting (solid lines). d Keff versus electric-field curve.
Interfacial DMI is essential for stabilizing skyrmions in Pt/Co/Ta (see ref. 8), and we used Brillouin light spectroscopy (BLS)21,22 to measure it under different electric fields. By measuring the wave-vector dependence of the frequency difference Δf between the anti-Stokes and Stokes peaks, the interfacial DMI strength of the Pt/Co/Ta multilayer (D) can be determined by the following equation:
| 1 |
where k is the in-plane wave vector, γ is the gyromagnetic ratio, and MS is the saturation magnetization. Figure 2b shows the wave-vector dependence of Δf under different electric fields (raw spectra in Supplementary Fig. 7) for the +4 kV/cm to −4 kV/cm loop and the inset is variation of D with electric field. A D value of 0.772 mJ/m2 can be found when removing electric field, comparable to the report14. The DMI value is a little bit small. However, for magnetic multilayer structures, the dipolar interaction can become significant. It has been shown that both the dipolar interaction and the DMI are important for skyrmions in magnetic multilayer structures37. The value of D reduces from 0.772 to 0.585 mJ/m2 (24% reduction) when electric field changes from +0 kV/cm to −4 kV/cm, which is much larger than the 6% variation from 0.727 mJ/m2 (at +4 kV/cm) to 0.772 mJ/m2 (at +0 kV/cm). To exclude the influence of electric-field polarity on the interfacial DMI measurements, we also measured the interfacial DMI at −1.4 kV/cm (+4 kV/cm to −4 kV/cm branch) because the associated strain is comparable to that of +4 kV/cm (see +4 kV/cm to −4 kV/cm branch in Fig. 2a). It can be seen from the inset of Fig. 2b that the interfacial DMI 0.713 mJ/m2 for −1.4 kV/cm is comparable to the interfacial DMI value (0.727 mJ/m2) of +4 kV/cm, excluding the possible influence of electric-field polarity on the interfacial DMI measurements. The similarities in the volatility and asymmetry between interfacial DMI and strain behaviors indicate a strain-mediated electric-field control of interfacial DMI. Some reports showed importance of charge accumulation/depletion22 or ion migration21 in controlling Rashba-type interfacial DMI (see ref. 38) with a sizable modulation via electric-field gating on the dielectric/FM interface21,22. This is different from the strain-mediated modulation of the Fert–Levy DMI at the HM/FM (Pt/Co) interface2,39 in our work, where electric-field-gating effect is negligible for HM/FM (Pt/Co) interface in our PMN-PT/Ta(4.7 nm)/[Pt/Co/Ta]5 heterostructure because the charge-screening length in metallic layers is very short and the 4.7-nm-thick metallic Ta layer should effectively screen all the polarization charges at the PMN-PT surface. Thus, strain transferred from the PMN-PT to the Pt/Co/Ta multilayer is the only likely means to modulate the Fert–Levy DMI of the HM/FM (Pt/Co) interface. Specifically, the tensile out-of-plane strain transferred from the PMN-PT increases the distance between Co and Pt atom across the interface, thereby reducing the strength of the orbital hybridization among the Co–Pt–Co atoms. Since the strength of Fert–Levy DMI is proportional to the strength of such interfacial hybridization11,12,40, the strength of the interfacial DMI of the Pt/Co interface (D) is also reduced. It should be mentioned that possible nonreciprocal effects due to the dipolar interaction were excluded in our BLS measurement (more details can be found in Supplementary Fig. 8). Overall, our work provides strong experimental evidence for a strain-mediated electric-field control of the interfacial DMI of the HM/FM interface. Such modulation of interfacial DMI strength will in turn modulate the stability of the skyrmion state.
Besides the interfacial DMI, the effective PMA of the multilayer is also critical to the control of skyrmion41,42. To determine the variation of the effective PMA with electric fields, we performed angular dependent FM resonance (FMR) measurements under different electric fields (see detailed experimental configuration in Supplementary Fig. 9). For each angle θ, a resonance field Hr(θ) can be determined from the FMR spectrum, as shown in Fig. 2c. The effective PMA (denoted as Keff) can then be determined by fitting Hr(θ) with the Kittel formula (see text accompanying Supplementary Fig. 9), and the fitting results are plotted by the lines in Fig. 2c. The variation of the Keff with electric field is shown in Fig. 2d, which resembles the variation of the interfacial DMI strength (inset of Fig. 2b) and is consistent with the strain variation (Fig. 2a). Thus, it can be concluded that strain transferred from the PMN-PT alters both the interfacial DMI strength of the Pt/Co interface and the effective PMA of the Pt/Co/Ta multilayer.
Nonvolatile electric-field-induced creation of multiple skyrmions
For investigating electric-field control of skyrmions using MFM, pretreatment procedures have been done for the sample. First, the sample was poled by varying electric fields between +4 kV/cm and −4 kV/cm for two cycles with a step of 0.2 kV/cm. Electric fields of +4 kV/cm or −4 kV/cm were then removed, yielding two remanent polarization states, denoted as +0 kV/cm and −0 kV/cm, respectively. After then, the sample was magnetically poled to saturation, followed by reducing the bias magnetic field Bbias to a lower value for subsequent in situ MFM measurement.
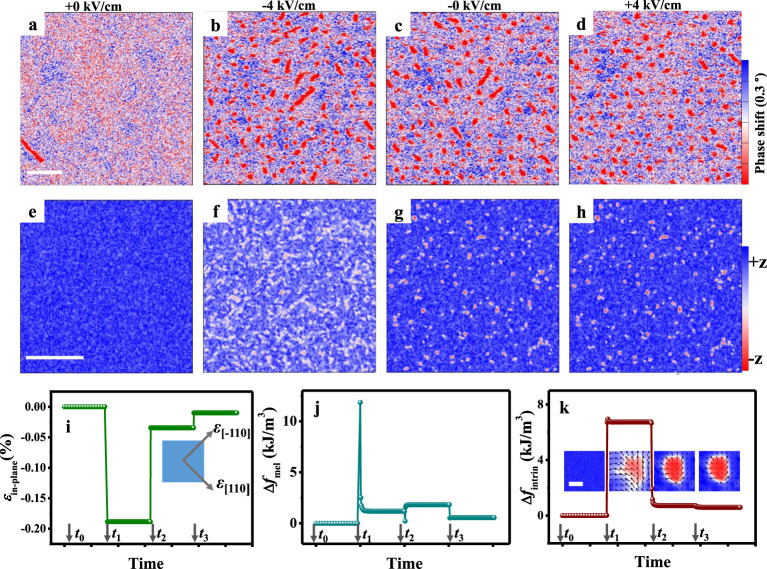
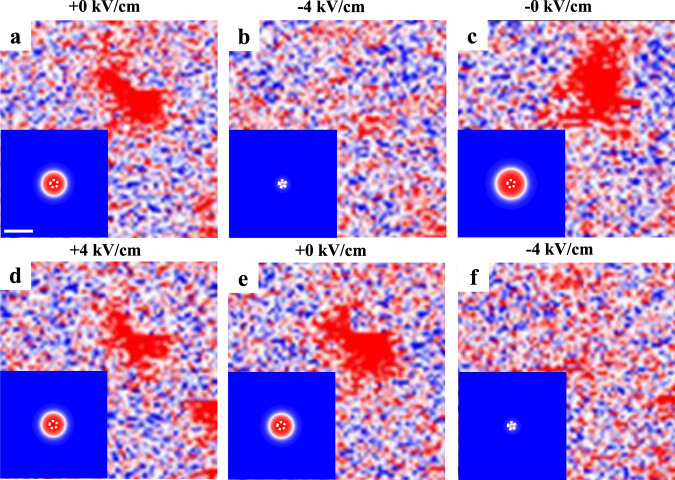
Figure 3 shows the electric-field-induced creation of skyrmions with Bbias = 60 mT. Initially, at E = +0 kV/cm, the sample is almost an FM single domain (Fig. 3a), and skyrmions appear (Fig. 3b) when applying E = −4 kV/cm. It has been suggested that the stray magnetic field from the scanning magnetic tip can alone lead to the creation of skyrmions32, but this possibility has been ruled out based on our control experiment (Supplementary Fig. 10). Notably, the skyrmion state remains after removing −4 kV/cm (Fig. 3c, at which E = −0 kV/cm). When further applying E = +4 kV/cm, the skyrmion state barely changes (Fig. 3d). Similar behaviors of skyrmion creation were also observed in sample starting from E = −0 kV/cm (Supplementary Fig. 11), that is, the creation of skyrmions can only occur when applying E = −4 kV/cm, under which the electric-field-induced strain from the PMN-PT is much larger than that the case of +4 kV/cm (see Fig. 2a). It was shown that the MFM images in Fig. 3a–d were taken from the same location on the sample (Supplementary Fig. 12). Moreover, the creation of skyrmions under other Bbias are shown in Supplementary Fig. 13.
Fig. 3. Skyrmion creation.
MFM images at E = +0 kV/cm (a), −4 kV/cm (b), −0 kV/cm (c), and +4 kV/cm (d) with Bbias = 60 mT. Corresponding simulation results of strain-mediated skyrmion creation with (initial state) and D = 0.772 mJ/m2 (e), and D = 0.585 mJ/m2 (f), and D = 0.685 mJ/m2 (g), and and D = 0.727 mJ/m2 (h), with the blue and red contrasts corresponding to magnetizations pointing up and down, respectively. The scale bar is 1 μm. Evolutions of in-plane biaxial compressive strain (i), magnetoelastic energy density fmel (j), and intrinsic energy density fintrin (k). The time stages are t0 (E = +0 kV/cm), t1 (E = −4 kV/cm), t2 (E = −0 kV/cm), and t3 (E = + 4 kV/cm), respectively. The insets of k are the corresponding individual skyrmion evolutions with a scale bar of 50 nm.
We performed micromagnetic simulations to elucidate the strain-mediated electric-field creation of skyrmions in polycrystalline [Pt/Co/Ta] × 5 multilayers, based on the strain-mediated electric-field modulation of effective PMA (Keff) and interfacial DMI strength (D). Since D decreases sizably when sample was switched from +0 kV/cm (or −0 kV/cm) to −4 kV/cm, which by itself would impede the stabilization of skyrmions, the observed skyrmion creation/stabilization must be attributed to the modulation of Keff. Here, (see ref. 29), where KU is the uniaxial magnetic anisotropy, μ0 is vacuum permeability, is the magnetoelastic coupling coefficient of the magnetic multilayer, and are its elastic stiffness coefficient, and εin-plane is the isotropic in-plane strain the magnetic multilayer experiences when the underlying PMN-PT substrate deforms under applied electric fields. We use MuMax3 (version: 3.10β, which incorporates the module of magnetoelastic coupling) for simulating the evolution of local magnetization in polycrystalline Pt/Co/Ta multilayers under such isotropic in-plane strains transmitted from PMN-PT (see “Methods”).
Figure 3e–h shows the simulated magnetization states at equilibrium under different in-plane biaxial compressive strains obtained from Supplementary Fig. 6, with E = +0, −4, −0, and +4 kV/cm, respectively. The average interfacial DMI strength under these electric fields, D = 0.772, 0.585, 0.685, and 0.727 mJ/m2, respectively, are directly extracted from Fig. 2b. Overall, the simulations (Fig. 3e–h) agree well with results from MFM imaging (Fig. 3a–d). Figure 3e shows the equilibrium magnetization state under zero strain and D = 0.772 mJ/m2 (+0 kV/cm), relaxed from a uniform upward (+z) magnetization. When applying and D = 0.585 mJ/m2 (−4 kV/cm), multiple skyrmions appear (Fig. 3f). As mentioned above, since the reduction of D does not favor the formation of skyrmions, the observed skyrmion creation is attributed to the reduction of the Keff by the compressive in-plane compressive strains (note that the Pt/Co/Ta multilayer has a negative magnetostriction24). Being consistent with experiments, the created skyrmions can be retained (Fig. 3g) after turning off the electric field (−0 kV/cm), at which and D = 0.685 mJ/m2. However, neither this small remanent strain nor the slightly enhanced D are the key factors for retaining the skyrmions, because the simulations shows that created skyrmions can be retained even when εin-plane is set to 0 and D remains to be 0.585 mJ/m2 (Supplementary Fig. 14). This control study indicates that the spatially heterogenous magnetic parameters in a polycrystalline system are the key to the retainment of the created skyrmions. For example, the spatial variation of uniaxial local magnetic anisotropy mimics the presence of local pinning sites. Simulations results studying the influence of such parametric heterogeneity, average grain size, size of computation cell, and room-temperature (298 K) thermal fluctuation on skyrmion creation are provided in Supplementary Figs. 15—19. Finally, when applying and D = 0.727 mJ/m2 (+4 kV/cm), the overall morphology of the skyrmion state (Fig. 3h) remains largely the same compared to that in Fig. 3g, partly because the reduced εin-plane and the slightly enhanced D act against and in favor of stabilizing the skyrmion state, respectively.
For demonstrating that strain-mediated control of effective PMA plays a dominant role in such skyrmion creation process, Fig. 3i–k shows the evolution of εin-plane, magnetoelastic energy density fmel and intrinsic energy density fintrin, respectively. The evolution of the constituent energy terms (fanis, fexch, fstray, fZeeman, fDMI, see their expressions in “Methods”) of fintrin are shown in Supplementary Fig. 20. At t0 (E = +0 kV/cm), the system has an almost uniform perpendicular magnetization (Fig. 3e). At t1 (E = −4 kV/m), fmel increases to 11.85 kJ/m3 associated with the sudden rise of strain to −0.189%. To minimize the fmel, perpendicular magnetization would then start to rotate toward the film plane (the magnetic easy plane). Indeed, fmel drops to 1.19 kJ/m3 at equilibrium. During this process, the interfacial DMI energy fDMI also needs to be minimized (Supplementary Fig. 20), which favors the formation of a Néel domain wall (inset in Fig. 3k). It is the simultaneous reduction of fmel and fDMI that provides the thermodynamic driving force for the creation of skyrmions (Fig. 3f). Furthermore, the energy cost is Δfintrin = 6.74 kJ/m3, while energy reduction is Δfmel = −10.66 kJ/m3, yielding Δftot = Δfintrin + Δfmel = −3.92 kJ/m3 < 0. Therefore, the skyrmion creation is favored.
Upon removing the applied large strain at t2 (E = −0 kV/cm), fmel increases by 0.63 kJ/m3 because of the increase in the magnitude of perpendicular magnetization (Fig. 3g) and fintrin decreases by 6.03 kJ/m3. Moreover, fintrin increases by 0.71 kJ/m3 compared with the initial state (t0), suggesting that the system in which skyrmions are maintained (Fig. 3g) is metastable. Similarly, further reducing the compressive strain from −0.034 to −0.01% and increasing D slightly from 0.685 to 0.727 mJ/m2 at t3 (E = +4 kV/cm), the corresponding fmel and fDMI both decreases, but the former shows a more sizable change (see Supplementary Fig. 20), indicating a stronger strain effect. Since the reduction of an in-plane compressive strain (hence larger Keff) reduces the stability of skyrmions, some smaller skyrmions annihilate. From the magnetization vector distributions in the local region of the multilayer (insets in the bottom panel), it can be seen that most of the magnetization vectors near the domain wall are perpendicular to the wall, directing from inside of the skyrmion to the outside. This indicates a DMI-stabilized left-chirality Néel wall, which is further confirmed by our asymmetric domain expansion study using L-TEM (Supplementary Fig. 21).
Deformation and annihilation of isolated skyrmions
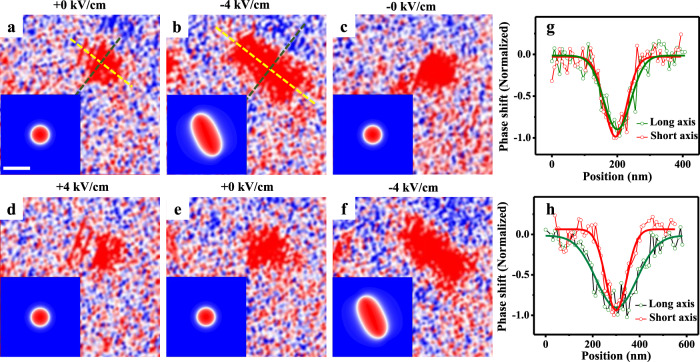
We also investigated deformation and annihilation of isolated skyrmions using MFM, with a high-spatial resolution via a smaller scanning size (2 μm), which is likely unperceived in Fig. 3 due to the larger scanning size (5 μm). The sample was in the remanent polarization state after positive electric poling (E = +0 kV/cm) with Bbias = 55 mT. Figure 4 demonstrates the anisotropic skyrmion deformation induced by in situ electric fields. The anisotropic deformation factor f is defined as f = 1 − r1/r2, with r1 and r2 the minor and major axes of the elliptic skyrmion, respectively. In the initial state (E = +0 kV/cm), the skyrmion is circular (Fig. 4a) with the line-cut profiles shown in Fig. 4g. At −4 kV/cm, the skyrmion exhibits evident anisotropic deformation (Fig. 4b) along the diagonal direction of magnetic multilayer, i.e., the [110] direction of PMN-PT, with f ~ 48% (r1 = 180 ± 12 nm, r2 = 346 ± 22 nm) deduced from Fig. 4h. At −0 kV/cm (after removing −4 kV/cm), the skyrmion becomes circular again with a size similar to its initial state. A subsequent application of +4 kV/cm (Fig. 4d) followed by its removal (+0 kV/cm, Fig. 4e), there is no appreciable deformation. However, the deformation occurs again upon applying −4 kV/cm (Fig. 4f), suggesting that the deformation is repeatable and appears only under −4 kV/cm. This is consistent with the earlier-discussed observation that the creation of multiple skyrmions also occurs only under −4 kV/cm, where both the strain and interfacial DMI show the most significant change (Fig. 2a, b). Note that the phase contrast in Fig. 4d is somewhat pale, which may be attributed to the influence of magnetic tip32, but this does not contradict the main finding.
Fig. 4. Skyrmion deformation.
Isolated skyrmion morphology at E = +0 kV/cm (a), −4 kV/cm (b), −0 kV/cm (c), +4 kV/cm (d), +0 kV/cm (e), and −4 kV/cm (f) with Bbias = 55 mT. g, h Skyrmion line-cut profiles along the major and minor axes in a and b with Gaussian fittings (solid lines), respectively. The insets in a–f show the simulation results of strain-mediated deformation of one single skyrmion with D = 0.772 mJ/m2 for +0 kV/cm (a), , , D = 0.585 mJ/m2 for −4 kV/cm (b), D = 0.685 mJ/m2 for −0 kV/cm (c), and D = 0.727 mJ/m2 for +4 kV/cm (d). The scale bar is 100 nm.
The experimental work on skyrmion deformation is rather limited43. A deformation factor of 30% was reported for B20 compound FeGe under a uniaxial strain of 0.3% (see ref. 43). This exotic emergent elasticity of skyrmions in FeGe was attributed to either the anisotropic magnetoelastic energy44,45 or the anisotropic DMI strength43 induced by the uniaxial strain. In magnetic multilayers with interfacial DMI, there is only one computational report on such emergent elasticity of isolated skyrmion46, which was attributed to anisotropic magnetoelastic energy.
In our sample, although the average in-plane strains from a [001]-poled (001)PMN-PT crystal are expected to be isotropic based on its crystal symmetry34, the local in-plane strain at the PMN-PT surface, arising from the 109° ferroelectric domain switching25,36, should be anisotropic. It is such local strain anisotropy that leads to the deformation of a single local skyrmion, which is much smaller than the micron-sized ferroelectric domain at the PMN-PT surface. Specifically, such local anisotropic strains, which are along the [110] and [−110] axes of the PMN-PT, would lead to anisotropic Néel wall energy (refs. 8,20) along these two axes by modulating either the local magnetoelastic anisotropy (which contributes to Keff) or the local DMI strength D, or both. Here, Aex is the exchange stiffness. Regardless of the details, the skyrmion radius is always smaller along the axis with a lower σw (see ref. 46). This is analogous to Wulff construction: lower surface energy (wall energy) of a crystal (skyrmion) yields shorted vector length (skyrmion radius) at thermodynamic equilibrium.
With these in mind, we simulate the deformation of one single skyrmion by applying biaxial in-plane anisotropic strains. The anisotropic magnetoelastic energy fmel was automatically considered (see expression of fmel in “Methods”), but the local DMI strength D was assumed to be isotropic for simplicity. The simulation results, which agree well with experimental observations, are shown in the insets of Fig. 4.
We also observed repeatable annihilation and creation of isolated skyrmion (Fig. 5). The initial state (Fig. 5a) shows the skyrmion with irregular shape implying presence of local inhomogeneity. At E = −4 kV/cm, there is no phase contrast (Fig. 5b), indicating the annihilation of skyrmion. Upon the removal of this negative poling field, the skyrmion reappears at E = −0 kV/cm (Fig. 5c). Then, applying +4 kV/cm, the skyrmion shrinks in size (Fig. 5d). After removing this positive poling field (now at E = +0 kV/cm), the skyrmion returns to its initial state (Fig. 5e). Applying −4 kV/cm again, the skyrmion annihilates again (Fig. 5f).
Fig. 5. Skyrmion creation/annihilation.
Isolated skyrmion morphology at E = +0 kV/cm (a), −4 kV/cm (b), −0 kV/cm (c), +4 kV/cm (d), +0 kV/cm (e), and −4 kV/cm (f) with Bbias = 55 mT. The insets in a–f show the simulation results of strain-mediated annihilation and reappearance of one single skyrmion with , D = 0.772 mJ/m2 for E = +0 kV/cm (a, e); , D = 0.585 mJ/m2 for E = −4 kV/cm (b, f); , D = 0.685 mJ/m2 for E = −0 kV/cm (c); and , D = 0.727 mJ/m2 for E = +4 kV/cm (d). A 20-nm diameter pinning site with ~5% lower perpendicular anisotropy was specified, as indicated by the dashed circle in the center. The scale bar is 100 nm.
The insets in Fig. 5 show the simulation results for the processes discussed above. Notably, for simulating the reappearance of the skyrmion from exactly the same location where it annihilates, we found that it is necessary to introduce a small pinning site (20 nm in diameter herein) with moderately (~5%) lower perpendicular anisotropy. The critical role of lower-anisotropy pinning site in achieving localized skyrmion deletion/re-creation has been demonstrated in systems with Rashba-type DMI arising from the FM/dielectric interface19. As shown in the inset of Fig. 5b, this lower-anisotropy pinning site leads to the stabilization of a tiny (diameter ~10 nm) skyrmion, which is too small to discern with our MFM (with a spatial resolution of ~10 nm as well), yet can function as the nucleus for the reappearance (growth) of skyrmion at exactly the same location after the removal of electric field (the inset of Fig. 5c). Our simulation results suggest the possibility of harnessing pinning sites for realizing a spatially precise control of skyrmions in continuous magnetic layer, which could be useful for device applications.
It is worth noting that there is an existing report on tuning the density and stability of the skyrmions in BaTiO3/SrRuO3 bilayer heterostructures by ferroelectric polarization switching47. In that work, voltage-controlled topological Hall effect (THE) measurement to provide an indirect evidence for skyrmion manipulation at low temperatures (<100 K), but a direct observation via in situ imaging is missing. Moreover, the origin of the so-called THE signal in SrRuO3 is still an open question48,49. After completing our manuscript, we noticed a very recent report on creation of micron-sized skyrmion bubbles (3–6 μm) with in-plane radiofrequency voltages by employing surface acoustic waves in multilayers of Pt/Co/Ir grown on LiNbO3, where it was found that static electric fields hardly affect skyrmions50. By contrast, in our work, we show manipulations of nanometer-scale skyrmions by using static and vertical electric fields. The use of static and vertical electric field is generally more compatible with existing manufacturing platform of spintronics, and is more energy efficient.
Discussion
In conclusion, we have demonstrated the electric-field control of skyrmions, especially the first observation of nanoscale skyrmion creation and Fert–Levy DMI variations, in FM/ferroelectric multiferroic heterostructures. Electric-field-induced variations of both the magnetic anisotropy (by FMR) and the interfacial DMI at the Pt/Co interface (by BLS) are consistent with the trend of electric-field-induced strain (by XRD), indicating that the electric-field control of both quantities is strain mediated. Specifically, the experimentally observed electric-field control of the Pt/Co interface DMI is explained by the weakening of Pt–Co hybridization at the interface induced by the out-of-plane tensile strain. Furthermore, we demonstrate nonvolatile electric-field creation of skyrmions. Micromagnetic simulations indicate the dominant role of strain-mediated control of magnetoelastic anisotropy (with respect to the control of interfacial DMI) in skyrmion creation, as well as the importance of polycrystal inhomogeneity (specifically, the local pinning sites) in retaining these metastable skyrmions at zero electric fields. We also observe electric-field-induced large and reversible deformation (up to 48%), repeatable annihilation, and reappearance of one isolated skyrmion. These observations are also interpreted using micromagnetic simulations. These findings could stimulate more research into the strain-mediated electric-field control of skyrmions or other topologically nontrivial spin textures, and pave the way toward more energy-efficient skyrmion-based spintronic devices.
Methods
Sample preparation
PMN-PT FE single-crystal substrates are (001)-cut and one-side polished with a size of 5 × 3 × 0.5 mm3. Ta(4.7 nm)/[Pt(4 nm)/Co(1.6 nm)/Ta(1.9 nm)] × 5 multilayers were grown by magnetic sputtering at room temperature with a base pressure of 1 × 10−6 Pa without a magnetic field. The first layer, Ta, was used to flat the surface of PMN-PT and promote the interface quality of Pt/Co. The top Ta layer is a capping layer preventing oxidation of Co and also as the top electrode. Au layer with a thickness of 300 nm was deposited on the bottom of the PMN-PT as the electrode.
Magnetic property measurement system
Out-of-plane and in-plane magnetic hysteresis loops were measured with a magnetic property measurement system (MPMS 7 T; Quantum Design).
Magnetic force microscopy
MFM was performed in ambient conditions with an Infinity Asylum Research AFM. The stray field of magnetic tip will inevitably interact with magnetic domain and distort them32. To reduce the influence of magnetic tip on domain, an optimized magnetic tip (SSS-MFMR)51 has been used in our work, which has a radii of 30 nm with a low coercivity ~ 12 mT and ultralow magnetic moment ~ 8 × 104 A/m. MFM images were taken in tapping/lift mode with a lift height of 30 nm.
The safety voltage for MFM is 200 V. Therefore, we apply ±4 kV/cm to the sample with a thickness of 0.5 mm.
Lorentz transmission electron microscopy
L-TEM imaging was carried out on Lorentz TEM (JEOL 2100F) under perpendicular magnetic fields by gradually increasing the objective lens current.
Scanning transmission electron microscopy
STEM and EDS mapping were performed on an ARM-200F (JEOL) operated at an acceleration voltage of 200 kV and equipped with double-spherical aberration (Cs) correctors. The TEM sample was prepared by using a focused ion beam with the cross-sectional lamella thinned down to 100 nm.
X-ray diffraction
XRD was operated on a Rigaku D/max-RB X-ray diffractometer with Cu Kα radiation.
Brillouin light spectroscopy
The principle of BLS is that52 the wave-vector direction of the magnetostatic surface spin wave in FM layer has a spatial chirality depending on the cross products of the normal direction and the direction of the magnetization, thus a pair of symmetric Stokes and anti-Stokes peaks are present in the BLS spectra corresponding to a fixed wave vector but opposite direction. However, the interfacial DMI favors certain spatial chirality same with only one of the wave vector, which induces an asymmetric modification of the frequency dispersion relation of Stokes and anti-Stokes peaks. The wave-vector dependence of the frequency difference between the Stokes and anti-Stokes peaks, Δf, has a linear relation with the in-plane wave vector k, and the slope is determined by D, see Eq. (1).
BLS was performed by using a single-mode solid-state laser with a wavelength of 532 nm and a power of 30 mW. The 180°-backscattered light was analyzed using a JRS Sandercock-type multipass tandem Fabry–Pérot interferometer. An external magnetic field of 500 mT was applied parallel to the sample surface plane and perpendicular to the in-plane wave vector (DE mode configuration).
FMR measurement
FMR measurements were performed by using the JEA-FS200 ESR spectrometer of JEOL Co., equipped with an X-band microwave generator with a frequency of 9.1 GHz and a cylindrical microwave resonant cavity. The sample was mounted to a rotating stage with the magnetic field direction unchanged.
Micromagnetic simulation
We use MuMax3 (see ref. 53) (version: 3.10β, which incorporates the module of magnetoelastic coupling) for simulating the evolution of local magnetization in polycrystalline [Pt(4 nm)/Co(1.6 nm)/Ta(1.9 nm)] × 5 multilayers under voltage-induced strains transmitted from the underlying piezoelectric PMN-PT substrate. In the simulations, the total free energy density ftot = fanis + fexch + fstray + fZeeman + fmel + fDMI is contributed by the following energy densities: the magnetocrystalline uniaxial anisotropy energy density , where u is the unit vector of the uniaxial anisotropy and m is the normalized local magnetization, Ku is the uniaxial anisotropy constant; the magnetic exchange energy density , where Aex is magnetic exchange coupling coefficient; the magnetostatic stray field energy density , where MS is the saturation magnetization and Bstray is the magnetostatic stray field; the Zeeman energy density associated with the externally applied magnetic field Bext, i.e., ; the magnetoelastic energy density , where B1 and B2 are magnetoelastic coupling coefficients, but the B2-related term can be omitted in our case because average shear strains are set to be zero ; the interfacial DMI energy density , where D is the interfacial DMI strength. The variation of ftot with respect to the change in m gives rise to the effective magnetic field , which drives the motion of the local magnetization m in a way described by the Landau–Lifshitz–Gilbert equation. The influence of thermal fluctuation at room temperature (298 K) on the switching of m can be considered by adding a thermal fluctuation field Btherm to the total effective magnetic field Beff, that is, . Here, , where α is the damping parameter, kB is Boltzmann constant, T is temperature, γ is the gyromagnetic ratio, ΔV is the volume of simulation cell, and Δt is time step in real unit, , where ηx, ηy, ηz are random numbers that have a standard normal distribution and a mean of zero, and are uncorrelated in both space and time. It is found that adding Btherm (with T = 298 K) yields overall similar behaviors of strain-mediated skyrmion creation to the case where Btherm = 0 (by setting T = 0 K), as shown in Supplementary Fig. 19. The simulations shown in the main paper are performed at Btherm = 0 for investigating and analyzing the energetics of the skyrmion switching more clearly.
The simulations simultaneously consider strain-induced changes in both the magnetic anisotropy and the interfacial DMI strength D. Unless stated otherwise, the former was considered by using average strains measured using strain gauge under different electric fields (Fig. 2a), which are related to the magnetoelastic energy density fmel. The latter was considered by using the D values measured using BLS under different electric fields (Fig. 2b), which are relate to the interfacial DMI energy density fDMI. The influence of strain on the magnetic anisotropy can be interpreted in a way that the strain is modulating the effective PMA of the multilayer as discussed in the main text.
The multilayer is described by 3D discretized computational cells of , where nx′ and ny′ are numbers of computational cells, and Δx′, Δy′, and Δz′ are cell sizes. Along the thickness direction (z′ axis), the bottom five layers and top two layers of grids with Δz′ = 0.8 nm are set as nonmagnetic materials to describe the Pt and Ta layer, while the middle two layers describe the magnetic Co layer. In-plane periodic boundary conditions are applied by adding one repetition of the simulation system along both x′ and y′ axes. Five repetitions of the simulation system are set along z′ axis to describe five repetitions of the Pt/Co/Ta tri-layer. The coordinate systems used in the experiment and simulations are different, shown in Supplementary Fig. 1b. Specifically, we only consider the strain along the diagonal direction of PMN-PT(001), and , as discussed later. We use in the main text.
For simulating strain-mediated electric-field control of multiple skyrmions, we first relax an initially uniform [001] magnetization under a bias external magnetic field Bbias. The obtained equilibrium magnetization distribution is used as the initial state. We then apply a spatially uniform strain to the entire magnetic multilayer. A complete transmission of the voltage-induced strain from the PMN-PT surface to the magnetic multilayer is considered26, yielding , . The out-of-plane strain of the magnetic layer is calculated by according to the thin-film boundary condition.
For the simulation of skyrmions creation in Fig. 3, we describe the system as a polycrystal considering the heterogeneity in a polycrystalline sample, with a mean grain size of 20 nm, , and and Bbias = 60 mT. We define grain-like regions with region-specific uniaxial magnetic anisotropy constant (KU), uniaxial magnetic anisotropy direction, and interfacial DMI strength (D) using Voronoi tessellation. Specifically, we generate 256 different KU obeying a uniform distribution around KU0 = 6.5 × 105 J/m3 (based on our own measurement, see Supplementary Fig. 2) within the range of (0.9–1.1KU0), 256 different θ (the angle between the axis of uniaxial magnetic anisotropy and the z′-axis) obeying a uniform distribution around 0° within the range of (−20°–20°), 256 different φ (the angle between +x′-axis and the projection of axis of uniaxial magnetic anisotropy on the x′y′ plane) obeying uniform distribution within the range of (0°–360°), and 256 different D obeying a uniform distribution around D0 within the range of (0.9–1.1D0). For each parameter set (KU, θ, φ, D), the 256 different numbers are randomly assigned to the grain-like regions. Note that the D is the averaged interfacial DMI strength of the entire sample, which is taken from our own experimental measurement and dependent on the applied electric fields (see inset of Fig. 2b). Furthermore, for a (001)-oriented PMN-PT single crystal, the average in-plane strain induced by electric field is expected to be biaxial isotropic54, i.e., . Assuming volume conservation, can be calculated from the experimentally measured , which is the average out-of-plane strain induced by electric field, via , with Poisson’s ratio (see ref. 34), shown in Supplementary Fig. 6.
However, given the local strain variations on the PMN-PT surface caused by spatially heterogenous ferroelectric domain switching25,36, we introduce anisotropic in-plane strain to simulate the deformation and annihilation of one single skyrmion as discussed in the Figs. 4 and 5 and Supplementary Fig. 22. In these cases, we use and as well as spatially homogenous magnetic parameters (KU = 6.5 × 105 J/m3; D varies with electric fields) for simplicity; the bias magnetic field Bbias = 30 mT. Under this setup, a circular-shaped 68-nm diameter skyrmion can be stabilized under zero strain. Anisotropic in-plane strains are then applied.
The rest of the magnetic parameters are all set to be spatially uniform in both the polycrystal and single-crystal (i.e., spatially uniform Ku and D) model. These parameters include: saturation magnetization MS = 9.48 × 105 A/m (from our own experimental measurement), magnetic exchange coupling coefficient Aex = 1.0 × 10−11 J/m (see ref. 14), magnetostriction constant λS = −180 ppm (which leads to best fit of the experimentally measured skyrmion morphology), and elastic stiffness coefficients and , which are calculated from thickness-weighted average of the Young’s modulus and Poisson’s ratio of the Pt, Co, and Ta layers55. Young’s modulus are , , and , and Poisson’s ratio are , , and (https://periodictable.com/Properties/A/YoungModulus.html).
Note added to proof
After submission of this work and during the period of preparation for the response to the reviewers’ comments, an article reporting study on electric-field control of skyrmions in multiferroic ferromagnetic/ferroelectric nanostructures56 has appeared. We focus on skyrmions in continuous thin films, while they focus on nanopatterned confined skyrmions and the behaviors of the skyrmions in these two cases are different.
Supplementary information
Acknowledgements
This work was supported by the Science Center of National Science Foundation of China (Grant No. 51788104) and National Science Foundation of China (Grant No. 51831005). J.-M.H. acknowledges support from the National Science Foundation under award CBET-2006028, and a start-up fund from the University of Wisconsin-Madison. Micromagnetic simulations were performed using Bridges at the Pittsburgh Supercomputing Center through allocation TG-DMR180076, which is part of the Extreme Science and Engineering Discovery Environment (XSEDE) and supported by NSF grant ACI-1548562. W.J. acknowledges support from Tsinghua University Initiative Scientific Research Program and the Beijing Advanced Innovation Center for Future Chip (ICFC). The authors acknowledge X. Yuan for support for MFM data difference process, Y. Liang for the helpful discussion of MFM measurement, and Y. Zhou for discussion of PMN-PT ferroelectric domain switching. The authors acknowledge C. Feng, W. Sun, and Q. Liu for useful discussion during this work.
Author contributions
Y.Z. and Y.B. conceived the project and designed the research. W.J. and H.Z. planed and deposited the multilayers. Y.B. performed the MPMS, XRD, and MFM measurement with the help of Yike.Z. and Y.W. Authors M.C., J.-M.H., and C.N. gave help for the MFM measurement. G.C., Y.G., and Yike.Z. carried out the BLS measurement. Ying.Z. performed the L-TEM measurement. H.T. contributed to the STEM measurement. H.D. measured asymmetric domain expansion under in-plane magnetic field by L-TEM. S.Z. and J.-M.H. performed the micromagnetic simulation. Yike.Z., W.S., Y.W., and Q.L. performed the FMR measurement. Y.B., S.Z., Yike.Z., Y.W., J.-M.H., and Y.Z. prepared the manuscript with contributions from all coauthors.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Competing interests
The authors declare no competing interests.
Footnotes
Peer review information Nature Communications thanks Jun Woo Choi and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
These authors contributed equally: You Ba, Shihao Zhuang, Yike Zhang.
Contributor Information
Jia-Mian Hu, Email: jhu238@wisc.edu.
Yonggang Zhao, Email: ygzhao@tsinghua.edu.cn.
Supplementary information
Supplementary information is available for this paper at 10.1038/s41467-020-20528-y.
References
- 1.Nagaosa N, Tokura Y. Topological properties and dynamics of magnetic skyrmions. Nat. Nanotech. 2013;8:899–911. doi: 10.1038/nnano.2013.243. [DOI] [PubMed] [Google Scholar]
- 2.Fert A, Cros V, Sampaio J. Skyrmions on the track. Nat. Nanotech. 2013;8:152–156. doi: 10.1038/nnano.2013.29. [DOI] [PubMed] [Google Scholar]
- 3.Dzyaloshinskii I. Thermodynamic theory of weak ferromagnetism in antiferromagnetic substances. Sov. Phys. JETP. 1957;5:1259–1271. [Google Scholar]
- 4.Moriya T. Anisotropic superexchange interaction and weak ferromagnetism. Phys. Rev. 1960;120:91–98. doi: 10.1103/PhysRev.120.91. [DOI] [Google Scholar]
- 5.Mühlbauer S, et al. Skyrmion lattice in a chiral magnet. Science. 2009;323:915–919. doi: 10.1126/science.1166767. [DOI] [PubMed] [Google Scholar]
- 6.Yu XZ, et al. Real-space observation of a two-dimensional skyrmion crystal. Nature. 2010;465:901–904. doi: 10.1038/nature09124. [DOI] [PubMed] [Google Scholar]
- 7.Nii Y, et al. Uniaxial stress control of skyrmion phase. Nat. Commun. 2015;6:8539. doi: 10.1038/ncomms9539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Woo S, et al. Observation of room-temperature magnetic skyrmions and their current-driven dynamics in ultrathin metallic ferromagnets. Nat. Mater. 2016;15:501–506. doi: 10.1038/nmat4593. [DOI] [PubMed] [Google Scholar]
- 9.Legrand W, et al. Room-temperature current-induced generation and motion of sub-100 nm skyrmions. Nano Lett. 2017;17:2703–2712. doi: 10.1021/acs.nanolett.7b00649. [DOI] [PubMed] [Google Scholar]
- 10.Torrejon J, et al. Interface control of the magnetic chirality in CoFeB/MgO heterostructures with heavy-metal underlayers. Nat. Commun. 2014;5:4655. doi: 10.1038/ncomms5655. [DOI] [PubMed] [Google Scholar]
- 11.Yang H, Thiaville A, Rohart S, Fert A, Chshiev M. Anatomy of Dzyaloshinskii-Moriya interaction at Co/Pt interfaces. Phys. Rev. Lett. 2015;115:267210. doi: 10.1103/PhysRevLett.115.267210. [DOI] [PubMed] [Google Scholar]
- 12.Belabbes A, Bihlmayer G, Bechstedt F, Blugel S, Manchon A. Hund’s rule-driven Dzyaloshinskii-Moriya interaction at 3d-5d interfaces. Phys. Rev. Lett. 2016;117:247202. doi: 10.1103/PhysRevLett.117.247202. [DOI] [PubMed] [Google Scholar]
- 13.Moreau-Luchaire C, et al. Additive interfacial chiral interaction in multilayers for stabilization of small individual skyrmions at room temperature. Nat. Nanotech. 2016;11:444–448. doi: 10.1038/nnano.2015.313. [DOI] [PubMed] [Google Scholar]
- 14.Wang L, et al. Construction of a room-temperature Pt/Co/Ta multilayer film with ultrahigh-density skyrmions for memory application. ACS Appl. Mater. Interfaces. 2019;11:12098–12104. doi: 10.1021/acsami.9b00155. [DOI] [PubMed] [Google Scholar]
- 15.Ma C, et al. Electric field-induced creation and directional motion of domain walls and skyrmion bubbles. Nano Lett. 2019;19:353–361. doi: 10.1021/acs.nanolett.8b03983. [DOI] [PubMed] [Google Scholar]
- 16.Hsu PJ, et al. Electric-field-driven switching of individual magnetic skyrmions. Nat. Nanotech. 2017;12:123–126. doi: 10.1038/nnano.2016.234. [DOI] [PubMed] [Google Scholar]
- 17.Yu G, et al. Room-temperature creation and spin-orbit torque manipulation of skyrmions in thin films with engineered asymmetry. Nano Lett. 2016;16:1981–1988. doi: 10.1021/acs.nanolett.5b05257. [DOI] [PubMed] [Google Scholar]
- 18.Jiang W, et al. Blowing magnetic skyrmion bubbles. Science. 2015;349:283–286. doi: 10.1126/science.aaa1442. [DOI] [PubMed] [Google Scholar]
- 19.Bhattacharya D, et al. Creation and annihilation of non-volatile fixed magnetic skyrmions using voltage control of magnetic anisotropy. Nat. Electron. 2020;3:539. doi: 10.1038/s41928-020-0432-x. [DOI] [Google Scholar]
- 20.Schott M, et al. The skyrmion switch: turning magnetic skyrmion bubbles on and off with an electric field. Nano Lett. 2017;17:3006–3012. doi: 10.1021/acs.nanolett.7b00328. [DOI] [PubMed] [Google Scholar]
- 21.Srivastava T, et al. Large-voltage tuning of Dzyaloshinskii-Moriya interactions: a route toward dynamic control of skyrmion chirality. Nano Lett. 2018;18:4871–4877. doi: 10.1021/acs.nanolett.8b01502. [DOI] [PubMed] [Google Scholar]
- 22.Zhang W, et al. Electrical field enhanced interfacial Dzyaloshinskii-Moriya interaction in MgO/Fe/Pt system. Appl. Phys. Lett. 2018;113:122406. doi: 10.1063/1.5050447. [DOI] [Google Scholar]
- 23.Hu J, Chen LQ, Nan CW. Multiferroic heterostructures integrating ferroelectric and magnetic materials. Adv. Mater. 2016;28:15–39. doi: 10.1002/adma.201502824. [DOI] [PubMed] [Google Scholar]
- 24.Sun Y, et al. Electric-field modulation of interface magnetic anisotropy and spin reorientation transition in (Co/Pt)3/PMN-PT heterostructure. ACS Appl. Mater. Interfaces. 2017;9:10855–10864. doi: 10.1021/acsami.7b00284. [DOI] [PubMed] [Google Scholar]
- 25.Ghidini M, et al. Shear-strain-mediated magnetoelectric effects revealed by imaging. Nat. Mater. 2019;18:840–845. doi: 10.1038/s41563-019-0374-8. [DOI] [PubMed] [Google Scholar]
- 26.Finizio S, et al. Magnetic anisotropy engineering in thin film Ni nanostructures by magnetoelastic coupling. Phys. Rev. Appl. 2014;1:021001. doi: 10.1103/PhysRevApplied.1.021001. [DOI] [Google Scholar]
- 27.Herrera Diez L, et al. Nonvolatile ionic modification of the Dzyaloshinskii-Moriya interaction. Phys. Rev. Appl. 2019;12:034005. doi: 10.1103/PhysRevApplied.12.034005. [DOI] [Google Scholar]
- 28.Li Z, et al. Strain-controlled skyrmion creation and propagation in ferroelectric/ferromagnetic hybrid wires. J. Magn. Magn. Mater. 2018;455:19–24. doi: 10.1016/j.jmmm.2017.07.008. [DOI] [Google Scholar]
- 29.Hu J, Yang T, Chen L. Strain-mediated voltage-controlled switching of magnetic skyrmions in nanostructures. npj Comput. Mater. 2018;4:62. doi: 10.1038/s41524-018-0119-2. [DOI] [Google Scholar]
- 30.Yanes R, et al. Skyrmion motion induced by voltage-controlled in-plane strain gradients. Appl. Phys. Lett. 2019;115:132401. doi: 10.1063/1.5119085. [DOI] [Google Scholar]
- 31.Kim N, et al. Improvement of the interfacial Dzyaloshinskii-Moriya interaction by introducing a Ta buffer layer. Appl. Phys. Lett. 2015;107:142408. doi: 10.1063/1.4932550. [DOI] [Google Scholar]
- 32.Zhang S, et al. Direct writing of room temperature and zero field skyrmion lattices by a scanning local magnetic field. Appl. Phys. Lett. 2018;112:132405. doi: 10.1063/1.5021172. [DOI] [Google Scholar]
- 33.Zhang S, Zhang J, Wen Y, Chudnovsky EM, Zhang X. Determination of chirality and density control of Néel-type skyrmions with in-plane magnetic field. Commun. Phys. 2018;1:36. doi: 10.1038/s42005-018-0040-5. [DOI] [Google Scholar]
- 34.Chen Q, et al. Electric-field control of phase separation and memory effect in Pr0.6Ca0.4MnO3/Pb (Mg1/3Nb2/3)0.7Ti0.3O3 heterostructures. Appl. Phys. Lett. 2011;98:172507. doi: 10.1063/1.3584025. [DOI] [Google Scholar]
- 35.Chen A, et al. Giant nonvolatile manipulation of magnetoresistance in magnetic tunnel junctions by electric fields via magnetoelectric coupling. Nat. Commun. 2019;10:243. doi: 10.1038/s41467-018-08061-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Zhang S, et al. Electric-field control of nonvolatile magnetization in Co40Fe40B20 / Pb(Mg1/3Nb2/3)0.7Ti0.3O3 structure at room temperature. Phys. Rev. Lett. 2012;108:137203. doi: 10.1103/PhysRevLett.108.137203. [DOI] [PubMed] [Google Scholar]
- 37.Li W, et al. Anatomy of skyrmionic textures in magnetic multilayers. Adv. Mater. 2019;31:1807683. doi: 10.1002/adma.201807683. [DOI] [PubMed] [Google Scholar]
- 38.Kim KW, Lee HW, Lee KJ, Stiles MD. Chirality from interfacial spin-orbit coupling effects in magnetic bilayers. Phys. Rev. Lett. 2013;111:216601. doi: 10.1103/PhysRevLett.111.216601. [DOI] [PubMed] [Google Scholar]
- 39.Fert A, Levy PM. Role of anisotropic exchange interactions in determining the properties of spin-glasses. Phys. Rev. Lett. 1980;44:1538–1541. doi: 10.1103/PhysRevLett.44.1538. [DOI] [Google Scholar]
- 40.Kashid V, et al. Dzyaloshinskii-Moriya interaction and chiral magnetism in 3d−5d zigzag chains: tight-binding model and ab initio calculations. Phys. Rev. B. 2014;90:054412. doi: 10.1103/PhysRevB.90.054412. [DOI] [Google Scholar]
- 41.Büttner F, et al. Field-free deterministic ultrafast creation of magnetic skyrmions by spin-orbit torques. Nat. Nanotech. 2017;12:1040–1044. doi: 10.1038/nnano.2017.178. [DOI] [PubMed] [Google Scholar]
- 42.Woo S, et al. Deterministic creation and deletion of a single magnetic skyrmions observed by direct time-resolved X-ray microscopy. Nat. Electron. 2018;1:288–296. doi: 10.1038/s41928-018-0070-8. [DOI] [Google Scholar]
- 43.Shibata K, et al. Large anisotropic deformation of skyrmions in strained crystal. Nat. Nanotech. 2015;10:589–592. doi: 10.1038/nnano.2015.113. [DOI] [PubMed] [Google Scholar]
- 44.Wang J, Shi Y, Kamlah M. Uniaxial strain modulation of the skyrmion phase transition in ferromagnetic thin films. Phys. Rev. B. 2018;97:024429. doi: 10.1103/PhysRevB.97.024429. [DOI] [Google Scholar]
- 45.Hu Y, Lan X, Wang B. Nonlinear emergent elasticity and structural transitions of a skyrmion crystal under uniaxial distortion. Phys. Rev. B. 2019;99:214412. doi: 10.1103/PhysRevB.99.214412. [DOI] [Google Scholar]
- 46.Hu J, Yang T, Chen L. Stability and dynamics of skyrmions in ultrathin magnetic nanodisks under strain. Acta Mater. 2020;183:145–154. doi: 10.1016/j.actamat.2019.11.005. [DOI] [Google Scholar]
- 47.Wang L, et al. Ferroelectrically tunable magnetic skyrmions in ultrathin oxide heterostructures. Nat. Mater. 2018;17:1087–1094. doi: 10.1038/s41563-018-0204-4. [DOI] [PubMed] [Google Scholar]
- 48.Wu, L. et al. Berry phase manipulation in ultrathin SrRuO3 films. Preprint at http://arxiv.org/abs/1907.07579 (2019).
- 49.Kimbell G, et al. Two-channel anomalous Hall effect in SrRuO3. Phys. Rev. Mater. 2020;4:054414. doi: 10.1103/PhysRevMaterials.4.054414. [DOI] [Google Scholar]
- 50.Yokouchi T, et al. Creation of magnetic skyrmions by surface acoustic waves. Nat. Nanotech. 2020;15:361–366. doi: 10.1038/s41565-020-0661-1. [DOI] [PubMed] [Google Scholar]
- 51.Soumyanarayanan A, et al. Tunable room-temperature magnetic skyrmions in Ir/Fe/Co/Pt multilayers. Nat. Mater. 2017;16:898–904. doi: 10.1038/nmat4934. [DOI] [PubMed] [Google Scholar]
- 52.Nembach HT, Shaw JM, Weiler M, Jué E, Silva TJ. Linear relation between Heisenberg exchange and interfacial Dzyaloshinskii-Moriya interaction in metal films. Nat. Phys. 2015;11:825–829. doi: 10.1038/nphys3418. [DOI] [Google Scholar]
- 53.Vansteenkiste A, et al. The design and verification of MuMax3. AIP Adv. 2014;10:107133. doi: 10.1063/1.4899186. [DOI] [Google Scholar]
- 54.Thiele C, Dörr K, Bilani O, Rödel J, Schultz L. Influence of strain on the magnetization and magnetoelectric effect in La0.7A0.3MnO3/PMN-PT(001) (A = Sr,Ca) Phys. Rev. B. 2007;75:054408. doi: 10.1103/PhysRevB.75.054408. [DOI] [Google Scholar]
- 55.Hashimoto S, Ochiai Y, Aso K. Perpendicular magnetic anisotropy and magnetostriction of sputtered Co/Pd and Co/Pt multilayered films. J. Appl. Phys. 1989;66:4909–4916. doi: 10.1063/1.343760. [DOI] [Google Scholar]
- 56.Wang Y, et al. Electric-field-driven non-volatile multi-state switching of individual skyrmions in a multiferroic heterostructure. Nat. Commun. 2020;11:3577. doi: 10.1038/s41467-020-17354-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.