Highlights
-
•
Ultrasound vaporizes the PFC phase in phase shift emulsions via ADV.
-
•
Classical nucleation theory predicted the stability of ADV-generated bubbles against condensation.
-
•
Bubble stability was dependent on the PFC species and ultrasound parameters.
-
•
Sequential payload delivery was achieved by generating transient and stable bubbles.
-
•
This technique could stimulate tissue regeneration via delivery of biomolecules.
Keywords: Acoustic droplet vaporization, Nucleation, Condensation, Ultrasound, Fibrin, Drug delivery
Abstract
Acoustically-responsive scaffolds (ARSs), which are fibrin hydrogels containing monodispersed perfluorocarbon (PFC) emulsions, respond to ultrasound in an on-demand, spatiotemporally-controlled manner via a mechanism termed acoustic droplet vaporization (ADV). Previously, ADV has been used to control the release of bioactive payloads from ARSs to stimulate regenerative processes. In this study, we used classical nucleation theory (CNT) to predict the nucleation pressure in emulsions of different PFC cores as well as the corresponding condensation pressure of the ADV-generated bubbles. According to CNT, the threshold bubble radii above which ADV-generated bubbles remain stable against condensation were 0.4 µm and 5.2 µm for perfluoropentane (PFP) and perfluorohexane (PFH) bubbles, respectively, while ADV-generated bubbles of any size in perfluorooctane (PFO) condense back to liquid at ambient condition. Additionally, consistent with the CNT findings, stable bubble formation from PFH emulsion was experimentally observed using confocal imaging while PFO emulsion likely underwent repeated vaporization and recondensation during ultrasound pulses. In further experimental studies, we utilized this unique feature of ADV in generating stable or transient bubbles, through tailoring the PFC core and ultrasound parameters (excitation frequency and pulse duration), for sequential delivery of two payloads from PFC emulsions in ARSs. ADV-generated stable bubbles from PFH correlated with complete release of the payload while transient ADV resulted in partial release, where the amount of payload release increased with the number of ultrasound exposure. Overall, these results can be used in developing drug delivery strategies using ARSs.
1. Introduction
Regenerative processes are typically stimulated by multiple, endogenous bioactive agents (e.g., cytokines) presented in distinct spatiotemporal patterns and expression sequences. Hydrogel-based delivery systems can provide sequential delivery of multiple, exogenous bioactive agents. A critical limitation of this approach is that release kinetics of the therapeutic agents are designed a priori via the manipulation of physiochemical properties of the hydrogel scaffold. Thus, release kinetics cannot be actively modulated after the hydrogel is implanted in situ. Alternatively, delivery systems that enable active control of release parameters such as dose, temporal profile, and spatial localization of multiple agents within the scaffold microenvironment would be beneficial in achieving modulation of release post-implantation and ultimately personalization of therapy. Integrating focused ultrasound (US), as a non-invasive therapeutic tool, with acoustically-responsive particles enables the on-demand release of therapeutic agents in a spatially- and temporally-controlled manner. One application of focused US is the phase transition of volatile perfluorocarbon (PFC) emulsions into gas bubbles in a process known as acoustic droplet vaporization (ADV) [1]. The vaporization of the PFC liquid using acoustic waves occurs above a threshold value of the rarefactional pressure (i.e., the ADV threshold) at which the phase transition becomes energetically favorable.
For therapeutic applications like drug delivery for tissue regeneration, ADV can be utilized for spatiotemporally-controlled delivery from payload-carrying PFC emulsions, thus enabling local delivery while increasing treatment efficacy and decreasing off-target effects. Depending on the intended application, PFC emulsions with different physical properties (i.e., size and bulk boiling point) have been designed [2], [3]. The effects of emulsion size and bulk boiling point of the PFC phase on the ADV threshold are well documented [4], [5]. Although the ultimate fate of ADV-generated bubbles (i.e., irreversible vaporization, re-condensation, collapse (i.e., bubbles filled with non-condensable gases), or fragmentation) is determined by acoustic parameters (i.e., excitation pressure, frequency, and pulse duration) [6], medium rheology (i.e., elasticity) [7], and physical properties of droplets (i.e., size and bulk boiling point) [8], two distinct types of behaviors have been observed: irreversible ADV (i.e., stable bubble formation) [9], [10] and reversible ADV (i.e., transient bubble formation) [11], [12].
In our prior publications, we utilized ADV to control the release of therapeutic agents encapsulated in phase-shift double emulsions (PSDEs) with a structure of water-in-PFC-in-water (W1/PFC/W2) [13]. The deliverable payload is contained within the innermost water phase (i.e., W1). Suprathreshold US disrupts the morphology of the PSDE by phase-transitioning the PFC phase, thereby releasing the payload. PSDEs can be incorporated into fibrin scaffolds to produce a composite hydrogel, termed an acoustically-responsive scaffold (ARS). ARSs have been used in conjunction with ADV in both in vitro [14] and in vivo [15] studies to control release of single payloads and sequential release of two payloads like fluorescently-labeled dextrans as well as regenerative growth factors (e.g., basic fibroblast growth factor (bFGF), platelet-derived growth factor (PDGF)) as shown previously [16], [17], [18]. Two major limitations of the previous sequential release strategies are 1) the attenuating effects of the ADV-generated bubbles following the first payload release, thus shadowing subsequent US exposures, as well as 2) the necessity of a bi-layer ARS. Understanding the physical and acoustic parameters resulting in stable or transient bubble formation via ADV could be utilized to overcome the current limitations in sequential delivery of multiple payloads from ARSs, thus refining their use in regenerative applications.
In this work, we use classical nucleation theory (CNT) [19], the most commonly-used theory of nucleation [20], to study the nucleation threshold in different PFC emulsions − perfluoropentane (PFP), perfluorohexane (PFH), and perfluorooctane (PFO) − as well as the condensation pressure of the corresponding ADV-generated bubbles. In addition, using CNT, we report the threshold bubble radii above which the ADV-generated bubbles remain stable against condensation for three different PFC emulsions. CNT has been used previously to study cavitation in biological fluids and tissues [21] as well as nucleation of a bubble in nano- [22] and micron-sized [4], [23] PFP emulsions. ADV-generated stable and transient bubble formation from different PFC emulsions at different acoustic parameters (i.e., excitation frequency and pulse duration) was further investigated experimentally using confocal imaging. Using the findings from CNT and confocal imaging, we present an ADV-triggered sequential delivery approach from PFC emulsions in ARSs.
2. Theoretical development
2.1. Nucleation of a bubble in a metastable liquid
Liquids are capable of withstanding tensile stresses (i.e., negative pressures) of considerable magnitude and remaining in a metastable state (i.e., below their saturated vapor pressure) for a finite period [24]. For such a state, the system is stable to small amplitude fluctuations in thermodynamic variables, which are stochastic in both space and time. At sufficiently high negative pressures, the liquid phase becomes unstable, vapor bubbles nucleate spontaneously, and grow until the pressure reaches the equilibrium vapor pressure of the liquid [21]. Transition from a metastable state to a state of stable equilibrium requires overcoming an activation energy barrier, computed by the change in the Helmholtz free energy of the system [25]. According to CNT, bubble nuclei are only stable after reaching a critical radius (). Subcritical nuclei () collapse and re-dissolve while those larger than the critical radius grow spontaneously. The mathematical definitions for and the corresponding critical work (), required to overcome the activation energy barrier, are given by [19], [26]:
| (1) |
| (2) |
where is the liquid–vapor interfacial tension, is the total pressure inside the critical bubble nucleus in unstable equilibrium with the surrounding liquid–gas solution, and is the pressure in the surrounding liquid–gas solution.
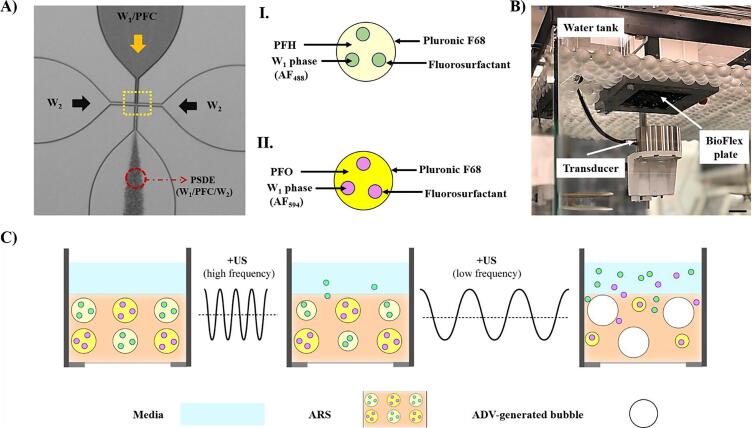
Since the pre-existing interfaces of the embedded W1 phase inside the PSDE (Fig. 1A) may increase the probability of heterogeneous nucleation, a geometric factor of is considered which depends on the physical properties (i.e., hydrophobicity or hydrophilicity) of the interface through the contact angle () as follows [27], [28]:
| (3) |
Fig. 1.
(A) An image of the microfluidic chip showing the flow focusing geometry of the junction (14 µm × 17 µm, highlighted in a yellow dotted box). The phase-shift double emulsion (PSDE) was generated by pumping the inner (W1/PFC) and outer (W2) fluids at 1 and 10 µL/min, respectively. The enlarged features display schematics of two similarly-sized PSDEs each containing a different PFC phase and payload: (I) perfluorohexane (PFH) and Alexa Fluor 488-labeled dextran (AF488), and (II) perfluorooctane (PFO) and Alexa Fluor 594-labeled dextran (AF594). (B) Picture of ultrasound (US) exposure setup. The plastic balls at the water surface maintain the temperature and dissolved gas concentration in the water tank. Acoustically-responsive scaffolds (ARSs), containing PSDEs, were polymerized in a BioFlex plate which was positioned on the surface of the water tank. US was applied through the silastic well bottom. (C) Schematics of side views of ARSs containing PFH-AF488 as well as PFO-AF594 exposed to different US parameters (i.e., frequency and pulse duration) resulting in different responses in PSDEs. Sequential release of AF488 and AF594 was achieved using high frequency US followed by low frequency US, respectively. Scale bar: 20 mm. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
Variation of the geometric factor with contact angle is shown in Fig. S1(A). At = 0, tends to zero, while at , the interface is not catalytic for phase change and becomes similar to homogenous nucleation. This shows that the presence of an external interface strongly favors nucleation. A contact angle of 100°, which was measured for bubble nucleation at a hydrophobic interface [24], was used here due to similar properties of fluorosurfactants at the interface between the PFC and W1 phases inside the PSDE. Nucleation of bubbles in PFC liquids can be influenced considerably by the presence of dissolved gases. According to Ward, et al. [29], total pressure inside the critical bubble nucleus can be written as:
| (4) |
where is the vapor pressure of the liquid and is the partial pressure of the non-condensable dissolved gas. Note that the effects of negative pressure as well as the dissolved gas on the actual vapor pressure of the liquid are not considered here [19], [25]. According to Henry’s law, the partial pressures of non-condensable dissolved gases in the bubble nucleus can be written as [30]:
| (5) |
where and refer to Henry’s law volatility constant and concentration of the i-th type of dissolved gas, respectively, in the corresponding liquid. Gas solubility in PFCs decreases in the order CO2 ≫ O2 > CO > N2 correlating with the decrease in molecular weight of the solute [31]. Values of in PFH and PFO were taken from Schürmann, et al. [32]. To calculate and in PFH and PFO, the corresponding values in water were normalized by the solubility of carbon dioxide and nitrogen in liquid PFCs, respectively (Table S1) [33], [34]. The number of moles of oxygen and carbon dioxide in the surrounding medium (water) at standard temperature and pressure were taken from Pilarek [31]. To calculate , the number of moles were normalized by the total volume of PFC emulsion present in the ARSs, calculated from the particle concentration and size distribution data, according to Radhakrishnan, et al. [35]. To account for the effect of elevated pressure inside the PFC emulsions on gas solubility, according to Henry’s law, the calculated concentrations were multiplied by a correction factor that accounts for the total internal pressure inside the PSDE (diameter: 6 µm, interfacial tension for PFC droplets stabilized by Pluronic copolymers: 42 mN/m [36], and atmospheric pressure: 100 kPa).
Dissolved gases may also lower the surface tension of liquids as a result of positive adsorption (in accordance with Gibbs adsorption isotherm) [28], [37]. At low pressures, the rate of change of surface tension of water with dissolved gas content has been experimentally measured as follows [38]:
| (6) |
where is the surface tension of pure liquid, P is the pressure (i.e., total internal pressure inside the PSDE), and b is a coefficient which significantly depends on the nature of the gas (−0.8 mN m−1 atm−1, −0.07 mN m−1 atm−1, and −0.08 mN m−1 atm−1 for carbon dioxide, oxygen, and nitrogen, respectively).
According to CNT, nucleation rate (), which is defined as the number of nucleation events () in the volume () and the duration () of the experiment, depends exponentially on as follows:
| (7) |
where is the nucleation rate, is Boltzmann’s constant, T is ambient temperature, is the kinetic pre-factor, is the volume of the PSDE, and is the time that the liquid is under negative pressure (i.e., one half of the acoustic period). accounted for the surface available for heterogenous nucleation per unit volume of liquid according to [39], [40]. Nucleation pressure (pl) was solved numerically by setting the number of nucleation equal to one.
The vapor pressures of PFC liquids () at 37 °C were estimated using the Antoine equation with the constant parameters obtained from the National Institute of Standards and Technology (USA) [41], as given in Table S1. The surface tension of pure PFC liquids () were taken from Freire, et al. [42].
2.2. Vapor condensation
Using CNT, the pressure required to condense a bubble into a droplet following the initial vaporization can be estimated. Similar to the case of bubble nucleation in a metastable liquid, the work required for the formation of a spherical liquid droplet () of critical radius () in a supersaturated vapor is [43]:
| (8) |
| (9) |
where is the density of liquid PFC [44], R is the gas constant, and S is the supersaturation ratio − the ratio of the actual pressure of the vapor (i.e., pressure inside the ADV-generated bubble) to the equilibrium vapor pressure (i.e., ). The number of condensation events in an ADV-generated bubble over a defined time period (as described in section 2.1) can be written as [45], [46]:
where is the condensation rate, is the internal pressure of the ADV-generated bubble, and is the molecular mass of PFC. Similarly, condensation pressure was solved numerically as described in section 2.1. A complete list of parameters along with their definitions and values is given in Table S1.
3. Experimental methods
3.1. Preparation and characterization of PSDE
Micron-sized PSDEs with a W1/PFC/W2 structure were prepared using a microfluidic-based technique following a previously described method [47]. Perfluorohexane (PFH, CAS# 355–42-0, bulk boiling point: 56 °C, Strem Chemicals) or perfluorooctane (PFO, CAS# 307–34-6, bulk boiling point: 100 °C, Sigma-Aldrich, St. Louis, MO, USA) was used as the PFC phase. A fluorosurfactant copolymer, synthesized using a 2:1 M ratio of Krytox 157 FSH (CAS# 51798–33-5, DuPont, Wilmington, DE, USA) and poly(ethylene glycol) bis(amine) (MW: 1000 g/mol, CAS# 24991–53-5, Alfa Aesar, Ward Hill, MA, USA), was dissolved at 2% (w/w) in PFC. The PFC solution was combined at 2:1 (v/v) with a W1 phase containing 1.66 mg/mL Alexa Fluor 488-labeled dextran (AF488, MW: 10,000 Da, Life Technologies, Grand Island, NY, USA) or Alexa Fluor 594-labeled dextran (AF594, MW: 10,000 Da, Life Technologies) in phosphate buffered saline (PBS, Life Technologies), and then sonicated (Q55 with CL-188 immersion probe, QSonica, LLC, Newton, CT, USA) for 30 s while on ice. In this work, each emulsion is designated by its respective PFC and payload (e.g., PFH-AF488).
To produce PSDEs, the primary emulsion (i.e., W1/PFC) and W2 phase, which was 50 mg/mL Pluronic F68 (CAS# 9003–11-6, Sigma-Aldrich, St. Louis, MO, USA) in PBS, were pumped at 1 µL/min and 10 µL/min, respectively, through a quartz microfluidic chip (Cat# 3200146, junction: 14 µm 17 µm, Dolomite, Royston, United Kingdom), as shown in Fig. 1A. Using a Coulter Counter (Multisizer 4, Beckman Coulter, Brea, CA, USA) with a 50 µm aperture tube, the average diameter (∅), coefficient of variation, and concentration were 6.3 ± 0.06 μm, 16.2 ± 0.3%, and (7.1 ± 1.1) × 109 particles /mL, respectively, for PFH-AF488. There were no significant differences in mean diameter among the PSDEs made with different PFC phases and payloads as was shown previously [16], [48].
3.2. Preparation of ARSs
ARSs were prepared by first dissolving bovine fibrinogen (Sigma-Aldrich) in FluoroBrite Dulbecco’s modified Eagle’s medium (DMEM, Life Technologies) at 20 mg/mL clottable protein while under gentle vortex mixing for 30 s. The fibrinogen solution and additional DMEM were degassed separately in a vacuum chamber (Isotemp vacuum oven, Model 282A, Fisher Scientific, Dubuque, IA, USA) at ~ 6 kPa for 60 min to minimize the amount of dissolved gas. ARSs were made by combining the prepared fibrinogen, DMEM, PSDE, bovine lung aprotinin (Sigma-Aldrich), and bovine thrombin (Thrombin-JMI, King Pharmaceuticals, Bristol, TN, USA). The final concentrations of fibrinogen, aprotinin, and bovine thrombin in the ARSs were 10 mg/mL, 0.05 U/mL, and 2 U/mL, respectively. Concentrations of PSDEs in ARSs were 0.005% (v/v) and 0.5% (v/v) for confocal imaging and payload release studies, respectively. To enable visualization of the matrix, 39 µg/mL Alexa Fluor 647-labeled fibrinogen (fibrinogen647) was added to each ARS prior to polymerization. Aliquots (volume = 0.35 mL, height (h) ~ 2 mm) of the ARS mixture were added to each well of 24-well BioFlex plates (total well diameter: 15 mm, membrane thickness: 0.2 mm, and total height: 15 mm, Flexcell International, Burlington, NC, USA), and allowed to polymerize for 15 min at room temperature. ARSs were then covered with 0.5 mL overlying media consisting of DMEM supplemented with 100 U/mL penicillin, 100 µg/mL streptomycin, and 2.5 µg/mL amphotericin B (Life Technologies). The height of the overlying media was chosen such that the ARSs were at least 3 mm away from the air interface to minimize the interference patterns caused by a standing wave field at these acoustic settings [16].
3.3. US exposure setup and parameters
All US experiments were conducted in a water tank (30 cm × 60 cm × 30 cm) filled with degassed (12–22% O2 saturation, where 100% O2 means equilibrium with air), deionized water at 37 °C. A calibrated, focused transducer (H-108, f-number = 0.83, radius of curvature = 50 mm, Sonic Concepts Inc., Bothell, WA, USA) was driven at either fundamental (2.5 MHz) or 3rd harmonic (8.6 MHz) mode to generate ADV within the ARSs. Pulsed waveforms (pulse duration: 1.5–5.4 µs; pulse repetition frequency: 100 Hz; duty cycle: 0.01%-0.05%) were generated by a function generator (33500B, Agilent Technologies, Santa Clara, CA, USA) and amplified by a gated radiofrequency (RF) amplifier (68 dB gain for the fundamental or 60 dB gain for the 3rd harmonic mode, GA-2500A Ritec Inc., Warwick, RI, USA). The generated amplified signals were viewed and monitored in real-time on an oscilloscope (HDO4034, Teledyne LeCroy, Chestnut Ridge, NY, USA). To reduce the impedance mismatch between the transducer and the amplifier, a matching circuit (H108_3 MN, Sonic Concepts) was used. The transducer was calibrated in free field at the focus in the range of 1–8 MPa and 1–7 MPa peak rarefactional pressure at the fundamental and 3rd harmonic, respectively, using an in-house fiber optic hydrophone (sensitivity: 16.6 mV/MPa) with a fiber diameter of 105 µm [49].
Experiments were conducted by placing the BioFlex plate containing the ARSs in the water tank such that only the bottom of the plate was in contact with water (Fig. 1B). ARSs were kept in the water tank at 37 °C for 15 min (verified by calculation of thermal boundary layer thickness) prior to ADV studies to reach thermal equilibrium. The transducer was positioned under the plate and connected to a three-axis positioning system controlled by MATLAB (The MathWorks, Natick, MA, USA). To localize the transducer axially with respect to the ARSs, a pulse echo technique was utilized whereby the transducer was driven by a pulser-receiver (5077PR, Olympus, Center Valley, PA, US) at low pressures to avoid ADV. The axial focus of the transducer was positioned and maximized either with respect to reflections from the well bottom (silicone elastomer membrane with a characteristic impedance (Z) of ~1.2 MRayl) or the overlying media-air interface (Z ~ 0.43 MRayl) [50]. Once the signal was maximized at either of the boundaries, the transducer was axially moved to place the focus in the middle of the ARS. The transducer was continuously rastered at 5 mm/s. The lateral raster spacing (0.5 mm at 2.5 MHz and 0.2 mm at 8.6 MHz) was chosen according to the full width half maximum (FWHM) of the beam width at the focus [16]. For all ADV experiments, the axial focus of the transducer was positioned at mid-height of each ARS. Unless otherwise noted, all acoustic pressures are listed as peak rarefactional pressure (Pr). In this study, all the US experiments were conducted at Pr = 8 MPa (at 2.5 MHz) and Pr = 7 MPa (at 8.6 MHz), which are suprathreshold for PFH (ADV threshold: 2.2 ± 0.2 MPa at 2.5 MHz, and 5.2 ± 0.3 MPa at 8.6 MHz) and for PFO (ADV threshold: 3.0 ± 0.4 MPa at 2.5 MHz) emulsions [16], [48], [51]. Note that, no ADV threshold was detected in ARSs containing PFO at an excitation frequency of 8.6 MHz across the range of pressures (Pr = 1–7 MPa) interrogated here [16].
3.4. Confocal imaging
ARSs, containing 0.005% (v/v) either PFH-AF488 or PFO-AF488, were imaged before and after ADV. Each well in the BioFlex plate was coated with 1% (w/v) solution of bovine serum albumin (CAS# 9048-46-8, Sigma-Aldrich) in PBS (for ~30 min) prior to polymerization of the ARSs to facilitate removal of the scaffolds. Scaffolds were imaged in a cell chamber (Attofluor, A7816, Thermo Fisher Scientific, Waltham, MA, USA) with a laser scanning confocal microscope (LSM800, Zeiss, Pleasanton, CA, USA) with an environmental chamber (37 °C). For intensity measurements, the laser power was set to the lowest non-zero setting (0.2%, 600 V gain) to minimize saturation. Similar exposure settings were used for imaging the ARSs. Fluorescence intensity measurements (reported as average intensity of the entire PSDE area) were performed on selected confocal images using ZEN lite software (Zeiss).
3.5. Single- and dual-payload release
All payload release studies were conducted in ARSs (h ~ 2 mm). Single release studies were performed at 8.6 MHz (pulse duration: 1.5–5.4 µs) on ARSs containing 0.5% (v/v) PFH-AF488. For dual release studies, ARSs contained two dextran payloads: 0.5% (v/v) PFH-AF488 (first payload) and 0.5% (v/v) PFO-AF594 (second payload). The first payload was released on day 0 at 8.6 MHz (Pr: 7 MPa, pulse duration:1.5 µs), while the second payload was released on day 4 at 2.5 MHz (Pr: 8 MPa, pulse duration: 5.4 µs). Immediately after US exposure, ARSs were placed in a standard tissue culture incubator (37 °C, 5% carbon dioxide) throughout the duration of the experiments. Overlying media was sampled daily, including three hours post exposure, by collecting half of the media and replacing it with an equal volume of fresh media until 10 days (14 days for dual release) after US exposure. The concentration of dextran in the collected media was measured using a fluorometer (Molecular Devices Spectramax M2e, Sunnyvale, CA, USA). All calculations were made using a mass balance approach for the payload (i.e., dextran), which accounted for mass removed (i.e., mass removed when sampling the media) and subsequent dilution of the overlying media due to addition of fresh media [15].
3.6. Statistical analyses
Statistical analyses were performed using GraphPad Prism software (GraphPad Software, Inc., La Jolla, CA, USA). Data are expressed as the mean ± standard deviation. To determine a rate constant (K) for dextran diffusion, the data were fit to a first-order exponential approximation of solute diffusion in a highly porous hydrogel following previously described methods [48]. The number of independent replicates is listed in the caption for each figure. Significant differences between groups were determined using one-way ANOVA followed by Tukey’s multiple comparisons test, with a significance level of 0.05.
4. Results and discussion
4.1. Theory
4.1.1. Bubble nucleation
In Fig. 2A, is plotted for three PFC liquids at varying liquid pressures (). As the magnitude of negative pressure in the liquid increases, the degree of metastability increases, resulting in significantly smaller critical radii and consequently lower activation energies for bubble nucleation. At very high negative pressures in the liquid (), the dependence of the critical radius on the saturated vapor pressure of PFC liquids is greatly reduced (Eq. 1 & Eq. 4).
Fig. 2.
Classical nucleation theory (CNT), including the effects of dissolved gas concentration as well as possibility of heterogeneous nucleation, was used to predict the threshold of bubble nucleation in phase-shift double emulsions (PSDEs) made with three different perfluorocarbon liquids. (A) Critical radius for bubble nucleation () in perfluoropentane (PFP), perfluorohexane (PFH), and perfluorooctane (PFO) emulsions as a function of applied rarefactional pressure in the liquid. (B) Nucleation threshold pressures () predicted by CNT (Eq. 7) for bubble formation in various PSDEs, PFP (: 1.6 MPa), PFH (: 2.4 MPa), and PFO (: 3.4 MPa) at 2.5 MHz (contact angle: 100°, geometric factor: 0.64).
Fig. 2B shows the predicted nucleation threshold pressures for PFP (1.6 MPa), PFH (2.4 MPa), and PFO (3.4 MPa) emulsions. The experimentally measured ADV thresholds were 1.3 ± 0.3, 2.2 ± 0.2 MPa, and 3.0 ± 0.4 MPa for PFP, PFH, and PFO emulsions, respectively, at 2.5 MHz [16], [48]. Variation of the geometric factor () with the contact angle () and its effect on the nucleation threshold pressure are shown in Fig. S1. The hydrophobic tails and surface irregularities at the interface of the W1 phase may act as nucleation sites and facilitate liquid–gas transition by lowering the nucleation energy barrier. Incorporation of nucleation seeds such as silica-coated quantum dots [11] and iron oxide nanoparticles [52] in PFC emulsions was found to lower the ADV threshold. The effects of surface irregularities, impurities, and microcavities as nucleation sites have been studied in details [19], [53].
Additionally, the effect of dissolved gas content in the liquid, which was considered both for the pressure in the critical bubble nucleus as well as the liquid surface tension, reduced the nucleation pressure by 2.24 MPa. The knowledge of the compositional dependence of the surface tension of the liquid mixture is crucial, as positive adsorption of dissolved gases can lower the surface tension considerably compared to the surface tension of the pure liquid [37], [54], [55]. The extent of lowering surface tension depends on the chemical nature of the gas as well as its solubility (as shown in Eq. 6). Because of the low polarizability of fluorine, the van der Waals interactions between fluorinated chains are weak, resulting in low cohesive energy, low surface tension, and exceptionally large gas-dissolving capacity of PFC liquids [56]. As discussed in section 2, any change in the surface tension will have a significant effect on (~σ), (~σ3), and nucleation threshold pressure (~σ3/2). In boiling nucleation, the presence of dissolved gases in liquids resulted in a significant decrease in the nucleation temperature [40], [57]. The effect of dissolved gas content on reducing the tensile strength of water and therefore the acoustic cavitation threshold has been extensively studied [58], [59]. A 2-fold increase in oxygen concentration reduced the cavitation threshold by ~2 MPa in water at 1 MHz [60].
Note that increasing the excitation frequency from 2.5 MHz to 8.6 MHz, which reduced the acoustic period under which PFC experiences negative pressure (i.e., τ), resulted in only a 2% increase in the nucleation pressure. Such weak dependence of the nucleation threshold pressure on the acoustic period can be seen in studies using CNT in the context of cavitation and ADV [4], [22], [24]. However, the experimentally measured ADV thresholds, particularly via acoustic techniques, are not capable of detecting nano-sized nuclei (7–10 nm in radius according to Fig. 2A). Longer pulse durations as well as lower frequency US pulses provide a longer window for growth of the nucleated bubbles via rectified diffusion, making them easier to be detected experimentally. Furthermore, at higher frequencies, more attenuation as well as a significantly smaller focal volume (reducing the probability of nucleation) might affect the experimental detection of the ADV threshold, which are not considered in CNT.
4.1.2. Bubble condensation
Upon ADV, the PFC phase undergoes a volumetric expansion, which is approximately 125-fold in water for sufficiently-sized emulsions [61], [62]. The presence of a viscoelastic medium such as gels reduces this expansion factor [63]. Assuming complete vaporization of the PFC phase and neglecting in-gassing during ADV, a ~6 µm PSDE (containing 67% (v/v) PFC) is expected to yield a ~20 µm bubble. Knowing the internal pressure of a ~20 μm bubble and assuming retention of the shell post-ADV [64], a hydrostatic pressure of 100 kPa, and the saturated vapor pressure for each PFC liquid at 37 °C (Table S1), then S is 0.8, 2.3, and 132 for PFP, PFH, and PFO, respectively.
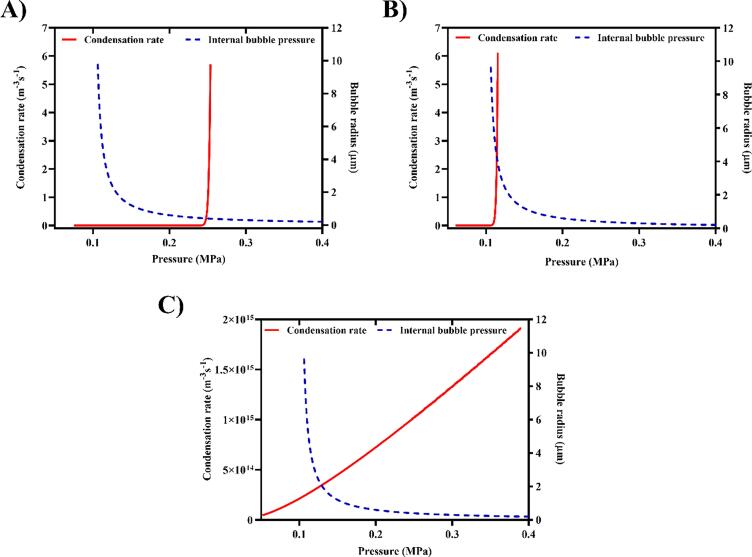
Fig. 3 shows the condensation rate (Eq. 10) of an ADV-generated bubble from different PFC liquids as a function of pressure (solid red lines). The pressure required to condense the ADV-generated PFP and PFH bubbles back to the liquid state was estimated to be 0.25 MPa (Fig. 3A) and 0.11 MPa (Fig. 3B), respectively. Bubble radius is plotted as a function of total internal pressure inside the ADV-generated bubble in the same figure (blue dashed lines). As can be seen in Fig. 3A & B, there is a threshold bubble radius (intersection of the two curves), Rstable (0.4 µm for PFP and 5.2 µm for PFH), where the internal pressure of the generated bubble is less than the condensation pressure. Above Rstable, the ADV-generated bubbles are stable against condensation.
Fig. 3.
Classical nucleation theory (CNT) was used to predict the condensation pressure as well as the threshold radius for stable bubbles generated via acoustic droplet vaporization (ADV). Condensation rate (Eq. 10) of bubbles generated from (A) perfluoropentane (PFP), (B) perfluorohexane (PFH), and (C) perfluorooctane (PFO) phase-shift double emulsions (red curves). For comparison, bubble radius is plotted as a function of the corresponding internal pressure in blue dashed lines. The pressure required to induce a condensation event (i.e., condensation pressure (), Eq. 10) in a bubble, within a time period of 1 µs, was estimated to be 0.25 MPa for PFP and 0.11 MPa for PFH. Due to a significantly higher supersaturation ratio, the ADV-generated bubbles of any size from PFO condense back to liquid at ambient condition. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
The condensation rate of a bubble generated from PFO demonstrated a significantly different behavior (Fig. 3C). Having a significantly higher supersaturation ratio (S = 132), an ADV-generated bubble from PFO is not thermodynamically stable at ambient condition. Therefore, after the US pulse is off, a PFO bubble condenses back to a liquid state. Note that stability against condensation was not significantly affected by . Increasing from 1 µs to 100 ms changed the condensation threshold pressure by only 30 kPa (~0.09 µm change in Rstable).
Dissolution or condensation due to increased Laplace pressure has been suggested as the ultimate fate of ADV-generated bubbles from submicron-sized PFP emulsion with an average diameter of ~0.2 µm [65], while stable bubble formation was observed for those in the range of 0.4–1 µm in diameter [8]. Micron-sized PFP emulsion has repeatedly shown stable bubble formation post-ADV [9], [14], [66]. Bubbles generated from higher bulk boiling point PFCs, such as PFH, exhibited repeated vaporization and recondensation at diameters smaller than 3 µm [8], [12] and stable bubble formation at diameters above 6 µm [48], [51]. The transient nature of vaporization of sufficiently-sized PFH emulsions and therefore insufficient time for sustained oscillation was reported to be the reason for the lack of subharmonic response [67]. These experimental findings are consistent with CNT predictions discussed above.
There are many factors determining the stability of the resulting ADV-generated bubbles, including US pulse parameters (e.g., frequency, pressure, and pulse duration), medium bulk properties (e.g., temperature, gas concentration, and stiffness), as well as emulsion physical properties (e.g., size, concentration, and surface tension). In this study, stability of an ADV-generated bubble is defined as its survival against condensation post-ADV. Understanding the parameters inducing stable or transient bubble formation via ADV could be beneficial for applications that utilize PSDEs for localized drug delivery, as will be discussed in the following section.
4.2. Confocal imaging
4.2.1. ADV at 2.5 MHz
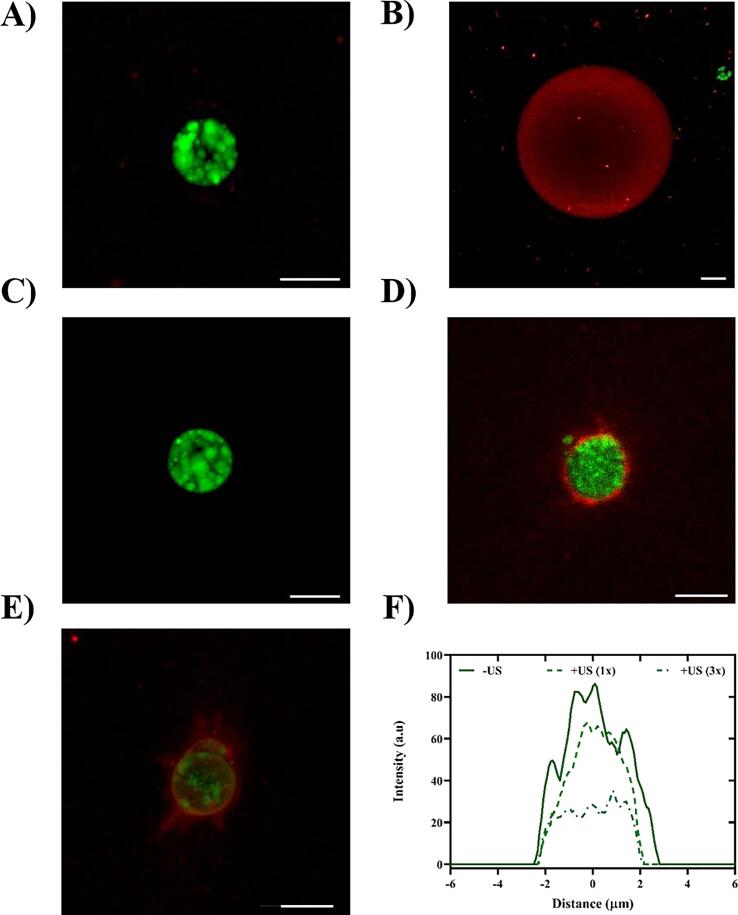
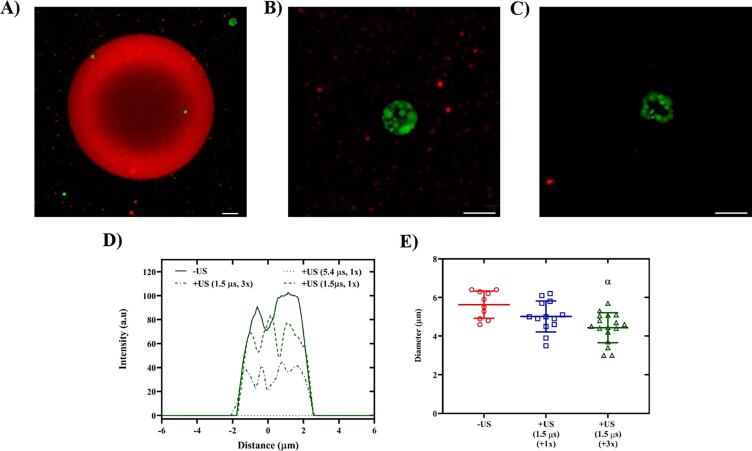
Maximum intensity projections of confocal images of ARSs containing different PSDEs are shown in Fig. 4. The W1 phase within the PSDE is displayed in green due to the presence of AF488, while the fibrin matrix, which surrounded the PSDE, is shown in red due to the inclusion of fibrinogen647. A PFH-AF488 emulsion (∅: 5.3 μm, Fig. 4A) was phase transitioned into a stable bubble (∅ ~45 μm, Fig. 4B) via ADV. Such stable bubble formation was consistent with the threshold bubble size obtained theoretically for PFH (i.e., Rstable > 5.2 µm) using CNT. At 2.5 MHz, ADV consistently resulted in stable bubble formation from PFH emulsion at different suprathreshold pressures (i.e., 2.2–8 MPa) and number of cycles (N = 2–13) (data not shown). ARSs containing PFH emulsion of a larger size distribution (∅: 13.2 ± 0.8) also resulted in stable bubble formation [51]. Furthermore, stable bubble formation was associated with complete release of the payload through AF488 intensity measurements [68], as can be seen here as well (Fig. 4B). An ARS containing PFO-AF488 (Fig. 4C), exposed to a suprathreshold pressure, displayed a different response post-ADV (Fig. 4D).
Fig. 4.
Acoustic droplet vaporization (ADV) in acoustically-responsive scaffolds (ARSs) resulted in stable bubble formation in sufficiently-sized perfluorohexane (PFH) emulsion and transient bubble formation in perfluorooctane (PFO) emulsion at 2.5 MHz (pulse duration: 5.4 µs). (A) Maximum intensity projection of confocal z-stacks of an ARS containing PFH emulsion. The fibrin matrix contained Alexa Flour 647-labeled fibrinogen (shown in red) while the phase-shift double emulsion contained Alexa Flour 488-labeled dextran (AF488, shown in green). (B) ADV resulted in stable bubble formation in ARSs containing PFH emulsion. ARSs with PFO emulsion (C) before and (D) after ADV behaved differently (no stable bubble formation). Similar acoustic settings were used in (B) and (D). (E) Repeated ultrasound (US) exposures (3x) in ARSs with PFO emulsion resulted in more AF488 release, thus indicating repeated vaporization and recondensation during US pulses. AF488 intensity measurements, comparing payload release from PFO over multiple US exposures, is shown in F. Scale bar for all panels: 5 µm. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
Unlike PFH, ADV does not yield stable bubble formation with PFO emulsion since ambient pressure is sufficient to condense the PFO bubble back into a liquid droplet once the US pulse is off (see Fig. 3C). The reduction in the intensity of AF488 in Fig. 4D compared to Fig. 4C indicates that repeated vaporization and recondensation occurred. The amount of payload inside the PFO emulsion significantly decreased following triplicate US applications (+US 3x, Fig. 4E). AF488 intensity in PFO-AF488 was quantified before and after US exposures (Fig. 4F). Both stable and transient bubble formation, which depends on the size and PFC species, can be used to tune the kinetics of release from PSDEs for therapeutic applications. We previously showed that payload release rate was significantly lower in ARSs with micron-sized PFP and PFH emulsions and correlated directly in ARSs with higher PFC boiling points, such as PFO [48]. A potential explanation is that in an ARS with ADV-induced stable bubbles, the path length for diffusion would be longer since released payloads cannot diffuse through a bubble, but rather must diffuse around it.
Although PFO did not generate stable bubbles, the repeated volumetric expansion and recondensation of the PFC phase during US pulses elevated the fluorescence intensity of fibrinogen647 in the surrounding fibrin, which qualitatively increased with the number of US exposures (Fig. 4D & E). Fibrin is known to exhibit strain stiffening, which is a characteristic of semiflexible filamentous networks [69]. Depending on the amount of strain, different stress-response mechanisms are proposed [70]. For ARSs containing PFH emulsion, consolidation of fibrin at the bubble-fibrin interface, likely due to the ADV-induced mechanical strain, increased in intensity and FWHM thickness as the generated bubbles grew due to static diffusion over time [68].
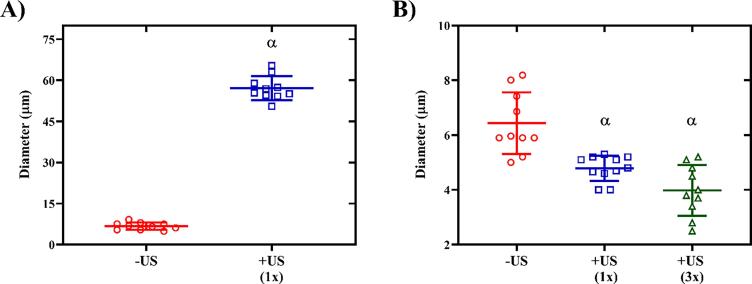
The average diameter of the ADV-generated bubbles from PFH-AF488 emulsion (∅ = 6.3 ± 0.3 µm) reached 57.14 ± 4.3 µm 1 h post-ADV (Fig. 5A), while the average diameter of the PFO-AF488 emulsion (∅ = 6.1 ± 0.2 µm) decreased to 4.8 ± 0.45 µm after one US raster (1x) and 3.9 ± 0.9 µm after three US rasters (3x) (Fig. 5B).
Fig. 5.
Acoustic droplet vaporization (ADV) resulted in (A) stable bubble formation in perfluorohexane and (B) repeated vaporization and recondensation in perfluorooctane (PFO) double emulsions at 2.5 MHz (pulse duration: 5.4 µs). The average size of PFO emulsion decreased over multiple exposures (x) of ultrasound (US). Statistically significant difference (p < 0.05) is denoted as follows: α: vs. -US (n = 10).
4.2.2. ADV at 8.6 MHz
Frequency of excitation impacts both the ADV threshold [1], [67] as well as the generated bubble response [71]. Lower frequency US provides a longer time window for nucleation, growth, and further influx of air from the surroundings. However, the use of higher frequency ultrasound to generate ADV within ARSs would enable more tightly focused ADV as well as minimize any cavitation-related damage to large molecular payloads or adjacent cells.
ARSs containing PFH-AF488 were exposed to suprathreshold US at 8.6 MHz at different pulse durations of 5.4 µs (1x, Fig. 6A), 1.5 µs (1x, Fig. 6B), and 1.5 µs (3x, Fig. 6C). Similar stable bubble formation, which resulted in consolidation of the fibrin at the interface, can also be seen at this acoustic setting (8.6 MHz and 5.4 µs) for PFH emulsion. ADV-generated bubbles at this acoustic setting reached 80 ± 3.1 µm in diameter 1 h post-ADV. A shorter pulse duration (1.5 µs) at this frequency did not generate stable bubbles (Fig. 6B & C). It is likely that at this acoustic setting, transient, partial ADV occurred in which a subvolume of PFH was phase transitioned. ADV-generated bubbles at 8.6 MHz with a short pulse duration (1.5 µs) may not have reached the theoretically determined critical radius of stability (Fig. 3B) due to insufficient in-gassing provided at this acoustic setting compared to a longer pulse duration (5.4 µs). The intensity of the payload inside the PSDE decreased as the number of US exposures increased (Fig. 6D). The effect of pulse duration on the size of PFH emulsion undergoing the hypothesized transient, partial ADV is shown in Fig. 6E. No significant change in the fibrinogen647 fluorescence intensity was observed in the case of high frequency (i.e., 8.6 MHz) and short pulse duration (i.e., 1.5 µs), which was possibly due to partial vaporization and therefore insufficient ADV-induced, mechanical strain on fibrin. Note that the ADV threshold was shown to be independent of pulse duration [72], [73] in microsecond ranges. However, it may take a longer time for the microdroplets to completely vaporize at high excitation frequencies. Using high speed imaging, Haworth and Kripfgans [74] showed that a two-cycle vaporization pulse at 3.5 MHz resulted in the phase transition of a subvolume of PFC within a micron-sized PFP emulsion, whereas with a thirteen-cycle vaporization pulse, the entire droplet phase transitioned. Using the Rayleigh-Plesset equation, Lacour, et al. [6] showed that a combination of surface tension, heat transfer, and acoustic modulation resulted in multiple rebounds of the PFC vapor bubble before complete vaporization. Note that the number of cycles did not result in any significant change in the US waveform and the amplitude of peak rarefactional and compressional pressures (Fig. S2).
Fig. 6.
Depending on the pulse duration, acoustic droplet vaporization (ADV) using high frequency ultrasound (US, 8.6 MHz) resulted in stable bubble (complete release) as well as presumably transient, partial vaporization (partial release) of perfluorohexane (PFH) double emulsion containing Alexa Flour 488-labeled dextran (AF488, shown in green). Maximum intensity projection confocal images of (A) an ADV-generated stable bubble at pulse duration: 5.4 µs one time (x) US exposure, and (B) partial ADV at pulse duration: 1.5 µs (1x, +US), and (C) pulse duration:1.5 µs (3x) in acoustically-responsive scaffolds with Alexa Flour 647-labeled fibrinogen (shown in red). Confocal image of a PFH-AF488 before ADV (i.e., -US) is shown in Fig. 4A. AF488 intensity measurements before and after ADV at 8.6 MHz and varying pulse durations is shown in D. (E) Average diameter of PFH-AF488 emulsion before and after US exposure at 8.6 MHz. ADV-generated bubbles at 8.6 MHz and pulse duration of 5.4 µs reached 80 ± 3.1 µm 1 h post-ADV. Statistically significant difference (p < 0.05) is denoted as follows: α: vs. -US (n = 10–16 per group). Scale bar: 5 µm for all panels. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
While PFH emulsion underwent stable, complete vaporization at 5.4 µs (8.6 MHz) and transient, partial vaporization at 1.5 µs (8.6 MHz), ARSs containing PFO emulsion did not show any significant change in the payload intensity before and after ADV at 8.6 MHz (data not shown). As mentioned earlier, no ADV threshold was detected in ARSs containing PFO at an excitation frequency of 8.6 MHz across the range of pressures (Pr = 1–7 MPa). In the subsequent section, this selectivity of release based on the frequency of excitation and the PFC species was used to release one payload without disturbing the other for sequential, dual release studies.
4.3. Payload release studies
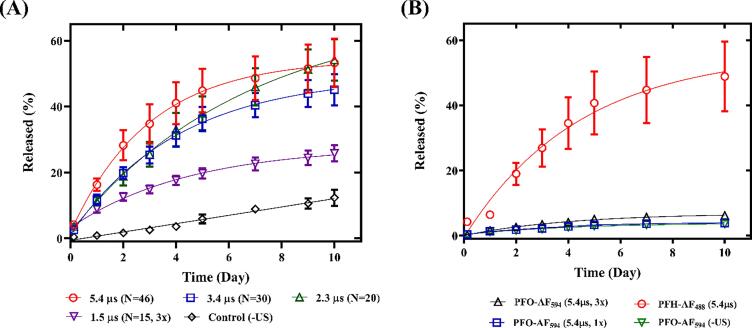
Release profiles of ARSs containing PFH-AF488 at various pulse durations (with the corresponding number of cycles (N)) at 8.6 MHz is shown in Fig. 7A. Consistent with the confocal images, significantly higher release was achieved at 5.4 µs (53.3 ± 7.4%), than at 1.5 µs with multiple US exposure (3x, 25.8 ± 2.4%). There was no significant difference in the release profiles for the pulse durations above 1.5 µs (N > 20). K was not significantly different between ARSs exposed to different acoustic settings in Fig. 7A.
Fig. 7.
Release profiles from acoustically-responsive scaffolds (ARSs) containing (A) one dextran payload: 0.5% (v/v) perfluorohexane (PFH)-Alexa Fluor 488-labeled dextran (AF488) (n = 4) and (B) two dextran payloads: 0.5% (v/v) PFH-AF488 and 0.5% (v/v) perfluorooctane (PFO)-Alexa Fluor 594 labeled dextran (AF594) (n = 8) exposed to ultrasound (US) at 8.6 MHz (7 MPa peak rarefactional pressure) and varying pulse durations with the corresponding number of cycles (N) and the number of US exposures (x).
Release profiles of ARSs containing PFH-AF488 and PFO-AF594 exposed to 8.6 MHz (5.4 µs) are compared in Fig. 7B. Percent release from ARSs containing PFO-AF594 at these acoustic parameters was not significantly different than the -US control.
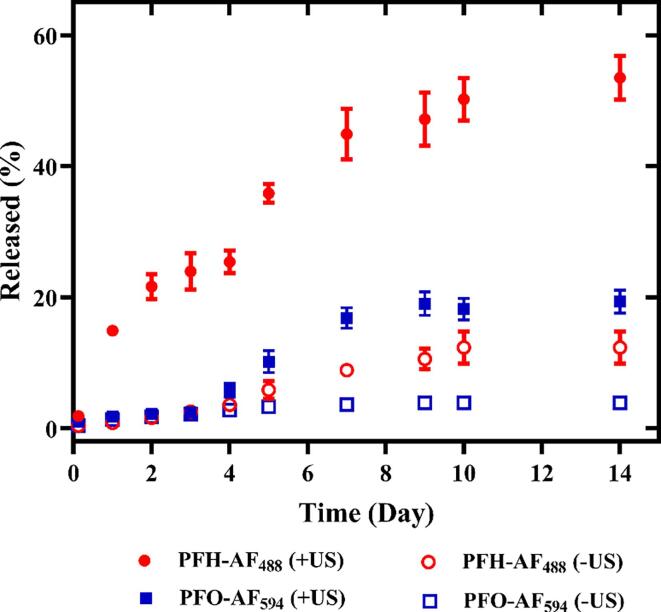
Fig. 8 displays the sequential, dual release profiles in ARSs where US exposure at 8.6 MHz (1.5 µs, +3x) selectively released PFH-AF488 on day 0. The second US exposure at 2.5 MHz (5.4 µs, +3x) on day 4 resulted in more release from the remaining PFH-AF488 as well as release from PFO-AF594.
Fig. 8.
Frequency-dependent, sequential release from acoustically-responsive scaffolds (ARSs) using acoustic droplet vaporization. The first dextran payload was released from emulsion with perfluorohexane (PFH)-Alexa Fluor 488-labeled dextran (AF488) on day 0 at 8.6 MHz (peak rarefactional pressure: 7 MPa, pulse duration: 1.5 µs). The second payload was activated from emulsion with perfluorooctane (PFO)-Alexa Fluor 594-labeled dextran (AF594) at 2.5 MHz (peak rarefactional pressure: 8 MPa pulse duration: 5.4 µs) on day 4 (n = 4).
Given the necessity for multiple payload release in tissue regeneration, we explored several strategies for dual release studies in our prior publications. In our first study of dual-payload release, we used a single excitation frequency to sequentially release two payloads from a single layer ARS containing two emulsions [18]. The first payload was incorporated into an emulsion with a lower bulk boiling point PFC (e.g., PFP or PFH) while the second payload was contained in an emulsion with a higher bulk boiling point PFC (e.g., perfluoroheptane). A lower excitation pressure was used to release the first payload, which relied on the direct dependence of the ADV threshold with PFC bulk boiling point. The major limitation of this approach was the presence of ADV-generated bubbles following the first payload release, thus shadowing subsequent US exposures. To eliminate the attenuating effects of the ADV-generated bubbles on subsequent exposures, a bi-layer ARS was designed such that the first payload in the upper layer was released in the presence of a standing wave field, followed by release of the second payload from the lower layer [16]. In the current approach, by adjusting the frequency of excitation and the pulse duration, the first payload (i.e., PFH emulsion) underwent transient, partial vaporization, where payload release increased with the number of US exposures without generation of stable bubbles or the disruption of the second payload. Additionally, the presented approach uses a single-layer ARS, offering the advantage of in situ polymerization during in vivo studies, unlike a bi-layer ARS, which must be polymerized ex situ and then implanted. Ultimately, designing PSDEs that would undergo partial vaporization or repeated vaporization under specific US parameters may provide sustained therapeutic benefits which are unattainable through irreversible ADV alone.
5. Conclusions
In this study, CNT was used to predict the nucleation and condensation pressures for ADV-generated bubbles in PSDEs with different PFC cores. The threshold bubble radii above which the ADV-generated bubbles remain stable against condensation were predicted to be 0.4 µm and 5.2 µm for PFP and PFH bubbles, respectively. Unlike PFP and PFH, ADV-generated bubbles of any size in PFO condense back to liquid at ambient condition. Consistent with the CNT findings, stable bubble formation from sufficiently-sized PFH emulsion was observed using confocal imaging while PFO emulsion underwent repeated vaporization and recondensation during US pulses. Intensity analysis of confocal images of PFH-AF488 showed complete release of the payload upon stable bubble formation either at 2.5 MHz (1.5–5.4 µs) or 8.6 MHz (only at 5.4 µs). At 8.6 MHz and a shorter pulse duration (1.5 µs), PFH underwent partial vaporization where the payload release increased with the number of US exposures. PFO did not vaporize at 8.6 MHz in the pressure range interrogated here. The selectivity of release based on the frequency of excitation and the species of the PFC liquid was used for dual release studies where the first payload (i.e., PFH-AF488) was activated at 8.6 MHz on day 0 followed by the second payload release (i.e., PFO-AF594) at 2.5 MHz on day 4.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
This work was supported by NIH Grant R01HL139656 (M.L.F.) and R00HL124322 (B.M.B). W.Y.W. acknowledges financial support from the University of Michigan Rackham Merit Fellowship and the National Science Foundation Graduate Research Fellowship Program (DGE1256260). Special thanks to Dr. Allen Brooks (Department of Radiology) for assisting with the synthesis of the fluorosurfactant, the Fabrication Studio at the Duderstadt Center and Dr. William Weadock (Department of Radiology) for helping with 3D printing of materials related to the US exposure setup.
Footnotes
Supplementary data to this article can be found online at https://doi.org/10.1016/j.ultsonch.2020.105430.
Appendix A. Supplementary data
The following are the Supplementary data to this article:
References
- 1.Kripfgans O.D., Fowlkes J.B., Miller D.L., Eldevik O.P., Carson P.L. Acoustic droplet vaporization for therapeutic and diagnostic applications. Ultrasound. Med. Biol. 2000;26(7):1177–1189. doi: 10.1016/S0301-5629(00)00262-3. [DOI] [PubMed] [Google Scholar]
- 2.Kawabata K.-I., Sugita N., Yoshikawa H., Azuma T., Umemura S.-I. Nanoparticles with multiple perfluorocarbons for controllable ultrasonically induced phase shifting. Jpn. J. Appl. Phys. 2005;44(6B):4548–4552. doi: 10.1143/JJAP.44.4548. [DOI] [Google Scholar]
- 3.Martz T.D., Sheeran P.S., Bardin D., Lee A.P., Dayton P.A. Precision manufacture of phase-change perfluorocarbon droplets using microfluidics. Ultrasound Med. Biol. 2011;37(11):1952–1957. doi: 10.1016/j.ultrasmedbio.2011.08.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Miles C.J., Doering C.R., Kripfgans O.D. Nucleation pressure threshold in acoustic droplet vaporization. J. Appl. Phys. 2016;120(3):034903. doi: 10.1063/1.4958907. [DOI] [Google Scholar]
- 5.Shpak O., Verweij M., Vos H.J., de Jong N., Lohse D., Versluis M. Acoustic droplet vaporization is initiated by superharmonic focusing. PNAS. 2014;111(5):1697–1702. doi: 10.1073/pnas.1312171111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Lacour T., Valier-Brasier T., Coulouvrat F. Ultimate fate of a dynamical bubble/droplet system following acoustic vaporization. Phys. Fluids. 2020;32(5):051702. doi: 10.1063/5.0004375. [DOI] [Google Scholar]
- 7.Fabiilli M.L., Haworth K.J., Fakhri N.H., Kripfgans O.D., Carson P.L., Fowlkes J.B. The role of inertial cavitation in acoustic droplet vaporization. IEEE Trans. Ultrason., Ferroelect., Freq. Contr. 2009;56(5):1006–1017. doi: 10.1109/TUFFC.2009.1132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Asami R., Kawabata K. 2012 IEEE International Ultrasonics Symposium. IEEE; 2012. Repeatable vaporization of optically vaporizable perfluorocarbon droplets for photoacoustic contrast enhanced imaging; pp. 1200–1203. [Google Scholar]
- 9.Kripfgans O.D., Fabiilli M.L., Carson P.L., Fowlkes J.B. On the acoustic vaporization of micrometer-sized droplets. J. Acoust. Soc. Am. 2004;116(1):272–281. doi: 10.1121/1.1755236. [DOI] [PubMed] [Google Scholar]
- 10.Sheeran P.S., Matsunaga T.O., Dayton P.A. Phase-transition thresholds and vaporization phenomena for ultrasound phase-change nanoemulsions assessed via high-speed optical microscopy. Phys. Med. Biol. 2013;58(13):4513–4534. doi: 10.1088/0031-9155/58/13/4513. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Matsuura N., Williams R., Gorelikov I., Chaudhuri J., Rowlands J., Hynynen K., Foster S., Burns P., Resnik N. 2009 IEEE International Ultrasonics Symposium. IEEE; 2009. Nanoparticle-loaded perfluorocarbon droplets for imaging and therapy; pp. 5–8. [Google Scholar]
- 12.Hannah A.S., Luke G.P., Emelianov S.Y. Blinking phase-change nanocapsules enable background-free ultrasound imaging. Theranostics. 2016;6(11):1866–1876. doi: 10.7150/thno.14961. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Fabiilli M.L., Lee J.A., Kripfgans O.D., Carson P.L., Fowlkes J.B. Delivery of water-soluble drugs using acoustically triggered perfluorocarbon double emulsions. Pharm. Res. 2010;27(12):2753–2765. doi: 10.1007/s11095-010-0277-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Fabiilli M.L., Wilson C.G., Padilla F., Martín-Saavedra F.M., Fowlkes J.B., Franceschi R.T. Acoustic droplet–hydrogel composites for spatial and temporal control of growth factor delivery and scaffold stiffness. Acta Biomater. 2013;9(7):7399–7409. doi: 10.1016/j.actbio.2013.03.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Moncion A., Arlotta K.J., O’Neill E.G., Lin M., Mohr L.A., Franceschi R.T., Kripfgans O.D., Putnam A.J., Fabiilli M.L. In vitro and in vivo assessment of controlled release and degradation of acoustically responsive scaffolds. Acta Biomater. 2016;46:221–233. doi: 10.1016/j.actbio.2016.09.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Aliabouzar M., Jivani A., Lu X., Kripfgans O.D., Fowlkes J.B., Fabiilli M.L. Standing wave-assisted acoustic droplet vaporization for single and dual payload release in acoustically-responsive scaffolds. Ultrason. Sonochem. 2020;66:105109. doi: 10.1016/j.ultsonch.2020.105109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Lu X., Jin H., Quesada C., Farrell E.C., Huang L., Aliabouzar M., Kripfgans O.D., Fowlkes J.B., Franceschi R.T., Putnam A.J., Fabiilli M.L. Spatially-directed cell migration in acoustically-responsive scaffolds through the controlled delivery of basic fibroblast growth factor. Acta Biomater. 2020;113:217–227. doi: 10.1016/j.actbio.2020.06.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Moncion A., Lin M., Kripfgans O.D., Franceschi R.T., Putnam A.J., Fabiilli M.L. Sequential payload release from acoustically-responsive scaffolds using focused ultrasound. Ultrasound Med. Biol. 2018;44(11):2323–2335. doi: 10.1016/j.ultrasmedbio.2018.06.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Blander M, Katz JL. Bubble nucleation in liquids. AIChE J. 1975; 21:833-48.
- 20.Karthika S., Radhakrishnan T.K., Kalaichelvi P. A review of classical and nonclassical nucleation theories. Cryst. Growth Des. 2016;16(11):6663–6681. doi: 10.1021/acs.cgd.6b00794. [DOI] [Google Scholar]
- 21.Church C.C. Spontaneous homogeneous nucleation, inertial cavitation and the safety of diagnostic ultrasound. Ultrasound Med. Biol. 2002;28(10):1349–1364. doi: 10.1016/S0301-5629(02)00579-3. [DOI] [PubMed] [Google Scholar]
- 22.Vlaisavljevich E., Aydin O., Lin K.-W., Durmaz Y.Y., Fowlkes B., ElSayed M., Xu Z. The role of positive and negative pressure on cavitation nucleation in nanodroplet-mediated histotripsy. Phys. Med. Biol. 2016;61(2):663–682. doi: 10.1088/0031-9155/61/2/663. [DOI] [PubMed] [Google Scholar]
- 23.Kumar KN, Aliabouzar M, Sarkar K. Study of acoustic droplet vaporization using classical nucleation theory. The Journal of the Acoustical Society of America 2017; 141:3953-53.
- 24.Fisher J.C. The fracture of liquids. J. Appl. Phys. 1948;19(11):1062–1067. doi: 10.1063/1.1698012. [DOI] [Google Scholar]
- 25.Forest T.W., Ward C.A. Effect of a dissolved gas on the homogeneous nucleation pressure of a liquid. J. Chem. Phys. 1977;66(6):2322–2330. doi: 10.1063/1.434267. [DOI] [Google Scholar]
- 26.Kalikmanov V.I. Springer; Nucleation theory: 2013. Classical Nucleation Theory; pp. 17–41. [Google Scholar]
- 27.Kelton K., Greer A.L. Elsevier; 2010. Nucleation In Condensed Matter: Applications In Materials And Biology. [Google Scholar]
- 28.Lubetkin S.D. Why is it much easier to nucleate gas bubbles than theory predicts? Langmuir. 2003;19(7):2575–2587. doi: 10.1021/la0266381. [DOI] [Google Scholar]
- 29.Ward C, Balakrishnan A, Hooper F. On the thermodynamics of nucleation in weak gas-liquid solutions. 1970.
- 30.Li D., Liu S., Wei Y., Ren T., Tang Y. A turbulent two-phase model for predicting cavitating flow based on homogenous nucleation theory. Int. Commun. Heat Mass Transfer. 2018;97:17–29. doi: 10.1016/j.icheatmasstransfer.2018.06.001. [DOI] [Google Scholar]
- 31.Pilarek M. Liquid Perfluorochemicals as Flexible and Efficient Gas Carriers Applied in Bioprocess Engineering: An Updated Overview and Future Prospects. Chemical and Process Engineering 2014; 35:463-87.
- 32.Schürmann A., Haas R., Murat M., Kuritz N., Balaish M., Ein-Eli Y., Janek J., Natan A., Schröder D. Diffusivity and solubility of oxygen in solvents for metal/oxygen batteries: a combined theoretical and experimental study. J. Electrochem. Soc. 2018;165(13):A3095–A3099. doi: 10.1149/2.0601813jes. [DOI] [Google Scholar]
- 33.Eibl D, Eibl R. Disposable Bioreactors II. 2014.
- 34.Nemec T, Marsik F. The classical multicomponent nucleation theory for cavitation in water with dissolved gases. 2009.
- 35.Radhakrishnan K., Holland C.K., Haworth K.J. Scavenging dissolved oxygen via acoustic droplet vaporization. Ultrason. Sonochem. 2016;31:394–403. doi: 10.1016/j.ultsonch.2016.01.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Rapoport N.Y., Efros A.L., Christensen D.A., Kennedy A.M., Nam K.-H. Microbubble generation in phase-shift nanoemulsions used as anticancer drug carriers. Bubble Sci. Eng. Technol. 2009;1(1-2):31–39. doi: 10.1179/175889709X446516. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Lubetkin S.D., Akhtar M. The variation of surface tension and contact angle under applied pressure of dissolved gases, and the effects of these changes on the rate of bubble nucleation. J. Colloid Interface Sci. 1996;180(1):43–60. doi: 10.1006/jcis.1996.0272. [DOI] [Google Scholar]
- 38.Massoudi R., King A.D. Effect of pressure on the surface tension of water. Adsorption of low molecular weight gases on water at 25.deg. J. Phys. Chem. 1974;78(22):2262–2266. doi: 10.1021/j100615a017. [DOI] [Google Scholar]
- 39.Vehkamäki H, Määttänen A, Lauri A, Napari I, Kulmala M. The heterogeneous Zeldovich factor. 2007. [DOI] [PubMed]
- 40.Ghosh DP, Raj R, Mohanty D, Saha SK. Onset of Nucleate Boiling, Void Fraction, and Liquid Film Thickness. Microchannel Phase Change Transport Phenomena: Elsevier, 2016. 5-90.
- 41.Barber E.J., Cady G.H. Vapor Pressures of Perfluoropentanes. J. Phys. Chem. 1956;60(4):504–505. doi: 10.1021/j150538a030. [DOI] [Google Scholar]
- 42.Freire M.G., Carvalho P.J., Queimada A.J., Marrucho I.M., Coutinho J.A.P. Surface Tension of Liquid Fluorocompounds. J. Chem. Eng. Data. 2006;51(5):1820–1824. doi: 10.1021/je060199g. [DOI] [Google Scholar]
- 43.Bakhtar F., Young J.B., White A.J., Simpson D.A. Classical nucleation theory and its application to condensing steam flow calculations. Proc. Inst. Mech. Eng., Part C: J. Mech. Eng. Sci. 2006;219:1315–1333. [Google Scholar]
- 44.Hall C.S., Lanza G.M., Rose J.H., Kaufmann R.J., Fuhrhop R.W., Handley S.H., Waters K.R., Miller J.G., Wickline S.A. Experimental determination of phase velocity of perfluorocarbons: Applications to targeted contrast agents. IEEE Trans. Ultrason., Ferroelect., Freq. Contr. 2000;47(1):75–84. doi: 10.1109/58.818750. [DOI] [PubMed] [Google Scholar]
- 45.Allen L.B., Kassner J.L., Jr. The nucleation of water vapor in the absence of particulate matter and ions. J. Colloid Interface Sci. 1969;30(1):81–93. doi: 10.1016/0021-9797(69)90381-6. [DOI] [Google Scholar]
- 46.Oriani R.A., Sundquist B.E. Emendations to nucleation theory and the homogeneous nucleation of water from the vapor. J. Chem. Phys. 1963;38(9):2082–2089. doi: 10.1063/1.1733936. [DOI] [Google Scholar]
- 47.Moncion A., Lin M., O'Neill E.G., Franceschi R.T., Kripfgans O.D., Putnam A.J., Fabiilli M.L. Controlled release of basic fibroblast growth factor for angiogenesis using acoustically-responsive scaffolds. Biomaterials. 2017;140:26–36. doi: 10.1016/j.biomaterials.2017.06.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Lu X., Dong X., Natla S., Kripfgans O.D., Fowlkes J.B., Wang X., Franceschi R., Putnam A.J., Fabiilli M.L. Parametric study of acoustic droplet vaporization thresholds and payload release from acoustically-responsive scaffolds. Ultrasound Med. Biol. 2019;45(9):2471–2484. doi: 10.1016/j.ultrasmedbio.2019.05.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Parsons J.E., Cain C.A., Fowlkes J.B. Cost-effective assembly of a basic fiber-optic hydrophone for measurement of high-amplitude therapeutic ultrasound fields. J. Acoust. Soc. Am. 2006;119(3):1432–1440. doi: 10.1121/1.2166708. [DOI] [PubMed] [Google Scholar]
- 50.Burke M.P., Smith J.D., Carroll N.L., Townend D.J., Porter D., Hoskins P.R. Acoustic properties of butadiene and silicone elastomers at megahertz frequencies. Plast., Rubber Compos. 2009;38(8):343–348. doi: 10.1179/146580109X12473409437020. [DOI] [Google Scholar]
- 51.Aliabouzar M., Lu X., Kripfgans O.D., Fowlkes J.B., Fabiilli M.L. Acoustic droplet vaporization in acoustically responsive scaffolds: effects of frequency of excitation, volume fraction and threshold determination method. Ultrasound Med. Biol. 2019;45(12):3246–3260. doi: 10.1016/j.ultrasmedbio.2019.08.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Lee J.Y., Carugo D., Crake C., Owen J., de Saint Victor M., Seth A., Coussios C., Stride E. Nanoparticle-loaded protein-polymer nanodroplets for improved stability and conversion efficiency in ultrasound imaging and drug delivery. Adv. Mater. 2015;27(37):5484–5492. doi: 10.1002/adma.201502022. [DOI] [PubMed] [Google Scholar]
- 53.Dominguez A., Bories S., Prat M. Gas cluster growth by solute diffusion in porous media. Experiments and automaton simulation on pore network. Int. J. Multiph. Flow. 2000;26(12):1951–1979. doi: 10.1016/S0301-9322(00)00006-9. [DOI] [Google Scholar]
- 54.Němec T. Homogeneous bubble nucleation in binary systems of liquid solvent and dissolved gas. Chem. Phys. 2016;467:26–37. doi: 10.1016/j.chemphys.2016.01.003. [DOI] [Google Scholar]
- 55.Hsu J.J.C., Nagarajan N., Robinson R.L. Equilibrium phase compositions, phase densities, and interfacial tensions for carbon dioxide + hydrocarbon systems. 1. Carbon dioxide + n-butane. J. Chem. Eng. Data. 1985;30(4):485–491. doi: 10.1021/je00042a036. [DOI] [Google Scholar]
- 56.Kovalchuk N.M., Trybala A., Starov V., Matar O., Ivanova N. Fluoro- vs hydrocarbon surfactants: Why do they differ in wetting performance? Adv. Colloid Interface Sci. 2014;210:65–71. doi: 10.1016/j.cis.2014.04.003. [DOI] [PubMed] [Google Scholar]
- 57.Li J., Peterson G.P. Microscale heterogeneous boiling on smooth surfaces—from bubble nucleation to bubble dynamics. Int. J. Heat Mass Transf. 2005;48(21-22):4316–4332. doi: 10.1016/j.ijheatmasstransfer.2005.05.022. [DOI] [Google Scholar]
- 58.Crum L. Acoustic cavitation thresholds in water. Cavitation and inhomogeneities in underwater acoustics: Springer, 1980. 84-89.
- 59.Rooze J., Rebrov E.V., Schouten J.C., Keurentjes J.T.F. Dissolved gas and ultrasonic cavitation – A review. Ultrason. Sonochem. 2013;20(1):1–11. doi: 10.1016/j.ultsonch.2012.04.013. [DOI] [PubMed] [Google Scholar]
- 60.Li B., Gu Y., Chen M. An experimental study on the cavitation of water with dissolved gases. Exp. Fluids. 2017;58(12) doi: 10.1007/s00348-017-2449-0. [DOI] [Google Scholar]
- 61.Kripfgans O.D., Orifici C.M., Carson P.L., Ives K.A., Eldevik O.P., Fowlkes J.B. Acoustic droplet vaporization for temporal and spatial control of tissue occlusion: a kidney study. IEEE Trans. Ultrason., Ferroelect., Freq. Contr. 2005;52(7):1101–1110. doi: 10.1109/TUFFC.2005.1503996. [DOI] [PubMed] [Google Scholar]
- 62.Sheeran P.S., Wong V.P., Luois S., McFarland R.J., Ross W.D., Feingold S., Matsunaga T.O., Dayton P.A. Decafluorobutane as a phase-change contrast agent for low-energy extravascular ultrasonic imaging. Ultrasound Med. Biol. 2011;37(9):1518–1530. doi: 10.1016/j.ultrasmedbio.2011.05.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Qamar A., Wong Z.Z., Fowlkes J.B., Bull J.L. Dynamics of acoustic droplet vaporization in gas embolotherapy. Appl. Phys. Lett. 2010;96(14):143702. doi: 10.1063/1.3376763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Reznik N., Seo M., Williams R., Bolewska-Pedyczak E., Lee M., Matsuura N., Gariepy J., Foster F.S., Burns P.N. Optical studies of vaporization and stability of fluorescently labelled perfluorocarbon droplets. Phys. Med. Biol. 2012;57(21):7205–7217. doi: 10.1088/0031-9155/57/21/7205. [DOI] [PubMed] [Google Scholar]
- 65.Reznik N., Shpak O., Gelderblom E.C., Williams R., de Jong N., Versluis M., Burns P.N. The efficiency and stability of bubble formation by acoustic vaporization of submicron perfluorocarbon droplets. Ultrasonics. 2013;53(7):1368–1376. doi: 10.1016/j.ultras.2013.04.005. [DOI] [PubMed] [Google Scholar]
- 66.Yu J., Chen X., Villanueva F.S., Kim K. Vaporization and recondensation dynamics of indocyanine green-loaded perfluoropentane droplets irradiated by a short pulse laser. Appl. Phys. Lett. 2016;109(24):243701. doi: 10.1063/1.4972184.13. [DOI] [Google Scholar]
- 67.Aliabouzar M., Kumar K.N., Sarkar K. Effects of droplet size and perfluorocarbon boiling point on the frequency dependence of acoustic vaporization threshold. J. Acoust. Soc. Am. 2019;145(2):1105–1116. doi: 10.1121/1.5091781. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Aliabouzar M., Davidson C.D., Wang W.Y., Kripfgans O.D., Franceschi R.T., Putnam A.J., Fowlkes J.B., Baker B.M., Fabiilli M.L. Spatiotemporal control of micromechanics and microstructure in acoustically-responsive scaffolds using acoustic droplet vaporization. Soft Matter. 2020;16(28):6501–6513. doi: 10.1039/D0SM00753F. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Hudson N.E., Houser J.R., O'Brien E.T., III, Taylor R.M., II, Superfine R., Lord S., Falvo M.R. Stiffening of individual fibrin fibers equitably distributes strain and strengthens networks. Biophys. J . 2010;98(8):1632–1640. doi: 10.1016/j.bpj.2009.12.4312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Piechocka I.K., Bacabac R.G., Potters M., MacKintosh F.C., Koenderink G.H. Structural hierarchy governs fibrin gel mechanics. Biophys. J. 2010;98(10):2281–2289. doi: 10.1016/j.bpj.2010.01.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Leighton T. Academic press; 2012. The Acoustic Bubble. [Google Scholar]
- 72.Lo A., Kripfgans O., Carson P., Rothman E., Fowlkes J. Acoustic droplet vaporization threshold: effects of pulse duration and contrast agent. IEEE Trans. Ultrason., Ferroelect., Freq. Contr. 2007;54(5):933–946. doi: 10.1109/TUFFC.2007.339. [DOI] [PubMed] [Google Scholar]
- 73.Zhang P., Porter T. An in vitro study of a phase-shift nanoemulsion: a potential nucleation agent for bubble-enhanced HIFU tumor ablation. Ultrasound Med. Biol. 2010;36(11):1856–1866. doi: 10.1016/j.ultrasmedbio.2010.07.001. [DOI] [PubMed] [Google Scholar]
- 74.Haworth K.J., Kripfgans O.D. 2008 IEEE Ultrasonics Symposium. IEEE; 2008. Initial growth and coalescence of acoustically vaporized perfluorocarbon microdroplets; pp. 623–626. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.