CT quantification of the heterogeneity of fibrosis boundaries in idiopathic pulmonary fibrosis

Abstract

Objectives

To quantify the heterogeneity of fibrosis boundaries in idiopathic pulmonary fibrosis (IPF) using the Gaussian curvature analysis for evaluating disease severity and predicting survival.

Methods

We retrospectively included 104 IPF patients and 52 controls who underwent baseline chest CT scans. Normal lungs below − 500 HU were segmented, and the boundary was three-dimensionally reconstructed using in-house software. Gaussian curvature analysis provided histogram features on the heterogeneity of the fibrosis boundary. We analyzed the correlations between histogram features and the gender-age-physiology (GAP) and CT fibrosis scores. We built a regression model to predict diffusing capacity of carbon monoxide (DLCO) using the histogram features and calculated the modified GAP (mGAP) score by replacing DLCO with the predicted DLCO. The performances of the GAP, CT-GAP, and mGAP scores were compared using 100 repeated random-split sets.

Results

Patients with moderate-to-severe IPF had more numerous Gaussian curvatures at the fibrosis boundary, lower uniformity, and lower 10th to 30th percentiles of Gaussian curvature than controls or patients with mild IPF (all p < 0.0033). The 20th percentile was most significantly correlated with the GAP score (r = − 0.357; p < 0.001) and the CT fibrosis score (r = − 0.343; p = 0.001). More numerous Gaussian curvatures, higher entropy, lower uniformity, and 10th to 30th percentiles (p < 0.001–0.041) were associated with mortality. The mGAP score was comparable to the GAP and CT-GAP scores for survival prediction (mean C-indices, 0.76 vs. 0.79 vs. 0.77, respectively).

Conclusions

Gaussian curvatures of fibrosis boundaries became more heterogeneous as the disease progressed, and heterogeneity was negatively associated with survival in IPF.

Key Points

• Gaussian curvature of the fibrotic lung boundary was more heterogeneous in patients with moderate-to-severe IPF than those with mild IPF or normal controls.

• The 20th percentile of the Gaussian curvature of the fibrosis boundary was linearly correlated with the GAP score and the CT fibrosis score.

• A modified GAP score that replaced the diffusing capacity of carbon monoxide with a composite measure using histogram features of the Gaussian curvature of the fibrosis boundary showed a comparable ability to predict survival to both the GAP and the CT-GAP score.

Supplementary Information

The online version contains supplementary material available at 10.1007/s00330-020-07594-y.

Introduction

Idiopathic pulmonary fibrosis (IPF) is a chronic, progressive, fibrosing interstitial lung disease of unknown etiology [1, 2]. IPF patients typically have a median survival of about 3 years after diagnosis. Nevertheless, disease severity may vary considerably at the time of IPF diagnosis, and patients’ clinical course after diagnosis can likewise show variation [3]. The gender-age-physiology (GAP) model is a well-validated clinical model for staging disease severity and predicting survival in IPF patients; this model consists of four clinical variables, including age, sex, forced vital capacity (FVC), and diffusing capacity of carbon monoxide (DLCO) [4, 5].

The radiologic abnormalities of IPF on chest CT can be utilized not only for diagnosis [1, 6], but also for staging its severity and prognostication. The visually assessed extent of fibrosis on CT images is a predictor of survival in IPF patients [7–10]. Furthermore, the CT-derived extent of fibrosis can be used as a supplement to the GAP score to improve the capability of predicting survival [11], or as a substitute for DLCO in the GAP model [12]. However, the visual evaluation of fibrosis on CT can be limited by the subjective interpretation or degree of experience of the reader, causing inter-observer variation [13]. Accordingly, several computer-based algorithms for the quantification of fibrosis have been developed [14–16] and shown to predict survival or disease progression in IPF better than visual assessments [17–21].

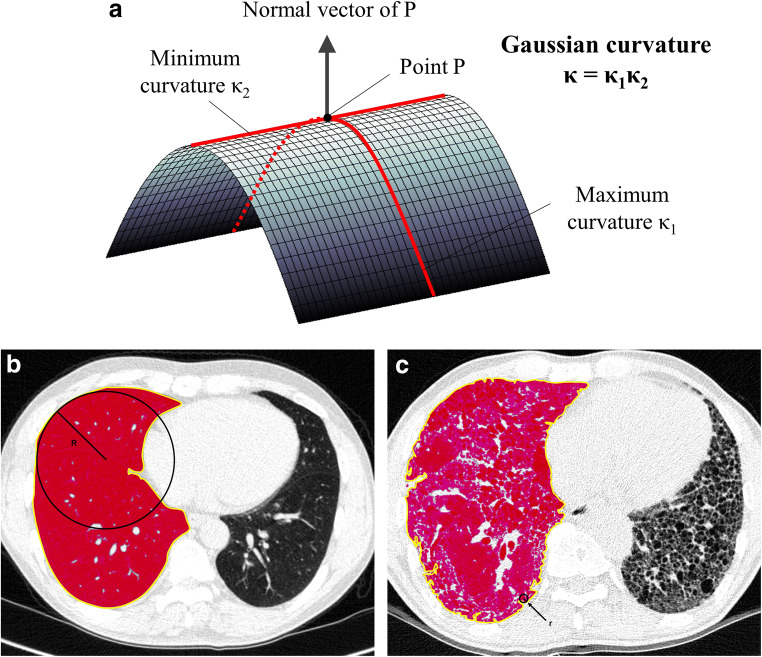
Pre-existing techniques for visual assessment or automatic quantification have focused on the presence and degree of fibrosis [22]. The temporal and spatial heterogeneity of interstitial fibrosis is considered a pathognomonic histologic finding of IPF [23]. Gaussian curvature is defined as the product of the minimum and maximum curvatures (i.e., the reciprocal of the radius) and is one of the local geometric descriptors of surface roughness in classical differential geometry (Fig. 1a and Supplementary figure 1) [24], which has been applied to analyze curvature in the developing brain using brain MRI [25]. We hypothesized that the similar approach could be applied for IPF patients by quantifying the heterogeneity of the fibrosis. Thus, the purpose of our study was to quantify the spatial heterogeneity of the fibrosis boundary on chest CT in IPF using the Gaussian curvature analysis for evaluating disease severity and predicting survival.

Fig. 1.

Schematic diagram of (a) Gaussian curvature of the fibrosis boundaries of (b) the normal lung and (c) the fibrotic lung. a Gaussian curvature is defined as the product of two principal curvatures which are the maximum (κ₁) and minimum (κ₂) of curvatures that intersect the normal plane—a plane containing the normal vector of the surface at a certain point (P). b In the normal lung, fibrotic areas do not exist; therefore, the boundary (colored in yellow) of non-fibrotic areas (below − 500 HU is colored in red) corresponds to pleural surfaces, which are smoothly elliptic and have a radius of the tangent sphere (R) that is mostly larger than 1 mm. c In IPF, the fibrosis boundary (colored in yellow) is irregular and the radius of the tangent sphere (r) is much smaller. Thus, the frequency of either positive or negative Gaussian curvature (according to the direction of the boundary curvature) is higher, although overall concavity of the boundary is maintained along pleural surfaces

Materials and methods

Our institutional review board approved this retrospective study (IRB No. H-1803-120-932), and informed consent was waived.

Patients

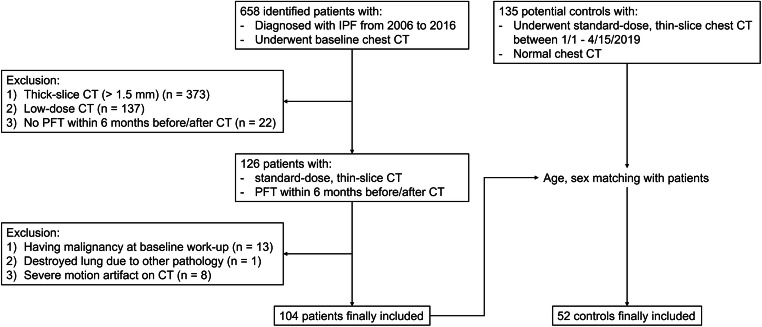
A study coordinator initially searched electronic medical records to identify patients who were diagnosed with IPF and underwent chest CT scans from 2006 to 2016 at a single tertiary hospital. The diagnosis of IPF was made according to the 2011 ATS/ERS/JRS/ALAT guideline since 2012 [26]. IPF was diagnosed by surgical pathology until 2011. We applied the following inclusion criteria to determine eligibility: (a) available baseline standard dose thin-section chest CT scans with a slice interval of 1.5 mm or shorter, and (b) available baseline pulmonary function test (PFT) results within 6 months before or after the baseline chest CT scan. We excluded patients who had (a) malignancy at the baseline workup, (b) a destroyed lung due to other pathology, or (c) profound motion artifacts on their CT images. Finally, a total of 104 patients (mean age, 68.2 ± 9.4; male-to-female ratio, 71:33; 56 diagnosed by pathology, 12 by multidisciplinary diagnosis, and 36 by typical usual interstitial pneumonia CT findings after excluding other differential diagnoses) were included in this study (Fig. 2).

Fig. 2.

Study diagram for the inclusion of patients and controls

For normal controls, we searched consecutive subjects who underwent chest CT scans from January 1 to April 15, 2019, and had few respiratory symptoms and CT abnormalities except for small benign nodules or linear atelectasis. We applied the same inclusion criteria except for PFT, as PFT was rarely performed for the normal controls without respiratory complaints. After age- and sex-matching with the IPF patients, 52 control subjects (mean age, 67.5 ± 9.4; male-to-female ratio, 35:17) were included in this study (Fig. 2).

Clinical risk assessment and CT visual analysis

The GAP stage and score were calculated using the baseline PFT results, including the percent of predicted FVC (FVC%) and DLCO (DLCO%) [4], with the following distribution: GAP stage I, 64 patients; stage II, 34 patients; stage III, 5 patients. Since there were few GAP stage III patients, we classified the patients as having mild IPF (GAP stage I, n = 64) or moderate-to-severe IPF (GAP stage II–III, n = 40). The mean interval between the baseline PFT and the CT scans was 21.2 ± 38.2 days.

Two thoracic radiologists (with 13 and 6 years of thoracic CT experience, respectively) blinded to the clinical data analyzed the CT images visually by a consensus reading. The radiologists reviewed axial CT images containing lung parenchyma at a PACS workstation (INFINITT PACS Version 5.0.0) with a lung window setting (level, − 700 HU; width, 1500 HU). A whole-lung extent of ground-glass opacity (GGO), consolidation, reticular abnormality, honeycombing, emphysema, and total fibrosis (including both reticular abnormality and honeycombing) were scored to the nearest 10% [27].

Gaussian curvature histogram analysis of the fibrosis boundaries

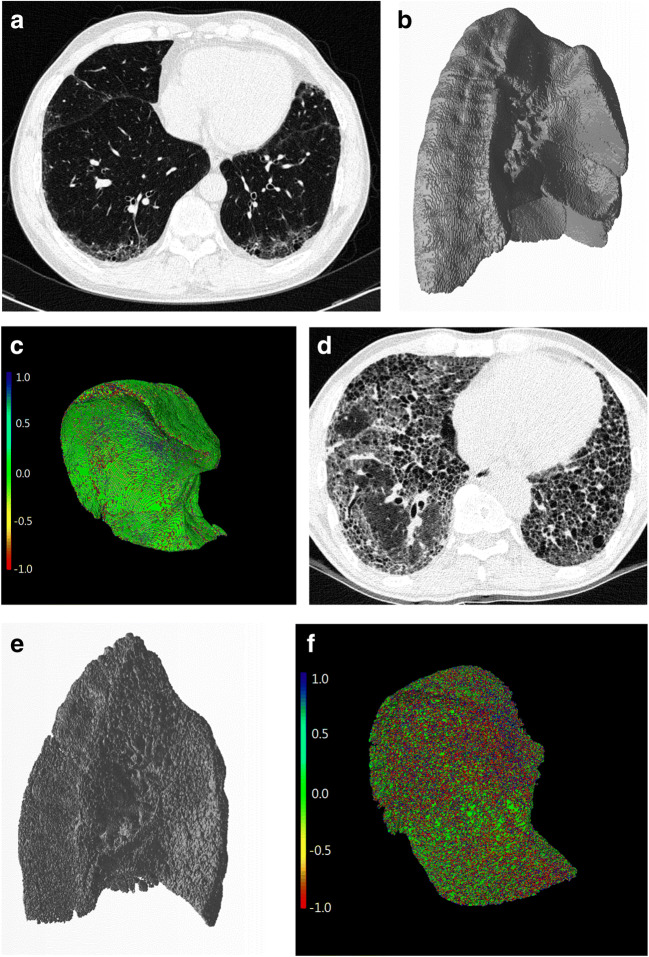
Gaussian curvature analysis of the fibrosis boundaries was performed by one researcher using in-house software (Supplementary figure 2). After loading the CT images, the non-fibrotic areas of both lungs were segmented with a threshold value of − 500 HU [28]. Next, the subpleural boundary between the fibrotic and non-fibrotic areas was automatically reconstructed by using the marching cube algorithm [29], which is one of the most commonly used algorithms for reconstructing a polygonal mesh from three-dimensional medical data (Fig. 3). This algorithm was performed after the volumetric segmentation of the structure of interest, and by “marching” through all the cubic cells intersected by the isosurface, the algorithm calculated the intersection points along the edges and produced a triangular mesh to fit the points. Finally, Gaussian curvature histogram analysis was performed to provide the following histogram parameters of the Gaussian curvature of the fibrosis boundary [24]: mean, standard deviation, skewness, kurtosis, entropy, uniformity, minimum, maximum, and 10th to 90th percentile values [30].

Fig. 3.

Representative images of extracting the boundaries between fibrotic and non-fibrotic lung areas. a, d Baseline chest CT images of patients with (a) mild IPF (GAP stage I) and (d) severe IPF (GAP stage III). b, e After segmenting into fibrotic and non-fibrotic areas using a threshold value of − 500 HU, the fibrosis boundary was automatically extracted and reconstructed three-dimensionally by applying marching cube. c, f The Gaussian curvature analysis was performed at the fibrosis boundary. The Gaussian curvature value at each point of the boundary was coded into red (negative), green (near-zero), and blue (positive). Note that the fibrosis boundary in severe IPF is more irregular than in mild IPF

Survival analysis

All patients were followed up until December 31, 2017. We obtained survival data regarding whether the patients were alive until December 31, 2017, and the date of death if the patients died earlier from the Ministry of the Interior and Safety of South Korea. The mean follow-up period was 47.8 ± 35.2 months.

Prediction of DLCO using the CT histogram parameters of Gaussian curvature

To predict DLCO using the histogram parameters, the least absolute shrinkage and selection operator (LASSO) was used to select features and to build a regression model [31]. First, study participants were split randomly into training and validation sets (6:4). Then, a linear regression model for predicting DLCO was built using the training set, and the tuning parameter for model shrinkage (i.e., lambda) was obtained based on the four-fold cross-validation error. The model was assessed on the validation set.

Statistical analysis

One-way ANOVA was used to compare the histogram parameters between IPF patients and controls. The Tukey honest significant difference test was used as a post hoc test. The Pearson or Spearman rank correlation coefficient was used to analyze the correlations of the histogram parameters with the GAP score and CT visual analysis score. A Cox proportional hazard model was used to investigate the effects of the histogram parameters, CT visual analysis score, and clinical parameters on patient survival. A p < 0.05 was selected to determine statistical significance, and the Bonferroni correction was applied for comparison of the histogram parameters between IPF patients and controls.

The DLCO prediction model was evaluated with respect to the following metrics: (1) root mean square error (RMSE) and (2) R-square. The modified GAP (mGAP) score was calculated by replacing DLCO% with the predicted DLCO% in the GAP score formula. We compared the C-indices and their 95% confidence intervals (CIs) of the GAP, CT-GAP, and mGAP scores using 100-times repeated random splitting of the study population [32]. The comparison was considered to be significant when p < 0.05.

Statistical analyses were carried out using the SPSS software (version 25; IBM Corp.) and R software (version 3.5.1, R Project for Statistical Computing; packages: caret and glmnet).

Results

Baseline characteristics and CT visual analysis

The patients with moderate-to-severe IPF were significantly older (71.4 ± 7.8 vs. 66.2 ± 9.8 years, p = 0.014) and had lower FVC% (63.4 ± 11.4% vs. 83.4 ± 14.8%, p < 0.001) and DLCO% (49.4 ± 18.1% vs. 69.9 ± 16.4%, p < 0.001) than those with mild IPF. Furthermore, patients with moderate-to-severe IPF had a larger extent of reticular opacities and honeycombing, as well as a higher CT fibrosis score (p < 0.001–0.002) than patients with mild IPF, but the extent of GGO, consolidation, and emphysema did not significantly differ between the groups (Table 1).

Table 1.

Summary of clinical parameters and CT visual analysis scores

Variables	Control (n = 52)	Mild IPF (n = 64)	Moderate-to-severe IPF (n = 40)	p value†
Clinical parameters
Age (years)	67.5 ± 9.4	66.2 ± 9.8	71.4 ± 7.8	0.018*a
Male sexb	35 (67.3%)	40 (62.5%)	31 (77.5%)	0.278
FVC (L)	-	2.74 ± 0.76	2.09 ± 0.57	< 0.001*
DLCO (mL/mmHg/min)	-	12.04 ± 3.28	7.72 ± 2.46c	< 0.001*
FVC%	-	83.4 ± 14.8	63.4 ± 11.4	< 0.001*
DLCO%	-	69.9 ± 16.4	49.4 ± 18.1c	< 0.001*
Unable to perform DLCO testb	-	0 (0.0%)	1 (2.5%)	0.385
CT visual analysis score (%)
GGO	-	11.1 ± 9.3	13.5 ± 8.6	0.190
Consolidation	-	3.0 ± 6.1	4.8 ± 7.8	0.225
Reticular abnormality	-	27.8 ± 7.2	32.5 ± 6.7	0.001*
Honeycombing	-	13.0 ± 10.5	21.3 ± 13.8	0.002*
Total fibrosis (CT fibrosis score)	-	32.0 ± 8.8	41.8 ± 10.1	< 0.001*
Emphysema	-	6.3 ± 8.6	10.3 ± 12.1	0.073

Unless otherwise indicated, data are mean ± standard deviation. Asterisks indicate statistical significance (p < 0.05)

IPF idiopathic pulmonary fibrosis, FVC forced vital capacity, DLCO diffusing capacity of carbon monoxide, FVC% percent of predicted FVC, DLCO% percent of predicted DLCO, GGO ground-glass opacity

^†p values were obtained using one-way ANOVA for age, chi-square test for “male sex,” Fisher’s exact test for “unable to perform DLCO test,” and Student’s T test for other variables

^aPost hoc test for age: p = 0.733 (normal control vs. mild IPF), p = 0.104 (normal control vs. moderate-to-severe IPF), and p = 0.014 (mild IPF vs. moderate-to-severe IPF)

^bData are absolute numbers, with percentages in parentheses

^cOne patient who was unable to perform the DLCO test was excluded

Quantitative analysis of the heterogeneity of fibrosis boundaries

Among the histogram parameters of the Gaussian curvature, the overall number, mean, entropy, uniformity, and the 10th to 30th percentiles were significantly different across controls, patients with mild IPF, and those with moderate-to-severe IPF (p < 0.0033) (Table 2, Supplementary table 1, and Figs. 4 and 5). In the post hoc test, the 10th and 20th percentiles were lower in patients with mild IPF than in controls (p < 0.001–0.002), and those values were also lower in patients with moderate-to-severe IPF than in patients with mild IPF (p ≤ 0.001). Patients with moderate-to-severe IPF had a significantly larger number of curvatures, higher entropy and lower uniformity, and 30th percentile than controls (p < 0.001) and larger number of curvatures, lower uniformity, and 30th percentile than patients with mild IPF (p < 0.001–0.003), but there was no significant difference of those parameters between controls and patients with mild IPF. Histogram parameters of the Gaussian curvature did not significantly differ depending on contrast enhancement (Supplementary table 2).

Table 2.

Summary of comparison of the histogram parameters of the Gaussian curvature of fibrosis boundaries

Histogram parameters	Control (n = 52)	Mild IPF (n = 64)	Moderate-to-severe IPF (n = 40)	p value†	p value for post hoc test††
					Control vs. mild IPF	Control vs. moderate-to-severe IPF	Mild vs. moderate-to-severe IPF
Overall no. of curvatures (×106)	1.587 ± 0.342	1.799 ± 0.593	2.429 ± 1.030	< 0.001*	0.215	< 0.001*	< 0.001*
Mean	0.700 ± 0.263	0.545 ± 0.211	0.575 ± 0.201	0.001*	0.001*	0.027	0.792
Entropy	1.549 ± 0.317	1.620 ± 0.347	1.831 ± 0.317	< 0.001*	0.480	< 0.001*	0.005
Uniformity	0.572 ± 0.083	0.550 ± 0.086	0.494 ± 0.077	< 0.001*	0.325	< 0.001*	0.003*
10th percentile	− 0.995 ± 0.326	− 1.243 ± 0.405	− 1.531 ± 0.417	< 0.001*	0.002*	< 0.001*	0.001*
20th percentile	− 0.410 ± 0.197	− 0.589 ± 0.226	− 0.792 ± 0.261	< 0.001*	< 0.001*	< 0.001*	< 0.001*
30th percentile	− 0.036 ± 0.122	− 0.130 ± 0.162	− 0.278 ± 0.210	< 0.001*	0.008	< 0.001*	< 0.001*
Other parameters	-	-	-	N.S.	N.S.	N.S.	N.S.

Data are mean ± standard deviation. Asterisks indicate statistical significance (p < 0.0033, applying the Bonferroni correction). Complete data are available in Supplementary table 1

IPF idiopathic pulmonary fibrosis, N.S. not significant

^†p values were obtained using one-way ANOVA

^††p values were obtained using the Tukey honest significant difference test

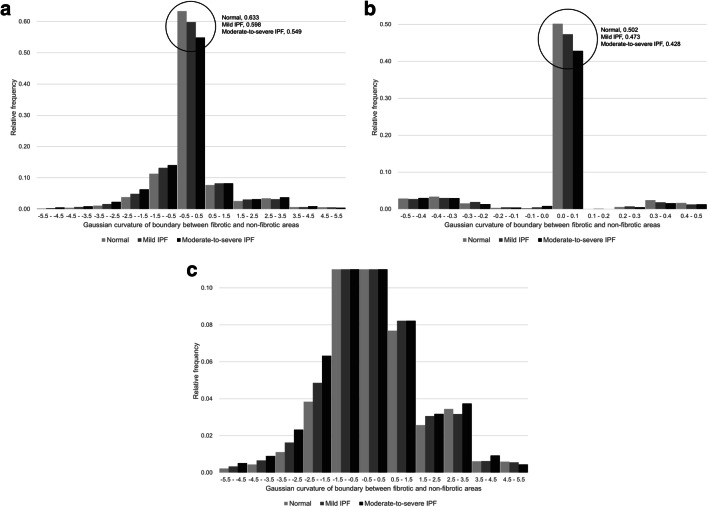
Fig. 4.

Summary histogram of the Gaussian curvature of the fibrosis boundaries in healthy controls and patients with mild and moderate-to-severe IPF. a, b The general shape of the histogram of the Gaussian curvature of the fibrosis boundaries is similar across groups, as the overall concavity of the boundaries is maintained along pleural surfaces, resulting in a dominant peak of Gaussian curvature at 0. c When the upper bound of the relative frequency on the Y-axis is adjusted in the same graph, it becomes clear that positively or negatively skewed Gaussian curvatures with a smaller radius exist primarily in IPF patients

Fig. 5.

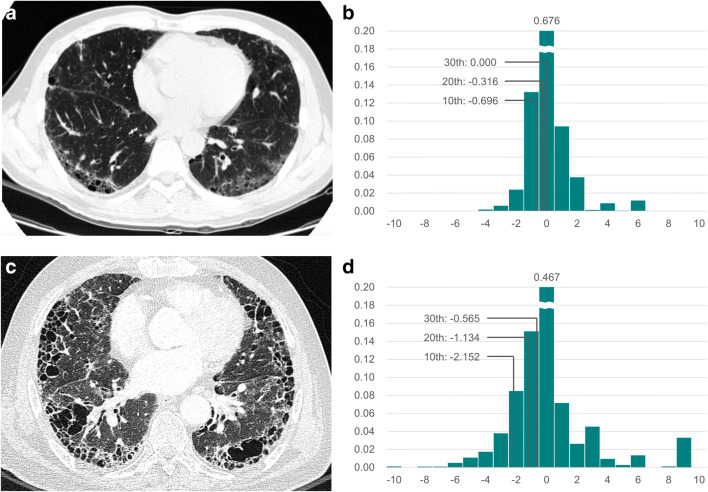
Representative images of (a, b) mild and (c, d) severe IPF. a Baseline chest CT image of a 50-year-old man with mild IPF (GAP stage I). b The histogram of the Gaussian curvature of the subpleural fibrosis boundary is shown: entropy, 1.141; uniformity, 0.664; 10th to 30th percentiles, − 0.696, − 0.316, and 0.000, respectively (data with Gaussian curvature < − 10.5 or > 10.5 are cropped for visibility). c Baseline chest CT image of a 66-year-old man with severe IPF (GAP stage III). d The histogram of the Gaussian curvature of the subpleural fibrosis boundary is shown: entropy, 2.231; uniformity, 0.400; 10th to 30th percentiles, − 2.152, − 1.134, and − 0.565, respectively (data with Gaussian curvature < − 10.5 or > 10.5 are cropped for visibility)

Association between the GAP score, CT visual analysis, and heterogeneity of fibrosis boundaries

The overall number of the curvatures and entropy showed significant positive correlations with the GAP score (r = 0.308, p = 0.002; r = 0.200, p = 0.043, respectively), while uniformity and the 10th to 30th percentiles showed significant negative correlations with the GAP score (r ranging from − 0.357 to − 0.219, p < 0.05). The 20th percentile of Gaussian curvature showed the most significant correlation with the GAP score (r = − 0.357; p < 0.001). However, histogram parameters did not have a significant correlation with the CT-GAP score except for the overall number of curvatures (r = 0.236, p = 0.016) (Table 3 and Supplementary table 3).

Table 3.

Summary of correlations between the histogram parameters of the Gaussian curvature of fibrosis boundaries and the GAP, CT-GAP, and mGAP scores

Histogram parameters	GAP score		CT-GAP score		mGAP scorea
	Pearson’s correlation coefficient	p value†	Pearson’s correlation coefficient	p value†	Pearson’s correlation coefficient	p value†
Overall no. of curvatures	0.308	0.002*	0.236	0.016*	0.341	< 0.001*
Entropy	0.200	0.043*	0.069	0.487	0.222	0.025*
Uniformity	− 0.219	0.026*	− 0.083	0.404	− 0.235	0.017*
10th percentile	− 0.275	0.005*	− 0.136	0.170	− 0.285	0.004*
20th percentile	− 0.357	< 0.001*	− 0.187	0.059	− 0.357	< 0.001*
30th percentile	− 0.321	0.001*	− 0.182	0.066	− 0.326	0.001*
Other parameters	-	N.S.	-	N.S.	-	N.S.

Asterisks indicate statistical significance (p < 0.05). Complete data are available in Supplementary table 3

GAP gender-age-physiology, mGAP modified GAP, N.S. not significant

^†p values were obtained using the Pearson’s correlation coefficient

^amGAP score was calculated based on a single random split: Predicted DLCO% = 74.456 + 18.227*mean + 33.553*20th percentile − 0.003*maximum

The 20th percentile showed the most significant correlation with the CT fibrosis score (r = − 0.343; p = 0.001) and the extent of honeycombing on CT (r = − 0.362; p < 0.001). A larger number of the curvatures, smaller minimum or 10th to 30th percentile values, and larger maximum or 90th percentile values were associated with a greater extent of at least one lung abnormality, including consolidation, reticular abnormality, honeycombing, and total fibrosis (Table 4 and Supplementary table 4). However, none of the histogram parameters displayed significant correlations with the extent of GGO or emphysema.

Table 4.

Summary of correlation between the histogram parameters of the Gaussian curvature of fibrosis boundaries and CT visual analysis score

Variables	Consolidation	Reticular abnormality	Honeycombing	Total fibrosis
Overall no. of curvatures	N.S.	N.S.	0.364 (< 0.001*)	0.324 (0.001*)
Minimum	− 0.204 (0.038*)	N.S.	N.S.	− 0.206 (0.036*)
10th percentile	− 0.224 (0.022*)	N.S.	− 0.286 (0.003*)	− 0.309 (0.001*)
20th percentile	N.S.	− 0.231 (0.019*)	− 0.362 (< 0.001*)	− 0.343 (< 0.001*)
30th percentile	N.S.	N.S.	− 0.353 (< 0.001*)	− 0.313 (0.001*)
90th percentile	0.198 (0.044*)	N.S.	N.S.	N.S.
Maximum	0.214 (0.029*)	N.S.	N.S.	N.S.
Other parameters	N.S.	N.S.	N.S.	N.S.

Data are Spearman’s ρ coefficients between each histogram parameter and the CT visual analysis score, with p values in parentheses. Asterisks indicate statistical significance (p < 0.05). None of the histogram parameters displayed significant correlations with the extent of ground-glass opacity (GGO) or emphysema. Complete data are available in Supplementary table 4

CT computed tomography, N.S. not significant

Survival analysis with the prediction of DLCO using the histogram features of Gaussian curvature

There were 56 (53.8%) deaths among the IPF patients during follow-up. The 1-, 2- and 3-year survival rates were 87%, 74%, and 61%, respectively. In univariate survival analysis, a higher GAP score (p < 0.001), as well as the clinical parameters included in the GAP score—older age, male sex, lower FVC%, and DLCO% (p < 0.001–0.007)—were associated with worse survival. Among the CT visual analysis parameters, a greater extent of reticular abnormality and honeycombing, the total fibrosis score, and emphysema were associated with worse survival (p < 0.001), while GGO and consolidation were not associated with survival. Among the histogram parameters, the overall number of the curvatures (p < 0.001), higher entropy (p = 0.041), lower uniformity (p = 0.027), and lower 10th to 30th percentiles (p < 0.001–0.010) were significant survival predictors (Table 5).

Table 5.

Univariate survival analysis for clinical parameters, the CT visual analysis score, and the histogram features of the Gaussian curvature of fibrosis boundaries

Variables	Hazard ratio	95% CI	p value†
Clinical parameters
Age (years)	1.039	1.010–1.069	0.007*
Male sex	2.482	1.279–4.816	0.007*
FVC%	0.962	0.944–0.980	< 0.001*
DLCO%a	0.974	0.959–0.990	0.001*
GAP score	3.722	2.467–5.615	< 0.001*
CT visual analysis score (%)
Ground-glass opacity	0.992	0.965–1.021	0.597
Consolidation	1.023	0.989–1.059	0.190
Reticular abnormality	1.083	1.040–1.128	< 0.001*
Honeycombing	1.050	1.029–1.072	< 0.001*
Total fibrosis	1.095	1.061–1.129	< 0.001*
Emphysema	1.047	1.022–1.073	< 0.001*
Histogram features
Overall no. of curvatures (×106)	1.605	1.230–2.095	< 0.001*
Mean	0.894	0.237–3.374	0.868
Standard deviation	1.163	0.804–1.682	0.424
Skewness	0.903	0.727–1.123	0.359
Kurtosis	0.995	0.983–1.008	0.478
Entropy	2.175	1.034–4.578	0.041*
Uniformity	0.031	0.001–0.667	0.027*
Minimum	0.962	0.923–1.004	0.075
10th percentile	0.482	0.276–0.841	0.010*
20th percentile	0.215	0.084–0.554	0.001*
30th percentile	0.173	0.049–0.612	0.007*
70th percentile	39.493	0.058–26919.670	0.269
80th percentile	1.553	0.690–3.495	0.287
90th percentile	1.212	0.874–1.681	0.249
Maximum	1.000	0.960–1.041	0.987

Asterisks indicate statistical significance (p < 0.05)

CI confidence interval, FVC% percent-predicted forced vital capacity, DLCO% percent-predicted diffusing capacity of carbon monoxide, GAP gender-age-physiology.

^†p values were obtained using a univariate Cox proportional hazard model

^aOne patient who was unable to perform the DLCO test was excluded

The regression equation for the prediction of DLCO% based on a single random split was as follows:

$$\text{Predicted DLCO}\%=74.456+18.227\ast \text{mean}+33.553\ast 20\mathrm{th}\text{percentile}-0.003\ast \text{maximum}$$

The median values of DLCO% and predicted DLCO% of the 100 repeated random-split set were 60% (interquartile range, 48–74%) and 63% (interquartile range, 57–67%), respectively. The mean R-square value between DLCO% and predicted DLCO% was 0.296 (95% CI, 0.275–0.317), and the RMSE was 16.69 (95% CI, 16.40–16.97). The predicted DLCO% was significantly associated with patient survival in univariate survival analysis using validation set (hazard ratio, 0.905; 95% CI, 0.845–0.969; p = 0.004 based on a single random split), and the mGAP score with the predicted DLCO% was also significantly associated with worse survival (hazard ratio, 34.0; 95% CI, 7.0–165.7; p < 0.001 based on a single random split).

The mean C-indices in the GAP and CT-GAP scores were 0.79 (95% CI, 0.71–0.86) and 0.77 (95% CI, 0.68–0.85), respectively. The mGAP score calculated with the predicted DLCO% using the composite of the histogram features of the Gaussian curvature instead of DLCO% had a mean C-index of 0.76 (95% CI, 0.69–0.84). All three GAP scores showed a comparable ability to predict survival without a significant difference in the C-index (p > 0.05; 95% CI of difference, − 0.09 to 0.05 when compared with the GAP score) (p > 0.05; 95% CI of difference, − 0.04 to 0.04 with the CT-GAP score).

Discussion

Gaussian curvature is positive for elliptic surfaces and negative for saddle surfaces, and the absolute value of Gaussian curvature increases as the radius becomes smaller. In normal lungs, as fibrotic areas do not exist, the boundary of non-fibrotic areas corresponds to the pleural surfaces, which typically have a smooth convexity with some acute peaks between the chest wall pleura and mediastinal or diaphragmatic pleura (Fig. 1b). Therefore, the Gaussian curvature of normal lungs is predominantly distributed around 0, followed by curvatures larger than 0. In contrary, IPF typically involves a predominant subpleural pattern of fibrosis, resulting in irregular boundaries between fibrotic and non-fibrotic areas. The irregular boundaries of fibrosis make more numerous Gaussian curvatures and result in many positively or negatively skewed Gaussian curvatures with a smaller radius, which is represented as higher entropy, lower uniformity, lower 10th to 30th percentiles, and higher 70th to 90th percentiles (Fig. 1c).

The overall number and 10th to 30th percentiles of Gaussian curvatures showed significant correlations with the extent of honeycombing and total fibrosis on CT, and entropy and uniformity also tended to be higher and lower with a greater extent of honeycombing and total fibrosis, respectively. In addition, these parameters were shown to be associated with disease severity and survival in IPF patients. These results are consistent with the aforementioned theoretical relationship between the Gaussian curvature of subpleural surfaces and the extent of fibrosis in IPF. Interestingly, the 70th to 90th percentiles of Gaussian curvature did not show any significant correlations with fibrosis. The 70th to 90th percentiles reflect peaks or pits, whereas the 10th to 30th percentiles reflect saddle points. Considering that even normal lungs have acute peaks at the flexure of the pleura at the transition between the diaphragm and mediastinum, while saddle points are scarce in normal lungs, the 10th to 30th percentiles seem more meaningful.

A previous study by Iwasawa et al reported that the CT analysis of subpleural fibrosis had a prognostic implication in IPF [33]. Despite the similar prognostic implication of subpleural fibrosis, the analyzing methodology of subpleural fibrosis was different between ours and theirs. We analyzed the curvature of fibrosis boundary caused by subpleural fibrosis, and their work analyzed the CT morphology of subpleural fibrosis. The result of the two studies seems to emphasize the importance of preferential subpleural involvement in the disease course of IPF.

The mGAP score calculated with predicted DLCO% showed a similar ability to predict survival to the GAP and CT-GAP scores. These results imply that the spatial heterogeneity of the fibrosis boundary in IPF can provide similar prognostic information to the degree of fibrosis on CT. The GAP score is a well-validated model for predicting survival in IPF patients, and the CT-GAP model is a useful alternative for the original GAP model [4, 12]. However, the DLCO test can suffer from intra- and inter-session variability, and some patients with lung disease cannot perform the maneuver of the DLCO test adequately [34, 35]. Furthermore, during a regular follow-up, IPF patients typically perform CT scans and spirometry but less undergo a DLCO test. The CT-GAP model allows predicting survival without performing the DLCO test, but visual assessment of the fibrosis on CT requires experienced radiologists and potentially be affected by inter-observer variability. Either the DLCO test or time-consuming visual grading of the experienced radiologist is limitedly applicable in clinical practice during coronavirus disease 2019 [36]. In our method of analysis, on the other hand, inter-observer variability was unlikely to occur since non-fibrotic areas were segmented using a threshold of − 500 HU and the entire process of analysis, from lung segmentation to the Gaussian curvature analysis, was fully automated. A combined analysis of the degree and spatial heterogeneity of fibrosis may provide better prognostication of IPF, and further investigations such as a head-to-head comparison between the GAP scores are warranted.

Our study has several limitations. First, our study was designed retrospectively and included a relatively small population of patients and controls. Second, the CT system and protocols were variable, including both contrast-enhanced and non-enhanced CT, although we excluded low-dose CT scans. Of particular note, CT attenuation of the lung changes depending on the use of intravenous contrast, which may affect the automatic segmentation of the lung using a specified HU threshold [37]. However, the resulting difference would be minimal since the difference between the attenuation of the lung with or without contrast enhancement is much smaller than the difference between fibrotic and non-fibrotic lung tissues [37]. Third, although patients were instructed to achieve full inspiration when undergoing chest CT, the degree of inspiration may have varied among the patients. Insufficient inspiration may increase the CT attenuation of the lung, thereby affecting the Gaussian curvature. Fourth, the reproducibility of our analyzing method was not evaluated in this study. Although thought to be minimal, inter-scan variability can occur depending on CT imaging conditions. Fifth, the example of the regression equation mentioned in the result was derived from a single random split, and different parameters may be selected in the other split of the population or external validation. Finally, we analyzed Gaussian curvature of the outmost boundary between fibrotic and non-fibrotic lungs. It predominantly reflected subpleural fibrosis in IPF patients, with a minor exception of the wall of honeycombing cysts which might not be included as a fibrotic area due to smaller HU. Thus, the entire boundary of fibrosis may not have been fully reflected in the analysis. Particularly, a central boundary between fibrotic and non-fibrotic lungs cannot be evaluated with our analyzing method. Further study using the central boundary may be meaningful.

In conclusion, the spatial heterogeneity of the fibrosis boundary in IPF could be quantitatively measured using the Gaussian curvature histogram analysis, and irregular fibrosis boundaries were represented as more numerous curvatures and heterogeneous distribution of Gaussian curvature on histograms. Heterogeneity was negatively associated with disease severity and survival in IPF patients. The quantitative analysis of the spatial heterogeneity of fibrosis boundaries in IPF shows promise as a potential imaging biomarker for staging disease severity and prognostication.

Abbreviations

CI

Confidence interval

DLCO

Diffusing capacity of carbon monoxide

DLCO%

Percent of predicted diffusing capacity of carbon monoxide

FVC

Forced vital capacity

FVC%

Percent of predicted forced vital capacity

GAP

Gender-age-physiology

GGO

Ground-glass opacity

IPF

Idiopathic pulmonary fibrosis

LASSO

Least absolute shrinkage and selection operator

mGAP

Modified gender-age-physiology

PFT

Pulmonary function test

RMSE

Root mean square error

Funding

This study has received funding by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (2016R1C1B1015761).

Compliance with ethical standards

Guarantor

The scientific guarantor of this publication is Soon Ho Yoon.

Conflict of interest

Soon Ho Yoon is the chief medical officer of MEDICAL IP Co. Ltd. outside this work. Other authors of this manuscript declare no relationships with any companies whose products or services may be related to the subject matter of the article.

Statistics and biometry

One of the authors has significant statistical expertise.

Informed consent

Written informed consent was waived by the Institutional Review Board.

Ethical approval

Institutional Review Board approval was obtained.

Methodology

• retrospective

• case-control study/diagnostic or prognostic study

• performed at one institution