Abstract
We introduce the first-ever statistical framework for estimating the age of Multiple Sclerosis (MS) lesions from magnetic resonance imaging (MRI). Estimating lesion age is an important step when studying the longitudinal behavior of MS lesions and can be used in applications such as studying the temporal dynamics of chronic active MS lesions. Our lesion age estimation models use first order radiomic features over a lesion derived from conventional T1 (T1w) and T2 weighted (T2w) and fluid attenuated inversion recovery (FLAIR), T1w with gadolinium contrast (T1w+c), and Quantitative Susceptibility Mapping (QSM) MRI sequences as well as demographic information. For this analysis, we have a total of 32 patients with 53 new lesions observed at 244 time points. A one or two step random forest model for lesion age is fit on a training set using a lesion volume cutoff of 15 mm3 or 50 mm3 . We explore the performance of nine different modeling scenarios that included various combinations of the MRI sequences and demographic information and a one or two step random forest models, as well as simpler models that only uses the mean radiomic feature from each MRI sequence. The best performing model on a validation set is a model that uses a two-step random forest model on the radiomic features from all of the MRI sequences with demographic information using a lesion volume cutoff of 50 mm3 . This model has a mean absolute error of 7.23 months (95% CI: [6.98, 13.43]) and a median absolute error of 5.98 months (95% CI: [5.26, 13.25]) in the validation set. For this model, the predicted age and actual age have a statistically significant association (p-value <0.001) in the validation set.
1. Introduction
Multiple Sclerosis (MS) is an autoimmune disease of the central nervous system characterized by lesions in the brain and spinal cord, and magnetic resonance imaging (MRI) is used to monitor these lesions (Sahraian and Radue, 2007). New MS lesion are identified on MRI through T1-weighted (T1w) imaging with intravenous gadolinium of acute blood-brain-barrier (BBB) disruption, with lesion enhancement typically lasting for less than eight weeks (He et al., 2001). However, lesions can accumulate silently for years prior to a patient’s first clinical symptoms and MRI evidence (Thompson et al., 2018), making accurate determination of the age of the lesion and the onset of the disease difficult. Even after a MS patient starts to have MRIs for disease monitoring, the age estimation of a new non-enhancing lesion detected on a follow-up scan has considerable uncertainty determined by the time interval between subsequent MRIs (Traboulsee et al., 2016). The inability to determine the age of a chronic MS lesion may delay diagnosis (Thompson et al., 2018), limit an accurate assessment of treatment response (Traboulsee et al., 2016), and impede longitudinal study of MS lesion dynamics.
A number of studies have described the temporal behavior of lesion signal captured on conventional qualitative MRI (Sweeney et al., 2016; Meier and Guttmann, 2003; Meier and Guttmann, 2006; Ghassemi et al., 2015) or advanced quantitative MRI such as quantitative susceptibility mapping (QSM) (Zhang et al., 2019a, Zhang et al., 2016a). Currently there is much interest in studying the longitudinal behavior of chronic active lesions on MRI. These lesions have a rim of iron-enriched activated pro-inflammatory microglia/macrophages as identified on histology and a characteristic rim appearance on gradient echo (GRE) phase or QSM image (Langkammer et al., 2013; Stüber et al., 2016; Wisnieff et al., 2015; Absinta et al., 2019; Kuhlmann et al., 2017; Absinta et al., 2016; Dal-Bianco et al., 2017). The date of lesion incidence must be known with sufficient precision and accuracy to prevent temporal misalignment in the longitudinal information from the lesions, which can mask the true temporal behavior due to the underlying biological differences or treatment effects (Marron et al., 2015; Ramsay and Silverman, 1997). Previous longitudinal studies have either ignored this temporal misalignment (Sweeney et al., 2016; Ghassemi et al., 2015) or have been limited to small cohorts of new enhancing lesions (Zhang et al., 2016b, 2019b) or those with frequent scanning (Meier and Guttmann, 2003, 2006).
The objective of this study is to develop a machine-learning based algorithm for MS lesion age prediction from a single MRI study, which is currently not available. A novel feature of our algorithm is the use of QSM in addition to the radiomic features of T1w without and with gadolinium contrast (T1w+c), T2-weighted (T2w), and fluid attenuated inversion recovery (FLAIR) images, as well as demographic information. QSM (de Rochefort et al., 2010; Wang and Liu, 2014; Wang et al., 2017) is a promising MRI technique for mapping tissue susceptibility changes related to myelin breakdown and iron deposition in MS lesions (Langkammer et al., 2013; Stüber et al., 2016; Wisnieff et al., 2015; Deh et al., 2018) and has recently been shown to predict lesion enhancement status with high diagnostic accuracy without using gadolinium (Zhang et al., 2016b, 2018). Previous cross-sectional and longitudinal studies have also observed that the QSM signal increases rapidly as a new lesion transitions from enhancing to non-enhancing phase, reaching a peak value approximately two years after lesion formation and then slowly decaying away in the final stages of a glial scar (Zhang et al., 2019b; Chen et al., 2014). This unique temporal activity on the QSM makes it potentially useful for estimating the age of an MS lesion.
2. Materials and methods
2.1. Study population
This is a retrospective image review study of 32 MS patients who were enrolled in an ongoing prospective MRI and clinical MS database. The database was approved by the Weill Cornell Medicine institutional review board and subjects provided written informed consent prior to enrollment. Patients were selected for this study if they met the inclusion criteria of having at least one new gadolinium enhancing MS lesion on MRI, which is considered the baseline scan (time = 0). A total of 53 new enhancing lesions were identified for a total of 244 imaging time points. Fig. 1 shows the time of the longitudinal observations for each lesion, with the scan at observed lesion incidence, marked as gadolinium enhancement on the plot, considered to be time zero for the lesion. Two MRI scanners were used to acquire data for this analysis, a GE scanner and a Siemens scanner. Of the 244 time points used in this analysis, 77 were imaged on the GE scanner and 167 on the Siemens scanner. Of the 32 patients in the analysis, 14 were scanned entirely on the Siemens scanner and 3 entirely on the GE scanner. The remaining 15 patients had scans on both scanners. Clinical data collected for patients included gender, age, Expanded Disability Status Scale (EDSS) scores, disease duration, disease subtype, an indicator of steroid use within thirty days of MRI, and information about disease-modifying treatment. Disease-modifying treatment was put into three categories: no treatment, milder immunomodulators and suppressors, and stronger immunosuppressants. Table 1 summarizes the clinical information for the subjects at the baseline visit considered for this study and also provides information about mean follow-up duration and number of follow-up visits for each patient.
Fig. 1. The MRI time points (shown as black dots) for each of the 53 lesions included in this study.
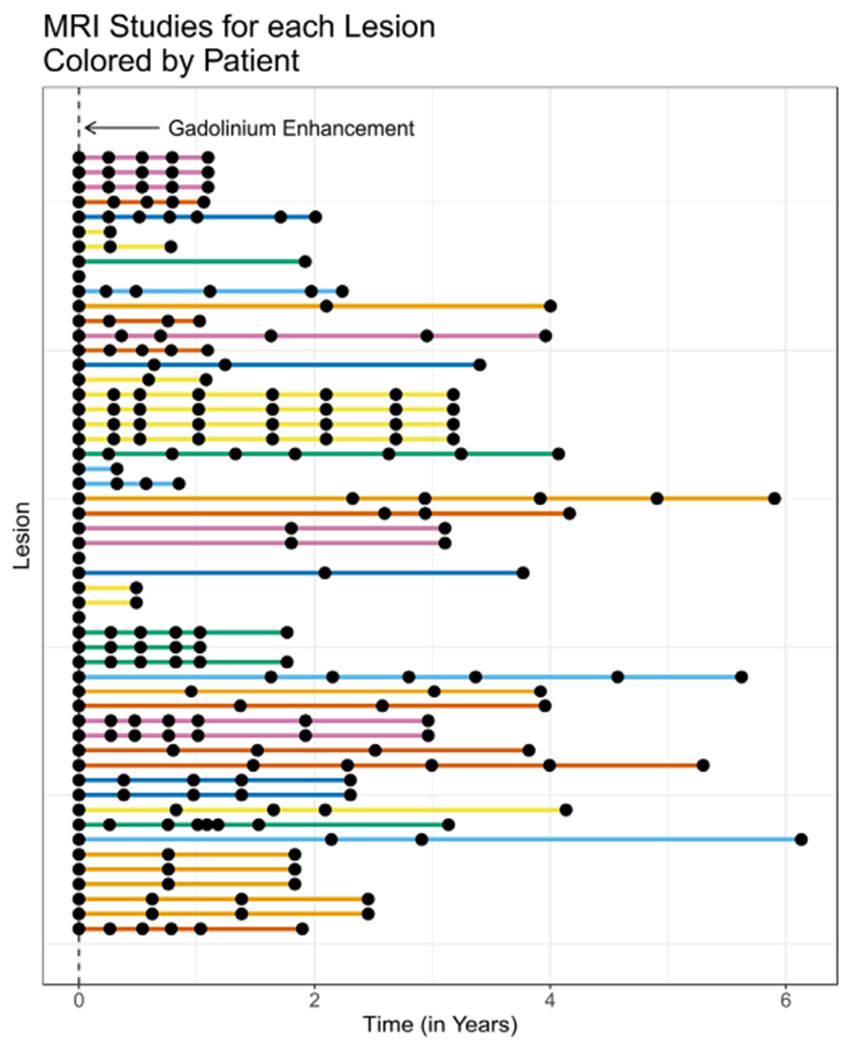
Each line on the plot represents the follow-up time for a particular lesion and each of the points along the line represents a time when a MRI study was performed. Time zero is defined as the time of first observed gadolinium enhancement. The colors in the plot denote different patients. Colors are repeated, but consecutive colored lines are from the same patient.
Table 1. Baseline characteristics.
The demographic characteristics of the patients during their baseline scan used in this analysis. Mean (sd) is reported for continuous demographic variables and number (%) is reported for binary demographic variables.
| Female [n (%)] | 22 (75.9%) |
| Age [mean (sd)] | 36.99 (8.86) |
| EDSS | 1.19 (1.64) |
| Disease duration | 6.42 (4.72) |
| Disease subtype | RRMS – 28 (96.6%), RIS – 1 (3.4%) |
| Steroids at baseline | 3 (10.3%) |
| Disease-modifying treatment at baseline | None – 11 (34.4%) |
| Milder – 7 (21.9%) | |
| Stronger – 14 (43.8%) | |
| Follow-up (in years) | 2.87 (1.65) |
| Number of visits | 4.84 (1.82) |
2.2. MRI protocol and image processing
Brain MRI was performed on 3T MRI systems (Signa HDxt, GE Healthcare, Waukesha, Wisconsin, USA, with an 8-channel head coil; Magnetom Skyra, Siemens, Erlangen, Germany, with a 20-channel head/neck coil). The scanning protocol consisted of 3D T1w BRAVO or MPRAGE sequence obtained pre-contrast for anatomical structures and post-contrast (T1w+c) for detecting BBB breakdown, 2D T2w fast spin echo and 3D T2w FLAIR sequences for lesion detection, and 3D multi-echo GRE sequence for QSM. The typical acquisition parameters were the following: 1) 3D sagittal T1W: TR/TE/TI = 8.8/3.4/450 ms (GE) and 2300/2.3/900 ms (Siemens), flip angle (FA) = 15° (GE) and 8° (Siemens), readout bandwidth (rBW) = 195.3 Hz/pixel (GE) and 200 Hz/pixel (Siemens), voxel size = 1.0–1.2 mm isotropic, parallel imaging acceleration factor (R) = 1.5 (GE) and 2.0 (Siemens); 2) 2D axial T2W: TR/TE = 5917/86 ms (GE) and 5840/93 ms (Siemens), FA = 90°, rBW = 195.3 Hz/pixel (GE) and 225 Hz/pixel (Siemens), echo train length (ETL) = 23 (GE) and 18 (Siemens), number of signal averages (NSA) = 2, voxel size = 0.6 × 0.9 × 3 mm3 ; 3) 3D sagittal T2W FLAIR: TR/TE/TI = 6000/133/1850 ms (GE) and 7600/448/2450 ms (Siemens), FA = 90° (GE) and 120° (Siemens), rBW = 139.5 Hz/pixel (GE) and 780 Hz/pixel (Siemens), ETL = 140 (GE) and 273 (Siemens), voxel size = 1.0–1.2 mm isotropic, R = 1.6 (GE) and 2.0 (Siemens); 4) QSM: FOV = 24 cm, TR = 57 ms (GE) and 48 ms (Siemens), TE1/ΔTE = 4.3/4.8 ms (GE) and 6.3/4.1 ms (Siemens), number of TEs = 11 (GE) and 10 (Siemens), FA = 20° (GE) and 15° (Siemens), rBW = 244 Hz/pixel (GE) and 260 Hz/pixel (Siemens), voxel size = 0.7 × 0.7 × 3 mm3 , R = 2, scan time = approximately 5 min. The QSM imaging protocol was harmonized for both manufacturers and was demonstrated to be reproducible across manufacturers (Deh et al., 2019, 2015). QSM was reconstructed from complex GRE images using a fully automated morphology-enabled dipole inversion (MEDI+0) algorithm zero-referenced to the ventricular CSF (Liu et al., 2018).
At each time point, the T1w, T2w, FLAIR, T1w+c and GRE magnitude images were brain extracted using the BET algorithm (Smith, 2002) and bias field corrected using the FAST algorithm (Zhang et al., 2001). The T2w, FLAIR, T1w+c, GRE and QSM (which is in the same space as GRE) images were then linearly coregistered to the T1w image at that time point using the FLIRT algorithm (Jenkinson et al., 2002) with 6-degrees of freedom. The coregistration matrices and their inversions were computed and saved for the next step. For longitudinal image coregistration, the brain-extracted T1w image at a later time point was linearly coregistered to the brain-extracted T1w image at the baseline using the FLIRT algorithm with 12-degrees of freedom. The resulting longitudinal coregistration matrix was combined with the cross-sectional coregistration matrices saved in the previous step to calculate the transformation matrices between the T1w, T2w, FLAIR, T1w+c and GRE/QSM images at a later time point and the baseline GRE/QSM image (using FSL convert_xfm command). These coregistration matrices were then applied to the corresponding images to align them with the baseline GRE/QSM image using the FLIRT command with spline interpolation. Intensity normalization was performed on all of the conventional MRI and the T1w+c image (Shinohara et al., 2014). Intensity normalization was not performed on the QSM image which has physical units of parts per billion (ppb).
2.3. Lesion segmentation
New gadolinium enhancing MS lesions were identified on the T1w+c images. For each lesion, longitudinal manual lesion segmentation was performed on the coregistered T2w image at each available imaging time point using the ITK-SNAP software (Version 3.6.0; http://www.itksnap.org/). These masks were drawn on the T2w image to avoid potential over-estimation of lesion area due to edema on the FLAIR image, especially for lesions less than one year old. Fig. 2 shows an example of the longitudinally coregistered QSM, T1w+c and conventional MRI for an axial slice of the entire brain as well as a lesion on this slice along with the lesion masks at each time point.
Fig. 2. The MRI sequences at each time point for the whole brain (A) and lesions (B).
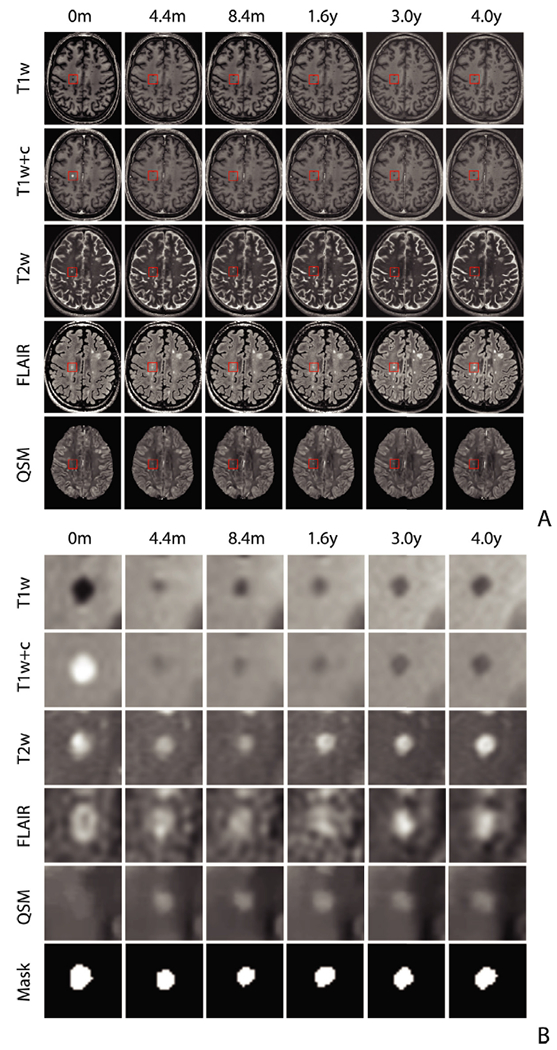
Example of the longitudinal brain scans and lesion evolution on conventional T1w, T2w, FLAIR, as well as T1w+c and QSM images over a 4-year period. Lesion age is estimated from the image intensity within the lesion masks drawn on the T2w image at each time point as shown in the bottom row of (B).
2.4. Radiomic features
A total of 44 first-order radiomic features for each MRI sequence were calculated over each lesion at each time point using the RIA R package (Kolossváry et al., 2017, 2018). These features collapse the information over a lesion into a number of scalar summary statistics. These features include 37 features that describe the average and spread of the data (the mean, median, mode, harmonic mean, three geometric means, trimmed mean, tri mean, mean absolute deviation from the median, median absolute deviation from the median, mean absolute deviation from the mean, median absolute deviation from the mean, median absolute deviation, maximum absolute deviation from the median, maximum absolute deviation from the mean, root mean square, minimum, maximum, the quartiles, the interquartile range, lower notch, upper notch, the deciles, and range), 4 features describing the shape of the distribution of the data (the variance, skewness, standard deviation, and kurtosis), and 3 features describing the diversity of the data points (the energy, entropy, and uniformity). A comprehensive list of all the radiomic features, including equations to calculate the features, can be found in the Supplemental material of Kolossváry et al. (2017). Fig. 3 shows one of the commonly used radiomic features, the mean intensity over the lesion, for the 5 different sequences, at all time points. Observations from the same lesion are connected by a line to illustrate the temporal patterns in this particular radiomic feature, but it is important to note that each of the radiomic features is calculated independently at each time point.
Fig. 3. Mean radiomic feature for the 15 mm3 cutoff.
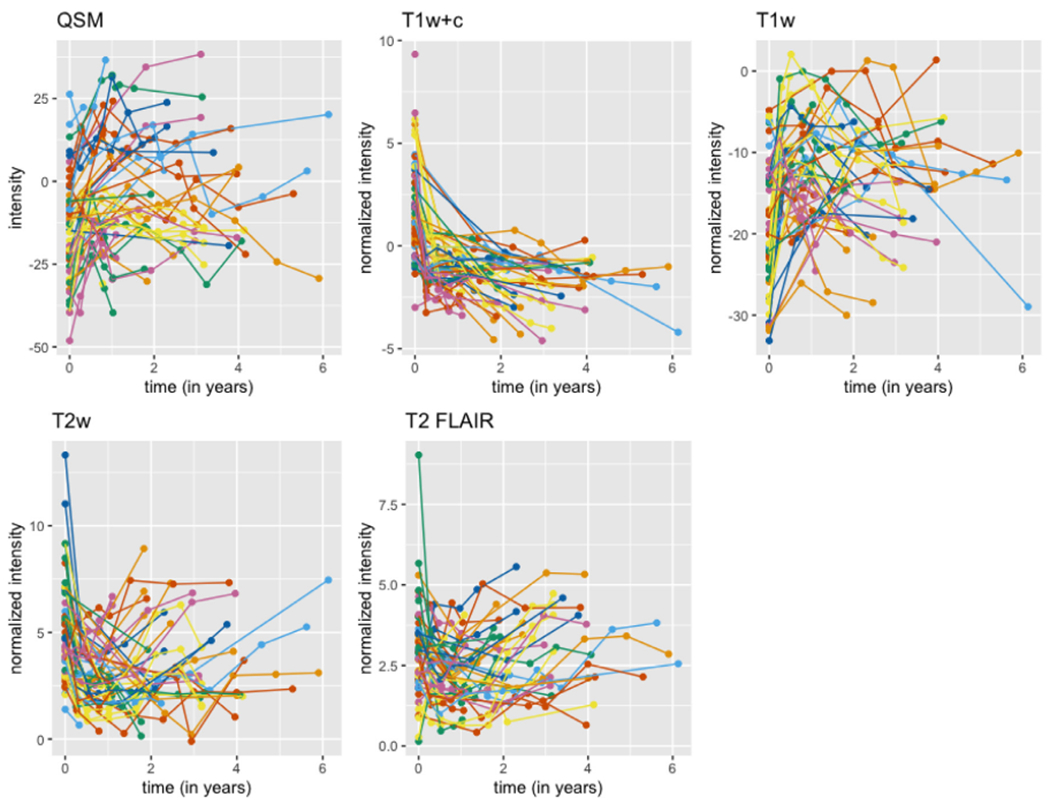
The plot shows the mean radiomic feature, the mean intensity over time entire lesion, for each of the 5 sequences at all time points. Time points for the same lesion are connected with lines. The colors in the plot denote different patients, but colors are repeated.
2.5. Statistical methods for lesion age prediction
We performed all modeling in the R environment (version 3.5.0, R Foundation for Statistical Computing, Vienna, Austria). For this analysis, we were interested in predicting the age of a lesion using only information from a single MRI scan. The age of a lesion is defined as the time interval between a scan and the baseline scan (first appearance of lesion with gadolinium enhancement). This process can be seen at the top of Fig. 2B. Given that we are interested in predicting the age of a lesion at a specific time point using only information from the scan performed at that particular time, a lesion from a patient contributes multiple observations to the analysis. For example, the lesion featured in Fig. 2B contributes 5 observations to the analysis. Demographic information was also included in the models, namely age, gender, disease duration, an indicator of being administered steroids, and disease-modifying treatment category. EDSS was not included in the model, as EDSS was missing for a number of time points and we did not wish to exclude these observations from the modeling.
We used two different inclusion criteria for the modeling; lesions having a volume of greater than 15 mm3 and greater than 50 mm3 . The 15 mm3 cutoff was calculated assuming a spherical shape with a diameter of 3 mm in accordance with the currently accepted minimum size on MRI (Filippi et al., 2016). The more stringent 50 mm3 cutoff (approximately 4.6 mm in lesion diameter) was chosen based on the recommendation that lesion size should be at least five times larger than the slice thickness for lesion geometry to be captured reliably between scans (Firbank et al., 1999). Using the 15 mm3 cutoff, 53 new lesions were identified in 32 patients for a total of 232 time points. Using the 50 mm3 cutoff, 44 new lesions were identified in the 29 patients for a total of 174 time points. To avoid correlation between the training and validation set, we assigned all the lesions and time points from a particular patient to either the training or validation set. Two thirds of the patients were randomized to a training set (15 mm3 cutoff: 21 patients, 36 lesions, 163 time points; 50 mm3 cutoff: 19 patients, 22 lesions, 90 time points) and the remaining one third of patients to a validation set (15 mm3 cutoff: 11 patients, 17 lesions, 69 time points; 50 mm3 cutoff: 10 patients, 22 lesions, 84 time points).
For this analysis, nine different modeling scenarios were considered. These scenarios involve using different sets of the MRI sequences and radiomic features and also using different modeling choices (namely a two-step random forest classification and regression model versus a one-step random forest regression model which are described in detail in the following two paragraphs). The modeling scenarios are: (1) a scenario utilizing all of the sequences, including the first order radiomic features from the conventional MRI (T1w, T2w, FLAIR), T1w+c, and QSM along with demographic information with a two-step random forest model (2) a scenario utilizing all of the sequences and demographic information with a random forest regression model, (3) a scenario excluding the QSM sequence with a two-step random forest model, (4) a scenario excluding the QSM sequence with a random forest regression model, (5) a scenario excluding the T1w+c sequence with a random forest regression model, (6) a model fit only using the conventional MRI sequences and demographic information with a random forest regression model, (7) a random forest regression model fit with only demographic information, (8) a two-step random forest model fit with only the mean radiomic features and (9) a random forest regression model fit with only the mean radiomic features. We refer to these models as ‘All Sequences (TS)’, All Sequences (R)’ ‘No QSM (TS)’, No QSM (R)’, ‘No T1w+c’, ‘Conventional’, ‘Demographic’, ‘Mean (TS)’, Mean (R)’ respectively, where ‘TS’ stands for two-step and ‘R’ stands for regression. These nine modeling scenarios were considered to evaluate the contribution in terms of predictive performance that the QSM and T1w+c MRI sequences contribute above conventional MRI and demographic information as well as just demographic information. The Mean (TS) and Mean (R) modeling scenarios enable us to evaluate the contribution of the radiomic features above just using the mean radiomic feature.
For the modeling scenarios that included T1w+c radiomic features, we were able to fit a two-step random forest model for predicting lesion age. These are the modeling scenarios that are followed by a ‘(TS)’ in the name. A two-step random forest model was fit on the training set for both the 15 mm3 and 50 mm3 cutoffs. The first step of the model estimates whether a lesion is new (age of zero) versus if it is not new (age greater than zero). For this first step model, we fit a random forest classification model (Ho, 1995) with the randomForest R package (Liaw and Wiener, 2002). The second step of the model is a regression model that estimates the age of the lesion. This model was fit only on time points for a lesion that had an age greater than zero (15 mm3 cutoff: 118 time points; 50 mm3 cutoff: 68 time points). For the second step model, we fit random forest regression model using the randomForest R package. Predictions for the validation set were made by first making a prediction from the random forest classification model. For those observations that were determined not to have an age of zero, predictions of the age were then made using the random forest regression model. A two-step random forest model was not used for modeling scenarios that did not include T1w+c radiomic features, as classification of new versus older lesions for the models excluding T1w+c features did not perform well.
For the modeling scenarios that excluded the T1w+c features, only a one-step random forest modeling procedure was used. Models were again fit for both the 15 mm3 and 50 mm3 cutoffs. A regression model was fit using data from all time points. We also fit a one-step random forest regression model for modeling scenarios that included T1w+c features for comparison and to 3ustify the use of the two-step random forest model. These are the modeling scenarios followed by an ‘R’. As described in the preceding paragraph, a random forest regression model was fit in the training set and predictions were made in the validation set.
Mean absolute error and median absolute error were reported in the training and validation set for all nine modeling scenarios for both volume cutoffs. To assess variability, the training and validation sets were re-assigned 1000 times, and 95% confidence intervals were calculated. We also report the relative ranking of the models in terms of median absolute error for both cutoffs. Variable importance for the ten most important features in the random forest regression models are also reported. For the classification and regression models variable importance is reported by MeanDecreaseGini and IncNodePurity respectively. Both measures are the total decrease in node impurities from splitting on the variables over all trees. For the classification model the node impurity is measured by the Gini index. For the regression model the node impurity is measured by residual sum of squares. We also investigated the stability of the variable importance for the best performing modeling scenarios, the All Sequences (TS) and (R) for the 50 mm3 cutoff. We report the 10 most frequently occurring features for the top three variable importance rankings and the percentage of times in which these occurred in the 1000 re-assigned training and validation sets.
We investigated the relationship between the model predicted age and actual age in each modeling scenario to assess if there was a statistically significant association between the two measures. To account for correlation from multiple lesions per patient, we fit a linear mixed effects model with predicted age as the outcome, actual age as a fixed effect, and patient as a random effect. We fit the model using the lme4 R package (Bates et al., 2014) and calculated p-values from the models using the lmerTest R package (Kuznetsova et al., 2017). We report the coefficient for age and the p-value from the model. We also explored adding an indicator for scanner (GE versus Siemens) as a fixed effect to the model to determine if scanner was related to predicted age after adjusting for actual age.
3. Results
We compared the age predictions from the nine different modeling scenarios in the validation set versus the true age of the lesions. For the subjects in the validation set, Fig. 4 shows the predicted age versus the true age for each lesion at each time point for the nine modeling scenarios for both the 15 mm3 and 50 mm3 cutoffs. The lesions are colored by subject and the predictions from the same lesion are connected with a line, although it is important to note that these predictions are made independently for each time point and do not use longitudinal information. Qualitatively, from the plots, the All Sequences (TS) and (R) and the No QSM (TS) and (R) scenarios have the best performance. Scenarios that exclude the T1w+c image (No T1w+c, Conventional, and Demographic) do not perform as well. The Demographic scenario shows very poor performance, predicting almost the same age for the lesions at all of the time points. This is to be expected as the demographic information for a patient does not change much over time. The Mean (TS) and (R) scenarios that use only the mean radiomic features perform well but do not perform as well as those that use more radiomic features, justifying the use of the additional radiomic features. Also, the more stringent cutoff of 50 mm3 has better performance than the 15 mm3 cutoff.
Fig. 4. Prediction in validation set for the 15 mm3 (A) and 50 mm3 (B) cutoff.
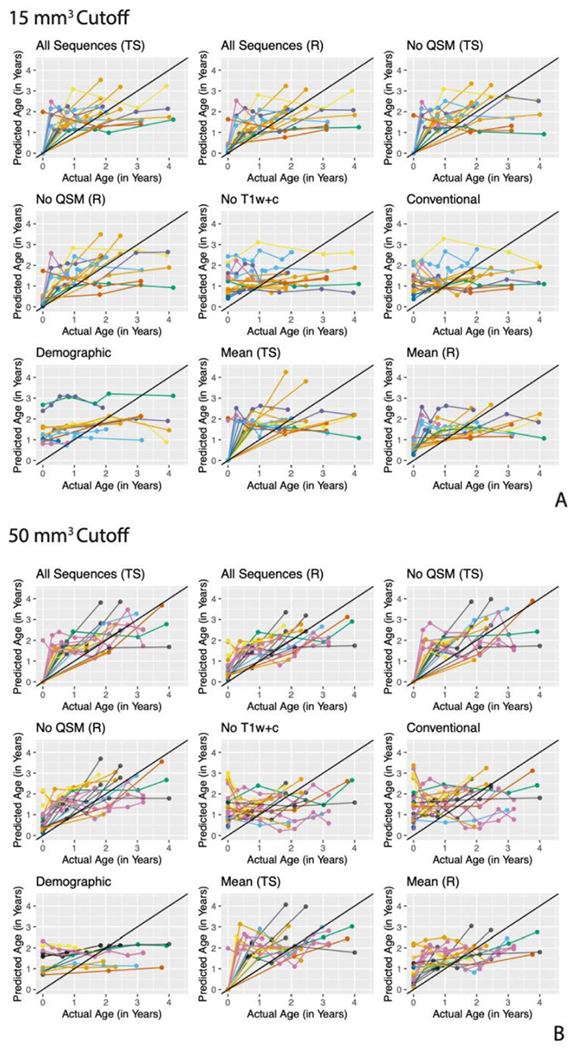
The predicted lesion age versus the actual lesion age for observations in the validation set for the nine modeling scenarios for each of the two cutoffs. Observations are colored by subject and observations from the same lesion are connected by lines.
The mean and median absolute error from the models in the validation set is reported in Table 2. Confidence intervals for the table are reported using reassignment of the training and validation set 1000 times. In terms of mean and median absolute error, the model with the best performance for the 15 mm3 cutoff is the All Sequences (R) model and for the 50 mm 3 cutoffs is the All Sequence (TS) model. The next best performing model for is the All Sequence (TS) for the 15 mm3 and the All Sequence (R) for the 50 mm3 cutoff. The scenarios that perform worst are those that exclude the T1w+c sequence for both cutoffs (No T1w+c, Conventional, and Demographic). These models have errors around a year. The simpler models that use only the mean features do not perform as well as the models that use all of the radiomic features for either of the cutoffs, indicating that performance is gained by using the large number of radiomic features. Note that the confidence intervals for all of the modeling scenarios have overlap. We also report the mean and median absolute error from the models in the training set in Table 3 for comparison. As expected, the error in the training set is lower than that in the validation set.
Table 2. Validation set mean and median absolute error for the models.
The mean and median absolute error for all modeling scenarios for the two cutoffs in the validation set. The 95% confidence intervals from 1000 reassignments to the training and validation as also shown for the two measures.
| 15 mm3 Cutoff |
50 mm3 Cutoff |
|||
|---|---|---|---|---|
| Modeling scenario | Mean absolute error (in months) | Median absolute error (in months) | Mean absolute error (in months) | Median absolute error (in months) |
| All Sequences (TS) | 8.84 (8.14, 13.74) | 6.74 (6.16, 13.58) | 7.23 (6.98, 13.43) | 5.98 (5.26, 13.25) |
| All Sequences (R) | 8.78 (8.47, 13.5) | 5.79 (6.15, 12.35) | 8.94 (7.87, 13.19) | 8.58 (5.34, 12.05) |
| No QSM (TS) | 9.07 (8.58, 13.92) | 6.58 (6.56, 13.73) | 8.19 (8.05, 13.84) | 8.22 (5.29, 13.75) |
| No QSM (R) | 9.07 (8.6, 13.52) | 6.44 (6.05, 12.42) | 9.93 (8.01, 13.48) | 10.06 (5.22, 12.51) |
| No T1w+c | 12.46 (11.4, 15.8) | 9.83 (8.99, 14.16) | 12.36 (11.22, 15.87) | 10.07 (8.86, 14.58) |
| Conventional | 12.00 (11.26, 15.91) | 9.57 (8.85, 14.35) | 13.87 (11.16, 16.38) | 12.00 (9.14, 15.32) |
| Demographics | 11.93 (10.48, 18.51) | 10.92 (7. 49, 18.59) | 12.66 (11.25, 18.02) | 12.00 (9.05, 17.67) |
| Mean features (TS) | 10.16 (9.79, 14.16) | 9.70 (7.49, 14.2) | 9.21 (8.66, 13.3) | 7.76 (6.14, 12.29) |
| Mean features (R) | 10.19 (10.13, 14.92) | 8.28 (7.43, 12.77) | 10.36 (8.97, 14.62) | 9.99 (6.65, 12.11) |
Table 3. Training set mean and median absolute error for the models.
The mean and median absolute error for all modeling scenarios for the two cutoffs in the training set.
| 15 mm3 Cutoff |
50 mm3 Cutoff |
|||
|---|---|---|---|---|
| Modeling scenario | Mean absolute error (in months) | Median absolute error (in months) | Mean absolute error (in months) | Median absolute error (in months) |
| All Sequences (TS) | 2.93 | 2.10 | 3.81 | 2.86 |
| All Sequences (R) | 3.35 | 2.70 | 4.64 | 3.62 |
| No QSM (TS) | 3.06 | 2.27 | 3.78 | 2.66 |
| No QSM (R) | 3.45 | 2.66 | 4.50 | 3.45 |
| No T1w+c | 4.24 | 3.12 | 5.13 | 3.78 |
| Conventional | 4.27 | 3.12 | 4.83 | 3.62 |
| Demographics | 6.12 | 4.41 | 6.44 | 5.00 |
| Mean features (TS) | 4.67 | 3.48 | 4.83 | 3.29 |
| Mean features (R) | 5.36 | 4.67 | 5.98 | 4.64 |
Fig. 6 shows the percent of the reassignments to the training and validation set with a lower median absolute error for the models. The model with the higher median absolute error is shown on the x-axis and the model with the lower median absolute error is shown on the y-axis. The percent of times this relationship is held in the 1000 reassignments of the training and validation set is reported. From this plot we see that for the 15 mm3 and 50 mm3 cases the All Sequences (R) modeling scenario performs better (lower median absolute error) than the other modeling scenarios in more than 50% of the reassignments. We also see that the No T1w+c, Conventional and Demographics modeling scenarios perform substantially worse than the other modeling scenarios.
Fig. 6. Percent of reassignments with lower median absolute error for the 15 mm3 (left) and 50 mm3 (right) cutoff.
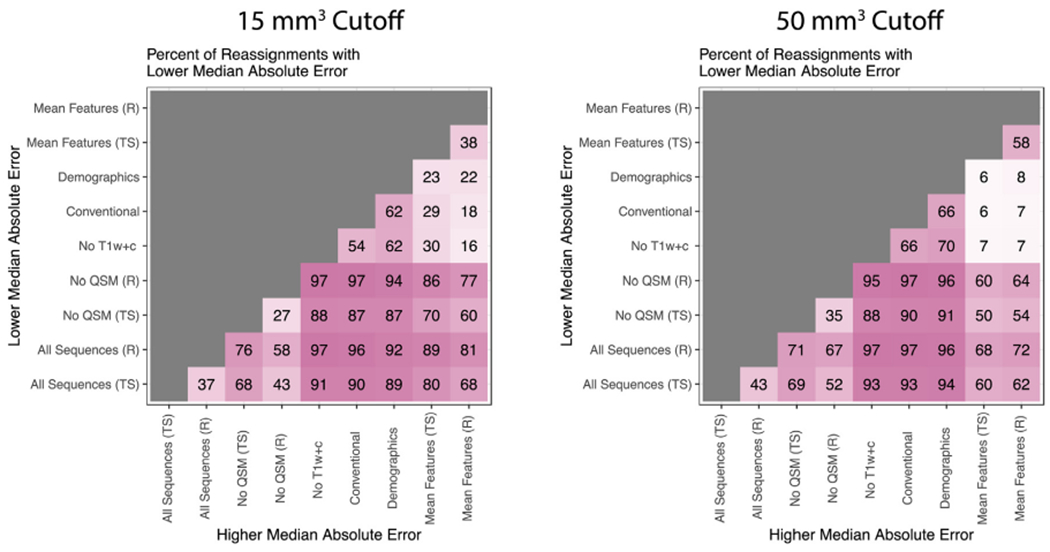
The model with the higher median absolute error is shown on the x-axis and the model with the lower median absolute error is shown on the y-axis. The percent of times this relationship is held in the 1000 reassignments of the training and validation set is reported.
The variable importance plots for the ten most important variables from the random forest classification models are shown in Fig. 5. For both the 15 mm3 cutoff (A) and the 50 mm3 cutoff (B) all of the top 10 features are derived from the T1w+c sequence. As expected, this indicates that the T1w+c sequence is important for detecting new lesions, as new lesions are enhancing on the T1w+c sequence.
Fig. 5. Variable importance for the classification models for the 15 mm3 (A) and 50 mm3 (B) cutoff.

The variable importance from the random forest classification models for the 10 most important variables for the three two step modeling scenarios for each of the two cutoffs.
The variable importance plots for the ten most important variables from the random forest regression models with the 15 mm3 cutoff are shown in Fig. 7A. For the All Sequence (TS) model with the 15 mm3 cutoff, the ten most important variables are derived from the QSM, T1w, T2w and FLAIR sequences. The demographic variable of age is also included in the top ten. The T1w+c is not among the ten most important variables for predicting lesion age above zero, but it is important to note that this sequence is very important for the first step classifier model to determine whether the lesion is at age zero (enhancing on T1w+c) or not. We see that T1w+c features are among the top 10 variables for the All Sequence (R) model, as this model does not separate the classification and regression tasks. For the No QSM (TS) modeling scenario with the 15 mm3 cutoff, all sequences in the model are part of the top ten most important variables except for the T1w+c. For the No QSM (R) modeling scenario with the 15 mm3 cutoff, all sequences in the model are part of the top ten most important variables except for the T2w. Patient’s age is again part of the top ten variables for both No QSM modeling scenarios. In the No T1w+c and Conventional modeling scenarios with the 15 mm3 cutoff, patient’s age is the most important variable. QSM, FLAIR, and T1w comprise the other top ten variables in the No T1w+c scenario, while FLAIR and T1 comprise the top variables in the Conventional scenario. For the Demographic scenario, age is the most important variable. For the Mean (TS) the T2w mean is the most important, while for the Mean (R) the T1w+c is the most important.
Fig. 7. Variable importance for the regression models for the 15 mm3 (A) and 50 mm3 (B) cutoff.
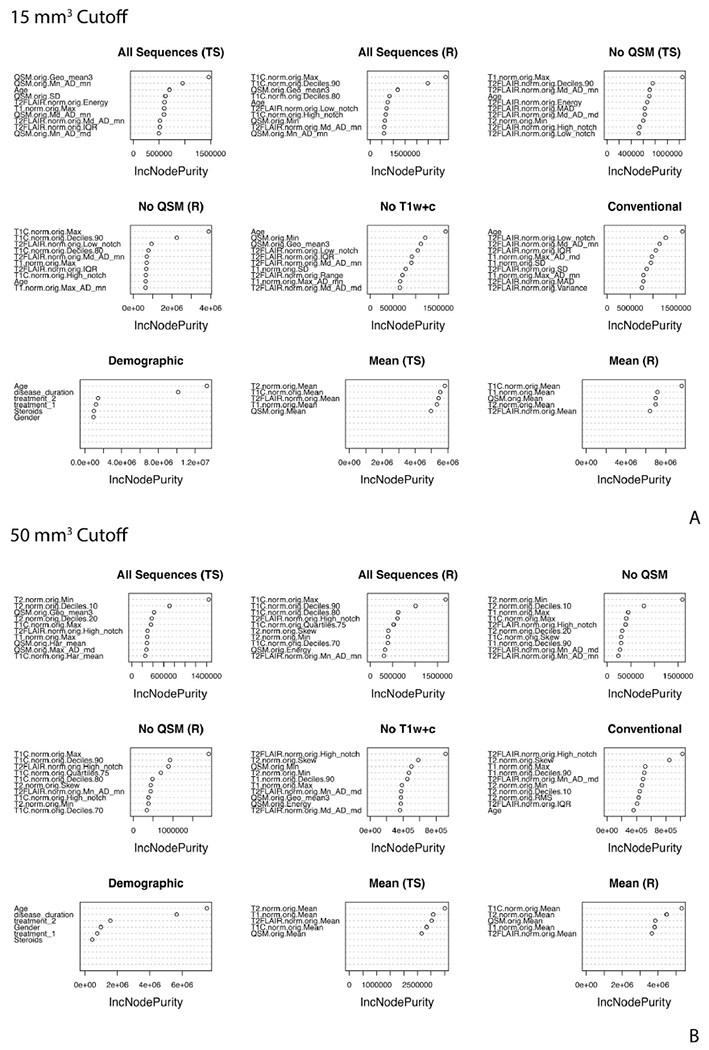
The variable importance from the random forest regression models for the 10 most important variables for the nine modeling scenarios for each of the two cutoffs.
The variable importance plots for the ten most important variables from the random forest regression models with the 50 mm3 cutoff are shown in Fig. 7B. For the All Sequence (TS) model with the 50 mm3 cutoff the ten most important variables are derived from all of the MRI sequences. The demographic information is not among the top ten. For the All Sequences (R) scenario, the T1w+c dominates the most important variables, with FLAIR, T2, and QSM also appearing in the list. For the No QSM (TS) all of the sequences are included in the top ten variables, while the No QSM (R) does not include T1w features and is also dominated by the T1w+c features. The No T1w+c and Conventional include all of the MRI sequences. For the Conventional scenario age is also one of the top ten features. For the Demographic scenario, age is the most important variable. For the Mean (TS) the T2w mean is the most important, while for the Mean (R) the T1w+c is the most important.
Table 4 examines the stability of the top features for the 1000 reassignments of the training and validation set for the All Sequences (TS) and (R) modeling scenarios for the 50 mm3 cutoff. The percentage of times the variable appeared as first, second, or third most important variable in the 1000 re-assignments is reported. We report for the ten most frequently occurring variables. We see that for the first-step classification model for the All Sequences (TS) and for the All Sequences (R) model, the most important features are mainly from the T1w+c features and these stay very stable. The most important variable for each of these is the T1w+c maximum over the lesion. For the All Sequences (TS) regression step the important variables are a mix of T1w, T2w, and QSM, with less stability than in the classification step and the All Sequences (R) model. The T1w+c maximum is also found among the most important variables and was found to be the third most important variable 11.2% of the 1000 re-assignments.
Table 4. Stability of variable importance.
The top three most important variables for the All Sequences (TS) and All Sequences (R) models for the 50 mm3 cutoff from 1000 reassignments to the training and validation set. The percentage of times the variable appeared as first, second, or third most important is reported. We report for the ten most frequently occurring variables.
| All Sequences (TS) classification step variable importance 50 mm3 cutoff | ||
|---|---|---|
| First | Second | Third |
| T1C.norm.orig.Max (73.3%) | T1C.norm.orig.Deciles.90 (63.6%) | T1C.norm.orig.Deciles.80 (45.4%) |
| T1C.norm.orig.Deciles.90 (23.8%) | T1C.norm.orig.Max (20.0%) | T1C.norm.orig.Quartiles.75 (17.2%) |
| T1C.norm.orig.Deciles.80 (1.2%) | T1C.norm.orig.Deciles.80 (8.2%) | T1C.norm.orig.Deciles.70 (11.5%) |
| T1C.norm.orig.Deciles.70 (0.7%) | T1C.norm.orig.Deciles.70 (2.7%) | T1C.norm.orig.Deciles.90 (8.3%) |
| T1C.norm.orig.Quartiles.75 (0.3%) | T1C.norm.orig.Quartiles.75 (2.5%) | T1C.norm.orig.high_notch (5.0%) |
| T1C.norm.orig.High_notch (0.2%) | T1C.norm.orig.High_notch (0.9%) | T1C.norm.orig.Max (3.4%) |
| T1C.norm.orig.Deciles.60 (0.1%) | T1C.norm.orig.Deciles.60 (0.3%) | T1C.norm.orig.Mean (2.2%) |
| T1C.norm.orig.Trim_mean_5 (0.3%) | T1C.norm.orig.Trim_mean_5 (1.7%) | |
| T1C.norm.orig.Median (0.2%) | T1C.norm.orig.Median (1.0%) | |
| T1C.norm.orig.Trim_mean_10 (0.2%) | T1C.norm.orig.Deciles.60 (0.9%) | |
| All Sequences (TS) regression step variable importance 50 mm3 cutoff | ||
| First | Second | Third |
| T1.norm.orig.Max (43.8%) | T2.norm.orig.Min (22.2%) | T1C.norm.orig.Max (11.2%) |
| T2.norm.orig.Min (34.1%) | T1.norm.orig.Max (19.5%) | T2.norm.orig.Min (10.4%) |
| QSM.orig.Min (3.5%) | T2.norm.orig.Deciles.10 (9.3%) | T1.norm.orig.Max (8.7%) |
| Age (3.1%) | T1C.norm.orig.Max (7.6%) | T2.norm.orig.Deciles.10 (7.7%) |
| T2.norm.orig.Deciles.10 (2.7%) | QSM.orig.Low_notch (5.0%) | QSM.orig.Max_AD_md (6.0%) |
| QSM.orig.Low_notch (2.0%) | QSM.orig.Max_AD_md (5.0%) | QSM.orig.Min (5.9%) |
| T1C.norm.orig.Deciles.20 (1.5%) | QSM.orig.Min (4.5%) | QSM.orig.Low_notch (5.5%) |
| QSM.orig.Geo_mean2 (1.1%) | Age (3.8%) | T2FLAIR.norm.orig.High_notch (4.6%) |
| QSM.orig.Variance (1.1%) | QSM.orig.Geo_mean3 (2.8%) | QSM.orig.Geom_mean3 (4.4%) |
| QSM.orig.Mn_Ad_mn (0.8%) | T2FLAIR.norm.orig.High_notch (2.8%) | Age (4.2%) |
| All Sequences (R) variable importance 50 mm3 cutoff | ||
| First | Second | Third |
| T1C.norm.orig.Max (72.8%) | T1C.norm.orig.Deciles.90 (69.1%) | T1C.norm.orig.Deciles.80 (38.8%) |
| T1C.norm.orig.Deciles.90 (25%) | T1C.norm.orig.Max (23%) | QSM.orig.Min (11.8%) |
| QSM.orig.Min (0.4%) | T1C.norm.orig.High_notch (2.0%) | QSM.orig.Low_notch (5.8%) |
| T1C.norm.orig.Geo_mean2 (0.4%) | T1C.norm.orig.Deciles.80 (1.9%) | T1C.norm.orig.High_notch (5.6%) |
| T1C.norm.orig.Deciles.20 (0.3%) | QSM.orig.Low_notch (0.6%) | T1C.norm.orig.Quartiles.75 (5.2%) |
| T1C.norm.orig.Deciles.80 (0.2%) | QSM.orig.Min (0.6%) | T1C.norm.orig.Deciles.90 (4.3%) |
| T1C.norm.orig.High_notch (0.2%) | T1C.norm.orig.Deciles.20 (0.5%) | T2.nor.orig.Min (3.7%) |
| T1C.norm.orig.Deciles.40 (0.1%) | T1C.norm.orig.Deciles.70 (0.4%) | T1.norm.orig.Max (3.2%) |
| T1C.norm.orig.Deciles.70 (0.1%) | T1C.norm.orig.Quartiles.75 (0.3%) | T2FLAIR.norm.orig.High_notch (2.9%) |
| T1C.norm.orig.Quartiles.70 (0.1%) | Age (0.2%) | T1C.norm.orig.Geo_mean2 (2.8%) |
Fig. 8 shows the smoothed trends for the three most important variables over the 1000 training and validation set re-assignments for the All Sequence (TS) model for the 50 mm3 cutoff for all of the data (training and validation set). The top row shows boxplots for the first-step classification model features for new versus older lesions. The bottom row shows smoothed normalized intensity over time for the second step regression model features. In the bottom row, a loess smoother has been fit to the data in order to show the temporal trends for each of the variables. For the T1w+c features in the classification model (maximum, ninth and eighth decile) we see higher intensities in the newer lesions, consistent with lesion enhancement. For the regression model, for The T1w maximum, we observe an increase in the value of the features followed by a decrease after a year. For the T2w minimum feature we see a decrease up until 1 year followed by an increase in the values. For the T1w+c maximum, we see a sharp decrease followed by a more subtle decrease over time.
Fig. 8. Most important variables from the All Sequences (TS) 50 mm3 cutoff for the 1000 training and validation set reassignments.
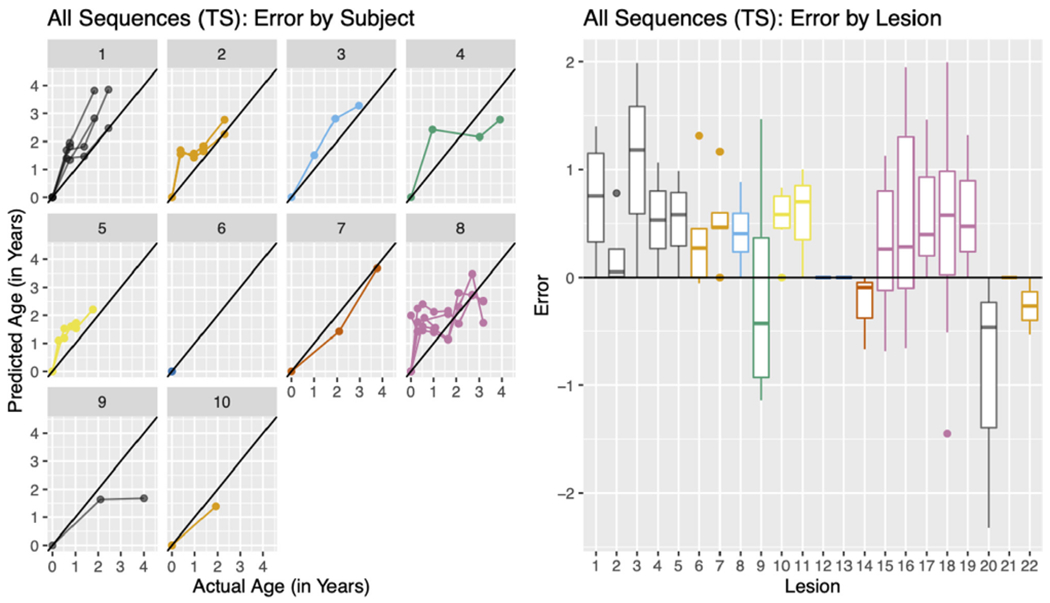
The plots show smoothed data from the three most important RIA features for the All Sequence (TS) modeling scenario over the 1000 reassignments to the training and validation set results from Table 4. The top row is for the first-step classification model and the bottom row the second-step regression model. Smoothing was performed with a loess smoother.
We further examined the errors from the best performing modeling scenario, the All Sequences (TS) with the 50 mm3 cutoff. Fig. 9 (left) shows the predicted age versus the true age in the validation set stratified by subject for the All Sequences (TS) modeling scenario. From the plot, we see that for each subject the errors in prediction are in general all positive or negative (lying entirely above or below the identity line). Fig. 9 (right) shows the error for each lesion colored by subject, using the same colors as the plot on the left. Again, we see in general all positive or negative errors for a lesion as well as for a subject. These results indicate systematic error by subject.
Fig. 9. All Sequences (TS) errors by subject and lesion for 50 mm 3 cutoff.
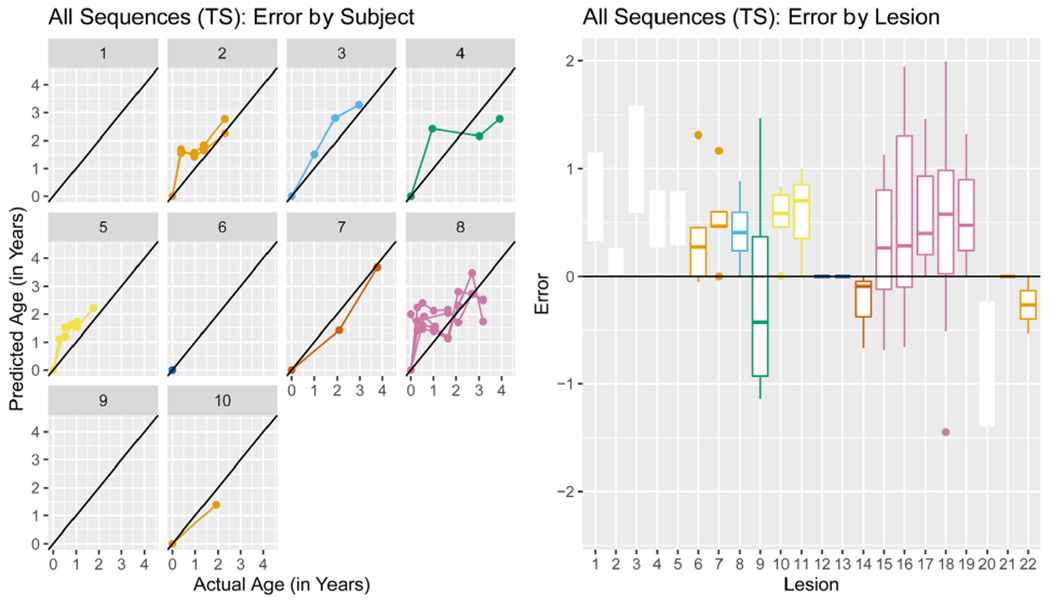
The predicted age versus the actual age (left) stratified by subject. The error by lesion (right) colored by subject, using colors that correspond to the plot on the left.
Table 5 shows the results from the linear mixed effect model regressing predicted age onto actual age. The beta coefficient and associated p-value are reported. For the 15 mm3 cutoff, we see statistically significant associations between predicted age and actual age in all modeling scenarios except the Conventional. For the 50 mm3 cutoff, we only see statistically significant associations between predicted age and actual age in models that included the T1w+c features. In the No T1w+c, Conventional, and Demographics modeling scenarios the association was not found to be statistically significant and the beta coefficient takes a value close to zero. We would ideally like to see a beta coefficient that takes a value close to one. The All Sequences (TS) modeling scenario for the 50 mm3 cutoff is the closest to one, with a value of 0.73. We also explored adding in an indicator of scanner (GE versus Siemens) to the model. This was not found to be statistically significant in any of the models and we therefore do not report these results.
Table 5. Association between predicted age and actual age.
The beta coefficients and p-values for the linear mixed effect model with predicted age as an outcome, fixed effect for actual age, and a random effect for patient in each of modeling scenarios for the two cutoffs. P-values that fall below a 0.05 significance threshold are bolded.
| 15 mm 3 Cutoff |
50 mm3 Cutoff |
|||
|---|---|---|---|---|
| Modeling scenario | Beta | p-Value | Beta | p-Value |
| All Sequences (TS) | 0.49 | <0.001 | 0.73 | <0.001 |
| All Sequences (R) | 0.44 | <0.001 | 0.51 | <0.001 |
| No QSM (TS) | 0.49 | <0.001 | 0.67 | <0.001 |
| No QSM (R) | 0.48 | <0.001 | 0.51 | <0.001 |
| No T1w+c | 0.07 | 0.0393 | 0.08 | 0.208 |
| Conventional | 0.08 | 0.0669 | 0.07 | 0.300 |
| Demographics | 0.12 | <0.001 | 0.05 | 0.056 |
| Mean features (TS) | 0.41 | <0.001 | 0.59 | <0.001 |
| Mean features (R) | 0.28 | <0.001 | 0.30 | <0.001 |
4. Discussion
For all metrics in this analysis, the model using all of the MRI sequences had the best performance. The performance was improved with the more stringent cutoff of 50 mm3 over 15 mm3 , indicating that the model had more difficulty estimating the age of smaller lesions. This estimation could be potentially be improved with increased spatial resolution in the imaging sequences at the cost of longer acquisition time or reduced signal-to-noise ratio. The models excluding the T1w+c sequence had poorer performance, indicating that the T1w+c sequence is the most important for predictive accuracy in estimating the age of MS lesions. These models had performance near to the model that only included demographic information, indicating how important the T1w+c features are for this problem. This is especially true for the identification of new lesions, which show up as enhancing on the T1w+c scan. In the validation set, the two-step regression and classification model had better performance than the one-step regression model, justifying our use of the two-step model. Yet, the one-step regression models for scenarios that include the T1w+c sequence still performs better those scenarios that do not include this sequence, indicating that not all of the increased performance is a result of the classification step. All of the intervals from reassignment of the training and validation set were overlapping, indicating that we do not have enough data to detect a significant difference in the performance between the models. Also, it is important to note that in general in the reassignments from the training and validation set, the one-step models outperformed the two step models in terms of median absolute error in more of the reassignments. Again, more data is needed to determine which modeling scenario has the best performance.
For this analysis, we used 44 radiomic features that were generated for each MRI sequence for each lesion. For the All Sequence modeling scenario, that is a total of 220 radiomic features in addition to demographic information. This large number of features allows for an accurate description of the image intensity distribution over each lesion in each sequence. This allows us to pick up the subtle changes in a lesion as it ages, which may not be apparent when looking only at only one of the radiomic features, such as the mean intensity used in the Mean (TS) and Mean (R) modeling scenarios. In addition to first-order radiomic features, we also evaluated the performance of radiomic features that described the spatial distribution of voxels and the geometry of the lesion in the model. These additional features did not improve performance and were therefore not included in the final model.
The proposed models can be used to temporally register longitudinal information from MRI for the study of longitudinal lesion behavior. If lesion age is known, the longitudinal signal of the lesions will be more easily uncovered and heterogeneity in the lesion behavior will not be ascribed to the misalignment of the lesions in time and will instead be attributed to underlying biological differences or treatment effects (Marron et al., 2015; Ramsay and Silverman, 1997). One example is the study of the longitudinal behavior chronic active or slowly expanding MS lesions (Dal-Bianco et al., 2017; Kaunzner et al., 2019), wherein it has been shown that the average intensities of these lesions increases on QSM after lesion incidence, peaks at the ‘chronic active’ stage (around one to two years after incidence), and then eventually decays away as the lesions transitions to the chronic inactive stage, all over a period of four to five years (S. Zhang et al., 2019a, Zhang et al., 2016a). These descriptive studies have been limited to enhancing lesions, where the age of lesions is known, and the data is therefore temporally aligned. When studying the impact of treatment on these lesions it will be necessary to look at a large population of lesion, many of which will not have enhancement. Temporal alignment of the data with lesion age estimation will allow for accurate treatment effect estimation. It is crucial to get the estimation of the lesion age as precise as possible, we therefore advocate for using the scenario that utilizes all of the MRI sequences, including QSM if possible. These best performing models, the All Sequences models for both cutoffs, have median absolute error ranging between six and 8.5 months. As the longitudinal activity of QSM lesions takes place over a period of around four to five years, we anticipate having a median registration error of around 10 to 15% of the total period will not have a great impact on our estimate of the average behavior. Further investigation into the impact is necessary and will be explored in future work with simulation analysis.
The McDonald criteria (McDonald et al., 2001) and its subsequent revisions (Thompson et al., 2018; Polman et al., 2011, 2005) are the current criteria used to diagnose MS. In addition to other findings, the current McDonald diagnostic criteria require that lesions be observed on MRI at different time points – referred to as the dissemination of lesions in time (Thompson et al., 2018). To have the timeliest diagnosis of MS, it is advantageous to be able to demonstrate dissemination in time using only one MRI scan. Given the potential for the proposed models to estimate the age of the lesions, integration of this into the diagnostic criteria may provide information regarding dissemination in time without the need for longitudinal scans. MS diagnosis is a very important problem, with serious ramifications for patients with a misdiagnosis. Our best performing models have a median absolute error ranging between six and 8.5 months and it is necessary to perform further validation to determine if this is accurate enough to determine dissemination in time. In Fig. 9, we see that errors are correlated within a patient, indicating that we may do better at ordering the lesion occurrences in time rather than estimating their exact age.
In Fig. 9, we see systematic error in the All Sequences modeling scenario by subject. This indicates that a model using more subject-level demographic features could perform better. In addition, if training data were available for all subjects, a subject-specific effect could be learned in the random forest model and could potentially have better performance. More data is necessary in order to fit a model of this kind.
For this analysis we used an affine registration with 12 degrees of freedom to register all images to the space of the baseline QSM. More sophisticated methods for longitudinal registration, such as those described in Smith et al. (2001), have been shown to perform better for longitudinal registration, especially for cases where quantitative measures of brain size and shape were of interest. This would be especially useful for incorporating geometric radiomic features of lesions which were not found to increase performance in our dataset. For future work we plan to investigate the impact of registration on the lesion radiomic features.
One limitation of this analysis is that two different MRI scanning platforms were used to acquire data. The protocol for the QSM was harmonized for both scanners and was demonstrated to be reproducible across scanners (Deh et al., 2019, 2015). For the qualitative images, T1w, T1w+c, T2w, and FLAIR, an intensity normalization procedure was used that has been shown to be robust to scanner differences (Shinohara et al., 2014). Because of this normalization, data from the two scanning platforms can be used together for the modeling of lesion age, allowing for a larger sample size. Error in the model could potentially be reduced by using data acquired with only one scanner. When investigating the relationship between predicted age and age and scanner using linear mixed effects models, we found no relationship with scanner in any of the modeling scenarios. We further investigated the median and mean absolute errors from the models stratified by scanner and did not observe differences in the performance.
A second limitation of this analysis is that we assumed that gadolinium enhancement signifies initial lesion formation, which may underestimate the actual lesion age. Studies have indicated that changes can occur months prior to gadolinium enhancement (Fazekas et al., 2002; Wiggermann et al., 2013), however detecting the earliest stages of lesion development would require frequent, serial MRI which is not clinically feasible. Gadolinium enhancement is an accepted measure of BBB disruption associated with the acute inflammatory response and will last approximately eight weeks (He et al., 2001). For these reasons, our lesion age estimates may have an error of a few months; however, considering the chronicity of MS, this is unlikely to have clinical significance.
Another limitation to this study is the relatively small sample size. For this analysis, we had data from 53 lesions from 32 patients. The strength of our study was the use of gadolinium enhancing lesions, which allowed for the calculation of an approximate age for each individual lesion. However, it is difficult to identify a large cohort of patients with gadolinium enhancing lesions in the era of effective anti-inflammatory disease modifying treatments for MS. With an increase sample size, significant differences in model performance could be obtained as well as the creation of models that would include subject-specific effects. Also, with a larger sample size, the effect of disease-modifying treatment on lesion age estimation could be further explored beyond the three categories (none, milder, and stronger) that were used in this analysis.
5. Conclusion
We demonstrate a novel machine-learning based approach to estimate the age of new and chronic MS lesions. The models presented are the first proposed in the literature to 1) estimate the age of MS lesions and 2) do so from a single MRI scan. Lesion age is estimated using a large number of radiomic features derived from different MRI sequences and a one or two step random forest model. We compared models with different combinations of the QSM sequence, the T1w+c sequence, conventional MRI, and demographic information. The best performance is obtained when all of the sequences and the demographic information are used together in the model. Future work involves utilizing these age prediction models to aid in the study of longitudinal behavior and treatment effects on chronic MS lesions.
Acknowledgments
This work was supported in part by grants from the National Institutes of Health (R01 NS090464, R01 NS105144, and R01 NS104283) and the National Multiple Sclerosis Society (RR-1602-07671)
Footnotes
Data availability
The imaging, clinical data, and code that support the findings of this study are not publicly available to protect the privacy of research participants in accordance with good clinical practice. The developed codes are available upon reasonable request from the corresponding author, EMS.
References
- Absinta M, et al. , 2016. Persistent 7-tesla phase rim predicts poor outcome in new multiple sclerosis patient lesions. J. Clin. Invest 126 (7), 2597–2609 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Absinta M, et al. , 2019. Association of chronic active multiple sclerosis lesions with disability in vivo. JAMA Neurol. 76 (12), 1474–1483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bates D, et al. , Fitting Linear Mixed-Effects Models Using lme4. arXiv preprint arXiv:1406.5823, 2014. [Google Scholar]
- Chen WW, et al. , 2014. Quantitative susceptibility mapping of multiple sclerosis lesions at various ages. Radiology 271 (1), 183–192 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dal-Bianco A, et al. , 2017. Slow expansion of multiple sclerosis iron rim lesions: pathology and 7 T magnetic resonance imaging. Acta Neuropathol. 133 (1), 25–42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Rochefort L, et al. , 2010. Quantitative susceptibility map reconstruction from MR phase data using bayesian regularization: validation and application to brain imaging. Magn. Reson. Med 63 (1), 194–206. [DOI] [PubMed] [Google Scholar]
- Deh K, et al. , 2015. Reproducibility of quantitative susceptibility mapping in the brain at two field strengths from two vendors. J. Magn. Reson. Imaging 42 (6), 1592–1600 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deh K, et al. , 2018. Magnetic susceptibility increases as diamagnetic molecules breakdown: myelin digestion during multiple sclerosis lesion formation contributes to increase on QSM. J. Magn. Reson. Imaging 48 (5), 1281–1287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deh K, et al. , 2019. Multicenter reproducibility of quantitative susceptibility mapping in a gadolinium phantom using MEDI+ 0 automatic zero referencing. Magn. Reson. Med 81 (2), 1229–1236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fazekas F, et al. , 2002. Quantitative magnetization transfer imaging of pre-lesional white-matter changes in multiple sclerosis. Mult. Scler. J 8 (6), 479–484. [DOI] [PubMed] [Google Scholar]
- Filippi M, et al. , 2016. MRI criteria for the diagnosis of multiple sclerosis: MAGNIMS consensus guidelines. Lancet Neurol. 15 (3), 292–303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Firbank M, et al. , 1999. Partial volume effects in MRI studies of multiple sclerosis. Magn. Reson. Imaging 17 (4), 593–601. [DOI] [PubMed] [Google Scholar]
- Ghassemi R, et al. , 2015. Quantitative measurement of tissue damage and recovery within new T2w lesions in pediatric-and adult-onset multiple sclerosis. Mult. Scler. J 21 (6), 718–725. [DOI] [PubMed] [Google Scholar]
- He J, et al. , 2001. Enhancing patterns in multiple sclerosis: evolution and persistence. Am. J. Neuroradiol 22 (4), 664–669. [PMC free article] [PubMed] [Google Scholar]
- Ho TK, 1995. Random decision forests. In: Proceedings of 3rd International Conference on Document Analysis and Recognition IEEE. [Google Scholar]
- Jenkinson M, et al. , 2002. Improved optimization for the robust and accurate linear registration and motion correction of brain images. NeuroImage 17 (2), 825–841. [DOI] [PubMed] [Google Scholar]
- Kaunzner UW, et al. , 2019. Quantitative susceptibility mapping identifies inflammation in a subset of chronic multiple sclerosis lesions. Brain 142 (1), 133–145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kolossváry M, et al. , 2017. Radiomic features are superior to conventional quantitative computed tomographic metrics to identify coronary plaques with napkin-ring sign. Circ.: Cardiovasc. Imaging 10 (12), e006843. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kolossváry M, et al. , 2018. Cardiac computed tomography radiomics. J. Thorac. Imaging 33 (1), 26–34. [DOI] [PubMed] [Google Scholar]
- Kuhlmann T, et al. , 2017. An updated histological classification system for multiple sclerosis lesions. Acta Neuropathol. 133 (1), 13–24. [DOI] [PubMed] [Google Scholar]
- Kuznetsova A, Brockhoff PB, Christensen RH , 2017. lmerTest package: tests in linear mixed effects models. J. Stat. Softw 82 (13), 1–26. [Google Scholar]
- Langkammer C, et al. , 2013. Quantitative susceptibility mapping in multiple sclerosis. Radiology 267 (2), 551–559. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liaw A , Wiener M, 2002. Classification and regression by randomForest. R News 2 (3), 18–22. [Google Scholar]
- Liu Z, et al. , 2018. MEDI+ 0: morphology enabled dipole inversion with automatic uniform cerebrospinal fluid zero reference for quantitative susceptibility mapping. Magn. Reson. Med 79 (5), 2795–2803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marron JS, et al. , 2015. Functional data analysis of amplitude and phase variation. Stat. Sci 468–484. [Google Scholar]
- McDonald WI, et al. , 2001. Recommended diagnostic criteria for multiple sclerosis: guidelines from the International Panel on the diagnosis of multiple sclerosis. Ann. Neurol.: Off. J. Am. Neurol. Assoc. Child Neurol. Soc 50 (1), 121–127. [DOI] [PubMed] [Google Scholar]
- Meier DS, Guttmann CR , 2003. Time-series analysis of MRI intensity patterns in multiple sclerosis. NeuroImage 20 (2), 1193–1209. [DOI] [PubMed] [Google Scholar]
- Meier DS, Guttmann CR, 2006. MRI time series modeling of MS lesion development. NeuroImage 32 (2), 531–537. [DOI] [PubMed] [Google Scholar]
- Polman CH, et al. , 2005. Diagnostic criteria for multiple sclerosis: 2005 revisions to the “McDonald Criteria”. Ann. Neurol.: Off. J. Am. Neurol. Assoc. Child Neurol. Soc 58 (6), 840–846. [DOI] [PubMed] [Google Scholar]
- Polman CH, et al. , 2011. Diagnostic criteria for multiple sclerosis: 2010 revisions to the McDonald criteria. Ann. Neurol 69 (2), 292–302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramsay JO, Silverman BW, 1997. Functional data analysis Springer Series in Statistics. Springer. [Google Scholar]
- Sahraian MA, Radue E-W, 2007. MRI Atlas of MS Lesions. Springer Science & Business Media; . [Google Scholar]
- Shinohara RT, et al. , 2014. Statistical normalization techniques for magnetic resonance imaging. NeuroImage: Clin. 6, 9–19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith SM, et al. , 2001. Normalized accurate measurement of longitudinal brain change. J. Comput. Assist. Tomogr 25 (3), 466–475. [DOI] [PubMed] [Google Scholar]
- Smith SM, 2002. Fast robust automated brain extraction. Hum. Brain Mapp 17 (3), 143–155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stüber C, Pitt D, Wang Y, 2016. Iron in multiple sclerosis and its noninvasive imaging with quantitative susceptibility mapping. Int. J. Mol. Sci 17 (1), 100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sweeney EM, et al. , 2016. Relating multi-sequence longitudinal intensity profiles and clinical covariates in incident multiple sclerosis lesions. NeuroImage: Clin. 10, 1–17 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thompson AJ, et al. , 2018. Diagnosis of multiple sclerosis: 2017 revisions of the McDonald criteria. Lancet Neurol. 17 (2), 162–173. [DOI] [PubMed] [Google Scholar]
- Traboulsee A, et al. , 2016. Revised recommendations of the consortium of MS centers task force for a standardized MRI protocol and clinical guidelines for the diagnosis and follow-up of multiple sclerosis. Am. J. Neuroradiol 37 (3), 394–401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y, Liu T, 2014. Quantitative susceptibility mapping (QSM): decoding MRI data for a tissue magnetic biomarker. Magn. Reson. Med 73(1), 82–101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y, et al. , 2017. Clinical quantitative susceptibility mapping (QSM): biometal imaging and its emerging roles in patient care. J. Magn. Reson. Imaging 46 (4), 951–971. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wiggermann V, et al. , 2013. Magnetic resonance frequency shifts during acute MS lesion formation. Neurology 81 (3), 211–218 . [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wisnieff C, et al. , 2015. Quantitative susceptibility mapping (QSM) of white matter multiple sclerosis lesions: interpreting positive susceptibility and the presence of iron. Magn. Reson. Med 74 (2), 564–570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang YY, Brady M, Smith S, 2001. Segmentation of brain MR images through a hidden Markov random field model and the expectation-maximization algorithm. IEEE Trans. Med. Imaging 20 (1), 45–57 [DOI] [PubMed] [Google Scholar]
- Zhang Y, et al. , 2016a. Longitudinal change in magnetic susceptibility of new enhanced multiple sclerosis (MS) lesions measured on serial quantitative susceptibility mapping (QSM). J. Magn. Reson. Imaging 44 (2), 426–432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y, et al. , 2016b. Longitudinal change in magnetic susceptibility of new enhanced multiple sclerosis (MS) lesions measured on serial quantitative susceptibility mapping (QSM). J. Magn. Reson. Imaging 44 (2), 426–432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang S, et al. , 2018. Diagnostic accuracy of semiautomatic lesion detection plus quantitative susceptibility mapping in the identification of new and enhancing multiple sclerosis lesions. Neuroimage Clin. 18, 143–148 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang S, et al. , 2019a. Quantitative susceptibility mapping of time-dependent susceptibility changes in multiple sclerosis lesions. Am. J. Neuroradiol 40 (6), 987–993 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang S, et al. , 2019b. Quantitative susceptibility mapping of time-dependent susceptibility changes in multiple sclerosis lesions. AJNR Am. J. Neuroradiol 40 (6), 987–993. [DOI] [PMC free article] [PubMed] [Google Scholar]


