ICLRBBN: a tool for accurate prediction of potential lncRNA disease associations

Abstract

Growing evidence has elucidated that long non-coding RNAs (lncRNAs) are involved in a variety of complex diseases in human bodies. In recent years, it has become a hot topic to develop effective computational models to identify potential lncRNA-disease associations. In this article, a novel method called ICLRBBN (Internal Confidence-Based Local Radial Basis Biological Network) is proposed to detect potential lncRNA-disease associations by adopting an internal confidence-based radial basis biological network. In ICLRBBN, a novel internal confidence-based collaborative filtering recommendation algorithm was designed first to mine hidden features between lncRNAs and diseases, which guarantees that ICLRBBN can be more effectively applied to predict new diseases. Then, a unique three-layer local radial basis function network consisting of diseases and lncRNAs was constructed, based on which the association probability between diseases and lncRNAs was calculated by combining different characteristics of lncRNAs with local information of diseases. Finally, we compared ICLRBBN with 6 state-of-the-art methods based on two different validation frameworks. Simulation results showed that area under the receiver operating characteristic curve (AUC) values achieved by ICLRBBN outperformed all competing methods. Furthermore, case studies illustrated that ICLRBBN has a promising future as a powerful tool in the practical application of lncRNA-disease association prediction. A web service for prediction of potential lncRNA-disease associations is available at http://leelab2997.cn/.

Graphical Abstract

Wang et al. developed a tool called ICLRBBN to detect potential lncRNA-disease associations by adopting an internal confidence-based radial basis biological network. This paper compared ICLRBBN with 6 state-of-the-art methods based on two different validation frameworks. Simulation results demonstrated the reliability and superiority of the prediction performance of ICLRBBN.

Introduction

Historically, the hypothesis that genetic information is stored in protein-coding genes has been commonly accepted as the unerring central principle of molecular biology.¹ However, with the continuous development of sequencing technology and the completion of various sequencing projects, researchers have found that more than 98% of the human genome does not encode protein sequences but produces a large number of non-coding RNAs (ncRNAs).^2,3 Among them, long non-coding RNAs (lncRNAs) are an important class of non-coding transcripts with lengths longer than 200 nt.^4,5 Specially, they are also critical regulators involved in various important biological processes such as cell proliferation, cell apoptosis, transcription, translation, cell cycle control, and epigenetic regulation.^6,7 Therefore, it is not surprising that a growing number of studies have corroborated the existence of a significant association between the mutations and abnormalities of lncRNAs and various complex human diseases.8, 9, 10 It is obvious that disease-related lncRNAs can not only provide valuable insights into the research on the pathogenesis of complex diseases at the lncRNA level but also contribute to the diagnosis, treatment, and prognosis of diseases. However, considering that traditional biological experimental methods are time consuming and expensive, it is necessary to develop computational models to infer potential lncRNA-disease associations, since it can reduce costs and save time in biological experiments.

In the past few years, some advanced computational models have been proposed to predict potential lncRNA-disease associations successfully. So far, according to the different strategies adopted, these models can be roughly divided into three major categories. The first category is composed of the network-based approaches, in which different kinds of lncRNA-disease heterogeneous networks are constructed to discover potential associations between lncRNAs and diseases based on known lncRNA-disease associations. For instance, Li et al.¹¹ presented a prediction model called LRWHLDA by implementing the local random walk method on a newly constructed lncRNA-disease heterogeneous network.¹¹ However, due to limited known lncRNA-disease associations, these network-based methods cannot be used to predict correlations between new lncRNAs (lncRNAs without known associated diseases) and new diseases (diseases without known associated lncRNAs). Hence, in recent years, some computational models that do not rely on known lncRNA-disease associations have been proposed. For example, Wang et al.¹² developed a tool called lncDisease to infer potential correlations between lncRNAs and diseases based on disease enrichment analysis of microRNAs (miRNAs) interacting with specific lncRNAs. These models constitute the second category. Although these models broke through the limitations of limited known lncRNA-disease association samples, they cannot be applied to infer potential associations between diseases and lncRNAs without any known related genes or miRNAs. Hence, the third category of computational models is proposed based on machine learning schemes in recent years. For example, Fu et al.¹³ developed a generic data fusion model based on matrix decomposition called MFLDA, which can explore and utilize the intrinsic structure of heterogeneous data sources to apply to correlation prediction between various types of entities. However, the performance of these machine learning-based models depends on the selection of optimal parameters, which have not been solved efficiently up to now.

Inspired by the above models, in this article, a novel method called ICLRBBN (Internal Confidence-Based Local Radial Basis Biological Network) was proposed to uncover potential lncRNA-disease associations. In ICLRBBN, considering the limited known lncRNA-disease associations and the applicability of new diseases, a new measure for estimating the similarities between diseases was designed first based on the concept of internal confidence. Then, an internal confidence collaborative filtering recommendation algorithm was developed to extract features of diseases. Next, a novel three-layer complex radial basis biological network was further constructed, based on which the probability matrix of associations between lncRNAs and diseases was calculated by integrating different characteristics of lncRNAs with local information of diseases. Finally, in order to evaluate the prediction performance of ICLRBBN, two different kinds of frameworks, including the leave-one-out cross-validation (LOOCV) and the 5-fold cross-validation (5-fold CV), were implemented separately. Experimental results indicated that ICLRBBN achieved reliable area under the receiver operating characteristic (ROC) curve (AUC) values of 0.9510 and 0.9043 ± 0.0019, respectively. Furthermore, case studies of two specific diseases, breast cancer and osteosarcoma, demonstrated that ICLRBBN was an effective tool for predicting potential lncRNA-disease associations as well.

Results

Performance evaluation

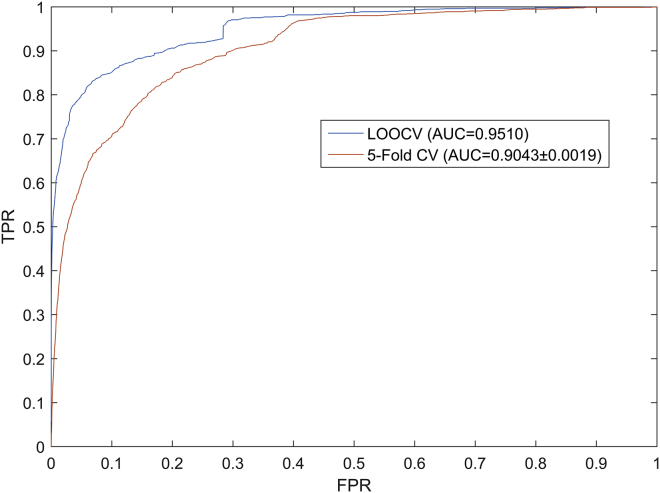
Two common validation frameworks, LOOCV and 5-fold CV, were adopted to evaluate model performance of ICLRBBN. Both LOOCV and 5-fold CV were performed on ICLRBBN based on 1,695 known lncRNA-disease associations obtained from the lncRNADisease database.¹⁴ First, in LOOCV, each known lncRNA-disease association was taken as a test sample in turn, while the remaining 1,694 known associations were taken as training samples. In addition, all lncRNA-disease pairs with no known association in the dataset were considered as candidate samples. Subsequently, we ranked the test sample together with all the candidate samples based on the scores predicted by ICLRBBN. If the test sample ranked higher than a given threshold, the prediction of the test sample was considered successful; otherwise, the prediction was considered failed. Then, through the setting of different thresholds, we calculated the corresponding true-positive rates (TPRs or sensitivity) and false-positive rates (FPRs or 1-specificity). Here, TPR represented the ratio of test samples ranked above a given threshold, and FPR represented the ratio of candidate samples ranked above a given threshold. Finally, the ROC curve was drawn according to the TPRs and FPRs corresponding to these different thresholds. The AUC was used as an evaluation indicator to evaluate the prediction performance of the model, where an AUC value of 1 indicated an ideal perfect prediction, while an AUC value of 0.5 indicated a completely random prediction. The closer the AUC value was to 1, the better the prediction performance of the model. The simulation experiment result is illustrated in Figure 1. ICLRBBN obtained a reliable AUC of 0.9510 under the LOOCV framework, which showed that our model had outstanding prediction performance.

Figure 1.

ROC curves and AUCs achieved by ICLRBBN under the framework of LOOCV and the framework of 5-fold CV

Additionally, unlike LOOCV, all 1,695 known lncRNA-disease associations in the 5-fold CV were randomly and evenly divided into 5 groups, with each group taking a turn as the test set, with the remaining 4 groups as the training set. Considering that the randomness of dividing the groups may have led to deviation in the experimental results, we performed 5-fold CV 100 times to obtain the average AUC values. As illustrated in Figure 1, ICLRBBN obtained a reliable AUC of 0.9043 ± 0.0019 under the 5-fold CV framework.

Effects of parameters

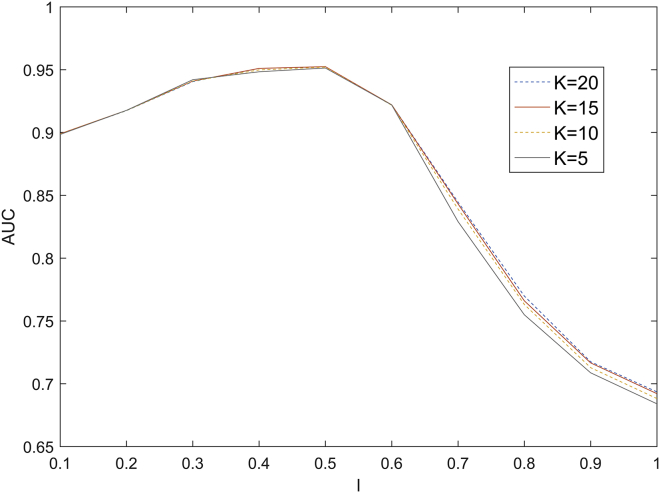
In ICLRBBN, there are two main parameters: the parameter K and the overlap coefficient factor $l$. The parameter K determines the size of the chum set of diseases, while the overlap coefficient factor $l$ controls the coverage of the basis function scope in the hidden layer. We considered $l\in \left\{0.1,0.2,0.3\cdots 1\right\}$ and $K\in \left\{\mathrm{5,10,15,20}\right\}$ and implemented ICLRBBN several times in LOOCV and 5-fold CV based on the dataset DS1 to evaluate their effects. Since the division of the test set and the verification set in 5-fold CV was random, 5-fold CV was performed 100 times under each group of parameters K and $l$ to obtain the average AUC values. As illustrated in Figure 2 below, we found that for all values of K, the AUC values in LOOCV increased slightly when l varied from 0.1 to 0.5, and the AUC values decreased significantly when $l$ varied from 0.6 to 1. Additionally, as shown in Table 1, we demonstrated that when K = 15 and $l$ = 0.4, ICLRBBN performed best in 5-fold CV. Hence, K and $l$ were set to 15 and 0.4 in ICLRBBN, respectively.

Figure 2.

Effects of parameters K and l under the framework of LOOCV

Table 1.

Effects of parameters K and l under the framework of 5-fold CV

K (AUC)	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0
5	0.8249	0.8561	0.8922	0.9025	0.8911	0.8177	0.7346	0.6656	0.6253	0.6046
10	0.8326	0.8562	0.8908	0.9036	0.8919	0.8196	0.7456	0.6784	0.6378	0.6175
15	0.8224	0.8566	0.8909	0.9043	0.8922	0.8208	0.7499	0.6837	0.6431	0.6232
20	0.8227	0.8565	0.8899	0.9040	0.8924	0.8206	0.7523	0.6872	0.6440	0.6246

Comparison with other state-of-the-art methods

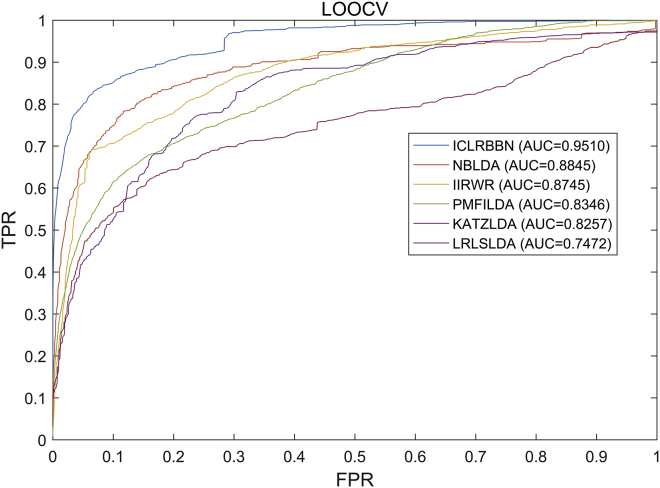
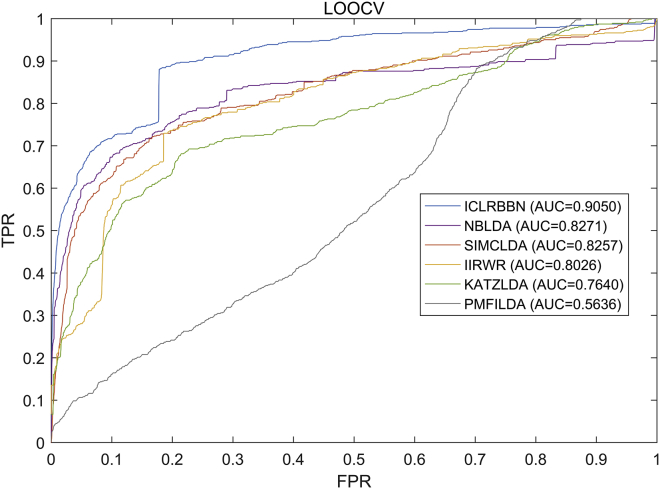
In order to better demonstrate the superior performance of ICLRBBN, we compared it with 6 state-of-the-art methods, including NBLDA,¹⁵ IIRWR,¹⁶ SIMCLDA,¹⁷ PMFILDA,¹⁸ KATZLDA,¹⁹ and LRLSLDA,²⁰ based on the same two datasets obtained above. As a result, the comparative experiment results under the LOOCV framework and the 5-fold CV framework are illustrated in Figures 3 and 4 and Table 2. As shown in Figure 3, we found that ICLRBBN achieved the optimal reliable AUC of 0.9510 in LOOCV based on dataset DS1, which considerably outperformed the AUCs of other methods (NBLDA: 0.8845; IIRWR: 0.8745; PMFILDA: 0.8346; KATZLDA: 0.8257; and LRLSLDA: 0.7472). As shown in Table 2, ICLRBBN achieved the optimal mean AUC of 0.9043 on dataset DS1 in 5-fold CV, which was still far superior to the other five methods (PMFILDA: 0.8337; IIRWR:0.8082; KATZLDA: 0.7994; LRLSLDA: 0.7154; and NBLDA:0.5547). Moreover, the results of multiple metrics including the Area Under the Precision-Recall curve (AUPR), F1 and Precision also demonstrated the superior performance of ICLRBBN. As shown in Figure 4, on dataset DS2, ICLRBBN also performed much better than other methods, with a reliable AUC of 0.9050 (NBLDA: 0.8271; SIMCLDA: 0.8257; IIRWR: 0.8026; KATZLDA: 0.7640; and PMFILDA: 0.5636).

Figure 3.

ROC curves and AUCs achieved by ICLRBBN, NBLDA, IIRWR, PMFILDA, KATZLDA, and LRLSLDA under the framework of LOOCV based on DS1

Figure 4.

ROC curves and AUCs achieved by ICLRBBN, NBLDA, SIMCLDA, IIRWR, KATZLDA, and PMFILDA under the framework of LOOCV based on DS2

Table 2.

Performance of ICLRBBN, PMFILDA, IIRWR, KATZLDA, LRLSLDA and NBLDA under the framework of 5-fold CV

Metrics and methods	ICLRBBN	PMFILDA	IIRWR	KATZLDA	LRLSLDA	NBLDA
AUC	0.9043	0.8337	0.8082	0. 7994	0.7154	0.5547
AUPR	0.1355	0.0641	0.0473	0.0868	0.0822	0.1807
F1	0.0016	0.0009	0.0007	0.0013	0.0010	0.0013
PRE	0.1268	0.0660	0.0483	0.0764	0.0742	0.1816

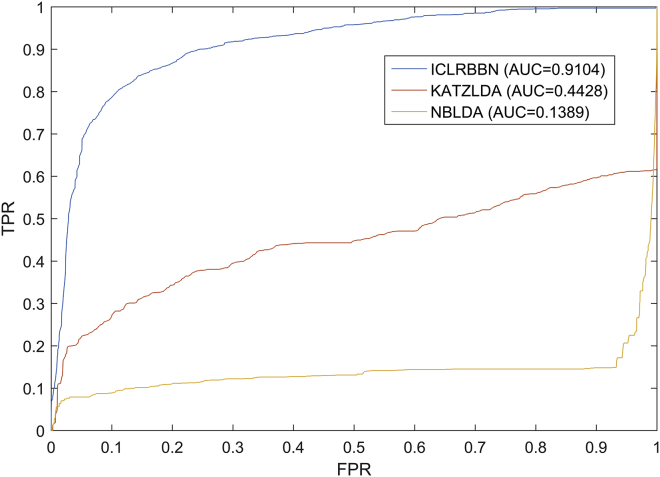
Moreover, in order to evaluate the performance of ICLRBBN in predicting lncRNAs related to new diseases, we further compared it with competing methods under the framework of leave-one-out verification. During experiments, for any disease d_i, when calculating the association scores between it and each lncRNA, we excluded all known associations of d_i and only relied on the remaining known associations for prediction. As illustrated in Figure 5, ICLRBBN still achieved a reliable AUC of 0.9104 for new disease-related lncRNA prediction, which considerably outperformed AUCs achieved by KATZLDA and NBLDA. That is to say, ICLRBBN had much better performance on prediction of new disease-related lncRNAs. Overall, the performance of ICLRBBN was significantly better than all these methods.

Figure 5.

The performance of ICLRBBN, KATZLDA and NBLDA on prediction of new disease-related lncRNAs

Case study

We selected two important cancers, breast cancer and osteosarcoma, for case studies on the dataset DS1 to further evaluate the prediction performance of ICLRBBN. During simulation, all known associations in the dataset were treated as training sets. In addition, for any given disease, all lncRNAs that have no known association with the disease were considered candidate-related lncRNAs for the disease. Then, according to the correlation probability score calculated by ICLRBBN, all candidate lncRNAs for the given disease were ranked. As a result, we list the top 15 candidate lncRNAs and some relevant evidence found in the PubMed literature.

Breast cancer is a malignant tumor developed from the epithelial tissue cells of the breast. Its signs include breast lumps, changes in breast shape, nipple depression, nipple discharge, etc. Breast cancer is the most common malignant tumor in women, which seriously threatens the health of women worldwide.²¹ However, breast cancer is a very heterogeneous disease; thus, its pathogenesis is still unclear, and the treatment is still incomplete. In recent years, more and more studies have demonstrated that lncRNAs are involved in the biological process of breast cancer’s generation and development.²² Therefore, we implemented ICLRBBN to predict lncRNAs associated with breast cancer. As a result, as illustrated in Table 3 below, 8 of the top 10 candidate lncRNAs related to breast cancer predicted by ICLRBBN have been experimentally confirmed recently, while 13 of the top 15 candidate lncRNAs have been confirmed. For instance, Shi et al.²³ utilized western blot to discover that HULC is highly expressed in triple-negative breast cancer (TNBC) tissues and is closely related to the poor prognosis of TNBC patients. Through a series of experiments in vivo and in vitro, it was found that the expression of HOTTIP was significantly upregulated in breast cancer cell lines, and HOTTIP could participate in breast cancer cell proliferation, migration, and apoptosis processes by regulating HOXA11 to some extent.²⁴ It was proved that BANCR was overexpressed in breast cancer cell lines, and the proliferation, invasion, and migration ability of breast cancer cells could be reduced by BANCR knockdown.^25,26

Table 3.

The top 15 potential breast cancer-related lncRNAs predicted by ICLRBBN and relevant evidence for these predicted associations

Rank	lncRNA	Evidence	Expression pattern
1	HOTTIP	29415429	upregulated
2	BANCR	29565494, 29805676	upregulated
3	HULC	27986124	upregulated
4	AFAP1-AS1	29439313, 29974352	upregulated
5	MIAT	29100300, 29345338, 29792859	upregulated
6	DRAIC	25288503	regulation
7	HNF1A-AS1	unconfirmed	unconfirmed
8	PCAT1	28989584	upregulated
9	PCAT29	unconfirmed	unconfirmed
10	TUSC7	23558749	differential expression
11	CASC2	29523222	downregulated
12	CRNDE	28469804	upregulated
13	PTENP1	29085464, 29212574	downregulated
14	TINCR	29614984	upregulated
15	HIF1A-AS1	26339353	upregulated

Osteosarcoma is the most common type of bone malignancy, usually occurring during adolescence. Although chemotherapy can greatly improve the survival rate of patients with osteosarcoma, about 40% of patients will experience tumor recurrence and tumor metastasis.²⁷ Hence, it is particularly important to thoroughly study the pathogenesis of osteosarcoma so as to explore more effective treatment strategies. As a result, as illustrated in Table 4, 9 of the top 10 candidate lncRNAs related to osteosarcoma predicted by ICLRBBN have been confirmed by recent experiments, while 13 of the top 15 candidate lncRNAs related to osteosarcoma have been confirmed. For example, it was found that the expression level of GAS5 was significantly reduced in osteosarcoma tissue cells and GAS5 could act as an inhibitor of osteosarcoma, which can inhibit the growth and migration of osteosarcoma by sponging miR-203a or regulating miR-22.^28,29 Ruan et al.³⁰ adopted Kaplan-Meier survival analysis and log rank testing to demonstrated that the expression of CCAT2 in osteosarcoma tissue was significantly increased compared to normal bone tissues and related to the TNM stage of tumors in osteosarcoma patients. Some studies have indicated that NEAT1 is an oncogene, and its overexpression will downregulate the osteosarcoma inhibitor miR-34c and enhance cisplatin (DDP)-based chemotherapy resistance.³¹

Table 4.

The top 15 potential osteosarcoma-related lncRNAs predicted by ICLRBBN and relevant evidence for these predicted associations

Rank	lncRNA	Evidence	Expression pattern
1	GAS5	29414815, 28519068	downregulated
2	PVT1	28602700	upregulated
3	NEAT1	28295289, 29654165	upregulated
4	SPRY4-IT1	28078006	upregulated
5	CCAT1	28549102	upregulated
6	CCAT2	29863240	upregulated
7	XIST	29384226, 28409547, 28682435, 29254174	upregulated
8	PANDAR	28011477	upregulated
9	AFAP1-AS1	31002124	upregulated
10	LINC-ROR	unconfirmed	unconfirmed
11	BCYRN1	unconfirmed	unconfirmed
12	SOX2-OT	28960757	upregulated
13	MIAT	32196573	downregulated
14	PCAT1	29430187	upregulated
15	ATB	28469952	upregulated

Discussion

In recent years, it has become increasingly clear that lncRNAs are involved in various biological processes in the human body and have an inseparable connection with many major diseases. The identification of potential lncRNA-disease association pairs has become a hot research topic in bioinformatics, which can deepen people’s understanding of the pathogenesis of various diseases at the molecular level and promote the research progress of treatment and prognosis strategies for complex diseases.

In this article, we developed a novel prediction model called ICLRBBN to infer potential lncRNA-disease associations. First, we designed an internal confidence collaborative filtering recommendation algorithm by introducing two confidence factors, which solved the problem that the known lncRNA-disease association information is too sparse and reduced the dependence of our model on the known association information. Second, by combining the radial basis function network with the information of lncRNAs and diseases and assigning biological significance to each node in the radial basis function network, we constructed a unique local radial basis function network, based on which we could predict the association probabilities between lncRNAs and the diseases according to the characteristics of lncRNAs and the local information of diseases. In addition, various experiments have been done, and experimental results have demonstrated the reliability and superiority of the prediction performance of ICLRBBN as well. Meanwhile, a web server that implements the method of ICLRBBN is available at http://leelab2997.cn/.

Of course, there are still certain limitations in ICLRBBN that need to be improved and optimized in future work. For instance, ICLRBBN still has a certain dependence on known lncRNA-disease associations. However, we believe that integrating a variety of biological indicators may solve this problem to a great extent and can further improve the prediction performance of the model to make it better applicable to the case of sparse known associations. Therefore, this problem will be the focus of discussion and study in the future.

Materials and methods

We first downloaded two different datasets of known lncRNA-disease associations from two versions of the lncRNADisease database (http://www.cuilab.cn/lncrnadisease).¹⁴ After removing non-human data and redundant association records, we finally obtain a dataset containing 1,695 distinct experimentally verified human lncRNA-disease associations between 314 diseases and 828 lncRNAs, and a dataset containing 621 distinct lncRNA-disease associations between 226 diseases and 285 lncRNAs. For convenience, we denote these two datasets as DS₁ and DS₂, respectively. Next, for any given dataset of known lncRNA-disease associations, we further converted it into an original incidence matrix A, where A(i,j) = 1 if and only if there is a known association between the i-th disease and the j-th lncRNA; otherwise A(i,j) = 0. In addition, for simplicity, we defined N_D and N_L as the number of diseases and the number of lncRNAs in the given dataset, respectively.

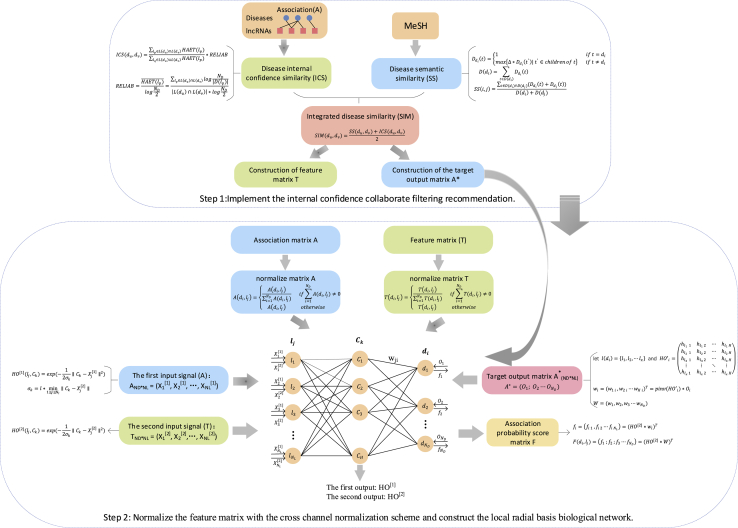
The flow chart of ICLRBBN is illustrated in Figure 6. In ICLRBBN, based on known lncRNA-disease associations, an original incidence matrix A was obtained first. To overcome the effect of limited known lncRNA-disease associations, a novel internal confidence-based collaborative filtering recommendation algorithm was designed to mine potential associations between lncRNAs and diseases without known related lncRNAs, and thus a new target output matrix A∗ and a new feature matrix T were constructed based on the original incidence matrix A. Finally, a novel three-layered local radial basis biological network was designed to infer potential lncRNA-disease associations.

Figure 6.

The flowchart of ICLRBBN

Internal confidence-based collaborative filtering recommendation algorithm

Considering that known lncRNA-disease associations are quite limited, the association matrix A was very sparse. Hence, to make ICLRBBN applicable to detect potential associations between lncRNAs and new diseases (i.e., diseases without any known related lncRNAs), an internal confidence-based collaborative filtering recommendation algorithm was proposed first to excavate potential indirect features between lncRNAs and diseases. As shown below, the recommendation algorithm consists of three major parts.

Part 1: calculation of similarities between diseases

Internal confidence-based similarity for diseases

The concept of internal confidence and two factors of internal confidence, including reliability and heat, were introduced first to measure the similarities between diseases. For any given two different diseases $d_u$ and $d_v$, let $L\left(d_u\right)$ and $L\left(d_v\right)$ represent the two sets of all lncRNAs with known associations with $d_u$ and $d_v$, respectively, and |$L\left(d_u\right)$| denote the number of elements in $L\left(d_u\right)$. We define two different diseases as “close friends” if and only if these two diseases have known associations with at least one common lncRNA. Based on the concept of close friends, it is reasonable to assume that: (1) the larger the number of elements in $L\left(d_u\right)\cap L\left(d_v\right)$, the more similar these two different diseases $d_u$ and $d_v$ will be; and (2) supposing that there is $L\left(d_u\right)\cap L\left(d_v\right)$ = $L\left(d_u\right)\cap L\left(d_w\right)$, then the similarity between $d_u$ and $d_v$ will be higher than the similarity between $d_u$ and $d_w$, if the number of elements in $L\left(d_v\right)$ is less than that in $L\left(d_w\right)$. Thereafter, based on the above two assumptions, we can calculate the similarity between $d_u$ and $d_v$ as follows:

$$IC{S}^1\left(d_u,d_v\right)=\frac{\left|L\left(d_u\right)\cap L\left(d_v\right)\right|}{\left|L\left(d_u\right)\cup L\left(d_v\right)\right|}.$$ (Equation 1)

Next, for a given lncRNA $l_k$, let $D\left(l_k\right)$ denote the set of all diseases that have known associations with $l_k$. Then we define $HEAT\left(l_k\right)$ as the heat score of lncRNA $l_k$, which can be obtained as follows:

$$HEAT\left(l_k\right)=\log \frac{N_D}{\left|D\left(l_k\right)\right|}.$$ (Equation 2)

According to Equation 2, it is obvious that the lncRNAs with higher heat scores will have known associations with fewer diseases. Moreover, based on the concept of heat score for lncRNAs, for any two given lncRNAs $l_p$ and $l_q$, where $l_p\in$ $L\left(d_u\right)\cap L\left(d_v\right)$ and $l_q\in$ $L\left(d_u\right)\cup L\left(d_v\right)$, it is reasonable that Equation 1 can be modified as follows:

$$ICS\left(d_u,d_v\right)=\frac{{\sum }_{l_p\in L\left(d_u\right)\cap L\left(d_v\right)}HAET\left(l_p\right)}{{\sum }_{l_q\in L\left(d_u\right)\cup L\left(d_v\right)}HAET\left(l_q\right)}.$$ (Equation 3)

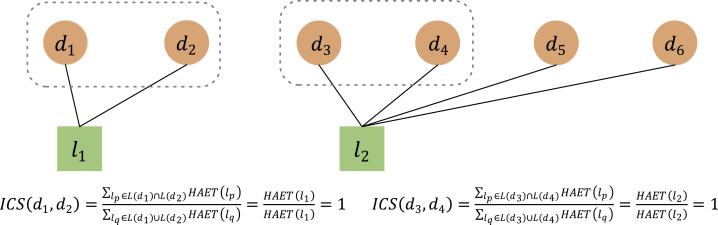
In addition, taking the situation in Figure 7 as an example, if the similarity calculation is performed according to Equations 2 and 3, the similarity between $d_1$ and $d_2$ and the similarity between $d_3$ and $d_4$ will both be 1. However, the lncRNA $l_1$ is associated with two different diseases, while the lncRNA $l_2$ is associated with four different diseases. Obviously, it is reasonable to assume that the similarity between $d_1$ and $d_2$ shall be higher than that between $d_3$ and $d_4$. Hence, we further introduced another confidence factor called RELIAB for different lncRNAs, which represents the average heat reliability of those lncRNAs with known association with both $d_u$ and $d_v$ and can be obtained as follows:

$$RELIAB=\frac{\overline{HEAT\left(l_p\right)}}{\log \frac{N_D}{2}}=\frac{{\sum }_{l_p\in L\left(d_u\right)\cap L\left(d_v\right)}\log \frac{N_D}{\left|D\left(l_p\right)\right|}}{\left|L\left(d_u\right)\cap L\left(d_v\right)\right|\ast \log \frac{N_D}{2}}.$$ (Equation 4)

Here, $\overline{HEAT\left(l_p\right)}$ denotes the average heat score of those lncRNAs with known association with both $d_u$ and $d_v$.

Figure 7.

The example of similarity calculation

According to Equation 4, the final internal confidence-based similarity between any two given diseases $d_u$ and $d_v$ can be calculated as follows:

$$ICS\left(d_u,d_v\right)=\frac{{\sum }_{l_p\in L\left(d_u\right)\cap L\left(d_v\right)}HEAT\left(l_p\right)}{{\sum }_{l_q\in L\left(d_u\right)\cup L\left(d_v\right)}HEAT\left(l_p\right)}\ast RELIAB.$$ (Equation 5)

Semantic similarity for diseases

For each disease in a given dataset, we downloaded its corresponding MeSH descriptor from the MeSH database of the National Medical Library (https://www.nlm.nih.gov/). According to the strict classification information provided by the MeSH descriptor and the concept of directed acyclic graph (DAG) between different diseases, we can obtain the semantic similarity³² between diseases as follows.

First, any disease $d_i$ can be represented in the form of a graph:$DAG\left(d_i\right)=\left(d_i,D\left(d_i\right),E\left(d_i\right)\right)$. Among them, $D\left(d_i\right)$ represents a set of nodes composed of $d_i$ itself and its ancestor nodes, and $E\left(d_i\right)$ represents the corresponding set of directed edges from the parent nodes to the child nodes. Thereafter, for any node t in the graph $DAG\left(d_i\right)$, its semantic contribution to the disease $d_i$ can be calculated as follows:

$$D_{d_i}\left(t\right)=\{\begin{array}{l}1ift=d_i\\ max\left\{\Delta \ast D_{d_i}\left(t^{\prime }\right)|t^{\prime }\in childrenoft\right\}ift\ne d_i\end{array}.$$ (Equation 6)

where Δ is a semantic contribution factor whose value is between 0 and 1, and previous experimental results have indicated that its value is set to 0.5 optimal.³²

Furthermore, for any disease $d_i$, its semantic value can be calculated as follows:

$$D\left(d_i\right)=\sum _{t\in D\left(d_i\right)}{D}_{d_i}\left(t\right).$$ (Equation 7)

Finally, based on the assumption that two diseases that share more structure in the DAG tend to have higher semantic similarity, the semantic similarity of any two different diseases $d_i$ and $d_j$ can be calculated as follows:

$$SS\left(i,j\right)=\frac{{\sum }_{t\in D\left(d_i\right)\cap D\left(d_j\right)}\left(D_{d_i}\left(t\right)+D_{d_j}\left(t\right)\right)}{D\left(d_i\right)+D\left(d_j\right)}.$$ (Equation 8)

Integrated similarity for diseases

According to Equations 5 and 8, for any two given diseases $d_u$ and $d_v$, we can obtain the integrated similarity between them as follows:

$$SIM\left(d_u,d_v\right)=\frac{SS\left(d_u,d_v\right)+ICS\left(d_u,d_v\right)}{2}.$$ (Equation 9)

Part 2: construction of the feature matrix T

According to the integrated disease similarity matrix SIM obtained above, for any given disease $d_u$, we can obtain “the circle of K-closest friends” of $d_u$, that is, a set of K diseases with the highest integrated similarities to $d_u$. Let $Chum\left(d_u\right)$ represent the “circle of K-closest friends” of $d_u$; then for any given lncRNA $l_p$, we can calculate a possible score of association between $d_u$ and $l_p$, even if there is no known association between $d_u$ and $l_p$. Thereafter, we can obtain a feature matrix T as follows:

$$T\left(d_u,l_p\right)=\{\begin{array}{l}1:if{d}_{u}isknowntobeassociatedwith{l}_p\\ \sum _{d_v\in Chum\left(d_u\right)}SIM\left(d_u,d_v\right)\ast \frac{SIM\left(d_u,d_v\right)}{{\sum }_{d_v\in Chum\left(d_u\right)}SIM\left(d_u,d_v\right)}\ast c_{vp}:otherwise\end{array}.$$ (Equation 10)

Here, $c_{vp}$ denotes the score of known association between the disease $d_v$ and lncRNA $l_p$, where $c_{vp}$ = 1 if and only if there is known association between $d_v$ and $l_p$. Otherwise, $c_{vp}$ = 0.

Part 3: construction of the target output matrix A∗

For new diseases, since there are no known association between these diseases and lncRNAs, we cannot extract any useful information about these new diseases from the original incidence matrix A to make effective predictions. Therefore, for any given new disease $d_u$, we utilize the “circle of K-closest friends” of $d_u$ to recommend the most likely associations for it first and then construct a new target output matrix A∗ from the original incidence matrix A according to the following steps:

• Step 1: let A∗ = A, and then for any given new disease $d_u$, we obtain a new association score vector ${\mathit{C}}_{{\mathit{d}}_{\mathit{u}}}^1$ based on the “circle of K-closest friends” of $d_u$ as follows:

$${\mathit{C}}_{{\mathit{d}}_{\mathit{u}}}^1=\sum _{d_v\in Chum\left(d_u\right)}A\left(d_v,:\right).$$ (Equation 11)

• Step 2: let ${\mathit{C}}_{{\mathit{d}}_{\mathit{u}}}^1=\left(c_{d_u,l_1},c_{d_u,l_2},c_{d_u,l_3}\cdots c_{d_u,l_t}\cdots c_{d_u,l_{N_L}}\right)$, and $T^1\left(d_u\right)=\left\{l_k|c_{d_u,l_k}=\text{maximum}\left\{c_{d_u,l_1},c_{d_u,l_2},c_{d_u,l_3}\cdots c_{d_u,l_t}\cdots c_{d_u,l_{N_L}}\right\}\wedge c_{d_u,l_k}\ne 0\right\}$. If the set is not empty (i.e., $T^1\left(d_u\right)\ne \varnothing$), then these lncRNAs in $T^1\left(d_u\right)$will be recommended to $d_u$ as the most likely candidates.

• Step 3: if $T^1\left(d_u\right)$ = $\varnothing$, then we will traverse each of these lncRNAs in the “circle of K-closest friends” of $d_u$ and further obtain another new association score vector ${\mathit{C}}_{{\mathit{d}}_{\mathit{u}}}^2$ based on the “circle of K-closest friends” of each lncRNA in the “circle of K-closest friends” of $d_u$ as follows:

$${\mathit{C}}_{{\mathit{d}}_{\mathit{u}}}^2=\sum _{\begin{array}{l}{d}_v\in Chum\left(d_u\right)\hfill \\ d_p\in Chum\left(d_v\right)\hfill \end{array}}A\left(d_p,:\right).$$ (Equation 12)

Similar to above step 2, let $T^2\left(d_u\right)$ denote the set of lncRNAs with the maximum score in ${\mathit{C}}_{{\mathit{d}}_{\mathit{u}}}^2$, and at the same time, the scores of these lncRNAs are greater than 0. Then if $T^2\left(d_u\right)\ne \varnothing$, all the lncRNAs in $T^2\left(d_u\right)$ will be recommended to $d_u$ as the most likely candidates as well.

Hence, according to the above steps, we can obtain a new matrix A∗ from the original incidence matrix A as follows:

$$A^{\ast }\left(d_u,l_k\right)=\{\begin{array}{l}1:ifA\left(d_u,l_k\right)=1\hfill \\ 1:elseif{l}_k\in T^1\left(d_u\right)and{T}^1\left(d_u\right)\ne \varnothing \hfill \\ 1:elseif{l}_k\in T^2\left(d_u\right)and{T}^2\left(d_u\right)\ne \varnothing \hfill \\ 0:Otherwise\hfill \end{array}.$$ (Equation 13)

Construction of the local radial basis function network

The radial basis function network (RBF network) is an artificial neural network utilizing radial basis functions as activation functions. It was first proposed by Broomhead and Lowe in 1988.³³ At present, the radial basis function network has been widely used in many fields, such as time series prediction, system control, and classification problems. Inspired by the superior performance of the radial basis function network, we designed a novel local radial basis function network for lncRNA-disease association prediction.

As illustrated in Figure 6, the local radial basis function network is divided into three layers: the input layer, the hidden layer, and the output layer. Among them, there are $N_L$ nodes in the input layer, representing $N_L$ lncRNAs, and each node will accept a $N_D$-dimensional vector (i.e., the eigenvector between the lncRNA and diseases) as the input. The hidden layer consists of H nodes corresponding to H distinct feature vectors in the input matrix. In addition, the output layer consists of $N_D$ nodes representing $N_D$ diseases, and the output of each node in the output layer is an $N_L$-dimensional vector, which consists of probabilities of $N_L$ associations between this disease and $N_L$ lncRNAs. In ICLRBBN, the hidden layer adopts the nonlinear optimization strategy, which maps the low-dimensional eigenvectors of the input layer to the high-dimensional space through the nonlinear function. Afterward, in this high-dimensional space, the output layer adopts the linear optimization strategy, which makes linear weighted adjustment to the hidden layer’s output information to approximate the target output.

In addition, the local radial basis function network is input twice, where the original incidence matrix A will be regarded as the initial eigenmatrix to be used as the input matrix for the first input of the local radial basis biological network, and the feature matrix T obtained in Equation 10 will be utilized for the second input of the local radial basis biological network. Furthermore, the target output matrix A∗ will be adopted as the first output target matrix of the local radial basis biological network, while the second output matrix of the local radial basis biological network will be regarded as the predicted lncRNA-disease association probability score matrix.

Particularly, before adopting them as the inputs of the local radial basis biological network, we will normalize these two feature matrices A and T with the cross-channel normalization scheme as follows:

$$A\left(d_i,l_j\right)=\{\begin{array}{l}\frac{A\left(d_i,l_j\right)}{{\sum }_{i=1}^{N_D}A\left(d_i,l_j\right)}if\sum _{i=1}^{N_D}A\left(d_i,l_j\right)\ne 0\\ A\left(d_i,l_j\right)otherwise\end{array}.$$ (Equation 14)

$$T\left(d_i,l_j\right)=\{\begin{array}{l}\frac{T\left(d_i,l_j\right)}{{\sum }_{i=1}^{N_D}T\left(d_i,l_j\right)}if\sum _{i=1}^{N_D}T\left(d_i,l_j\right)\ne 0\hfill \\ T\left(d_i,l_j\right)otherwise\hfill \end{array}.$$ (Equation 15)

Based on above descriptions, the prediction process based on the newly constructed local radial basis function network can be mainly divided into the following steps.

Step 1: determining the number of nodes for the hidden layer

The normalized incidence matrix A is a $N_D$∗$N_L$-dimensional matrix, which will be used as the initial input matrix of the local radial basis biological network. In the local radial basis biological network, these $N_L$ nodes in the input layer represent $N_L$ lncRNAs, and each node will accept a corresponding $N_D$-dimensional feature vector as the input. In addition, supposing that after removing duplicated columns in the normalized incidence matrix A, a unique $N_D$∗H-dimensional feature matrix containing H different $N_D$-dimensional feature vectors will be obtained; then we will assign H nodes to form the hidden layer of the local radial basis biological network, which correspond to these H different $N_D$-dimensional feature vectors separately.

Step 2: calculating the first output of the hidden layer

After determining the number of nodes for the hidden layer, the output matrix of the hidden layer can be calculated. The role of the hidden layer is to take kernel function as the basis function and map each feature vector of the input layer from low dimension to high dimension to make it linearly separable. In ICLRBBN, we adopt the Gaussian kernel function as the basis function, and for each node in the hidden layer, its output will be a $N_L$-dimensional vector. Let the output vector of the k-th node in the hidden layer be $h_k^{\left[1\right]}={\left(h_{k1},h_{k2},\cdots ,h_{k{N}_L}\right)}^T$; then each element $h_{kj}$ in $h_k^{\left[1\right]}$ can be calculated according to the Euclidean distance as follows:

$$h_{kj}=exp\left(-\frac{1}{2{\sigma }_k}{\Vert C_k-X_j^{\left[1\right]}\Vert }^2\right).$$ (Equation 16)

Here, $C_k$ represents the center of the k-th basis function (i.e., $N_D$-dimensional feature vector corresponding to the k-th node in the hidden layer). $X_j^{\left[1\right]}$ represents the feature vector input by the j-th node in the input layer for the first time. Additionally, σ is the bandwidth parameter of the basis function, which controls the radial range of the basis function. ${\sigma }_k$ represents the bandwidth of the k-th basis function, and its value can be obtained as follows:

$${\sigma }_k=l\ast \underset{1\le j\le N_l}{\min }\Vert C_k-X_j^{\left[2\right]}\Vert .$$ (Equation 17)

Here, $X_j^{\left[2\right]}$ represents the j-th column of the eigenmatrix T, and $l$ is an overlap coefficient factor with value ranging from 0 to 1. Obviously, the larger the value of $l$ is, the more the scope of each basis function will overlap.

According to above Equations 16 and 17, for each node in the hidden layer, an $N_L$-dimensional output vector can be obtained. Thereafter, considering all the nodes of the hidden layer, we will obtain an output matrix $H{O}^{\left[1\right]}$ as follows:

$$H{O}^{\left[1\right]}\left(l_j,C_k\right)=exp\left(-\frac{1}{2{\sigma }_k}{\Vert C_k-X_j^{\left[1\right]}\Vert }^2\right).$$ (Equation 18)

Step 3: obtaining the weight matrix W

From the above steps, we obtained the N_L∗H-dimensional output matrix $H{O}^{\left[1\right]}$of the hidden layer. For convenience, let $H{O}^{\left[1\right]}=\left(\begin{array}{llll}{h}_{11}\hfill & h_{12}\hfill & \cdots \hfill & h_{1H}\hfill \\ h_{21}\hfill & h_{22}\hfill & \cdots \hfill & h_{2H}\hfill \\ ⋮\hfill & ⋮\hfill & \ddots \hfill & ⋮\hfill \\ h_{N_{L}1}\hfill & h_{N_{L}2}\hfill & \cdots \hfill & h_{N_{L}H}\hfill \end{array}\right)$. It is obvious that the j-th row of $H{O}^{\left[1\right]}$ represents the output vector of the j-th node in the hidden layer. In addition, let $L\left(d_i\right)=\left\{l_1,l_2,\cdots l_x\right\}$. Then, for any given disease $d_i$, a system of equations can be locally generated according to the lncRNAs that are known to be related to it as follows:

$$\left(\begin{array}{llll}{h}_{l_{1}1}\hfill & h_{l_{1}2}\hfill & \cdots \hfill & h_{l_{1}H}\hfill \\ h_{l_{2}1}\hfill & h_{l_{2}2}\hfill & \cdots \hfill & h_{l_{2}H}\hfill \\ h_{l_{3}1}\hfill & h_{l_{3}2}\hfill & \cdots \hfill & h_{l_{3}H}\hfill \\ ⋮\hfill & ⋮\hfill & \ddots \hfill & ⋮\hfill \\ h_{l_{x}1}\hfill & h_{l_{x}2}\hfill & \cdots \hfill & h_{l_{x}H}\hfill \end{array}\right)\ast \left(\begin{array}{l}{w}_{1i}\hfill \\ w_{2i}\hfill \\ ⋮\hfill \\ w_{Hi}\hfill \end{array}\right)=\left(\begin{array}{l}{A}^{\ast }\left(i,l_1\right)\hfill \\ A^{\ast }\left(i,l_2\right)\hfill \\ A^{\ast }\left(i,l_3\right)\hfill \\ ⋮\hfill \\ A^{\ast }\left(i,l_x\right)\hfill \end{array}\right).$$ (Equation 19)

For convenience, Equation 19 can be rewritten as follows:

$$HO{\text{'}}_i\ast w_i=O_i.$$ (Equation 20)

In Equation 20, the right side in the system of equations is a $l_x$ dimensional column vector. Therefore, we can solve the system of equations based on the pseudo-inverse to obtain the weight vector as follows:

$$w_i={\left(w_{1i},w_{2i}\cdots w_{Hi}\right)}^T=pinv\left(HO{\text{'}}_i\right)\ast O_i.$$ (Equation 21)

Here, pinv represents the function to solve the pseudoinverse.

According to Equation 21, for any given disease $d_i$, it is easy to see that the corresponding weight vector $w_i$ can be calculated out. Moreover, considering the weight vectors of all diseases, then it is obvious that we can obtain a weight matrix W as follows:

$$W=\left(w_1,w_2,w_3\cdots w_{N_D}\right)=\left(\begin{array}{llll}{w}_{11}\hfill & w_{12}\hfill & \cdots \hfill & w_{1N_D}\hfill \\ w_{21}\hfill & w_{22}\hfill & \cdots \hfill & w_{2N_D}\hfill \\ ⋮\hfill & ⋮\hfill & \ddots \hfill & ⋮\hfill \\ w_{H1}\hfill & w_{H2}\hfill & \cdots \hfill & w_{H{N}_D}\hfill \end{array}\right).$$ (Equation 22)

Step 4: calculating the second output of the hidden layer

In ICLRBBN, the feature matrix T obtained by the internal confidence-based collaborative filtering recommendation algorithm will be used as the input matrix for the second input of the local radial basis biological network. Similar to the first input, the $N_L$ nodes in the input layer will accept the feature vectors corresponding to the $N_L$ lncRNAs in the feature matrix as their inputs. For convenience, for any node k in the hidden layer, let the output vector of its second output be $h_k^{\left[2\right]}={\left(h_{k1}^{\prime },h_{k2}^{\prime },\cdots ,h_{k{N}_L}^{\prime }\right)}^T$. Then, considering all the nodes of the hidden layer, we will obtain another output matrix $H{O}^{\left[2\right]}$ as follows:

$$H{O}^{\left[2\right]}\left(l_j,C_k\right)=exp\left(-\frac{1}{2{\sigma }_k}{\Vert C_k-X_j^{\left[2\right]}\Vert }^2\right).$$ (Equation 23)

Step 5: calculating the output matrix of the output layer

Let l_j denote the j-th node in the input layer and$H{O}^{\left[2\right]}\left(j\right)$ denote the j-th row in the output matrix $H{O}^{\left[2\right]}$ of the hidden layer. It is obvious that $H{O}^{\left[2\right]}\left(j\right)$ represents the output vector of l_j in the hidden layer, which can be express as $\left(h_{j1},h_{j2},h_{j3}\cdots h_{jH}\right)$. Thereafter, for any given lncRNA $l_j$, we can obtain the association probabilities between $l_j$ and diseases as follows:

$$\left(f_{j1},f_{j2}\cdots f_{j{N}_D}\right)=\left(h_{j1},h_{j2}\cdots h_{jH}\right)\ast \left(\begin{array}{llll}{w}_{11}\hfill & w_{12}\hfill & \cdots \hfill & w_{1N_D}\hfill \\ w_{21}\hfill & w_{22}\hfill & \cdots \hfill & w_{2N_D}\hfill \\ ⋮\hfill & ⋮\hfill & \ddots \hfill & ⋮\hfill \\ w_{H1}\hfill & w_{H2}\hfill & \cdots \hfill & w_{H{N}_D}\hfill \end{array}\right).$$ (Equation 24)

Moreover, based on Equation 24, taking all lncRNAs into account, we can obtain a matrix F as follows:

$$F\left(d_i,l_j\right)={\left(H{O}^{\left[2\right]}\ast W\right)}^T=\left(\begin{array}{llll}{f}_{11}\hfill & f_{12}\hfill & \cdots \hfill & f_{1N_L}\hfill \\ f_{21}\hfill & f_{22}\hfill & \cdots \hfill & f_{2N_L}\hfill \\ f_{31}\hfill & f_{32}\hfill & \cdots \hfill & f_{3N_L}\hfill \\ ⋮\hfill & ⋮\hfill & \ddots \hfill & ⋮\hfill \\ f_{N_{D}1}\hfill & f_{N_{D}2}\hfill & \cdots \hfill & f_{N_D{N}_L}\hfill \end{array}\right).$$ (Equation 25)

Here, the matrix F is the final association probability matrix between lncRNAs and diseases, and $F\left(d_i,l_j\right)$ represents the association probability score between the i-th disease$d_i$ and the j-th lncRNA $l_j$.