Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2020 Dec 28;6(1):55–64. doi: 10.1021/acsomega.0c01199

Density Functional Study of Metal-to-Ligand Charge Transfer and Hole-Hopping in Ruthenium(II) Complexes with Alkyl-Substituted Bipyridine Ligands

Salmahaminati †,§, Minori Abe †,*, Indra Purnama ‡,∥,#, Jacob Yan Mulyana ‡,⊥, Masahiko Hada †
PMCID: PMC7807472  PMID: 33458459

Abstract

graphic file with name ao0c01199_0007.jpg

In this study, we present a density functional study of four ruthenium complexes by means of UV–visible spectroscopy and Marcus theory. These molecules, [RuII(bipyP)(bipy)2] (P1), [RuII(bipyP)(dmb)2] (P2), [RuII(bipyP)(dtbb)2] (P3), and [RuII(bipyP)(dnb)2] (P4), where bipyP = 2,2′-bipyridine-4,4′-diphosphonic acid, bipy = 2,2′-bipyridine, dmb = 4,4′-dimethyl-2,2′-bipyridine, dtbb = 4,4′-di-tert-butyl-2,2′-bipyridine, and dnb = 4,4′-dinonyl-2,2′-bipyridine, are photosensitizers for applications in dye-sensitized photo-electrochemical cells (DSPECs). Because of the undetermined P4 conformation in the experiment, we modeled three P4 conformers with straight (P4-straight) and bent nonyl chains (P4-bend1 and bend2). UV–vis absorption spectra by time-dependent density functional theory showed intense metal-to-ligand charge transfer to anchor bipyridine ligands (MLCT-anchoring) at 445–460 nm, which accurately reproduce experimental data. The largest light-harvesting efficiency of the MLCT-anchoring state was observed in the P4-bend1 conformer, which has the lowest P4 energy. This may relate to greater electron injection in the P4 and supports experimental results of dye-only systems (do-DSPEC). The calculated charge transfer rates agree well with the experimental trend. The largest rate was obtained for P2, which was attributed to the expansion of the highest-occupied molecular orbital toward the ancillary bipy ligands and also to the short distances between dyes on the TiO2 surface. These results also support experimental results for P2, which was the best compound for lateral hole-hopping in a sacrificial agent-containing system (sa-DSPEC).

Introduction

Ruthenium or organic photosensitizers are promising compounds for dye-sensitized photo-electrochemical cell (DSPECs) because they absorb light in the visible spectrum and have sufficient excited-state potentials to inject electrons into the conduction band of TiO2.1−3 Additionally, they are capable of driving water oxidation in properly designed complexes4−7 and it is also possible without a water oxidation catalyst.2,3,8,9 New structures of ruthenium dyes have been investigated in dye-sensitized solar cells (DSSCs).10,11 In DSSCs, the excited-state potential of the dye is designed to be appropriate for electron injection. The presence of electron-donating substituents in the bipyridine (bipy) ancillary ligand generally shifts the excited-state potential to more negative values, resulting in faster electron injection.1 Our recent experimental study of DSPECs3 investigated four ruthenium polypyridyl dyes (P1, P2, P3, and P4). P2, P3, and P4 contain electron-donating substituents (methyl, t-butyl, and n-nonyl groups, respectively) in the bipy ancillary ligand, while P1 has no substituents. In our experiments, different solvents were used. For measuring the photocurrent, incident photon-to-current conversion efficiency (IPCE), and reorganization energy, buffered phosphate (pH = 7) in water was used, while methanol was used to solubilize the dyes for acquiring absorption and emission spectra. In the former case, the dyes were also attached to TiO2 nanoparticles.

Previously observed features of P1–P4 dyes were noteworthy.3 (i) In the dye-only system (do-DSPEC), the magnitude of photocurrent and hydrogen production was in the order P4 > P3 > P2 > P1, where that for P4 was approximately twice that of P1–P3 (Figure S1a). (ii) In the case where the electrolyte solution was loaded with ethylenediaminetetraacetic acid (EDTA) as a sacrificial agent (sa-DSPEC), the hydrogen production performance of P4 was now the lowest and P2 was the highest, in the following order P2 > P1 > P3 > P4 (Figure S1b). However, the photocurrents of all the dyes increased by a factor of 10 in the presence of EDTA (sa-DSPECs), relative to when it was absent (do-DSPECs) (Figure S1). This may indicate the following scenario depicted in Figure 1: (a) The RuII dye close to fluorine-doped tin oxide (FTO) absorbs the light, injects an electron to the TiO2 nanoparticle, and becomes RuIII. (b) The RuIII close to FTO becomes RuII via hole-hopping. (c) The hole-hopping continues toward the RuII where the EDTA sacrificial agent can be accessed. (d) The EDTA reduces RuIII and the regenerated RuII returns to (a). The hole percolation that occurs from the FTO side to the top of the film has been modeled previously.12 Under this hypothesis, the recombination rates1,12,13 of dye molecules following electron injection may not be dominant, rather the hole-hopping efficiency between two dyes may be more important for better IPCE in sa-DSPECs. This is consistent with experimental observation that by introducing the sacrificial agent, the dye with the highest performance changes from P4 to P2. (iii) With respect to the self-exchange of RuII–RuIII dyes on the TiO2 surface, the RuIII/RuII reorganization energies were obtained using temperature-dependent cyclic voltammetry based on the nonadiabatic Marcus theory. The experimental reorganization energy of P4 was the largest, which may be related to suppressed hole-hopping on TiO2 and lower IPCE performance of P4 in the case of sa-DSPEC.

Figure 1.

Figure 1

Open in a new tab

Schematic of photo-electrochemistry in the sa-DSPECs. Upon electron injection by the excited-state dye, hole-hopping occurs toward the semiconductor–solution interface, where the dye molecule interacts with EDTA.

The abovementioned features of P4 are surprising because the electron-donating strength of alkyl chains is considered to be saturated beyond four carbon atoms. Hence, we performed density functional theory (DFT)/time-dependent (TD)-DFT calculations to complement the experimental results and verify whether the subtle alkyl-chain variation of the ruthenium photosensitizers could fine-tune the electron injection capacity. DFT/TD-DFT calculations are frequently used to understand transition-metal complexes, and several previous reports have examined ligand effects on the photosensitization properties of Ru(II) complexes.14−18 Here, we focus on DFT calculations of light-harvesting efficiency (LHE) because the IPCE is proportional to LHE, as given by19

graphic file with name ao0c01199_m001.jpg 1

where ϕ is the charge injection quantum yield and η is the charge-collecting efficiency of the photoanode. We calculated LHE from oscillator strengths f(15) and analyzed LHEs for metal-to-ligand charge transfer (MLCT) in excited states to elucidate the high performance of the P4 dye in do-DSPECs. We also calculated the electronic coupling J and the reorganization energy λ to examine hole mobility, which can be applied to the experimental results of sa-DSPECs to discuss the best efficiency in P2.20−22

Theory of Hole-Hopping

The efficiency of hole-hopping depends on a number of factors, including the chemical structure of the dye,23 the nature of the attachment to the surface,24 dye loading,25,26 and the dielectric environment.27,28 One of the simplest methods to characterize hole transfer is the temperature-dependent cyclic voltammetry experiment based on nonadiabatic Marcus theory.29,30 The rate constant of the charge-transfer reaction is described using the following equation

graphic file with name ao0c01199_m002.jpg 2

where kB is Boltzmann’s constant, T is the temperature, h is Planck’s constant, J is the electronic coupling between two identical molecules, ΔG is the free energy of a hole-transfer reaction, which is zero for two identical molecules, and λ is the total reorganization energy. From eq 2, hole-hopping occurs more easily in systems with larger J and smaller λ. λ consists of two terms, λi and λo. λi is the reorganization energy from the inner sphere contribution that reflects the energy needed to adjust the intramolecular geometry. λo is the outer sphere energy contribution from the polarization of the medium.31 The total reorganization energy λ and λi may be calculated using the following equations.32

graphic file with name ao0c01199_m003.jpg 3
graphic file with name ao0c01199_m004.jpg 4

Here, E is the total electronic energy and G accounts for the geometry of the system. The subscripts “0” and “+” correspond to neutral (RuII) and cationic (RuIII) states, respectively. “med” refers to calculations incorporating the effect of the surrounding medium; here, water was considered using the polarizable continuum model (PCM). For λi, we performed the calculations in the gas phase. The static dielectric constant εst for the medium was used for the initial equilibrium states. In contrast, the optical dielectric constant εop was used in the nonequilibrium states at the instant of charge transfer.33 The abovementioned method using the PCM was previously proposed by Vaissier et al.32 and used for DSSCs.

Computational Details

The program Gaussian 0934 was used to perform DFT-D (G3DBJ) and time-dependent DFT (TD-DFT)35,36 calculations on complexes P1–P4. Solvent environmental effects were determined using the PCM.37 Geometry optimizations of the lowest singlet and triplet states, and 50 singlet–singlet transitions using TD-DFT, were calculated. Calculations were run using the B3LYP functional, with the Stuttgart-ECP basis set38,39 for Ru, the 6-31G* basis set40 for C, N, O, and P atoms, and the 6-31G** basis sets for H atoms.

For the calculation of electronic coupling J, we used a conventional perturbation method based on highest occupied molecular orbital (HOMO)–HOMO coupling because it reproduced the experimental trend of Γ in Ru dyes.32 The constrained DFT methods did not use Kohn–Sham orbitals and could be more elaborate;41−43 however, we could not use them because they were not available as distributed software. We obtained the electronic coupling J using a program provided by Dr. Y. Imamura, based on the molecular orbital integral files created in Gaussian. Because of the limitation of the program, we computed J as the HOMO–HOMO coupling of two neutral dyes (not as a neutral and cationic pair) in water, assuming that the HOMO of the cationic dye is similar to the neutral one.

The program GaussSum 3.044 was used to analyze transition contributions and extract electron density difference maps (EDDMs).45 The Avogadro 1.2.0 program46 was adopted to visualize molecules and their electronic state.

We use methanol as the solvent for absorption and emission spectra calculations and water for the ionization energy, reorganization energy, and electron coupling to reproduce the experimental conditions.

Results and Discussion

Molecular Structures of P1–P4

Figure 2a–c depicts the P1–P3 structures, their atomic labels, and their optimized geometries in the S0 electronic ground states, respectively. Although P1–P3 each has one conformation, P4 has many because of the nonyl chains. Here, we selected a straight conformation (P4-straight) and two bending conformations (P4-bend1 and P4-bend2) as examples and optimized their geometries with and without dispersion correction (GD3BJ),47,48 as shown in Figure 3. With the dispersion correction, the ordering of electronic and free energies was P4-bend1 < P4-straight < P4-bend2, while P4-straight was lower than P4-bend1 and P4-bend2 without the dispersion correction (Table S1). P4-bend1 exhibited a greatly folded alkyl–alkyl confirmation, which is similar to alkyl–alkyl contacts reported by Yang et al.49 We also compared the relative energies in second-order Møller–Plesset perturbation theory (MP2) for six geometries in Table S2, where the lowest was P4-bend1 optimized with dispersion. If we estimate each population of the three P4 models using Boltzmann’s distribution, the P4-bend1 is overwhelmingly dominant at approximately 1014 times larger than those of the others. However, in reality, greater numbers of conformations must be taken into account and the dispersion effect might be overestimated in the MP2 and GD3BJ calculations.49,50 Hence, in the following section, we calculated three P4 systems optimized with dispersion, in addition to the P4-bend1. Table S3a compiles the critical bond lengths and angles for P1–P4. Most of the geometrical structures around the Ru and bipyridine ligands were the same for the four dyes, except for the P4-bend1 structure. The largest differences were 0.4 and 0.5%, between P1 and P4-bend1 in Ru–N(anchoring) and Ru–N(ancillary) bond lengths, respectively. All the other differences were less than 0.3%.

Figure 2.

Figure 2

Open in a new tab

Molecular structures of P1–P3. (a) Anchoring, ancillary bipyridine, and Ru units are in blue, purple, and brown frames, respectively. (b) Atomic labels. (c) Density-functional-optimized geometries (c) of P1, P2, and P3.

Figure 3.

Figure 3

Open in a new tab

Molecular structures of (a) P4-bend1, (b) P4-bend2, and (c) P4-straight, without dispersion correction, and (d) P4-bend1, (e) P4-bend2, and (f) P4-straight, with dispersion correction.

Excited-State Properties

Figure 4a,b plots experimental absorption spectra and those calculated via scalar relativistic TD-DFT using Gaussian, respectively. Table 1 lists the absorption energies of the two lowest excited singlet states with the highest calculated oscillator strength. The experimental wavelengths of the absorption peaks attributed to the first excited states (S5 or S3) agree well with the calculations, while the transition to the second excited state (S8) is blue-shifted in the calculations. S5 and S8 in P1 were confirmed as 1MLCT-anchoring and 1MLCT-ancillary states from the EDDM maps shown in Figure S3. The experimental absorption spectra had a red-shifted character, that is, the wavelengths were in the order P4 ≈ P3 ≈ P2 > P1 in the 1MLCT bands at 400–500 nm. The calculated spectra of 1MLCT-anchoring in Table 1 also indicated red shifts of P2–P4 relative to P1, but the ordering of P2–P4 was not exactly the same as the experiment because of the very subtle energy differences relative to the accuracy of the ab initio calculations. In Figure 4a, the experimental molar extinction coefficients (ε) were the largest in P4 molecules, which can be an important factor in the high P4 efficiency. We observed this trend in the calculated oscillator strength (f) and the LHE for the first peak of P4-bend1, although the differences among P1–P4 are not largely relative to the experimental ε differences. The calculated emission wavelengths and lifetimes (see the Supporting Information) showed no significant differences among P2–P4.

Figure 4.

Figure 4

Open in a new tab

(a) Experimental and (b) Gaussian TD-DFT-calculated absorption spectra of P1–P4-bend1 and (c) Gaussian TD-DFT-calculated absorption spectra of P4-bend1, P4-bend2, and P4-straight in methanol.

Table 1. TD-DFT-Calculated and Experimental Absorption Wavelengths (λ) and Energies (E), Experimental Molar Extinction Coefficients (ε), Calculated Oscillator Strengths (f), LHEs, and Major Contributions to the Excited States.

  theoretical results
 experimental results
dye state λ (nm) E (eV) f LHE major contributiona 1MLCT transition to λ (nm) E (eV) ε (M–1 cm–1)
P1 S5 448 2.770 0.147 0.287 H – 2–L (86%) Anchoring 455 2.72 9578.33
  S8 407 3.049 0.123 0.247 H – 2 → L + 2 (53%), H – 1 → L + 1 (46%) ancillary      
P2 S3 460 2.693 0.111 0.226 H – 2 → L (71%), H → L + 2 (21%) Anchoring 458 2.70 11,506.7
  S8 408 3.036 0.127 0.254 H – 2 → L + 2 (69%), H – 1 → L + 1 (30%) ancillary      
P3 S3 457 2.711 0.141 0.277 H – 2 → L (87%) Anchoring 459 2.70 14,421.7
  S8 399 2.799 0.138 0.272 H – 2 → L + 2 (70%), H – 1 → L + 1 (28%) ancillary      
P4 bend1 S5 451 2.751 0.149 0.290 H – 2 → L (72%), H → L + 2 (18%) Anchoring 460 2.69 16,326.7
  S8 406 3.053 0.095 0.196 H – 2 → L + 2 (69%), H – 1 → L + 1 (27%) ancillary      
P4 bend2 S3 460 2.695 0.148 0.289 H – 2 → L (88%) Anchoring 460 2.69 16,326.7
  S8 404 3.069 0.082 0.173 H – 2 → L + 2 (85%), H – 1 → L + 1 (12%) ancillary      
P4 straight S3 461 2.690 0.139 0.274 H – 2 → L (89%) Anchoring 460 2.69 16,326.7
  S8 398 3.115 0.141 0.276 H – 2 → L + 2 (66%), H – 1 → L + 1 (32%) ancillary      
Open in a new tab
a

H: HOMO, L: LUMO.

Electron Population

We calculated the electron populations using natural population analysis (NPA) in Gaussian to examine electron-donating effects of the ancillary ligand substituents. We divided each dye molecule into three fragments (anchoring, ancillary, and Ru units), as defined in Figure 2a, summed up the effective atomic charges in each fragment, and listed the fragment charges of the ground and first excited state, as shown in Table 2. We could not obtain the electron population of P4-bend1 in the excited state because the NPA calculation did not converge to the original 1MLCT-anchoring state obtained in the absorption spectra.

Table 2. Total Charge Using Natural Population Analysis in Neutral Dyes (Dye2+)a.

NPA ground state
 1MLCT excited state
dyes ancillary Ru anchoring ancillary Ru Anchoring
P1 1.256 (0) 0.184 (0) 0.560 (0) 1.208 (0) 0.507 (0) 0.285 (0)
P2 1.273 (+0.017) 0.183 (−0.001) 0.544 (−0.016) 1.375 (+0.167) 0.488 (−0.019) 0.137 (−0.148)
P3 1.277 (+0.021) 0.180 (−0.004) 0.543 (−0.017) 1.419 (+0.211) 0.481 (−0.026) 0.100 (−0.185)
P4-bend1 1.267 (+0.011) 0.182 (−0.002) 0.550 (−0.010)      
P4-bend2 1.270 (+0.014) 0.179 (−0.005) 0.549 (−0.011) 1.394 (+0.186) 0.480 (−0.027) 0.124 (−0.161)
P4-straight 1.278 (+0.022) 0.179 (−0.005) 0.541 (−0.019) 1.427 (+0.219) 0.479 (−0.028) 0.093 (−0.192)
Open in a new tab
a

Values in parentheses are differences from P1.

In both the ground and excited states, the ancillary units were more positively charged than the anchoring units, implying that electron populations were concentrated in the anchoring ligands. Moreover, in the 1MLCT-anchoring excited state, the concentration of electron density on the anchoring unit was much greater in P2–P4 than in P1 and the difference was about 0.2. This increase in electron population may be related to the effectiveness of electron injection because the anchoring unit was directly attached to TiO2. However, the difference in NPA among P2–P4 is not so large to identify the best performance of P4.

Ionization Potentials

The ionization properties of the dyes are closely related to the reorganization energies. Table 3 shows the comparison of the calculated and experimental ionization potential (IP) energies. The calculated IPs in vacuum significantly overshot the experimental values from cyclic voltammetry, whereas the calculated IPs in water exhibited better agreement. Although the PCM can fail to represent solvation energies for hydrogen bonding, the agreement in IPs suggested that the PCM for water was applicable for IPs and also for the estimation of reorganization energies. The IPs of P2–P4 were smaller than those of P1 in the calculations. This can be explained by the hyper-conjugation effect of the electron-donating alkyl chain, which destabilized the HOMO composed of the Ru d orbital. Howeve r, there was no trend of increasing IP in P4 compared with P2 and P3, as observed experimentally, especially in the calculations of P4-bend1 and P4-straight. This result may indicate an overestimation of the solvent effect (i.e., an underestimation of the hydrophobic effect) in our P4 calculations. If we increase the cavity size of the PCM van der Waals radius to increase the hydrophobic environment, the IP values increase and become closer to the experiment (Table S4). In a real system, nonyl chains in P4 would be freely rotating at room temperature and water molecules may not be able to locate close to the center of P4. In addition, as discussed in the latter section, dyes may completely cover the TiO2 surface and be located close to each other. Therefore, the hydrophobic effect in the real system may be more enhanced than that estimated by the monomer calculations in solution.

Table 3. IP Energies (eV).

  solvent P1 P2 P3 P4-bend1 P4-bend2 P4-straight
calcd vacuum 11.844 11.442 11.153 11.068 11.016 11.003
  water 5.673 5.551 5.549 5.545 5.600 5.529
exp. water 5.830 5.720 5.730 5.820 5.820 5.820
Open in a new tab

Reorganization Energy

We calculated the reorganization energies (λ) in PCM water, accounting for the effect of the shape of the cavity at an isovalue of 0.02 electron Å–3.32Table 4 lists the theoretical λ values (inner, outer, and total) and the experimental total λ estimated from least-squares fitting of the temperature dependence of the charge-transfer rates.29,30 The electronic energies contributing to λ in eqs 2 and 3 are shown in Table S5. The internal reorganization energies λi, calculated in vacuum, were 0.12–0.16 eV, being relatively small in all the dyes. The λi reflected the magnitude of molecular structural changes between the neutral and cationic dyes (Table S3b,c). The dominant contribution of the outer sphere effects λo in λ may be attributed to the large solvent–solute interaction with the highly polar water and the electronic states of cationic dyes.32

Table 4. Reorganization Energies (eV).

  calcd calcd exp. calcd
    water
  λi λtot λo
P1 0.146 1.627 2.741 1.481
P2 0.150 1.589 2.165 1.439
P3 0.152 1.549 2.409 1.398
P4-bend1 0.149 1.548 2.886 1.399
P4-bend2 0.153 1.522 2.886 1.370
P4-straight 0.125 1.559 2.886 1.434
Open in a new tab

Vaissier et al.32 and Moia et al.29 did some pioneering calculations of reorganization energies using the PCM. Specifically, in ref (29), ruthenium dyes with NCS ligands, that is, N820 (two bipyridines including a nonyl ligand) and Z907 (two bipyridines including a methyl ligand), had similar structures to P4 and P2, respectively. Their results (λ = 0.976 and 0.979 eV for N820 and Z907) and the present results in Table S10 indicated that the substituent effect on reorganization energy was small in the PCM calculations. The absolute values obtained by Moia et al. (1.0 eV) were smaller than the results mentioned here (1.5 eV); however, this was because of the different PCM energy scheme for nonequilibrium systems. If we used the present method for N820 and Z907, the λ values were close to 1.5 eV and similar to those of P1–P4 (see the Supporting Information for details).

In comparison with the calculations, the experimental absolute values of λ were larger (2.1–2.8 eV) and the differences of λ among the four dyes were greater. Also, the trend of λ ordering in the experimental data (P4 > P1 > P3 > P2) was quite different from the calculations. The same tendency was observed for λ in acetonitrile (see the Supporting Information), performed to confirm the feasibility of the PCM in water. The experimental λ was obtained from the method used by Moia et al.29 The squares of the correlation coefficients (R2) were >0.98 when fitting λ to the temperature dependence of the Marcus equation in previous experiments, which suggested that the statistical errors were well-suppressed (See the Supporting Information for details). However, during that fitting, some of the experimental J values were unexpectedly large (1–10 eV), especially for P4. As discussed below, the maximum theoretical J values were in the order of 10–3 eV. This indicated that there were some systematic errors created by another temperature-dependent source and that the Marcus theory, combined with the simple model of the semi-infinite slab approximation,29 may not work here. Many low-frequency modes of P4 nonyl chains also may degrade the validity of the Marcus model.

Electronic Coupling (J) and Charge-Transfer Rate (Γ)

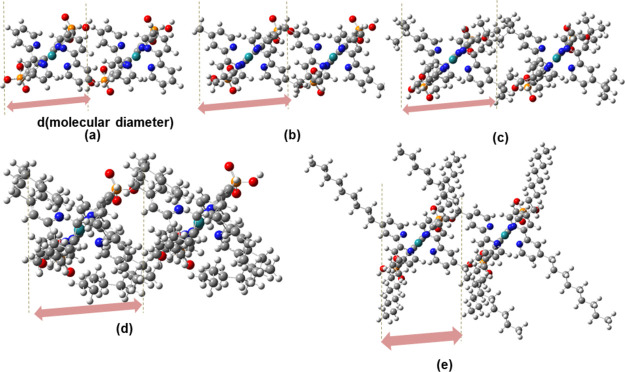
Calculations of electronic couplings depended on two monomer distances (R) that could not be determined precisely from the experiment. Dimarco et al. suggested three ways to estimate R, as follows.30 (i) The upper limit of R may be calculated from experimental values of dye loading (c0), using the relationship R = (c0)−1/3.33 Here, they were 21, 21, 23, and 24 Å, for P1, P2, P3, and P4, respectively. This provides the upper limit because the volume of the film used for the calculation of c0 also contains the TiO2 nanoparticles, where the dyes were not located (see the Supporting Information for more details). (ii) The R value in case (i) may be corrected as R = fp1/3 (c0)−1/3 by introducing a porosity factor (fp), which is generally unknown. (iii) The shortest R may be derived from the molecular diameters shown in Figure 5.

Figure 5.

Figure 5

Open in a new tab

Configurations for pairs of ruthenium dye molecules at short distances for P1 (a), P2 (b), P3 (c), P4-bend1 (d), and P4-straight (e).

Hence, we calculated the J values at the longest R [that is, case (i)] and the shorter R as 9.4, 9.6, 12.2, and 10.5 Å for P1, P2, P3, and P4-bend1 or P4-straight, respectively. The latter distances were selected so that the two monomers were close without overlap. These distances are also similar to those used previously (around 10 Å),32 which may correspond to a complete monolayer on the TiO2.51 We did not discuss J and Γ values for P4-bend2 because the monomers overlapped at 14.5 Å distances, and the calculated electronic coupling at 15 Å was very small (∼10–4 meV) and not realistic. The conformations of the two monomers are shown in Figure 5, where the planes of their anchoring bipys are parallel. We could also confirm in our shorter models of P1–P4 that the oxygens in anchoring phosphates can be attached to titanium atoms on the TiO2(101) surface (Figures S4–S8).

Table 5 shows calculated J values and charge-transfer rates Γ obtained from the calculated λ at 282 K. They are compared with experimental Γ values. The calculated J and Γ values are too small at the longest distances, which indicates that these distances are not realistic. At the shorter distances, the calculated Γ for P1–P4 agrees well with the experiment. The agreement becomes slightly worse for P4-straight, and the calculated Γ is about 12 times lower than the experimental value. This may be because we did not consider the conformational changes of the nonyl chains as a dimer on TiO2. However, the overall calculation reproduced the qualitative trend of the largest Γ for P2. Because of the P3 and P4 bulky structures, we could easily expect that their J and Γ could be smaller than those of P2. However, P1 was also smaller than P2. To understand why J is larger for P2 than that for P1, we analyzed the MO coefficients (CMO) of the HOMO in Table 6. The summation of (CMO)2 for the Ru basis sets decreased by 0.9–2.3% and that for the ancillary bipys basis sets increased by 1.0–1.7% in P2, P3, and P4, relative to that in P1. This suggests that the HOMO in P2, P3, and P4 is more expanded than that in P1 perhaps because of the electron-donating effect of the methyl substituents. This results in a larger overlap of HOMOs and J values between two monomers. We also verified that HOMO – 1, which is another molecular orbital consisting of Ru 5d with ancillary bipy ligands, showed similar trends of expansion in P2, P3, and P4 (Table 6) and J values (Table S6). Hence, in conclusion, our result is consistent with the experimental finding that P2 has the largest transfer rate and the best photocurrent performance in the sa-DSPEC experiment containing the sacrificial agent EDTA.

Table 5. Calculated Electronic Coupling J and Charge-Transfer Rates Γ at Long and Short Distances (Shown in Parentheses), Compared with Experimental Γ.

dye J (meV) Γcalc (s–1) at 287 K Γexpa (s–1)
P1 2.01 × 10–8 2.93 6.50 × 10–14 1389.29 1370.709
  (21 Å) (9.4 Å) (21 Å) (9.4 Å)  
P2 4.19 × 10–7 6.15 4.22 × 10–11 9081.32 16,066.88
  (21 Å) (9.6 Å) (21 Å) (9.6 Å)  
P3 3.87 × 10–7 1.16 5.44 × 10–11 1010.46 1339.271
  (23 Å) (12.2 Å) (23 Å) (12.2 Å)  
P4-bend1 0.0 1.33 0.0 852.54 1213.03
  (24 Å) (10.5 Å) (24 Å) (10.5 Å)  
P4-straight 1.00 × 10–9 0.54 4.81 × 10–16 95.01 1213.03
  (24 Å) (10.5 Å) (24 Å) (10.5 Å)  
Open in a new tab
a

Experimental Γ was obtained as averages of three or four samples with slightly different temperatures (285–289 K) because of the limitation of experimental data.

Table 6. Percentage of Squared Molecular Orbital Coefficients (CMO)2 in Each Fragment at HOMO and HOMO – 1 Levels.

level dye Ru ancillary anchoring
HOMO P1 82.6 11.5 5.9
  P2 81.5 12.7 5.8
  P3 80.3 13.2 6.5
  P4-bend1 81.0 12.9 6.1
  P4-straight 81.7 12.5 5.8
HOMO – 1 P1 78.4 16.8 4.8
  P2 76.6 18.5 4.9
  P3 76.2 18.1 5.7
  P4-bend1 77.8 17.4 4.8
  P4-straight 76.6 18.6 4.8
Open in a new tab

Conclusions

We have presented a theoretical study of the electronic parameters and hole-hopping properties of four ruthenium molecular complexes with alkyl-substituted bipyridine ligands (P1, P2, P3, and P4) used as photosensitizers for DSPECs. The aim was to elucidate why P4, with nonyl substituents, had the best photosensitization efficiency in dye-only experiments, while P2, with methyl substituents, was the best in the presence of the sacrificial agent EDTA.

The lowest peak in the absorption spectra (450 nm) corresponded to the 1MLCT-anchoring state, which shows that P4-bend1 had the largest LHE. This may relate to the high P4 efficiency. Analysis of the electron population in the excited state revealed more population in the P2–P4 anchoring unit than in P1, which may relate to better electron injection in do-DSPECs. However, the differences among P2–P4 were very small, and there was no clear evidence for the best performance of P4 in the do-DSPEC experiment. Different trends were sometimes observed among the three P4 models. Hence, a molecular dynamics study considering nonyl conformations with surrounding water molecules will be needed to assess the ensemble average and to capture the hydrophobic effect more precisely. The experimental high performance of P4 in do-DSPEC may also relate to its weak monomer–monomer interactions, as small Γ values of P4 in both calculation and experiment suggested. This weak interaction inhibits self-quenching and increases the photocurrent density.52

To investigate the hole-hopping properties, we calculated the reorganization energies λ using the PCM. Because the total λ was much larger than the inner λ, the outer effect of the solvent was dominant and the methodological accuracy of the PCM was important. Our results showed similar λ values for all four dyes around 1.5 eV, whereas in the experiment, the values varied widely (2.1–2.8 eV) and P4 showed the largest λ (2.8 eV). Our calculations may contain some systematic errors as a result of using the PCM and excluding the TiO2 surface from the molecular model.53,54 However, we believe that the disagreement with the experimental λ mainly derives from the experimental fitting procedure, which used a simple model of charge transfer based on the Marcus theory, without considering the effects of low-frequency modes of long alkyl chains. In support of this, the experimental values of electronic coupling J were obtained as unphysically large (on the order of 10 eV) for P4 when we fitted the data of Γ to obtain λ and J. In contrast, the calculated J values were relatively small (∼10–3 eV), even at the shorter distances between two monomers. The calculated Γ values at the shorter distances agreed well with the experimental values, and the J and Γ values for P2 were the largest, consistent with the sa-DSPEC experiment. The reason that P2 had a larger J than that of P1 was attributed to the P2-HOMO expansion into the ancillary bipy units in our analysis of MO coefficients.

Acknowledgments

We would like to thank Dr. Y. Imamura for giving us his original program of electron coupling calculation. We would like to thank Dr. Noel, Prof. Luca, Prof. Gjergi, Prof. C. Daniel, Prof. Remco, Prof. Nadia Rega, Dr. Sergentu C, and Dr. Antonio F for their kind communication and discussion via emails. We would like to specially thank Dr. V. Vaissier and Dr. R. Fukuda for valuable discussions about reorganization energy calculation using the PCM. We would also like to thank Prof. Akiko Inagaki for valuable discussions about lifetime. Finally, we thank S. Kanno, R. Murata, and Ataru Sato for their kind discussions about computational problems. A part of calculations was performed at the Research Center for Computational Science, Okazaki, Japan. Salmahaminati is a Ph.D. student in the Tokyo Metropolitan University and gets partial scholarship from Indonesian government (BU Kemdiknas). This work was supported by JSPS KAKENHI grant numbers JP18K05040 and JP17H03011. We thank Leo Holroyd, Ph.D., from Edanz Group (www.edanzediting.com/ac) for editing a draft of this manuscript.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.0c01199.

  • Optimized geometrical coordinates: ground state (S0) in water and methanol; triplet excited state (T1) in water; and cationic state in water (XLSX)

  • P4 conformations and dispersion correction with and without GD3BJ, important bond length and bond angles, IP of P4, electronic energy in au for λ and resulting λ in eV, electronic coupling, photocurrent density do and sa-DSPEC, molecular orbitals of dyes in S0, selected transition using EDDMs, top and side views of the P1–P3 dimer at a short distance and adsorbed on TiO2, discussion about experimental fitting of λ and J, J values obtained from the experimental Γ and T and theoretical λ, theoretical λ values for N820 and Z907, theoretical calculation of λ, IP and J in acetonitrile using the PCM, and emission properties (PDF)

The authors declare no competing financial interest.

Supplementary Material

ao0c01199_si_001.xlsx (394.8KB, xlsx)
ao0c01199_si_002.pdf (2.4MB, pdf)

References

  1. Zigler D. F.; Morseth Z. A.; Wang L.; Ashford D. L.; Brennaman M. K.; Grumstrup E. M.; Brigham E. C.; Gish M. K.; Dillon R. J.; Alibabaei L.; et al. Disentangling the Physical Processes Responsible for the Kinetic Complexity in Interfacial Electron Transfer of Excited Ru(II) Polypyridyl Dyes on TiO 2. J. Am. Chem. Soc. 2016, 138, 4426–4438. 10.1021/jacs.5b12996. [DOI] [PubMed] [Google Scholar]
  2. Purnama I.; Kubo Y.; Mulyana J. Y. A robust ruthenium complex with nonyl-substituted bpy ligand for dye-sensitized photoelectrochemical cell application. Inorg. Chim. Acta 2018, 471, 467–474. 10.1016/j.ica.2017.11.052. [DOI] [Google Scholar]
  3. Purnama I.; Salmahaminati S.; Abe M.; Hada M.; Kubo Y.; Mulyana J. Y. Factors Influencing the Photoelectrochemical Device Performance Sensitized by Ruthenium Polypyridyl Dyes. Dalton Trans. 2019, 48, 688–695. 10.1039/c8dt03502d. [DOI] [PubMed] [Google Scholar]
  4. Swierk J. R.; Mallouk T. E. Design and Development of Photoanodes for Water-Splitting Dye-Sensitized Photoelectrochemical Cells. Chem. Soc. Rev. 2013, 42, 2357–2387. 10.1039/c2cs35246j. [DOI] [PubMed] [Google Scholar]
  5. Thompson D. W.; Ito A.; Meyer T. J. [Ru(Bpy)3]2+* and Other Remarkable Metal-to-Ligand Charge Transfer (MLCT) Excited States. Pure Appl. Chem. 2013, 85, 1257–1305. 10.1351/pac-con-13-03-04. [DOI] [Google Scholar]
  6. Yam V. W.-W.; Lee V. W.-M.; Ke F.; Siu K.-W. M. Synthesis, Photophysics, and Electrochemistry of Ruthenium(II) Polypyridine Complexes with Crown Ether Pendants. Inorg. Chem. 1997, 36, 2124–2129. 10.1021/ic961400j. [DOI] [PubMed] [Google Scholar]
  7. Tandon R.; Nigst T. A.; Zipse H. Inductive Effects through Alkyl Groups - How Long Is Long Enough?. Eur. J. Org. Chem. 2013, 2013, 5423–5430. 10.1002/ejoc.201300486. [DOI] [Google Scholar]
  8. Takijiri K.; Morita K.; Nakazono T.; Sakai K.; Ozawa H. Highly Stable Chemisorption of Dyes with Pyridyl Anchors over TiO2: Application in Dye-Sensitized Photoelectrochemical Water Reduction in Aqueous Media. Chem. Commun. 2017, 53, 3042–3045. 10.1039/c6cc10321a. [DOI] [PubMed] [Google Scholar]
  9. Morita K.; Takijiri K.; Sakai K.; Ozawa H. A Platinum Porphyrin Modified TiO2 Electrode for Photoelectrochemical Hydrogen Production from Neutral Water Driven by the Conduction Band Edge Potential of TiO2. Dalton Trans. 2017, 46, 15181–15185. 10.1039/c7dt03710d. [DOI] [PubMed] [Google Scholar]
  10. Duchanois T.; Liu L.; Pastore M.; Monari A.; Cebrián C.; Trolez Y.; Darari M.; Magra K.; Francés-Monerris A.; Domenichini E.; et al. NHC-Based Iron Sensitizers for DSSCs. Inorganics 2018, 6, 63. 10.3390/inorganics6020063. [DOI] [Google Scholar]
  11. Lundqvist M. J.Quantum Chemical Modeling of Dye-Sensitized Titanium Dioxide. Ph.D. Thesis, Uppsala University, 2006. [Google Scholar]
  12. Hu K.; Meyer G. J. Lateral Intermolecular Self-Exchange Reactions for Hole and Energy Transport on Mesoporous Metal Oxide Thin Films. Langmuir 2015, 31, 11164–11178. 10.1021/acs.langmuir.5b02129. [DOI] [PubMed] [Google Scholar]
  13. Sampaio R. N.; DiMarco B. N.; Meyer G. J. Activation Energies for Electron Transfer from TiO 2 to Oxidized Dyes: A Surface Coverage Dependence Correlated with Lateral Hole Hopping. ACS Energy Lett. 2017, 2, 2402–2407. 10.1021/acsenergylett.7b00759. [DOI] [Google Scholar]
  14. Ali B. A.; Sharmoukh W.; Elnagar M. M.; Hassan Z. M.; Allam N. K. Experimental and Density Functional Theory Insights into the Effect of Withdrawing Ligands on the Fluorescence Yield of Ru(II)-Based Complexes. Appl. Organomet. Chem. 2019, 33, e4677 10.1002/aoc.4677. [DOI] [Google Scholar]
  15. Ali B. A.; Allam N. K. Propping the Optical and Electronic Properties of Potential Photo-Sensitizers with Different π-Spacers: TD-DFT Insights. Spectrochim. Acta, Part A 2018, 188, 237–243. 10.1016/j.saa.2017.07.009. [DOI] [PubMed] [Google Scholar]
  16. Elmorsy M. R.; Su R.; Fadda A. A.; Etman H. A.; Tawfik E. H.; El-Shafei A. Effect of Terthiophene Spacer Position in Ru(II) Bipyridyl Complexes on the Photocurrent and Photovoltage for High Efficiency Dye-Sensitized Solar Cells. Dyes Pigm. 2018, 156, 348–356. 10.1016/j.dyepig.2018.04.005. [DOI] [Google Scholar]
  17. Backler F.; Wilson G. J.; Wang F. Rational Use of Ligand to Shift the UV–Vis Spectrum of Ru-Complex Sensitiser Dyes for DSSC Applications. Radiat. Phys. Chem. 2019, 161, 66–71. 10.1016/j.radphyschem.2019.01.012. [DOI] [Google Scholar]
  18. Tsaturyan A. A.; Budnyk A. P.; Ramalingan C. DFT Study of the CNS Ligand Effect on the Geometry, Spin-State, and Absorption Spectrum in Ruthenium, Iron, and Cobalt Quaterpyridine Complexes. ACS Omega 2019, 4, 10991–11003. 10.1021/acsomega.9b00921. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Guo M.; Xie K.; Lin J.; Yong Z.; Yip C. T.; Zhou L.; Wang Y.; Huang H. Design and Coupling of Multifunctional TiO2 Nanotube Photonic Crystal to Nanocrystalline Titania Layer as Semi-Transparent Photoanode for Dye-Sensitized Solar Cell. Energy Environ. Sci. 2012, 5, 9881–9888. 10.1039/c2ee22854h. [DOI] [Google Scholar]
  20. Xu M.; Wenger S.; Bala H.; Shi D.; Li R.; Zhou Y.; Zakeeruddin S. M.; Grätzel M.; Wang P. Tuning the Energy Level of Organic Sensitizers for High-Performance Dye-Sensitized Solar Cells. J. Phys. Chem. C 2009, 113, 2966–2973. 10.1021/jp809319x. [DOI] [Google Scholar]
  21. Li R.; Lv X.; Shi D.; Zhou D.; Cheng Y.; Zhang G.; Wang P. Dye-Sensitized Solar Cells Based on Organic Sensitizers with Different Conjugated Linkers: Furan, Bifuran, Thiophene, Bithiophene, Selenophene, and Biselenophene. J. Phys. Chem. C 2009, 113, 7469–7479. 10.1021/jp900972v. [DOI] [Google Scholar]
  22. Zhao G.; Wu G.; He C.; Bai F.-Q.; Xi H.; Zhang H.-X.; Li Y. Solution-Processable Multiarmed Organic Molecules Containing Triphenylamine and DCM Moieties: Synthesis and Photovoltaic Properties. J. Phys. Chem. C 2009, 113, 2636–2642. 10.1021/jp809795p. [DOI] [Google Scholar]
  23. Geng H.; Niu Y.; Peng Q.; Shuai Z.; Coropceanu V.; Brédas J.-L. Theoretical Study of Substitution Effects on Molecular Reorganization Energy in Organic Semiconductors. J. Chem. Phys. 2011, 135, 104703. 10.1063/1.3632105. [DOI] [PubMed] [Google Scholar]
  24. Pastore M.; Mosconi E.; De Angelis F.; Grätzel M. A Computational Investigation of Organic Dyes for Dye-Sensitized Solar Cells: Benchmark, Strategies, and Open Issues. J. Phys. Chem. C 2010, 114, 7205–7212. 10.1021/jp100713r. [DOI] [Google Scholar]
  25. Wang Q.; Zakeeruddin S. M.; Nazeeruddin M. K.; Humphry-Baker R.; Grätzel M. Molecular Wiring of Nanocrystals: NCS-Enhanced Cross-Surface Charge Transfer in Self-Assembled Ru-Complex Monolayer on Mesoscopic Oxide Films. J. Am. Chem. Soc. 2006, 128, 4446–4452. 10.1021/ja058616h. [DOI] [PubMed] [Google Scholar]
  26. Bonhôte P.; Gogniat E.; Tingry S.; Barbé C.; Vlachopoulos N.; Lenzmann F.; Comte P.; Grätzel M. Efficient Lateral Electron Transport inside a Monolayer of Aromatic Amines Anchored on Nanocrystalline Metal Oxide Films. J. Phys. Chem. B 1998, 102, 1498–1507. 10.1021/jp972890j. [DOI] [PubMed] [Google Scholar]
  27. Hamann T. W.; Gstrein F.; Brunschwig B. S.; Lewis N. S. Measurement of the Dependence of Interfacial Charge-Transfer Rate Constants on the Reorganization Energy of Redox Species at n-ZnO/H 2 O Interfaces. J. Am. Chem. Soc. 2005, 127, 13949–13954. 10.1021/ja0515452. [DOI] [PubMed] [Google Scholar]
  28. Lewis N. S. Chemical Control of Charge Transfer and Recombination at Semiconductor Photoelectrode Surfaces. Inorg. Chem. 2005, 44, 6900–6911. 10.1021/ic051118p. [DOI] [PubMed] [Google Scholar]
  29. Moia D.; Vaissier V.; López-Duarte I.; Torres T.; Nazeeruddin M. K.; O’Regan B. C.; Nelson J.; Barnes P. R. F. The Reorganization Energy of Intermolecular Hole Hopping between Dyes Anchored to Surfaces. Chem. Sci. 2014, 5, 281–290. 10.1039/c3sc52359d. [DOI] [Google Scholar]
  30. DiMarco B. N.; Motley T. C.; Balok R. S.; Li G.; Siegler M. A.; O’Donnell R. M.; Hu K.; Meyer G. J. A Distance Dependence to Lateral Self-Exchange across Nanocrystalline TiO 2 . A Comparative Study of Three Homologous Ru III/II Polypyridyl Compounds. J. Phys. Chem. C 2016, 120, 14226–14235. 10.1021/acs.jpcc.6b04438. [DOI] [Google Scholar]
  31. Metri N.; Sallenave X.; Plesse C.; Beouch L.; Aubert P.-H.; Goubard F.; Chevrot C.; Sini G. Processable Star-Shaped Molecules with Triphenylamine Core as Hole-Transporting Materials: Experimental and Theoretical Approach. J. Phys. Chem. C 2012, 116, 3765–3772. 10.1021/jp2098872. [DOI] [Google Scholar]
  32. Vaissier V.; Barnes P.; Kirkpatrick J.; Nelson J. Influence of Polar Medium on the Reorganization Energy of Charge Transfer between Dyes in a Dye Sensitized Film. Phys. Chem. Chem. Phys. 2013, 15, 4804–4814. 10.1039/c3cp44562c. [DOI] [PubMed] [Google Scholar]
  33. Fukuda R.; Ehara M.; Nakatsuji H.; Cammi R. Nonequilibrium Solvation for Vertical Photoemission and Photoabsorption Processes Using the Symmetry-Adapted Cluster-Configuration Interaction Method in the Polarizable Continuum Model. J. Chem. Phys. 2011, 134, 104109. 10.1063/1.3562211. [DOI] [PubMed] [Google Scholar]
  34. Frisch M.; Trucks G.; Schlegel H.; Scuseria G.. Gaussian 09W, Revision A. 1; Gaussian: Wallingford (CT), 2009.
  35. Garino C.; Terenzi A.; Barone G.; Salassa L. Teaching Inorganic Photophysics and Photochemistry with Three Ruthenium(II) Polypyridyl Complexes: A Computer-Based Exercise. J. Chem. Educ. 2016, 93, 292–298. 10.1021/acs.jchemed.5b00801. [DOI] [Google Scholar]
  36. Fumanal M.; Daniel C. Electronic and Photophysical Properties of [Re (L)(CO) 3 (Phen)] + and [Ru(L) 2 (Bpy) 2 ] 2+ (L = Imidazole), Building Units for Long-Range Electron Transfer in Modified Blue Copper Proteins. J. Phys. Chem. A 2016, 120, 6934–6943. 10.1021/acs.jpca.6b06438. [DOI] [PubMed] [Google Scholar]
  37. Tomasi J.; Mennucci B.; Cammi R. Quantum Mechanical Continuum Solvation Models. Chem. Rev. 2005, 105, 2999–3094. 10.1021/cr9904009. [DOI] [PubMed] [Google Scholar]
  38. Schuchardt K. L.; Didier B. T.; Elsethagen T.; Sun L.; Gurumoorthi V.; Chase J.; Li J.; Windus T. L. Basis Set Exchange: A Community Database for Computational Sciences. J. Chem. Inf. Model. 2007, 47, 1045–1052. 10.1021/ci600510j. [DOI] [PubMed] [Google Scholar]
  39. Feller D. The role of databases in support of computational chemistry calculations. J. Comput. Chem. 1996, 17, 1571–1586. . [DOI] [Google Scholar]
  40. Hehre W. J.; Ditchfield R.; Pople J. A. Self—Consistent Molecular Orbital Methods. XII. Further Extensions of Gaussian—Type Basis Sets for Use in Molecular Orbital Studies of Organic Molecules. J. Chem. Phys. 1972, 56, 2257–2261. 10.1063/1.1677527. [DOI] [Google Scholar]
  41. Lu S.-Z.; Li X.-Y.; Liu J.-F. Molecular Orbital Analysis in Evaluation of Electron-Transfer Matrix Element by Koopmans’ Theory. J. Phys. Chem. A 2004, 108, 4125–4131. 10.1021/jp0380374. [DOI] [Google Scholar]
  42. Curtiss L. A.; Miller J. R. Distance Dependence of Electronic Coupling through Trans Alkyl Chains: Effects of Electron Correlation. J. Phys. Chem. A 1998, 102, 160–167. 10.1021/jp972210c. [DOI] [Google Scholar]
  43. Wu Q.; Van Voorhis T. Extracting Electron Transfer Coupling Elements from Constrained Density Functional Theory. J. Chem. Phys. 2006, 125, 164105. 10.1063/1.2360263. [DOI] [PubMed] [Google Scholar]
  44. O’boyle N. M.; Tenderholt A. L.; Langner K. M. Cclib: A Library for Package-Independent Computational Chemistry Algorithms. J. Comput. Chem. 2008, 29, 839–845. 10.1002/jcc.20823. [DOI] [PubMed] [Google Scholar]
  45. Brooks B. R. III; Brooks C. L.; Petrella R. J.; Roux B.; Won Y.; Archontis G.; Bartels C.; Boresch S.; Caflisch A.; et al. CHARMM: The biomolecular simulation program. J. Comput. Chem. 2009, 30, 1545–1614. 10.1002/jcc.21287. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Hanwell M. D.; Curtis D. E.; Lonie D. C.; Vandermeersch T.; Zurek E.; Hutchison G. R. Avogadro: An Advanced Semantic Chemical Editor, Visualization, and Analysis Platform. J. Cheminf. 2012, 4, 17. 10.1186/1758-2946-4-17. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Li H.; Zhang L.; Lin H.; Fan X. A DFT-D Study on the Electrochromic Mechanism of Ruthenium Sulfoxide Complexes. RSC Adv. 2014, 4, 45635–45640. 10.1039/c4ra06047d. [DOI] [Google Scholar]
  48. Peter S. K.; Kaulen C.; Hoffmann A.; Ogieglo W.; Karthäuser S.; Homberger M.; Herres-Pawlis S.; Simon U. Stepwise Growth of Ruthenium Terpyridine Complexes on Au Surfaces. J. Phys. Chem. C 2019, 123, 6537–6548. 10.1021/acs.jpcc.8b12039. [DOI] [Google Scholar]
  49. Yang L.; Adam C.; Nichol G. S.; Cockroft S. L. How Much Do van Der Waals Dispersion Forces Contribute to Molecular Recognition in Solution?. Nat. Chem. 2013, 5, 1006–1010. 10.1038/nchem.1779. [DOI] [PubMed] [Google Scholar]
  50. Wodrich M. D.; Corminboeuf C.; Schleyer P. V. R. Systematic Errors in Computed Alkane Energies Using B3LYP and Other Popular DFT Functionals. Org. Lett. 2006, 8, 3631–3634. 10.1021/ol061016i. [DOI] [PubMed] [Google Scholar]
  51. Li X.; Nazeeruddin M. K.; Thelakkat M.; Barnes P. R. F.; Vilar R.; Durrant J. R. Spectroelectrochemical Studies of Hole Percolation on Functionalised Nanocrystalline TiO2 Films: A Comparison of Two Different Ruthenium Complexes. Phys. Chem. Chem. Phys. 2011, 13, 1575–1584. 10.1039/c0cp01013h. [DOI] [PubMed] [Google Scholar]
  52. Föhlinger J.; Maji S.; Brown A.; Mijangos E.; Ott S.; Hammarström L. Self-Quenching and Slow Hole Injection May Limit the Efficiency in NiO-Based Dye-Sensitized Solar Cells. J. Phys. Chem. C 2018, 122, 13902–13910. 10.1021/acs.jpcc.8b01016. [DOI] [Google Scholar]
  53. Shepard R.; Minkoff M. Optimization of nonlinear wave function parameters. J. Quantum Chem. 2006, 106, 3190–3207. 10.1002/qua.21140. [DOI] [Google Scholar]
  54. Persson P.; Lundqvist M. J.; Ernstorfer R.; Goddard W. A.; Willig F. Quantum Chemical Calculations of the Influence of Anchor-Cum-Spacer Groups on Femtosecond Electron Transfer Times in Dye-Sensitized Semiconductor Nanocrystals. J. Chem. Theory Comput. 2006, 2, 441–451. 10.1021/ct050141x. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao0c01199_si_001.xlsx (394.8KB, xlsx)
ao0c01199_si_002.pdf (2.4MB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES