Evaluation of localized region-based segmentation algorithms for CT-based delineation of organs at risk in radiotherapy

Abstract

Background and purpose

In radiation therapy, defining the precise borders of cancerous tissues and adjacent normal organs has a significant effect on the therapy outcome. Deformable models offer a unique and robust approach to medical image segmentation. The objective of this study was to investigate the reliability of segmenting organs-at-risk (OARs) using three well-known local region-based level-set techniques.

Methods and materials

A total of 1340 non-enhanced and enhanced planning computed tomography (CT) slices of eight OARs (the bladder, rectum, kidney, clavicle, humeral head, femoral head, spinal cord, and lung) were segmented by using local region-based active contour, local Chan-Vese, and local Gaussian distribution models. Quantitative metrics, namely Hausdorff Distance (HD), Mean Absolute Distance (MAD), Dice coefficient (DC), Percentage Volume Difference (PVD) and Absolute Volumetric Difference (AVD), were adopted to measure the correspondence between detected contours and the manual references drawn by experts.

Results

The results showed the feasibility of using local region-based active contour methods for defining six of the OARs (the bladder, kidney, clavicle, humeral head, spinal cord, and lung) when adequate intensity information is available. While the most accurate results were achieved for lung (DC = 0.94) and humeral head (DC = 0.92), a poor level of agreement (DC < 0.7) was obtained for both rectum and femur.

Conclusion

Incorporating local statistical information in level set methods yields to satisfactory results of OARs delineation when adequate intensity information exists between the organs. However, the complexity of adjacent organs and the lack of distinct boundaries would result in a considerable segmentation error.

1. Introduction

The main goal of radiotherapy is to deliver a prescribed dose to the target volume, while sparing normal tissue including organs-at-risk (OARs). To achieve this aim, it is necessary to perform all elements of radiotherapy, from CT simulation to plan verification, in an accurate manner [1], [2], [3], [4]. One of the most fundamental elements of this process is the localization of the target volume and OAR, the effects of which on the treatment quality are highly significant. However, a manual delineation of the regions-of-interest (ROIs) is an error-prone procedure owing to the fact that it is cumbersome, time intensive, and prone to intra- and inter-observer variability [3], [4].

Medical image segmentation is a wide field that can play a key role in clinical diagnosis and therapy, the applications of which are quite extensive [5], [6], [7], [8], [9], [10], from computer-aided diagnosis systems, to improving and facilitating delineation tasks for radiotherapy. With the advent of new radiotherapy techniques such as image-guided radiation therapy (IGRT), this field has remained an active area of research in radiation therapy, and different classes of image segmentation methods have been proposed, implemented, and clinically evaluated [3], [4], [11]. A significant amount of research has been clinically applied to OAR delineation, most of which has focused on deformable shape and atlas-based models owing to their ability to reduce inter- and intra-observer variability [12], [13], [14], [15], [16], [17].

Active contour models based on a level set are another class of segmentation techniques whose application in radiotherapy has received growing attention in terms of both the target volume and OAR delineation [3], [18], [19], [20], [21], [22]. The main idea underlying these methods is to initialize a contour around the boundaries of the object as a parametric curve, and to deform this contour toward the desired boundaries through a minimization of the energy functional [23], [24], [25], [26]. Despite the better accuracy of region-based level-set segmentation methods, as compared to gradient-based methods, for use with medical images, they cannot provide suitable results for tumor images with a non-uniform intensity distribution [4]. Thus, local region-based active contours may be the preferred approach to evaluating their clinical performance in radiotherapy treatment planning [3], [18].

Moreover, various local region-based segmentation algorithms have been proposed. The main goal of this paper was to evaluate the validity and reliability of three robust local region-based algorithms to delineate eight OARs throughout the whole body, namely, the bladder, rectum, kidney, clavicle, humeral head, femoral head, spinal cord, and lung, which are visible in CT images.

2. Materials and methods

2.1. Patients and computed tomography (CT) images

A CT dataset of 20 patients diagnosed with different types of cancer, including breast, prostate, esophagus, lung and pancreatic cancer, were used to delineate the above-mentioned OARs. All images acquired for treatment planning were scanned using an Aquilion One (Canon, formerly Toshiba Medical Systems Co.), and all patients were treated using standard three-dimensional conformal therapy (3D-CRT). The properties extracted from the studied CT images were shown in an axial view, with a slice spacing of 3–5 mm, resolution of $0.5\text{mm}\times 0.5\text{mm}$, and a scan matrix of $512\times 512$.

2.2. Manual contouring

Three radiation oncologists manually delineated the eight OARs on 1340 non-enhanced and enhanced planning CT slices of 20 patients using an Oncentra MasterPlan (version 4.3, Elekta AB, Stockholm, Sweden) except for the lung delineation, for which the oncologists employed automatic segmentation tools available with the treatment planning system. The inter-observer variability was assessed, and the reference contour was defined as the baseline and obtained from the averages of the oncologists’ contours based on a method defined by Chalana and Kim [27].

2.3. Local region-based segmentation algorithms

The semi-automatic segmentations of all slices were conducted by two users experienced with the algorithms. First, three to four points were selected around the desired organ in each slice, and the initial contour was automatically interpolated and fitted between these points. The initial curve reached the boundary of the organ by minimizing the energy functional. In this study, three robust localized energy functionals were used, and all three models were evaluated against all eight OARs to assess the applicability and accuracy of each model. One of the most effective features of the algorithms applied is their ability to segment cancer-related images with non-uniform intensity distributions. However, because the localized energy functional is based on the image intensity, this class of segmentation can only be applicable to organs whose pixel intensities are distinguishable from adjacent organs. It should be mentioned that all the implementations were conducted on a 2.8 GHz desktop computer, with 8 GB of random access memory, using MATLAB 7.12 software (MathWorks, Natick, MA).

2.3.1. Localizing region-based active contour (LRBAC)

LRBAC, proposed by Lankton and Tannenbaum [28], is considered one of the most efficient local region-based techniques. The energy functional for this model uses image statistics in a local neighborhood along with the zero-level set and a curvature-based regularization term.

$$\frac{\partial \phi }{\partial t}(x)=\delta (\phi (x))\left[\int B(x\text{,}y)\nabla F(I\text{,}\phi \text{,}y)\mathit{dy}+\mathit{REG}(\phi )\right]$$ (1)

$$F(I\text{,}\phi \text{,}y)=H(\phi (y)){(I(y)-c_1)}^2(1-H(\phi (y))){(I(y)-c_2)}^2$$ (2)

In these equations, and throughout the remainder of the paper, $c_1$ and $c_2$ represent the average image intensity inside and outside of the local window, respectively, which were defined through a Heaviside function, H(.). The $\phi$ symbol refers to the level set function, the zero levels of which were obtained through a Dirac Delta function, $\delta (.)$. The term $\mathit{REG}(.)$ denotes the length minimization energy that controls the smoothness of the evolving contour. Moreover, I represents the main image in the above formulae, and the subsequent formulae provided in the following sections.

2.3.2. Local chan–vese model (LCV)

LCV is a generalization of the Chan–Vese model, which is one of the most robust region-based methods available. Different local versions of the CV model have been proposed, among which an efficient LCV model, suggested by Xiao Wang et al. [29], was used in this study. The energy functional for this model consists of a global statistical term, local statistical term, and regularization term. Therefore, appropriate segmentation results can be achieved in images with either homogenous or inhomogeneous intensity.

$$\frac{\partial \phi }{\partial t}=\delta (\phi (x))[{(G_k\ast I(x)-I(x)-d_1)}^2+{(G_k\ast I(x)-I(x)-d_2)}^2+\mathit{REG}(\varphi )]$$ (3)

In this equation, $d_1$ and $d_2$ represent the global image intensity calculated from a contrast-enhanced image, $G_k$ is square-shaped averaging mask with a size of k, and $\ast$ signifies the convolution operator.

2.3.3. Local Gaussian distribution fitting (LGDF)

Li Wang et al. [30] proposed the LGDF method by assuming that the local average intensity along with the local standard deviation is capable of achieving segmentation in regions with a non-uniform intensity and different variances with higher accuracy.

$$\frac{\partial \phi }{\partial t}(x)=\delta (\phi (x)[(e_1-e_2)+\mathit{REG}(\phi )]$$ (4)

$$e_i(x)=\int w(y-x)[\log ({\sigma }_i(y))+\frac{{(m_i(y)-I(x))}^2}{2{\sigma }_i^2(y)}]\mathit{dy}\text{;}i=1\text{,}2$$ (5)

In Eqs. (4), (5), $w(.)$ refers to the localizing Gaussian kernel, and $m_i$ and ${\sigma }_i^2$ are its average and standard deviation, respectively.

Because all eight OARs investigated in this research were segmented using all three local region-based functionals described herein, the energy functional that provided the most accurate results for each OAR was chosen as the optimum algorithm for that particular OAR.

2.4. Quantitative analysis for evaluation

Three error metrics that are usually used in reporting the segmentation performance were applied to compare the semi-automatic results with the manual reference contours: the Dice coefficient (DC) which measures the spatial overlap between two regions; the Hausdorff distance (HD), which quantifies the largest minimum distance between two contours; and the mean absolute distance (MAD), which measures the average of the absolute signed distance between two contours. Additionally, to compare the volumes, two parameters, namely, the percentage absolute volumetric difference (AVD) and the percentage volume difference (PVD), for each organ were calculated [3], [31], [32]. Because poor results were obtained from the femur and rectum, they were not considered further in the quantitative analysis.

It should be noted that the paired sample t-test (with significance level set at α=0.05) was applied to all OAR volumes to compare the average manual volumes and average semiautomatic volumes.

3. Results

3.1. Manual and semi-automatic results

A review of the measured quantitative error metrics revealed that the highest inter-observer Dice similarity criteria were obtained for the lung (0.94 ± 0.04) and bladder (0.93 ± 0.03), and the lowest agreements were observed for the spinal cord (0.81 ± 0.04) and clavicle (0.87 ± 0.02) (Fig. 1).

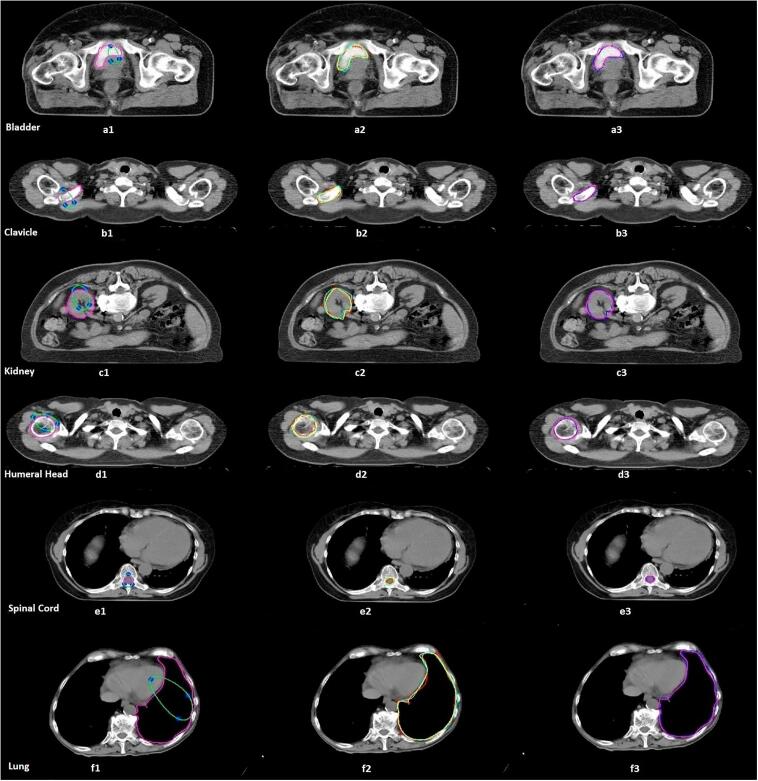
Fig. 1.

Example of the results from both manual and semi-automatic delineations of an image slice of six OARs. The first column (a1, b1, c1, d1, e1, f1) represents the initial contours defined by two experienced users and the final semi-automatic results; the second column (a2, b2, c2, d2, e2, f2) represents the manual contours defined by three oncologists (red, oncologist 1; yellow, oncologist 2; cyan, oncologist 3), demonstrating the inter-observer variability in the OAR delineation. The last column (a3, b3, c3, d3, e3, f3) shows a contour overlap of the semi-automatic (magenta) results, and the average of the oncologists’ contours (blue). All image datasets were exported from the PACS at a university hospital of Trieste, Italy. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Table 1 shows all error metric values between the manual and semi-automatic results. Based on the optimum algorithm for each OAR, the most accurate results were as follows: the mean ± standard deviation of the DC between the manual and semi-automatic contours was 0.9 ± 0.04 for the bladder, 0.92 ± 0.12 for the humeral head, 0.81 ± 0.04 for the spinal cord, 0.84 ± 0.04 for the clavicle, 0.90 ± 0.04 for the kidney, and 0.94 ± 0.02 for the lung. A poor level of agreement ($\text{DC < 0}.7$) was demonstrated for both the rectum and femur. The highest values (between the manual and semi-automatic results), excluding the femur and rectum, for HD and MAD were in the lung (HD, 9.7 ± 6.1 mm) and bladder (MAD, 3.2 ± 0.9 mm). However, the lowest values were obtained for the spinal cord (HD, 3.9 ± 0.9 mm, MAD, 1.8 ± 0.3).

Table 1.

Error metrics (DC, HD, and MAD) analysis of semi-automatic results compared to manual reference contours.

OAR	LRBAC			LCV			LGDF
	DC	HD (mm)	MAD (mm)	DC	HD (mm)	MAD (mm)	DC	HD (mm)	MAD (mm)
Clavicle	0.73	6.8	3.1	0.84	4.6	2	0.78	6.1	2.8
Bladder	0.83	12.7	5.6	0.67	17.6	8.4	0.90	9.5	3.2
Humeral Head	0.92	4.7	2.1	0.53	14.4	11.2	0.67	12.6	6.8
Kidney	0.73	13.4	9.4	0.62	14.1	13.2	0.90	8.4	2.6
Lung	0.76	17.6	10.9	0.83	14.7	8.4	0.94	9.7	2.4
Spine	0.59	6.6	3.8	0.81	3.9	1.8	0.72	5.6	2.3
Femoral Head	0.54	24.3	17.6	0.38	32.7	24.3	0.47	26.1	23.8
Rectum	0.52	19.5	10.2	0.46	19.9	13.7	0.61	17.4	8.8

The total OAR volumes derived from the manual and semi-automatic techniques, AVD and PVD, are shown in Table 2, and the results were averaged for each organ. According to the results, all volumes obtained from the semi-automatic methods were lower than those obtained from the manual delineation except for the bladder (with the lowest AVDaverage time for defining each with the largest AVD).

Table 2.

Comparison of volumes obtained from manual and semiautomatic methods along with PVD and AVD.

OAR	Manual volume (cm3)	Semi-automatic volume (cm3)	Percentage mean AVD	PVD	P value
Clavicle	25 ± 4	23 ± 3	8.5 ± 1.3	0.91 ± 0.01	0.3
Bladder	174 ± 40	177 ± 40	4.1 ± 1.8	1.02 ± 0.04	0.85
Humeral Head	43 ± 7	45 ± 5	9.8 ± 2.5	1.05 ± 0.09	0.6
Kidney	184 ± 87	176 ± 85	4.9 ± 2.5	0.95 ± 0.02	0.6
Lung	1950 ± 60	1901 ± 62	4.1 ± 2.6	0.98 ± 0.04	0.85
Spine	48 ± 11	44 ± 11	7 ± 3.3	0.92 ± 0.03	0.2

The average time for defining each OAR per slice using the semi-automatic method was 2.8 ± 0.8 s for the lung, 1.9 ± 0.3 s for the clavicle, 1.4 ± 0.6 s for the humeral head, 3.1 ± 0.3 s for the kidney, 2.4 ± 0.6 s for the bladder, and finally, 0.7 ± 0.3 s for the spinal cord. Compared with manual delineation, in which the contouring time was recorded manually, these algorithms can reduce the time for organ delineation by 20–40% (Table 3). The only exception was the lung, which was delineated using the automatic segmentation tools available in TPS and was segmented faster than with the other algorithms; however, delineation through the automatic segmentation tools in the TPS required a pre-processing to adjust the grey level, and finally, some slices required slight modifications. In contrast, the LGDF algorithm used for delineating the lung boundaries achieved more precise and reliable results.

Table 3.

Computational time expended for segmenting each OAR.

OAR	Average # of slices for each OAR	Time per slice	Time (s)
Clavicle (L + R)	16 × 2	1.9	60.8
Bladder	12	2.4	28.8
Humeral Head (L + R)	18 × 2	1.4	50.4
Kidney (L + R)	20 × 2	3.1	124
Lung (L + R)	38 × 2	2.8	212.8
Spine	75	0.7	52.5

4. Discussion

To the best of our knowledge, this study was the first evaluation of localized region-based algorithms for CT-based OAR delineation in radiation therapy treatment planning.

As shown in Table 1, the LRBAC led to better results for the humeral head and femur bone delineation. This was due to the fact that the humeral head had a ball shape, and the gradient of intensity between the ball portion and adjacent neighboring structure was negligible; therefore, a shape constraint was required to define this OAR. Of the three local-region based algorithms, the LRBAC energy functional could be easily combined with a shape constraint. The results demonstrated that LCV is the most accurate model for spinal cord and clavicle segmentation. This might be because it applies a high-pass filter and can intensify the edges of the image. A high intensity gradient and intense inhomogeneity are present in some organs including the (non-contrast enhanced) bladder, as well as portions of the kidney and lung; thus, not only is the average intensity required, the local contrast criteria should also be applied to obtain a better delineation, and as a result, LGDF can segment these three OARs more precisely compared to the other methods.

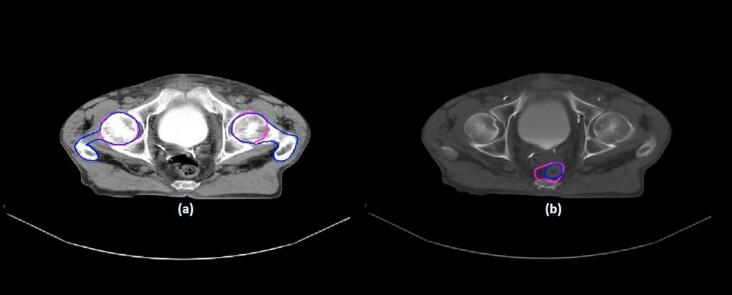
Rectum and femur segmentation results obtained by any of the above algorithms have been poor and unacceptable. The main reason for this is believed to be an inability to distinguish the boundaries between the rectum and nearby structures, as well as a portion of the femur from the adjacent tissue, owing to a lack of intensity information in certain image slices. Although combining the shape term with the LRBAC energy functional allows segmenting certain parts of the femur, it is still impossible to simultaneously segment the femoral head and pelvic bone using such algorithms (Fig. 2).

Fig. 2.

(a) Difficulty in simultaneously segmenting the femoral head and pelvic bone, and (b) a lack of distinct boundaries between the rectum and nearby structures (manual contour, blue; semi-automatic contour, magenta). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

In comparison to other common active contours, particularly edge-based active contour models, the aforementioned three local region-based methods are less sensitive to the initialization. However, they still depend on the initialization parameters and initial contours. In this study, the initial contours were defined by two experts experienced with the algorithms, and the results of a semi-automatic segmentation were observed by oncologists and approved as acceptable. Accordingly, one of the major limitations of using the active contours is their vulnerability to initialization; thus, oncologists need to be trained in this procedure when utilizing the algorithms. To a certain extent, this drawback can be handled by defining the blocking regions, as proposed by Wang [33].

The pros and cons of this study can be highlighted through a subjective comparison between our results and the results obtained from other related researches. In the first step, a quantitative comparison with a recent algorithm proposed by Wang [33] was conducted. The reason for choosing this robust level algorithm for comparison is its ability to locally converge at the boundaries of the target regions. By comparing the most accurate results from the three considered local region-based methods with the results obtained from Wang’s algorithm, it can be inferred that utilizing only image-based information for a segmentation task is insufficient for all eight OARs. Because the evolution of the surface when applying Wang’s method is driven by the threshold-based energy, each OAR can be segmented by setting the threshold range according to the specific CT number. Although the results are promising for six of the OARs, the humeral head and clavicle have not been segmented as accurately as with the investigated region-based methods. These results can be interpreted as follows. The rectum and lungs are filled with air and have distinct CT numbers compared with their adjacent tissues; therefore, to a certain extent, they can be segmented more accurately. Because none of the neighboring tissues of the spine have the same CT number, improved results have been easily achieved. For cases of the femoral head, bladder, and kidney, the availability of a blocking option helps prevent the surface from growing toward other tissue. However, the existence of several bony structures that are connected to the humeral head and clavicle result in a leak in the evolving surface and a deviation from the target boundaries.

Zhang et al. [22] segmented the prostate, rectum and seminal vesicle separately through a robust and fast active contour model by defining a restricted region around each target. However, defining a number of restriction regions adds increased demand to the initialization process. This can occur for a lung segmentation, which requires the right and left ventricle areas, vena cava, thoracic aorta, and other tissue types to be defined as restricted regions for a contour evolution. Pekar et al. [13] used a 3D deformable surface model for segmenting the bladder, rectum, and femoral head. The results are heavily dependent on a manual correction and the image resolution. In addition, the computational time takes up to 15 min, which is five times longer than our implementations. In another study, Pekar et al. [14] used a model-based approach with a shape constraint to segment the bladder, rectum, and femoral head. The shape information in this research was acquired by training the dataset, which makes it an offline method; in contrast, we used a variational-based energy shape model that can be fitted to the level set evolution algorithm in real time. El Naqa et al. [21] applied a segmentation framework to multimodal images (PET-CT or PET-CT-MR); however, the accuracy of the segmented regions was almost within the same range as our results using only CT images.

The first conclusion drawn here is that, although CT images have a lower tissue contrast resolution compared to that of an MRI [34], such segmentation techniques are still able to reveal adequately satisfactory results when a reasonable amount of intensity information of diverse tissue types exists. In addition, the potential and limitations of this class of segmentation were investigated in this paper. The results demonstrated that this class of segmentation achieves a good deformability and a significant ability to delineate OARs when adequate intensity information exists. However, the two main drawbacks of this class are sensitivity to the initialization and an inability to segment the images when insufficient intensity information is available.

In this study, the possibility of using local region-based level-set methods for segmentation of the OARs was investigated by applying three different energy functionals to eight OARs in CT images. The accuracy of the semi-automatic segmentations was compared against manual delineations by experts in terms of Dice, MAD, and HD, as well as through volumetric measurements, such as AVD and PVD. Although promising results were obtained for six of the OARs, segmentation of the rectum and femoral head remain a challenging task owing to a lack of distinct boundaries and intensity information. As indicated, deformable models have both benefits and drawbacks in handling the task of OAR segmentation; however, using model-based segmentation tools along with active contours, the shortcomings presented in this paper might be overcome [35], [36], [37]. A possible optimal solution could be using a coupled framework to utilize the benefits of both active contours and atlas-based algorithms. Although such a combination has been applied using classical parametric active contours [38], their inability to segment sharp concavities as well as handle images with inhomogeneous intensity can be solved by replacing the parametric active contours with local region-based energy functionals, as suggested by Gao and Tannenbaum [39]. Therefore, an evaluation of the clinical application of an atlas-based method coupled with local region-based active contours for use in radiation therapy treatment planning can be addressed in future studies.

Conflict of interest

All the authors declare no conflicts of interest.

Appendix A. Supplementary data

Supplementary data

Data profile.