Investigating the potential of conical scintillation detectors for patient-specific verification of intensity-modulated radiotherapy plans

Abstract

Background and purpose

Conical scintillation detectors are frequently used to measure geometric characteristics of radiotherapy modalities. However, their application to verify intensity-modulated radiotherapy plan delivery has not been investigated and requires a more detailed understanding of device response. This work evaluated the novel application of a conical scintillation detector to plan-specific quality assurance (QA) for intensity-modulated photon plans by evaluating device dependence on beam delivery and device acquisition parameters.

Materials and methods

Measurements were made with a conical scintillation detector using beam delivery parameters of five photon beams (6–15 MV, including flattening filter free), three field sizes (1 × 1–5 × 5 cm²), and several dose rates (100–2000 MU/min) combined with device acquisition parameters of two frame rates (10 and 20 fps) and three gains (18–22 dB). A standardization equation to correct for gain and frame rate was investigated, and the remaining dose rate dependence was characterized. Device precision was evaluated using replicate measurements, and spatial uniformity was determined by irradiating different parts of the device.

Results

For each parameter combination, measurement reproducibility was 1.3%, and spatial uniformity was 1–2%. Scintillation intensity varied with gain, frame rate, and dose rate. Standardizing measurements for gain and frame rate was effective, but a dependence on dose rate caused errors at non-reference conditions (root mean squared error, RMSE: 0–152%). An additional dose rate correction specific to each combination of gain and frame rate improved accuracy (RMSE 0–17%).

Conclusions

To consider the detector for plan-specific QA of intensity-modulated radiotherapy plans, correction factors are imperative to mitigate effects of delivery and acquisition parameters.

1. Introduction

The need for dosimetric and geometric accuracy in radiotherapy is well established [1], [2], [3], and the presence, magnitude, and influence of uncertainties on dosimetric accuracy are well described [4]. The International Commission of Radiation Units and Measurements (ICRU) recommends the dose delivered to be within 5% of the prescribed value [1]. A rigorous quality assurance protocol is required to ensure this accuracy and includes periodic tests like those in the AAPM’s TG-40 [5] and TG-142 [6] as well as plan-specific quality assurance (PSQA) for treatment plans featuring modulated fluence intensity such as IMRT and SBRT plans. PSQA verifies that the dose resulting from delivery of a complex treatment plan matches the desired dose despite the presence of uncertainties in machine precision and machine and dose modeling. To this end, a wide variety of quality assurance (QA) methods and devices are used to quantitatively compare measured values with their treatment plan predictions [7].

A conical scintillation detector is an example of such a QA device. One end features a hollow conical housing, the inside of which is lined with a scintillating phosphor. The opposite end features a CCD camera with a complete view of the scintillating layer from the central axis of the cone. When radiation is incident on the cone, interactions with the structural housing initiate secondary radiation that interacts with the scintillating layer. The CCD camera observes the pattern of scintillation photons as the beam enters and exits the cone, and a video of the irradiation is captured and analyzed with software. A thorough description of this kind of device has been published previously and is available in Cai et al. [8].

Heretofore, applications of conical scintillation detectors have exploited their unique shape to measure geometric properties (e.g. radiation beam size, shape, and isocentricity) of CyberKnife and proton beams [8], [9], [10], [11], [12], [13]. By identifying the entry and exit spots of a narrow beam, software can determine the beam’s directional vector, making the device well suited for tests like Winston-Lutz [14].

In addition, these devices have several attributes that may extend their utility to additional QA applications. These traits include high spatial resolution, 3D measurement capabilities, independence from the treatment delivery system, and minimal collision risk. These characteristics could provide important benefits to the evaluation of intensity-modulated radiotherapy plans if used for PSQA. However, for this new application, the device response must be understood to a degree beyond that necessary to determine beam vectors. Establishing the beam vector merely requires determination of the position of the entrance and exit spot. Beyond their location, little information is required about the scintillation spots. To be used for PSQA, however, the measured scintillation intensity must be well-characterized with regards to device performance (e.g. position and angle of incidence), beam delivery parameters (e.g. energy, flattening filter, and dose rate), and device acquisition parameters (e.g. gain and frame rate). Failing to account for these factors may result in misinterpretation of measurement results. As these variables do not affect the ability of software to determine the beam vector, their influence on scintillation intensity remains largely unexplored. The application of a scintillation detector to PSQA for proton pencil beam scanning treatments has been described previously by Cai et al. [8], however to our knowledge, the considerations necessary for PSQA of intensity-modulated photon plans have not been described.

The purpose of this work was to investigate how the performance of a conical scintillation detector depends on beam delivery parameters and device acquisition parameters in order to investigate its potential application for PSQA of intensity-modulated photon radiotherapy plans.

2. Materials and methods

2.1. Device setup and measurement parameters

To investigate potential application to PSQA, numerous measurements were made with a conical scintillation detector (XRV-124, Logos Systems International, Scott Valley, CA) using a conventional c-arm medical linear accelerator (TrueBeam v2.5, Varian Medical Systems, Palo Alto, CA). The device was extended beyond the end of the treatment couch with the tip of the cone oriented towards the gantry. External markings were used to place the machine’s isocenter along the cone’s central axis near its base (Supplementary Figs. S1 and S2). In this configuration, measurements were made using all combinations of beam delivery and device acquisition parameters listed in Table 1, including complete datasets for 6 MV, 6MV FFF (flattening filter free), and 10 MV FFF beams. After each irradiation, the vendor-provided software was used to identify the entrance spot in each image frame and to calculate the maximum cumulative intensity integrated across all frames. Measurements were made in triplicate (acquired in immediate succession without adjusting the device), and the average, standard deviation, and coefficient of variation (CV, standard deviation divided by the mean) were calculated for measurements at each set of parameters.

Table 1.

Beam delivery and device acquisition parameters.

Parameter	Values
Beam	6 MV, 6 MV FFF, and 10 MV FFF
Field Size	1 × 1 cm2, 3 × 3 cm2, and 5 × 5 cm2
Dose Rate	100, 200, 400, and 600 MU/min (6 MV)
	400, 600, 1000, 1400 MU/min (6 MV FFF)
	400, 800, 1200, and 2000 MU/min (10 MV FFF)
Monitor Units	50
Frame Rate	10 and 20 fps
Gain	18, 20, 22 dB

*FFF – Flattening Filter Free.

2.2. Measurement of spatial uniformity of scintillation intensity

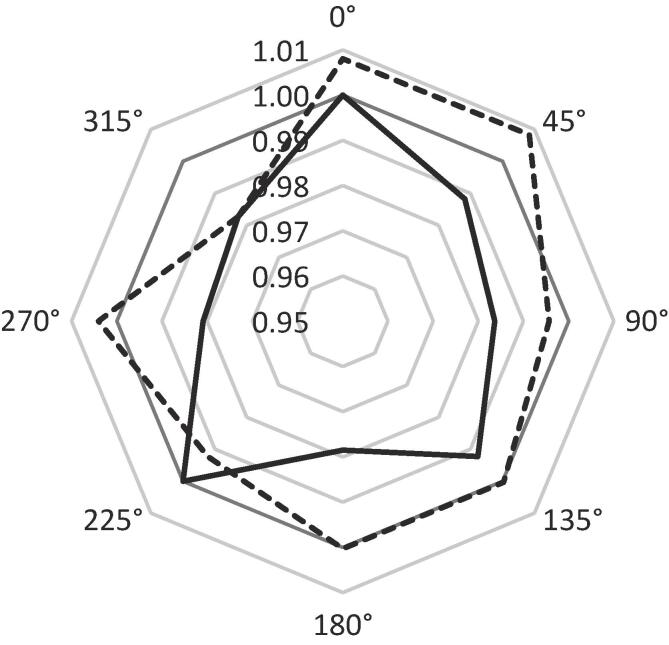
Additional measurements were acquired to determine uniformity across different parts of the device. A 6 MV, 3 × 3 cm² photon beam was used to deliver 50 MU at 600 MU/min with acquisition parameters of 24 dB gain and 5 fps frame rate at multiple gantry angles and longitudinal couch positions. These acquisition parameters were optimized for this individual experiment featuring a single energy, field size, and dose rate; they therefore differ from those listed in Table 1 used for the broader experiment where energy, field size, and dose rate vary. Seven gantry angles, starting at 0° and increasing to 315° in 45° increments, were considered, along with two longitudinal couch positions which placed measurements either near the base of the cone or near the middle of the cone, approximately 5 cm apart. These scintillation intensity measurements were made in triplicate, averaged, and normalized to the measurement acquired at 0° near the base of the cone.

2.3. Analytical equation to standardize measurements for gain and frame rate

As gain and frame rate are known to affect the measured scintillation intensity, we used a vendor-provided equation (Eq. (1)) to standardize the measurements from combinations of parameters in Table 1 to vendor-suggested reference parameters (20 dB and 20 fps). In Eq. (1), the measured scintillation intensity standardized to reference device acquisition parameters of frame rate and gain (${\mathit{Intensity}}_{\mathit{FR},G}$) is the product of the maximum cumulative scintillation intensity integrated over all frames (${\mathit{Intensity}}_{\mathit{Raw}}$), the ratio of the measurement and reference frame rates (${\mathit{FrameRate}}_{\mathit{Meas}}$ and ${\mathit{FrameRate}}_{\mathit{Ref}}$, respectively), and a logarithmic comparison of the measured and reference gains (${\mathit{Gain}}_{\mathit{Meas}}$ and ${\mathit{Gain}}_{\mathit{Ref}}$, respectively).

$${\mathit{Intensity}}_{\mathit{FR},G}={\mathit{Intensity}}_{\mathit{Raw}}\ast \frac{{\mathit{FrameRate}}_{\mathit{Meas}}}{{\mathit{FrameRate}}_{\mathit{Ref}}}\ast {10}^{\left(\frac{{\mathit{Gain}}_{\mathit{Ref}}-{\mathit{Gain}}_{\mathit{Meas}}}{20}\right)}$$ (1)

Measurements standardized for gain and frame rate using Eq. (1) were normalized to the 3 × 3 cm² measurement acquired at 600 MU/min and reference conditions (20 dB and 20 fps) for each beam. Because the 10 MV FFF beam is not configured to deliver beam at 600 MU/min, values at this dose rate were approximated by linear interpolation of measurements acquired at 400 MU/min and 800 MU/min. Specifically for the 20 fps reference frame rate, because the device was not sensitive enough to detect the 400 MU/min measurement at 20 fps, the interpolation was conducted using the 10 fps measurements and scaled according to the ratio of 800 MU/min measurements acquired at 20 fps and 10 fps.

2.4. Linear regression to standardize measurements for dose rate

In addition to the known influences of gain and frame rate, it was hypothesized that dose rate would also affect the scintillation intensity. Therefore, measurements standardized for gain and frame rate as described in Section 2.3 were subsequently analyzed with respect to dose rate. The dependence on dose rate was determined for each combination of beam, gain, and frame rate across all field sizes using linear regression.

2.5. Evaluation of standardization methods

To assess the methods of standardizing measurements for gain and frame rate alone (Section 2.3), or for gain, frame rate, and dose rate (Section 2.4), the root mean squared error (RMSE) was calculated between the standardized measurements acquired at non-reference conditions and those acquired under reference conditions for the same beam and field size. This was conducted for each combination of beam, gain, and frame rate.

3. Results

Across the replicate measurements for parameter combinations of Table 1, the average CV was 1.3% (standard deviation = 1.2%, range = 0.0–6.1%), and was similar for all beams.

3.1. Observed spatial uniformity of scintillation intensity

Scintillation intensity varied across different parts of the device. Measurements at different gantry angles and longitudinal couch positions were within 1–2% of the reference value at 0° near the base of the cone (Fig. 1). Measurements near the middle of the cone were generally larger than those at the base for the corresponding gantry angle.

Fig. 1.

Polar plot of the relative scintillation intensity as a function of gantry angle and longitudinal position. Solid line: measurements acquired near the base of the cone. Dotted line: measurements acquired near the middle of the cone. The unity line is thickened for emphasis. All measurements were normalized to that of 0° gantry angle near the base of the cone.

3.2. Effect of analytical equation for gain and frame rate

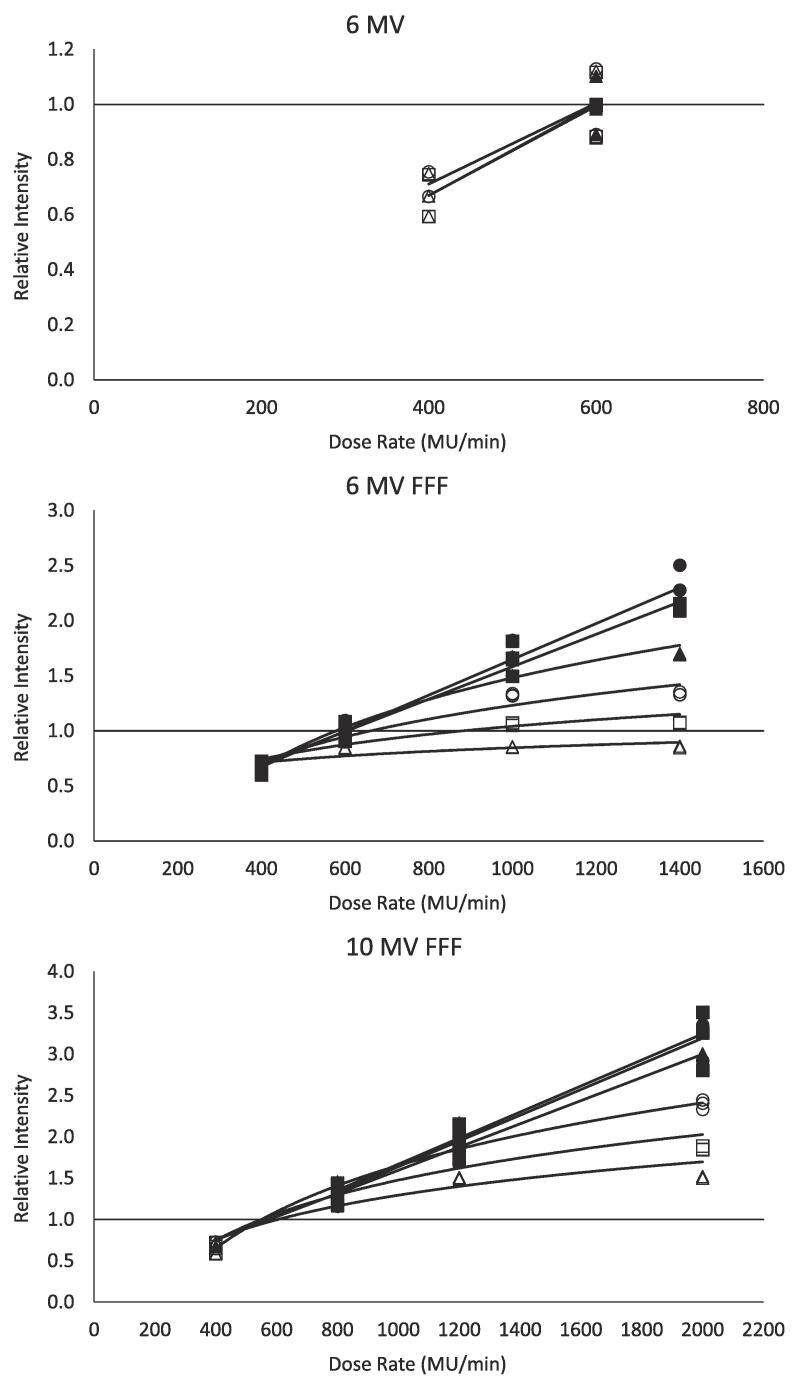
Fig. 2 depicts the relative scintillation intensity measurements standardized with respect to gain and frame rate as a function of dose rate. As described in Section 2.3, all data was normalized to 20 dB, 20 fps, 600 MU/min, and 3 × 3 cm² field size. Each combination of gain and frame rate is depicted as an individual series and is fit with its own regression function. The figure reveals that scintillation intensity increases as a function of dose rate. For some combinations of gain and frame rate, a regression line was determined to provide the best characterization of the dose rate dependence, while for others, the regression function took the form of a logarithmic curve ($y=A\times ln(x)+B$). The slope and curvature of the regression functions is driven largely by the high dose rates of the 6 MV FFF and 10 MV FFF beams, and is more prevalent for measurements acquired at higher gains and the slower 10 fps frame rate. Equations for all regression functions are provided in Table 2.

Fig. 2.

Relative scintillation intensity for 6 MV (top), 6 MV FFF (middle), and 10 MV FFF (bottom) measurements standardized with respect to gain and frame rate as a function of dose rate. Individual series represent different combinations of gain and frame rate, and are each fit with either a linear or logarithmic regression function. Regression function equations are presented in Table 2. Circle, square, and triangle markers represent 18 dB, 20 dB, and 22 dB gains, respectively. Unfilled and filled markers represent 10 fps and 20 fps frame rates, respectively. Data is normalized to beam-specific measurements at 20 fps, 20 dB, 600 MU/min, and 3 × 3 cm² field size.

Table 2.

Form and parameters of dose rate regression functions.

Beam	Frame Rate	Gain	Form	Parameters
				A	B
6 MV
	10 fps
		18 dB	Linear1	0.002	0.124
		20 dB	Linear	0.002	0.009
		22 dB	Linear	0.002	0.022
	20 fps
		20 dB	*	*	*
		22 dB	*	*	*
6 MV FFF
	10 fps
		18 dB	Exponential2	0.560	−2.634
		20 dB	Exponential	0.326	−1.210
		22 dB	Exponential	0.146	−0.163
	20 fps
		18 dB	Linear	0.002	0.024
		20 dB	Linear	0.002	0.110
		22 dB	Exponential	0.879	−4.590
10 MV FFF
	10 fps
		18 dB	Exponential	1.094	−5.904
		20 dB	Exponential	0.796	−4.024
		22 dB	Exponential	0.582	−2.728
	20 fps
		18 dB	Linear	0.002	0.090
		20 dB	Linear	0.002	0.081
		22 dB	Linear	0.001	0.191

* Measurements could only be acquired at 600 MU/min. No regression function needed.

¹Linear regression functions were of the form: $y=A\times x+B$.

²Exponential regression functions were of the form: $y=A\times ln(x)+B$.

When compared with measurements of the corresponding energy and field size at 600 MU/min, measurements standardized with respect to gain and frame rate alone resulted in errors ranging from 0% to 152%. The error observed for each beam, gain, and frame rate are presented in Table 3. As depicted in Fig. 2 and Table 3, the error tends to increase with decreasing gain, increasing frame rate, and increasing dose rate.

Table 3.

Root mean squared error of measurements acquired at non-reference conditions when standardized for gain and frame rate alone or with dose rate.

		Standardized for gain and frame rate			Standardized for gain, frame rate, and dose rate
Beam	Frame Rate	Gain			Gain
		18 dB	20 dB	22 dB	18 dB	20 dB	22 dB
6 MV
	10 fps	22%	21%	24%	4%	2%	1%
	20 fps	*	0%	1%	*	0%	1%
6 MV FFF
	10 fps	29%	19%	22%	10%	8%	7%
	20 fps	75%	68%	49%	3%	8%	10%
10 MV FFF
	10 fps	91%	65%	43%	13%	17%	14%
	20 fps	152%	140%	122%	5%	7%	11%

* Device was not sensitive enough to detect measurements at 18 dB and 20 fps.

3.3. Effect of regression functions for dose rate

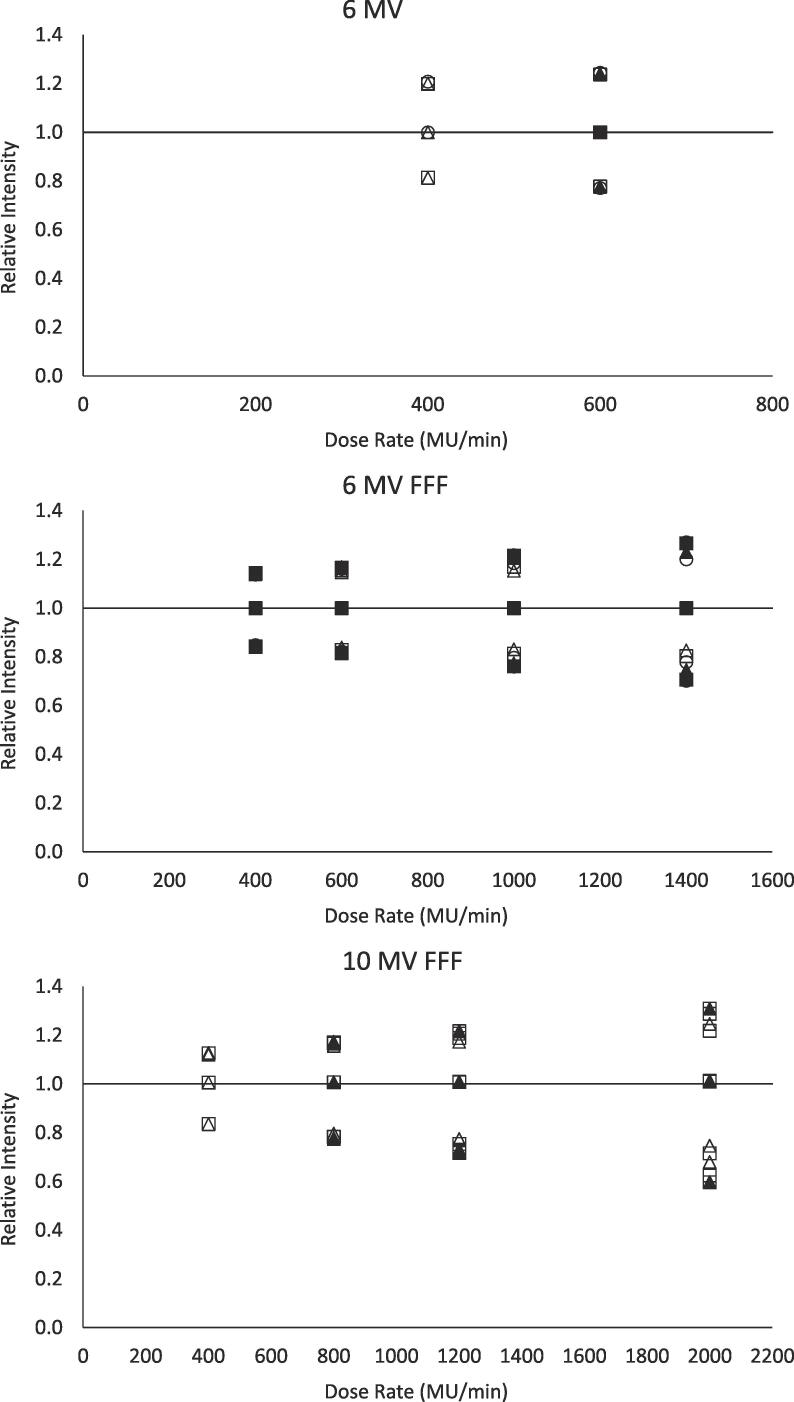
Similar to Fig. 2, Fig. 3 depicts the relative scintillation intensity measurements standardized with respect to gain and frame rate, but also with respect to dose rate according to the observed regression functions. The figure reveals that the dependence on dose rate observed in Fig. 2 has largely been removed by the additional standardization step. This is also observed by the considerable decrease in the RMSE depicted in Table 3 when compared to measurements standardized for gain and frame rate alone. The range in error for measurements standardized for gain, frame rate, and dose rate is between 0% and 17%. Also apparent in Table 3 is that the errors are more consistent across gains and frame rates. The three distinct levels visible at each dose rate in Fig. 3 correspond to the three field sizes, as these values are all normalized to the 3 × 3 cm² measurement. While the dependence on dose rate was determined without consideration of field size – as the regression functions were fit to measurements from all field sizes – when applied to standardize measurements, the regression functions were applied to each field size individually. The RMSE, therefore, reflects the error in regards to the corresponding field size acquired at reference conditions, not the 3 × 3 cm² field sized used for normalization.

Fig. 3.

Relative scintillation intensity for 6 MV (top), 6 MV FFF (middle), and 10 MV FFF (bottom) measurements standardized with respect to gain, frame rate, and dose rate as a function of dose rate. Individual series represent different combinations of gain and frame rate. Three distinct levels at each dose rate represent 1 × 1 cm², 3 × 3 cm², and 5 × 5 cm² field sizes. Circle, square, and triangle markers represent 18 dB, 20 dB, and 22 dB gains, respectively. Unfilled and filled markers represent 10 fps and 20 fps frame rates, respectively. Data is normalized to beam-specific measurements at 20 fps, 20 dB, 600 MU/min, and 3 × 3 cm² field size.

4. Discussion

This work evaluated the potential of using conical scintillation detectors for PSQA of intensity-modulated photon plans by measuring the dependence of scintillation intensity on beam delivery and device acquisition parameters. While conical scintillation detectors are in routine clinical use, to our knowledge, this is the first evaluation of such a device for PSQA of intensity-modulated photon plans and of considerations unique to this application. Measurements standardized to reference conditions with respect to gain and frame rate demonstrated a considerable dependence on beam delivery dose rate. Furthermore, the magnitude and nature of this dependence varied between different combinations of gain and frame rate. Consideration of gain, frame rate, and dose rate are all required to accurately compare measurements acquired with different parameters using a conical scintillation detector. Even when accounting for the considerable dependence on dose rate, residual errors ranged between 0% and 17% depending on the beam, gain, and frame rate.

Several anticipated advantages of using this kind of device for PSQA were observed, including high spatial resolution, the ability to encode 3D information during acquisition, independence from the treatment delivery system, and minimal collision risk. In addition, replicate measurements showed adequate reproducibility on the order of 1% for identical beam delivery and device acquisition parameters.

Some variation in the measured scintillation intensity was observed when different parts of the device were irradiated. While this non-uniformity alone was relatively small, a strategy to mitigate its contribution to the total uncertainty would be advantageous. Reasons for this non-uniformity might include variations in the construction of the scintillating layer as well as geometric effects due to the angle and curvature of the cone that might have introduced the systematic discrepancy between longitudinal couch positions. Considering the observed measurement precision, it is possible that this non-uniformity could be characterized to map the relative response over the device. For geometric considerations, this may be achieved specific to the device model. For construction variations, it would need to be performed specific to each individual unit. This process could resemble our method of irradiating different parts of the device with constant delivery and acquisition parameters to assess the spatial variation of device’s response.

The observed dependencies on gain, frame rate, and dose rate were logical due to the understanding that instantaneous scintillation intensity is proportional to the incident fluence (i.e. dose rate), and that the scintillation intensity measured in each frame depends on the duration of the frame (i.e. inverse of the frame rate) and the degree of signal amplification (i.e. gain). Therefore, the vendor-provided equation is well directed, but it should also consider correction factors for measurements acquired at different dose rates. Incorporating models of dose rate dependence derived from the regression functions in Fig. 2 greatly improved the accuracy when standardizing measurements acquired at non-reference conditions. It was observed that the curvature of the regression functions, necessary to fit the data acquired at higher dose rates, was more severe for measurements acquired at the higher gains and with the lower 10 fps frame rate. As this curvature represented a bend back towards scintillation intensity values similar to those measured at the reference dose rate, combinations of gain and frame rate with regression functions exhibiting more severe curvature were associated with smaller errors.

To date, conical scintillation detectors have predominantly been used for measuring geometric properties of a limited number of treatment modalities [8], [9], [10], [11], [12], [13]. However, Jenkins et al. has measured the effects of dose rate on a similar scintillator for the purpose of real-time treatment beam visualization [15]. The scintillator they investigated was created in-house, and while of a similar gadolinium-based composition, featured a flat-film geometry, not a conical geometry. With this film, they observed that the relative scintillation intensity increased linearly as a function of dose rate for 200–600 MU/min using 6 MV and 10 MV beams. This is consistent with our observations at 400 and 600 MU/min using the 6 MV beam. We also observed linear dependences on dose rate for the 6 MV FFF and 10 MV FFF beams when acquired using the 20 fps dose rate. This was the dose rate used by Jenkins et al., although experimental camera setups varied with the camera we used having been integrated into the conical device. In addition to the linear dependences on dose rate, we observed logarithmic dependences on dose rate for the slower 10 fps dose rate and at higher dose rates achievable by FFF beams, however these dose rates and FFF beams were not included in Jenkins et al. analysis. Lastly, we observed that the parameters of the dose rate regression functions, regardless of form, varied between sets of delivery and acquisition parameters, such that these parameters must be considered to correctly characterize the response of the device.

With the current data acquisition software available with the device used here, the gain and frame rate are set prior to acquisition and remain constant for the duration of the measurement. The range of these parameters is large and many irradiation conditions can be captured successfully as a result. However, it was observed that no particular combination of gain and frame rate covered the entire range of beam delivery parameters investigated here. This resulted in insufficient data acquired using 10 MV and 15 MV beams which prevented their analysis in this work. A user will likely need to tune these parameters for specific irradiation conditions prior to the measurement to ensure complete data acquisition.

The dependence on dose rate warrants further note. When not accounted for, the dose rate of the delivered beam was observed to greatly compromise the accuracy of the vendor-provided standardization equation. Tuning the parameters to consider dose rate is therefore key for optimal data acquisition. One challenge, however, is that the dose rate may vary during treatment plan delivery. It is plausible that this variation could result in a measurement signal outside of detectable range. As a result, to use the device for PSQA, the sensitivity must either have a range broad enough to encompass the full range of dose rates possible during delivery of the plan, or it must adjust dynamically. Regardless, the effect of dose rate and the effect of the combination of dose rate with other acquisition parameters on scintillation intensity must be considered to provide accurate quantitative measurements.

One aspect presented here that was not fully addressed was the larger measurement error observed for 6 MV FFF and 10 MV FFF beams that persisted even after normalizing the measurements to the standardized reference parameters. This suggests that additional factors and/or additional complexity in modeling the effects of those factors remains necessary. That the error for 6 MV FFF measurements was greater than in the 6 MV measurements suggests that this variability might at least in part be attributable to the effect of the flattening filter, which affects the energy spectra and fluence incident on the device. It may also be the case that while the current correction factors largely account for variations in measured scintillation intensity due to frame rate and dose rate, they may not be able to capture higher order effects or interactions of these dependences, and increasingly sophisticated models may be necessary to decrease the observed variation. We avoided adding further complexity to our models of the scintillation intensity dependence on beam delivery and device acquisition due to limitations of our data set and a concern of overfitting.

Other practical considerations that will be important if the device is to be considered for PSQA include factors regarding the geometry of the device and nature of the physical quantity of its signal. It was observed that due to the curvature of the cone, there was an upper limit on the field size of the beam that could be measured by the device. At field sizes greater than this limit, the entrance and exit scintillation spots merge proving challenging for the software to analyze, and portions of the field miss the cone entirely. The largest field size tested here, 5 × 5 cm², was able to be measured provided the beam was directed near the bottom half of the cone. This limitation might make the device most appropriate for treatment plans of relatively small field sizes such as SBRT.

Another consideration pertains to how the results of the PSQA are to be quantified and evaluated. Conventional QA systems are capable of generating an anticipated measurement to be verified with the actual measurement. This comparison could relate to the scintillation intensity along the surface of the cone or to a volumetric description of fluence or dose within it. Measurements with conical scintillation detectors inherently describe the radiation incident on their surface. However, neither conventional treatment planning systems nor the associated software currently provide a convenient workflow for establishing the anticipated value of this signal based on the parameters of an individual treatment plan. The associated software does currently allow for the determination of a volumetric distribution of cumulative fluence within the cone derived from the scintillation intensity observed at its surface. This is a potential domain in which the QA assessment may take place. However, it is worth noting that again, there is not currently an established workflow to generate the anticipated distribution from a treatment plan, as this distribution is not equivalent to the planned dose due to incomplete consideration of attenuation and scatter. Once the anticipated measurement can be created along with a measurement in the appropriate domain – be it scintillation intensity on the cone surface, or a description of fluence or dose within the volume of the cone – the device could, in principle, be used for quantitative evaluation of PSQA. To fully extend the application of the device to PSQA, however, the effects of dose rate and residual sources of variations in the measured scintillation intensity along with practical considerations like field size limitations must be addressed, and an appropriate domain for quantitative evaluation must be identified and fully supported.

Conical scintillation detectors have several advantages for PSQA measurements, but demonstrate considerable dependence on beam delivery and device acquisition parameters. This work demonstrates that consideration of dose rate and combinations of dose rate with gain and frame rate are integral to the standardization of measurements acquired under different parameters, however, parameter-dependent errors remain for flattening filter free beams.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following are the Supplementary data to this article: