Abstract
Background and purpose
In adaptive radiotherapy, deformable image registration (DIR) is used to propagate delineations of tumors and organs into a new therapy plan and to calculate the accumulated total dose. Many DIR accuracy metrics have been proposed. An alternative proposed here could be a local uncertainty (LU) metric for DIR results.
Materials and methods
The LU represented the uncertainty of each DIR position and was focused on deformation evaluation in uniformly-dense regions. Four cases demonstrated LU calculations: two head and neck cancer cases, a lung cancer case, and a prostate cancer case. Each underwent two CT examinations for radiotherapy planning.
Results
LU maps were calculated from each DIR of the clinical cases. Reduced fat regions had LUs of 4.6 ± 0.9 mm, 4.8 ± 1.0 mm, and 4.5 ± 0.7 mm, while the shrunken left parotid gland had a LU of 4.1 ± 0.8 mm and the shrunken lung tumor had a LU of 3.7 ± 0.7 mm. The bowels in the pelvic region had a LU of 10.2 ± 3.7 mm. LU histograms for the cases were similar and 99% of the voxels had a LU < 3 mm.
Conclusions
LU is a new uncertainty metric for DIR that was demonstrated for clinical cases. It had a tolerance of <3 mm.
Keywords: Deformable image registration, Uncertainty, Deformation vector field correctness, Radiotherapy
1. Introduction
Adaptive radiotherapy (ART) is commonly employed in head and neck cancer [1], [2], [3], prostate cancer [4], [5], and other sites [6], [7] and modalities [8], [9]. Deformable image registration (DIR) is an important ART tool because it helps to delineate organs and targets for therapy re-planning [10], [11], [12], [13].
DIR has been used for summing dose accumulations over treatment courses. To measure daily dose distributions, structures are propagated to cone beam CT images or megavoltage CT images acquired for patient setup and dose calculations [12], [13], [14], [15], [16], [17], [18], [19]. DIR has been used to calculate accumulated dose distributions using daily dose distributions [20], [21], [22]. Daily distributions are deformed according to the deformation vector field (DVF), and then summed to obtain a total dose distribution. This assumes that DIRs work accurately. However, issues of sliding organs [23] and uniform-density regions [24] are well known. Specifically, DIR deformation at the interface between a fixed organ and a sliding organ was inaccurate because these organs could move separately. The incorrect deformation may be visually obvious. The issue of uniform-density regions is that the interior of these regions could be deformed and incorrect deformation is difficult to identify because the pixels have the same density. There is little information on the accuracy of deformation in the interior, especially for clinical cases. Hence, an accuracy check does not work, which is more serious for dose accumulation because it may lead to incorrect dose summations.
The most frequently used metric for DIR accuracy is the Dice similarity coefficient (DCS) [25]. It indicates the similarity in volume and shape between organs in reference and deformed images, which is the resulting image of DIR [26], [27]. Target registration error (TRE) quantification, which shows the distance error for fiducial markers and/or anatomical landmarks between a reference image and a deformed image, is also frequently calculated [28], [29], [30], [31], [32]. The Hausdorff distance and surface errors [27], [33] use boundaries of organs and fiducial markers in the reference image as the ground truth, and thus only assess deformation accuracies of the boundaries and markers. If deformation in the interior of a uniform-density organ is incorrect when the organ in the resulting deformed image is grossly similar to the reference image, the evaluations will assess the result as good. DSC, Hausdorff distances, TRE, and surface errors cannot assess the correctness of interior deformation in organs. Intensity differences between two images have not been effective when a voxel in the organ is moved to a wrong place. Elsewhere, a known deformation was performed on a reference image to generate a moving image that was deformed to fit the reference image [27], [28]. The deformation calculated by DIR methods and the given deformation were compared. However, it is difficult to follow anatomical motion such as respiration.
In a DVF assessment, Varadhan et al. [27] used inverse consistency error, Jacobians, and harmonic energy. The inverse consistency error revealed the difference between a DVF from image A to image B calculated with a DIR, and another DVF from image B to image A as a consistency metric [34], [35]. The Jacobian and the harmonic energies indicated the deformation magnitude and DVF smoothness. Schreibmann et al. evaluated a DVF directly by using the Curl operation [36] that detected unrealistic deformation. For an accurate quantification of dose accumulation, accuracy evaluation of an individual DIR result is necessary. However, because of the lack of deformation ground truth, that assessment in clinical cases is impossible.
For DIR uncertainty evaluation, Murphy et al. [24] used randomly defined volumes of interest (VOIs) in a pair of CT image sets and obtained DVFs for the VOIs with DIR. The mean DVF was calculated from the DVFs in overlapping regions of the VOIs and the DVF error was the difference from the mean. This method required 50 repeated DIR executions for one pair of images. Another study calculated the DIR uncertainty by using at least five image sets [37]. These methods revealed variations in multiple DVFs and the comprehensive uncertainty of the DIR method. However, they could be used for DIR quality assurance and not for results.
Here, a local uncertainty (LU) metric was calculated from a moving image and a DVF; it required one DIR execution. It evaluated uncertainties in uniform-density regions and was applied to four clinical cases.
2. Methods
2.1. Local uncertainty
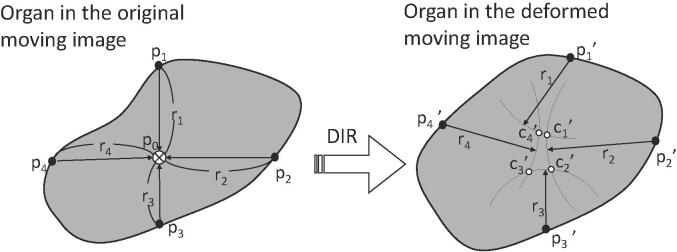
The LUs represented positional variations of candidates for a target position, which were calculated from surrounding organ edges after DIR. Hence, organ edges were used to determine candidate positions in organ interiors.
A moving image was defined as one of the initial images for DIR and was deformed to match a reference image. A reference image was defined as another initial image to which the moving image was matched. A deformed image was a deformed moving image and a DIR result.
To calculate the LU for target position p0, neighboring positions p1, p2, p3,…pn were searched radially from p0 in an initial moving image Isrc (before DIR). The neighboring positions were set on organ edges that had sufficient contrast with the pixel density at p0 (Eq. (1)):
| (1) |
Here, was a unit vector of arbitrary direction that originated on p0, k was the minimum number to satisfy the third condition in Eq. (1), and cnt was the minimum contrast needed to resolve a pixel on an organ edge.
Distances from p1, p2, p3,…pn to p0 were r1, r2, r3,…rn, respectively (Eq. (2)). The DIR mapped p0, p1, p2, p3,… pn to p′0, p′1, p′2, p′3,… p′n, respectively, with a DVF T in Eq. (3):
| (2) |
| (3) |
Then, a candidate position c'i in a deformed image was calculated as the intersection of the p'i-centered sphere with radius ri, the p'i+1-centered sphere with radius ri+1, and the p'i+2-centered sphere with radius ri+2. The p'i-centered sphere with radius ri was defined as:
| (4) |
The intersection of the three spheres was then calculated from:
| (5) |
where A was an arbitrary value. The intersection gj could have two positions (g′j_0 and g′j_1) at the maximum. The closer of the two positions to p′0 was chosen as candidate c'i (Eq. (6)):
| (6) |
where d(p′0, g′j_0) and d(p′0, g′j_1) was the distance between p′0 and g′j_0 or g′j_1.
Finally, the LU value at p'0 was calculated from the coordinates of the candidates (Eqs. (7), (8), (9), (10)):
| (7) |
| (8) |
| (9) |
| (10) |
where m was the number of candidate positions, and were the mean values of the x, y, and z candidate coordinates. The coordinates of the ith candidate were xi, yi, and zi. Hence, the LU value represented the positional variation of a target position, shown schematically in Fig. 1 for 2D images.
Fig. 1.
Schematic of candidate position determination in two-dimensional images for a local uncertainty calculation.
In Fig. 1 of the Supplementary Material, a uniform-density region in a reference image was shifted by one pixel in a moving image. DIR software often provides a resulting DVF that exhibited deformation only in areas close to the boundary of the uniform-density region. In this case, the Dice coefficient was one because the shape of the region in the deformed image completely matched that in the reference image. However, the actual positions of the stationary portion of the uniform-density region were incorrect, and rigid shifting of the uniform-density region was the correct deformation. When LU calculations were performed, the stationary portion had a high LU. The portions close to the boundary had zero or low LU because of better deformation.
2.2. Cases
The LU calculation was applied to the DIR results of two head and neck cancer patients (#1, 2), one lung cancer case (#3), and one prostate cancer case (#4). Each underwent two CT examinations for radiotherapy planning and re-planning. The CT scanner (Aquilion LB, Toshiba Medical Systems, Nasu, Tochigi, Japan) had a tube voltage of 120 kV and a current of 100 mA. Each scan required 2 s, the field of view was 450-mm × 450-mm (512 × 512 pixels), and the section thickness was 2 mm.
In Supplementary Material Fig. 2, the first CT images for the initial radiotherapy plan (green) were rigidly translated and superimposed onto the second CT images for re-planning (magenta). In Case #1, the patient had experienced weight loss before the second CT image set. Hence, the fat regions around the mandible bone were shrunken. Additionally, the right shoulder was higher, the neck was flexed leftward, and the head was rotated counter-clockwise with the mouth opened slightly relative to the first CT images (Supplementary Material Fig. 2a–c). In Case #2, the tongue was positioned higher in the mouth and the left parotid gland was shrunken in the second CT images (Supplementary Material Fig. 2d–f). Otherwise, the two sets of CT images matched. In Case #3, the volume of the tumor in the left lung was reduced during the treatment course (Supplementary Material Fig. 2g–i). In Case #4, the patient suffered from pelvic bone metastasis. A large deformation was seen in the bladder volume and in the bowel. The amount of urine in the bladder was lower in the reference image, and the rectum and colon moved in a complex way. There were also different stools in the rectum and the sigmoid colon (Supplementary Material Fig. 2j–l).
DIR was performed for each case. The second CT images were used as the reference images, and the first CT images were used as the moving images, which were deformed to fit the reference images. The DIR software (MIM Maestro version 6.7, MIM Software Inc., Cleveland OH, USA) was used to obtain DVFs. All cases underwent automatic DIR processing without manual refinement. The CT images and DVFs were exported in Digital Imaging and Communications in Medicine (DICOM) format. The LU map was calculated with an in-house ImageJ plugin from the moving CT image and the DVF.
To find neighboring positions on organ edges in the LU calculation, voxels having a difference of ≥30 Hounsfield units (HU) with respect to the intensity of a target voxel (cnt = 30 HU) were identified along each of the eighteen neighboring voxel directions () in three dimensions. The air regions in the CT images had a standard deviation of 15 HU; therefore, the difference of twice the standard deviation (≥30 HU) was used. Twenty-six or more neighboring radial voxel directions could be used. Three of the neighboring positions on edges were used for the calculation of one candidate. The grid size of the LU map was 2.6-mm × 2.6-mm × 6-mm.
The LU map image for each case was visually assessed. It was placed beside the DVF data on the moving images to find deformation correspondences with the LU values.
3. Results
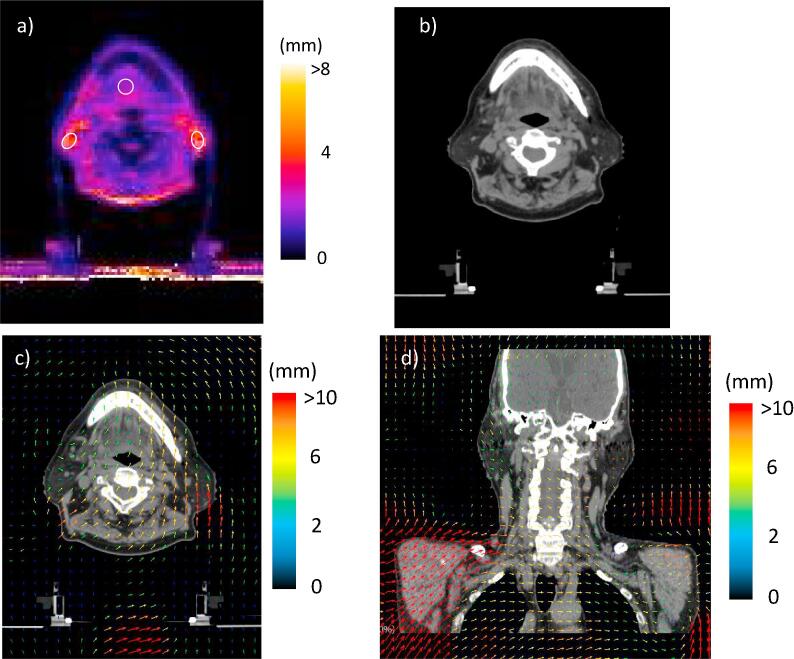
Fig. 2 shows the LU map, the deformed image, and the DVF data on the moving images for Case #1. The DVF data included body position shifts between the two CT exams. The LU map had high values for the fat regions around the mandible bone and the back of the neck (Fig. 2a). The left and right fat regions, the back of the neck, and a tongue region had LUs of 4.6 ± 0.9 mm, 4.8 ± 1.0 mm, 4.5 ± 0.7 mm, and 2.7 ± 0.5 mm, respectively. The fat regions in the deformed image seemed to be correctly deformed (Fig. 2b). However, the DVF data for the axial image revealed that the deformation vectors around the left region varied in length (4–10 mm). Similarly, the region in the back of the neck had deformation vectors that varied over 0–6 mm. Meanwhile, in the coronal image (Fig. 2d), the deformation vectors for the right region were directed towards the middle line of the body. There was a 5-mm body shift in the anterior-posterior direction between the two CT image sets.
Fig. 2.
The local uncertainty (LU) map, the deformed image, and deformation vector field (DVF) for Case #1; a) the LU map, b) the deformed image and c) the DVF on the moving images. In the LU map, the LU value was represented in color as shown by the color bar and the white circles were the regions of interest for the determination of the mean LU value. The DVF was represented as colored arrows on the moving images and the color showed the magnitude of the deformation vector.
In Case #2 (Supplementary material Fig. 3), the right and left parotid glands had high LU values of 3.3 ± 0.5 mm and 4.1 ± 0.8, respectively (Supplementary material Fig. 3a). The glands in the deformed image seemed to be correctly deformed (Supplementary material Fig. 3b). The DVF data for the axial and coronal planes revealed deformation vectors directed towards the middle line of the body in the left gland region. In contrast, the vectors in the right gland region were <2 mm (Supplementary material Fig. 3c and d), which indicated that it had not moved. However, the entire body was moved by 4 mm in the interior direction between two CT exams.
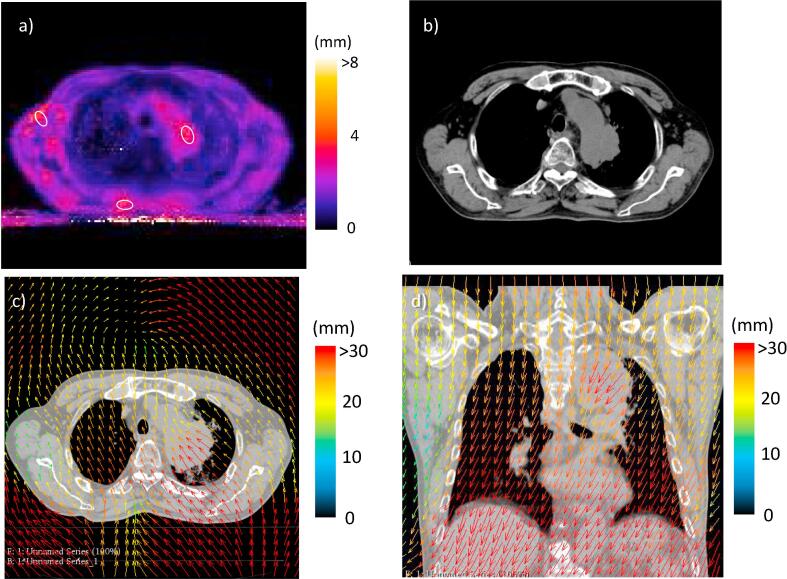
In Case #3 (Fig. 3), which had a tumor located next to the aorta arch, a back muscle, and the fat region of the right axillary had LUs of 3.7 ± 0.7 mm, 4.1 ± 0.8 mm, and 3.7 ± 1.0 mm, respectively (Fig. 3a). Although the DVF data globally represented large displacements due to a body shift, the deformation vectors in the tumor region were larger, corresponding to shrinkage, relative to those in the surrounding region. In contrast, deformation vectors in the fat region in the axial right, as well as part of the back muscle, were smaller than those in the surrounding regions (Fig. 3c and d). Despite the partial deformation, unnatural distortion was not observed for the muscle in the deformed image (Fig. 3b).
Fig. 3.
The local uncertainty (LU) map, the deformed image, and deformation vector field (DVF) for Case #3; a) the LU map, b) the deformed image and c) the DVF on the moving images. On the LU map, the LU value was represented in color as shown by the color bar and the white circles were the regions of interest for the determination of the mean LU value. The DVF was represented as colored arrows on the moving images and the color showed the magnitude of the deformation vector.
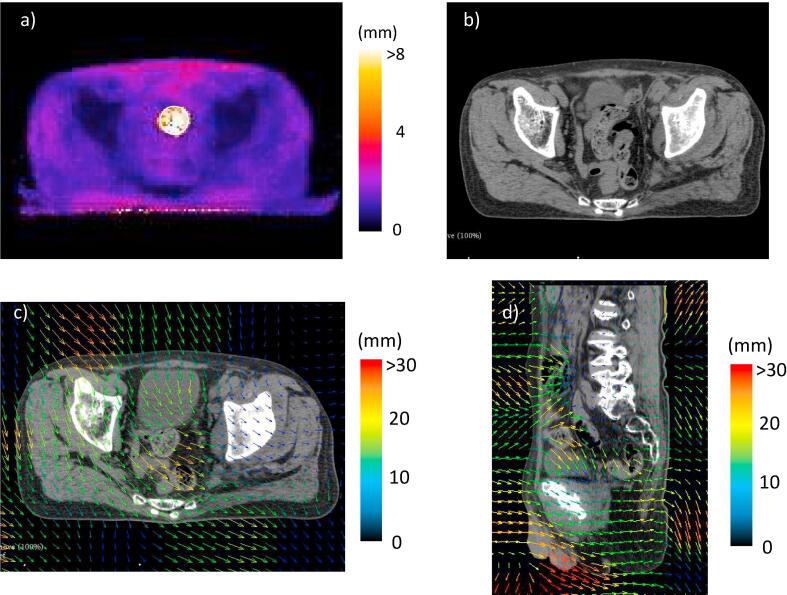
In Case #4 (Fig. 4), there was a high LU region (10.2 ± 3.7 mm) at the center of the pelvis (Fig. 4a). The region included the rectum and the sigmoid colon, which could move in a complex way. Hence, the DIR method could not match these tissues between two CT images (Fig. 4b). The deformation vectors around the region were relatively smooth, which indicated that the DIR could not cover their complex movements (Fig. 4c and d).
Fig. 4.
The local uncertainty (LU) map, the deformed image, and deformation vector field (DVF) for Case #4; a) the LU map, b) the deformed image and c) the DVF on the moving images. On the LU map, the LU value was represented in color as shown by the color bar and the white circles were the regions of interest for the determination of the mean LU value. The DVF was represented as colored arrows on the moving images and the color showed the magnitude of the deformation vector.
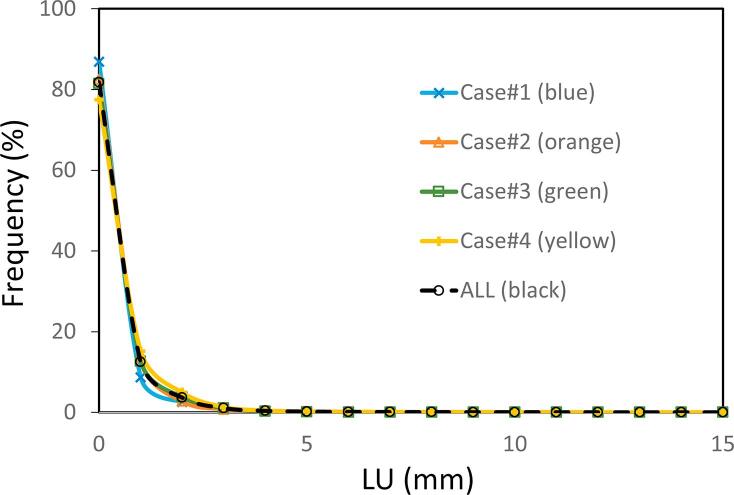
Histograms of LU values for all the cases were plotted in Fig. 5. They were normalized by the number of voxels in each case. In the plot, 95% of the voxels had a LU < 1.2 mm, and 99% had a LU < 3 mm.
Fig. 5.
Histograms of the local uncertainty value for the four cases. The frequency of each local uncertainty bin was normalized by the total number of voxels.
4. Discussion
LU maps of DIR results evaluated local uncertainties in uniform-density regions and could represent position uncertainties for a DIR method. Other uncertainty evaluation methods [24], [37] provided the total DIR uncertainty. The distance discordance metric (DDM) of Saleh et al. [37] was similar to the LU. They reported high DDM of >6 mm for a head and neck cancer patient; whereas the tolerance of LU was 3 mm. This difference derives from the definitions, the DIR algorithms, and the number of the datasets. The DDM represented the mean distance between candidate positions and the LU represented a standard deviation of candidate position coordinates. Saleh et al. used a B-spline-based DIR algorithm, while MIM maestro was used here. The DDM was calculated from five to ten CT image sets, while the LU was calculated from one pair of CT images. The advantage of the LU calculation was that it required only one pair, which meant that it could represent the uncertainty of individual DIRs.
Quantitative accuracy validation of the uncertainty map calculated by the LU metric was difficult because there was no ground truth of DIR uncertainty. Additionally, the uncertainty of deformation did not necessarily relate to DSC, TRE, and intensity differences. Thus, the limitation here was that the validation of LU maps was simply visual inspection of the deformations.
Thus, high LU values were observed in uniform-density regions, fat regions, muscles, in the parotid glands, and in tumors that shrunk or were deformed relative to surrounding regions. These results suggested that an LU could be calculated for each organ. In LU maps for Cases #1, #2, and #3, regions and tissues that were shrunken or stretched because of volume change or motion had high LUs similar to the example in Fig. 1 of the Supplementary Material. There, the LU represented the uncertainty of deformation in uniform-density regions. However, further analysis may be necessary for Case #4 because the DIR examination could not match the bowels in the pelvis in the moving image with those in the reference image. Therefore, the DIR produced a completely erroneous DVF. The LU value of an organ that was deformed incorrectly might not represent the correct uncertainty for that organ, which suggested that the LU depended on DIR accuracy.
A LU calculation could depend on organ volume. For a calculation position in a large organ, the distance to an organ edge may be long and thus affect the LU value. However, because many organ edges are depicted in a CT image, this concern may not be important. For example, the LU calculations for three different sites of the four cases produced the same histograms (Fig. 5). The LU calculations also produced stable values independent of body site. Finally, 99% of the voxels had LU < 3 mm; thus, 3 mm could be considered the LU tolerance for a DIR result.
For assessing dose accumulation, a LU map would be effective. Multiple DIR executions and dose summations are required to obtain a total accumulated dose distribution for a treatment course. A LU map could be summed to obtain a total LU by means of root-sum-square.
The LU calculations do not necessarily need to use MIM software to perform DIR executions. If DIR software is able to save the DVF, the LU could be calculated using the DVF and moving CT images. In addition, the contrast of >30 HU could be used to detect organ edges. If there were two contacting tissues with no difference in density, then the two tissues would be treated as an organ. The LU could be incorrect if these tissues moved independently. To avoid this issue, the detection of organ edges needs to be improved
In conclusion, an uncertainty metric LU for DIR was demonstrated using DIR results from four clinical cases. Organs with uniform density that had shrunk or were deformed had LU values ≥ 3 mm. An LU of 3 mm could be the tolerance value because 99% of all volumes had <3 mm. Because the LU calculations depended on the DIR accuracy, a combination of LU calculation and accuracy evaluation might be necessary.
Acknowledgments
Acknowledgements
This work was supported by The Japan Society for the Promotion of Science, Grant-in-Aid for Scientific Research (C) (JSPS KAKENHI Grant Number JP 26460724). We thank Alan Burns, PhD, from the Edanz Group (www.edanzediting.com/ac) for editing a draft of this manuscript.
Conflict of interest
The authors report no conflicts of interest.
Footnotes
Supplementary data associated with this article can be found, in the online version, at https://doi.org/10.1016/j.phro.2018.05.005.
Appendix A. Supplementary data
References
- 1.Castelli J., Simon A., Louvel G., Henry O., Chajon E., Nassef M. Impact of head and neck cancer adaptive radiotherapy to spare the parotid glands and decrease the risk of xerostomia. Radiat Oncol. 2015;10:6. doi: 10.1186/s13014-014-0318-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Yip C., Thomas C., Michaelidou A., James D., Lynn R., Lei M. Co-registration of cone beam CT and planning CT in head and neck IMRT dose estimation: a feasible adaptive radiotherapy strategy. Br J Radiol. 2014;87:20130532. doi: 10.1259/bjr.20130532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Nishi T., Nishimura Y., Shibata T., Tamura M., Nishigaito N., Okumura M. Volume and dosimetric changes and initial clinical experience of a two-step adaptive intensity modulated radiation therapy (IMRT) scheme for head and neck cancer. Radiother Oncol. 2013;106:85–89. doi: 10.1016/j.radonc.2012.11.005. [DOI] [PubMed] [Google Scholar]
- 4.Nijkamp J., Pos F.J., Nuver T.T., de Jong R., Remeijer P., Sonke J.-J. Adaptive radiotherapy for prostate cancer using kilovoltage cone-beam computed tomography: first clinical results. Int J Radiat Oncol Biol Phys. 2008;70:75–82. doi: 10.1016/j.ijrobp.2007.05.046. [DOI] [PubMed] [Google Scholar]
- 5.Westendorp H., Hoekstra C.J., Immerzeel J.J., van de Pol S.M.G., Niël C.G.H.J., Kattevilder R.A.J. Cone-beam CT-based adaptive planning improves permanent prostate brachytherapy dosimetry: an analysis of 1266 patients. Med Phys. 2017 doi: 10.1002/mp.12156. [DOI] [PubMed] [Google Scholar]
- 6.Xiao L., Liu N., Zhang G., Zhang H., Gao S., Fu Z. Late-course adaptive adjustment based on metabolic tumor volume changes during radiotherapy may reduce radiation toxicity in patients with non-small cell lung cancer. PLoS One. 2017;12:e0170901. doi: 10.1371/journal.pone.0170901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Arnesen M.R., Hellebust T.P., Malinen E. Impact of dose escalation and adaptive radiotherapy for cervical cancers on tumour shrinkage-a modelling study. Phys Med Biol. 2017;62 doi: 10.1088/1361-6560/aa5de2. N107–19. [DOI] [PubMed] [Google Scholar]
- 8.Veiga C., Janssens G., Teng C.-L., Baudier T., Hotoiu L., McClelland J.R. First clinical investigation of cone beam computed tomography and deformable registration for adaptive proton therapy for lung cancer. Int J Radiat Oncol. 2016;95:549–559. doi: 10.1016/j.ijrobp.2016.01.055. [DOI] [PubMed] [Google Scholar]
- 9.Kraus K.M., Jäkel O., Niebuhr N.I., Pfaffenberger A. Generation of synthetic CT data using patient specific daily MR image data and image registration. Phys Med Biol. 2017;62:1358–1377. doi: 10.1088/1361-6560/aa5200. [DOI] [PubMed] [Google Scholar]
- 10.Hvid C.A., Elstrøm U.V., Jensen K., Alber M., Grau C. Accuracy of software-assisted contour propagation from planning CT to cone beam CT in head and neck radiotherapy. Acta Oncol. 2016;55:1324–1330. doi: 10.1080/0284186X.2016.1185149. [DOI] [PubMed] [Google Scholar]
- 11.Hardcastle N., Tomé W.a., Cannon D.M., Brouwer C.L., Wittendorp P.W., Dogan N. A multi-institution evaluation of deformable image registration algorithms for automatic organ delineation in adaptive head and neck radiotherapy. Radiat Oncol. 2012:7–90. doi: 10.1186/1748-717X-7-90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Lu W., Olivera G.H., Chen Q., Ruchala K.J., Haimerl J., Meeks S.L. Deformable registration of the planning image (kVCT) and the daily images (MVCT) for adaptive radiation therapy. Phys Med Biol. 2006;51:4357–4374. doi: 10.1088/0031-9155/51/17/015. [DOI] [PubMed] [Google Scholar]
- 13.Petit S.F., van Elmpt W.J.C., Nijsten S.M.J.J.G., Lambin P., Dekker A.L.A.J. Calibration of megavoltage cone-beam CT for radiotherapy dose calculations: correction of cupping artifacts and conversion of CT numbers to electron density. Med Phys. 2008;35:849–865. doi: 10.1118/1.2836945. [DOI] [PubMed] [Google Scholar]
- 14.Veiga C., McClelland J., Moinuddin S., Lourenço A., Ricketts K., Annkah J. Toward adaptive radiotherapy for head and neck patients: feasibility study on using CT-to-CBCT deformable registration for “dose of the day” calculations. Med Phys. 2014;41:31703. doi: 10.1118/1.4864240. [DOI] [PubMed] [Google Scholar]
- 15.Yoo S., Yin F.-F. Dosimetric feasibility of cone-beam CT-based treatment planning compared to CT-based treatment planning. Int J Radiat Oncol Biol Phys. 2006;66:1553–1561. doi: 10.1016/j.ijrobp.2006.08.031. [DOI] [PubMed] [Google Scholar]
- 16.Yang Y., Schreibmann E., Li T., Wang C., Xing L. Evaluation of on-board kV cone beam CT (CBCT)-based dose calculation. Phys Med Biol. 2007;52:685–705. doi: 10.1088/0031-9155/52/3/011. [DOI] [PubMed] [Google Scholar]
- 17.Onozato Y., Kadoya N., Fujita Y., Arai K., Dobashi S., Takeda K. Evaluation of on-board kV cone beam computed tomography-based dose calculation with deformable image registration using Hounsfield unit modifications. Int J Radiat Oncol Biol Phys. 2014;89:416–423. doi: 10.1016/j.ijrobp.2014.02.007. [DOI] [PubMed] [Google Scholar]
- 18.Guan H., Dong H. Dose calculation accuracy using cone-beam CT (CBCT) for pelvic adaptive radiotherapy. Phys Med Biol. 2009;54:6239–6250. doi: 10.1088/0031-9155/54/20/013. [DOI] [PubMed] [Google Scholar]
- 19.Usui K., Ichimaru Y., Okumura Y., Murakami K., Seo M., Kunieda E. Dose calculation with a cone beam CT image in image-guided radiation therapy. Radiol Phys Technol. 2013;6:107–114. doi: 10.1007/s12194-012-0176-z. [DOI] [PubMed] [Google Scholar]
- 20.Eiland R.B., Maare C., Sjöström D., Samsøe E., Behrens C.F. Dosimetric and geometric evaluation of the use of deformable image registration in adaptive intensity-modulated radiotherapy for head-and-neck cancer. J Radiat Res. 2014:1–7. doi: 10.1093/jrr/rru044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Akino Y., Yoshioka Y., Fukuda S., Maruoka S., Takahashi Y., Yagi M. Estimation of rectal dose using daily megavoltage cone-beam computed tomography and deformable image registration. Int J Radiat Oncol Biol Phys. 2013;87:602–608. doi: 10.1016/j.ijrobp.2013.06.2054. [DOI] [PubMed] [Google Scholar]
- 22.Godley A., Ahunbay E., Peng C., Li X.A. Accumulating daily-varied dose distributions of prostate radiation therapy with soft-tissue-based kV CT guidance. J Appl Clin Med Phys. 2012;13:3859. doi: 10.1120/jacmp.v13i3.3859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Fu Y., Liu S., Li H.H., Li H., Yang D. An adaptive motion regularization technique to support sliding motion in deformable image registration. Med Phys. 2018;45:735–747. doi: 10.1002/mp.12734. [DOI] [PubMed] [Google Scholar]
- 24.Murphy M.J., Salguero F.J., Siebers J.V., Staub D., Vaman C. A method to estimate the effect of deformable image registration uncertainties on daily dose mapping. Med Phys. 2012;39:573–580. doi: 10.1118/1.3673772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Dice L.R. Measures of the amount of ecologic association between species. Ecology. 1945;26:297–302. [Google Scholar]
- 26.Veiga C., Lourenço A.M., Mouinuddin S., van Herk M., Modat M., Ourselin S. Toward adaptive radiotherapy for head and neck patients: uncertainties in dose warping due to the choice of deformable registration algorithm. Med Phys. 2015;42:760–769. doi: 10.1118/1.4905050. [DOI] [PubMed] [Google Scholar]
- 27.Varadhan R., Karangelis G., Krishnan K., Hui S. A framework for deformable image registration validation in radiotherapy clinical applications. J Appl Clin Med Phys. 2013;14:4066. doi: 10.1120/jacmp.v14i1.4066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Lawson J.D., Schreibmann E., Jani A.B., Fox T. Quantitative evaluation of a cone-beam computed tomography-planning computed tomography deformable image registration method for adaptive radiation therapy. J Appl Clin Med Phys. 2007;8:2432. doi: 10.1120/jacmp.v8i4.2432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Brock K.K. Deformable registration accuracy consortium. Results of a multi-institution deformable registration accuracy study (MIDRAS) Int J Radiat Oncol Biol Phys. 2010;76:583–596. doi: 10.1016/j.ijrobp.2009.06.031. [DOI] [PubMed] [Google Scholar]
- 30.Latifi K., Zhang G., Stawicki M., van Elmpt W., Dekker A., Forster K. Validation of three deformable image registration algorithms for the thorax. J Appl Clin Med Phys. 2013;14:3834. doi: 10.1120/jacmp.v14i1.3834. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Hoffmann C., Krause S., Stoiber E.M., Mohr A., Rieken S., Schramm O. Accuracy quantification of a deformable image registration tool applied in a clinical setting. J Appl Clin Med Phys. 2014;15:4564. doi: 10.1120/jacmp.v15i1.4564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Mencarelli A., Van Kranen S.R., Hamming-Vrieze O., Van Beek S., Nico Rasch C.R., Van Herk M. Deformable image registration for adaptive radiation therapy of head and neck cancer: Accuracy and precision in the presence of tumor changes. Int J Radiat Oncol Biol Phys. 2014;90:680–687. doi: 10.1016/j.ijrobp.2014.06.045. [DOI] [PubMed] [Google Scholar]
- 33.Kadoya N., Nakajima Y., Saito M., Miyabe Y., Kurooka M., Kito S. Multi-institutional validation study of commercially available deformable image registration software for thoracic images. Int J Radiat Oncol Biol Phys. 2016;96:422–431. doi: 10.1016/j.ijrobp.2016.05.012. [DOI] [PubMed] [Google Scholar]
- 34.Chen M., Lu W., Chen Q., Ruchala K.J., Olivera G.H. A simple fixed-point approach to invert a deformation field. Med Phys. 2008;35:81–88. doi: 10.1118/1.2816107. [DOI] [PubMed] [Google Scholar]
- 35.Bender E.T., Tomé W.A. The utilization of consistency metrics for error analysis in deformable image registration. Phys Med Biol. 2009;54:5561–5577. doi: 10.1088/0031-9155/54/18/014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Schreibmann E., Pantalone P., Waller A., Fox T. A measure to evaluate deformable registration fields in clinical settings. J Appl Clin Med Phys. 2012;13:3829. doi: 10.1120/jacmp.v13i5.3829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Saleh Z.H., Apte A.P., Sharp G.C., Shusharina N.P., Wang Y., Veeraraghavan H. The distance discordance metric-a novel approach to quantifying spatial uncertainties in intra- and inter-patient deformable image registration. Phys Med Biol. 2014;59:733–746. doi: 10.1088/0031-9155/59/3/733. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.