Deriving the mean excitation energy map from dual-energy and proton computed tomography

Abstract

The mean excitation energy, I, is an essential quantity for proton treatment planning. This work investigated the feasibility of extracting the spatial distribution of I by combining two computed tomography (CT) modalities, dual-energy CT and proton CT, which provided the spatial distribution of the relative electron density and the stopping power relative to water, respectively. We provided the analytical derivation of I as well as its uncertainty. Results were validated on simulated X-ray and proton CT images of a digital anthropomorphic phantom. Accuracy was below 15% with a large uncertainty, which demonstrated the potential and limits of the technique.

1. Introduction

The mean excitation energy, sometimes referred to as the average ionization potential and noted I in the following, is an essential parameter for proton treatment planning but controversial as there is no consensus on how to establish reference values for different media. Although I is a well-defined quantity for a given material and it only depends on the properties of the medium [1], there are large uncertainties associated to its determination. Elemental I is generally derived from experimental data [1] such as stopping-power or range measurements for several charged particle beams, but there is limited experimental data for compounds and mixtures except water. Moreover, even for liquid water, which is highly investigated, there is no consensus on the mean excitation energy [2] with variations up to 20%, and values deduced from experiments are higher than theoretical derivations [3]. Experimental values for water range between 75 eV [4] and 81.8 eV [5] and recommended values range from 67.2 eV (ICRU Report 73 [6]) to 78 eV (Errata ICRU Report 73 [7]) with 75 eV in between (ICRU Reports 37 [8] and 49 [1]). When the I value of a medium is not known, it is computed by Bragg’s additivity rule based on its tabulated chemical composition and mass density. As this rule is an approximation and it ignores the effects of chemical bonds, I estimates of human tissues have large uncertainties (up to 15%) [8], [9]. The available reference human tissue compositions [10], [11], [12], [13] are average values obtained under different conditions and are expected to be approximate [9]. Moreover, there is a large variability on I values of similar human tissues reported in publications of the International Commision on Radiation Units (ICRU) [8], [12], [14]. There is currently no solution to image the spatial distribution of I in a heterogeneous object (e.g. a patient). In this work, we evaluate the feasibility of an experimental setup designed to derive the I map by combining two computed tomography (CT) imaging modalities: dual-energy CT (DECT) and proton CT.

2. Materials and methods

2.1. Phantom

The adult female (AF) reference computational phantom of the International Commission on Radiological Protection (ICRP) [13] was selected as a virtual patient. This anthropomorphic phantom represented an average female subject divided into 140 organs made of 52 standard human tissues, with known mass densities and chemical compositions. It had voxel dimensions of 1.775 × 1.775 × 4.84 mm³. For this study, three slices were selected at different locations: head, thorax and pelvis.

2.2. RED determination

Virtual X-ray CT acquisitions of the AF phantom were obtained using deterministic simulations in Gate v7.2 [15]. The DECT spectra employed in the simulation were 80 kV and 140 kV  + 0.4 mm Sn which corresponds to the Siemens Flash spectra [16]. The simulated detector response was accounted for in the deterministic simulation by weighting each source spectrum by the detector response. Poisson noise was applied to the projections corresponding to a central dose of about 20 mGy with the DECT acquisition while keeping a balanced dose between the low and the high energy acquisitions, as described in [17]. The basis material decomposition method proposed in [18] was implemented in the projection domain to extract the relative electron density (RED) map. The RED image was reconstructed using filtered backprojection with 380 × 380 × 1 voxels of size 1 × 1 × 1 mm³. For further details on the DECT simulations and the RED reconstruction, the reader is referred to [19].

2.3. SPR determinaton

The proton CT scanner described in [20] was simulated using the same Gate v7.2. The conceptual design of the simulated scanner consisted of two ideal detectors, one before and one after the phantom, measuring the position, the direction and the energy of each proton (list-mode). An incident proton beam of 300 MeV was used, which is sufficient for the proton beam to pass through in any direction of the three selected slices of the AF phantom. The delivered dose was recorded during the Gate simulation from the energy deposition in a voxelized map aligned with the ICRP lattice and it was about 5 mGy. The effect of multiple Coulomb scattering was mitigated by estimating the most likely path of each proton from the measured positions and directions following [21] and including it in a filtered backprojection reconstruction algorithm [20]. Stopping power relative to water (SPR) images were reconstructed on a 380 × 380 × 1 mm³ lattice like the DECT images. Protons which underwent nuclear interactions were filtered out using 3σ cuts on the exit energy and angular distributions before image reconstruction [21]. For further details on the proton CT scanner simulation and the SPR reconstruction, the reader is referred to [22].

2.4. I determination

The I map was estimated based on Bethe’s equation without correction terms [23]

$$S=4\pi r_e^2{m}_e{c}^2{\rho }_e\frac{z^2}{{\beta }^2}\left(\ln \frac{2m_e{c}^2{\beta }^2}{I(1-{\beta }^2)}-{\beta }^2\right)$$ (1)

where S is the stopping power of the medium, $r_e$ the classical electron radius, $m_e$ the mass of an electron, c the speed of light in vacuum, ${\rho }_e$ the electron density of the medium, z the charge of the projectile, and $\beta =v/c$ with v the velocity of the projectile.

The mean excitation energy of the object was computed pixel-by-pixel by computing

$$I(\mathit{x})=\frac{2m_e{c}^2{\beta }^2}{1-{\beta }^2}\exp \left(-\frac{\text{SPR}(\mathit{x})}{\text{RED}(\mathit{x})}\left(\ln \frac{2m_e{c}^2{\beta }^2}{I_{\text{w}}(1-{\beta }^2)}-{\beta }^2\right)-{\beta }^2\right)$$ (2)

with SPR = S/S_w the stopping power ratio and $S_w$ the stopping power of water, $I_{\text{w}}$ the mean excitation energy of water, which was set to 78 eV in Geant4, and ${\beta }^2=0.43$ corresponding to an energy of 300 MeV. This latter choice outlines the energy dependence of Eq. 2 which stems from the energy dependence of S propagating to the SPR. It can easily be seen that there is no energy dependence when SPR/RED = 1, i.e., for water. For other tissues, the calculated I will depend on the choice of the energy-dependent β. However, for human tissues, the SPR variations are small in the 80–300 MeV energy range [24]. For the AF tissues, the difference between I values for ${\beta }^2=0.18$ (100 MeV) and ${\beta }^2=0.43$ (300 MeV) was at maximum 6.1% (for the teeth) and below 1% for 44 of the 52 tissues.

2.5. Uncertainty of I

The uncertainty of I computed from SPR and RED using Eq. (2) was calculated using the first-order Taylor series expansion known as the propagation of uncertainty. We assumed that RED and SPR were independent variables since they were computed from independent measurements. The variance of ${\sigma }_I^2$ was then given by

$${\sigma }_I^2={\left(\frac{\partial I}{\partial \text{SPR}}\right)}^2{\sigma }_{\text{SPR}}^2+{\left(\frac{\partial I}{\partial \text{RED}}\right)}^2{\sigma }_{\text{RED}}^2$$ (3)

with ${\sigma }_{\text{SPR}}$ and ${\sigma }_{\text{RED}}$ the standard deviation of the SPR and the RED, respectively. We obtained

$${\sigma }_I^2=\frac{I^2}{{\text{RED}}^2}{\left(\ln \frac{2m_e{c}^2{\beta }^2}{I_{\text{w}}(1-{\beta }^2)}-{\beta }^2\right)}^2\left({\sigma }_{\text{SPR}}^2+{\left(\frac{\text{SPR}}{\text{RED}}\right)}^2{\sigma }_{\text{RED}}^2\right)\text{.}$$ (4)

2.6. Quantitative evaluation

The reconstructed CT images (SPR, RED) and the I map were quantitatively evaluated in four to five homogeneous regions-of-interest (ROIs) per slice (Table 1). Reference SPR, RED and I values were retrieved from Geant4 which used Bragg’s additivity rule and ICRU49 elemental I [1]. The reconstructed I was measured in the ROIs and compared to the reference values in terms of average (Eq. 2) and standard deviation (Eq. (4)). For I, the median was used instead of the mean for robustness to outliers and because, unlike the SPR and the RED, I was not normally distributed in 9 out of 14 ROIs (Shapiro–Wilk normality test, p <0.05) due to the non-linearity of Eq. 2 stemming from the logarithm and the exponential.

Table 1.

Quantitative evaluation of I in the ROIs drawn in the first column on top of RED images. The relative I error (last column) is obtained as the difference of the measure with the reference divided by the reference.

	ROI	Tissue	RED (unitless)		SPR (unitless)		I (eV)		${\sigma }_I$ (eV)	I error
			Ref.	$\mu \pm \sigma$	Ref.	$\mu \pm \sigma$	Ref.	Med ± σ	Eq. (4)	(%)
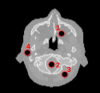	1	Adipose	0.95	0.95 ± 0.02	0.97	0.97 ± 0.02	63	60 ± 13	14	−5.0
	2	Brain	0.04	1.05 ± 0.02	1.06	0.06 ± 0.02	69	71 ± 20	17	3.0
	3	Muscle	1.04	1.04 ± 0.02	1.05	1.05 ± 0.02	69	74 ± 14	15	7.2
	4	Salivary gland	1.02	1.02 ± 0.02	1.04	1.04 ± 0.02	68	67 ± 15	14	−1.2
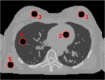	1	Mammary gland	1.02	1.02 ± 0.02	1.04	1.05 ± 0.02	64	62 ± 20	22	−3.1
	2	Blood	1.05	1.05 ± 0.02	1.06	1.06 ± 0.02	70	70 ± 24	21	0.8
	3	Mammary gland	1.02	1.02 ± 0.02	1.04	1.04 ± 0.02	64	65 ± 24	21	1.6
	4	Compressed lings	0.38	0.38 ± 0.02	0.39	0.39 ± 0.02	70	54 ± 46	49	−21.8
	5	Muscle	1.04	1.03 ± 0.04	1.05	1.04 ± 0.04	69	65 ± 36	37	−6.9
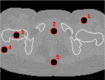	1	Muscle	1.04	1.04 ± 0.03	1.05	1.05 ± 0.03	69	67 ± 29	30	−2.9
	2	Urine	1.03	1.03 ± 0.05	1.05	1.04 ± 0.05	70	60 ± 37	33	−14.5
	3	Femora spongiosa	1.04	1.03 ± 0.05	1.06	1.05 ± 0.05	67	62 ± 39	36	−7.1
	4	Muscle	1.04	1.05 ± 0.05	1.05	1.06 ± 0.05	69	78 ± 38	47	−12.3
	5	Adipose	0.95	1.95 ± 0.04	1.97	0.98 ± 0.04	63	59 ± 37	35	−6.5

3. Results

The errors in extracting I (Table 1), computed as the percentage relative difference of I inside each ROI with respect to the reference values, were below 10% for the head and thorax slices, except for the lung tissue which exhibited a larger relative error. For the pelvis slice, errors within 15% were obtained. The theoretical standard deviation of I (Eq. (4)) was in good agreement with the measurements.

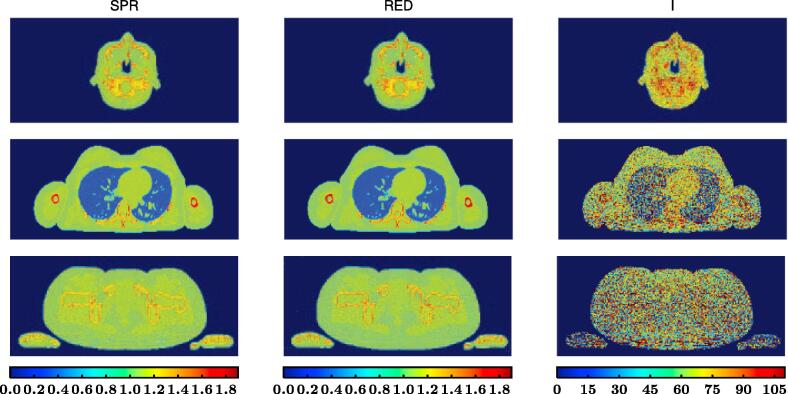
For all three anatomical sites, the reconstructed SPR image obtained through proton CT, the RED image obtained through DECT and the derived ionization potential image determined combining both imaging modalities (Fig. 1) displayed similar anatomical information but the amount of image noise was visually much more predominant for I than for SPR and RED.

Fig. 1.

From left to right: reconstructed SPR image (unitless) obtained through proton CT, reconstructed RED image (unitless) obtained through dual-energy CT and computed I map (in eV) determined using Bethe’s equation.

4. Discussion

The difficulty of experimentally extracting the mean excitation energy of compounds or mixtures has long been discussed [2], [8], [9], [12], [14]. Bragg’s additivity rule, which neglects chemical bonds and assumes a constant and general chemical composition for human tissues, is used instead of experimental measurements [2], [9], [25]. We conducted a feasibility study based on simulations to extract the I map of an object combining DECT and proton CT acquisitions. From these preliminary results, it seems feasible.

Errors in estimating I were below 15% for all anatomical regions, except for lung tissue. The accuracy of I was found to be very sensitive on the accuracy of the RED and the SPR. This was consistent with Eq. (2): for example, 1% error on the RED or the SPR caused 9% error on I with SPR/RED = 1. Larger errors were obtained in the pelvis ROIs which could be explained by the higher noise levels.

We computed (Eq. (4)) and validated (Table 1) an analytical expression of the uncertainty of I according to the uncertainties of the SPR and the RED. It can be seen that the contribution of the RED uncertainty is weighted by an additional SPR/RED term with respect to the SPR uncertainty but since both the SPR and the RED are around 1 for human tissues, the SPR and RED have about the same contributions to the uncertainty on I. The formula also indicates that the uncertainty on I is about 11 times larger than that of the SPR and RED. In the simulations, we used a DECT dose of 20 mGy at the center of a cylindrical phantom of similar diameter as the considered anatomical region [17] which is common in clinical routine for CT acquisitions. A similar SPR image noise was obtained with a proton CT dose of 5 mGy. Higher imaging doses should reduce the uncertainty of I according to Eq. (4). The I accuracy will not only be limited by the statistical uncertainty and inaccuracies are expected even with infinite doses due to the energy dependence in Eq. (2) and the reference value for water $I_w$ in the same equation. Note also that both pCT and CT have non-uniform spatial distributions of noise which are different from each other and which will therefore lead to another non-uniform distribution of the noise of I. The study of this distribution was out of the scope of this work.

At present, there is no clear consensus on which SPR expression is the most appropriate for computing the theoretical SPR values [26], [27]. In this study, we calculated the theoretical SPR using the equation proposed by Schneider et al. [23], which neglects shell, density, Barkas and Bloch correction terms and energy dependency. This approximation of the Bethe-Bloch theory [28], [29] has been proven to be valid and is widely used in proton therapy to compute the stopping power of human tissues [23]. Bethe-Bloch theory is not valid for proton energies below 1 MeV but it was found to have a negligible clinical impact [27]. Ödén et al. [26] compared Schneider’s approach with the SRIM software [30], which incorporates all mentioned corrections, and concluded that Bethe’s equation without correction terms could safely be used because SPR errors below 0.1% were obtained across 72 biological tissues. In a recent work, Doolan et al. [27] did an inter-comparison of four existing SPR models for proton therapy: Bichsel’s [31], Janni’s [32] and ICRU’s formulas [1] to compute the absolute stopping power of tissues, and Schneider’s [23] to compute the relative stopping power. The SPR value of eleven plastic materials was experimentally determined and it was compared against the four theoretical approaches. The first three approaches account for different effects (i.e. shell and/or density corrections) and they used different sets of elemental I. To determine the relative SPR, the absolute stopping power of the tissue was divided by the absolute stopping power of water over the same range of energies. They concluded that Bichsel’s approach [31] and Schneider’s approximation [23] using ICRU’s elemental I values [1] lead to the lowest errors. Therefore, based on these studies, Bethe’s equation without correction terms seems to be a safe choice to determine the SPR and, therefore, to derive I as done in this study.

One obvious limitation of this simulation-based study was the fact that the considered proton CT scanner was assumed to have perfect energy and position detectors. Even though many efforts have been made in improving proton CT scanner prototypes [33], [34], no clinical proton CT scanners are available at the moment. As a consequence, the clinical implementation of this technique is far from being immediate. Nevertheless, proton CT radiography is already possible with commercial multi-layer ionization chambers [35] and, consequently, I radiographies would be immediately available with current technology. The X-ray CT simulation was also idealized since we assumed perfect scatter correction and perfect knowledge of the source spectra and the detector response.

The accuracy results in Table 1 do not include bone tissues which thickness never exceeded two pixels in the ICRP phantom and which inaccuracy was therefore dominated by partial volume effects. In a previous work (chapter 6 of [19]), we simulated the I map of the Gammex phantom using the same approach as the one presented here and the results in bone were in accordance: with 1.2% error on the RED of the high density bone-equivalent tissue (SB3) and 12% error on I.

One immediate application of I maps is to determine the intra-organ or intra-tissue I variability by performing organ or tissue segmentation. Furthermore, if the proposed imaging technique is applied to a large number of individuals, representative of different population groups (e.g. infants, children, female adults, male adults, ill and healthy individuals, etc.), it would be possible to derive the intra-group and inter-group variability of I for a given organ or tissue. Consequently, the proposed imaging technique could be used to extract valuable experimental reference data for I which is currently lacking. Proton therapy could also benefit from this information as the determination of the proton range in the patient lacks of accuracy because of the limited knowledge on I, which is one of the components required to compute proton stopping powers [36].

In conclusion, in this simulation study, we demonstrated the feasibility of computing an I map from DECT and proton CT images. The error on the I values measured in several ROIs of the digital human phantom were below 15% with a large uncertainty on the derived I, which demonstrated the potential and the limits of the technique.

Conflict of interest

The authors declare that they have no conflicts of interest to disclose.