Analyses of regional radiosensitivity of white matter structures along tract axes using novel white matter segmentation and diffusion imaging biomarkers

Abstract

Background and purpose

Brain radiotherapy (RT) can cause white matter damage and downstream neurocognitive decline. We developed a computational neuroimaging tool to regionally partition individual white matter tracts, then analyze regional changes in diffusion metrics of white matter damage following brain RT.

Materials and methods

RT dose, diffusion metrics and white matter tract structures were extracted and mapped to a reference brain for 49 patients who received brain RT, and underwent diffusion tensor imaging pre- and 9–12 months post-RT. Based on their elongation, 23 of 48 white matter tracts were selected. The Tract-Crawler software was developed in MATLAB to create cross-sectional slice planes normal to a tract’s computed medial axis. We then performed slice- and voxel-wise analysis of radiosensitivity, defined as percent change in mean diffusivity (MD) and fractional anisotropy (FA) as a function of dose relative to baseline.

Results

Distinct patterns of FA/MD radiosensitivity were seen for specific tracts, including the corticospinal tract, medial lemniscus, and inferior cerebellar peduncle, in particular at terminal ends. These patterns persisted for corresponding tracts in left and right hemispheres. Local sensitivities were as high as 40%/Gy (e.g., voxel-wise: −39 ± 31%/Gy in right corticospinal tract FA, −45 ± 25%/Gy in right inferior cerebellar peduncle FA), p < 0.05.

Conclusions

Tract-Crawler, a novel tool to visualize and analyze cuts of white matter structures normal to medial axes, was used to demonstrate that particular white matter tracts exhibit significant regional variations in radiosensitivity based on diffusion biomarkers.

1. Introduction

Brain radiotherapy is standard of care for most primary and metastatic brain tumors. However, the decline of neurocognitive function is an unfortunate sequelae among brain tumor patients treated with radiotherapy, likely driven in part by damage to white matter, cortex, and neurogenic stem cell niches [1]. In particular, radiation-induced damage to normal-appearing white matter has been studied using advanced diffusion imaging [2], [3], [4], [5], [6], with evidence associating diffusion biomarkers of white matter damage with neurocognitive decline after brain radiation. How to prevent such neurocognitive decline in terms of selective avoidance of white matter regions is unclear. The QUANTEC report [7] on radiation dose-effects in the brain stipulates constraints for radiation necrosis, but acknowledges that there is limited data on constraints to avoid neurocognitive decline. It encourages the use of advanced neuroimaging to identify signatures of microstructural damage and relate these imaging biomarkers to functional changes.

We have previously reported on radiation-induced damage to white matter following brain RT for primary brain tumors [8]. Specifically, using diffusion tensor imaging, it was demonstrated that changes in water diffusion characteristics correlate with dose and that these changes are observed for the full dose range, including <10 Gy [5]. We further investigated whether these changes vary regionally across the brain [4]. Overall, 21 structures were identified and mean values for fractional anisotropy (FA), axial diffusivity (AD), radial diffusivity (RD), and mean diffusivity (MD) were calculated for each structure for scans acquired before and 9–12 months after RT. These changes were shown to correlate with maximum and mean dose for some, but not all structures, with the corpus callosum, cingulum bundle and fornix showing the most pronounced dose-response. Traditionally, diffusivity metrics are averaged over the volume of the structure, and so any information on spatial variation of the sensitivity of the tract along its principal (primary) axis is lost. Studies employing a more sophisticated along-tract analysis have been reported in the neuroimaging literature. For example, the superiority of along-tract analysis of diffusion imaging metrics over the tract-averaged approach has been demonstrated in a study of children with fetal alcohol spectrum disorders vs typically developing controls [9]. The emphasis of the along-tract analysis of FA and MD following brain radiotherapy is different. Literature, including our preliminary results [10], suggests that diffusion tensor imaging predicts decline in cognitive function [11]. If differential radiosensitivity along the tract axis is demonstrated, this would pave way to tract-geometry driven, rather than tract-averaged-driven constraints to guide radiotherapy planning.

In order to determine how radiation sensitivity measures change along a tract, the tract must first be correctly partitioned, which is a complex procedure. In the case of perfectly cylindrical geometry, this problem can be solved by a basic rotation of the volume. However, tracts are often curved in 3-dimensional space and so traditional parallel (axial, sagittal, coronal) slice planes neither uniformly subdivide a tract nor provide a true representation of a local cross-section. In the extreme case of curved tracts which subtend an angle >180°, parallel slicing would sometimes result in these tracts being sampled in two disconnected locations at once, regardless of any possible rotations. Computation of an anatomical central axis to calculate normal-tissue metrics to correlate with the risk of radiation-induced complications has been attempted for reasonably well shaped structures. Hoogeman et al. [12] used the minimum distance field approach to define the axis of a rectum to guide digital unfolding of the rectal wall. White matter tracts present a more complicated challenge as they are not necessarily cylindrical, and vary in size and shape.

In this report we describe a novel method to define the tract axis, and use this method to explore differential sensitivity to radiation along the axes for 23 white matter tracts.

2. Material and methods

2.1. Study design

A detailed description of the study patients and MRI image pre-processing can be found elsewhere [4]. In brief, 49 patients with pre- and post-RT MRI imaging were selected for analysis. The MRI acquisition protocol consisted of a T1-weighted, T2-weighted FLAIR, and a diffusion-weighted sequence. Diffusion data (TE, 97 ms, TR, 1700 ms; diffusion time, ∼90 ms; matrix, 128 × 128 × 48; resolution (mm), 1.875 × 1.875 × 2.5) were acquired with b = 0, 500, 1500, and 4000 s/mm². One instance of the non-diffusion weighted images (b = 0 s/mm²) was acquired, while 6, 6, and 15 unique gradient directions were acquired for b = 500, 1500, and 4000 s/mm², respectively. Anatomical scans were corrected for distortions arising from gradient nonlinearities [13] while diffusion-weighted scans were corrected for distortions arising from static field inhomogeneity [14] using in-house algorithms. A diffusion tensor was fit, per-voxel, to the diffusion data, from which the mean diffusivity (MD) and fractional anisotropy (FA) were extracted. The anatomical scans were used to register the patient data set, including the MD and FA maps, into the standard space, from which the white matter tracts could be segmented using the JHU-ICBM 1 mm atlas [15], [16], [17]. RT planning data, including the planning CT and volumetric calculated dose, were also non-linearly registered to the standard space. The quality of the final registrations was manually assessed by visual inspection. Overall, 48 tracts (left and right) were automatically segmented using a non-linear registration to the JHU-ICBM atlas [18]. The study was approved by the institutional review board.

Tumor, tumor bed, surgical cavity, and surgical scars were manually censored on each patient. A white matter mask was computed from the T1-weighted sequence at the baseline time-point using automatic segmentation software [19]. In order to avoid partial volume effects from gray matter and CSF at the edges of the volume, the mask was shrunk to its six-connected voxels (voxels whose six face neighbors were also white matter) [5].

2.2. Fractional anisotropy and mean diffusivity analysis

A computational neuroimaging tool, Tract-Crawler, was developed in MATLAB (Mathworks, Natick, MA) to create slice planes for individual white matter tracts in the brain normal to the tract’s computed medial axis. This software requires the definition of terminal points of a tract, and therefore only tracts where clear identification of these points was possible could be used. Following a visual examination, 23 of 48 white matter tracts were selected for this analysis, as described in Table 1. These data demonstrate that the selected tracts are indeed narrow, elongated structures for which there are clear terminal ends.

Table 1.

Medial axis lengths for each of the 23 tracts analyzed and maximum and mean tract diameters, calculated from the cross-sectional area assuming circular geometry.

Tract	Length along Medial Axis (mm)	Maximum Diameter (mm)	Mean Diameter (mm)
Fornix (column and body of fornix)	31	5	3
Corticospinal Tract L/R	37	9	5
Medial Lemniscus L/R	21	7	5
Inferior Cerebellar Peduncle L/R	37	5	4
Superior Cerebellar Peduncle L/R	29	6	5
Anterior Corona Radiata L/R	54	14	11
Sagittal Stratum (includes inferior longitudinal fasciculus and inferior fronto-occipital fasciculus) L/R	53	9	6
Cingulum (cingulate gyrus) L/R	107	6	4
Cingulum (hippocampus) L/R	51	5	3
Fornix (cres) L/R	43	6	4
Superior Longitudinal Fasciculus L/R	81	12	8
Superior Fronto-Occipital Fasciculus L/R	28	5	4

The final shape of the medial axis is not sensitive to small variations in the selection of terminal endpoints. The preferred step size (mm) between the final slice planes was determined for each tract, so that the resulting slice planes were as close as possible without intersecting. The medial axis for each tract was computed in several steps. Each structure first underwent a medial axis transform by thinning [20]. Typically, undesired medial axis skeleton branches were created due to noisy surfaces and thus it was necessary to perform post-processing by a 3-dimensional curve fitting process to remove the unwanted branches [21]. The vertex points of the medial axis were taken as a 3-dimensional point cloud, and an algorithm was run which created a final curve of 'n' equally spaced control points between the previously determined terminal points. Initially, ‘n’ was set as the number of original points in the point cloud, and was typically of order 100. An initial set of control points was defined along a straight line between the terminal points of the tract. All of the original points (sample points) in the point cloud were assigned to their nearest control point, and the control point was then shifted to the mean of its sample points. Any control points without sample points in its domain were linearly distributed between its neighbors which did have sample points in their domains [22]. A 3-dimensional parametric cubic spline was then fit to the curve, such that each point was spaced apart equally by the step size. The number of control points, 'n', was varied until the medial axis was acceptably smooth, typically resulting in values of ‘n’ around five. Slice planes were then computed normal to the medial axis. Each of our user inputs for each tract was recorded as a tract parameter, such that Tract-Crawler could then operate automatically. Fig. S1 (supplementary material) shows the process progression for the right inferior cerebellar peduncle.

Two methods were used to analyze the data: a slice-wise analysis in which the 2-dimensional slice planes were 3-dimensionally linearly interpolated into the data volume and a voxel-wise analysis taking the volume between each slice plane. For the slice-wise analysis, DTI data, FA and MD, and RT dose data were mapped to the angled slices with interpolated pixel spacing of 0.25 mm after restricting these data to the masked white matter tracts for each patient, and a radiosensitivity measure was calculated as the percent change in mean FA or MD per patient and slice divided by the mean RT dose per patient and slice, scaled by the mean over all the slices, and averaged over all 49 patients studied. Similarly, for the voxel-wise analysis, masked FA, MD, and dose data were partitioned into volumetric sections between slice planes and the sensitivity measure was calculated as the percent change in mean FA or MD per patient and volumetric section divided by the mean RT dose per patient and section, scaled by the mean over all the voxels, and averaged over all 49 patients studied.

2.3. Statistical analysis

All statistical tests were performed in MATLAB. Diffusion (FA/MD) radiosensitivity at each slice or volumetric section location was tested for statistical significance using a one-sample t-test. Pearson correlation coefficients, R, and their corresponding p-values were calculated for the association between the FA/MD sensitivities of the left and right hemispheres for each of 23 tracts used in this study. Correlation was also calculated between the two analysis methods used.

3. Results

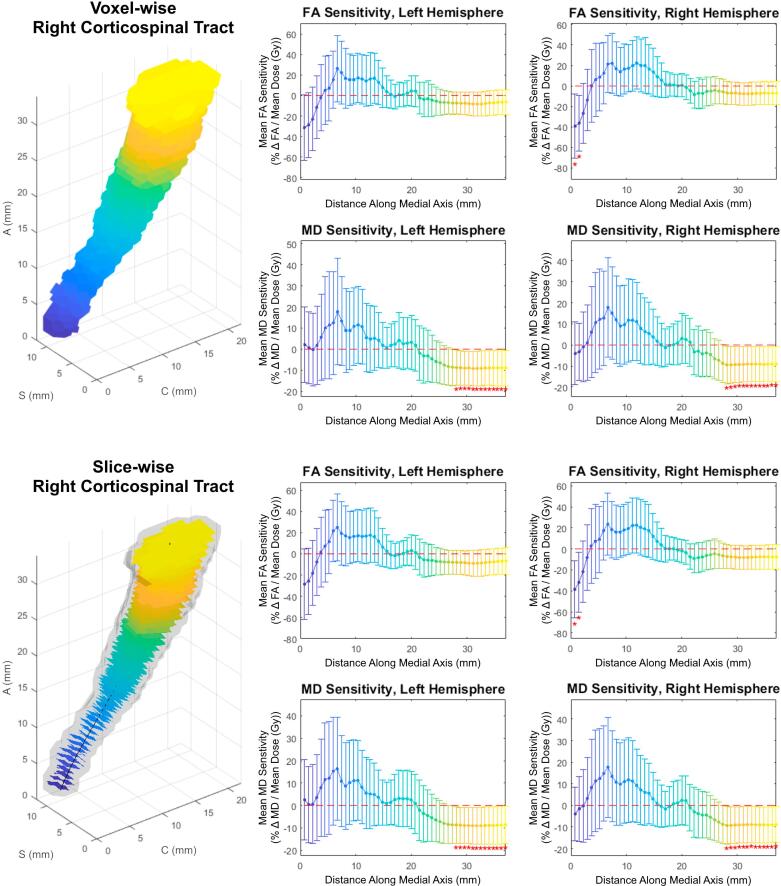
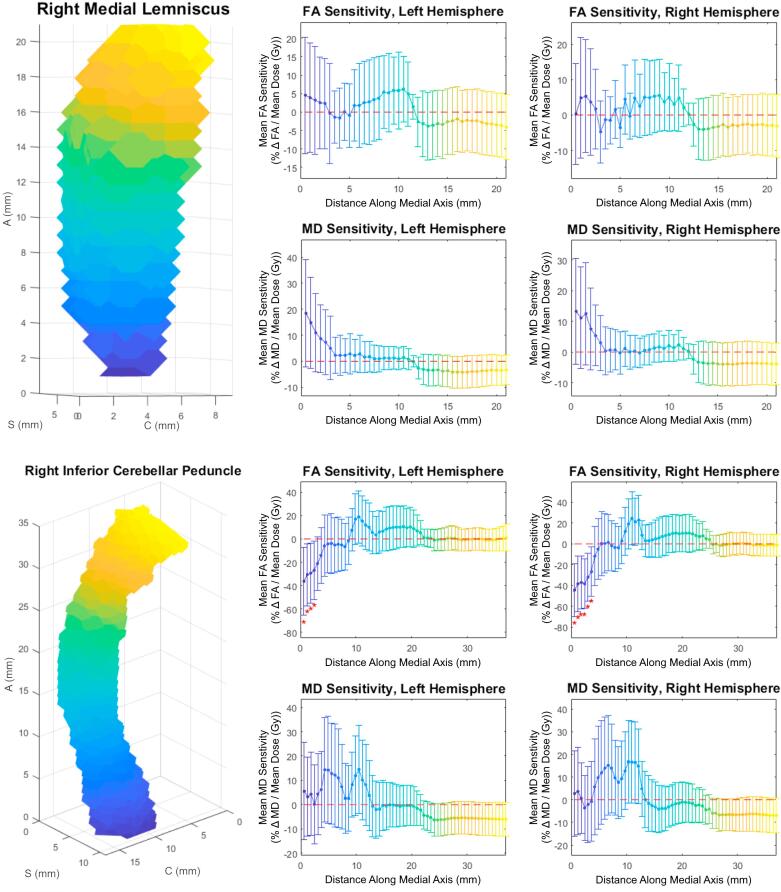
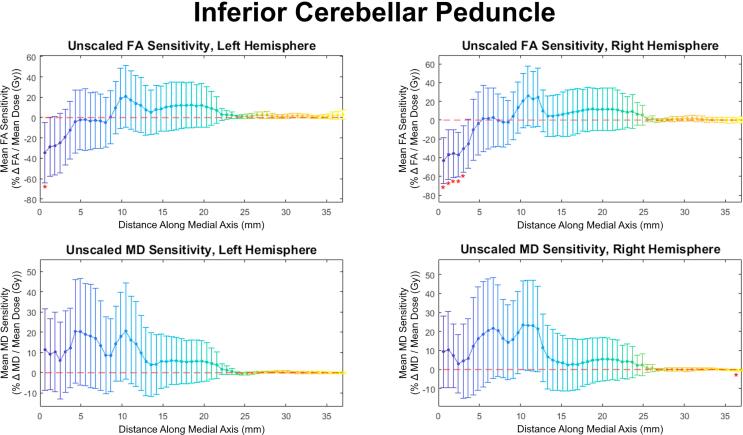
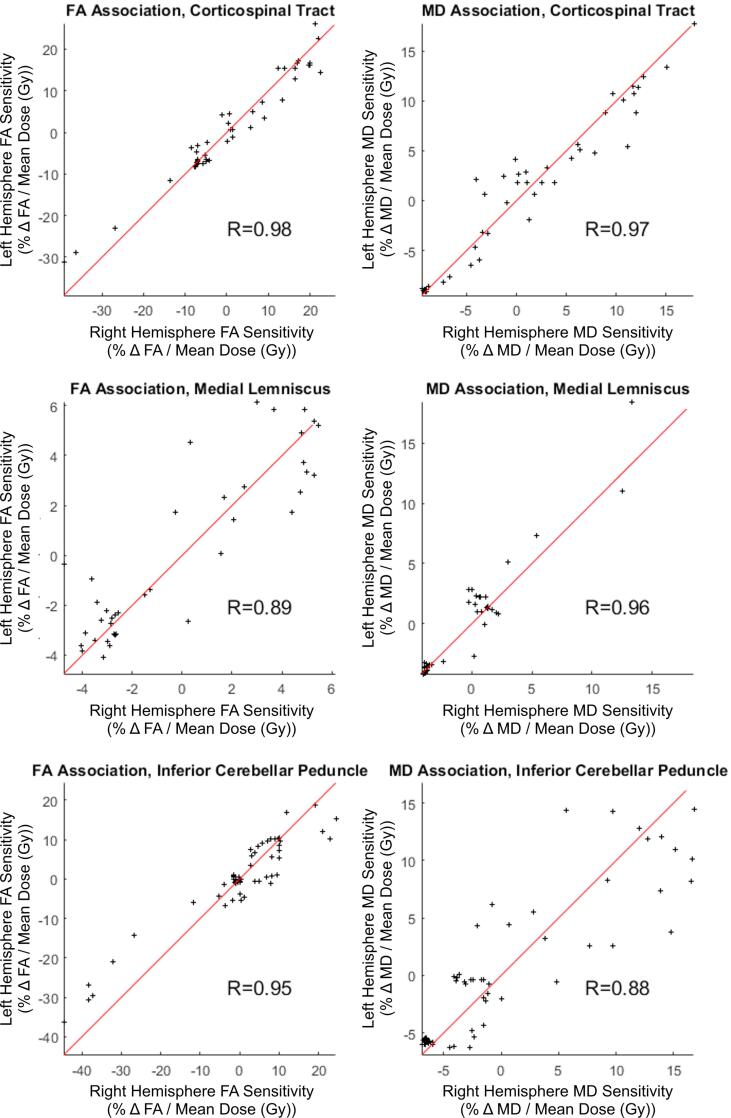
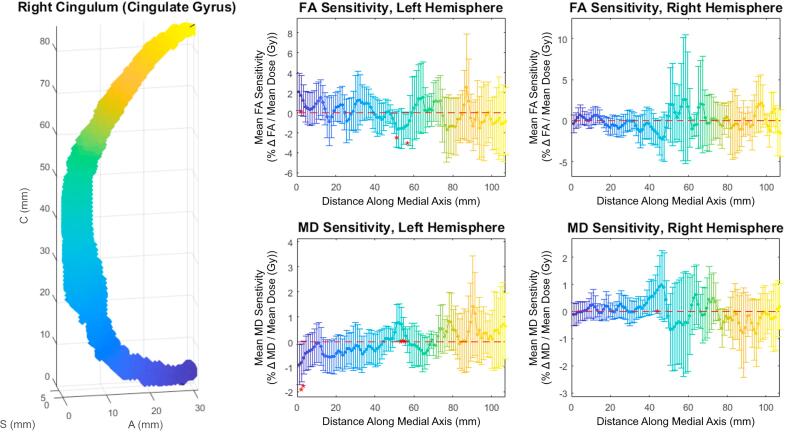
Both slice-wise and voxel-wise analysis yielded very similar results (R > 0.98, p < 0.01). Under both methods, distinct patterns of FA/MD sensitivity to dose (percent change in diffusivity per Gy, relative to the tract’s mean) along the tract axis were seen for the corticospinal tract, medial lemniscus, and inferior cerebellar peduncle. Fig. 1 shows FA and MD sensitivity calculated using both the slice-wise and voxel-wise approaches. Fig. 2 shows the results for medial lemniscus and inferior cerebellar peduncle obtained using the voxel-based method. Notably, a statistically significant difference from baseline was observed on consecutive data points in the corticospinal tract and inferior cerebellar peduncle, and these stretches of differential sensitivity were constrained to the terminal ends of the tracts. Fig. 1, Fig. 2 show that the sensitivity patterns persisted for corresponding tracts in both the left and right brain hemispheres. Sensitivity as given in Fig. 1, Fig. 2 is formulated in a manner relative to the mean over a tract to demonstrate deviations from the mean, therefore absolute changes in diffusion metrics cannot be ascertained. Fig. 3 shows absolute along-tract changes in FA and MD for the inferior cerebellar peduncle without referencing to the tract’s mean. A persistent, but not significant, increase in MD is notable and consistent between the left and right hemispheres. All other structures analyzed did not display any clear trends, an example being the cingulate gyrus, as shown voxel-wise in Fig. S2 (supplementary material). Fig. 4 illustrates the voxel-wise correlation between the left and right hemispheres for the corticospinal tract, medial lemniscus and inferior cerebellar peduncle (R > 0.88, p < 0.01 for all structures). Table 2 summarizes data for these three structures at their terminal ends.

Fig. 1.

Voxel-wise (top) and slice-wise (bottom) analysis for the corticospinal tract; Top Left: 3D view of Tract-Crawler volumetric sections; Axes are labeled such that A (Axial), S (Sagittal) and C (Coronal) represent the Superior-Inferior, Left-Right and Anterior-Posterior directions, respectively. Bottom Left: 3D view of Tract-Crawler slices overlaid on right hemisphere tract structure; Middle column: FA (rows 1 and 3) and MD (rows 2 and 4) relative sensitivities versus distance along the medial axis for the left hemispheres; Right column: FA (rows 1 and 3) and MD (rows 2 and 4) relative sensitivities versus distance along the medial axis for the right hemispheres; Error bars are 95% confidence intervals. Asterisks denote data with p < 0.05.

Fig. 2.

Voxel-wise analyses for the medial lemniscus (top) and inferior cerebellar peduncle (bottom); Top and Bottom Left: 3D view of Tract-Crawler volumetric sections; Axes labeling as in Fig. 1. Middle column: FA (rows 1 and 3) and MD (rows 2 and 4) relative sensitivities versus distance along the medial axis for the left hemispheres; Right column: FA (rows 1 and 3) and MD (rows 2 and 4) relative sensitivities versus distance along the medial axis for the right hemispheres; Error bars are 95% confidence intervals. Asterisks denote data with p < 0.05.

Fig. 3.

Voxel-wise analysis for the inferior cerebellar peduncle relative to the pre-RT FA without scaling relative to the tract mean.

Fig. 4.

Voxel-wise association scatterplots for sensitivities in FA (left) and MD (right) for right versus left hemisphere, parametrized by distance along the medial axis, for the corticospinal tract, medial lemniscus, and inferior cerebellar peduncle, p < 0.01 in all cases.

Table 2.

Slice-wise and voxel-wise sensitivity results for the corticospinal tract, medial lemniscus, and inferior cerebellar peduncle with 95% confidence intervals.

Tract	Hemisphere	Measure	Slice-Wise Relative Sensitivity at Terminal Ends: (%Δ/Gy)		Voxel-Wise Relative Sensitivity at Terminal Ends: (%Δ/Gy)
Corticospinal Tract	Right	FA	−39 ± 27 (p < 0.01)	−8 ± 12 (p > 0.10)	−39 ± 31 (p = 0.02)	−7 ± 11 (p > 0.10)
		MD	−4 ± 12 (p > 0.10)	−9 ± 8 (p = 0.04)	−4 ± 15 (p > 0.10)	−9 ± 8 (p = 0.04)
	Left	FA	−29 ± 33 (p = 0.10)	−7 ± 12 (p > 0.10)	−31 ± 32 (p = 0.06)	−7 ± 12 (p > 0.10)
		MD	3 ± 18 (p > 0.10)	−9 ± 8 (p = 0.05)	2 ± 18 (p > 0.10)	−9 ± 8 (p = 0.04)
Medial Lemniscus	Right	FA	1 ± 15 (p > 0.10)	−3 ± 9 (p=>0.10)	0 ± 14 (p > 0.10)	−3 ± 9 (p > 0.10)
		MD	14 ± 18 (p > 0.10)	−4 ± 7 (p > 0.10)	13 ± 17 (p > 0.10)	−4 ± 7 (p > 0.10)
	Left	FA	4 ± 15 (p > 0.10)	−4 ± 9 (p > 0.10)	5 ± 16 (p > 0.10)	−4 ± 9 (p > 0.10)
		MD	17 ± 19 (p = 0.09)	−4 ± 6 (p > 0.10)	19 ± 21 (p = 0.09)	−3 ± 6 (p > 0.10)
Inferior Cerebellar Peduncle	Right	FA	−42 ± 26 (p < 0.01)	−2 ± 11 (p > 0.10)	−45 ± 25 (p < 0.01)	−1 ± 11 (p > 0.10)
		MD	3 ± 18 (p > 0.10)	−7 ± 8 (p = 0.09)	3 ± 19 (p > 0.10)	−7 ± 8 (p = 0.08)
	Left	FA	−34 ± 28 (p = 0.02)	1 ± 12 (p > 0.10)	−36 ± 29 (p = 0.02)	1 ± 11 (p > 0.10)
		MD	5 ± 18 (p > 0.10)	−6 ± 7 (p > 0.10)	6 ± 20 (p > 0.10)	−6 ± 7 (p = 0.10)

4. Discussion

Neurocognitive decline following brain RT has been acknowledged for a long time, which is driven in part by dose dependent damage to white matter. Previous work has demonstrated the exquisite dose sensitivity of white matter based on diffusion biomarkers of white matter damage [5] and the regional sensitivity among discrete white matter tracts in the brain [2], [3], [4]. Our group has also previously demonstrated that there exist component-wise differences in the associations between radiation dose and directional diffusion coefficients in the 9 months after radiotherapy [8]. However, many questions remain. How can we evaluate dose dependency to radiation-associated damage along a white matter tract? Are the terminal ends of the tract more sensitive than the middle? Is the exterior portion of a given white matter tract more or less sensitive to dose than the interior portion? In order to answer these questions, we needed a tool to regionally segment white matter tracts along their curvatures. We have successfully created a novel neuroanatomic segmentation tool which meets these needs by creating cross-sectional slice planes normal to a computed medial axis, similar to methodology developed for application in the rib cage [23] and rectum [12].

In this study we have demonstrated that some, but not all, white matter structures clearly exhibit non-uniform sensitivity to radiation dose along their axes. It is notable that this pattern has been highly reproducible in such tracts between the left and right hemispheres. Even for locations where the change from baseline was not statistically significant, the overall pattern persisted in both hemispheres, Fig. 1, Fig. 2. There are at least two ways to interpret that long stretches of tracts show similar sensitivity. One is that sensitivity is indeed slowly changing along the tract axis. Another, which may numerically lead to the same result but is mechanistically different, is that changes in FA and MD are influenced by those of the neighboring regions. This question cannot be answered with our data.

The along-tract approach revealed clear variations in sensitivity. In contrast, the volume-averaged approach did not show significant changes. Specifically, the volume-averaged mean FA and MD changes and 95% confidence intervals, in percent per Gy, were 6 ± 35 and 9 ± 27 for the right corticospinal tract, 4 ± 30 and 4 ± 25, right medial lemniscus, and 1 ± 34 and 7 ± 27, right cerebellar peduncle. Similar results were observed for the left hemisphere.

Our formulation of sensitivity is designed to reveal local deviations in response compared to the tract mean. It can be seen from the data, Table 2, that local radiosensitivity compared to the tract mean can reach magnitudes as high as ∼40% per Gy, which could constitute a very significant effect, depending on dose. For example, a locus with a relative sensitivity of 40% per Gy exposed to only 20 Gy would experience a change in the diffusion metric of 800% in addition to that of the tract mean.

Imaging-driven treatment planning has been making its way into radiation therapy. The premise is that tumors and normal tissues are heterogeneous in their properties. For tumors this can be cell density, proliferation rate, hypoxia [24], [25], [26]. These properties can be visualized using modern positron emission tomography and MRI means. For normal tissue this can be functional burden distribution [27] or preferred location of stem cells [28] to preserve the function. Clinical trials are in progress and the emphasis thus far has been on tumor properties [29]. This study demonstrates that white matter tracts exhibit variation in dose sensitivity of diffusion metrics along their principal axis. Regions with increased sensitivity may be at greater risk for microstructural changes following irradiation. Although no associations between neurocognitive outcomes and dose sensitivity were examined in this study, there are several examples within the literature in both oncology [2] and other disease states [30], demonstrating the association between changes in diffusion properties of white matter and cognitive function. Together, these results can help inform the identification of new organs-at-risk for treatment planning optimization whose value can be assessed using prospective clinical trials.

Limitations to our study include its retrospective nature and potential confounding effects from chemotherapy or surgery. These data are from a single institution using a standardized imaging protocol. The generalization of both the method and the findings still need to be explored. It is also assumed, as a first approximation, throughout the analysis that changes in diffusivity vary linearly with RT dose. This assumption cannot be true for parameters with bound values, e.g. between zero and unity, as is FA. Therefore, extrapolation of our results to substantial variations from the mean would be incorrect. Our analysis is an advancement over the tract-averaged approach. However, slice-averaged or voxel-averaged approaches have been used. A detailed voxel-based analysis will require a more sophisticated voxel connectivity approach. This will require combining tract geometry with dosimetric data, for example minimum, maximum, or above/below pre-set threshold dose in any voxel in any slice. Voxel-based analysis will unavoidably introduce more statistical noise and a larger data set (number of patients) will be required.

The Tract-Crawler software is currently only semi-automated and required a fair amount of human intervention, i.e. determination of tract terminal ends and medial axis smoothness. The former can be solved using computer vision, while the latter requires an optimization algorithm. The association between regional radiosensitivity of diffusion metrics and neurocognitive or clinical function is yet to be explored.

The Tract-Crawler software was developed and used to calculate changes in MD and FA for 23 white matter tracts along the tract axes. Specific tracts, in particular the corticospinal tract, medial lemniscus and inferior cerebellar peduncle, exhibited strong regional dependence. This regional sensitivity was consistent between tracts in the left and right hemispheres.

Declaration of interest

Dr. Hattangadi-Gluth has a research grant from Varian Medical Systems, unrelated to the current study.

Appendix A. Supplementary data

Supplementary Fig. S1.

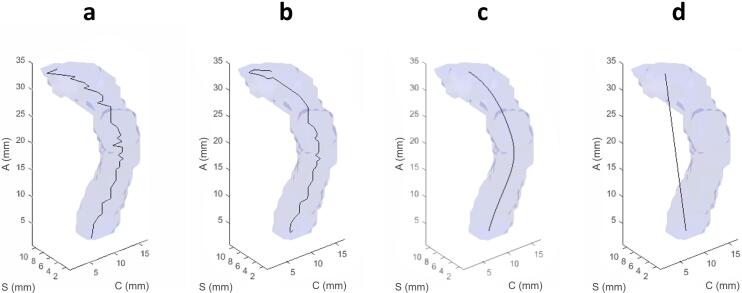
Visualization of the medial axis smoothing process performed on the right inferior cerebellar peduncle; Axes labeling as in Fig. 1. (a) Medial axis by thinning with no smoothing processes, (b) 3-dimensional parametric cubic spline fit to the medial axis with no resampling of points, (c) 3-dimensional parametric cubic spline fit to the medial axis with 6 control points (optimal smoothness), and (d) 3-dimensional parametric cubic spline fitted to the medial axis with only 2 control points, i.e. the endpoints of the tract.

Supplementary Fig. S2.

Voxel-wise cingulum (cingulate gyrus); Left Panel: 3D view of Tract-Crawler slices overlaid on the right hemisphere tract structure; Axes labeling as in Fig. 1. Middle and right columns: FA (top) and MD (bottom) relative sensitivities versus distance along the medial axis for the left (middle column) and right (right column) hemispheres. Error bars are 95% confidence intervals.