Clinical workflow for treating patients with a metallic hip prosthesis using magnetic resonance imaging-guided radiotherapy

Abstract

Background & purpose

Metallic prostheses distort the magnetic field during magnetic resonance imaging (MRI), leading to geometric distortions and signal loss. The purpose of this work was to develop a method to determine eligibility for MRI-guided radiotherapy (MRIgRT) on a per patient basis by estimating the magnitude of geometric distortions inside the clinical target volume (CTV).

Materials & methods

Three patients with prostate cancer and hip prosthesis, treated using MRIgRT, were included. Eligibility for MRIgRT was based on computed tomography and associated CTV delineations, together with a field-distortion (B0) map and anatomical images acquired during MR simulation. To verify the method, B0 maps made during MR simulation and each MRIgRT treatment fraction were compared.

Results

Estimates made during MR simulation of the magnitude of distortions inside the CTV were 0.43 mm, 0.19 mm and 2.79 mm compared to the average over all treatment fractions of 1.40 mm, 0.32 mm and 1.81 mm, per patient respectively.

Conclusions

B0 map acquisitions prior to treatment can be used to estimate the magnitude of distortions during MRIgRT to guide the decision on eligibility for MRIgRT of prostate cancer patients with metallic hip implants.

1. Introduction

Magnetic resonance imaging-guided radiotherapy (MRIgRT) takes advantage of the superior soft-tissue contrast provided by magnetic resonance imaging (MRI), with the promise to increase treatment efficacy [1], [2]. It provides opportunities for online plan adaptation, tumour tracking and trailing, and other techniques that might ultimately lead to toxicity reduction and/or an improvement of local control [3], [4], [5], [6].

Besides soft-tissue contrast, needed for anatomical differentiation, geometric fidelity of the imaging modality is a necessity for optimal MRIgRT [7]. Although MRI is subject to geometrical distortions, these can be kept within acceptable limits under normal circumstances [8], [9]. Implants, however, can heavily distort the magnetic field thereby introducing large geometric distortions that depend on the type and positioning of the implant, potentially making the patient ineligible for MRIgRT [10]. This is a growing problem, as the population of pelvic cancer patients with metallic implants that need some form of radiotherapy is expected to increase [11], [12], [13].

Computed tomography (CT) imaging data has been used to estimate field distortions in MRI by mapping Hounsfield units (HU) to magnetic susceptibility values for human tissues [14], [15]. Metallic implants, however, can take on a much larger range of HU and introduce artefacts in CT images reducing the efficacy of these methods. There are also multiple MRI acquisitions designed specifically to reduce metal artefacts, although individual adjustments are necessary in many patients to increase image quality and there is no guarantee scan and reconstruction times, image quality, and contrast are sufficient for MRIgRT purposes [16], [17].

Another way of estimating geometric distortions in MRI, on a per patient basis, is to acquire a field-distortion map, or B0 map, during the MR exam and converting frequency offsets to expected geometric distortions using the readout bandwidth of the MR image of interest. In principle, these B0 maps can be used to geometrically correct MR images made during the examination [18], [19]. The B0 map is based on phase differences of the spins in voxels between two acquisitions, for which information on complete cycles is lost. For high enough field distortions, this results in phase wraps (i.e., discontinuities in the B0 map along which the frequency offset ostensibly switches from the minimum to the maximum value), which prevents straightforward implementation of a geometric correction algorithm. There are algorithms available that ‘unwrap’ the B0 maps, most of which require extra data, like magnitude images or multiple phase-difference images [20], [21], [22], [23], that have been successfully applied to investigate tissue-induced field distortions in a radiotherapy setting [24], [25]. Near metallic implants, however, field distortions are typically much larger, so there might not be enough information to quickly and reliably acquire an accurate unwrapped B0 map.

An alternative to geometrically correcting for field distortions is to estimate the severity of the distortions to determine whether a patient can undergo MRIgRT. It is desirable to accurately ascertain eligibility prior to the decision on the course of treatment. This ensures an optimal treatment modality for all patients and prevents an unnecessary increase in burden, for the patient and the healthcare system, as a result of alterations at a later stage.

For pelvic cancer patients, it is recommended that MR images, acquired during an exam optimized for MR simulation, are available for treatment planning purposes [9], [26], [27]. Although patient anatomy changes over time and magnetic field strengths between the systems used for MR simulation (MRsim) and MRIgRT (MR-linac) might differ, our hypothesis was that a B0 map acquired on the MRsim could be used to guide treatment decisions by estimating geometric distortion effects of the implant on the MR images used for online plan adaptation. We therefore implemented a clinical workflow, based on a <2 min B0 map acquired per patient during MR simulation, to guide the decision on the course of treatment.

The aim of this study was to present this clinical workflow and evaluate the accuracy of the estimate of magnitude of distortions, sourced by the implant during MRIgRT, by comparing B0 maps acquired during MR simulation and each treatment fraction.

2. Materials and methods

2.1. Theory

The accumulated phase ($\phi =\gamma \text{B}\mathrm{T}\mathrm{E}\text{)}$ of spins after excitation depends on the gyromagnetic ratio ($\gamma /(2\pi )=$ 42.577 MHz/T for protons) and increases linearly with magnetic field strength ($B_0$) and echo-time ($\mathrm{T}\mathrm{E}$). From two acquisitions, a phase-difference map ($\mathrm{\Delta }\phi =\gamma \mathrm{\Delta }\text{B}\mathrm{\Delta }\mathrm{T}\mathrm{E}$) can be constructed that depends linearly on local field distortions ($\mathrm{\Delta }\text{B}$) and the difference in $\mathrm{T}\mathrm{E}$ ($\mathrm{\Delta }\mathrm{T}\mathrm{E}$) between the two acquisitions. By inverting the equation, a field-distortion map ($f$ in Hz), or B0 map, can be constructed

$$f\text{=}\gamma /(2\pi )\mathrm{\Delta }\text{B =}\mathrm{\Delta }\phi /(2\pi \mathrm{\Delta }\mathrm{T}\mathrm{E}).$$

Phase-differences have a range of $\pm \pi$ and so $f$ can only take on values between $\pm 1/(2\mathrm{\Delta }\mathrm{T}\mathrm{E})$.

Furthermore, in the linear response regime of magnetization, relative field distortions caused by materials/tissue are independent of field strength. Therefore, the effect of an implant, in terms of its magnetic field distortions, can be extrapolated to a certain field strength from measurements performed at a different field strength. For most commonly used acquisitions (Cartesian, non-EPI), geometric distortions due to field distortions can be calculated by taking the ratio frequency offset over the read-out bandwidth of the acquisition in question. The distortions are in the read-out direction. Using these well-known relations, the expected geometric offset $x$ (mm) during MRIgRT can be calculated as

$$x=(B_{0,\mathrm{M}\mathrm{R}\mathrm{L}}/B_{0,\mathrm{M}\mathrm{R}\mathrm{s}\mathrm{i}\mathrm{m}})(fl)/\text{BW}\text{,}$$

where the pre-factor is to account for magnetic field strength differences between the MRsim and MR-linac, $f$ is the B0 map acquired on the MRsim, $l$ (mm/px) is the acquisition pixel length in the read-out direction, and $\text{BW}$ (Hz/px) is the bandwidth in the read-out direction per pixel. Here, $l$ and $\mathrm{B}\mathrm{W}$ are parameters from the acquisition on an MR-linac for which $x$ is calculated.

2.2. Clinical workflow

To guide clinical target volume (CTV) delineation, CT images were registered to anatomical T₂-weighted images acquired during MR simulation. An additional B0 map was acquired during this session, which was thereby indirectly registered to the CT as well. The frequency range of the B0 map was arbitrarily chosen such that when no phase wraps occur inside the CTV, geometric distortions due to the prosthesis were well within acceptable limits (<0.35 mm) on the T₂-weighted image used during MRIgRT for online plan adaptation.

From the B0 map, an estimate of maximum distortion in the 3D T₂ TSE image used for MRIgRT between two voxels inside the CTV was calculated. Phase wrapping was accounted for by estimating the number of phase wraps, sourced by the implant, inside the CTV based on visual inspection of the images. The resulting estimation of the magnitude of geometric distortions throughout the CTV was subsequently used to determine eligibility for MRIgRT treatment. This workflow is summarized in Fig. 1.

Fig. 1.

Proposed workflow to decide on eligibility for MRIgRT for patients with metallic implants, based on planning CT and MR (including B0 map).

2.3. Patient data

Patients with prostate cancer, one hip-prosthesis, and who were treated with MRIgRT, were eligible for inclusion in this study. All patients that provided written informed consent, for using their data as part of an ethics review board approved observational study, were included. For these three patients, the planning CT, associated delineated structures and anatomical MR images used for clinical treatment planning, were available. The anatomical MR images used for position verification during MRIgRT were also accessible. Additionally, B0 maps were acquired on both the MRsim and during each subsequent treatment fraction. There were no patients that were deemed ineligible for MRIgRT based on the aforementioned workflow.

2.4. Imaging data

The MR simulation was performed with a 3 T Ingenia (Philips Healthcare, Best, The Netherlands). Patient positioning during the simulation was matched with the planning CT using a 2D T₂ turbo spin echo (TSE) image. The MR-linac used for MRIgRT was a 1.5 T Unity (Elekta AB, Stockholm, Sweden). Similarly as for MR simulation, patient position prior to each treatment fraction was matched to the planning CT using the 3D T₂ TSE image, conventionally used for position verification.

The B0 maps were automatically calculated on the MR console from two 3D TFE acquisitions with different echo-times. Echo-time differences were chosen such that, for both field-strengths, the range of the B0 maps were ± 1.7 ppm (corresponding to ± 217 Hz and ± 109 Hz on the 3 T and 1.5 T systems, respectively). Table 1 contains more details on the acquisition parameters.

Table 1.

Acquisition parameters for the sequences used for anatomical imaging and acquisition of B0 maps during MR simulation and MRIgRT.

	MR simulation		MRIgRT
	T2 TSE	B0	T2 TSE	B0
acq. voxel size (mm3)	0.7x0.7x3.0	2.0x2.0x6.0	1.2x1.2x2.4	4.0x4.0x4.0
field-of-view (mm3)	200x281x75	262x253x69	400x448x250	430x430x60
TE (ms)	120	2.2	128	4.6
TR (ms)	3960	6.6	1300	11
flip angle (˚)	90	21	90	15
readout bandwidth (Hz/px)	291	869	373	556
scan time (min:sec)	3:42	1:55	2:53	0:34

2.5. Data analysis

Matching was performed by an experienced radiation therapy technologist using Mirada (Mirada Medical, Oxford, United Kingdom) to rigidly match the planning CT to the anatomical MR images. The B0 map, acquired in the same MR scanning session, was thereby also registered to the delineated structures. Care was taken during registration to consider only structures uninfluenced by the distortions from the prosthesis, like the nonmetal hip and pubis, which were far removed from the hip prosthesis.

To show the effects of the hip-prostheses on the different images and imaging modalities, for each patient, the planning CT, B0 maps, and T₂ TSE images acquired during MR simulation and the first treatment fraction were visually compared at the slices for which distortions in the CTV were maximal in the T₂ TSE images acquired during MR simulation.

B0 maps from MR simulation and each treatment fraction during MRIgRT were qualitatively compared at the same slice location, to investigate the degree of agreement between field distortions, sourced by metallic implants, at different field strengths as well as anatomical changes during the course of treatment.

For a quantitative analysis, Mirada was used to extract minimal, average, and maximal values as well as the standard deviation from the B0 maps inside the CTV for each imaging session. These values were then converted to expected geometric distortions (in mm) for the 3D T₂ TSE image used for position verification during MRIgRT. The maximum distortion between voxels inside the CTV ($\delta x$) was calculated from the difference in maximal and minimal values in addition to an estimate of the number of phase wraps that occurred inside the CTV due to the nearby implant. Mean values of $\delta x$ over the course of treatment were compared to estimates made during MR simulation.

When no phase wraps occurred, the statistics on $f$ and $x$ were undistorted and could reliably be used for estimating $\delta x$ directly. When phase wraps occurred, however, minimal and maximal values of $f$ and $x$ were close to and within their respective ranges and only crude estimates of $\delta x$ could be calculated by incorporating distortions per complete phase wrap. Therefore, when phase wraps occurred, estimates of $\delta x$ were approximately multiples of 0.70 mm as that was the range of the B0 maps acquired, both for simulation and MRIgRT.

3. Results

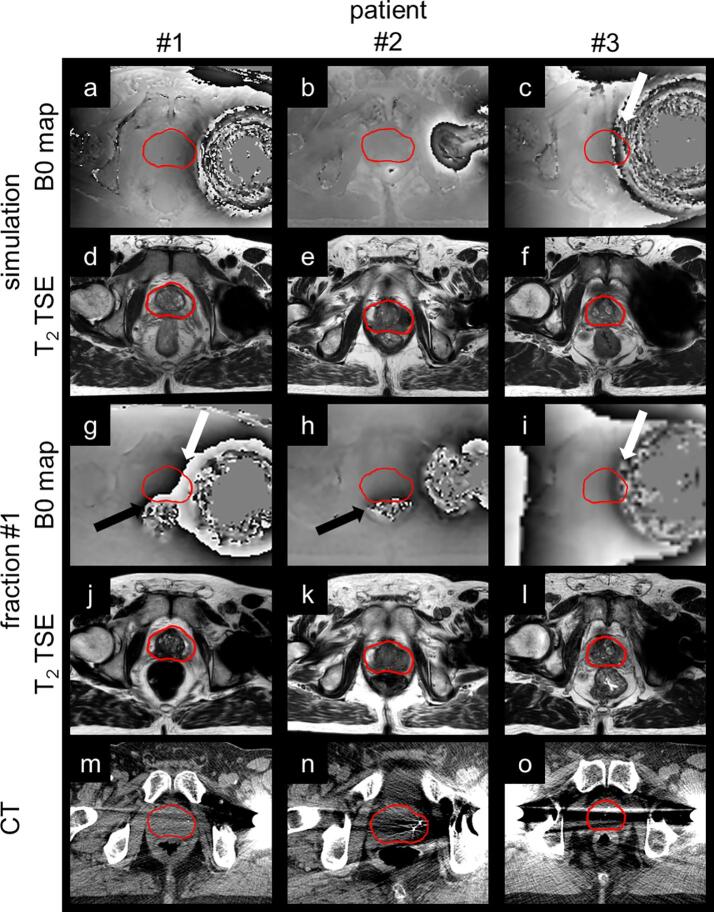
CTVs were located outside the region of signal voids during each MR imaging session for all patients. Geometric distortions, however, were expected inside the CTVs based on visual inspection of the B0 maps made during MR simulation, particularly for patient #3 (Fig. 2). Per patient, the general shape of the distortion caused by the implant was similar over time and between field strengths (Fig. 3). Changes in rectal filling occasionally resulted in notable changes between B0 maps acquired during different imaging sessions.

Fig. 2.

The B0 maps and T₂ TSE images, acquired during MR simulation (3 T system) and the first treatment fraction of MRIgRT (1.5 T system), are shown together with the planning CT to which they were registered. For direct comparison, the field distortions are shown relative to field strength (range ± 1.7 ppm). Black and white arrows point to phase wrapping inside the CTV due to rectal air and metallic implants, respectively. Bright streak artefacts throughout the whole imaging plane were a result of the implant in CT. In the T₂ TSE images acquired with MRI, signal voids, inside and nearby the implant as a consequence of magnetic field disturbances, were apparent.

Fig. 3.

B0 maps acquired during MR simulation and each treatment fraction of MRIgRT are shown for each patient. During the first treatment fraction, patient #1 and #2 had significant rectal filling resulting in phase wrapping near and inside the CTV (black arrows). Phase wrapping, sourced by the implant (white arrows), either occurs always or never inside the CTV, with the exception for patient #1 during simulation where the phase wrapping stops just outside of the CTV.

Maximum distortions inside the CTV were calculated for each MR imaging session based on the B0 map and estimated number of phase wraps that occurred inside the CTV (Table 2). For patient #1, no phase wrapping due to the implant occurred inside the CTV during simulation and once for each subsequent treatment fraction, resulting in an underestimation of the distortions by 1.03 mm. The difference between $\delta x$ estimated during MR simulation and averaged over all treatment fractions was 0.13 mm for patient #2. For patient #3, however, strong distortions led to multiple phase wraps inside the CTV due to the implant. Variety in the estimate on the number of phase wraps led to a range of $\delta x$ from 1.39 mm to 2.79 mm over the imaging sessions where on average, the prior estimation overestimated the magnitude of distortion in the CTV during MRIgRT with 0.98 mm.

Table 2.

Metrics on the field-distortions ($\mathit{f}$ in ppm) and derived expected geometric distortions $\mathit{x}$ (mm) for the 3D T₂ TSE image used for plan adaptation during MRIgRT inside the CTVs are reported as (minimum|mean ± standard deviation|maximum). The maximum distortion inside the CTV ($\delta x$) is calculated by including an estimate of the number of phase wraps sourced by the implant.

patient	time point	$\mathit{f}$(ppm)	$\mathit{x}$(mm)	phase wraps	$\mathit{\delta }\mathit{x}$(mm)
#1	simulation	(−1.36|−0.16 ± 0.34|0.72)	(−0.28|−0.03 ± 0.07|0.15)	0	0.43
	fraction #1	(−1.71|−0.44 ± 0.95|1.71)	(−0.35|−0.09 ± 0.20|0.35)	1	1.40
	#2	(−1.70|−0.51 ± 0.74|1.71)	(−0.35|−0.10 ± 0.15|0.35)	1	1.40
	#3	(−1.71|−0.55 ± 0.69|1.71)	(−0.35|−0.11 ± 0.14|0.35)	1	1.40
	#4	(−1.71|−0.45 ± 0.83|1.71)	(−0.35|−0.09 ± 0.17|0.35)	1	1.40
	#5	(−1.71|−0.53 ± 0.55|1.70)	(−0.35|−0.11 ± 0.11|0.35)	1	1.40
#2	simulation	(−0.29| 0.13 ± 0.19|0.64)	(−0.06| 0.03 ± 0.04|0.13)	0	0.19
	fraction #1	(−1.71|−0.28 ± 0.44|1.70)	(−0.35|−0.06 ± 0.09|0.35)	0	0.70
	#2	(−0.68|−0.10 ± 0.14|0.23)	(−0.14|−0.02 ± 0.03|0.05)	0	0.19
	#3	(−0.53| 0.05 ± 0.16|0.43)	(−0.11| 0.01 ± 0.03|0.09)	0	0.20
	#4	(−0.81| 0.01 ± 0.25|0.82)	(−0.17| 0.00 ± 0.05|0.17)	0	0.33
	#5	(−0.75|−0.17 ± 0.14|0.13)	(−0.15|−0.04 ± 0.03|0.03)	0	0.18
#3	simulation	(−1.70|−0.19 ± 0.81|1.70)	(−0.35|−0.04 ± 0.17|0.35)	3	2.79
	fraction#1	(−1.70|−0.06 ± 0.85|1.70)	(−0.35|−0.01 ± 0.17|0.35)	2	2.10
	#2	(−1.71|−0.06 ± 0.84|1.70)	(−0.35|−0.01 ± 0.17|0.35)	2	2.09
	#3	(−1.71|−0.13 ± 0.85|1.70)	(−0.35|−0.03 ± 0.17|0.35)	1	1.40
	#4	(−1.66|−0.02 ± 0.84|1.70)	(−0.34| 0.00 ± 0.17|0.35)	2	2.09
	#5	(−1.68|−0.01 ± 0.86|1.68)	(−0.34| 0.00 ± 0.18|0.35)	1	1.39

4. Discussion

With the clinical workflow presented in this work, estimates of the expected distortions in images acquired during MRIgRT were obtained during MR simulation to decide on the course of treatment with minimal extra burden on patient and health care professionals. We have shown that effects of metallic implants on imaging during MRIgRT can be predicted using B0 maps acquired during MR simulation.

Geometric distortions, sourced by metallic implants in a porcine thigh, have been corrected by extracting a distortion correction map from MR images of a grid phantom with known geometry with and without the implant inserted [28]. The method does not offer a population-based solution and is resource intensive, however, and might therefore be unsuitable for implementation in a clinical setting. In the MR simulation setting, geometric correction of images based on B0 maps have been successfully implemented [24], [25]. For MRIgRT, however, these corrections would have to be applied without impeding the online workflow. Since this feature was not yet clinically available, we implemented a workflow to decide if expected distortions during MRIgRT would be acceptable or not.

Phase wrapping poses a problem for accurate estimations of the distortions. Although we estimated the number of phase wraps that occurred inside the CTVs to reconstruct the total distortion, this increases variability in the estimate as well as possibly introduce human error in the workflow. The most straightforward way of reducing phase wraps is by increasing the range of the B0 maps to the maximum allowed by the system at the cost of reduced precision of the maps [22]. Far enough away from the implant, phase unwrapping algorithms can also be effective although their use was outside of the scope of this manuscript [21], [22], [23]. Note, however, that estimation on the number of phase wrapping was mostly a problem for the B0 maps acquired prior to treatment with MRIgRT, using a fast acquisition on a system with lower specifications than those typically used for diagnostic purposes. Nevertheless, an automatic phase unwrapping algorithm that is robust and fast enough is a requisite for the implementation of field distortion corrections in an online workflow.

Besides subject-related field distortions, the magnetic field created by the MR is never homogeneous throughout the whole imageable volume. Since measured and expected field distortions are compared between systems (with different machine-related B0 inhomogeneities) this workflow unjustly incorporates machine-related field distortions measured on the MRsim into the expected geometric distortions on the MR-linac. This effect, however, is expected to be negligible as field inhomogeneities are typically ≲1 ppm inside a sphere with a diameter of 40 cm for most clinical MR systems [29].

Contouring is performed using both CT and MR images, of which the latter are geometrically distorted by the prosthesis [27]. This leads to uncertainties in the estimation of distortions inside the CTV, particularly in regions where distortions are large. Consequently, it is important to use a conservative approach by matching regions outside of the distortions from the prosthesis and choosing a range for the B0 map such that phase wrapping occurs before field distortions lead to significant geometric distortions.

Whether or not a patient is deemed eligible for MRIgRT depends on the expected levels of distortions as well as the thresholds set at the treating institution. For patient #3, expected geometric distortions exceeded 2 mm and the clinical decision was made to increase margins anisotropically to account for distortions of the CTV on the side nearest the metallic implant. Alternatively, the decision could have been made to perform a simple dose shift, where one could argue that if a substantial part of the target is undisturbed, a rigid match is still feasible [30]. Similarly, full plan adaptation, with online recontouring of the CTV, could still have been performed [31], [32]. In both cases, the added uncertainty could have been mitigated by considering the distortion as a systematic error, resulting in an increased PTV margin [33], [34].

In conclusion, we have shown that metallic implants do not necessarily rule out MRIgRT treatment for prostate patients. The suggested framework is generalizable and not restricted to the pair of MR systems, site, implant, or region of interest as presented in this work. Care must be taken, however, to quantify the expected geometric distortions sourced by the implant to ensure they are within acceptable limits. In this paper, we described a method to estimate the magnitude of geometric distortions on a per patient basis, by adding a fast B0 map acquisition to the MR simulation protocol.

Declaration of Competing Interest

NKI-AvL is part of the Elekta MR-linac Consortium and we acknowledge financial and technical support from Elekta AB (Stockholm, Sweden) under a research agreement.