Evaluation of the influence of susceptibility-induced magnetic field distortions on the precision of contouring intracranial organs at risk for stereotactic radiosurgery

Highlights

• •45 data sets (18 on a 1.5 T MR and 27 on a 3 T MR) were evaluated for susceptibility induced distortions.
• •Maximum distortions of up to 1.7 mm were found for organs at risk in standard diagnostic settings.
• •Median distortions ranged between 0.1 and 0.2 mm for all organs at risk.
• •Active shimming was estimated to reduce distortions by a factor of 2.3 to 2.9.
• •A safety margin of 1 mm would have encompassed 99.8% of the distortions.

Abstract

Background and purpose

Magnetic resonance imaging (MRI) is a crucial factor in optimal treatment planning for stereotactic radiosurgery. To further the awareness of possible errors in MRI, this work aimed to investigate the magnitude of susceptibility induced MRI distortions for intracranial organs at risk (OARs) and test the effectiveness of actively shimming these distortions.

Materials and methods

Distortion maps for 45 exams of 42 patients (18 on a 1.5 T MRI scanner, 27 on a 3 T MRI scanner) were calculated based on a high-bandwidth double-echo gradient echo sequence. The investigated OARs were brainstem, chiasm, eyes, and optic nerves. The influence of active shimming was investigated by comparing unshimmed 1.5 T data with shimmed 3 T data and comparing the results to a model based prediction.

Results

The median distortion for the different OARs was found to be between 0.13 and 0.18 mm for 1.5 T and between 0.11 and 0.13 mm for 3 T. The maximum distortion was found to be between 1.3 and 1.7 mm for 1.5 T and between 1.1 and 1.4 mm for 3 T. The variation of values was much higher for 1.5 T than for 3 T across all investigated OARs. Active shimming was found to reduce distortions by a factor of 2.3 to 2.9 compared to the expected values.

Conclusions

Using a safety margin for OARs of 1 mm would have encompassed 99.8% of the distortions. Since distortions are inversely proportional to the readout bandwidth, they can be further reduced by increasing the bandwidth. Additional error sources like gradient nonlinearities need to be addressed separately.

1. Introduction

Radiotherapy (RT) planning is based on computed tomography (CT) images, enabling dose calculation based on individual patient anatomy. Magnetic resonance imaging (MRI) has become a crucial factor in RT planning for many indications because of its superior soft tissue contrast [1], [2], [3]. It allows for precise target delineation and is recommended for many forms of RT [4]. This is especially important for intracranial stereotactic radiotherapy (SRT), where the in-plane resolution and slice thickness should be ≤ 1 mm [5]. Furthermore, in addition to providing excellent soft tissue contrast, it is also possible to visualize physical and metabolic processes of the tumor environment with established MRI sequences, such as diffusion weighted imaging [6], [7] or perfusion weighted imaging [8]. Improved imaging of the underlying patho-physiology is to be expected since the development of new techniques is still ongoing [9]. For the interested reader, a large number of papers describing MRI basics and possible errors in an RT context are available [1], [10], [11], [12].

Recent developments in technology have brought to the market hybrid treatment machines, combining MRI and medical linear accelerators, termed magnetic resonance guided radiotherapy (MRgRT) [13]. The first patient treatments with these systems have demonstrated the ability for MRgRT to improve daily positioning as compared to conventional image guided RT with cone-beam CT [14], [15], [16]. Thus, with the increased application of MRI in RT, the importance of characterizing all possible imaging errors is becoming increasingly important.

These errors mainly consist of non-linear gradient fields and patient-induced magnetic field inhomogeneities caused by magnetic susceptibility differences within biological tissues [10], [11]. For intracranial tumors treated with stereotactic radiosurgery (SRS), geometrical accuracy is of utmost importance [17]. Studies showed that susceptibility-induced errors caused a shift of up to 4 mm, although extreme distortions only occur in small volumes [18]. The highest errors were found at tissue-air boundaries, for example in the sinuses. An additional critical point is the static magnetic field strength, as the distortions increase with higher field strength. Errors induced by non-linear gradient fields were shown to be up to 2 mm after distortion correction algorithms were applied [11], [19].

Distortion in MRI is a very important and well-researched aspect and there are several ways to measure distortion. Some techniques use phantom measurements that are compared to their well defined geometry [20], landmark comparison on MRI and CT images [21], by simulating the magnetic field distortions based on bulk assignment of magnetic susceptibilities [22], or by using a special sequence designed to measure frequency distortions [18], [23].

Recent studies on susceptibility-induced errors focused on an analysis of the brain as a whole [18]. However, for RT planning purposes, the contouring physician would profit from detailed information about where the image is less reliable. This information could then be a contributing factor for establishing safety margins for OARs, also called planning organ at risk volumes (PRVs) [24]. OARs are subject to the same errors as target volumes like inter-observer variability when contouring, distorted images, or imperfect positioning. This is especially important in SRT, where steep dose gradients can lead to significant overdosing in OARs when these errors occur.

Thus, the aim of this work was to derive estimates of spatial distortions in organs at risk (OARs) originating from susceptibility differences. To obtain this information, clinical data of 42 cancer patients presenting with an intra-cranial malignancy were analyzed retrospectively. The motivation of this study was to assess the quality of the sequences routinely used for RT planning. As different shimming techniques were used for 1.5 T and 3 T, we were able to investigate the influence of the main magnetic field strength on the image error and finally the impact of active shimming compared to passive shimming.

2. Materials and Methods

2.1. Patients

The data for this study resulted from 42 patients receiving an MRI scan over a period of three months (September 2018 - December 2018). All procedures performed were in accordance with the ethical standards of the institutional research committee and with the 1964 Helsinki declaration and its later amendments. Patient consent was not required for this retrospective study per institutional policy. Image data was only included in the analysis if those images had been used in the target delineation workflow. All patients were receiving SRS for intracranial lesions. The total number of patient examinations was 45, with three patients receiving multiple treatments in the study period. Of those 45 measurements, 18 were conducted on a 1.5 T MR-scanner and 27 on a 3 T MR-scanner. The median age of the 1.5 T patients was 61 years (29–88 years), the median age of the 3 T patients was 56 years (39–81 years).

2.2. Data acquisition

For all patients, MRI was performed no more than 5 days in advance of the day of treatment in order to reduce the risk of tumor growth or intracranial shifts after the target had been contoured [25]. The exams were performed on both a 1.5 T MR-scanner (Magnetom Aera, Siemens Healthineers, Erlangen, Germany) and a 3 T MR-scanner (Magnetom Trio Tim, Siemens Healthineers, Erlangen, Germany).

For contouring, a transversal high resolution 3D T1-weighted magnetization-prepared rapid acquisition with gradient echo (MPRAGE) was used. The data for reconstruction of error maps was acquired with a vendor-provided 2D transversal double-echo gradient echo (GRE) sequence. The detailed sequence parameters can be found in Table 1. In the analyzed period, all 1.5 T sequences used passive shimming, which creates a homogeneous magnetic field in the empty MRI, while all 3 T sequences used 2nd-order active shimming, which reduces the patient-induced magnetic field distortions to the second order. To keep the measurement time low, a lower resolution of 3.3 × 3.3 × 3.3 mm³ was chosen for the double-echo GRE sequence.

Table 1.

Detailed sequence parameters for the transversal T1-MPRAGE and the transversal double-echo GRE. All 1.5 T sequences used passive shimming, while all 3 T sequences used 2nd-order active shimming.

Scanner	TI [ms]	TR [ms]	TE [ms]	FA [°]	Voxel size [mm × mm × mm]	BW [Hz/Pixel]
	transversal T1-MPRAGE
1.5 T	1100	1900	3.02	15	1.0 × 1.0 × 1.0	160
3 T	1100	2010	3.35	15	1.1 × 1.1 × 1.1	180
	transversal double-echo GRE
1.5 T	500	4.76	9.52	90	3.3 × 3.3 × 3.3	1502
3 T	500	4.92	7.38	60	3.3 × 3.3 × 3.3	1502

2.3. Data processing

The location of a point in an MR image in frequency encoding direction is dependent on the local magnetic field. For sequences with special readouts like echo planar imaging distortion can also occur in the phase encoding direction. A distortion $\mathrm{\Delta }B$ in this field causes a misallocation of the point. Magnetic field distortions can be caused by distortions of the main magnetic field ($\mathrm{\Delta }{B}_0$), for example because of insufficient shimming, susceptibility changes ($\mathrm{\Delta }{B}_{\chi }$), or chemical shifts ($\mathrm{\Delta }{B}_{\mathit{CS}}$) [11]. The effective field distortion then consists of

$$\mathrm{\Delta }B=\mathrm{\Delta }{B}_0+\mathrm{\Delta }{B}_{\chi }+\mathrm{\Delta }{B}_{\mathit{CS}}.$$ (1)

These distortions can be determined by using a double-echo gradient echo sequence, with the echo times adjusted to prevent chemical shift artifacts caused by fat [26]. It is based on the phase difference $\mathrm{\Delta }\phi$ that accumulates between the two echo times. The effective field distortion can then be calculated by

$$\mathrm{\Delta }B=\frac{\mathrm{\Delta }\phi \left(\mathrm{\Delta }TE\right)}{\gamma \mathrm{\Delta }TE},$$ (2)

where $\gamma$ is the gyromagnetic ratio, $\mathrm{\Delta }TE=T{E}_2-T{E}_1$ is the echo time difference and $\mathrm{\Delta }\phi \left(\mathrm{\Delta }TE\right)$ is the phase difference that is accumulated between the two echoes.

The resulting error $\mathrm{\Delta }x$ in the spatial domain of a voxel in frequency encoding direction for a given sequence is

$$\mathrm{\Delta }x=\frac{\mathrm{\Delta }B}{2\pi BW}\gamma d,$$ (3)

where BW is the bandwidth in Hz/pixel and d is the size of the pixel along the frequency encoding direction. BW and d are sequence-dependent parameters and thus the resulting error needs to be calculated individually for each sequence. For an assessment of the error magnitude and a better statistical evaluation, the errors were calculated as absolute values.

To correct the phase wraps that occur because of the limited value range, a magnitude-sorted list, multi-clustering phase unwrapping algorithm [27] was used. The results were inspected manually and all images with abrupt phase jumps of multiples of 2π in the processed data that had no colocalized equivalent in the raw data were excluded. This removed the influence of limitations of the unwrapping algorithm. All calculations were performed in MatLab (MatLab, R2015b, MathWorks, Natick, USA). The spatial distortions presented in this work were calculated with the bandwidth of the respective MPRAGE sequence (160 Hz/Px for 1.5 T and 180 Hz/Px for 3 T) using Equation (3) and refer to the distortion in frequency encoding direction. For a more comprehensive graphic description of the workflow, see Supplementary Fig. 1.

To check the plausibility of the resulting values, it is possible to analytically calculate the distortions for simple geometric structures, such as an infinitely long cylinder, by solving the Maxwell equations. With the cylinder model used by Haacke and Reichenbach [28], the susceptibility induced field distortion outside the cylinder wall is given by

$$\mathrm{\Delta }B=\frac{{\chi }_{\mathrm{w}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}}{B}_0}{2}{\frac{{\mathrm{a}}^2}{\left|{\mathrm{r}}^2\right|}\sin }^2\theta \cos 2\varphi ,$$ (4)

where ${\chi }_{\mathrm{w}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}}$ is the magnetic susceptibility of water (${\chi }_{\mathrm{w}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}}=-9ppm$), $\theta$ the angle between the long axis of the cylinder and the external magnetic field, $\mathrm{a}$ the radius of the cylinder, and $\varphi$ the polar angle between the position vector $\mathrm{r}$ and the plane perpendicular to the cylinder axis. The resulting distortion in the spatial direction is then given by

$$\mathrm{\Delta }x=\frac{{\chi }_{\mathrm{w}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}}{B}_0}{2}{\frac{{\mathrm{a}}^2}{\left|{\mathrm{r}}^2\right|}\sin }^2\theta \cos 2\varphi \frac{\gamma d}{2\pi BW},$$ (5)

with a maximum value at the cylinder surface of

$$\mathrm{\Delta }x=\frac{{\chi }_{\mathrm{w}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}}{B}_0}{4\pi }\frac{\gamma d}{\mathit{BW}}.$$ (6)

2.4. Contours

All contours used in this work were taken from the clinical treatment plans. The choice regarding which OARs to include in the study was based on the OAR contour availability in the majority of patient plans investigated. Based on this consideration, the eyes, optic nerves, brainstem and chiasm were investigated. All contours were drawn in iPlan (iPlan RT Image, 4.1.2, Brainlab, Munich, Germany) on a contrast-enhanced T1w-MPRAGE and transferred onto the distortion maps for further calculation.

As the evaluated contours were taken from clinical plans of patients with various indications, not all OARs were present in every patient. For the 1.5 T measurements, contours of the chiasm were missing for one patient, two patients had no contours of the right optic nerve and one patient had no contours of the left optic nerve. For the 3 T measurements, one patient had no contours of the left optic nerve and two patients had no contours of the right optic nerve. These contours were added by an experienced radiation oncologist (Florian Putz) for the current analysis.

2.5. Efficiency of shimming

The efficiency of the shimming in our work could be estimated by comparing the values at 1.5 T for all OARs with those at 3 T. To scale up the 1.5 T data to reach expected artifact strengths at 3.0 T, the 1.5 T measured values needed to be doubled and the different BW and resolution was also required to be taken into account (see Equation (5)). As the maximum values only represent single points, which would not give a statistically significant comparison, we compared median values.

2.6. Statistical evaluation

For the statistical evaluation, the distortion values of the individual contours were exported from MatLab and then imported in R [29]. Median, mean and maximum values of the spatial error in mm for each OAR were calculated over the complete set of contours. Additionally, the cumulative distribution function $F\left(\mathrm{\Delta }x\right)$ of the distortion for each OAR was calculated. It denotes the probability that the distortion takes a value less than or equal to $\mathrm{\Delta }x$ and was evaluated voxelwise.

3. Results

3.1. Qualitative evaluation

A distribution of distortions that was representative for the average patient can be found in Fig. 1. Distortions were more pronounced in the second measurement, acquired on the 1.5 T MR-scanner. In both measurements, large distortions mostly colocalized with tissues adjacent to the air-filled sinus cavities, mastoid cells and the air-filled oro- and nasopharynx, as well as the nasal cavity.

Fig. 1.

Overlay of distortion maps (in units of mm) and a contrast enhanced T1-MPRAGE to show the morphological context of the distortions. Background voxels were masked based on the magnitude data from the T1w-MPRAGE. The images were taken 37 days apart on a 1.5 T and b 3 T. The distortions colocalize with air filled areas as well as cavity walls.

Distortions were particularly severe near the frontal and maxillary sinuses as well as near the sphenoid sinus and the ethmoidal cells. These distortions also reached parts of the optic nerves and optic chiasm as well as basal parts of the frontal lobes. In addition, distortions were shown to overlap with the external auditory canal, nuchal and occipital skin and subcutaneous tissues as well as the external nose.

Brain regions distant to the mastoid bone and sinus cavities showed only minimal distortions.

3.2. Quantitative evaluation

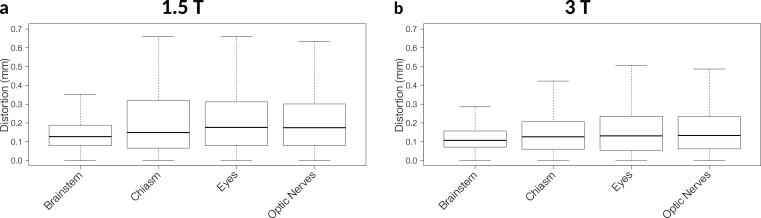
Fig. 2 shows boxplots of the distortions for all voxels of every patient for each investigated OAR. The median and maximum distortion values can be found in Table 2. The variation of values was much higher for 1.5 T than for 3 T across all investigated OARs. No patients had metal implants that showed artifacts in the investigated OARs.

Fig. 2.

Box plot of the distortions for each investigated OAR over all patients for a 1.5 T and b 3 T. The boxes contain 50% of the measured voxels for each OAR. Outliers were excluded for better readability.

Table 2.

Median and maximum distortion values in mm for all OARs investigated for 1.5 T and 3 T. The values were calculated based on the acquisition parameters of the respective T1-MPRAGE.

	Brainstem	Chiasm	Eyes	Optic nerves
	1.5 T
$\mathrm{\Delta }{x}_{\mathit{med}}$ [mm]	0.13	0.15	0.18	0.17
$\mathrm{\Delta }{x}_{\mathit{max}}$ [mm]	1.7	1.4	1.3	1.7
	3 T
$\mathrm{\Delta }{x}_{\mathit{med}}$ [mm]	0.11	0.13	0.13	0.13
$\mathrm{\Delta }{x}_{\mathit{max}}$ [mm]	1.1	1.3	1.4	1.4

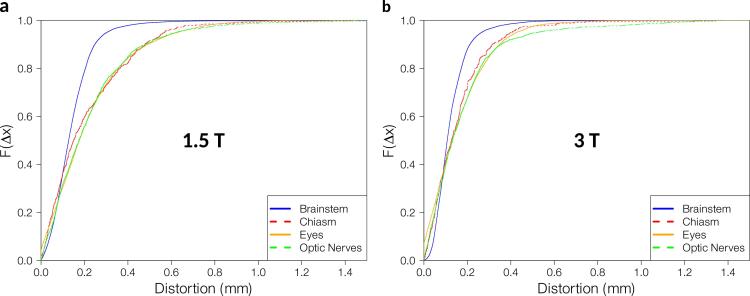
95% of the voxels for 1.5 T and 3 T respectively showed distortion values smaller than 0.30 mm and 0.27 mm in the brainstem, 0.57 mm and 0.40 mm in the chiasm, 0.63 mm and 0.43 mm in the eyes, and 0.62 and 0.53 mm in the optic nerves. 99.8% of the voxels showed distortions ≤ 1 mm, 95% of the voxels showed distortions ≤ 0.5 mm. A more detailed representation of the distribution of the distortions can be found in Fig. 3.

Fig. 3.

Cumulative distribution function for each investigated OAR over all patients for a 1.5 T and b 3 T. $F(\mathrm{\Delta }x)$ denotes the probability that the distortion takes on a value less than or equal to $\mathrm{\Delta }x$.

3.3. Theoretical prediction

The maximum expected distortion for 1.5 T was 1.8 mm. If we assumed the air filled sinuses to have a diameter of 10 mm, a voxel with 1 mm distance to the wall of the cylinder had an expected distortion value of 1.3 mm, while one with 1 cm distance had an expected distortion value of 0.20 mm. For 3 T the maximum expected distortion was 3.2 mm, over a distance of 1 mm the expected distortion is 2.2 mm, and in a distance of 10 mm, it is 0.36 mm. This did not, however take into account the dependence of the geometrical angles, which would have further decreased those values.

3.4. Efficiency of shimming

The expected ratio of 3 T to 1.5 T was 1.96. The ratios of median values were found to range between 0.67 and 0.87. Compared to the expected ratio this would mean that active shimming effectively reduced the distortions by a factor of 2.3 to 2.9.

4. Discussion

The aim of this study was to characterize errors in MRIs used for RT planning that occur because of locally-deviating magnetic field strengths. For this, a transversal double-echo gradient echo sequence was used. Based on the phase differences from the echoes, frequency distortion maps were calculated and converted into sequence-specific local distortion maps. The evaluation was done for various serial OARs that were taken from clinically-approved treatment plans and transferred onto the reconstructed distortion maps using a clinical treatment planning system.

As can be seen in Fig. 1, the highest distortions occurred at air-tissue boundaries, while the remaining parts of the head showed nearly no distortions. Hence, we verified that the largest artifacts were typically at air-tissue boundaries. The maximum distortion values found in this work were 1.7 mm in the optic nerve for 1.5 T and 1.4 mm for the eyes for 3 T, which are both structures that are very close to air-tissue boundaries. This is in accordance with several other studies that found distortions of up to 4 mm for unshimmed 3 T data [18], [23], as the maximum values found in our work were expected to be two times smaller for 1.5 T and the 3 T data was acquired with active shimming. To check the plausibility of our calculated distortions, we assumed that the main air cavities, primarily the sinus, could be modelled by an infinitely long air filled cylinder surrounded by water. To check this assumption, the main magnetic field only needed to be altered by the susceptibility effects. For this we were able to use the 1.5 T field maps that were acquired with the tune-up shim, which balanced out magnetic field inhomogeneities in the empty bore, without presence of a patient. In this case, all distortions could be assumed to be caused by the patient and therefore mainly by the susceptibility effects. The measured distortions matched the expected values closely. The highest expected distortion was 1.8 mm right at the surface of the cylinder, which is the sinus in this model. With 1.7 mm, the maximum measured value of the optic nerves was in good accordance with the expected value, as the optic nerves were in close proximity to the sinus. The median values of the distortions ranged between 0.13 and 0.18 mm, which was the expected value within a 1 cm distance to the sinus. As the brainstem and the chiasm were usually located more than 1 cm from the sinus, other effects like an imperfect tune-up shim or chemical shift artifacts were likely more dominant.

As the magnetic susceptibility artifacts are linearly-dependent on the field strength [30], artifacts will become more prominent at 3 T. To counteract this dependence, active shimming is often used. The efficiency of the shimming in our work could be estimated by comparing the values at 1.5 T for all OARs with those at 3 T. As the maximum values only represent single points, which would not give a statistically significant comparison, we compared median values. This means active shimming effectively reduced the distortions by a factor 2.3 to 2.9. Other studies also found significant improvements when using active shimming. Adjeiwaah et al. found a reduction in the number of voxels with a geometric shift over 2 mm from 15.4% to 2.7% [22], while Tijssen et al. found an improvement in magnetic field homogeneity by up to a factor of 3 [31].

The importance of this distortion reduction was highlighted since we compared the maximal expected distortions with the size of our OARs. For 3 T, the highest expected value was 3.21 mm, while the optic nerves had, on average, a diameter between 1.6 mm and 3.5 mm along their tract [32]. This means that, for some positions along the optic nerve, contours drawn on the distorted MR image would have had no overlap at all with the ground truth position of the optic nerve. On the other hand, the median distortion was small compared to the dimensions of all investigated OARs. This however did not decrease the significance of the maximum values, as distortions of these magnitudes, and thus the potential for over-dosing an OAR in the ensuing RT plan, could have led to significant damage to the respective OAR. However, the maximum values were reduced less than the factor found for the median values, as active shimming can in general only correct the field very locally.

We found that for 1.5 T a safety margin of 1 mm would have encompassed 99.8% of the voxels, while a margin of 0.5 mm would have encompassed 95% of all voxels. For 3 T, a safety margin of 1 mm would have encompassed 99.9% of the voxels, while a margin of 0.4 mm would have encompassed 95% of all voxels. Wang et al. found 97.4% of their voxels to have distortions less than 1 mm at 3 T [18]. The lower distortion in this work could be explained by the use of active shimming and a focus on the OARs instead of the whole brain, and therefore the inclusion of a lower proportion of voxels close to air-tissue boundaries. Theoretically, the distortion values should scale linearly with field strength and inversely linear with the bandwidth [33], [34], [35]. However, as in our study, different applied shimming types also affected the distortion magnitude. Furthermore, the safety margin proposed here is only one of many contributing factors when considering PRV margins [24]. Additional factors that contribute to the creation of PRVs include inter-observer variability, positioning uncertainties, gradient non-linearity, and others. At 1515 Hz/Pixel, the BW used in this work was very high compared to those routinely used in MRI protocols. This was chosen to decrease the influence of inhomogeneities on the acquisition of the field map itself. To achieve reasonable SNR values, the voxel size had to be increased up to 3.3 mm. This could have possibly led to partial volume effects for smaller OARs like the optic nerves, as for some regions the voxel size was larger than the nerve itself. However, this should not have led to unacceptable errors since the variation of distortion is small across the voxel size. If acquisition time had not been a limiting factor, the quality and resolution of the field maps could have been increased. The sequence parameters used in this work however enabled routine use of the sequence for every patient with a time cost of only 89 s.

We did not evaluate the influence of distortions in the phase and slice encoding directions as they are usually assumed to be negligible [11]. We also did not differentiate between susceptibility-induced artifacts and chemical shift artifacts, although we eliminated the fat–water shift by choosing specific echo times. Gradient non-linearities, imperfect excitation pulses and other possible sources of error were also not included in this work. Therefore, the proposed margins were only guidelines to circumvent this particular source of error and, thus, only represented one component of a PRV margin recommendation.

In this work, we showed that distortions in the main magnetic field would be accounted for to a large extent by adding a 1 mm safety margin to all serial OARs in the head region. We also discussed the use of high BWs and active shimming for MRIs in RT planning. This is especially important since the maximum distortion values in all OARs exceeded 1 mm, even in the brainstem. These parameters should be carefully chosen for every MRI sequence used for contouring stereotactic radiosurgery cases because of the high single fraction doses along with the inherently steep dose gradients generated in the treatment planning process. We are currently investigating a way to make the results of this very fast sequence available for routine clinical use in contouring software as opposed to the retrospective evaluation in this work. This should improve the quality of the contours by being able to locally adjust safety margins around the critical serial OARs.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following are the Supplementary data to this article: