Dosimetric impact of placement errors in optically stimulated luminescent in vivo dosimetry in radiotherapy

Abstract

Introduction

Studies have suggested that optically stimulated luminescent dosimeters (OSLDs) can be used for in vivo dosimetry of intensity-modulated radiation therapy (IMRT) and volumetric-modulated arc therapy (VMAT). Clinical uncertainties such as placement error have not been thoroughly investigated. The purpose of this work was to measure OSLD placement error in a clinical sample and analyze its dosimetric impact.

Methods and materials

The analysis consisted of three parts: first, quantification of placement error in a clinical sample of 128 patients yielding 293 cone-beam CT (CBCT) with visible OSLDs registered to the treatment plan; Second, correlation of placement error and clinical OSLD measurements; third, simulation of dosimeter placement in the treatment plan and correlation of recalculated dose with placement error.

Results

In the first analysis, average placement error was 9.7 ± 9.5 mm. In the second analysis, placement error and measured-to-planned dose agreement yielded no correlation (R² = 0.02) for a subsample of 77 CBCTs of 55 head-and-neck patients. Average placement error was 7.0 ± 6.0 mm. Several factors, including image-guided shifts, introduced uncharacterized uncertainty to the measured-to-planned dose agreement. The third analysis isolated placement error from these other effects. Average dosimetric error was −2.4 ± 19.3%. Simulated dosimetric impact was weakly correlated with placement error (R² = 0.39). Removing outliers reduced the average dosimetric error to −2.1 ± 10.9%, marginally improving the correlation (R² = 0.44).

Conclusion

Placement error can substantially impact measured-to-planned dose agreement of OSLDs in high gradient regions, demonstrating the criticality of accurate dosimeter placement for IMRT and VMAT treatments.

1. Introduction

Optically stimulated luminescent dosimeters (OSLDs) are increasingly utilized for in vivo dosimetry (IVD) of complex radiation therapy techniques such as intensity-modulated radiation therapy (IMRT) and volumetric-modulated arc therapy (VMAT). The OSLDs are disks with dimensions of 1 cm² infused with aluminum oxide doped with carbon (Al₂O₃:C). These OSLDs have a linear response with dose and minimal dose sensitivity with temperature. Linear response with absorbed dose is in the range of 1–300 cGy for which above 300 cGy, a small supra-linear behavior occurs [1]. Though the physical characteristics of these OSLDs have been well-documented, [1], [2], [3], [4], [5], [6] clinical experience and uncertainties have not been thoroughly investigated. Several authors have suggested accuracy of OSLD-based IVD between ±0.5% and ±3% depending on calibration procedures and treatment technique [7], [8]. The forthcoming American Association of Physicists in Medicine Task Group 191 report explores the use of OSLDs and TLDs in clinical IVD, characterizing several uncertainty parameters in a hypothetical “uncertainty budget.” The report proposes several strata of uncertainty based on different calibration procedures and clinical implementation ranging from approximately 1–5% [9].

In previous work, we investigated the accuracy and precision of OSLDs in a clinical setting with over 10,000 OSLD measurements [10]. The analysis included a variety of treatment techniques (including intensity-modulated delivery), modalities, anatomical sites and placement locations. We found the accuracy of OSLDs to be within 0.3% of planned doses but observed one-sigma precision over 10%, approximately twice the proposed uncertainty budget in TG-191 [10]. Given the high-dose gradients in IMRT and VMAT, placement error may have a considerable role in variability of measured-to-planned dose agreement. Placement error, however, is hard to detect and harder to quantify retrospectively. Dipasquale et al. used registered cone-beam computed tomography (CBCT) to estimate dose to intracavitary thermoluminescent dosimeters visualized on the acquired image [11]. The purpose of this work was to characterize OSLD placement error using clinical CBCT and estimate the resulting impact on measured-to-planned dose agreement.

2. Methods and materials

2.1. In vivo dosimetry procedure

The following section describes our institution’s clinical in vivo dosimetry protocol by which all retrospective data in the current work was collected. At the physician’s request, OSLDs were placed weekly throughout a patient’s radiotherapy treatment with locations determined by a physicist. The location of the dosimeters was treatment site specific and based on two factors: dosimetric homogeneity (avoiding field edges and sharp dose gradients) [12], [13] and reproducibility (specifying a practical, accessible location on the patient) [10]. Placement locations were recorded as gantry angle and a two-dimensional offset from the central axis of a specific isocenter to facilitate placement using the linear accelerator field light. Planned doses were calculated by placing a point of interest at the planned location in the clinical plan, applying a virtual tissue-equivalent bolus with dimensions of 50 by 50 by 5 mm³ at the projected location to establish dose buildup, and recalculating dose. In our clinical practice, placement uncertainty was estimated by measuring the standard deviation in dose in an arbitrary 5 mm radius around the planned dosimeter location.

Therapists centered and taped the OSLDs to a 50 by 50 by 5 mm³ slab of tissue-equivalent bolus. Therapists then positioned the patient at the correct isocenter, rotated the gantry to the required angle, placed the bolus/dosimeter bundle at the designated location using the field light, and secured it to the skin with masking tape. Dosimeters were placed after planned isocenter shifts, but before image-guided shifts, to increase clinical efficiency. Image-guided shifts are applied after appropriate treatment imaging for the patient for accurate patient positioning and localization of the treatment site. The patient was treated, the OSLD was removed and read at least one hour after irradiation, and the resulting measured dose was expressed as a percent difference from the planned dose. A detailed description of measured dose calculation and reader calibration is beyond the scope of the current work but can be found in prior work [10].

The following investigation was split into three analyses: first, measurement of placement error in a clinical sample; second, correlation of placement error with clinical OSLD measurements, and third, simulation of the dosimetric impact of clinical placement errors using the treatment planning system.

2.2. Measurement of placement error

We searched four years of cone-beam CTs (CBCTs) that were acquired on the standard weekly OSLD placement day for dosimeters that were clearly visible. Dosimeters were visible on 293 CBCTs of 128 patients over a four year time span of eight treatment sites. Rigid registration was utilized in Velocity version 3.2 (Varian Medical Systems, Atlanta, GA) to match the CBCT and CT simulation. Cone beam CTs and CT simulations were registered using final (treatment) isocenter setup coordinates before image-guided shifts were applied (in other words, as the patient was initially setup on the table when the dosimeter was placed). Visualized dosimeters were contoured on CBCTs and points-of-interest were generated at the center of each dosimeter contour. A reference beam was created en face to the planned dosimeter point-of-interest. Placement error was quantified by measuring the two-dimensional distance between the intended dosimeter location and observed dosimeter placement in the en face beam’s eye view.

The rationale behind using original setup coordinates before the image-guided shift requires some additional explanation. As described above in our clinical OSLD procedure, dosimeters were placed after setup to final isocenter and before image guidance. Pre-imaging setup coordinates were chosen to measure placement error because image-guided shifts could potentially move the OSLD relative to the isocenter after placement (Fig. S1), compounding any placement errors with additional translations. Using post-shift registration, the observed offset between the intended dosimeter location and the actual dosimeter location would be a vector sum of the placement error and the image-guided shift as shown in Fig. S1. To avoid this compounding effect and to isolate placement errors, we used the pre-shift coordinates for registration.

2.3. Correlation of placement error and clinical measured-to-planned dose agreement

In this preliminary and more limited analysis, a subset of the larger patient sample (head-and-neck patients only) was considered. Placement errors calculated in the previous section were correlated with clinical OSLD measurements expressed as measured-to-plan percent dose agreement. Grossly misplaced dosimeters were excluded from analysis. These included measurements where placement directions were not followed, such as wrong laterality, confusion in placement location between prescriptions, or placement off the incorrect isocenter.

2.4. Isolating placement error and simulating dosimetric impact

A limitation of the analysis described in the previous section is the inability to isolate the effect of placement error among all the physical uncertainties associated with the OSLD and clinical uncertainties introduced by our clinical IVD protocol. These additional uncertainties could mask the effect of placement error in clinical OSLD readings. Our third analysis was aimed at isolating placement error by utilizing OSLD placement information from CBCT to simulate placement in the treatment plan and recalculate dose to this simulated point. This technique is similar to the methodology of Dipasquale et al. [11].

For this analysis, we utilized the full sample of CBCTs where OSLDs were visible. Dosimeter placements on the registered CBCT images were analyzed in the original treatment plan in which the planned OSLD location was specified. Due to daily variations in source-to-skin distance, the actual placement location did not always align with the skin surface in the CT simulation. To calculate dose at the actual placement point, it was necessary to specify measurement points at the skin surface of the CT simulation under the applied bolus. The actual placement point was projected to the skin surface parallel to the central axis of the reference en face beam. A virtual tissue-equivalent bolus with dimensions of 50 by 50 by 5 mm³ was centered at the projected measurement point and a new dose distribution was calculated using the analytical anisotropic algorithm in Eclipse version 11. Percent dose differences were calculated from the planned dosimeter location and the surface projections of the actual OSLD placement. Placement and resulting dosimetric errors were also compared to the initial clinical reference (dosimetric variation within a 5 mm radius around the planned dosimeter location).

We investigated eight treatment sites (prostate, head-and-neck, lung, bladder, rectum/anus, brain, pelvis, and abdomen) with IMRT, VMAT, and 3D-conformal treatment techniques. The average and standard deviation of placement error and dosimetric impact for all placements were calculated. Placement errors and percent dose differences between planned and actual dosimeter locations were correlated. Outliers were identified in two ways: first, OSLDs that were grossly misplaced were excluded. Second, Cook’s distance was used to identify outliers in the correlation between placement error and dosimetric impact for further analysis.

The basis of Cook’s distance is to identify any influential points and measure the effect that the removal of those points would have on a given data set [14]. The formulism for Cook’s distance for an observation i is given by

$$D_i=\frac{{\sum }_{j=1}^n{\left({\widehat{y}}_j-{\widehat{y}}_{j\left(i\right)}\right)}^2}{p{\widehat{\sigma }}^2}$$ (1)

where $\widehat{y_j}$ is the estimated mean of y at observation j and ${\widehat{y}}_{j\left(i\right)}$ is the estimated mean of y at observation j based on the reduction of the data set with observation i. The value of ${\widehat{\sigma }}^2$ is the mean squared error of your data with p denoting the number of coefficients in the regression model. Then, D_i is the normalized measure of the influence of an observation i on $\widehat{y_j}$, denoting all predicted mean values (j = 1,…n.) [15]. This formula essentially provides a threshold value. When any observation in a given data set crosses this threshold value, it is identified as an influential value in the regression. An influential observation is one that would substantially affect the conclusion of the regression analysis once it is removed [14].

Cook’s distance essentially removes outliers to improve the regression model. In addition to improving the regression, we used this method to identify, investigate the root cause of, and assess the dosimetric impact of outlier OSLD measurements.

3. Results

3.1. Measurement of placement error

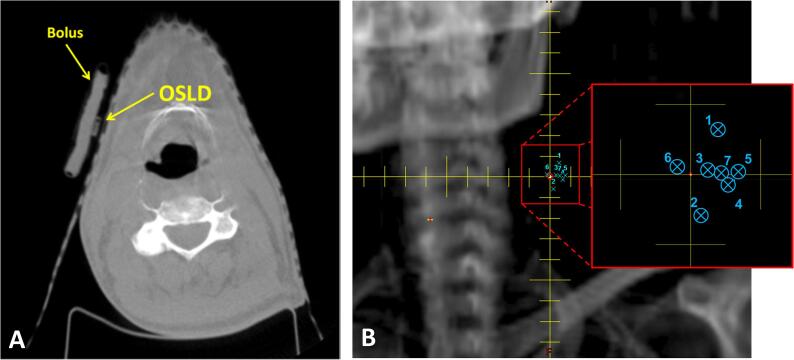
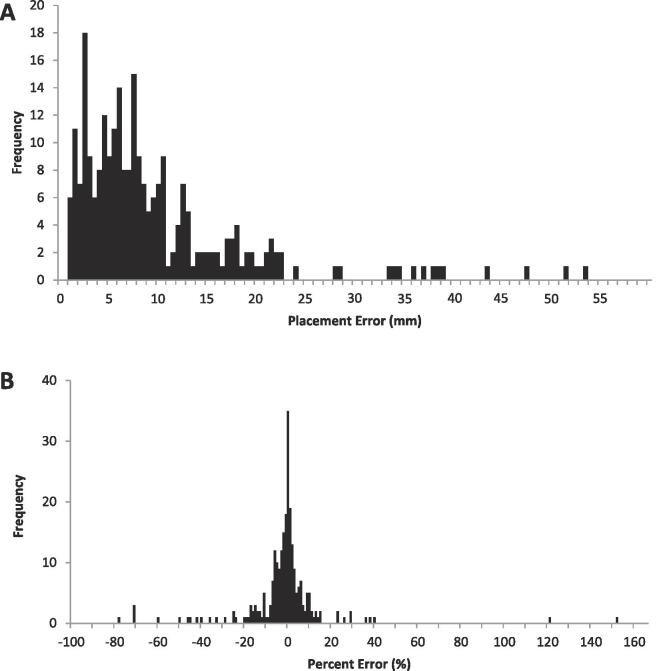
We measured placement error on the 293 CBCTs of 128 patients over a four year time span of eight treatment sites. Fig. 1A shows the placement of OSLD under the slab of bolus on the patient’s skin with Fig. 1B demonstrating the measurement of placement error in the beam's eye view. The average placement error was 9.7 ± 9.5 mm. Fig. 2A shows the frequency distribution of placement errors for all treatment sites with the greatest range of placement errors being in the range of 2–8 mm.

Fig. 1.

a) Cone beam CT with OSLD placed on thermoplastic mask. b) Beam’s eye view displaying planned OSLD location (central axis) and multiple OSLD placements observed on setup cone beam CTs (numbered blue x’s). (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Fig. 2.

a) Frequency distribution of 274 placement errors visualized using cone beam CT. b) Frequency distribution of simulated dosimetric errors for 274 OSLD placements. Gross misplacements were excluded.

3.2. Retrospective analysis of placement error and clinical measured-to-planned dose agreement

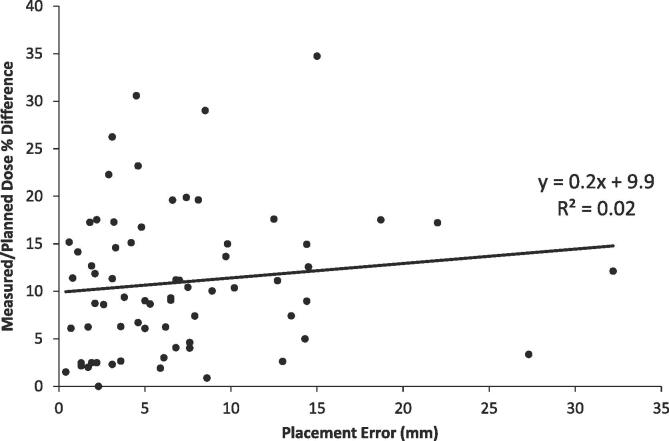
We identified 77 CBCTs of 55 head-and-neck patients where OSLDs were visible. Dosimeters were grossly misplaced on five of 77 placements. Of the remaining 72 placements, average placement error (plus or minus one standard deviation) was 7.0 ± 6.0 mm. Placement errors were not correlated with measured-to-planned percent dose difference (R² = 0.02, Fig. 3).

Fig. 3.

Correlation of placement error (cm) and percent difference (%) of measured and planned dose.

3.3. Isolating placement error and estimating dosimetric impact

Of the 293 CBCTs with visible OSLDs, nineteen (19) placements were excluded due to gross misplacements of the dosimeters. Placement locations were simulated and dose was recalculated for the remaining sample and the resulting average dosimetric error was −2.4 ± 19.3%. The frequency distribution of dosimetric errors for all treatment sites is shown in Fig. 2B. The 5 mm clinical reference radius around the planned dosimeter location yielded an average standard deviation of 4.6 ± 3.8% for all planned locations.

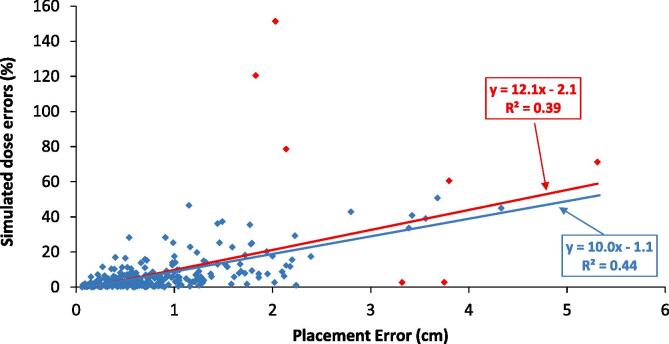
Placement error was weakly correlated with dose percent errors as seen in Fig. 4. The correlation was obtained with R² = 0.39 and seven outliers identified. Removing the seven outliers yielded a marginally improved correlation (R² = 0.44) and dosimetric error of −2.1 ± 10.9%.

Fig. 4.

Correlation of placement error and simulated dose errors with outliers (red line) and with outliers removed (blue line). Red data points represent the outliers identified by Cook’s Distance. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Results for placement and resulting dosimetric error for each treatment site are shown in Table 1. Placement error was comparable among treatment sites, ranging from 7 to 12 mm for brain and abdominal sites respectively. There was considerable variation in the dosimetric impact, with rectum/anal treatments yielding the largest dosimetric error at −7.8%. The smallest dosimetric error was abdominal treatments at −2.0%. Seven of eight treatment sites yielded negative dosimetric errors, implying that misplaced dosimeters measured lower doses than the planned dose on average. The standard deviation around the mean dosimetric error varied widely as well, ranging from 6.0% for abdominal sites to 21.4% for head and neck.

Table 1.

Treatment site specific data of placement and dosimetric errors with their corresponding standard deviations.

Treatment Site	Sample Size	Mean Placement Error (mm)	Standard Deviation of placement error (mm)	Mean Dosimetric Error (%)	Standard Deviation of dosimetric error (%)
Head-and-Neck	119	8	6	2.6	21.4
Lung	69	11	10	−5.8	17.2
Prostate	26	8	12	−6.4	16.3
Pelvis	25	11	9	−3.1	10.8
Abdominal	12	12	7	−2.0	5.9
Bladder	8	9	6	−5.7	14.4
Rectum/Anus	4	10	5	−7.8	11.7
Brain	11	7	6	−3.2	11.2

4. Discussion

To our knowledge, this work is the first investigation into the magnitude of placement errors and their effect on measured-to-planned dose agreement for OSLD-based in vivo dosimetry. Our initial clinical attempt to account for placement error consisted of measuring the standard deviation in dose in a 5 mm radius around the planned location. The current study has demonstrated 5 mm is not sufficient as the observed placement error was approximately twice this value at 9.7 mm. The dosimetric uncertainty likewise doubled from 4.6% at 5 mm to 10.9% at 9.7 mm after outliers were removed. Fig. 4 shows the correlation between the placement errors and the associated dosimetric errors. We concluded that there is a weak linear correlation between placement error and dosimetric error, with several outliers that when investigated, were found to be associated with large dose gradients and variability in dose distribution. This variation in dose distribution is specifically seen each anatomical site (Table 1).

Clinical CBCT images allowed us to identify the position of the OSLD placed during the radiotherapy treatments, similar to the intracavitary technique utilized by Dipasquale et al. in ano-rectal VMAT [11]. In the first analysis of the current work, we calculated placement error and compared to clinical OSLD readings and found practically no correlation (R² = 0.02). Upon further investigation, we found the image-guided shifts that occurred after dosimeter placement contributed substantial dosimetric variation which impeded our ability to tease out effects from placement errors alone. This prompted the need for the second analysis in this work.

In the second analysis, calculations of placement error and its dosimetric impact yielded a weak linear correlation after several outliers influencing this correlation were removed (R² = 0.44). Our analysis demonstrated dosimetric disagreement increased by approximately 10% per cm of placement error (Fig. 4). Dose heterogeneities including dose gradients and field edges demonstrated substantial influence in measured-to-planned dose agreement. It was observed that high dose gradients caused small misplacements to yield dramatic differences in measured dose, and large misplacements sometimes yielded small percent errors in regions of uniform dose. While this observation is certainly not new, the finding that placement errors can reach 1 cm or more is novel from our investigation and underscores both the criticality of choosing an appropriate measurement point and accurately placing the dosimeter at that point. In other words, one may think a measurement point is safe when in fact it may be subject to substantial variability. This is exactly what happened at our institution when we inaccurately assumed placement error was 5 mm, which, ultimately, provided the impetus for the current investigation.

As an example, Fig. S2 illustrates an erroneous placement (an outlier in Fig. 4) in a high dose gradient region of an IMRT treatment. Note that the planned position was on the central axis far away from any beam edge. The dosimeter placement, however, was several centimeters from the intended location and resulted in a large dosimetric change. Even when these extreme outliers were identified and removed via Cook’s Distance, placement errors caused substantial dose disagreement roughly on the order of 10% per cm. Using this finding as a definitive characterization of placement uncertainty, however, is cautioned due to the relatively weak correlation with the linear fit (Fig. 4). In our clinical procedure, planned locations were chosen specifically to avoid dosimetric heterogeneity. This is laborious and may not be feasible for all institutions. Standardized locations can increase clinical efficiency, but may induce higher dosimetric errors than observed in the current work because dosimetric heterogeneity is not considered when the location is chosen. However, large positional errors were found to originate in cases where there was a large variation in dose distribution leading to high dose gradients. Therefore, a small misplacement of the OSLD could potentially lead to inaccuracy in dosimeter readout and therefore, large percent differences with the expected point dose. Practical and reproducible OSLD placements can greatly reduce positioning uncertainties. For example, specifying OSLD placement to the therapist as G0 CAX (gantry angle = 0, central axis) is far more reproducible than G242, 2.5 cm superior from CAX. Reproducible placements help to reduce the positional uncertainty. Other methods on improving the OSLD clinical workflow, is having physicists present for specific OSLD placements such as electron treatments, which may incorporate small fields with high dose gradients.

Anatomical sites that generally required more intensity modulation, such as head and neck, demonstrated higher variability of dosimetric error despite smaller-than-average placement errors. Abdominal placements, in contrast, demonstrated the largest placement error (12 mm) but lowest dosimetric variation (5.9%), implying placement in more homogenous dose regions.

Task Group 191 is charged with producing recommendations for OSLD-based in vivo dosimetry [9]. This report introduces the concept of an “uncertainty budget” for OSLD-based IVD, which includes various well-studied physical dependencies added in quadrature but few clinical ones. In a previous study, we investigated over 10,000 clinical OSLD measurements and found that the variability was ±10.3%, nearly twice the uncertainty budget that TG-191 proposes (5.2%) [9], [10]. We hypothesized that placement error could explain the disagreement between the TG 191 uncertainty budget and our clinical findings [10]. If we add ±10.9% (dosimetric impact of placement error reported in this work) in quadrature to itemized sources of uncertainty from TG-191 (which add in quadrature to 5.2%), we obtain approximately ±12%. This rough estimate is within 2% of our clinically-observed precision of OSLD-based in vivo dosimetry which supports the hypothesis that placement error accounts for a portion of the discrepancy.

Challenges with dosimeter placement are not isolated just within the EBRT community. The dose gradients encountered in brachytherapy (BT) even more so emphasize the criticality of dosimeter placement for IVD. With the use of plastic scintillation detectors (PSDs) by Wootton et al. and metal oxide-silicon semiconductor field effect transistor (MOSFET) detectors by Carrara et al. for rectal wall in vivo measurements for prostate BT, there were similar gradient related challenges, showing an increase in variability in the agreement between measured and planned dose [16], [17]. The delivered dose to the target volume in prostate permanent implants can deviate from the planned dose due to two main uncertainties: needle placement and seed migration [18]. The investigation by Cherpak et al. used an in vivo dosimetry tool which combines MOSFET dosimetry and electromagnetic sensors to provide real time dose measurements with spatial position information. This tool further minimizes positioning uncertainties with the monitoring of dose at five points rather than just a single point. The main contributor to positioning errors is the positioning of the transrectal ultrasound probe. They found a dose variation of −66% to 36% with dependency on the position of the probe [18]. Methods to assess positioning errors in brachytherapy have been evaluated in work by Kertzscher et al. in which they introduce an adaptive error detection algorithm [19]. The goal of this algorithm is to mainly guide decisions in BT for cases in which IVD detected a potential treatment error. This error would be introduced as a positioning error of the dosimeter or the source. The error evaluation consists of the correspondence between the measured dose rate distribution from delivered dwell positions throughout treatment with those of simulated alternative dosimeter positions used as the reference for the treatment assessment [19].

Placement error could be addressed either by incorporating placement uncertainty into overall IVD uncertainty or by attempting to reduce placement errors directly. The former path is exemplified by our initial attempt of measuring dosimetric variation within a 5 mm radius of the planned dosimeter location. The results of this work suggest the radius should be closer to 10 mm instead of the arbitrarily chosen 5 mm. This is relatively easy to implement but yields more imprecise in vivo dosimetry. The latter path is more difficult to implement but will increase overall precision. One way to mitigate placement error would be to use the observed measurement point on CBCT to identify the corresponding dosimetric point on the treatment plan and compare measured-to-planned dose. In other words, the reference dose would be reassessed with each dosimeter placement. This would avoid placement error, but would be labor-intensive and would require CBCT for every dosimeter placement.

In the world of point detector systems, other dosimeters are recommended such as PSDs, and radiophotoluminescence glass detectors with in-room imaging for the verification of the position of the IVD detector relative to patient anatomy [20]. Beyond point-based dosimetry, utilizing technology such as electronic portal imaging device (EPID) to measure in vivo exit dosimetry can help to mitigate uncertainties associated with detector positioning [21], [22]. In a recent review of IVD in the UK, MacDougall et al. suggest that point-based IVD, most effective for conformal radiation treatments with uniform dose, may be phased out in favor of portal imaging for highly-modulated IMRT and VMAT [23]. Essentially all linacs come equipped with EPIDs, with EPID-based dosimetry having the advantage of providing 3D information for IMRT and VMAT treatments [20]. Given the placement errors documented in this work, migrating from point-based in vivo dosimetry to planar or volumetric methods may be prudent. Currently, however, exit portal dosimetry is not in widespread clinical use and point dosimeters such as OSLDs and diodes are quite common [23]. The main limitation of portal dosimetry with EPID technology presently is the limitation of the commercial software available [20].

In conclusion, the effect of placement error on measured-to-planned dose agreement is difficult to assess with clinical OSLD measurements due to numerous physical and clinical uncertainties. With the analysis of 293 CBCTs, 19 OSLDs were grossly misplaced and the remaining 274 CBCTs produced an average placement error of 9.7 ± 9.5 mm. High dose gradients caused small misplacements to yield dramatic differences in measured dose and vice versa. The exclusion of outliers produced an average measured-to-planned dose difference of −2.1 ± 10.9% which correlated weakly with placement error distance (R² = 0.44). With many previous works exploring physical uncertainties of OSLDs, this present work demonstrates the importance of placement accuracy as a critical factor in measured-to-planned dose agreement.

Appendix A. Supplementary data

The following are the Supplementary data to this article: