The impact of mass density variations on an electron Monte Carlo algorithm for radiotherapy dose calculations

Abstract

Background and Purpose

A key step in electron Monte Carlo dose calculation requires converting Computed Tomography (CT) numbers from a tomographic acquisition to a mass density. This study investigates the dosimetric consequences of perturbations applied to a calibration table between CT number and mass density.

Materials and Methods

A literature search was performed to define lower and upper bounds for physically reasonable perturbations to a reference CT number to mass density calibration table. Electron beam dose was calculated for ten patients using these variations and the results were compared to clinical plans originally derived with a reference calibration table. Dose differences both globally and in the Planning Target Volume (PTV) were assessed using dose- and volume-based metrics and 3- dimensional gamma analysis for each patient.

Results

Small but statistically significant differences were observed between perturbations and reference data for certain metrics including volume of the 50% prescription isodose. Upper and lower variations in CT number to mass density calibration yielded mean values of V50% that were 4.4% larger and 2.1% smaller than reference values respectively. Gamma analysis using 3%/3mm criteria indicated >99% passing rate for the PTV for all patients. Global gamma analysis for some patients showed larger discrepancies possibly due to large electron path lengths through inhomogeneities.

Conclusions

In most patients, physically reasonable perturbations in CT number to mass density curves will not induce clinically significant impact on calculated target dose distributions. Strong dependence of electron transport on voxel material may produce dose speckle throughout the volume. Care should be taken in evaluating critical structures at depths beyond the target volume in highly heterogeneous regions.

1. Introduction

Electron Monte Carlo schemes can be employed to compute radiation dose to cancer patients. Often, these methods use an electron beam source model to parameterize electrons and photons leaving the treatment head of the linear accelerator. Subsequently, these particles are transported through a Computed Tomography (CT) volume to calculate dose. Modeling inhomogeneities in CT data for electron beam transport depends on a conversion table between CT number and mass density. Treatment planning systems use this table for assigning regions of varying diameter in a CT volume to materials accordingly. The material and radius assignments depend on the average mass density within a sphere surrounding a sampled point which is determined by a conversion between CT number and mass density (throughout this text we refer to CT number to mass density as CT-to-density). Consequently, changes to this conversion in a treatment planning system (TPS) can impact material assignment in CT preprocessing and thus influence dose deposition calculated by the electron transport model. The impact of variations in the CT-to-density table on the computed dose in a patient is potentially of significant importance.

Site-specific CT-to-density calibrations are often required due to variations between CT scanners, techniques and reconstruction algorithms. Different CT scanner models and manufacturers have been shown to produce different measurements [1], [2], [3], [4], [5], [6], [7], [8], [9]. For a given scanner, choice of tube voltage can have a significant impact on measured CT numbers [1], [2], [3], [4], [5], [8], [10], [11], [12] while other parameters such as tube current have been shown to have minimal impact [4], [12]. Beyond scanner parameters, variables including software [13], reconstruction algorithm [3], [14] and object location [15] have also been demonstrated to alter CT numbers. Once a CT scanner has been calibrated properly, stable CT number over time can be achieved [6] and variations due to phantom variation are typically much lower than those from using different scanners and tube voltages [16].

The variability of CT number and the dependence of Monte Carlo dose calculation on mass density prompted the question of whether variations in CT number measurements from factors such as scanning technique and scanner model have any clinically significant impact on calculated dose. Many studies have investigated the sensitivity of dose calculation for photon and proton beams to conversion between CT number and electron density [17], [18], [19], [20], [21], [22]; however, the impact of conversion between CT number and density has not been rigorously investigated. A study by Verhaegen and Devic observed dose errors of up to 10% for photon beams and more than 30% for 18 MeV electron beams when using different assignments between CT number and mass density in Monte Carlo simulations of phantoms using DOSXYZnrc [23]. While this study indicated that the impact of calibration tables may be more pronounced for electron beams than photon beams, the study was limited to calculations in a test phantom using an experimental Monte Carlo scheme that is not necessarily representative of commercial platforms used in clinical practice.

Thus, dose perturbations in patients due to variation in CT-to-density calibration tables still merits investigation [24]. This study aims to ascertain the dosimetric impact of CT-to-density calibration on clinical patient plans calculated by a Monte Carlo dose calculation model within a clinical TPS. Ultimately, this investigation sought to address the question of whether natural perturbations in CT number measurements and concomitant CT-to-density tables have any considerable influence on patient treatments.

2. Materials and methods

2.1. CT number variation determination

To assess possible deviations of CT number measurements, a broad literature review of CT number measurements for various phantoms and materials of known composition was performed. For each material considered, the maximal and minimal CT number observed in two commonly used CT calibration phantoms, the CIRS 062 Phantom (Computerized Imaging Reference Systems Inc., Norfolk, VA) and Gammex Tissue Characterization Phantom (Gammex Inc., Middleton, WI), were recorded. These data were measured on various scanners with differing imaging parameters [9], [24], [25], [26].

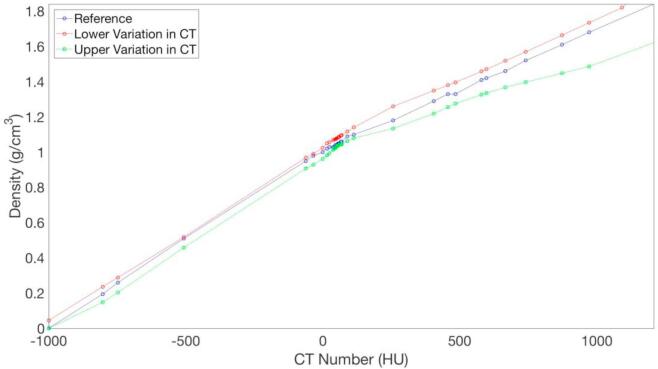
Using the data from the literature review, two different CT-to-density plots were generated. From both the maximal and minimal CT numbers observed for all inserts in the two phantoms, CT-to-density curves were generated by linearly interpolating between the discrete CT number measurements as shown in Fig. 1 The lower and upper variations in CT number are supplemented by a reference plot corresponding to the conversion table used at our institution for patient treatment planning purposes. This reference curve was obtained by averaging calibration measurements acquired on six different CT scanners across our clinics. The reference data has been extensively verified through comparison of phantom dose computation and in phantom dose measurements at our institution [1], [9], [27]. To be able to list the same CT numbers in the CT-to-density tables in the TPS for all three calibration curves, the curves for the maximal and minimal CT numbers (referred to as the upper and lower variation, respectively) were re-interpolated based on the CT numbers used in the interpolation for the reference curve and the corresponding density taken from the initial interpolate. That is, the data points in Fig. 1 for the upper and lower variation curves do not correspond to the retrieved CT number measurements. While these curves were chosen to capture the practical variations in CT-to-density calibration, larger systematic deviations are still possible.

Fig. 1.

Lower (red) and upper (green) variations in CT-to-density calibrations derived from literature review. The blue curve is a reference trace corresponding to measurements obtained at our institution. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

2.2. Clinical cases

The dosimetric impact of changing the reference CT-to-density table to the lower and upper variations described above was assessed on ten previously treated clinical cases (Table 1). Dose computation was performed using eMC in Eclipse version 13.7.14 with a target statistical uncertainty of 1% within the sub-volume where calculated dose exceeds 50% of the maximal dose, and an isotropic grid size of 1.5 mm. A fixed random number generator seed was used to suppress random variation between calculations using the different curves. Three-dimensional Gaussian smoothing was applied to calculated dose distributions via a setting within the treatment planning system. For each clinical case, all treatment parameters including gantry angle, beam energy, machine, field size, source to surface distance (SSD), and dose prescription were held constant. Differences in maximum dose, various isodose volumes (V90% and V50%, i.e. volumes of 90% and 50% isodoses relative to the prescription dose), conformity indices, and required monitor units (MUs) were recorded in each case. In this study, the conformity index CI_I is defined by

$${\mathit{CI}}_I=PTV/V_I$$ (1)

where PTV denotes the planning target volume and V_I is a specified isodose volume [28], [29].

Table 1.

Summary of 10 clinical patients considered in this study.

Patient no.	Treatment site	Energy (MeV)	Applicator (cm)	SSD (cm)	Prescription (cGy)
1	Nose	9	10	103.8	250 × 22
2	Nose	9	10	103.6	333 × 15
3	Scalp	16	15	103.4	200 × 15
4	Chest wall	16	25	101.5	200 × 8
5	Nose	9	10	102.9	333 × 15
6	Abdomen	9	15	104.1	300 × 15
7	Left Temple	12	15	103.9	200 × 30
8	Right Ear	12	15	105.0	200 × 30
9	Nose	9	10	104.0	275 × 20
10	Nose	9	10	103.4	275 × 20

Shapiro-Wilk test with hypothesis that data is normal was tested with (p < 0.05) used to reject hypothesis that data is normal. The data normality assumption works for all data except V90, CI90 in Table 2 and V90 in Supplementary Table S1 (identified by *). Student t-tests and one-sample Wilcoxon tests were performed to assess statistical significance of the different parameters relative to our reference values. The hypothesis that no difference between the calculated values for the perturbed calibrations and the reference calibration exists was tested. Percent differences in various quantities were calculated between lower/upper variations and reference CT-to-density curve.

Table 2.

Percent differences in various global dose metrics between lower, L (and upper, U) variations in CT-to-density curve and reference trace.

Global Percent Difference (%)
Patient no	Dmax		MU		V90%		V50%		CI90		CI50
	L	U	L	U	L	U	L	U	L	U	L	U
1	1.1	0.8	0.6	0.3	1.2	5.2	−1.3	4.1	−1.2	−4.9	1.3	−4.0
2	0.5	0.8	−0.1	0.1	−3.0	3.7	−2.0	4.0	3.1	−3.5	2.1	−3.9
3	0.5	−0.5	0.1	−0.1	−1.7	2.7	−2.4	4.3	1.7	−2.7	2.5	−4.1
4	−0.3	−0.6	−0.3	−0.4	−4.2	2.1	−2.9	5.8	4.3	−2.1	3.0	−5.5
5	−0.2	0.6	−0.4	0.5	−11.0	14.0	−2.3	4.8	12.3	−12.3	2.3	−4.5
6	−0.4	0.4	0.3	0.3	−0.3	6.0	−1.5	3.9	0.3	−5.7	1.5	−3.8
7	−0.8	0.4	0.5	0.6	−0.8	5.1	−2.5	4.9	0.8	−4.9	2.6	−4.7
8	0.4	−0.1	0.3	0.4	−1.9	6.8	−2.7	4.7	2.0	−6.3	2.8	−4.5
9	0.1	0.5	0.0	−1.0	−2.7	−12.9	−2.2	3.7	2.8	14.8	2.3	−3.6
10	0.0	0.1	0.2	0.5	0.1	6.0	−1.6	3.9	−0.1	−5.7	1.7	−3.7
Mean	0.1	0.2	0.1	0.1	−2.4	3.9	−2.1	4.4	2.6	−3.3	2.2	−4.2
P-Value (t-Test)	0.58	0.18	0.30	0.30	*0.02	*0.06	<0.001	<0.001	*0.02	*0.08	<0.001	<0.001

^*Data normality assumption is not strictly valid in these cases according to Shapiro-Wilk, Wilcox P value is reported instead of Student t-test.

Dose volume histograms (DVHs) were generated and compared using metrics proposed by Das et al. [1]. For example, fractional change in the volume of the PTV covered by the 90% isodose volume (relative to the total PTV volume) was determined for both variations with respect to the reference plan. Additionally, reference and perturbed dose distributions were compared by way of three-dimensional gamma analysis [30], [31]. Pass rates were quantified for three different criteria including 3% dose difference and 3 mm distance-to-agreement (DTA), 2% and 2 mm, and 1% and 1 mm. Pass rates were calculated within the PTV and also regions where dose exceeds thresholds of 10% and 50% of the prescription dose respectively. In addition to gamma analysis, the fraction of voxels with dose differences greater than 3% of the prescription dose (along with maximum absolute value of the dose difference) was recorded in each tested region of interest (ROI).

3. Results

Fig. 1 shows the upper and lower variation CT-to-density curves together with the reference trace from our institutional data. Of note, the reference curve is contained entirely between the lower and upper variations. The magnitude of density variation with CT number was greater for materials with density greater than water. In the physiological range between −120 HU (fat) and 300 HU (soft tissue), the upper variation has an average density 3.3% below the reference curve with a maximum deviation of 5.2%. The lower variation in CT number calibration has an average density 3.8% above the reference curve with a maximum deviation of 6.8%. At CT number equal to 1208, which corresponds to the density of bone, the upper and lower variations in CT number have densities 11.9% and 7.7% lower and greater than that of the reference respectively.

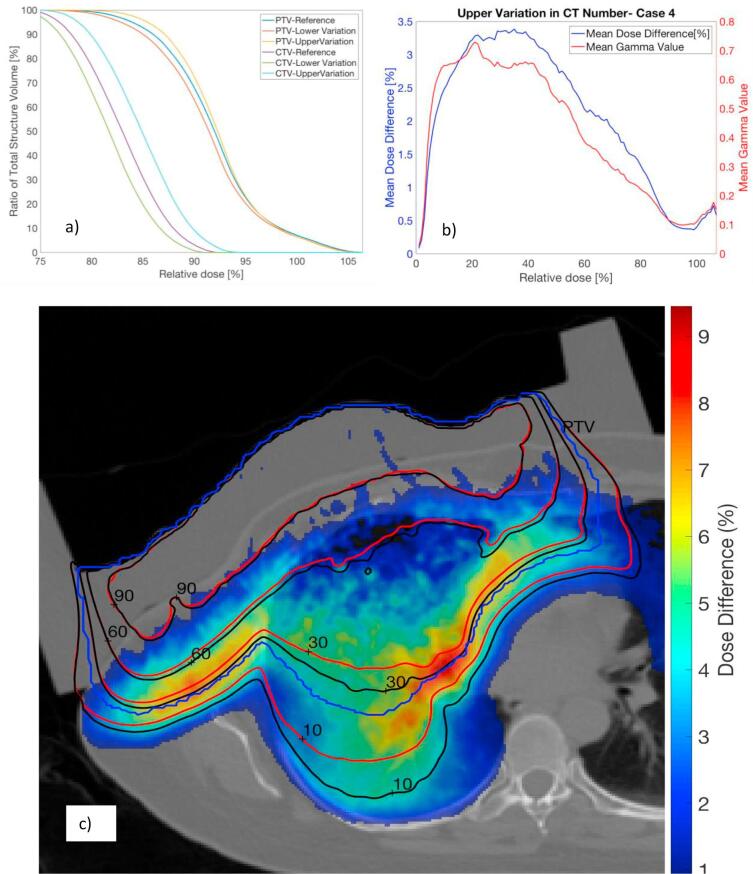
Table 2, which compares relative percent differences between values derived from perturbed and reference CT-to-density curves for all patients, shows that no significant statistical difference was observed for maximum dose or delivered MUs. In contrast, V50% and V90% were determined to be 4.4% and 3.9% larger on average for the upper variation relative to the reference curve. Likewise, these values were found to be 2.1% and 2.4% smaller on average for the lower variation (Table 2). The increase and decrease in dose resulting from the upper and lower variations in CT-to-density curves are exemplified in the DVHs. For case 4, Fig. 2a shows that for a given dose, the volume of all ROIs covered by that dose was larger (smaller) when the upper (lower) variation in the curve was applied.

Fig. 2.

For patient 4 (with a 16 MeV electron beam), Dose Volume Histograms for the CTV and PTV obtained using reference data and lower and upper variations (a). Mean percent difference in dose and gamma values between upper variation and reference data as a function of dose threshold for computation is shown in (b). An axial slice displays calculated isodose lines for the upper variation (black) and reference data (red) in (c). A wax compensator overlaid on the skin to shape the isodoses to the target is also shown. The PTV (in blue) and percent dose difference (color bar legend) are included for reference. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Several dose metrics were also calculated within the PTV. The mean percent difference in V90% within the PTV was −2.4% (p = 0.05) and 3.9% (p = 0.10) for the lower and upper variations respectively as shown in Supplementary Table S1. For each case considered, V50% fully covered the PTV. The upper and lower variations calculated higher and lower mean PTV doses (p = 0.18 for lower variation and p = 0.04 for upper variation) in 8 of 10 cases. The average minimum PTV dose calculated using the upper variation curve was 3.4% larger (p < 0.001) and 1.3% smaller using the lower variation curve (p = 0.04) compared to that calculated using the reference data. As shown in Table 3, dose differences greater than 3% of the prescription dose were observed in less than 1% of PTV voxels in all cases except for the upper variation applied to cases 5, 9 and 10. The maximum dose increase within the PTV for any voxel was 8.4% (specified relative to prescription).

Table 3.

Global gamma analysis and 3D Gamma analysis and voxel-by-voxel comparisons in the PTV for dose calculated using lower, L and upper, U variations.

Dose differences
Patient no/Metric	PTV Pass Rate (%)
	1	2	3	4	5	6	7	8	9	10
3%/3 mm	L	100	100	100	100	100	100	100	100	100	100
	U	100	100	>99.9	100	100	100	100	100	100	100
2%/2 mm	L	99.8	100	>99.9	100	100	100	>99.9	100	100	100
	U	100	99.9	99.8	100	100	>99.9	99.9	>99.9	99.8	100
1%/1 mm	L	91.3	99.8	97.6	97.3	99.6	99.0	96.3	99.3	99.2	97.7
	U	96.7	94.0	94.5	92.2	89.0	80.4	96.4	94.1	86.2	96.2
		PTV Voxel-Wise Differences
>3% (%)	L	0	0	0.2	0	0.2	0	0.1	0	0	0
	U	0.3	0.4	1.0	0.1	8.8	0.5	0.7	0	1.0	5.7
ΔDmax (%)	L	2.9	1.6	3.6	1.6	2.0	2.2	4.0	3.8	2.6	2.7
	U	3.3	3.2	4.6	3.4	5.4	4.0	8.4	2.8	4.5	5.0
		Global Pass Rate (%)
3%/3 mm (10% Threshold)	L	100	100	99.9	94.5	99.4	100	99.9	100	99.4	100
	U	>99.9	100	99.3	85.3	98.3	>99.9	99.3	99.9	99.5	>99.9
3%/3 mm (50% Threshold)	L	100	100	99.9	>99.9	100	100	>99.9	100	100	100
	U	100	100	99.7	99.1	>99.9	100	99.7	99.9	100	100
		Global Voxel-Wise Differences
>3% (%)	L	5.5	3.6	12.6	14.9	10.4	2.0	17.6	17.3	10.8	6.5
	U	26.2	22.7	26.2	35.0	28.0	21.0	31.3	31.8	26.4	21.6
ΔDmax (%)	L	5.0	4.4	8.2	7.1	8.2	4.0	−7.8	−7.2	−7.4	−5.8
	U	9.7	9.2	9.7	9.6	8.6	6.8	12.5	12.3	9.3	10.6

Even though large voxel-by-voxel dose differences were present in certain cases, these differences were largely not detectable by gamma analysis using a 3%/3 mm criterion. As indicated in Table 3, in general a 100% pass rate within the PTV was recorded for all perturbed curves using this criterion. For the PTV, the pass rate remains above 99% for all curves even for a 2%/2 mm criterion, although it decreased substantially at the 1%/1 mm level.

As summarized in Table 4, global gamma analysis was also performed for all voxels in which dose exceeded 10% or 50% of the prescribed dose. Except for case 4 with a 10% threshold, gamma pass rates exceeded 98% for all calculations. Despite high 3%/3mm pass rates, the dose deviated by more than 3% (relative to prescription) in a large fraction of the voxels for nearly every case, and this was seen especially for the upper variation. The maximum magnitude of this voxel-by-voxel variation was nearly 10% of the prescription dose in certain cases for the upper variation. As summarized in Fig. 2b, failing voxels in the comparison between the reference and upper CT-to-density calibration in case 4 are predominantly localized in regions receiving less than 50% of the prescription dose. In this case, the largest dose differences and mean gamma values are found in voxels receiving between 5% and 50% of the prescription dose. Fig. 2c compares isodose lines corresponding to the upper variation and reference data on an axial slice for case 4. Isodose lines in regions of higher dose showed good agreement; however agreement worsened between 60% and 10% isodose lines. The dose differences in the region between the 60% and 10% isodose lines correspond to the increasing differences between the isodose lines of the reference and perturbed calibration.

Table 4.

Global gamma analysis and voxel-by-voxel comparisons for dose calculated using lower, L and upper, U variations.

Global distributions
	Pass rate (%)
	1	2	3	4	5	6	7	8	9	10
3%/3 mm (10% Threshold)	L	100	100	99.9	94.5	99.4	100	99.9	100	99.4	100
	U	>99.9	100	99.3	85.3	98.3	>99.9	99.3	99.9	99.5	>99.9
3%/3 mm (50% Threshold)	L	100	100	99.9	>99.9	100	100	>99.9	100	100	100
	U	100	100	99.7	99.1	>99.9	100	99.7	99.9	100	100
		Voxel-Wise Differences
>3% (%)	L	5.5	3.6	12.6	14.9	10.4	2.0	17.6	17.3	10.8	6.5
	U	26.2	22.7	26.2	35.0	28.0	21.0	31.3	31.8	26.4	21.6
ΔDmax (%)	L	5.0	4.4	8.2	7.1	8.2	4.0	−7.8	−7.2	−7.4	−5.8
	U	9.7	9.2	9.7	9.6	8.6	6.8	12.5	12.3	9.3	10.6

4. Discussion

The impact of mass density variations on dose calculated within eMC was examined. This is the only report which evaluated the sensitivity of electron beam dose distributions using a commercial treatment planning Monte Carlo when varying the CT-to-density conversion curve. This has previously been investigated based on a non-commercial electron Monte Carlo code [23]. Mass density variations for a given CT number can be the result of using different scanners, scanning parameters, imaging objects and reconstruction techniques.

Gamma analysis is often used to evaluate clinical dose errors. In this study, the gamma passing rates with 3%/3mm criteria were higher than 99% for all patients; however, voxel-wise dose differences of up to 12.5% of prescription dose were observed in some cases. Significant dose differences were unsurprising given that it has been suggested that 57 tissue subsets are needed for accuracy at the 1% dose level in Monte Carlo simulations, which far exceeds the number used in our commercial package [32]. Dose differences of this magnitude are comparable to dose errors that may arise from conventional dose calculating algorithms as compared to eMC [33]. Other metrics also indicated meaningful differences in calculated dose distributions. For example, statistically significant differences were observed in V50% and CI₅₀ for calculations performed with the lower and upper variations relative to the reference calibration. In certain cases, the dose differed by more than 3% in over 20% of voxels for calculations performed with the upper variation and reference calibration. The peak magnitude of these voxel-by-voxel differences was 12.5% relative to the prescription dose. For case 4, the gamma pass rates was less than 95% for both upper and lower variations when all voxels with dose exceeding 10% of the prescription dose were considered.

This worsening agreement in regions of lower dose was likely a consequence of particle transport, where the radiation traversed large distances prior to depositing dose in these areas. For larger numbers of interactions per history, the differences in CT-to-density tables should be exacerbated and consequently greater deviations in calculated dose should be expected. Thus, while most metrics indicate good agreement between curves for dose calculated within the PTV, large variation should be expected in regions of lower dose which could correspond to locations of organs-at-risk (OARs) with strict dose constraints. For example, steepest variation between upper variation and reference data in Fig. 2c was most apparent at sharp interfaces in CT number. In more inhomogeneous regions eMC will define smaller sphere radii and the path length between interaction events will be less. Consequently, larger variation in calculated dose should be expected in these regions when various perturbations are applied to CT-to-density curves. Work that examined the mis-assignment of single material phantom inserts on eMC dose also postulated that large dose calculation errors could be found in high dose gradient areas due to material assignment errors [34]. It is important to note that some of the dose speckle in eMC arises due to the mis-assignment of media in some voxels possibly due to CT artifacts or air-tissue interfaces [35], [36].

Future work will more closely investigate dose differences in regions of lower dose. While this study confirmed that physically reasonable variations in CT-to-density calibrations do not meaningfully impact target volume dose in the studied cases, these density changes could clinically affect dose calculated to deeper critical structures.

Reasonable variation in CT-to-density calibration from factors such as tube voltage and CT machine was assessed through a comprehensive literature search. The highest and lowest CT number reported for materials of different mass density became the basis for upper and lower variations in CT number calibration curves. In the physiological range between −120 HU and 300 HU, mass density variations of up to 6.8% were observed. These variations in CT-to-density tables were used to assess the dosimetric impact of mass density variations in the Eclipse™ eMC algorithm. Statistically significant impact on metrics such as V50% and CI₅₀ were found when perturbed calibrations were substituted for a reference institutional calibration. These parameters are typically used to assess treatment plan quality and thus mass density variations observed due to calibration perturbations could influence treatment planning. As expected, the upper and lower variations in CT number calibration yielded higher and lower calculated doses relative to those computed with our reference calibration table.

Despite per voxel dose differences of up to 12.5% of the prescription dose, in practice these mass density variations may not impact treatment planning in a majority of electron treatments when looking at the target coverage alone. Gamma analysis with clinically-used criteria of 3% dose difference and 3 mm distance-to-agreement [37] suggested excellent dose agreement in the PTV between plans calculated with upper and lower variations with reference data. For electron treatments, the PTV is typically located at shallow depths where electrons have not propagated sufficiently far for variations in CT-to-density calibrations to manifest themselves strongly. In contrast, larger dose perturbations could be expected at greater depths where OARs are typically located. At larger depths due to electrons beam transport through some of the OAR voxels dose speckles may result throughout the volume. This must be taken into account while evaluating hot spots in critical structures at depths beyond the target volume, especially near extremely heterogeneous regions. This was consistent with previous reports that large heterogeneity corrections to dose are present at material interfaces [33].

In this study we evaluated the impact of perturbed mass density data on electron Monte Carlo dose calculations on a cohort of clinical cases. At the level of PTV, the dosimetric impact attributable to these perturbations was not clinically significant. However, the impact of perturbations may not be insignificant for organs beyond the target, especially in proximity of highly heterogeneous regions such as tissue interfaces.

Conflict of interest

None.

Appendix A. Supplementary material

The following are the Supplementary data to this article: