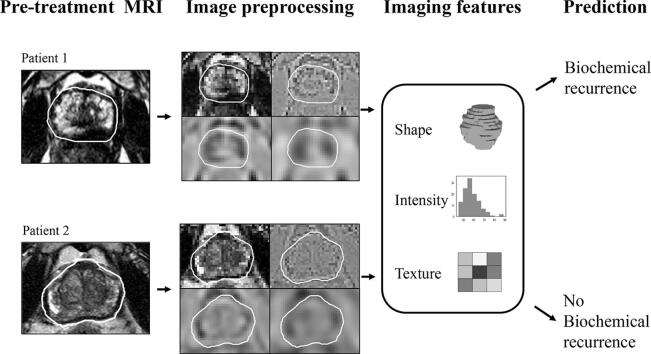
Graphical abstract
Keywords: Prostate cancer, T2-weighted MRI, Radiomics, External beam radiotherapy
Abstract
Background and purpose
High-risk prostate cancer patients are frequently treated with external-beam radiotherapy (EBRT). Of all patients receiving EBRT, 15–35% will experience biochemical recurrence (BCR) within five years. Magnetic resonance imaging (MRI) is commonly acquired as part of the diagnostic procedure and imaging-derived features have shown promise in tumour characterisation and biochemical recurrence prediction. We investigated the value of imaging features extracted from pre-treatment T2w anatomical MRI to predict five year biochemical recurrence in high-risk patients treated with EBRT.
Materials and methods
In a cohort of 120 high-risk patients, imaging features were extracted from the whole-prostate and a margin surrounding it. Intensity, shape and textural features were extracted from the original and filtered T2w-MRI scans. The minimum-redundancy maximum-relevance algorithm was used for feature selection. Random forest and logistic regression classifiers were used in our experiments. The performance of a logistic regression model using the patient’s clinical features was also investigated. To assess the prediction accuracy we used stratified 10-fold cross validation and receiver operating characteristic analysis, quantified by the area under the curve (AUC).
Results
A logistic regression model built using whole-prostate imaging features obtained an AUC of 0.63 in the prediction of BCR, outperforming a model solely based on clinical variables (AUC = 0.51). Combining imaging and clinical features did not outperform the accuracy of imaging alone.
Conclusions
These results illustrate the potential of imaging features alone to distinguish patients with an increased risk of recurrence, even in a clinically homogeneous cohort.
1. Introduction
High-risk primary prostate cancer (PCa) patients are commonly treated with radiotherapy (RT). According to the Phoenix definition, biochemical recurrence (BCR) after RT occurs within five years in 15–35% of all cases [1], [2], [3]. Aiming at better patient stratification, clinical nomograms, such as the Kattan nomogram [3], have been developed to predict biochemical recurrence after RT. These incorporate factors such as the PSA level and biopsy Gleason score, known to be good predictors of biochemical recurrence, but are often limited by the accuracy of the measured variables. The prognosis of high-risk PCa patients is heterogeneous, however the available clinical nomograms are not tailored to distinguish patients within a single risk group.
Magnetic resonance imaging (MRI) is well established for PCa diagnosis and staging. T2-weighted (T2w) anatomical scans are used to assess the extent of the tumour. Visually scored semantic attributes of PCa visible on T2w-MRI, such as seminal vesicle invasion or extracapsular extension, are predictors for five year biochemical recurrence free survival. By improving staging, these predictors augment the performance of predictive models which combine them together with clinical nomograms [4].
Radiomics has emerged as a field in which a high number of quantitative imaging features are extracted from a region of interest (ROI) to quantitatively describe its phenotype. Texture analysis based on the grey level co-occurrence matrix (GLCM) [5], using second order statistics to characterise the spatial dependence of grey-levels in an image, has been applied extensively to evaluate both the location and aggressiveness of PCa [6], [7] based on T2w-MRI. By assessing tissue micro-architecture and tumour aggressiveness, being the latest by definition related with BCR, this modality could provide insight on recurrence risk prediction.
Local recurrence after RT is reported to occur predominantly at the site of the index lesion [8], and imaging features from the primary tumour were found to strongly associate with the probability of BCR following RT [9], [10]. However, these studies have relatively small and inhomogeneous patient cohorts, with the study by Gnep et al. [9] having a median follow-up time of only four years. An early identification of increased recurrence risk can potentially impact clinical management and subsequent follow-up, particularly for high-risk disease as it is related with higher recurrence rates [11].
For many years, the standard for RT purposes was not multi-parametric MRI (mp-MRI) but anatomical imaging with the goal of prostate gland delineation. Thus, cohorts with longer follow-up are often restricted to T2w-MRI and the uncertainty in tumour localisation is high. Tumour delineations on mp-MRI are prone to inter-observer variations up to 2.3 mm with smaller satellite lesions being often missed [12]. No guidelines are yet available for this task. Prostate delineations are also prone to inter-observer variability but radiological guidance on how to delineate in T2w-MRI is available [13]. Evaluation of whole-prostate imaging features avoids delineation uncertainty, is not restricted to the visible tumour area and might therefore be sensitive to both micro- and macroscopical features predictive of recurrence.
We here aimed to investigate the potential of whole-prostate imaging features for five year BCR prediction after RT of local PCa, in a clinically homogeneous cohort of high-risk biopsy-proven PCa patients. We further analysed the predictive value of features in the margin surrounding the prostate, as the presence of extracapsular extension and seminal vesicle invasion is related to the risk of relapse. The performance of models using imaging features was compared to one using solely clinical features.
2. Materials and methods
2.1. Dataset
In a single centre, patients with high-risk PCa were selected retrospectively from a consecutive cohort treated with external-beam radiotherapy (EBRT) between 2007 and 2011. Risk classification was performed according to the D’Amico definition [14]. Further inclusion criteria involved having received hormonal therapy (HT), a dose of 78 Gy in 39 fractions and no other pelvic comorbidities before the treatment. Biochemical recurrence was diagnosed according to the Phoenix criteria [15] and all patients had five years of follow-up. A total of 120 patients satisfied the inclusion criteria.
Pre-treatment clinical predictors of biochemical recurrence after EBRT were chosen according to the input parameters of the Kattan nomogram [16].
2.2. MRI protocol
T2w anatomical MRI scans were acquired as part of the RT treatment planning procedure. Axial T2w turbo-spin echo (TSE) and T2w 3D VISTA (for nine patients) sequences were acquired on a 3T Philips Achieva MRI scanner (Philips Healthcare, Best, the Netherlands). For the TSE sequence the repetition times (TR) were longer than 3800 ms, the echo times (TE) between 120 and 150 ms and the scans had an in-plane pixel pitch of 0.27–0.49 mm and slice thickness of 2.3–3.3 mm. For the VISTA sequence the TR = 2034 ms and TE = 120 ms, with isotropic voxels of 0.8 mm width. Functional sequences were not part of the RT clinical workup.
2.3. ROI segmentation
Prostate delineations were performed for all patients with an atlas-based approach using a research software version of ADMIRE 1.13.5 (Elekta AB, Stockholm, Sweden), with visual verification by the researcher (four years of experience in prostate delineation) and manual correction whenever necessary.
Based on the prostate delineation intra-observer variability reported by Nyholm et al. [17], prostate ROIs were created by expanding the delineation by 2 mm to compensate for possible delineation uncertainties and to ensure whole-prostate coverage. The margin ROIs were defined as the region between an expansion and shrinkage of the prostate delineation by 2 mm.
2.4. Image feature extraction
The pyradiomics 1.2.0 toolbox [18] was used for region-wise 3D feature extraction. For a consistent calculation of 3D features, all images were resampled to an isotropic grid of 2x2x2 mm voxels using BSplines to avoid extreme image oversampling in the slice direction. Images were then normalised as described in Appendix A. The normalised images, as well as images obtained by further filtering with a Laplacian of Gaussians (LoG) with sigma = 1, 3, and 5 mm, were used as input for feature extraction. The extracted features were categorized in shape, intensity and texture. From the LoG filtered images only intensity and texture features were extracted.
Image discretization was performed by using a fixed bin width = 5. Rotational invariant textural features derived from the grey-level co-occurrence (GLCM) and run length (GLRLM) matrices were computed by averaging the values obtained over 13 angles (0, 45, 90 and 135° symmetrical angles in-plane and out-of-plane) using a displacement vector of one voxel. These features quantify regional heterogeneity.
A total of 254 region-level features were obtained per patient (Table 1 and Appendix B), all scaled as described in Appendix A.
Table 1.
Description of the features extracted for each region of interest (ROI). The index 1 and 2 in homogeneity and informal measure of correlation refer to the two used formulations used to calculate these measures. Further information about these features can be found in the Appendix B.
| Feature class | Description | Features extracted |
|---|---|---|
| Shape | 3D shape features | Sphericity, maximum 3D diameter, volume, spherical disproportion, surface area, surface volume ratio |
| Intensity | 1st order statistics (2D and 3D) | Root mean squared, maximum, median, standard deviation, variance, 90% percentile, minimum, mean absolute deviation, kurtosis, mean, energy, interquartile range, range, 10% percentile, skewness, total energy, robust mean absolute deviation, entropy, uniformity |
| Texture | Grey-level co-occurrence matrix, GLCM (2D and 3D) | Entropy, cluster tendency, inverse difference moment, inverse difference moment normalized, maximum probability, correlation, sum variance, homogeneity1, homogeneity2, energy, dissimilarity, informal measure of correlation1, informal measure of correlation2, inverse difference, inverse difference normalized, contrast, average intensity, difference average, sum squares, cluster shade, sum entropy, difference entropy, inverse variance, cluster prominence, auto correlation, sum average, difference variance |
| Grey level run length matrix, GLRLM | Short run emphasis (SRE), long run emphasis (LRE), grey-level non-uniformity (GLN), grey-level non-uniformity normalized (GLNN), run length non-uniformity (RLN), run length non-uniformity normalized (RLNN), run percentage (RP), run entropy (RE), low grey-level run emphasis (LGLRE), high grey-level run emphasis (HGLRE), short run low grey-level emphasis (SRLGLE), short run high grey-level emphasis (SRHGLE), long run low grey-level emphasis (LRLGLE), long run high grey-level emphasis (LRHGLE), grey-level variance (GLV), run length variance (RLV) | |
| Filtered | Laplacian of Gaussian filter | Order = 1, Sigma = 1,3,5 |
2.5. Models and validation
Independent models were created using either clinical or imaging features. Separate imaging models were generated for each ROI. The clinical model was developed using PSA, Gleason and clinical stage variables.
All models were independently validated using stratified 10-fold cross-validation (CV), ensuring the folds preserve the percentage of samples for each class. Receiver operating curve (ROC) analysis with the use of the area under the curve (AUC) values per fold was applied to assess the prediction accuracy for the different ROIs.
Clinical and imaging models were created based on different features, potentially offering complementary information about the pattern to be classified. Combining the results of the two to generate a consensus decision may improve efficiency and accuracy, as the sets of patterns misclassified by the different models would not necessarily overlap [19]. To evaluate this hypothesis, the posterior probabilities obtained for each patient for imaging and clinical models were averaged in one joint probability, and the performance of the combined models was assessed.
2.6. Feature ranking and selection
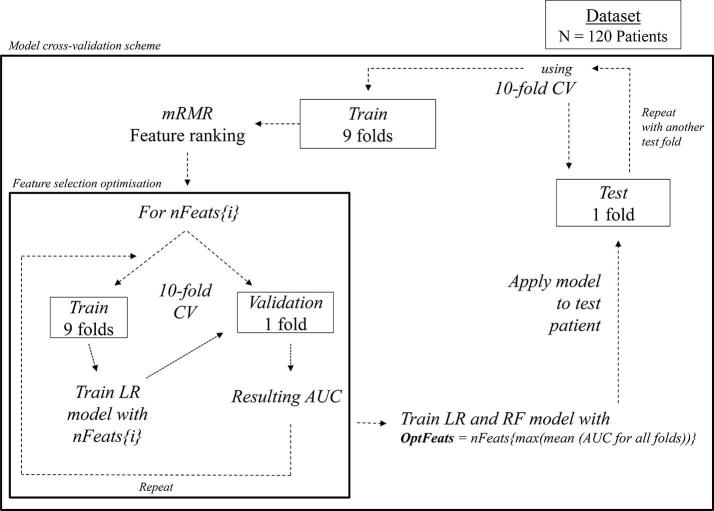
Due to the high dimensionality of the feature set, feature selection was implemented to address the curse of dimensionality [20]. Within the stratified 10-fold CV scheme we aimed at identifying a model hyperparameter – the number of features to select (nFeats). Firstly, feature ranking was performed in the training fold using the minimum-redundancy maximum-relevance (mRMR) algorithm [21]. This method maximizes the dissimilarity and minimizes the redundancy between features. To identify the hyperparameter nFeats, an inner stratified 10-fold CV scheme was implemented within the training set. Data was thus further split into training and test folds, and different sizes of features sets were tested: nFeats = {3,5,10,20,30,40,50,60,70,80,90,100,150,200,250,254}. The AUC performance of each feature set when used with a logistic regression (LR) classifier was recorded for each fold. The LR classifier was chosen for its simplicity. The AUC was averaged for all folds of each feature set, and the nFeats{i} with the highest value was chosen as being optimal. This optimal number of features was then selected from the outer training fold data, and given to train and test the model classifiers.
Pearson correlation between the top five features for the whole dataset was also calculated.
2.7. Classifiers
Parmar et al. [20] reported the Random Forest (RF) classifier to have obtained the highest prognostic performance with high stability against data perturbations. However, LR is by far one of the most widely used classification algorithms. Both algorithms are simple and computationally efficient, so the performance of RF and LR classifiers was evaluated here.
The LR model was built using a l2-penalty, tolerance = 0.0001 and C = 1. The RF model was built using 45 trees and a minimum of two samples per split. As ours is an imbalanced dataset (i.e. more non-recurrent than recurrent samples) for both classifiers the class weight was set to ‘balanced’ so that the weights are adjusted to be inversely proportional to the class frequencies in the input data. To investigate the stability of the RF model, the classification process was repeated 20 times, and the standard deviation (SD) of the obtained AUC values was calculated.
The stratified 10-fold CV was used to avoid overfitting by ensuring the test set was independent and not included in the feature selection process. A separate model was created for each of the ROIs and for both RF and LR classifiers, resulting in a total of 4 imaging models. The clinical model was developed using a LR classifier. A total of two combined models - using the predictions from RF and LR imaging classifiers combined with clinical predictions – were investigated per ROI.
Supplementary Fig. S1 and Table S1 associated with this article can be found, in the online version, at https://doi.org/10.1016/j.phro.2018.06.005.
Fig. S1 illustrates the different steps in optimizing feature selection, in classification and cross-validation.
Fig. S1.
Feature selection, classification and cross-validation pipeline. The stratified 10-fold cross validation (CV) separates the patients in 10 folds, and then iterates the use of 9 folds for training and the remaining fold as test set. Feature selection is performed using stratified 10-fold CV on the training set where different subsets of features are tested. Variable i = 1, 2…M, where M equals the total number of nFeats combinations to test. The number of features resulting in the maximum AUC value in the training set is used to train an LR and RF classifiers which are evaluated on the remaining independent test fold. This process is repeated 10 times
2.8. Statistics
To test for significant differences between clinical features of recurrent and non-recurrent patients, a T-test (for continuous variables) and a chi-square test (for categorical variables) was used. The patient’s clinical stage is decided in consensus between the urologist and radiologist, and is therefore potentially biased by the MRI findings. A bivariate Pearson correlation was calculated between the TNM stage and all MRI extracted features. The degree of correlation can help reason as to whether the clinical TNM stage provides similar information as the imaging features; if so, the two models cannot be considered to provide independent predictions. The same correlation measure was performed between Gleason score and the MRI extracted features.
3. Results
Patient characteristics are reported in Table 2. The follow-up time was five years or until biochemical recurrence. Median time to BCR was four years (range 1–5 years). Three recurrences were local [10%], six were locoregional [19%] (local with involved lymph nodes), two were regional [7%] (only lymph nodes), three were regional-distant [10%] and 11 were distant (typically bone metastasis) [35%]. For six [19%] recurrent patients the location was unreported. Table S1 reports the distribution of recurrence location according to T stage, Gleason score and PSA level. Recurrence location was determined by either Choline or 68Ga-PSMA PET, SPECT/CT and at times MRI and/or biopsy.
Table 2.
Patient characteristics. The numbers in brackets are the percentages rounded down to the nearest integer.
| Recurrent | Non-recurrent | |
|---|---|---|
| Number of patients (%) | 31 (26%) | 89 (74%) |
| Median pre-treatment PSA (ng/ml) [IQR] | 17 [25] | 15 [29] |
| PSA ≤ 10 | 9 (29%) | 31 (35%) |
| 10 < PSA ≤ 20 | 7 (23%) | 17 (19%) |
| PSA ≥ 20 | 15 (48%) | 41 (46%) |
| Clinical tumour stage | ||
| T1 | 2 (6%) | 10 (11%) |
| T2 | 9 (29%) | 20 (22%) |
| T3 + T4 | 20 (65%) | 59 (66%) |
| Primary Gleason grade | ||
| Gleason 5–6 | 6 (19%) | 20 (22%) |
| Gleason 7 | 9 (29%) | 31 (35%) |
| Gleason 8 | 9 (29%) | 28 (31%) |
| Gleason 9–10 | 7 (23%) | 10 (11%) |
IQR – Interquartile range.
Table S1.
Recurrence location according to primary clinical tumour stage, Gleason grade and pre-treatment PSA values.
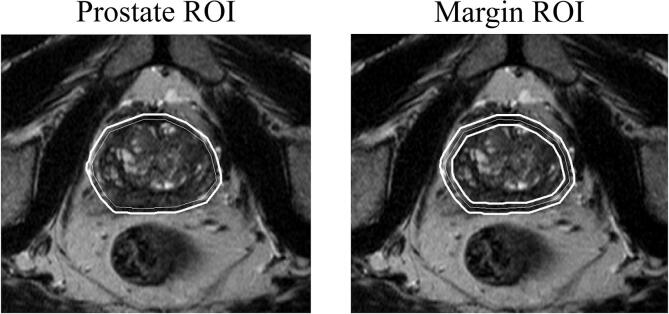
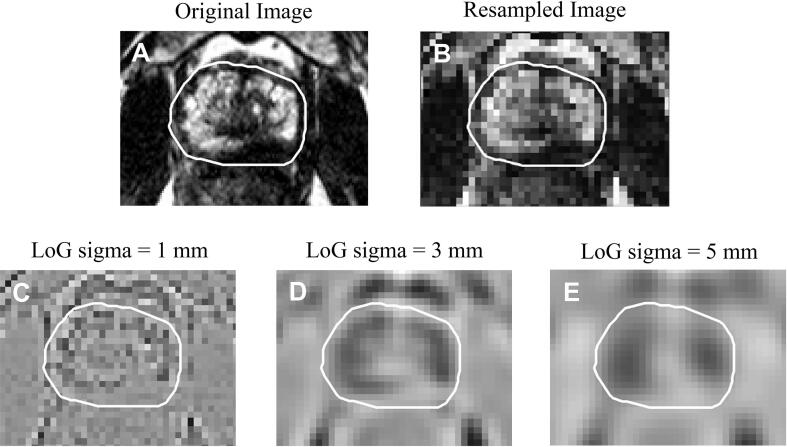
Fig. 1 illustrates the segmented ROIs from which imaging features were extracted. The original, as well as the resampled and filtered images provided for feature extraction are presented in Fig. 2 for a representative patient.
Fig. 1.
The different regions of interest (ROIs) used for feature extraction. The ROIs were created by expanding (and in the case of the margin also shrinking) the original delineations (thin lines) to obtain the final ROIs used for feature extraction (solid lines).
Fig. 2.
A. Original T2w image; B. Normalised and resampled image in the grid of 2 × 2 × 2 mm3; C–E Normalized and resampled images filtered with a Laplacian of Gaussian (LoG) with sigmas = 1,3 and 5 mm. The resampled image as well as the filtered images were used as input for feature extraction. The white contour represents the prostate ROI.
No significant differences were found between the clinical variables of recurrent and non-recurrent patients (p-values were 0.40 for PSA, 0.14 for Gleason and 0.62 for TNM stage) highlighting the clinical homogeneity of the high-risk cohort. TNM stage and Gleason score were weakly correlated (maximum absolute value of 0.30 and 0.35 respectively) with the MRI extracted features of any of the ROIs. Thus, the clinical model was considered to provide an independent prediction from the imaging models.
Table 3 shows the AUC values for the different classifiers; for RF, the value is averaged over the folds and for 20 runs with the corresponding SD between different runs. For a single run, using whole-prostate imaging features, the average AUC (SD between folds) for 10 folds was for the RF classifier 0.56 (0.21) and 0.63 (0.18) for the LR. Margin imaging features obtained for a single run of 10 folds an average AUC (SD between folds) of 0.57 (0.20) for the RF classifier and 0.59 (0.21) for the LR.
Table 3.
AUC values obtained with the different feature selection methods and classifiers. Numbers in brackets show the standard deviation for average AUC for all folds between different rounds when using random forest classifier.
| Clinical 0.51 |
||||
|---|---|---|---|---|
| AUC values (SD) | ||||
| Imaging |
Imaging + Clinical |
|||
| ROI | mRMR + RF | mRMR + LR | mRMR + RF | mRMR + LR |
| Prostate | 0.55 (0.03) | 0.63 | 0.54 (0.02) | 0.56 |
| Margin | 0.56 (0.02) | 0.59 | 0.58 (0.02) | 0.54 |
ROI – region of interest; SD – standard deviation; mRMR - minimum-redundancy maximum-relevance; RF – random forest; LR – logistic regression.
The clinical model had a poor performance with an AUC (SD between folds) = 0.51 (0.18). The best performance with imaging features was obtained for the whole-prostate region with a LR classifier. The highest AUC for the combination of imaging and clinical features was of 0.58, using margin imaging features.
The most prevalent optimal number of features was three for the margin, and either three, ten or 20 for the prostate (all were chosen by three folds each). There was inter-fold variability regarding the optimal number of features. For the prostate, the optimal number of features varied between three [30%], 10 [30%], 20 [30%] and 90 [10%]. For the margin the values were of three [60%], five [20%], 30 [10%] and 60 [10%].
Names and description of the highest ranking features for the two ROIs, when ranked in the whole dataset, can be found in Table 4. The majority of the top five prostate features originated from the filtered images and for the margin from the no filter image. The LoG filter enhanced boundaries and overall changes in intensities. First order statistics were mostly associated with extreme values (e.g. minimum, maximum). Textural based features were related to homogeneity (e.g. GLCM inverse difference moment normalized), heterogeneity (e.g. GLCM difference variance and GLCM dissimilarity) as well as skewness, asymmetry and uniformity of the GLCM (e.g. GLCM cluster prominence and GLCM cluster shade). The highest Pearson correlation for the top five features was 0.20 for the prostate and 0.51 for the margin.
Table 4.
Feature ranking for the different ROIs obtained using the mRMR method for the whole dataset.
| Prostate | Margin | |
|---|---|---|
| #1 | LoG sigma 3 GLRLM LGLRE | No filter image first order 10th percentile |
| #2 | No filter image first order minimum | No filter image GLCM cluster shade |
| #3 | LoG sigma 5 GLCM inverse difference normalized | No filter image shape surface area |
| #4 | LoG sigma 5 GLCM cluster prominence | LoG sigma 5 first order maximum |
| #5 | LoG sigma 5 first order mean | LoG sigma 3 GLCM difference variance |
4. Discussion
In this study we aimed at identifying high-risk PCa patients who are at a higher-risk of BCR up to five years after EBRT. The heterogeneous outcome reported in this homogeneously treated high-risk cohort raises the question of potential treatment intensification for a subgroup of very high-risk patients. A LR model with clinical features resulted in a poor performance predicting BCR. This is not surprising as no significant differences were found between clinical features of recurrent and non-recurrent patients, confirming the clinical homogeneity of the cohort and highlighting the difficulty in discriminating patients solely based on clinical information. Similar findings have been reported by Hegde et al. [22], stressing the importance of imaging in such a high-risk cohort. Literature reported values for the use of the Kattan nomogram are of AUC = 0.61 [23] and 0.58 [10], higher than our clinical model performance. The Kattan nomogram was originally developed using a combined population of intermediate and high-risk patients and the literature values reported above are obtained when applied in similarly mixed cohorts. We did not use the original Kattan nomogram but instead a model incorporating the same features and trained on our own clinically homogeneous cohort. Despite the differences in methodology and cohort characteristics, our findings are in line with the published literature.
Whole-prostate pre-treatment MRI radiomic features obtained an AUC of 0.63, outperforming standard clinical features in recurrence prediction. Several studies describe the association between tumour adjacent stroma and prostate microenvironment to relapse and disease progression [24], [25]. MRI is known to have limited accuracy in the detection of small tumour foci of less than 0.5 cm3 [12]. Thus it is impossible to rule out the presence of satellite lesions, not visible on MRI and missed by biopsy sampling, in the remaining prostatic region. Analysis of the prostate as a whole is less time consuming and takes into account all available information. The overall findings support the idea that relevant information can be found on a whole-prostate level as well as the potential of this region for BCR prediction. Due to the cohort’s clinical homogeneity, combining clinical with imaging features did not improve performance and introduced noise.
Despite the AUC values being relatively low to extrapolate significant clinical decisions, these results offer a proof of concept of the potential of radiological images in the context of precision medicine. Published literature on the use of radiomics for outcome prediction reported similar AUC values [20], [26]. For our cohort with five years follow up, only T2w anatomical scans were available for all patients, whereas to date mp-MRI is considered standard of care for diagnostics and treatment. Functional parameters extracted from DCE-MRI and DWI have been found to be predictive of response in other cancer sites [27], [28] and in pre-clinical studies [29]. In particular, the association between DWI-derived ADC maps and Gleason score has been extensively reported [30], [31]. The inclusion of functional imaging can potentially enhance the performance of biochemical recurrence prediction models.
The MRI protocol underwent slight changes during the period in which this patient cohort was treated. The influence of different MRI scanners, parameters and setup on the extracted radiomic features is still under-investigated. Standardizing the extraction and use of radiomic features as well as evaluating the repeatability of MR-based radiomic features are important subjects. Various reviews [32], [33] highlight important topics to be addressed in designing future radiomics studies. To tackle the curse of dimensionality we use a feature selection method, as commonly done in the radiomics field. Optimizing an RF classifier would be an alternative to regularize the model and address this issue.
Lastly, the results obtained in this study require external validation in similar cohorts, with our findings suggesting the use of a small number of features. Nonetheless these are encouraging findings as they provide pilot evidence of the relevance of imaging in outcome stratification of clinically homogeneous patients. The use of whole-prostate imaging characteristics to obtain information about five year biochemical recurrence risk can potentially be used to develop individualized treatment strategies.
Conflict of interest statement
The authors certify that they have No conflicts of interest in the subject matter or materials discussed in the manuscript entitled "Biochemical recurrence prediction after radiotherapy for prostate cancer with T2w magnetic resonance imaging radiomic features."
Acknowledgments
Acknowledgements
This work was supported by the Dutch Cancer Society; Grant number NKI 2013–5937.
We acknowledge the supply of a research software version of ADMIRE by Nicole O’Connell, Elekta AB.
Appendix A
A.1. Image normalisation
Images were normalised according to:
| (A.1) |
where x and f(x) are the original and normalised intensities, µx and σx are the ROI mean and standard deviation of the intensity values, and s is a scaling value here set to 100. Intensity values outside three standard deviations from the mean were considered outliers and set to µ + 3σ or µ − 3σ according to their location in the distribution.
A.2. Feature scaling
All imaging features were scaled by subtracting the median and scaling the data according to the interquartile range. This method provides increased robustness against outliers which can impact the estimation of the mean and variance used by typical scalers, and is implemented as a ‘robust scaler’ part of scikit-learn – a machine learning toolbox for Python.
Appendix B
The textural features homogeneity and informal measure of correlation were calculated using two different formulations:
| (B.1) |
| (B.2) |
| (B.3) |
| (B.4) |
where Ng is the number of discrete intensity levels in the image and therefore the size of the GLCM matrix; i and j are the elements from the matrix; p is the second-order joint probability function of an image region constrained by the mask; px is the marginal row probabilities; py is the marginal column probabilities; HX and HY are the entropy of px and py; HXY is the entropy of p(i,j) and
| (B.5) |
| (B.6) |
being ε an arbitrarily small non-negative number added to prevent log(0) which is undefined (-infinity).
Appendix C
C.1. Programs and settings
All programming and analysis were performed in Python 3.5 and MATLAB 2017a. The simple Insight Segmentation and Registration Toolkit was used to resample the images prior to feature extraction. An online available MATLAB implementation of the mRMR method by Peng et al. [34] was used. Feature scaling and the RF and LR classifiers were used as implemented in the scikit-learn 0.18.1 package for Python [35]. Statistics were performed using IBM SPSS Statistics 22.
References
- 1.Michalski J., Winter K., Roach M., Markoe A., Sandler H.M., Ryu J. Clinical outcome of patients treated with 3D Conformal Radiation Therapy (3D-CRT) for prostate cancer on RTOG 9406. Int J Radiat Oncol Biol Phys. 2012;83:e363–e370. doi: 10.1016/j.ijrobp.2011.12.070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Nomiya T., Tsuji H., Toyama S., Maruyama K., Nemoto K., Tsujii H. Management of high-risk prostate cancer: radiation therapy and hormonal therapy. Cancer Treat Rev. 2013;39:872–878. doi: 10.1016/j.ctrv.2013.04.003. [DOI] [PubMed] [Google Scholar]
- 3.Cahlon O., Zelefsky M.J., Shippy A., Chan H., Fuks Z., Yamada Y. (86.4 Gy) IMRT for localized prostate cancer: toxicity and biochemical outcomes. Int J Radiat Oncol Biol Phys. 2008;71:330–337. doi: 10.1016/j.ijrobp.2007.10.004. [DOI] [PubMed] [Google Scholar]
- 4.Fuchsjäger M.H., Pucar D., Zelefsky M.J., Zhang Z., Mo Q., Ben-Porat L.S. Predicting post-external-beam radiation therapy PSA relapse of prostate cancer using pre-treatment MRI. Int J Radiat Oncol Biol Phys. 2010;78:743–750. doi: 10.1016/j.ijrobp.2009.08.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Haralick R., Shanmugan K., Dinstein I. Textural features for image classification. IEEE Trans Syst Man Cybern. 1973:610–621. [Google Scholar]
- 6.Vignati A., Mazzetti S., Giannini V., Russo F., Bollito E., Porpiglia F. Texture features on T2-weighted magnetic resonance imaging: new potential biomarkers for prostate cancer aggressiveness. Phys Med Biol. 2015;60:2685–2701. doi: 10.1088/0031-9155/60/7/2685. [DOI] [PubMed] [Google Scholar]
- 7.Nketiah G., Elschot M., Kim E., Teruel J.R., Scheenen T.W., Bathen T.F. T2-weighted MRI-derived textural features reflect prostate cancer aggressiveness: preliminary results. Eur Radiol. 2017;27:3050–3059. doi: 10.1007/s00330-016-4663-1. [DOI] [PubMed] [Google Scholar]
- 8.Pucar D., Hricak H., Shukla-Dave A., Kuroiwa K., Drobnjak M., Eastham J. Clinically significant prostate cancer local recurrence after radiation therapy occurs at the site of primary tumor: magnetic resonance imaging and step-section pathology evidence. Int J Radiat Oncol Biol Phys. 2007;69:62–69. doi: 10.1016/j.ijrobp.2007.03.065. [DOI] [PubMed] [Google Scholar]
- 9.Gnep K., Fargeas A., Gutierrez-Carvajal R.E., Commandeur F., Mathieu R., Ospina J.D. Haralick textural features on T2-weighted MRI are associated with biochemical recurrence following radiotherapy for peripheral zone prostate cancer. J Magn Reson Imaging. 2017;45:103–117. doi: 10.1002/jmri.25335. [DOI] [PubMed] [Google Scholar]
- 10.Ginsburg S.B., Rusu M., Kurhanewicz J., Madabhushi A. Computer extracted texture features on T2w MRI to predict biochemical recurrence following radiation therapy for prostate cancer. SPIE Med Imaging. 2014;9035:903509–903513. [Google Scholar]
- 11.Vora S.A., Wong W.W., Schild S.E., Ezzell G.A., Andrews P.E., Ferrigni R.G. Outcome and toxicity for patients treated with intensity modulated radiation therapy for localized prostate cancer. J Urol. 2013;190:521–526. doi: 10.1016/j.juro.2013.02.012. [DOI] [PubMed] [Google Scholar]
- 12.Steenbergen P., Haustermans K., Lerut E., Oyen R., De Wever L., Van den Bergh L. Prostate tumor delineation using multiparametric magnetic resonance imaging: Inter-observer variability and pathology validation. Radiother Oncol. 2015;115:186–190. doi: 10.1016/j.radonc.2015.04.012. [DOI] [PubMed] [Google Scholar]
- 13.Villeirs G.M., Verstraete L K., De Neve W.J., De Meerleer G.O. Magnetic resonance imaging anatomy of the prostate and periprostatic area: a guide for radiotherapists. Radiother Oncol. 2005;76:99–106. doi: 10.1016/j.radonc.2005.06.015. [DOI] [PubMed] [Google Scholar]
- 14.D’Amico A., Whittington R., Malkowicz S., Al E. Biochemical outcome after radical prostatectomy, external beam radiation therapy, or interstitial radiation therapy for clinically localized prostate cancer. JAMA. 1998;280:969–974. doi: 10.1001/jama.280.11.969. [DOI] [PubMed] [Google Scholar]
- 15.Abramowitz M.C., Li T., Buyyounouski M.K., Ross E., Uzzo R.G., Pollack A. The Phoenix definition of biochemical failure predicts for overall survival in patients with prostate cancer. Cancer. 2008;112:55–60. doi: 10.1002/cncr.23139. [DOI] [PubMed] [Google Scholar]
- 16.Zelefsky M.J., Kattan M.W., Fearn P., Fearon B.L., Stasi J.P., Shippy A.M. Pretreatment nomogram predicting ten-year biochemical outcome of three-dimensional conformal radiotherapy and intensity-modulated radiotherapy for prostate cancer. Urology. 2007;70:283–287. doi: 10.1016/j.urology.2007.03.060. [DOI] [PubMed] [Google Scholar]
- 17.Nyholm T., Jonsson J., Söderström K., Bergström P., Carlberg A., Frykholm G. Variability in prostate and seminal vesicle delineations defined on magnetic resonance images, a multi-observer, -center and -sequence study. Radiat Oncol. 2013;8:126. doi: 10.1186/1748-717X-8-126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.van Griethuysen J.J.M., Fedorov A., Parmar C., Hosny A., Aucoin N., Narayan V. Radiomics system to decode the radiographic phenotype. Cancer Res. 2017 doi: 10.1158/0008-5472.CAN-17-0339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Kittler J., Hatef M., Duin R.P.W., Matas J. On combining classifiers. IEEE Trans Pattern Anal Mach Intell. 1998;20:226–239. [Google Scholar]
- 20.Parmar C., Grossmann P., Bussink J., Lambin P., Aerts H.J.W.L. Machine learning methods for quantitative radiomic biomarkers. Sci Rep. 2015;5:13087. doi: 10.1038/srep13087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ding C., Peng H. Minimum redundancy feature selection from microarray gene expression data. J Bioinform Comput Biol. 2005;3:185–205. doi: 10.1142/s0219720005001004. [DOI] [PubMed] [Google Scholar]
- 22.Hegde J.V., Demanes D.J., Veruttipong D., Raince J., Park S.-J., Kamrava M. Pre-treatment MRI staging predicts for biochemical failure in high-risk prostate cancer treated with combination high-dose-rate brachytherapy and external beam radiotherapy. Brachytherapy. 2017;16:S18–S19. doi: 10.1016/j.brachy.2017.07.008. [DOI] [PubMed] [Google Scholar]
- 23.Westphalen A.C., Koff W.J., Coakley F.V., Muglia V.F., Neuhaus J.M., Marcus R.T. Prostate cancer: prediction of biochemical failure after external-beam radiation therapy–Kattan nomogram and endorectal MR imaging estimation of tumor volume. Radiology. 2011;261:477–486. doi: 10.1148/radiol.11110457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Wikstrom P., Marusic J., Stattin P., Bergh A. Low stroma androgen receptor level in normal and tumor prostate tissue is related to poor outcome in prostate cancer patients. Prostate. 2009;69:799–809. doi: 10.1002/pros.20927. [DOI] [PubMed] [Google Scholar]
- 25.Leach D.A., Need E.F., Toivanen R., Trotta A.P., Palenthorpe H.M., Tamblyn D.J. Stromal androgen receptor regulates the composition of the microenvironment to influence prostate cancer outcome. Oncotarget. 2015;6:16135–16150. doi: 10.18632/oncotarget.3873. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Oakden-Rayner L., Carneiro G., Bessen T., Nascimento J.C., Bradley A.P., Palmer L.J. Precision Radiology: Predicting longevity using feature engineering and deep learning methods in a radiomics framework. Sci Rep. 2017;7:1648. doi: 10.1038/s41598-017-01931-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Teruel J.R., Heldahl M.G., Goa P.E., Pickles M., Lundgren S., Bathen T.F. Dynamic contrast-enhanced MRI texture analysis for pretreatment prediction of clinical and pathological response to neoadjuvant chemotherapy in patients with locally advanced breast cancer. NMR Biomed. 2014;27:887–896. doi: 10.1002/nbm.3132. [DOI] [PubMed] [Google Scholar]
- 28.Braman N.M., Etesami M., Prasanna P., Dubchuk C., Gilmore H., Tiwari P. Intratumoral and peritumoral radiomics for the pretreatment prediction of pathological complete response to neoadjuvant chemotherapy based on breast DCE-MRI. Breast Cancer Res. 2017;19:57. doi: 10.1186/s13058-017-0846-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Roe K., Kakar M., Seierstad T., Ree A.H., Olsen D.R. Early prediction of response to radiotherapy and androgen-deprivation therapy in prostate cancer by repeated functional MRI: a preclinical study. Radiat Oncol. 2011;6:65. doi: 10.1186/1748-717X-6-65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Boesen L., Chabanova E., Logager V., Balslev I., Thomsen H.S. Apparent diffusion coefficient ratio correlates significantly with prostate cancer gleason score at final pathology. J Magn Reson Imaging. 2015;42:446–453. doi: 10.1002/jmri.24801. [DOI] [PubMed] [Google Scholar]
- 31.Fehr D., Veeraraghavan H., Wibmer A., Gondo T., Matsumoto K., Vargas H.A. Automatic classification of prostate cancer Gleason scores from multiparametric magnetic resonance images. Proc Natl Acad Sci. 2015 doi: 10.1073/pnas.1505935112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Yip S.S.F., Aerts H.J.W.L. Applications and limitations of radiomics. Phys Med Biol. 2016;61:R150–R166. doi: 10.1088/0031-9155/61/13/R150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Gillies R.J., Kinahan P.E., Hricak H. Radiomics: images are more than pictures, they are data radiology. Radiology. 2016;278:563–577. doi: 10.1148/radiol.2015151169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Peng H., Long F., Ding C. Feature selection based on mutual information: criteria of max-dependency, max-relevance, and min-redundancy. IEEE Trans Pattern Anal Mach Intell. 2005;27:1226–1238. doi: 10.1109/TPAMI.2005.159. [DOI] [PubMed] [Google Scholar]
- 35.Pedregosa F., Varoquaux G., Gramfort A., Michel V., Thirion B., Grisel O. Scikit-learn: machine learning in Python. J Mach Learn Res. 2012;12:2825–2830. [Google Scholar]